В прямоугольном треугольнике найти угол между биссектрисой и медианой
В прямоугольном треугольнике катет и гипотенузе равны соответственно 16 и 20. Найдите другой катет этого треугольника. известны размеры одного катета и гипотенузы: а=16; с=20 Следовательно катет в =v20^2-16^2=v400-256=v144=12 Ответ: другой катет треугольника равен 12.
Помогите решить.
Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 24 градуса. Найдите меньший угол этого треугольника. Ответ дайте в градусах
- Попроси больше объяснений Следить Отметить нарушение
Mogsem 06.06.2014
Ответы и объяснения
В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы, соответственно:
Биссектриса делит прямой угол C на два равных угла ACD и BCD:
Угол ACD = угол BCD = 90 / 2 = 45 градусов
Угол DCM по условию 24 градуса, соответственно:
Угол ACM = 90 — угол BCD — угол DCM = 90 — 24 — 45 = 21 градус
Треугольник ACM равнобедренный, т. к. AM = CM, соотвественно угол A равен углу ACM:
Угол A = угол ACM = 21 градус
Так как сумма углов треугольника равна 180 градусов, соответственно:
Угол B = 180 — угол C — угол A = 180 — 90 — 21 = 69 градусов
Таким образом мы нашли все углы треугольника ABC, меньшим углом будет угол A равный 21 градус
В прямоугольном треугольнике найти угол между биссектрисой и медианой
В прямоугольном треугольнике найти угол между биссектрисой и медианой
В прямоугольном треугольнике угол между биссектрисой и медианой, проведенной из вершины прямого угла, равен 13. Найдите больший из двух острых углов треугольника.
- Попроси больше объяснений Следить Отметить нарушение
Siniz 04.03.2013
Ответы и объяснения
Биссектриса поделила 90/2=45гр
45-13=32 гр.-это угол при основании равнобедренного треугольника, так как медиана в данном случае — радиусописанной окружности и равна отрезкам треугольника которые поделилв пополам. И так один острый уГол равен 32гр , друго 90-32=58 гр.
Ответ:больший из двух острых углов треугольника равен 58 гр.
В прямоугольном треугольнике найти угол между биссектрисой и медианой
В прямоугольном треугольнике найти угол между биссектрисой и медианой
Задание 6. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Так как треугольник прямоугольный и медиана BM исходит из прямого угла B, то точка M является центром описанной окружности вокруг треугольника ABC. Следовательно, AM=MC=MB=r – радиус описанной окружности.
Найдем сначала угол MBC. Учитывая, что BD – биссектриса, то угол. Тогда угол
Рассмотрим равнобедренный треугольник MBC со сторонами MB=MC, в котором углы при основании BC равны, то есть. Так как сумма острых углов в прямоугольном треугольнике равна 90°, то
- Прямоугольный треугольник Все задания на прямоугольный треугольник Решения отдельных заданий
- Задание 6. В треугольнике ABC угол C равен 90°, AC=4,8, sinA=7/25. Найдите AB. Задание 6. В треугольнике ABC угол C равен 90°, AC=2, sinA=√17/17. Найдите BC. Задание 6. В треугольнике ABC угол C равен 90°, АС = 4, cosA=0,5. Найдите АВ. Задание 6. В треугольнике ABC угол C равен 90°, tgA=33/(4√33), АС = 4. Найдите АВ. Задание 6. В треугольнике ABC угол C равен 90°, АС = 8, tgA=0,5. Найдите BC. Задание 6. В треугольнике ABC угол C равен 90°, BC = 4, sinA=0,5. Найдите АВ. Задание 6. В треугольнике ABC угол C равен 90°, cosA=√17/17, ВС = 2. Найдите АС. Задание 6. В треугольнике ABC угол C равен 90°, tgA=0,5, ВС = 4. Найдите АС. Задание 6. В треугольнике ABC угол C равен 90°, AC = 24, BC = 7. Найдите sinA. Задание 6. В треугольнике ABC угол C равен 90°, CH – высота, AB=13,tgA=1/5. Найдите AH. Задание 6. В треугольнике АВС угол С равен 90°, СН — высота, AB=13, tgA=5. Найдите ВН. Задание 6. В треугольнике ABC угол C равен 90°, AB=13, tgA=1/5. Найдите высоту CH. Задание 6. В треугольнике АВС угол С равен 90°, CH — высота, BC=3, sinA=1/6. Найдите АН. Задание 6. В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, sinA=0,5. Найдите BH. Задание 6. В треугольнике АВС угол С равен 90°, BC=5, sinA=7/25. Найдите высоту СН. Задание 6. В треугольнике ABC угол C равен 90°, СН — высота, BC = 3, cosA=√35/6. Найдите АН. Задание 6. В треугольнике АВС угол С равен 90°, СН — высота, BC=5, cosA=7/25. Найдите ВН. Задание 6. В треугольнике АВС угол С равен 90°, BC=8, cosA=0,5. Найдите СН. Задание 6. В треугольнике ABC угол C равен 90°, CH – высота, AC=3, cosA=1/6. Найдите BH. Задание 6. В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, BH = 4. Найдите sinA. Задание 6. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите cosA. Задание 6. В треугольнике ABC угол C равен 90°, CH – высота, BC=4√5, BH=4. Найдите tgA. Задание 6. В треугольнике ABC угол C равен 90°, высота CH равна 20, BC = 25. Найдите sinA. Задание 6. В треугольнике ABC угол C равен 90°, высота CH равна 4, BC = 8. Найдите cosA. Задание 6. В треугольнике ABC угол C равен 90°, высота CH равна 4, BC=√17. На
poiskvstavropole.ru
Свойства биссектрисы и медианы треугольника. | Геометрия
Свойства биссектрисы и медианы треугольника. | Геометрия — просто!Здравствуйте, уважаемые читатели! Сегодня мы приступим к решению задач по свойствам биссектрисы и медианы треугольника. А для начала давайте вспомним, что такое биссектриса и медиана.
Биссектриса — это отрезок CD, который выходит из вершины угла треугольника, делит угол пополам и заканчивается на противоположной стороне.
Медиана – это отрезок СМ, который соединяет вершину треугольника с серединой противоположной стороны.
Поскольку в треугольнике вершин и сторон по три, то биссектрис медиан у него будет тоже три.
Задача 1. Дан прямоугольный треугольник АВС. Из вершины А к стороне ВС проведены медиана АД и биссектриса АМ. Угол между медианой и биссектрисой равен 17°. Найти острые углы треугольника.
Решение: Поскольку АМ — биссектриса, то угол ВАМ равен углу МАС и они равны 45°. Но угол ДАМ равен 17°. Отсюда, угол ВАД равен разности углов ВАМ и ДАМ, или 45-17 = 28°.
Мы знаем, что медиана, проведённая из вершины прямого угла прямоугольного треугольника, делит этот треугольник на 2 равнобедренных треугольника. А именно треугольники АВД и АДС.
И теперь, поскольку треугольник АВД равнобедренный, то углы при основании у него равны, т.е. угол ВАД равен углу АВД и они оба равны 28°.
А это значит, что в прямоугольном треугольнике угол В равен 28°.
Но сумма острых углов в прямоугольном треугольнике равна 90°. Отсюда, угол С будет равен 90 — 28 = 62°.
Ответ: острые углы в прямоугольном треугольнике равны 28° и 62°.
Задача 2. Докажите, что биссектрисы смежных углов перпендикулярны.
Решение: Мы знаем свойство измерения углов, которое гласит, что если внутри угла провести лучи, то они разобьют его на несколько углов и сумма градусных мер этих углов будет равна градусной мере первоначального угла.
Поэтому мы имеем: α+α+β+β = 180°.
Или 2α+2β = 180°.
Сокращаем правую и левую часть уравнения на 2, получим: α + β = 90°.
Т.е. угол ДВК между биссектрисами ВД и ВК смежных углов ВСЕГДА равен 90° независимо от величин смежных углов.
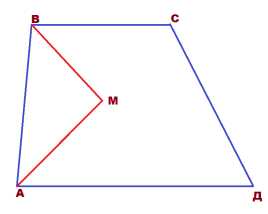
 Задача 3. Дана трапеция АВСД. Биссектрисы углов А и В пересекаются в точке М.
Задача 3. Дана трапеция АВСД. Биссектрисы углов А и В пересекаются в точке М.
Найти АВ, если АМ = 24, ВМ = 18.
Решение: Из предыдущей задачи мы узнали, что биссектрисы смежных углов всегда образуют угол 90°.
Биссектрисы, проведённые из углов трапеции, прилежащих к боковой стороне тоже образуют угол 90°.
В самом деле: углы А и В трапеции в сумме дают 180°, как односторонние углы при параллельных прямых АД и ВС и секущей АВ.
Значит, половины этих углов в сумме будут равны 90°.
А если в треугольнике 2 угла в сумме равны 90°, то третий угол будет равен 90°, ведь сумма внутренних углов треугольника равна 180°.
Значит, это треугольник — прямоугольный. Нам известно в нём 2 катета, найти гипотенузу можно по теореме Пифагора.
АВ² = АМ² + ВМ² = 24² + 18² = 900. Отсюда, АВ = 30.
Ответ: АВ = 30.
На сегодня мы заканчиваем решать задачи по свойствам биссектрисы и медианы треугольника. В следующий раз мы продолжим решать геометрические задачи.
Вам так же будет интересно:
Оставить комментарий
В прямоугольном треугольнике угол между медианой и биссектрисой
Перпендикулярность прямых и плоскостей. Из вершин А и В равностороннего треугольника АВС восстановлены перпендикуляры АА1 и ВВ1 к плоскости треугольника. Найдите расстояние от вершины С до середины отрезка А1B1, есл.
В прямоугольном треугольнике угол между биссектрисой и медианой, проведенными из вершины прямого угла равен 13°. Найдите больший из двух острых углов треугольника. Ответ дайте в градусах. ПОМОГИТЕ.
Ответы и объяснения
Пусть дан треугольник АВС (см. рисунок), угол С=90° и АС< BC. СО — медиана, СМ — биссектриса
АО=ОВ=ОС=R, где R — радиус описанной окружности и треугольники СОВ и АОС — равнобедренные.
Биссектриса СM делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. Так как АС < BC, то АM < MB.
Угол АСО равен углу ВСО и равны 45°. Угол ОСВ =45°-13°=32°.
Угол СВО=углу ОСВ=32°, так как ΔСОВ — равнобедренный.
В прямоугольном треугольнике угол между медианой и биссектрисой
В прямоугольном треугольнике угол между биссектрисой и медианой, проведенными из вершины прямого угла равен 13°. Найдите больший из двух острых углов треугольника. Ответ дайте в градусах. ПОМОГИТЕ.
Ответы и объяснения
Пусть дан треугольник АВС (см. рисунок), угол С=90° и АС< BC. СО — медиана, СМ — биссектриса
АО=ОВ=ОС=R, где R — радиус описанной окружности и треугольники СОВ и АОС — равнобедренные.
Биссектриса СM делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. Так как АС < BC, то АM < MB.
Угол АСО равен углу ВСО и равны 45°. Угол ОСВ =45°-13°=32°.
Угол СВО=углу ОСВ=32°, так как ΔСОВ — равнобедренный.
В прямоугольном треугольнике угол между медианой и биссектрисой
В прямоугольном треугольнике угол между медианой и биссектрисой
Задание 6. Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 19°. Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
Так как биссектриса делит угол пополам, то угол ACD будет равен
.
В прямоугольном треугольнике медиана, проведенная из вершины прямого угла равна половине основания, на которую она проведена. То есть треугольник ADC равнобедренный с равными сторонами AD=DC. У равнобедренного треугольника углы при основании равны, то есть угол A равен углу ADC и он является меньшим углом в треугольнике.
Другие задания варианта:
Частичное или полное копирование решений с данного сайта для распространения на других ресурсах,
В том числе и бумажных, строго запрещено. Все решения являются собственностью сайта

poiskvstavropole.ru
Найти угол в прямоугольном треугольнике между биссектрисой и медианой
Урок: периметр.Вы найдете разбор типовых примеров и задач. Запомните! ! Периметр прямоугольника — это сумма длины и ширины, умноженная на «2». P = (a + b) · 2. Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого.
Найти угол в прямоугольном треугольнике между биссектрисой и медианой
Задание 6. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Так как треугольник прямоугольный и медиана BM исходит из прямого угла B, то точка M является центром описанной окружности вокруг треугольника ABC. Следовательно, AM=MC=MB=r – радиус описанной окружности.
Найдем сначала угол MBC. Учитывая, что BD – биссектриса, то угол. Тогда угол
Рассмотрим равнобедренный треугольник MBC со сторонами MB=MC, в котором углы при основании BC равны, то есть. Так как сумма острых углов в прямоугольном треугольнике равна 90°, то
- Прямоугольный треугольник Все задания на прямоугольный треугольник Решения отдельных заданий
- Задание 6. В треугольнике ABC угол C равен 90°, AC=4,8, sinA=7/25. Найдите AB. Задание 6. В треугольнике ABC угол C равен 90°, AC=2, sinA=√17/17. Найдите BC. Задание 6. В треугольнике ABC угол C равен 90°, АС = 4, cosA=0,5. Найдите АВ. Задание 6. В треугольнике ABC угол C равен 90°, tgA=33/(4√33), АС = 4. Найдите АВ. Задание 6. В треугольнике ABC угол C равен 90°, АС = 8, tgA=0,5. Найдите BC. Задание 6. В треугольнике ABC угол C равен 90°, BC = 4, sinA=0,5. Найдите АВ. Задание 6. В треугольнике ABC угол C равен 90°, cosA=√17/17, ВС = 2. Найдите АС. Задание 6. В треугольнике ABC угол C равен 90°, tgA=0,5, ВС = 4. Найдите АС. Задание 6. В треугольнике ABC угол C равен 90°, AC = 24, BC = 7. Найдите sinA. Задание 6. В треугольнике ABC угол C равен 90°, CH – высота, AB=13,tgA=1/5. Найдите AH. Задание 6. В треугольнике АВС угол С равен 90°, СН — высота, AB=13, tgA=5. Найдите ВН. Задание 6. В треугольнике ABC угол C равен 90°, AB=13, tgA=1/5. Найдите высоту CH. Задание 6. В треугольнике АВС угол С равен 90°, CH — высота, BC=3, sinA=1/6. Найдите АН. Задание 6. В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, sinA=0,5. Найдите BH. Задание 6. В треугольнике АВС угол С равен 90°, BC=5, sinA=7/25. Найдите высоту СН. Задание 6. В треугольнике ABC угол C равен 90°, СН — высота, BC = 3, cosA=√35/6. Найдите АН. Задание 6. В треугольнике АВС угол С равен 90°, СН — высота, BC=5, cosA=7/25. Найдите ВН. Задание 6. В треугольнике АВС угол С равен 90°, BC=8, cosA=0,5. Найдите СН. Задание 6. В треугольнике ABC угол C равен 90°, CH – высота, AC=3, cosA=1/6. Найдите BH. Задание 6. В треугольнике ABC угол C равен 90°, CH — высота, BC = 8, BH = 4. Найдите sinA. Задание 6. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите cosA. Задание 6. В треугольнике ABC угол C равен 90°, CH – высота, BC=4√5, BH=4. Найдите tgA. Задание 6. В треугольнике ABC угол C равен 90°, высота CH равна 20, BC = 25. Найдите sinA. Задание 6. В треугольнике ABC угол C равен 90°, высота CH равна 4, BC = 8. Найдите cosA. Задание 6. В треугольнике ABC угол C равен 90°, высота CH равна 4, BC=√17. Найдите tgA. Задание 6. В треугольнике ABC угол C равен 90°, высота CH равна 24, BH=7. Найдите sinA. Задание 6. В треугольнике ABC угол C равен 90°, высота CH равна 7, BH=24. Найдите cosA. Задание 6. В треугольнике ABC угол C равен 90°, высота CH равна 8, BH=4. Найдите tgA. Задание 6. В треугольнике ABC угол C равен 90°, CH – высота, BH=12, sinA=2/3. Найдите AB. Задание 6. В треугольнике ABC угол C равен 90°, CH – высота, AH=12, cosA=2/3. Найдите AB. Задание 6. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10. Задание 6. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет. Задание 6. В треугольнике ABC угол ACB равен 90°, угол B равен 58°, CD — медиана. Найдите угол ACD. Задание 6. Острый угол прямоугольного треугольника равен 32°. Найдите острый угол, образованный биссектрисами Задание 6. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Задание 6. Один из углов прямоугольного треугольника равен 29°. Найдите угол между высотой и биссектрисой Задание 6. В прямоугольном треугольнике угол между высотой и биссектрисой Задание 6. Острые углы прямоугольного треугольника равны 24° и 66°. Задание 6. В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла Задание 6. Острые углы прямоугольного треугольника равны 24° и 66°. Задание 6. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла Задание 6. В треугольнике ABC угол C равен 90°, угол A равен 30°, AB=2√3. Найдите высоту CH. Задание 6. В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30°, AB=2. Найдите AH. Задание 6. В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30°, AB=4. Найдите BH.
Равнобедренный треугольник Все задания на равнобедренный треугольник Решения отдельных заданий
poiskvstavropole.ru

 Задача 3. Дана трапеция АВСД. Биссектрисы углов А и В пересекаются в точке М.
Задача 3. Дана трапеция АВСД. Биссектрисы углов А и В пересекаются в точке М.
Leave A Comment