Персональный сайт — C2
№1.В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найдите расстояние от точки C до прямой A1B1
Решение.1.doc
№2. В прямоугольном параллелепипедеABCDA1B1C1D1 заданы длины ребер AD=12 AB=5,AA1=8, Найдите объем пирамиды MB1C1D, если M — точка на ребре AA1, причемAM=5 .
Решение.2.doc
№3. В правильной треугольной пирамиде SABC с основанием ABC известны ребра AB=7V3, SC=25.Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC.
Решение.3.doc
№3.1. В правильной треугольной SABC пирамиде с основанием ABC известны ребраAB=24V3, SC=25. Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC.
Решение.4.doc
№4. Длины всех ребер правильной четырёхугольной пирамиды
PABCD с вершиной P равны между собой. Найдите угол между прямой BM и плоскостью BDP, если точка M — середина бокового ребра пирамиды AP.Решение.4.doc
№5.В прямоугольном параллелепипеде A-D1 известны ребра: AB=6 , AD=8 , CC1=16 .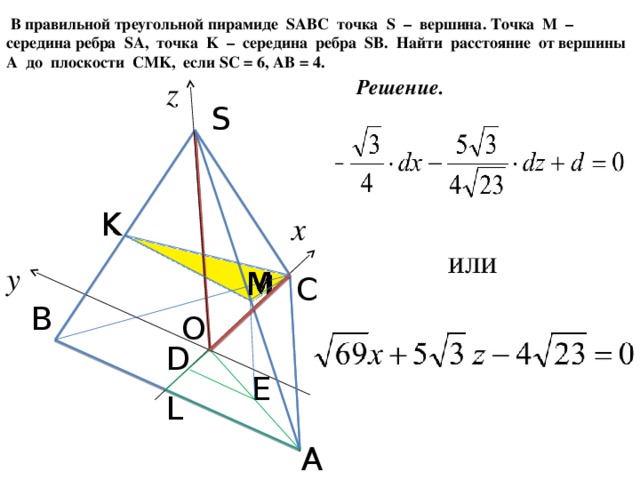 Найдите угол между плоскостями ABC и A1DB.
Найдите угол между плоскостями ABC и A1DB.
Решение5.doc
№6. В кубе A-D1 найдите косинус угла между плоскостями BA1C1 и BA1D .
Решение.6.doc
№7. В правильном тетраэдре ABCD найдите угол между высотой тетраэдра DH и медианой BM боковой грани BCD.
Решение.7.doc
№8.В правильном тетраэдре ABCD найдите угол между медианой BM грани ABD и плоскостью BCD.
Решение.8.doc
№9.В правильной треугольной призме ABCA1B1C1 все ребра которой равны 1, найдите расстояние между прямыми AA1 и BC1 .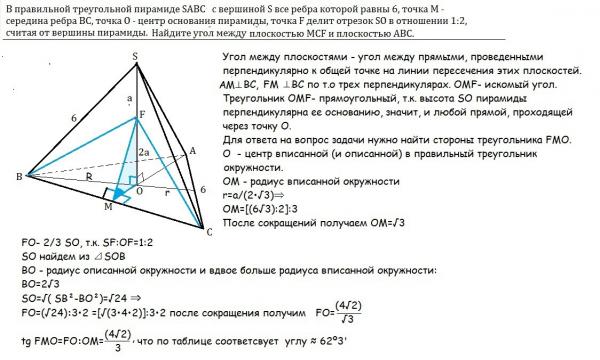
Решение.9.odt
№10.В правльной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между плоскостью SAD и плоскостью, проходящей через точку A перпендикулярно прямой BD.
Решение.10.doc
№11. В правильной шестиугольной призме A-F1 все ребра которой равны 1 найдите расстояние от точки B до прямой E1F1.
Решение.11.doc
№12. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите угол между прямыми SB и CD.
Решение.12.odt
Zadachnik_S2
И. В. Яковлев | Материалы по математике | MathUs.ru
Задачник С2
Здесь приведены задачи С2, которые предлагались на ЕГЭ по математике, а также на диагностических, контрольных и тренировочных работах МИОО начиная с сентября 2009 года.
1. (ЕГЭ, 2014 ) Радиус основания конуса с вершиной P равен 6, а длина его образующей равна 9.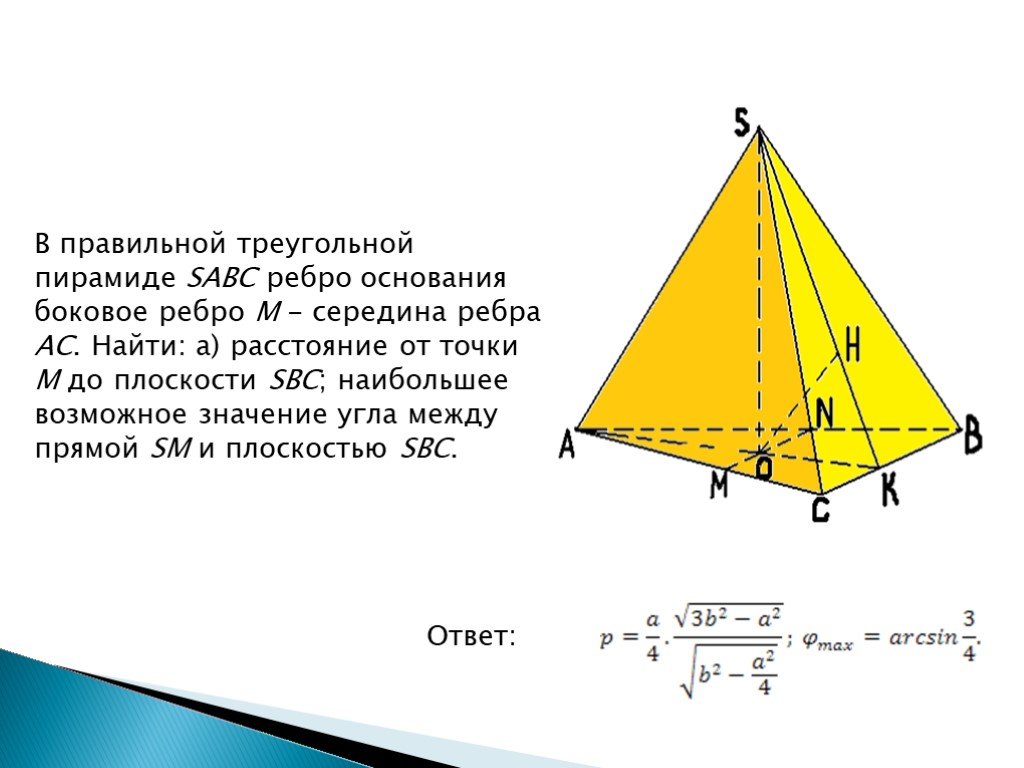 На окружности основания конуса выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1 : 3. Найдите площадь сечения конуса плоскостью ABP .
На окружности основания конуса выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1 : 3. Найдите площадь сечения конуса плоскостью ABP .
14 | 9 |
| p |
2. (МИОО, 2014) В правильной треугольной пирамиде SABC с основанием ABC боковое ребро равно 5, а сторона основания равна 6. Найдите расстояние от вершины A до плоскости SBC.
4 |
|
| |
| 39 | 3 | |
| p |
|
|
3. (Санкт-Петербург, пробный ЕГЭ, 2014) Отрезок AC диаметр основания конуса, отрезок AP образующая этого конуса и AP = AC. Хорда основания BC составляет с прямой AC угол 60 . Через AP проведено сечение конуса плоскостью, параллельной прямой BC.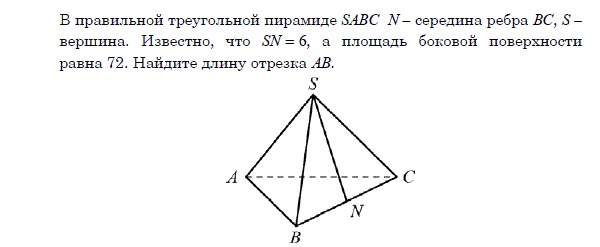 Найдите расстояние от центра основания конуса O до плоскости сечения, если радиус основания конуса равен 1.
Найдите расстояние от центра основания конуса O до плоскости сечения, если радиус основания конуса равен 1.
5
15 p
4. (МИОО, 2014) Высота SO правильной треугольной пирамиды SABC составляет 5/7 от высоты SM боковой грани SAB. Найдите угол между плоскостью основания пирамиды и её боковым ребром.
| 6 | 4 | arctg |
| p |
| |
| 5 |
|
|
5. (МИОО, 2014) Дана правильная четырёхугольная пирамида MABCD, рёбра основания | |||||
p |
|
| p |
| |
которой равны 5 2. Тангенс угла между прямыми DM и AL равен |
| 2, L середина ребра | |||
MB. |
|
|
| ||
|
|
| 5 | ||
6. (МИОО, 2013) Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 108, а площадь полной поверхности этой пирамиды равна 144. Найдите площадь сечения, проходящего через вершину S этой пирамиды и через диагональ её основания.
36
7. (МИОО, 2013) Дана правильная треугольная призма ABCA1B1C1, все рёбра основания ко- p
торой равны 2 7. Сечение, проходящее через боковое ребро AA1 и середину M ребра B1C1, является квадратом. Найдите расстояние между прямыми A1B и AM.
2
6 p
1
8. (МИОО, 2013) В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра AB = 5, AD = 4, AA1 = 9. Точка O принадлежит ребру BB1 и делит его в отношении 4 : 5, считая от вершины B. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки A, O и C1.
1281 p
9. (ЕГЭ, 2013 ) В правильной треугольной пирамиде MABC с вершиной M высота равна 3, а боковые рёбра равны 6. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середины сторон AB и AC параллельно прямой MA.
2 27
p
10. (ЕГЭ, 2013 ) В правильную шестиугольную пирамиду, боковое ребро которой равно 5, а высота равна 1, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
| 3 | 74 | 12 |
|
| p | |
|
|
11. (ЕГЭ, 2013) Радиус основания конуса равен 8, а его высота равна 15. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 14. Найдите расстояние от центра основания конуса до плоскости сечения.
4 15
12. (ЕГЭ, 2013 ) В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания равна 6, а боковое ребро AA1 = 1. Точка F принадлежит ребру C1D1 и делит его в отношении 2 : 1, считая от вершины C1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки A, C и F .
Точка F принадлежит ребру C1D1 и делит его в отношении 2 : 1, считая от вершины C1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки A, C и F .
2 | 12 |
| p |
13. (ЕГЭ, 2013 ) В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 3, а боковые рёбра равны 8. Найдите площадь сечения пирамиды плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AC.
14. (ЕГЭ, 2013) Две параллельные плоскости, расстояние между которыми равно 2, пересекают шар. Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0;84. Найдите радиус шара.
5
15. (ЕГЭ, 2013) Плоскость пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 7. Плоскость , параллельная плоскости , касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 5.
12
2
16. (МИОО, 2013) Правильные треугольники ABC и BCM лежат в перпендикулярных плоскостях, BC = 8. Точка P середина CM, а точка T делит отрезок BM так, что BT : T M = 1 : 3. Вычислите объём пирамиды MP T A.
24
p
17. (МИОО, 2013) В правильной треугольной призме ABCA1B1C1 боковое ребро равно 8 3, а ребро основания равно 1. Точка D середина ребра BB1. Найдите объём пятигранника
ABCA1D.
3
18. (ФЦТ, 2013) В правильной треугольной пирамиде SABC с основанием ABC проведено сечение через середины рёбер AB и BC и вершину S. Найдите площадь этого сечения, если боковое ребро пирамиды равно 7, а сторона основания равна 8.
29 | 2 |
| p |
19. (МИОО, 2013) В правильной четырёхугольной пирамиде SABCD точка S вершина. Точка M середина ребра SA, точка K середина ребра SC. Найдите угол между плоскостями
Найдите угол между плоскостями
BMK и ABC, если AB = 10, SC = 8.
| 10 | arctg |
7 | ||
| p |
|
20. (МИОО, 2013) В правильной треугольной пирамиде SABC с основанием ABC сторона основания равна 8, а угол ASB равен 36 . На ребре SC взята точка M так, что AM биссектриса угла SAC. Найдите площадь сечения пирамиды, проходящего через точки A, M и B.
3 | 16 |
| p |
21. (МИОО, 2012) В правильной треугольной призме ABCA1B1C1 стороны основания равны 8, p
а боковые рёбра равны 13. Изобразите сечение, проходящее через вершины A, C и середину ребра A1B1. Найдите его площадь.
30
22. (МИОО, 2012) В правильной четырёхугольной пирамиде SABCD с основанием ABCD проведено сечение через середины рёбер AB и BC и вершину S. Найдите площадь этого сечения, если все рёбра пирамиды равны 8.
Найдите площадь этого сечения, если все рёбра пирамиды равны 8.
23. (ЕГЭ, 2012) В прямоугольном параллелепипеде ABCDA1B1C1D1 AB = 2, AD = AA1 = 1. Найдите угол между прямой AB1 и плоскостью ABC1.
10 arcsinp1
24. (ЕГЭ, 2012) В правильной треугольной призме ABCA1B1C1 стороны основания равны 2, боковые рёбра равны 3, точка D середина ребра CC1. Найдите расстояние от вершины C до плоскости ADB1.
13 p3
3
25. (ЕГЭ, 2012) В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 2, а боковые рёбра равны 5. На ребре AA1 отмечена точка E так, что AE : EA1 = 3 : 2. Найдите угол между плоскостями ABC и BED1.
| 2 | arctg |
| 13 | |
| p |
|
26. (ЕГЭ, 2012 ) Точка E середина ребра AA1 куба ABCDA1B1C1D1. Найдите площадь сечения куба плоскостью C1DE, если рёбра куба равны 2.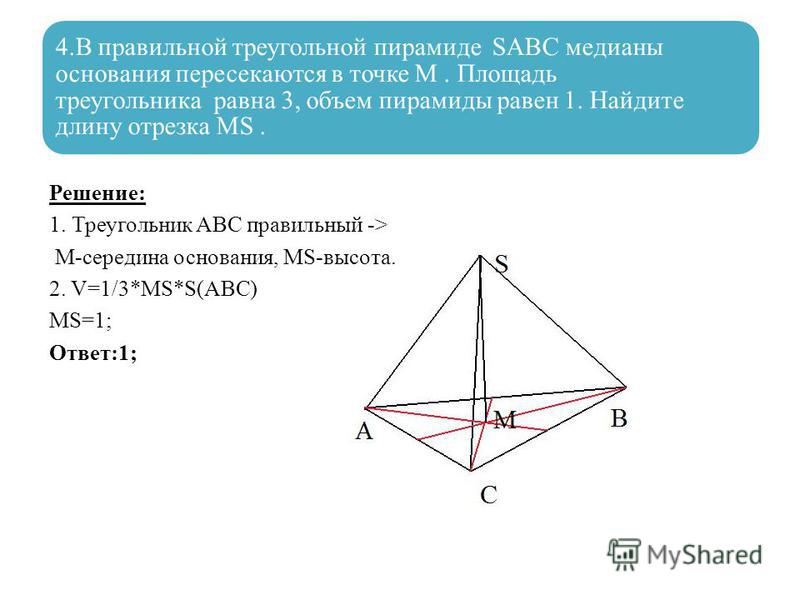
9/2
27. (ЕГЭ, 2012 ) На ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE : EC1 = = 1 : 2. Найдите угол между прямыми BE и AC1.
| 15 |
|
| arccos |
30 | 2 | |||
| p |
|
|
|
28. (ЕГЭ, 2012) Точка E середина ребра DD1 куба ABCDA1B1C1D1. Найдите угол между прямыми CE и AC1.
15 arccosp1
29. (Репетиционный ЕГЭ, 2012) В правильной четырёхугольной призме ABCDA1B1C1D1 со стороной основания 4 и высотой 7 на ребре AA1 взята точка M так, что AM = 2. На ребре BB1 взята точка K так, что B1K = 2. Найдите угол между плоскостью D1MK и плоскостью
CC1D1.
30. (Репетиционный ЕГЭ, 2012 ) Основанием прямого параллелепипеда ABCDA B C D яв-
p 1 1 1 1
ляется ромб ABCD, сторона которого равна 4 3, а угол BAD равен 60 . Найдите расстояние от точки A до прямой C1D1, если известно, что боковое ребро данного параллелепипеда равно 8.
Найдите расстояние от точки A до прямой C1D1, если известно, что боковое ребро данного параллелепипеда равно 8.
10
31. (ФЦТ, 2012) В прямоугольном параллелепипеде ABCDA1B1C1D1 AB = 2, AD = 4, AA1 = 3 и точка E середина ребра AB. Найдите угол между прямыми A1C1 и B1E.
50 arccosp1
32. (Юг, пробный ЕГЭ, 2012) В пирамиде DABC известны длины рёбер: AB = AC = DB = = DC = 13 см, DA = 6 см, BC = 24 см. Найдите расстояние между прямыми DA и BC.
4см
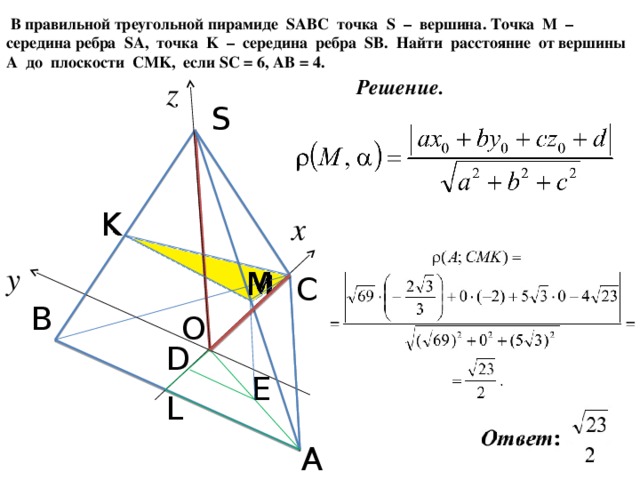
33. (МИОО, 2012) В правильной треугольной пирамиде SABC точка S вершина. Точка M середина ребра SA, точка K середина ребра SB. Найдите угол между плоскостями CMK и ABC, если SC = 6, AB = 4.
| 5 | arctg |
| 23 | |
| p |
|
4
34p. (МИОО, 2012) Дана правильная четырёхугольная пирамида SABCD. Боковое ребро SA = = 5, сторона основания равна 2.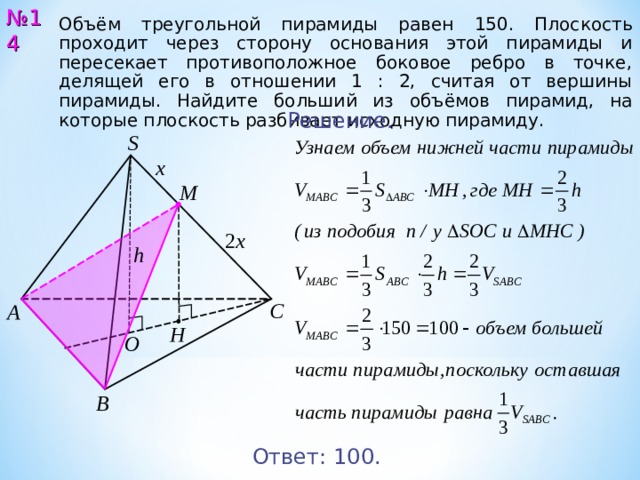 Найдите расстояние от точки B до плоскости ADM, где M середина ребра SC.
Найдите расстояние от точки B до плоскости ADM, где M середина ребра SC.
1
35. (МИОО, 2011) В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания p
равна 2, а высота равна 1. M середина ребра AA1. Найдите расстояние от точки M до плоскости DA1C1.
4
2 p
36. (МИОО, 2011) Основанием прямой призмы ABCA1B1C1 является равнобедренный треугольник ABC, AB = AC = 5, BC = 8. Высота призмы равна 3. Найдите угол между прямой A1B и плоскостью BCC1.
5 | arctg |
3 | |
|
|
37. (МИОО, 2011) Основание прямой четырёхугольной призмы ABCDA1B1C1D1 прямоугольник ABCD, в котором AB = 12, AD = 5. Найдите угол между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD перпендикулярно прямой BD1, если расстояние между прямыми AC и B1D1 равно 13.
38. (ЕГЭ, 2011) В правильной четырёхугольной призме ABCDA1B1C1D1, стороны основания которой равны 3, а боковые рёбра равны 4, найдите угол между прямой AB1 и плоскостью
BDD1.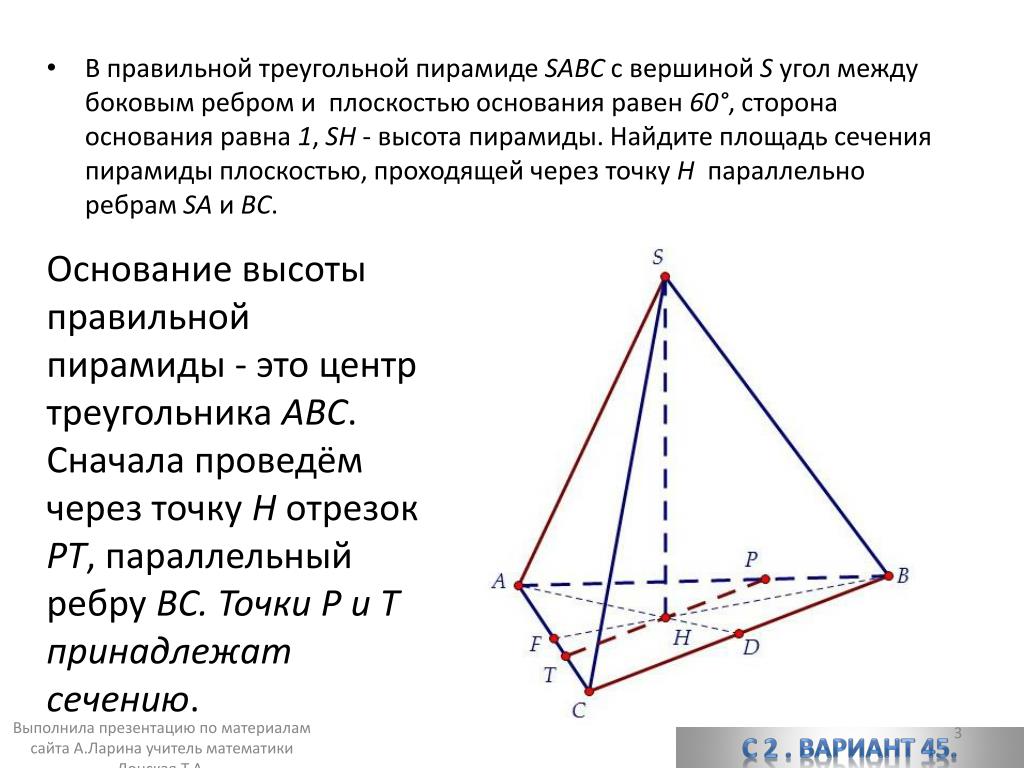
| 10 |
| arcsin | |
| 2 | 3 | ||
|
| p |
| |
39. (ЕГЭ, 2011 ) В правильной четырёхугольной пирамиде SABCD, все рёбра которой равны 1, точка E середина ребра SB. Найдите угол между прямой CE и плоскостью SBD.
2 | arctg |
| p |
40. (ЕГЭ, 2011 ) В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 1, найдите расстояние между прямыми AA1 и BC1.
2
3 p
41. (ЕГЭ, 2011 ) В правильной шестиугольной призме ABCDEF A1B1C1D1E1F1, стороны основания которой равны 3, а боковые рёбра равны 4, найдите расстояние от точки C до прямой D1E1.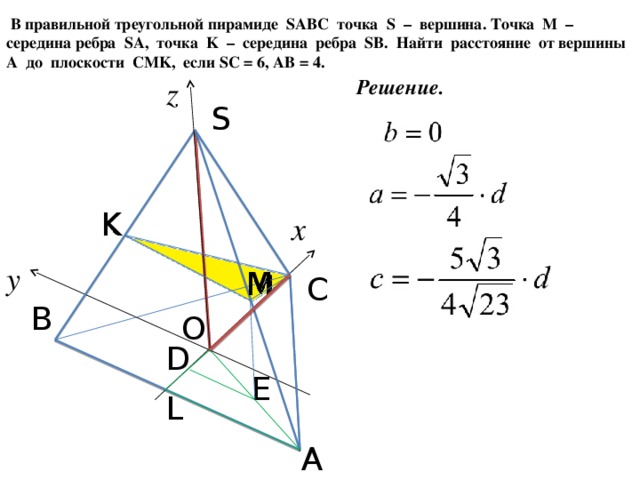
2
91 p
42. (ЕГЭ, 2011 ) В правильной шестиугольной призме ABCDEF A1B1C1D1E1F1, стороны основания которой равны 4, а боковые рёбра равны 1, найдите расстояние от точки B до прямой F1E1.
7
5
43. (ЕГЭ, 2011) В правильной четырёхугольной призме ABCDA1B1C1D1, стороны основания которой равны 3, а боковые рёбра равны 4, найдите угол между прямыми AC и BC1.
| 10 |
| arccos | |
| 2 | 3 | ||
|
| p |
| |
44. (Репетиционный ЕГЭ, 2011) В правильной треугольной пирамиде сторона основания равна 12. Найдите расстояние от центра основания до боковой грани, если двугранный угол при ребре основания равен =3.
3
45.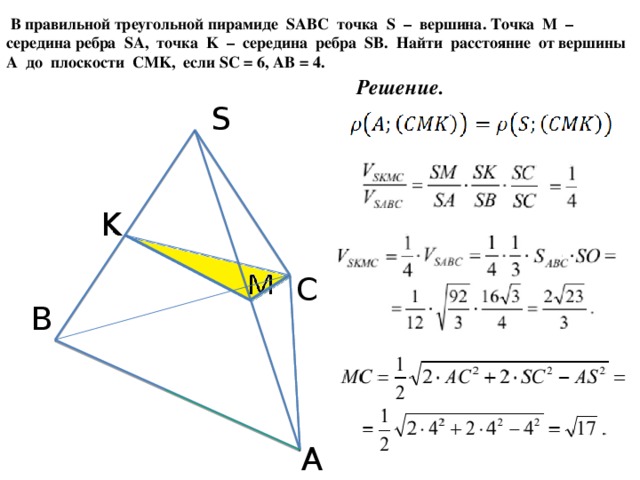 (Репетиционный ЕГЭ, 2011) Длины всех рёбер правильной четырёхугольной пирамиды P ABCD с вершиной P равны между собой. Найдите угол между прямой BM и плоскостью BDP , если точка M середина бокового ребра пирамиды AP .
(Репетиционный ЕГЭ, 2011) Длины всех рёбер правильной четырёхугольной пирамиды P ABCD с вершиной P равны между собой. Найдите угол между прямой BM и плоскостью BDP , если точка M середина бокового ребра пирамиды AP .
5 arctgp 1
46. (МИОО, 2011) Основанием прямой призмы ABCDA1B1C1D1 является ромб ABCD, у которого AB = 10, BD = 12. Высота призмы равна 6. Найдите расстояние от центра грани A1B1C1D1 до плоскости BDC1.
5 24
47. (МИОО, 2011) В основании прямой треугольной призмы ABCAp1B1C1 лежит равнобедрен-
ный прямоугольный треугольник ABC с гипотенузой AB, равной 2 10; высота призмы равна p
2 5. Найдите расстояние от точки C1 до плоскости BCM, где M середина ребра A1C1.
2
48. (МИОО, 2011) Длина ребра куба ABCDA1B1C1D1 равна 1. Найдите расстояние от вершины B до плоскости ACD1.
3
p 1
49. (МИОО, 2011) Дан куб ABCDA1B1C1D1 с ребром 1. Найдите расстояние от вершины A до плоскости A1BT , где T середина ребра AD.
6
p 1
50. (МИОО, 2011) Дан правильный тетраэдр MABC с ребром 1. Найдите расстояние между прямыми AL и MO, где L середина ребра MC, O центр грани ABC.
(МИОО, 2011) Дан правильный тетраэдр MABC с ребром 1. Найдите расстояние между прямыми AL и MO, где L середина ребра MC, O центр грани ABC.
14
7 p
51. (МИОО, 2010) Дан куб ABCDA1B1C1D1. Длина ребра куба равна 1. Найдите расстояние от середины отрезка BC1 до плоскости AB1D1.
3
p 1
52. (МИОО, 2010) В кубе ABCDA1B1C1D1 найдите угол между плоскостями AB1D1 и ACD1.
3 | arccos | |
1 | ||
| ||
|
|
6
p
53. (МИОО, 2010) В правильной треугольной призме ABCA1B1C1 известны рёбра: AB = 3 3, BB1 = 6. Точка M середина ребра B1C1, а точка T середина A1M. Найдите угол между плоскостью BCT и прямой AT .
8 | 2arctg | |
3 | ||
| ||
|
|
54.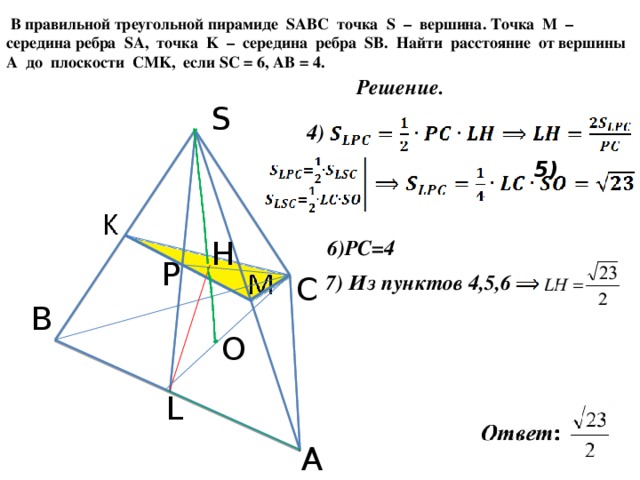 (МИОО, 2010) В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого AA1 = 3, AD = 8, AB = 6, найдите угол между плоскостью ADD1 и прямой EF , проходящей через середины рёбер AB и B1C1.
(МИОО, 2010) В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого AA1 = 3, AD = 8, AB = 6, найдите угол между плоскостью ADD1 и прямой EF , проходящей через середины рёбер AB и B1C1.
5 | arctg | |
3 | ||
|
p
55. (МИОО, 2010) Дан куб ABCDA1B1C1D1 с ребром 8 6. Найдите расстояние от середины ребра B1C1 до прямой MT , где точки M и T середины рёбер CD и A1B1 соответственно.
12
56. (ЕГЭ, 2010) Дан куб ABCDA1B1C1D1. Найдите тангенс угла между плоскостями AB1C и DCC1.
2 p
57. (ЕГЭ, 2010 ) В правильной треугольной пирамиде SABC с основанием ABC известны рёбра: | ||||||
p |
| , SC = 10. Точка N середина ребра BC. Найдите угол, образованный плоскостью | ||||
AB = 6 | 3 | |||||
основания и прямой AT , где T середина отрезка SN. |
|
| ||||
|
|
|
| |||
|
| 15 | arctg | |||
|
|
|
| 8 |
| |
|
|
|
| |||
|
|
| ||||
58. (ЕГЭ, 2010 ) В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра: AB = 8, | ||||||
AD = 6, CC1 = 6. Найдите угол между плоскостями CD1B1 и AD1B1. |
|
| ||||
|
|
|
| |||
| 41 | arccos | ||||
|
|
| 9 | |||
|
|
| ||||
59. | ||||||
AD = 6, CC1 = 5. Найдите угол между плоскостями BDD1 и AD1B1. |
|
| ||||
|
| |||||
| 25 | arctg | ||||
|
|
|
| 24 | ||
|
| |||||
|
|
|
|
|
|
|
60. (ЕГЭ, 2010 ) В правильной треугольной пирамиде SABC с основанием ABC известны рёбра: | ||||||||
p |
| , SC = 17. Найдите угол, образованный плоскостью основания и прямой, проходящей | ||||||
AB = 8 | 3 | |||||||
через середины рёбер AS и BC. |
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 16 | arctg | |
|
|
|
|
|
| 15 | ||
|
|
|
|
|
|
| ||
61. (ЕГЭ, 2010 ) В правильной шестиугольной призме ABCDEF A1B1C1D1E1F1 сторона осно- | ||||||||
вания равна 7, а высота равна 1. Найдите угол между прямой F1B1 и плоскостью AF1C1. |
| |||||||
|
| 151 |
| arcsin | ||||
|
|
| 1 | p | ||||
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
62.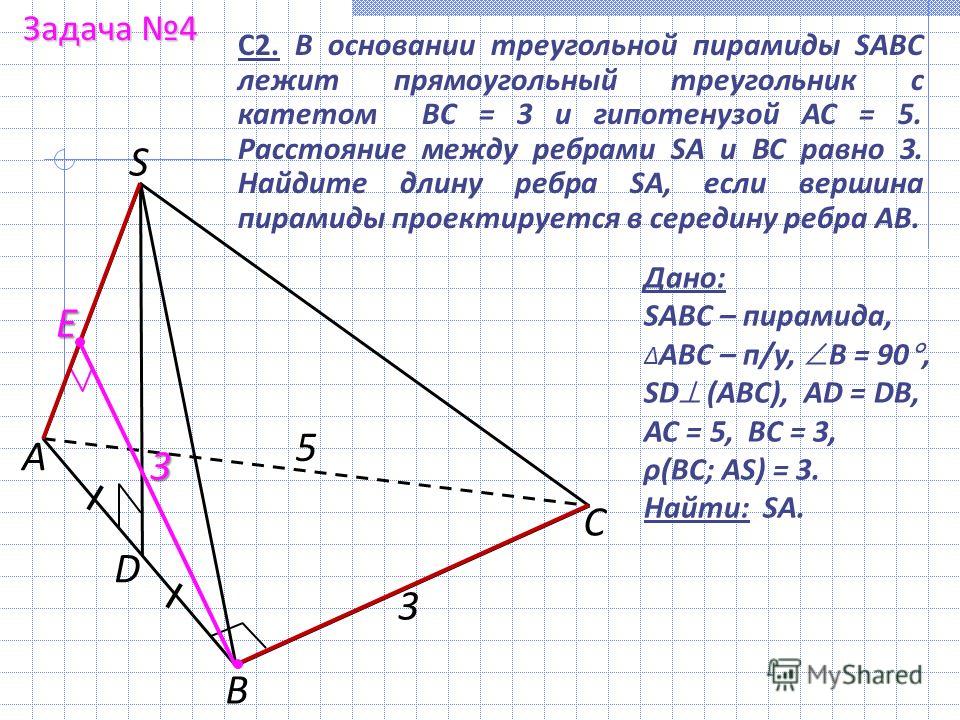 (МИОО, 2010) В правильной шестиугольной призме ABCDEF A1B1C1D1E1F1, все рёбра которой равны 1, найдите расстояние от точки C до прямой F1E1.
(МИОО, 2010) В правильной шестиугольной призме ABCDEF A1B1C1D1E1F1, все рёбра которой равны 1, найдите расстояние от точки C до прямой F1E1.
2
7
63. (МИОО, 2010) В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые рёбра равны 2, найдите расстояние от точки C до прямой SA.
4
39 p
64. (МИОО, 2010) В тетраэдре ABCD, все рёбра которого равны 1, найдите расстояние от точки A до прямой, проходящей через точку B и середину E ребра CD.
3
6 p
65. (Репетиционный ЕГЭ, 2010 ) В правильной четырёхугольной пирамиде SABCD с осно- p
ванием ABCD сторона основания равна 3 2, а боковое ребро равно 5. Найдите угол между плоскостями ABC и ACM, где точка M делит ребро BS так, что BM : MS = 2 : 1.
3 | arctg | |
8 | ||
| ||
|
|
66. (МИОО, 2010) В правильной четырёхугольной пирамиде SABCD сторона основания рав- p
(МИОО, 2010) В правильной четырёхугольной пирамиде SABCD сторона основания рав- p
на 1, а боковое ребро равно 3=2. Найдите расстояние от точки C до прямой SA.
3 2
q
67. (МИОО, 2010) В кубе ABCDA1B1C1D1 все рёбра равны 1. Найдите расстояние от точки C до прямой BD1.
3
6 p
68. (МИОО, 2010) В правильной треугольной призме ABCA1B1C1 высота равна 2, сторона основания равна 1. Найдите расстояние от точки B1 до прямой AC1.
10
95 p
69. (МИОО, 2010) Сторона основания правильной треугольной призмы ABCA1B1C1 равна 8. Высота этой призмы равна 6. Найдите угол между прямыми CA1 и AB1.
25 | arccos | |
1 | ||
|
70. (МИОО, 2010) В основании прямой призмы ABCA1pB1C1 лежит равнобедренный прямоугольный треугольник ABC с гипотенузой AB, равной 8 2. Высота призмы равна 6.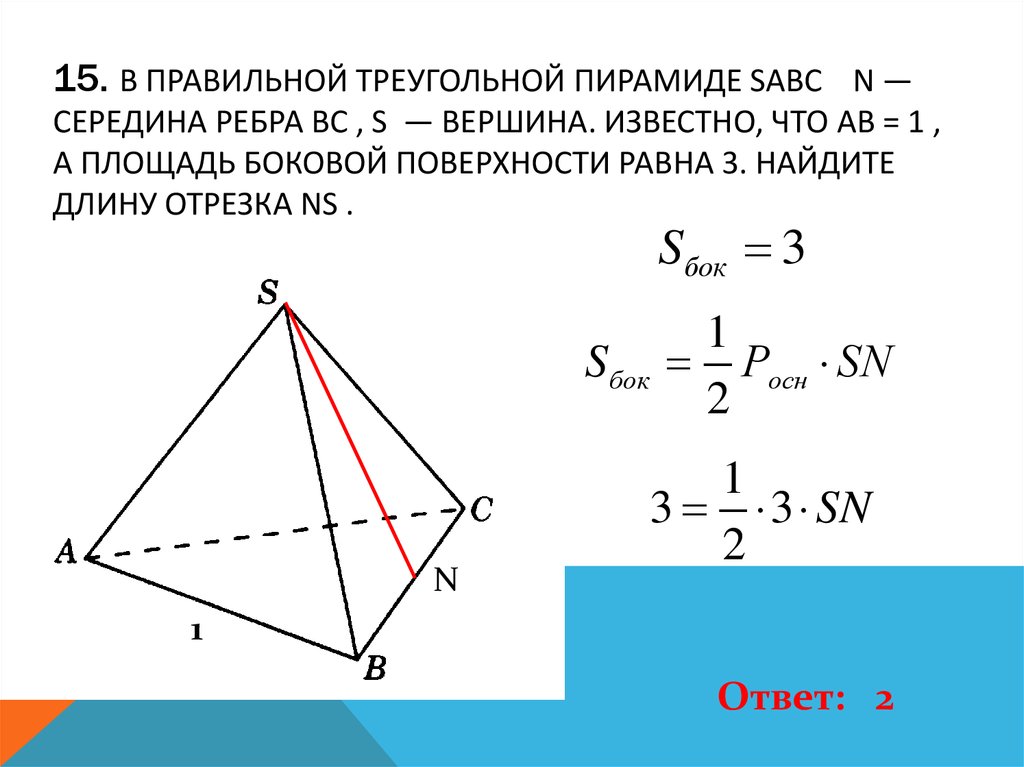 Найдите угол между прямыми AC1 и CB1.
Найдите угол между прямыми AC1 и CB1.
25 | arccos | |
9 | ||
| ||
|
|
71. (МИОО, 2009) В основании прямой призмы ABCA1B1C1 лежит прямоугольный треуголь- | |||||||||
p |
|
|
|
|
|
|
|
|
|
ник ABC, у которого угол C равен 90 , угол A равен 30 , AC = 10 3. Диагональ боковой грани | |||||||||
B1C составляет угол 30 с плоскостью AA1B1. Найдите высоту призмы. |
|
|
|
| |||||
| 2 |
| 10 |
|
| ||||
|
|
|
| p |
|
| |||
|
|
|
|
| |||||
72. | |||||||||
BC = 6, CC1 = 4, найдите тангенс угла между плоскостями ACD1 и A1B1C1. |
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
| 2 | 2 |
|
| ||
|
|
|
|
|
| p |
|
| |
8
73. (МИОО, 2009) В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого AB = 4, BC = 6, CC1 = 4, найдите тангенс угла между плоскостью ABC и прямой EF , проходящей через середины рёбер AA1 и C1D1.
(МИОО, 2009) В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого AB = 4, BC = 6, CC1 = 4, найдите тангенс угла между плоскостью ABC и прямой EF , проходящей через середины рёбер AA1 и C1D1.
10 p1
74. (МИОО, 2009) В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между плоскостью A1BC и прямой BC1, если AA1 = 8, AB = 6, BC = 15.
85 | arcsin | |
24 | ||
| ||
|
|
75. (МИОО, 2009) В правильной шестиугольной призме ABCDEF A1B1C1D1E1F1, все рёбра которой равны 1, найдите косинус угла между прямыми AB1 и BC1.
4 3
9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
15.11.2019209.41 Кб6YuridLOGIK_Semin2.doc
- #
25.08.201928.
 44 Кб1YuZhNAYa_AMERIKA.docx
44 Кб1YuZhNAYa_AMERIKA.docx - #
20.09.201973.07 Кб1Yuzhnyy_Federalnyy_Universitet_red.docx
- #
22.09.201985.09 Кб0zachet_po_integratsii.docx
- #
18.11.201940.58 Кб0Zachet_po_polovine.docx
- #
12.03.2016231.66 Кб22Zadachnik_S2.pdf
- #
19.08.201928.5 Кб0Zadania_Afrika.docx
- #
13.02.2015312.32 Кб19zadania_dlya_9_kl.doc
- #
15.09.2019288.06 Кб8Zadania_po_matematike_2_semestr_1_kurs.docx
- #
12.03.2016824.18 Кб234Zadanie_MA10_11022016_baza_copy.pdf
- #
12.03.20161.47 Mб596Zadanie_MA11_03032016_baza_zapad_copy.pdf
Задача о треугольной пирамиде
Задача о треугольной пирамиде Mathematics Magazine, , том 76 (2003 г.), стр. 319, включает следующее:
проблема, номер Q934, немного перефразированная здесь.
Mathematics Magazine, , том 76 (2003 г.), стр. 319, включает следующее:
проблема, номер Q934, немного перефразированная здесь.- Рассмотрим все треугольные пирамиды с неподвижным основанием со сторонами а, б, и в, и фиксированной высотой h. Какая из этих треугольных пирамид имеет наименьшую площадь поверхности,
и какова площадь этой поверхности?
Чтобы начать анализ ситуации, нарисуйте линии DE, DF, и DG от D перпендикулярно сторонам a, b, и c принадлежащий
треугольник с длинами x, y, и z, соответственно.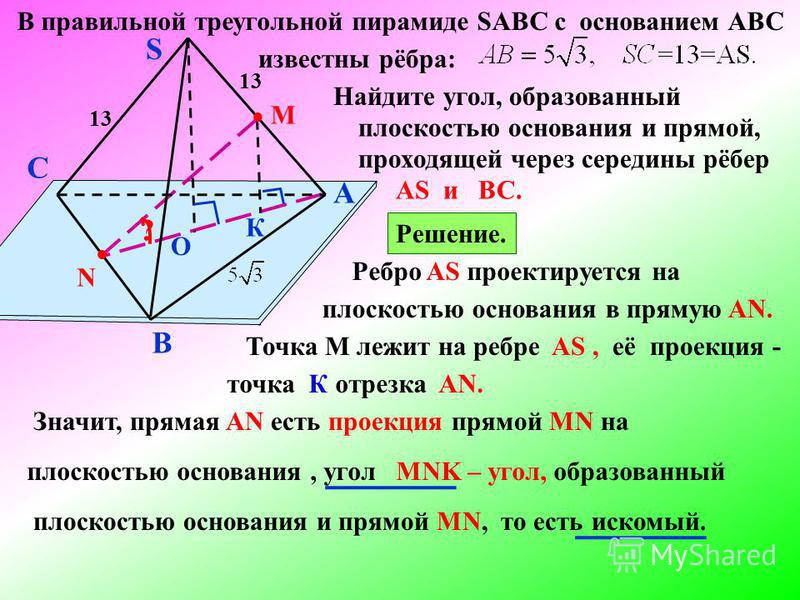 Кроме того, нарисуйте
линии
от D до вершин треугольника.
Кроме того, нарисуйте
линии
от D до вершин треугольника.
Обратите внимание, что длины x, y, и z не могут быть выбраны произвольно. так как любые два определяют третий. Первая проблема заключается в том, чтобы найти уравнение что их роднит. Треугольник ABC состоит из три треугольника BCD, ACD, и ABD. Эти три треугольника есть области ax /2, по /2 и cz /2 соответственно. Следовательно, площадь T треугольника ABC есть
Поскольку площадь T является фиксированной величиной, это уравнение является ограничением которая связывает переменные x, y, и г.
Пирамида. Далее мы можем найти формулу для площади поверхности
в
пирамида. мы только
касается боковой области, состоящей из
треугольники с тремя сторонами, так как
базовый треугольник зафиксирован. Боковой треугольник
на линии имеет высоту
который является квадратным корнем из ч 2 + x 2 ,
так что его площадь такова
раз и /2. Площади двух других боковых треугольников
иметь аналог
формулы, поэтому площадь боковой поверхности P пирамиды дано
к
формула
Площади двух других боковых треугольников
иметь аналог
формулы, поэтому площадь боковой поверхности P пирамиды дано
к
формула
Теперь нам нужно максимизировать это количество с учетом ограничения на x, y, и z , упомянутые выше.
Множители Лангранжа. Если бы у нас не было ограничения на переменные, тогда мы могли бы использовать базовое исчисление, чтобы найти решение. Все мы придется сделать, это взять три частные производные по х, у, и г, установить их все в 0, и одновременно решить получившиеся три уравнения, чтобы найти критические точки, в которых возникают экстремальные значения функции.
Но у нас есть это ограничение. К счастью, метод Лагранжа
множители
применяется только в этом случае. Введем новую переменную, давайте
назовите это w, и
образуют функцию четырех переменных x, y, z, и w , взяв
Формула функции, которую мы хотим максимизировать, и
вычитание w раза больше
ограничение, после того как мы перепишем ограничение
как функция, которая должна быть равна 0. Это дает нам функцию
Это дает нам функцию
Для метода множителей Лагранжа возьмите три частные производные с относительно x, y, и z, установите их все на 0 и одновременно решить получившиеся три уравнения вместе с ограничение уравнение, чтобы найти критические точки, в которых экстремальные значения функция возникает.
Три частные производные установить в 0 дать уравнения
Эти три уравнения можно легко решить, чтобы получить единственное решение x = y = z.
Центр треугольника. Делаем вывод, что точка D ниже вершина пирамиды с наибольшей площадью поверхности это точка, равноудаленная от три стороны треугольника. Это называется центром треугольника. Расстояние р от вписанный центр в любую сторону называется внутренним радиусом треугольника.
Для получения дополнительной информации о вписанном центре см. элемента Евклида, предложение .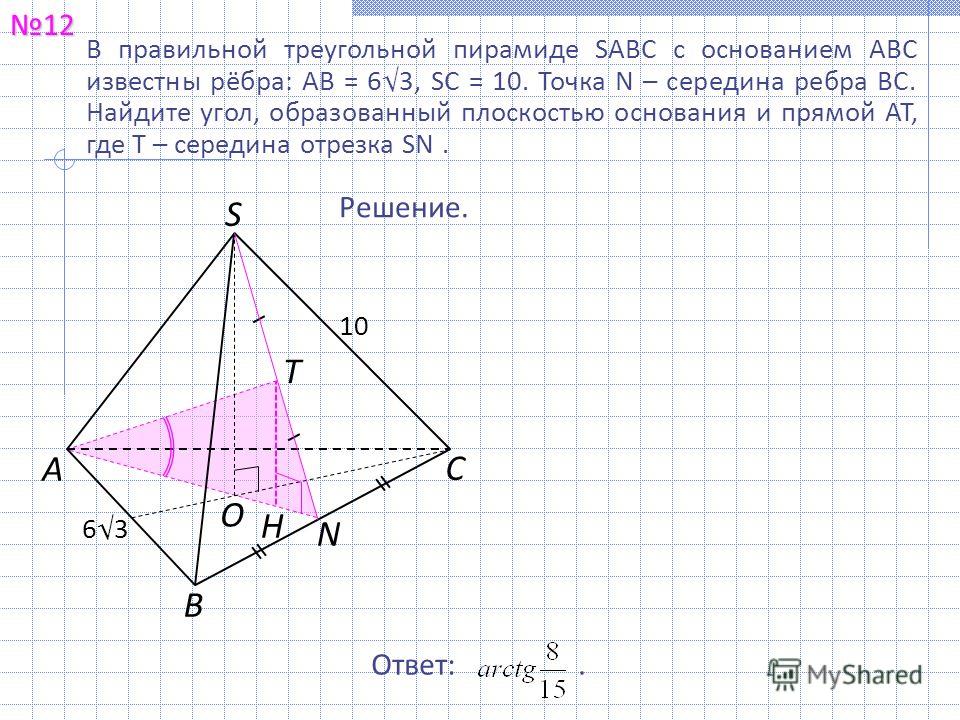 IV.4
в котором вписанная окружность треугольника строится как пересечение
любые два
биссектрисы треугольника. (Инцентр — не единственный «центр»
треугольника. См. также примечание о линия Эйлера треугольника для некоторых других центров треугольника.)
IV.4
в котором вписанная окружность треугольника строится как пересечение
любые два
биссектрисы треугольника. (Инцентр — не единственный «центр»
треугольника. См. также примечание о линия Эйлера треугольника для некоторых других центров треугольника.)
Обратите внимание, что площадь T треугольника является произведением радиуса r внутреннего радиуса и полупериметра с, который ( a + b + c )/2. Так T = р. В комментарии к предложению IV.4 упоминается выше также дает вывод Герона формула площади T треугольник по полупериметру с, и стороны а, б, и c, а именно, T равно квадратному корню из s ( s a )( s b )( s c ).
Назад к пирамиде минимальной площади. Теперь мы можем вычислить боковой поверхность площадь пирамиды минимальной площади. Это
Вернуться на страницу группы решения математических задач Кларка
Эта страница находится по адресу http://aleph0.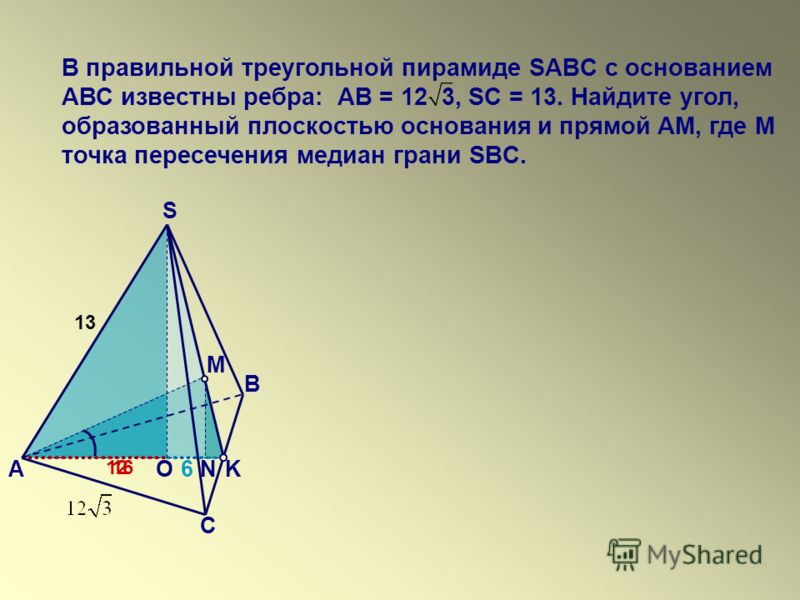

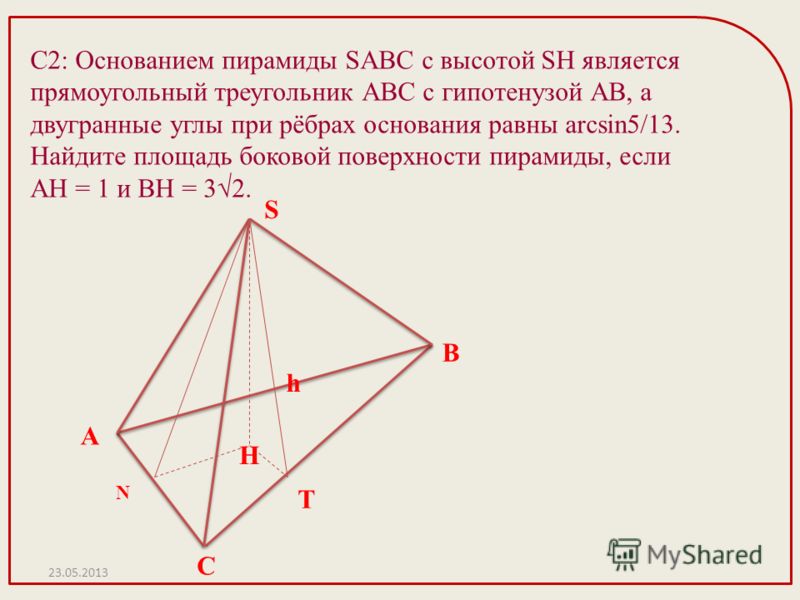
 Найдите высоту данной пирамиды.
Найдите высоту данной пирамиды.
 (ЕГЭ, 2010 ) В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра: AB = 8,
(ЕГЭ, 2010 ) В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра: AB = 8,
 (МИОО, 2009) В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого AB = 6,
(МИОО, 2009) В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого AB = 6,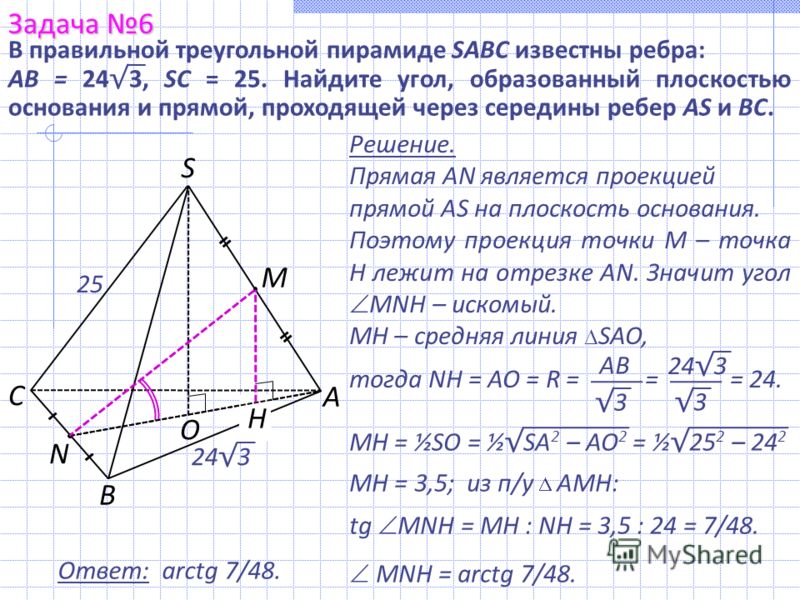 44 Кб1YuZhNAYa_AMERIKA.docx
44 Кб1YuZhNAYa_AMERIKA.docx
Leave A Comment