Пробная экзаменационная работа по математике для 9 класса «Модуль
Районная контрольная работа по геометрии
9 класс
Вариант 1
1часть
1. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
2. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором и . Найдите угол BOC. Ответ дайте в градусах.
3. В прямоугольном треугольнике один из катетов равен 35, а угол, лежащий напротив него равен 450. Найдите площадь треугольника.
4. Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
5. Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника
соответственно равны двум сторонам другого треугольника, то такие треугольники
равны.
2) Площадь круга меньше квадрата длины его диаметра.
3) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
6. Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Перечислите эти длины в ответе без пробелов в порядке возрастания.
7. В равнобедренном треугольнике . Найдите AC, если высота .
2 часть
8. В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона
9. В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOB.
10. Точки и лежат на стороне AC треугольника ABC на
расстояниях соответственно 18 и 40 от вершины А. Найдите радиус окружности, проходящей через точки и и
Найдите радиус окружности, проходящей через точки и и
касающейся луча AB, если
Вариант 2
1часть
1. Основания трапеции равны 1 и 11. Найдите бóльший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
2. Окружность с центром в точке
 Найдите величину угла BOC. Ответ дайте в градусах.
Найдите величину угла BOC. Ответ дайте в градусах.
3. В прямоугольном треугольнике один из катетов равен 29, а острый угол, прилежащий к нему, равен . Найдите площадь треугольника.
4. Найдите тангенс угла С треугольника ABC , изображённого на рисунке.
5. Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
6. Сторона ромба равна 24, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Перечислите эти длины в ответе без пробелов в порядке неубывания.
7. В равнобедренном
треугольнике . Найдите AC, если высота
.
2 часть
8. В трапеции ABCD основание AD вдвое больше основания
9. В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKB.
10. Точки и лежат на стороне AC треугольника ABC на расстояниях соответственно 18 и 22 от вершины Найдите радиус окружности, проходящей через точки и и
касающейся луча AB, если
Ответы и решения
Рекомендации к проведению работы и оцениванию работы:
Время проведения: 60- 90 минут.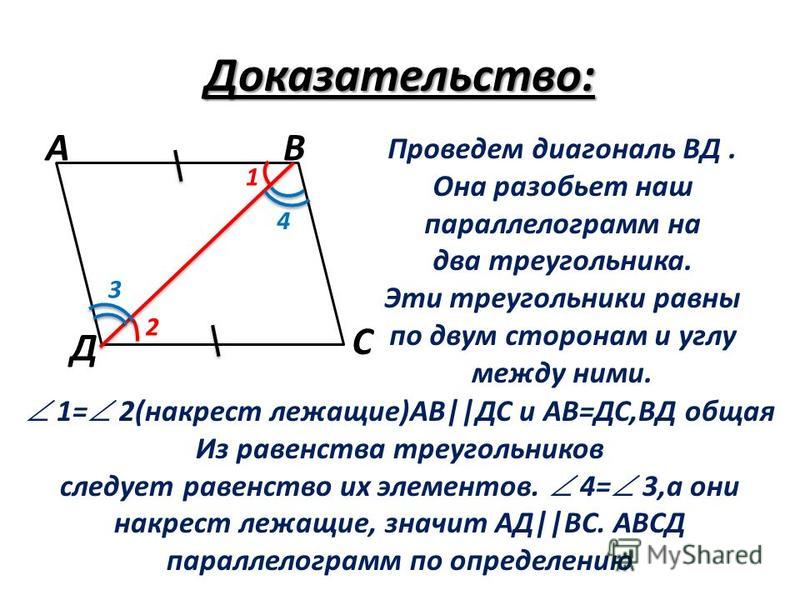
Задания 1- 7 первой части оцениваются в 1 балл, задания 8-10 второй части в 2 балла.
Решения 1- 7 заданий (1 часть) рекомендуется писать кратко или записывать только ответ. Решения заданий 8- 10 (2 часть) оформляем в развернутом виде со всеми обоснованиями, комментариями.
Максимальный балл- 13 баллов.
Оценивание:
«5»- 11-13
«4»- 8- 10
«3»- 3-7
«2»- 0- 2
Таблица ответов
№ задания | Вариант 1 | Вариант 2 |
1 | 5 | 5,5 |
2 | 86 | 114 |
3 | 612,5 | 420,5 |
4 | 3,5 | 0,75 |
5 | 2 | 13 |
6 | 1717 | 1212 |
7 | 13 | 12 |
Вариант 1
1. Введём обозначения, как показано на
рисунке. MN — средняя линия, поэтому, откуда по
теореме Фалеса Рассмотрим
Введём обозначения, как показано на
рисунке. MN — средняя линия, поэтому, откуда по
теореме Фалеса Рассмотрим
треугольник ABD MK — средняя линия, следовательно,
Ответ: 5.
2. Сумма углов треугольника равна 180°. Треугольник ABC — равнобедренный, следовательно, Угол
Ответ: 86.
3. Сумма углов в треугольнике равна
180°, поэтому второй острый угол равен 180° − 90° − 45° = 45°. Оба острых угла
равны, следовательно, данный треугольник — равнобедренный, откуда получаем, что
второй катет равен 35. Площадь прямоугольного треугольника можно найти как
половину произведения катетов:
Площадь прямоугольного треугольника можно найти как
половину произведения катетов:
Ответ: 612,5.
4. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Ответ: 3,5.
6. Введём обозначения, как показано на рисунке. Имеем:
Тогда
Ответ: 1717.
Примечание.
Высота делит сторону на два отрезка, и в ответе требуется указать длины обоих отрезков. Длина первого отрезка 17, и длина второго отрезка 17, поэтому ответ 1717.
7. В равнобедренном треугольнике высота, опущенная на основание делит основание пополам, то есть CH делит AB пополам. Тогда получаем прямоугольный треугольник
катетами и гипотенузой которого является искомая По теореме Пифагора найдем
Ответ: 13.
8. Пусть точка P — середина стороны Поскольку то
треугольник PCD — равнобедренный. Угол при вершине этого
треугольника равен 60°, следовательно, углы при основании равны значит,
треугольник PCD — равносторонний. Угол BCP равен Аналогично получаем,
что треугольник BCP — равносторонний. Найдём угол Аналогично
двум предыдущим треугольникам получаем, что треугольник ABP —
равносторонний. Получили, что площадь трапеции равна сумме площадей трёх равных
равносторонних треугольников:
Угол при вершине этого
треугольника равен 60°, следовательно, углы при основании равны значит,
треугольник PCD — равносторонний. Угол BCP равен Аналогично получаем,
что треугольник BCP — равносторонний. Найдём угол Аналогично
двум предыдущим треугольникам получаем, что треугольник ABP —
равносторонний. Получили, что площадь трапеции равна сумме площадей трёх равных
равносторонних треугольников:
Ответ:
Критерии проверки:
Критерии оценивания выполнения задания | Баллы |
Ход решения верный, все его шаги выполнены правильно, получен верный ответ | 2 |
Ход решения верный, чертёж соответствует условию задачи, но пропущены существенные объяснения или допущена вычислительная ошибка | 1 |
Другие случаи, не соответствующие указанным критериям | 0 |
Максимальный балл | 2 |
9. Проведём высоту MN так, чтобы она
проходила через точку Углы AOM и NOC равны
друг другу как вертикальные. Вспомним также, что диагонали делятся точкой
пересечения пополам, следовательно, Рассмотрим
треугольники AOM и NOC, они прямоугольные, имеют
равные углы и равные гипотенузы, следовательно, эти треугольники равны, а
значит равны отрезки MO и ON. Таким образом,
Проведём высоту MN так, чтобы она
проходила через точку Углы AOM и NOC равны
друг другу как вертикальные. Вспомним также, что диагонали делятся точкой
пересечения пополам, следовательно, Рассмотрим
треугольники AOM и NOC, они прямоугольные, имеют
равные углы и равные гипотенузы, следовательно, эти треугольники равны, а
значит равны отрезки MO и ON. Таким образом,
Площадь параллелограмм равна а площадь треугольника
Критерии проверки:
Критерии оценивания выполнения задания | Баллы |
Доказательство верное, все шаги обоснованы | 2 |
Доказательство в целом верное, но содержит неточности | 1 |
Другие случаи, не соответствующие указанным критериям | 0 |
Максимальный балл | 2 |
10.
Введём обозначения, как показано на рисунке. По теореме о касательной и
секущей:
Рассмотрим треугольник AEM, по теореме косинусов найдём сторону
Аналогично из треугольника AEN найдём сторону
В треугольнике AEN стороны AE и EN равны, следовательно, треугольник AEN — равнобедренный, откуда Из основного тригонометрического тождества найдём
Найдём искомый радиус окружности по теореме синусов:
Ответ: 13,5.
Критерии проверки:
Критерии оценивания выполнения задания | Баллы |
Ход решения верный, все его шаги выполнены правильно, получен верный ответ | 2 |
Ход решения верный, чертёж соответствует условию задачи, но пропущены существенные объяснения или допущена вычислительная ошибка | 1 |
Другие случаи, не соответствующие указанным критериям | 0 |
Максимальный балл | 2 |
Вариант 2
1. Введём обозначения, как показано на
рисунке. MN — средняя линия, AM = MB, откуда по
теореме Фалеса AK = KC. Рассмотрим треугольник ACD. KN —
средняя линия, следовательно,
Введём обозначения, как показано на
рисунке. MN — средняя линия, AM = MB, откуда по
теореме Фалеса AK = KC. Рассмотрим треугольник ACD. KN —
средняя линия, следовательно,
Ответ: 5,5.
2. Сумма углов треугольника равна 180°. Треугольник ABC — равнобедренный, следовательно, Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается. Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается. Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
Ответ: 114.
3. Сумма углов в треугольнике равна 180°, поэтому второй острый угол равен 180° − 90° − 45° = 45°. Оба острых угла равны, следовательно, данный треугольник — равнобедренный, откуда получаем, что второй катет равен 29. Площадь прямоугольного треугольника можно найти как половину произведения катетов: 420,5
Ответ: 420,5
4. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Ответ: 0,75.
6. Введём обозначения, как показано на рисунке. Треугольник ABH — прямоугольный, в нём угол A равен 60°. Тогда отрезок AH можно найти по формуле:
Найдём отрезок HD:
Оба отрезка имеют длину 12, в ответ необходимо записать длины обоих отрезков, следовательно, ответ 1212.
Ответ: 1212.
Примечание.
Высота делит сторону на два отрезка, и в ответе требуется указать длины обоих отрезков. Длина первого отрезка 12, и длина второго отрезка 12, поэтому ответ 1212.
7. По теореме Пифагора имеем:
Так как высота в равнобедренном треугольнике является медианой, то
Ответ: 12.
8. Опустим перпендикуляры BH и CK на
большее основания AD. По условию тогда Катет,
лежащий напротив в угла в равен половине
гипотенузы, тогда Так
как по условию, а HK=BC=CD, то Треугольники ABH и DCK равны
по двум катетам, следовательно, трапеция ABCD — равнобедренная.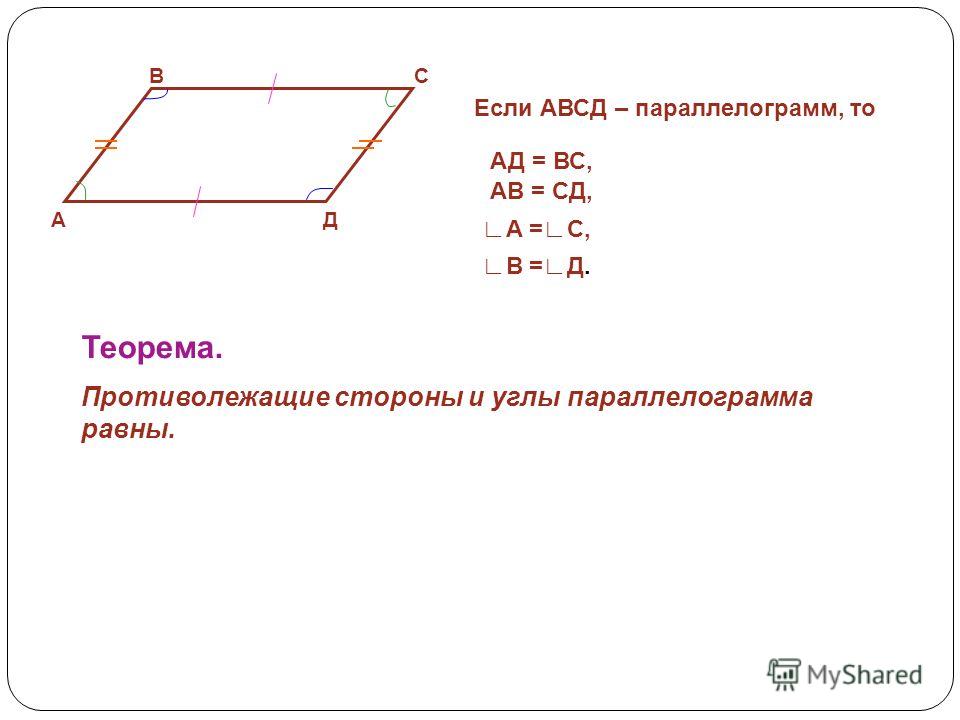 Таким образом, АВ=2, AD=4, BH=. Площадь трапеции равна
произведению полусуммы оснований на высоту, следовательно
Таким образом, АВ=2, AD=4, BH=. Площадь трапеции равна
произведению полусуммы оснований на высоту, следовательно
Ответ:
Критерии проверки:
Критерии оценивания выполнения задания | Баллы |
Ход решения верный, все его шаги выполнены правильно, получен верный ответ | 2 |
Ход решения верный, чертёж соответствует условию задачи, но пропущены существенные объяснения или допущена вычислительная ошибка | 1 |
Другие случаи, не соответствующие указанным критериям | 0 |
Максимальный балл | 2 |
9. Проведём высоту MN так, чтобы она
проходила через точку Углы AKM и NKC равны
друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения
пополам, следовательно, Рассмотрим треугольники AMK и KCN,
они прямоугольные, имеют равные углы и равные гипотенузы, следовательно, эти
треугольники равны, а значит равны отрезки MK и KN.
Таким образом,
Проведём высоту MN так, чтобы она
проходила через точку Углы AKM и NKC равны
друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения
пополам, следовательно, Рассмотрим треугольники AMK и KCN,
они прямоугольные, имеют равные углы и равные гипотенузы, следовательно, эти
треугольники равны, а значит равны отрезки MK и KN.
Таким образом,
Площадь параллелограмм равна а площадь треугольника
Критерии проверки:
Критерии оценивания выполнения задания | Баллы |
Доказательство верное, все шаги обоснованы | 2 |
Доказательство в целом верное, но содержит неточности | 1 |
Другие случаи, не соответствующие указанным критериям | 0 |
Максимальный балл | 2 |
10. Пусть K — точка касания окружности с
лучом AB (см. рис.). По теореме 2 о касательной и
секущей AK2 = AM · AN = 18 · 22 = 396.
Пусть K — точка касания окружности с
лучом AB (см. рис.). По теореме 2 о касательной и
секущей AK2 = AM · AN = 18 · 22 = 396.
По теореме косинусов
Значит, KM = 18. Треугольник AKM равнобедренный, поэтому
∠AKM = ∠KAM = ∠BAC.
По теореме об угле между касательной и хордой ∠KNM = ∠AKM = ∠BAC. Пусть R — радиус окружности, проходящей через точки M, N и K. По теореме синусов
Ответ: 10,8.
Критерии проверки:
Критерии оценивания выполнения задания | Баллы |
Ход решения задачи верный, получен верный ответ. | 2 |
Ход решения правильный, все его шаги присутствуют, но допущена
ошибка или описка вычислительного характера. | 1 |
Другие случаи, не соответствующие указанным критериям. | 0 |
Максимальный балл | 2 |
Анализ районной контрольной работы по математике (модуль геометрия)
Дата проведения:
Количество учащихся по списку:
Выполняли работу:
Успешность:
Качество:
Получили: «5»- . «4»- , «3»- , «2»- .
Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Проверяемая тема | Средняя линия трапеции, треугольника | Вписанные и
центральные углы. | Площадь прямоугольного треугольника | Нахождение тангенса острого угла | Выбор утверждений. | Ромб | Равнобедренный треугольник. Теорема Пифагора | Задача на нахождение площади трапеции | Задача на доказательство | Задача на вычисление |
Допустили ошибки |
|
|
|
|
|
|
|
|
|
|
Не приступали |
|
|
|
|
|
|
|
|
|
|
Учитель:
в параллелограмме ABCD сторона AB равна 7 корней из 2, а угол A равен 45.
 Найдите высоту BH — Знания.site
Найдите высоту BH — Знания.siteПоследние вопросы
Геометрия
7 минут назад
Якщо кулю вписано в циліндр, висота якого дорівнює 6 см, то площа поверхні кулі дорівнює А Б В Г Д 18 см² 32 см² 36 см² 64 см² Інша відповідьГеометрия
12 минут назад
Завдання на фото)))))))))Геометрия
17 минут назад
знайти гіпотенузу прямокутного трикутника якщо його катет дорівнює корень7 см і 3 смГеометрия
22 минут назад
Найдите четвёртый член геометрической прогрессии, у которой первый член равен 1/3 , а знаменатель равен 3.
Геометрия
33 минут назад
В треугольнике ABC угол C прямой, AC=9,
cosA=0,3. Найдите AB.
Геометрия
39 минут назад
В треугольнике ABC угол С равен 90 М-Середина стороны АВ.АВ=34 ВС=12 Найдите СМ
Геометрия
47 минут назад
контрольна робота пжж срочноГеометрия
1 час назад
Ширина будинку 7 м, довжина крокви 4,5 м. Під яким кутом крокви нахилені до стелі ? Дано: АС=7 м, АВ=ВС=4,5 м. Знайти кут А.
Знайти кут А.Геометрия
1 час назад
СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!!!
Геометрия
1 час назад
срочно геометрія пзззГеометрия
1 час назад
Решите пожалуйста задачу, правильно и с рисунком. Даю 100 баллов Основою похилої призми є правильний трикутник зі стороною 2 см. Бічне ребро призми дорівнює 5 см і утворює з двома сусідніми сторонами основи кути по 60°. Знайдіть об’єм призми.Геометрия
1 час назад
Помогите пожалуйста срочно спасибо заранее. Даю 100 баллов.
1. Знайдіть координати центра сфери, заданої рівням Baplanm 1.(x-1) + (y + 1) + (2-1) = 1.
2. Знайдіть радіус сфери, заданої рівнянням Bapianm 1.(x-1)+(y+1)+(2-1)-8.
3. Складіть рівняння сфери, радіус якої дорівнює 1, а й центр знахо диться в точці
Baplanm 1. A(-1; 0; 0).
4. Установіть відповідність між рівнянням сфери (1-3) і точкою (А-Г),
що лежить даній сфері.
Baplanm 1 1. (x-1)+g+2=1
A. (1; 1; 1)
2. x + (y -1) + d=1
B. (0; 0:-2)
3. x + y + (2+1) = 1
B. (0; 2; 0)
T. (2; 0; 0)
5. Складіть рівняния сфери в діаметром 48, якщо Baplewm 1. Ad:-23). 8 (8-21)
6. Эрдинати центра й радіус кола, по якому перетина сферу
(-1)+(-1)(z — 1) = 25 площина
Boplasm 1. y=-3
7. Що жилие собою геометричне місце точок простору, координати
задовольняють рівнянню
Baplanm 1. x + y +2 -2x+4y-62 — 2?
Даю 100 баллов.
1. Знайдіть координати центра сфери, заданої рівням Baplanm 1.(x-1) + (y + 1) + (2-1) = 1.
2. Знайдіть радіус сфери, заданої рівнянням Bapianm 1.(x-1)+(y+1)+(2-1)-8.
3. Складіть рівняння сфери, радіус якої дорівнює 1, а й центр знахо диться в точці
Baplanm 1. A(-1; 0; 0).
4. Установіть відповідність між рівнянням сфери (1-3) і точкою (А-Г),
що лежить даній сфері.
Baplanm 1 1. (x-1)+g+2=1
A. (1; 1; 1)
2. x + (y -1) + d=1
B. (0; 0:-2)
3. x + y + (2+1) = 1
B. (0; 2; 0)
T. (2; 0; 0)
5. Складіть рівняния сфери в діаметром 48, якщо Baplewm 1. Ad:-23). 8 (8-21)
6. Эрдинати центра й радіус кола, по якому перетина сферу
(-1)+(-1)(z — 1) = 25 площина
Boplasm 1. y=-3
7. Що жилие собою геометричне місце точок простору, координати
задовольняють рівнянню
Baplanm 1. x + y +2 -2x+4y-62 — 2?Геометрия
1 час назад
Помогите с кр по матешеГеометрия
1 час назад
срочно геометрия пжжжжГеометрия
1 час назад
2. Треугольники ABC и A B C1 подобны, причëм сторонам AB и ВС соответствуют сторонам А1В1 и B1C1. ВС=28 см, A1B1=5 см B1C1=7 см, A1C1=11 см. Найдите неизвестные стороны этих треугольников. 5
Треугольники ABC и A B C1 подобны, причëм сторонам AB и ВС соответствуют сторонам А1В1 и B1C1. ВС=28 см, A1B1=5 см B1C1=7 см, A1C1=11 см. Найдите неизвестные стороны этих треугольников. 5
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
How much to ban the user?
1 hour 1 day 100 years
Площадь параллелограммов: определение и формула
Задумывались ли вы, какую форму представляет воздушный змей? Воздушный змей обычно имеет четыре стороны, что делает его типом четырехугольника.
Теперь обратите внимание, как верхняя левая и нижняя правая стороны воздушного змея, показанного ниже, параллельны друг другу. Точно так же верхняя правая и нижняя левая стороны этого воздушного змея параллельны друг другу.
Есть предположения, что это за четырехугольник? Правильно! Это параллелограмм.
Допустим, вам сказали найти площадь этого воздушного змея. Поскольку это тип параллелограмма, мы могли бы использовать определенную формулу для вычисления площади этого воздушного змея.
Иллюстрация воздушного змея, StudySmarter Originals
В этой статье мы познакомимся с формулой площади параллелограмма и рассмотрим некоторые рабочие примеры, где она применяется.
Резюме параллелограммов
Прежде чем мы перейдем к нашему основному предмету, давайте проведем краткий обзор параллелограммов, чтобы облегчить себе задачу.
Как следует из названия, параллелограмм имеет параллельные стороны. Таким образом, мы можем определить параллелограмм, как показано ниже.
Параллелограмм представляет собой четырехугольник с двумя парами параллельных противоположных сторон. Параллелограмм является частным случаем четырехугольника.
Четырехсторонняя плоская фигура известна как четырехугольник.
На следующем рисунке показан параллелограмм со сторонами AB, BD, CD и AC.
Иллюстрация параллелограмма, StudySmarter Originals
Свойства параллелограммов
Вернемся к нашему параллелограмму ABCD выше. Давайте посмотрим на некоторые свойства, которые отличают эту форму.
Противоположные стороны треугольника ABCD параллельны. В этом случае АВ параллельна CD, а АС параллельна BD. Запишем это как AB // CD и AC // BD,
Противоположные углы ABCD равны. Здесь ∠CAB = ∠CDB и ∠ACD = ∠ABD,
Диагонали параллелограмма делят друг друга пополам в точке, скажем, M. Тогда AM = MD и BM = MC. This is shown below,
Property of a parallelogram , StudySmarter Originals
Types of parallelograms
There are three types of parallelograms we must consider throughout this syllabus, namely
Rectangle
Square
Ромб
Каждый из этих параллелограммов имеет свои особенности, которые отличают их друг от друга. Более подробное объяснение параллелограммов можно найти здесь, Параллелограммы.
Более подробное объяснение параллелограммов можно найти здесь, Параллелограммы.
Определение области параллелограмма
Площадь параллелограмма определяется как область, ограниченная параллелограммом в двумерном пространстве.
На приведенной выше диаграмме общая площадь, заключенная в ABCD, является площадью параллелограмма ABCD.
Площадь параллелограмма Формула
Ссылаясь на наш исходный параллелограмм ABCD, мы добавим к этой фигуре две новые компоненты, называемые b и h. Это показано на диаграмме ниже.
Параллелограмм с основанием b и высотой h, Study Smarter Originals
Переменная b называется основанием параллелограмма. В качестве основания можно использовать любую из длинных сторон ABCD. На приведенной выше диаграмме b может быть либо AB, либо CD. Здесь, здесь мы взяли b = AB.
Обратите внимание, что это понятие является соглашением, а не жестким правилом.
Переменная h называется высотой параллелограмма. Это также можно назвать высотой. Высота — это отрезок, перпендикулярный паре смежных сторон параллелограмма с одной конечной точкой на одной стороне и другой конечной точкой на другой стороне.
Это также можно назвать высотой. Высота — это отрезок, перпендикулярный паре смежных сторон параллелограмма с одной конечной точкой на одной стороне и другой конечной точкой на другой стороне.
Теперь, когда мы определили наши переменные b и h, мы можем представить площадь параллелограмма следующим образом.
Площадь любого параллелограмма определяется по формуле
A=b×h
, где b = основание и h = высота.
Примеры площади параллелограмма
Имея это в виду, давайте теперь рассмотрим следующие рабочие примеры, в которых используется эта формула.
Найдите площадь следующего параллелограмма:
Пример 1, StudySmarter Originals
Решение
Здесь основание b = 24 единицы, а высота h = 10 единиц. Используя формулу площади параллелограмма, мы получаем,
A=b×h=24×10=240единиц2
Таким образом, площадь этого параллелограмма составляет 240 единиц 2 .
Параллелограмм высотой 5 единиц длины имеет площадь 20 единиц 2 . Какова длина основания?
Решение
Здесь нам даны площадь параллелограмма и высота (или высота), то есть
A = 20 и h = 5.
Чтобы найти основание, нужно просто подставить эти значения в нашу область формулы параллелограмма и перестройте уравнение, как показано ниже.
A=b×h30=b×55b=20
Делая b предметом, получаем
b=205=4единицы
Таким образом, основание этого параллелограмма равно 4 единицам.
Нахождение площади параллелограмма из прямоугольника
Предположим, мы хотим найти площадь параллелограмма, высота (или высота) которого неизвестна. Вместо этого нам даны длины двух сторон параллелограмма, а именно длины АВ и АС.
Давайте попробуем рассмотреть этот сценарий графически. Возвращаясь к нашему исходному параллелограмму ABCD, давайте проведем две высоты для каждой пары смежных сторон, AC и AB, а также CD и BD.
Площадь параллелограмма из прямоугольника, StudySmarter Originals
Таким образом, мы получаем две новые точки на этом параллелограмме, а именно S и T. Теперь посмотрим на форму, образованную BTCS. Вам это кажется знакомым? Это верно! Это прямоугольник, который также является разновидностью параллелограмма. Теперь нам нужно найти способ получить длины либо CS, либо BT, чтобы мы могли вывести высоту этого параллелограмма.
Обратите внимание, что из построения этих двух отрезков мы получили пару прямоугольных треугольников, CAS и BDT. Поскольку CS = BT, нам достаточно вычислить только один из них. Рассмотрим треугольник CAS.
Треугольник CAS, StudySmarter Originals
Для простоты мы будем обозначать следующие стороны как: x = AS, y = CS и z = AC. Поскольку это прямоугольный треугольник, мы можем использовать теорему Пифагора, чтобы получить длину CS, которая является высотой параллелограмма ABCD. Учитывая длины AS и AC, имеем
x 2 + y 2 = z 2
Преобразовав это и применив квадратный корень, мы получим
y=z2-x2
Теперь мы можем найти длину CS, по нахождению площади параллелограмма ABCD по приведенной формуле. За основание возьмем длину АВ. Таким образом, площадь ABCD равна
За основание возьмем длину АВ. Таким образом, площадь ABCD равна
AreaABCD=AB×CS
Покажем это на примере.
Дан параллелограмм PQRS, найдите его площадь.
Пример 2, StudySmarter Originals
Линия OQ представляет собой высоту смежных сторон PQ и PS. Длины QR, PQ и PO равны 12 единицам, 13 единицам и 5 единицам соответственно.
Решение
Так как QR = PS, мы можем принять основание как QR = 12 единиц. Теперь нам нужно найти высоту этого параллелограмма, чтобы найти его площадь. Это дается отрезком OQ.
Из диаграммы видно, что треугольник QPO является прямоугольным. Поскольку у нас есть длина PO = 5 единиц, мы можем использовать теорему Пифагора, чтобы найти OQ.
PO2+OQ2=PQ252+OQ2=132
Переставляя это и применяя квадратный корень, мы получаем следующее значение для OQ:
OQ2=132-52OQ=132-52=169-25=144=12 единиц Таким образом, высота этого параллелограмма равна 12 единицам. Теперь мы можем найти площадь PQRS, как показано ниже,
ПлощадьPQRS=QR×OQ=12×12=144единиц2
Следовательно, площадь этого параллелограмма составляет 144 единицы 2 .
Пример параллелограмма, вписанного в прямоугольник
В этом примере мы рассмотрим случай, когда параллелограмм вписан в прямоугольник. Мы хотим определить площадь внутри прямоугольника, не занятую параллелограммом.
На рисунке ниже показан параллелограмм PXRY внутри прямоугольника PQRS. Найдите площадь области, заштрихованной синим цветом.
Пример 3. Исследование Smarter Originals
Отрезок линии XZ представляет собой высоту смежных сторон XP и PY. Здесь QP = RS = XZ, PX = RY и QR = PS. Длины QP, PY и SY равны 19 единицам, 21 единице и 7 единицам соответственно.
Решение
Здесь высота прямоугольника PQRS равна h = QP = 19 единиц. Основание равно PS, равному сумме длин PY и SY. Таким образом, основание равно
PS=PY+YS=21+7=28единиц
Таким образом, b = 28 единиц. Формула площади прямоугольника представляет собой произведение его основания и высоты. Таким образом, площадь прямоугольника PQRS равна
APQRS=b×h=PS×QP=28×19=532единиц2
Теперь найдем площадь параллелограмма PXRY. Высота параллелограмма равна XZ. Так как XZ = QP, то h = XZ = 19 единиц. База задается длиной PY. Таким образом, b = PY = 21 единица. Используя формулу площади параллелограмма, получаем
Высота параллелограмма равна XZ. Так как XZ = QP, то h = XZ = 19 единиц. База задается длиной PY. Таким образом, b = PY = 21 единица. Используя формулу площади параллелограмма, получаем
APXRY=b×h=PY×XZ=21×19=399единиц2
Таким образом, площади прямоугольника PQRS и параллелограмма PXRY составляют 532 единицы 2 и 399 единиц 2 соответственно.
Теперь нам нужно найти область, заштрихованную синим цветом, которая не занята параллелограммом внутри прямоугольника. Это можно найти, вычислив разницу между площадями прямоугольника PQRS и параллелограмма PXRY. При этом получаем
Ablueregion=APQRS-APXRY=532-399=133units2
Следовательно, площадь оставшейся области, заштрихованной синим цветом, составляет 133 единицы 2 .
Особый случай: площадь ромба
Ромб — это особый тип четырехугольника, у которого фактически есть собственная формула для вычисления его площади. Иногда его называют равносторонним четырехугольником. Напомним определение ромба.
Напомним определение ромба.
Ромб представляет собой параллелограмм, все четыре стороны которого имеют одинаковую длину.
Теперь рассмотрим ромб ниже. На этом параллелограмме построены две диагонали AD (голубая линия) и BC (синяя линия). Диагонали имеют длину d 1 и д 2 соответственно.
Площадь Rombus, StudySmarteroriGinals
Площадь Rombus
Площадь ромба дается формулой,
A = 12D1D2
, где A = область, D 5 1 = длина. диагональ AD и d 2 = длина диагонали BC.
Пример площади ромба
Вот пример, включающий площадь формулы ромба.
Диагонали ромба имеют длины 10 единиц и 15 единиц. Чему равна площадь ромба?
Раствор
Обозначим d 1 = 10 единиц и d 2 = 15 единиц. Применяя формулу выше, получаем
A=12d1d2=12×10×15=75единиц2
Таким образом, площадь этого ромба составляет 75 единиц 2 .
- Формула площади ромба также может быть использована для нахождения площади воздушного змея.
Мы закончим эту статью последним примером, касающимся площади параллелограмма или, точнее, воздушного змея.
Реальный пример площади параллелограмма
Теперь мы вернемся к нашему примеру в начале этой статьи. Поскольку теперь у нас есть базовая формула для вычисления площади параллелограмма, мы можем использовать ее, чтобы найти площадь нашего воздушного змея.
Вы решаете измерить длину двух диагоналей вашего воздушного змея рулеткой. Вы обнаружите, что горизонтальная диагональ и вертикальная диагональ равны 18 дюймам и 31 дюйму соответственно. Используя формулу площади ромба, найдите площадь этого воздушного змея.
Пример 4, исследование Smarter Originals
Решение
Let
d 1 = диагональ по горизонтали = 18 дюймов
d 2 = вертикальная диагональ = 31 дюйм
Применяя формулу для площади ромба, получаем
A=12d1d2=12×18×31=558 дюймов2 дюймов 2 .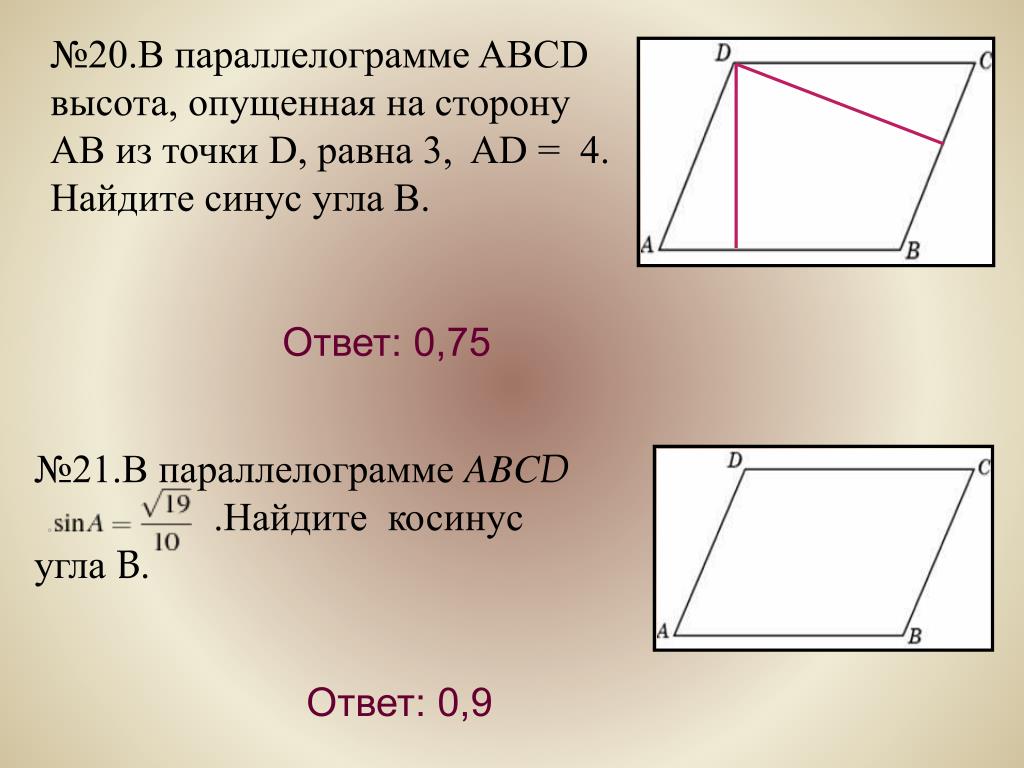
Площадь параллелограммов. Ключевые выводы
- Четырехугольник с двумя парами параллельных противоположных сторон называется параллелограммом.
- Параллелограммы бывают трех видов: прямоугольник, квадрат и ромб.
- Основные свойства параллелограмма:
Противоположные стороны параллельны
Противоположные углы равны
Диагонали делятся пополам как точка
7
Площадь ромба находится по формуле: A=12d1d2, где d 1 и d 2 — длины диагоналей ромба.
Постройте ромб, одна сторона которого равна 5 см, а один угол равен 45…
Перейти к
- Построение четырехугольников. Упражнение 14.1.
- Построение четырехугольников.
 Упражнение 14.2.
Упражнение 14.2.
- Рациональное число
- Показатели и силы
- Квадраты и квадратные корни
- Кубы и кубические корни
- Игра с числами
- Операции над множествами Диаграммы Венна
- Процент
- Простой и сложный процент
- Прямая и обратная вариация
- Алгебраические выражения и тождества
- Факторизация
- Линейные уравнения и неравенства с одной переменной
- Понимание четырехугольников
- Построения четырехугольников
- Круг
- Отражение и вращение симметрии
- Визуализация твердых фигур
- Измерение
- Обработка данных
Главная >
ML Aggarwal Solutions
Класс 8
Математика
>
Глава 14. Построение четырехугольников.
>
Построение четырехугольников. Упражнение 14.2.
>
Вопрос 8
Построение четырехугольников.
>
Построение четырехугольников. Упражнение 14.2.
>
Вопрос 8
Вопрос 8 Построение четырехугольников Упражнение 14.2
Постройте ромб, одна сторона которого равна 5 см, а один угол равен 45.
Ответ:
Этапы построения:
(i) Построить AB = 5 см.
(ii) В точке A начертите ∠BAP = 45.
(iii) Отрежьте AD = 5 см от AP.
(iv) Приняв B за центр и радиус 5 см, постройте дугу.
(v) Приняв D за центр и радиус 5 см, постройте дугу, которая пересекает предыдущую дугу в точке C.
(vi) Теперь соедините BC и CD.
Следовательно, ABCD искомый ромб.
Связанные вопросы
**Постройте параллелограмм ABCD так, чтобы AB = 4,8 см, BC = 4 см и диагональ BD = 5,4 см. **
**
**Постройте параллелограмм ABCD так, чтобы BC = 4,5 см, BD = 4 см и AC = 5,6 см.**
**Постройте параллелограмм ABCD так, что AC = 6 см, BD = 4,6 см и угол между ними равен 45 **
**Постройте прямоугольник, смежные стороны которого равны 5,6 см и 4 см.**
**Постройте прямоугольник так, чтобы одна сторона была 5 см, а одна диагональ 6,8 см**
**Постройте прямоугольник ABCD так, чтобы AB = 4 см и ∠BAC = 60 градусов**
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Конструкции четырехсторонних упражнений.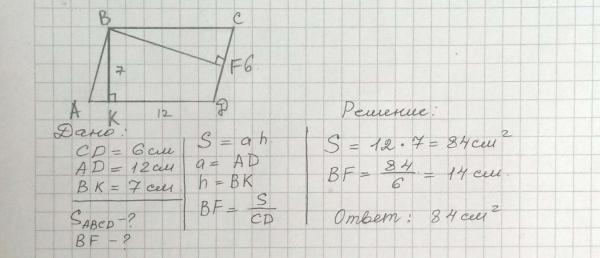




 Знайти кут А.
Знайти кут А.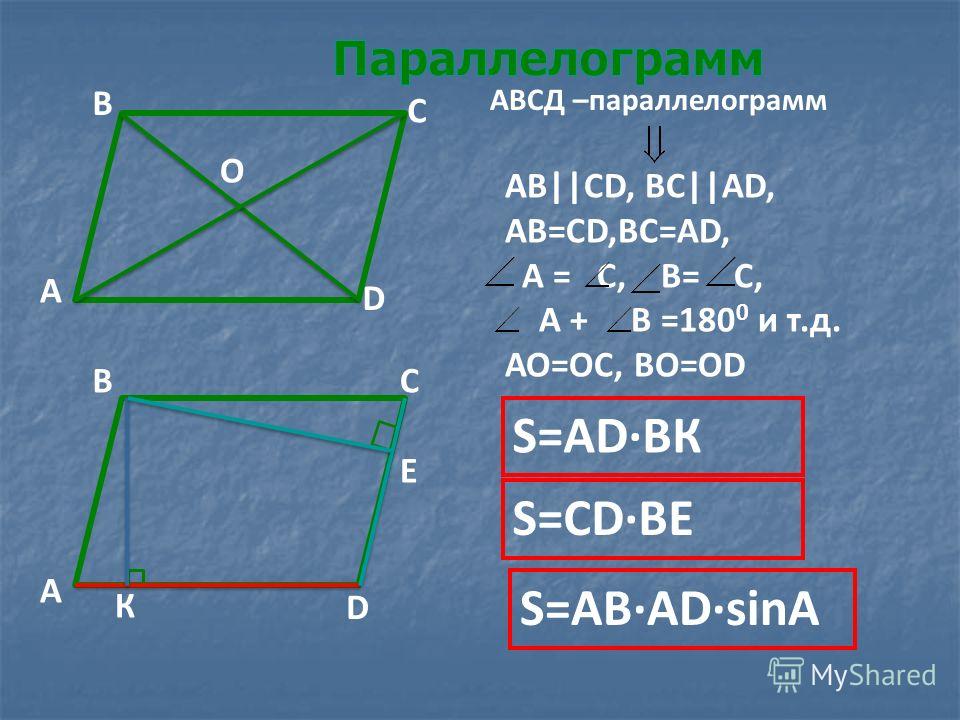 Даю 100 баллов.
1. Знайдіть координати центра сфери, заданої рівням Baplanm 1.(x-1) + (y + 1) + (2-1) = 1.
2. Знайдіть радіус сфери, заданої рівнянням Bapianm 1.(x-1)+(y+1)+(2-1)-8.
3. Складіть рівняння сфери, радіус якої дорівнює 1, а й центр знахо диться в точці
Baplanm 1. A(-1; 0; 0).
4. Установіть відповідність між рівнянням сфери (1-3) і точкою (А-Г),
що лежить даній сфері.
Baplanm 1 1. (x-1)+g+2=1
A. (1; 1; 1)
2. x + (y -1) + d=1
B. (0; 0:-2)
3. x + y + (2+1) = 1
B. (0; 2; 0)
T. (2; 0; 0)
5. Складіть рівняния сфери в діаметром 48, якщо Baplewm 1. Ad:-23). 8 (8-21)
6. Эрдинати центра й радіус кола, по якому перетина сферу
(-1)+(-1)(z — 1) = 25 площина
Boplasm 1. y=-3
7. Що жилие собою геометричне місце точок простору, координати
задовольняють рівнянню
Baplanm 1. x + y +2 -2x+4y-62 — 2?
Даю 100 баллов.
1. Знайдіть координати центра сфери, заданої рівням Baplanm 1.(x-1) + (y + 1) + (2-1) = 1.
2. Знайдіть радіус сфери, заданої рівнянням Bapianm 1.(x-1)+(y+1)+(2-1)-8.
3. Складіть рівняння сфери, радіус якої дорівнює 1, а й центр знахо диться в точці
Baplanm 1. A(-1; 0; 0).
4. Установіть відповідність між рівнянням сфери (1-3) і точкою (А-Г),
що лежить даній сфері.
Baplanm 1 1. (x-1)+g+2=1
A. (1; 1; 1)
2. x + (y -1) + d=1
B. (0; 0:-2)
3. x + y + (2+1) = 1
B. (0; 2; 0)
T. (2; 0; 0)
5. Складіть рівняния сфери в діаметром 48, якщо Baplewm 1. Ad:-23). 8 (8-21)
6. Эрдинати центра й радіус кола, по якому перетина сферу
(-1)+(-1)(z — 1) = 25 площина
Boplasm 1. y=-3
7. Що жилие собою геометричне місце точок простору, координати
задовольняють рівнянню
Baplanm 1. x + y +2 -2x+4y-62 — 2? Треугольники ABC и A B C1 подобны, причëм сторонам AB и ВС соответствуют сторонам А1В1 и B1C1. ВС=28 см, A1B1=5 см B1C1=7 см, A1C1=11 см. Найдите неизвестные стороны этих треугольников. 5
Треугольники ABC и A B C1 подобны, причëм сторонам AB и ВС соответствуют сторонам А1В1 и B1C1. ВС=28 см, A1B1=5 см B1C1=7 см, A1C1=11 см. Найдите неизвестные стороны этих треугольников. 5 Упражнение 14.2.
Упражнение 14.2.
Leave A Comment