Контрольные работы по геометрии 9кл Атанасян
Контрольная работа №1. Векторы. | Контрольная работа №1. Векторы. |
Вариант 1. | Вариант 2. |
1. ABCD – параллелограмм, Найдите разложение вектора по неколлинеарным векторам . 2. Дана трапеция ABCD с основаниями AD=20 и BC=8, О —точка пересечения диагоналей. Разложите вектор по векторам = и . 3. Диагонали ромба АС = а, BD = b.Точка K BD и BK : KD = 1 : 3. Найдите величину | |. 4. В равнобедренной трапеции острый угол равен 60 , боковая сторона равна 12 см, большее основание равно 30 см. Найдите среднюю линию трапеции. 5. В прямоугольнике ABCDизвестно, что AD=a, DC=b, O точка пересечения диагоналей. Найдите величину | 1. ABCD – параллелограмм, Найдите разложение вектора по неколлинеарным векторам . 2. Дана трапеция ABCD с основаниями AD=15 и BC=10, О —точка пересечения диагоналей. Разложите вектор по векторам = и . 3. Диагонали ромба АС = а, BD = b.Точка K AC и AK : KC = 2: 3. Найдите величину | |. 4. В равнобедренной трапеции острый угол равен 60 , боковая сторона равна 10 см, меньшее основание равно 14 см. Найдите среднюю линию трапеции. 5. В прямоугольнике ABCDизвестно, что AB=a, BC=b, O точка пересечения диагоналей. Найдите величину . |
Контрольная работа №2. Метод координат.
Метод координат.
Вариант 1
1. Установите связь между векторами
2. Векторы разложены по неколлинеарным векторам и . Разложите векторы по векторам .
3. Четырехугольник имеет вершины с координатами А (1;1), В (3;5), С(9;-1), D(7;-5). Определите вид четырехугольника (с обоснованием) и найдите его диагонали.
4. Напишите уравнение окружности с центром в точке С (-3;1), проходящей через точку А (2;3).
5. Прямая l проходит через точки А (-3;1) и В (1;-7). Напишите уравнение прямой m, проходящей через точку С(5;6) и перпендикулярной прямой l.
1. Установите связь между векторами
Вариант2
1 см у 1-го
2. Векторы разложены по неколлинеарным векторам и . Разложите векторы по векторам .
3. Четырехугольник имеет вершины с координатами А (-6;1), В (2;5), С(4;-1), D(-4;-5). Определите вид четырехугольника (с обоснованием) и найдите его диагонали.
Определите вид четырехугольника (с обоснованием) и найдите его диагонали.
4. Напишите уравнение окружности с центром в точке С (2;-3), проходящей через точку А (-1;-2).
5. Прямая l проходит через точки А (2;-1) и В (-3;9). Напишите уравнение прямой m, проходящей через точку С(3;10) и перпендикулярной прямойl.
Контрольная работа №3.Соотношение между сторонами и углами треугольника. Скалярное произведение вектор
.
Вариант1
1. Упростите выражение
2. В треугольнике АВС . Найдите площадь треугольника и радиус окружности, описанной около него.
3. В параллелограмме ABCD даны стороны АВ=4 см, AD=5 см и угол Найдите диагонали параллелограмма и его площадь.
4. Найдите координаты вектора , если а угол между вектором и положительным направлением оси абсцисс острый.
5. Вычислите скалярное произведение векторов , если
1. Упростите выражение
2. В треугольнике АВС . Найдите площадь треугольника и радиус окружности, описанной около него.
3. В параллелограмме ABCD даны стороны АВ=8 см, AD=3 см и угол Найдите диагонали параллелограмма и его площадь.
4. Найдите координаты вектора , если а угол между вектором и положительным направлением оси абсцисс тупой.
5. Вычислите скалярное произведение векторов , если
Контрольная работа №4. Длина окружности и площадь круга
Вариант 1.
Вариант 2.
1. Три последовательные стороны четырехугольника, описанного около окружности, относятся как 3:4:5. Периметр этого четырехугольника равен 48 см. Найдите длины его сторон.
2. Около правильного шестиугольника описана окружность и в него вписана окружность. Длина большей окружности равна 4π. Найдите площадь кольца и площадь шестиугольника.
Найдите площадь кольца и площадь шестиугольника.
3. Хорда окружности равна и стягивает дугу в 90 . Найдите длину дуги и площадь соответствующего сектора.
4. Найдите радиус сектора, если площадь соответствующего сегмента равна
.
5. В треугольник вписана окружность радиуса 3 см. Найдите длины сторон треугольника, если одна из них разделена точкой касания на отрезки длиной 4 см и 3 см.
1. Три последовательные стороны четырехугольника, описанного около окружности, относятся как 4:5:6. Периметр этого четырехугольника равен 80 см. Найдите длины его сторон.
2. Около правильного треугольника описана окружность и в него вписана окружность. Длина меньшей окружности равна 8π. Найдите площадь кольца и площадь треугольника.
3. Хорда окружности равна 6 и стягивает дугу в 60 . Найдите длину дуги и площадь соответствующего сектора.
4. Найдите радиус сектора, если площадь соответствующего сегмента равна
.
5. В треугольник вписана окружность радиуса 4 см. Найдите длины сторон треугольника, если одна из них разделена точкой касания на отрезки длиной 4 см и 5 см.
Контрольная работа №5. Движения.
Вариант 1.
Вариант 2.
1. Точка А (-2;3) симметрична точке А1 (6;-9) относительно точки В. Найдите координаты точки В.
2. Дан треугольник АВС с вершинами А(2;1), В(-6;1), С(-1;5). Треугольник А1В1С1 симметричен треугольнику АВС относительно прямой, заданной уравнением х=1. Найдите координаты вершин А1, В1,С1.
3. Найдите вектор параллельного переноса, при котором прямаяу=3х-2 переходит в прямую у=3х+4, а прямая 3х+2у=2 переходит в прямую 6х+4у=3.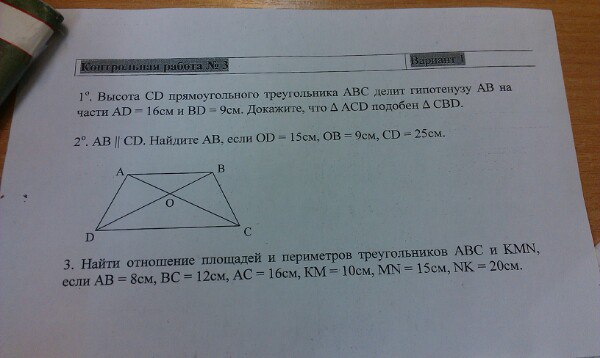
4. В результате поворота вокруг точки В(1;2) на 60 против часовой стрелки точка А(4;2) перешла в точку А1. Найдите координаты этой точки.
5. Прямая m задана уравнением 3х+2у-5=0. Прямая n симметрична прямой m относительно точки В(2;3). Напишите уравнение прямой n.
1. Точка А (-3;1) симметрична точке А1 (9;-5) относительно точки В. Найдите координаты точки В.
2. Дан треугольник АВС с вершинами А(-4;5), В(1;5), С(-3;-1). Треугольник А1В1С1 симметричен треугольнику АВС относительно прямой, заданной уравнением у=1. Найдите координаты вершин А1, В1,С1.
3. Найдите вектор параллельного переноса, при котором прямаяу=2х-1 переходит в прямую у=2х+3, а прямая 2х+3у=1 переходит в прямую 4х+6у=5.
4. В результате поворота вокруг точки В(2;1) на 30 против часовой стрелки точка А(6;1) перешла в точку А1. Найдите координаты этой точки.
5. Прямая m задана уравнением 2х+3у-7=0. Прямая n симметрична прямой m относительно точки В(3;2). Напишите уравнение прямой n.
Контрольная работа №6.
Итоговая по программе 9 класса.
Вариант 1.
Вариант 2.
1. В параллелограмме ABCD точка E, AE:EC=1:5. Разложите вектор по векторам
2. Найдите косинус угла между векторами , если и угол между векторами равен 30 .
3. Около круга радиусом R описан правильный шестиугольник. Найдите разность между площадью шестиугольника и круга.
4. Напишите уравнение окружности, симметричной относительно точкиА (-1;3) окружности, заданной уравнением х2+у2-4х+6у=0
5. Первая окружность радиуса 4 см касается трех сторон прямоугольника. Вторая окружность касается первой внешним образом, а также касается сторон прямого угла. Найдите максимальный радиус второй окружности, если стороны прямоугольника равны 8 см и 12 см.
Первая окружность радиуса 4 см касается трех сторон прямоугольника. Вторая окружность касается первой внешним образом, а также касается сторон прямого угла. Найдите максимальный радиус второй окружности, если стороны прямоугольника равны 8 см и 12 см.
1. В параллелограмме ABCD точка E, BE:ED=1:4. Разложите вектор по векторам
2. Найдите косинус угла между векторами , если и угол между векторами равен 30 .
3. Около круга радиусом R описан правильный треугольник. Найдите разность между площадью треугольника и круга.
4. Напишите уравнение окружности, симметричной относительно точкиА (-2;3) окружности, заданной уравнением х2+у2+6х-4у=0
5. Первая окружность радиуса 9 см касается трех сторон прямоугольника. Вторая окружность касается первой внешним образом, а также касается сторон прямого угла. Найдите максимальный радиус второй окружности, если стороны прямоугольника равны 18 см и 20 см.
Контрольная работа № 7. Итоговая по курсу геометрии (7-9 классы)
Контрольная работа № 7. Итоговая по курсу геометрии (7-9 классы)
Вариант 1.
Вариант 2.
1. В равнобедренный треугольник с основанием 10 см и боковой стороной 5 см вписан квадрат так, что две его вершины лежат на основании, а другие две вершины – на боковых сторонах. Найдите сторону квадрата.
2. Найдите площадь круга, вписанного в ромб с диагоналями, равными 12 см и 16 см.
3. Найдите длину медианы ВМ треугольника АВС, если координаты вершин треугольника А (2;5), В (0;0), С(4;3).
4. Точка М является серединой боковой стороны АВ трапеции ABCD. Найдите площадь трапеции, если площадь треугольника MCD равна 28 см2.
5. Окружность радиуса 2 см, центр О которой лежит на гипотенузе АСпрямоугольного треугольника АВС, касается его катетов. Найдите площадь треугольника АВС, если ОА= см.
Найдите площадь треугольника АВС, если ОА= см.
1. В равнобедренный треугольник с основанием 14 см и боковой стороной 7 см вписан квадрат так, что две его вершины лежат на основании, а другие две вершины – на боковых сторонах. Найдите сторону квадрата.
2. Найдите площадь круга, вписанного в ромб с диагоналями, равными 16 см и 30 см.
3. Найдите длину медианы СР треугольника АВС, если координаты вершин треугольника А (-3;-2), В (-13;14), С(0;0).
4. Точка М является серединой боковой стороны АВ трапеции ABCD. Найдите площадь треугольника MCD, если площадь трапеции равна 38 см2.
5. Окружность радиуса 3 см, центр О которой лежит на гипотенузе АСпрямоугольного треугольника АВС, касается его катетов. Найдите площадь треугольника АВС, если ОА= см.
геометрия — ABCD параллелограмм.
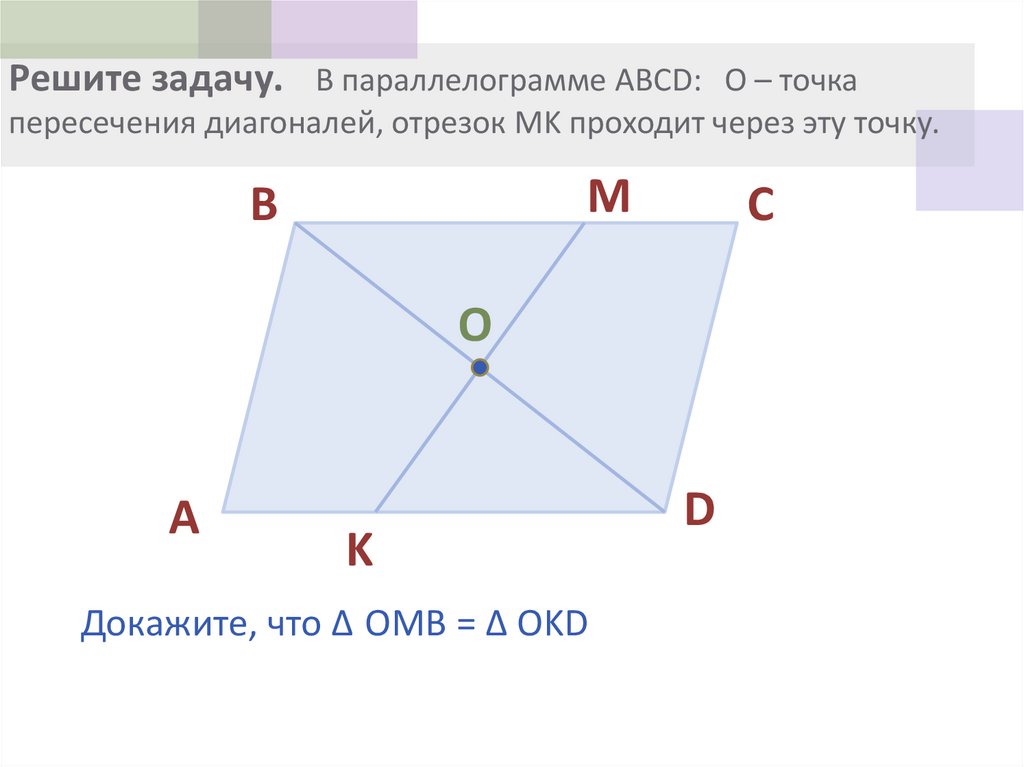 прямая, проходящая через A, пересекает BD в точке X, BC в точке Y и DC в точке Z. Докажите, что AX:XZ = AY:AZ
прямая, проходящая через A, пересекает BD в точке X, BC в точке Y и DC в точке Z. Докажите, что AX:XZ = AY:AZЗадавать вопрос
спросил
Изменено 1 год, 3 месяца назад
Просмотрено 457 раз
$\begingroup$
ABCD — параллелограмм. прямая, проходящая через A, пересекает BD в точке X, BC в точке Y и DC в точке Z. Докажите, что $$AX:XZ = AY:AZ$$
Мой подход
Я понял, что, поскольку вопрос кажется «недостаточным», нужно что-то делать с конструкциями . Увидев «соотношение», я подумал, что оно должно быть связано с подобными треугольниками.
Расширение $AB$
Опустите перпендикуляры из точек $X$,$Y$,$Z$ на $AB$.

Где моя ошибка и как решить эту проблему?
Дополнение
Когда я увидел, что предшествующее и последующее являются частью одного и того же отрезка, я не понял, что это можно решить без дополнительной конструкции (потому что если $∆ABC \sim ∆A’ B’C’$ можно написать $\frac{AB}{A’B’} = \frac{BC}{B’C’}$, а так как точки $A$,$B$,$C$ не могут лежать на одной прямой , поэтому члена отношения не могут быть частью одной и той же прямой линии). Всего ради любопытства , я хочу спросить, какой алгоритм следует использовать, чтобы найти требуемые треугольники, которые должны быть доказаны подобными?
- геометрия
$\endgroup$
$\begingroup$
Боюсь, вы меня потрясли на шаге 3. Вот что я с ним сделал.
Построить прямую через $B$ параллельно $XZ$.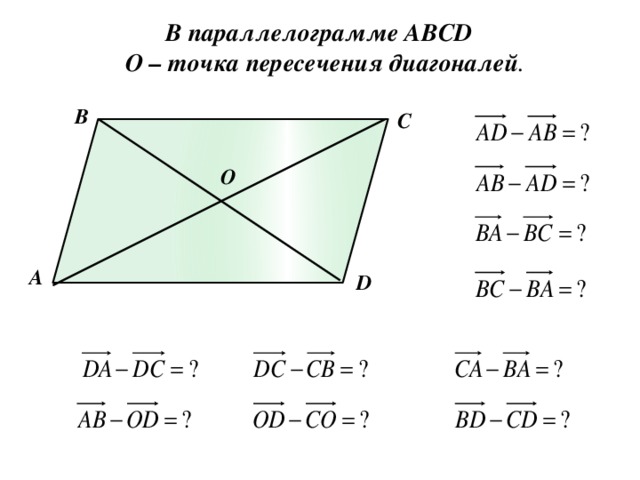 Пусть он встречается с $AD$ в точке $K$ и $CD$ в точке $L$. Получаются параллелограммы $ABLZ$ и $KAYB$.
Пусть он встречается с $AD$ в точке $K$ и $CD$ в точке $L$. Получаются параллелограммы $ABLZ$ и $KAYB$.
$KB=AY$ и $BL=AZ$ … (противоположные стороны параллелограмма)
$AX:XZ = KB:BL$ … (совпадающие секущие, пересекающие параллельные прямые)
$AX:XZ = AY:AZ$
$\endgroup$
$\begingroup$
В качестве альтернативы, вы можете просто использовать подобные треугольники, чтобы доказать это, без каких-либо дополнительных построений.
Как $\треугольник ADX\sim\треугольник YBX$, $\frac{XY}{AX} = \frac{BY}{AD} = \frac{BY}{BC} $
Добавление $1$ к обеим сторонам, $\frac{AY}{AX} = \frac{BC + BY}{BC} \tag1$
Также как $\triangle ADZ \sim \triangle YBA$,
$\frac{AZ}{AY} = \frac{AD}{BY} = \frac{BC}{BY} \tag2$
Умножение $(1)$ и $(2)$,
$\frac{AZ}{AX} = \frac{ BC+BY}{BY} \ подразумевает \frac{XZ}{AX} + 1 = \frac{BC}{BY} + 1$
Таким образом, $\frac{XZ}{AX} = \frac{BC} {BY} = \frac{AZ}{AY}$ (используя $2$)
$\endgroup$
2
$\begingroup$
Используя лемму о пересечении, получаем $$\frac{AX}{XZ} = \frac{[ABD]}{[BDZ]} = \frac{AB}{DZ}$$ и $$\frac{AY} {YZ} = \frac{[ABC]}{[BCZ]} = \frac {AB}{CZ}$$ Итак, $\frac{AY}{AZ} = \frac{AB}{CZ+AB} = \frac{AB}{CZ +CD}$
$\endgroup$
$\begingroup$
Ну, без лишних построений, попробую ответить.
$\endgroup$
$\begingroup$
Другое решение (убийство мухи базукой), используя перекрестное соотношение:
\begin{align}{AX\over XZ}\cdot {YZ\over AY}&= {AX\over XZ}: {AY\ над YZ}\\ &= (А, Z; X, Y)\\ & = (BA,BZ;BX,BY)\\ &= (B\infty, BZ;BD,BC)\\ &= (\infty,Z;D,C)\\ &={CZ\над DZ} \end{align}
Так как $\triangle CZY\sim \triangle DZA$, мы имеем ${CZ\over DZ }={YZ\over AZ}$ и все готово.
$\endgroup$
2
Математическая задача: Воздушный змей — вопрос №8390, алгебра, выражение переменной из формулы
ABCD — воздушный змей.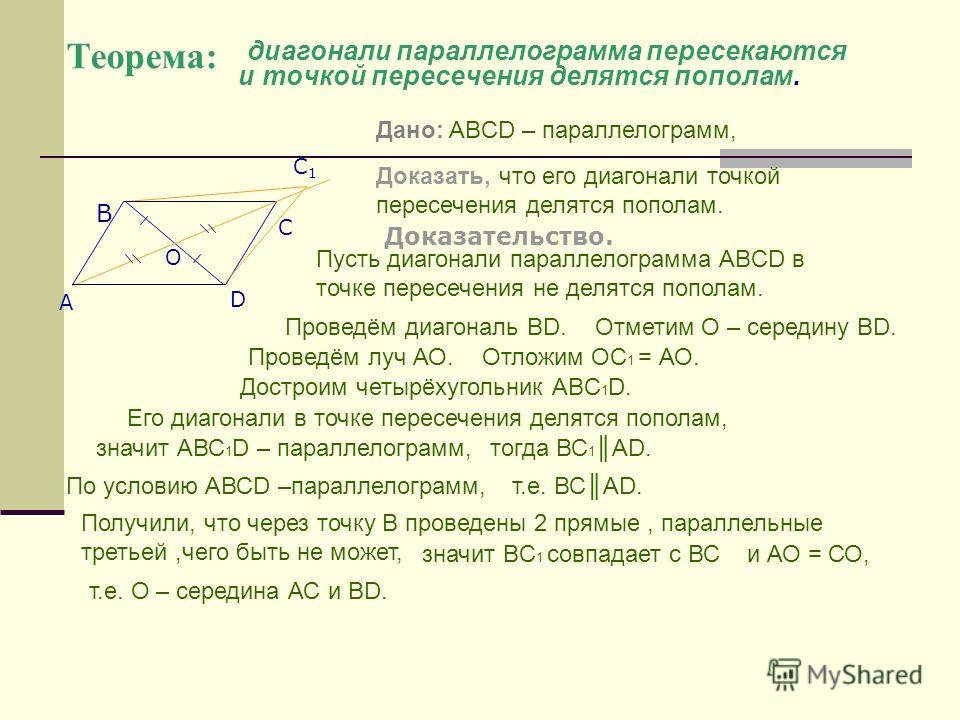 Угол OBC = 20° и угол OCD = 35°. О — пересечение диагоналей. Найдите угол ABC, угол ADC и угол BAD.
Угол OBC = 20° и угол OCD = 35°. О — пересечение диагоналей. Найдите угол ABC, угол ADC и угол BAD.
Правильный ответ:
x = 40 °y = 110 °
z = 55 °
Пошаговое объяснение:
∠OBC=20 ∘ ∠OCD=35 ∘ ∠OBA=∠OBC=20=20 ∘ ∠ABC=∠OBA+∠OBC=20+20=40 ∘ x=∠ABC=40=40∘
∠ОАД= ∠OCD=35=35 ∘ ∠ADO=90−∠OAD=90−35=55 ∘ ∠ODC=∠ADO=55=55 ∘ ∠ADC=∠ADO+∠ODC=55+55=110 ∘ y=∠ADC= 110=110∘
∠BAD=∠OBA+∠OAD=20+35=55 ∘ z=∠BAD=55=55∘
Нашли ошибку или неточность? Не стесняйтесь
написать нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
См. также наш калькулятор тригонометрического треугольника.
Для решения этой словесной задачи по математике необходимо знать следующие знания:
- алгебра
- выражение переменной из формулы
- планиметрия 9003 0
- прямоугольный треугольник
- треугольник
- трапеция
Единицы физических величин:
- угол
Уровень словесной задачи:
- практика для 13-летних
Рекомендуем посмотреть это обучающее видео по этой математической задаче: video1
- Параллелограмм
Мы знаем о параллелограмме ABCD: длина |AB| = 76см, |ВС| = 44 см, а угол ∢BAD = 30°.
- Пересечение 81594
Даны трапеция ABCD и размеры внутренних углов. Угол SDC 32° Угол SAD 33° Угол SDA 77° Угол CBS 29°, где S – пересечение диагоналей. Какова величина угла BSA? - Алмаз ABCD
В ромбе ABCD диагональ e = 24 см, а величина угла SAB равна 28 градусам, где S — пересечение диагоналей. Вычислите окружность алмаза. - Параллелограмм
Вычислите площадь параллелограмма ABCD, как показано, если |AB| = 13 см, |ВС| = 99 см и угол BAD = 100° - Параллелограмм 80761
- Координаты пересечения диагоналей
В прямоугольной системе координат нарисован прямоугольник ABCD. Эти координаты определяют вершины прямоугольника. A = (2.2) B = (8.2) C = (8.6) D = (2.6) Найдите координаты пересечения диагоналей прямоугольника ABCD. - Окружность 16933
В ромбе ABCD угол BAD равен 60°; длина диагонали BD равна 7 см. Вычислите окружность алмаза.
Вычислите окружность алмаза. - Четырехугольник 27693
Постройте четырехугольник ABCD с диагоналями AC = e 7см, BD = f = 6,2см, d = 4,3см, a = 5,3см и β = 125° - Диагонали трапеций
Дана трапеция ABCD с основаниями | АБ | = 12 см, |CD| = 8 см. Точка S — это пересечение диагоналей, для которых |AS| имеет длину 6 см. Вычислите длину полной диагонали АС. - Коэффициент подобия
Треугольники ABC и A’B’C’ подобны с коэффициентом подобия 2. Величина углов треугольника ABC равна α = 35° и β = 48°. Найдите величины всех углов треугольника A’B’C’. - Гамма-угол
Найдите модуль гамма-угла в треугольнике ABC, если: α = 38° 56′ и β = 47° 54′. - Равнобедренная
Равнобедренная трапеция ABCD ABC = 12 угол ABC = 40° b=6. Вычислите окружность и площадь. - Построение ромб
Построение параллелограмм (ромб) ABCD, | АБ | = 4 см альфа = 30° и | БД | = 5 см. - Найдите
Найдите третий внутренний угол треугольника ABC, где: α = 48°, γ = 65°.




 Вычислите окружность алмаза.
Вычислите окружность алмаза.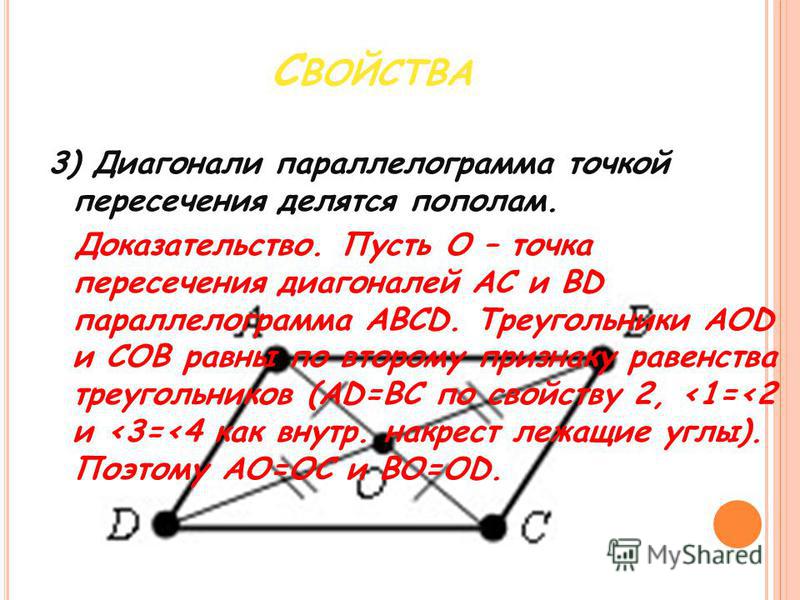
Leave A Comment