Параллелограмм: свойства его биссектрисы
МУНИЦИПАЛЬНАЯ XI УЧЕНИЧЕСКАЯ НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ « ЮНОСТЬ: ТВОРЧЕСТВО, ПОИСК, УСПЕХ»
Аннинский муниципальный район
Воронежская область
Секция: МАТЕМАТИКА
Тема: «Параллелограмм: свойства его биссектрисы»
Автор работы: Зубов Данил
МБОУ Аннинская СОШ № 3, 9 «А» класс
Место выполнения работы: МБОУ Аннинская СОШ № 3, 9 «А» класс,
Воронежская область, п.г.т. Анна
Научный руководитель:
Конюхова Галина Станиславовна,
учитель математики МБОУ Аннинская СОШ №3
г. АННА, 2020/2021 учебный год
Содержание
1. Введение………………………………………………………………………….. стр 3-4
2. Историческая справка…………………………………………………………….
….стр 5
3 Свойства параллелограмма……………………………………………………….….стр 6
4. Доказательство свойств биссектрисы параллелограмма………………………….стр 7-9
5. Способ построения биссектрисы параллелограмма без транспортира………… стр 10
6. Практическое применение свойств биссектрисы параллелограмма при
решении задач……………………………………………………………………….. стр 11-16
7. Проверь себя!……………………………………………………………………………………………….. стр 17
8. Методические аспекты решения задачи № 23 2 части ОГЭ по математике
(Модуль «Геометрия»)……………………………………………………………….. стр 18
9. Полезные советы учащимся для успешной подготовки к ОГЭ по математике… стр 19
10. Заключение…………………………………………………………………………стр 20
11. Библиографический список………………………………………………………..стр
1. Введение
Среди равных умов
при одинаковости прочих условий
превосходит тот, кто знает геометрию
Блез Паскаль
Во время изучения темы «Параллелограмм» на уроках геометрии в 8 классе мы рассмотрели свойства и признак параллелограмма, которые были в учебнике, но когда я начал подготовку к ОГЭ и стал решать задачи из КИМов, то оказалось, что этого материала недостаточно.
У меня возник вопрос, а есть ли у параллелограмма еще свойства, которые помогут мне при решении задач. И поставил перед собой цель: изучить дополнительные свойства биссектрисы параллелограмма и показать, как их можно применить для решения задач.
Предмет исследования: параллелограмм
Объект исследования: свойства биссектрисы параллелограмма
Цель работы:
1. Формулировка и доказательство свойств биссектрисы параллелограмма, которые не изучаются в школе;
2. Применение этих свойств для решения задач.
Задачи:
1. Изучить историю возникновения параллелограмма и историю развития его свойств;
2. Найти дополнительную литературу по исследуемому вопросу;
3. Изучить свойства биссектрисы параллелограмма и доказать их;
4. Показать применение этих свойств для решения задач;
5.
Рассмотреть применение свойств параллелограмма в жизни.
6. Показать применение данных свойств биссектрисы параллелограмма при решении заданий ОГЭ № 18 и № 23.
4. Создать медиаресурс для решения задач с биссектрисой параллелограмма.
Методы исследования:
1. Работа с учебной и научно – популярной литературой, ресурсами сети Интернет;
2. Изучение теоретического материала;
3. Выделение круга задач, которые можно решать с использованием свойств биссектрисы параллелограмма;
4. Наблюдение, сравнение, анализ, аналогия.
Актуальность исследования обусловлена тем, что при подготовке к олимпиадам и успешной сдачи ОГЭ и ЕГЭ, выпускники испытывают затруднения при выполнении заданий, где при решении необходимо применить свойства биссектрисы параллелограмма. Планируемый процент выполнения задания № 23 (повышенного уровня сложности) — 30-50%.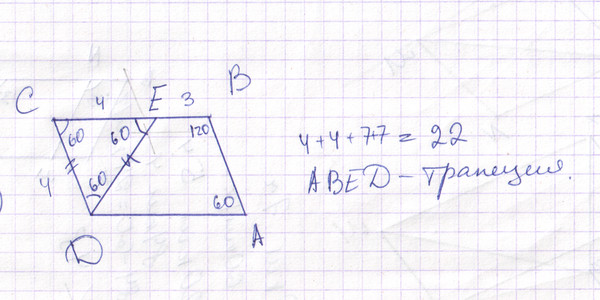
Актуальность выбранной темы заключается в том, что биссектриса параллелограмма имеет широкое применение в теории, что и является прикладной значимостью. Исследовательский характер работы состоит в решении задач с применением свойств биссектрисы параллелограмма, выходящих за рамки школьной программы.
Тема «Многоугольники» является одной из важных тем курса алгебры основной школы. Она отражена в заданиях 1-й (базового уровня) и 2-й (повышенного уровня) частях экзаменационной работы.
Практическая значимость моей работы заключается:
1. В использовании приобретенных знаний по данной теме, а также углубление их и применение к задачам;
2. В использовании навыков исследовательской работы в дальнейшей учебной деятельности.
Ключевые слова: параллелограмм, биссектриса, ОГЭ, геометрия.
2. Историческая справка
Оказывается термин «параллелограмм» греческого происхождения Parallelos — параллельный и gramme — линия.
Поэтому слово «параллелограмм» можно перевести как «параллельные линии». И, согласно древнегреческому философу Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам.
В «Началах» Евклида доказывается следующая теорема: в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам. Он не рассматривает ни прямоугольника, ни ромба.
Полная теория параллелограммов была разработана к концу средних веков и появились в учебниках лишь в XVII веке. Все теоремы о параллелограммах основываются непосредственно или косвенно на теореме Евклида о свойствах параллелограмма.
В учебнике геометрии мы читаем следующее определение параллелограмма: параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны, т.е. лежат на параллельных прямых.
3. Свойства биссектрисы параллелограмма
Биссектриса параллелограмма — это отрезок, соединяющий вершину параллелограмма с точкой на одной из двух противоположных сторон и делящий угол при вершине пополам.
В учебнике по геометрии даны только два свойства параллелограмма:
1. Противоположные углы и стороны равны
2.Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
В различных источниках по геометрии можно встретить следующие дополнительные свойства:
1. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник;
2. Биссектрисы противолежащих углов параллелограмма лежат на параллельных прямых;
3. Биссектрисы соседних углов параллелограмма пересекаются под прямым углом;
4.
Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник;
5. Биссектрисы соседних углов параллелограмма пересекаются на большей стороне параллелограмма, если она в два раза больше меньшей стороны;
6. Биссектрисы соседних углов параллелограмма пересекаются внутри параллелограмма, если меньшая сторона больше половины большей стороны;
7. Биссектрисы соседних углов параллелограмма пересекаются вне параллелограмма, если меньшая сторона меньше половины большей стороны;
8. Биссектрисы соседних углов параллелограмма могут пересекать противоположную сторону или ее продолжение.
4. Доказательство свойств биссектрисы параллелограмма
1 . Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник
Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
Д ано: ABCD — параллелограмм, AF — биссектриса ∠BAD, F ∈ BC.
Доказать: ∆ ABF — равнобедренный.
Доказательство:
1) ∠BAF=∠DAF (так как AF — биссектриса ∠BAD по условию).
2) ∠BFA=∠DAF (как внутренние накрест лежащие углы при BC ∥ AD м секущей AF).
РИС.3
3) Следовательно, ∠BAF=∠BFA.
4) Следовательно, треугольник ABF — равнобедренный с основанием AF (по признаку).
5) Следовательно, AB=BF ч.т.д.
2. Биссектрисы углов параллелограмма, прилежащих к одной стороне, взаимно перпендикулярны.
Д ано: ABCD — параллелограмм,
AF биссектриса ∠BAD, DK- биссектриса ∠ADC,
AF ∩ DK= M.
Доказать: ∠AMD=90º.
Доказательство:
∠BAD+∠ADC=180º (как внутренние односторонние углы при AB ∥ CD и секущей AD).
Так как биссектриса угла делит его пополам, то ∠DAM = 0,5∠BAD, ∠ADM = 0,5 ∠ADC
∠DAM + ∠ADM = 0,5∠BAD + 0,5 ∠ADC = 0,5 (∠BAD + ∠ADC) = 0,5 × 1800 = 900 Рассмотрим треугольник ADM.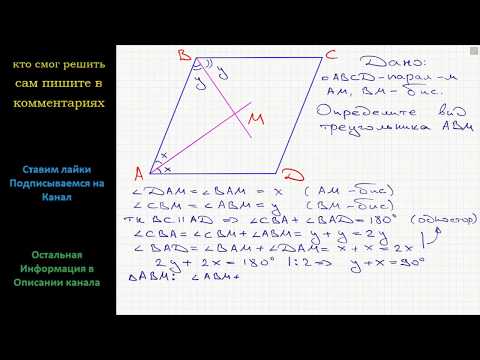
Так как сумма углов треугольника равна 180º, то
∠DAM+∠ADM+∠AMD=180º, 90º+∠AMD=180º, откуда ∠AMD=180º- 90º=90º,
т о есть биссектрисы углов параллелограмма, прилежащие к стороне AD, перпендикулярны
3
Дано: АВСD — параллелограмм, АК-биссектриса A,
DР-биссектриса D,
CM -биссектриса C,
BF -биссектриса B.
Доказать: KRNS-прямоугольник
Из предыдущего доказательства можно сделать ещё два вывода:
4. Биссектрисы параллелограмма пересекутся внутри параллелограмма, если меньшая сторона больше половины соседней стороны.
5. Биссектрисы соседних углов в параллелограмме пересекутся вне параллелограмма, если меньшая сторона меньше половины соседней стороны
6 .
Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых.
Дано: АВСD – параллелограмм
АК и СМ – биссектрисы
АВ = ВК = СD = DМ
Доказать:
АК = СМ; АК // СМ
5. Способ построения биссектрисы параллелограмма без транспортира.
На ОГЭ выпускник может пользоваться только линейкой, и поэтому хочу поделиться способом построения биссектрисы параллелограмма без транспортира.
Мы узнали, что биссектриса отсекает от параллелограмма равнобедренный треугольник.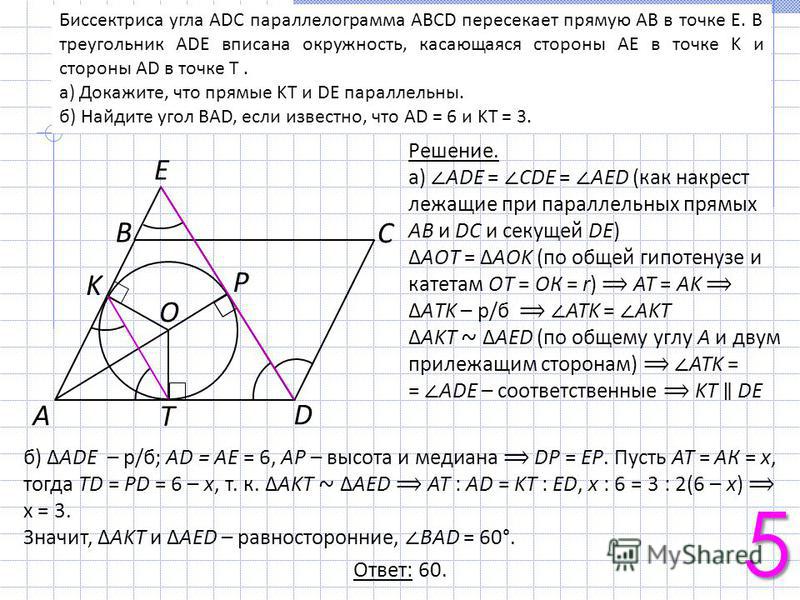
Линейкой измеряем сторону АВ и откладываем это расстояние из точки В на прямой ВС, делаем засечку, обозначаем точку буквой К. Таким образом АВ = ВК. Проводим биссектрису А – АК.
6. Практическое применение свойств биссектрисы параллелограмма при решении задач.
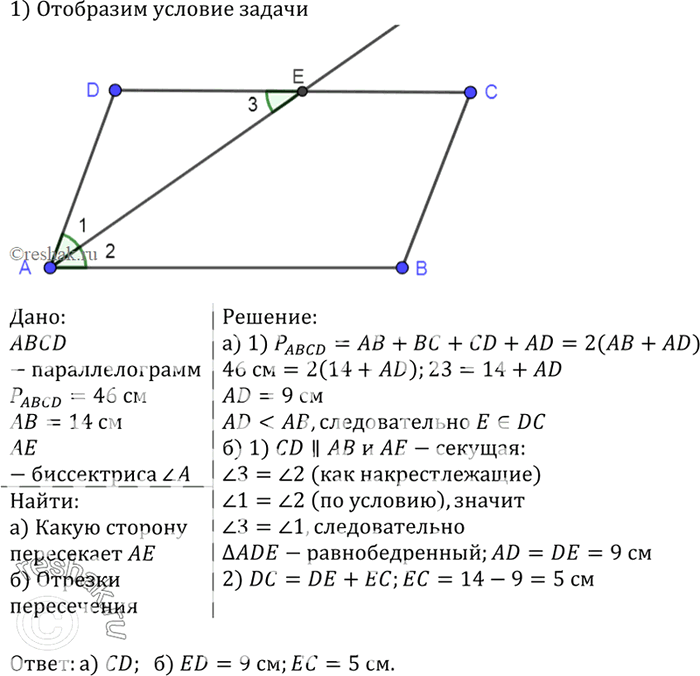
1 (№18). Биссектрисы углов B и C параллелограмма ABCD пересекаются на стороне AD. Найдите BC, если AB=4.
Д ано: Биссектрисы углов B и C параллелограмма ABCD пересекаются на стороне AD. AB=4.
Найдите: BC
РИС.11
Решение.
По свойству биссектрисы параллелограмма △ABK и △CDK – равнобедренные (AB=AK, CD=DK). Следовательно, BC=AD=AK+DK=AB+CD=2AB=8.
Ответ: 8.
2 (№ 24). В параллелограмме ABCD биссектриса, выходящая из вершины B, пересекает AD в точке K и равна 6. ∠BAD=60∘, AK:KD=3:2. Найдите периметр параллелограмма ABCD.
2
Дано: ABCD-параллелограмм, ∠BAD=60∘, AK:KD=3:2, ВК = 6, ВК-биссектриса
Найти: PАВСD
РИС.12
Решение.
Т.к. BK – биссектриса ∠ABC, то ∠KBC=∠BKA, т.к. это накрест лежащие углы при параллельных прямых. Тогда: ∠ABK=∠BKA=0,5(180∘−∠BAD)=0,5(180∘−60∘)=60∘ △ABK равносторонний, значит AB=BK=AK=6. Тогда AK:KD=6:KD=3:2⇒KD=4. AD=AK+KD=10, тогда PABCD=2⋅6+2⋅10=32
Ответ:32
3(№ 24) . В параллелограмме ABCD проведены биссектрисы AN и BE односторонних углов. Найдите BE, если AN=16, AB=10.
Дано: ABCD-параллелограмм, AN и BE – биссектрисы. AN=16, AB=10.
Найдите: BE
РИС.13
Решение.
По свойству биссектрисы параллелограмма △ABE и △ABN – равнобедренные, то есть AE=AB=BN=10.
Следовательно, AO – биссектриса, проведенная к основанию, значит, высота, то есть ∠AOB=90∘, а также и медиана, то есть BO=OE. Аналогично AO=ON=0,5AN=8. Тогда по теореме Пифагора AB2=ВO2+AO2, BO=6, следовательно ВЕ=12
Ответ: 12
4 (№ 18). В параллелограмме ABCD биссектриса ∠BAD пересекает сторону BC в точке K и делит ее пополам, а также пересекает продолжение стороны DC в точке L. Найдите периметр параллелограмма, если CL=3.
Дано: ABCD-параллелограмм, АК – биссектриса,
CL=3
Найти: PАВСD
РИС.15
Решение.
△CKL=△BKA и являются равнобедренными. AB=CL=3,BC=BK+KC=2⋅CK=2⋅CL=2⋅3=6. Тогда PABCD=2⋅3+2⋅6=18.
Ответ: 18
5 ( №18). В параллелограмме ABCD: точка K лежит на стороне AD, BK=3 – биссектриса ∠ABC, BC=5, ∠BKA=60∘. Найдите периметр параллелограмма.
Дано: ABCD-параллелограмм, BK=3,
BK– биссектриса ∠ABC,
BC=5, ∠BKA=60∘
Найти: PАВСD
РИС.
16
Решение
⇒ ∠BAD=60∘ ⇒ △ABK – равносторонний, тогда AB=BK=3 ⇒ PABCD=2⋅3+2⋅5=16.
Ответ: 16
6 (№ 24). Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4:3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
Дано: ABCD-параллелограмм, PАВСD = 88,
ВК- биссектриса, AK:KD=4:3
Найти: АD
РИС.17
Решение.
Из условия задачи следует, что AK:KD=4:3. Обозначим AK=4x, KD=3x. Следовательно, AD=7x. Так как в параллелограмме противоположные стороны параллельны, то ∠AKB=∠KBC как накрест лежащие при AD∥BC и секущей BK. Следовательно, ∠AKB=∠ABK, то есть △ABK равнобедренный: AK=AB. Отсюда AB=4x. Следовательно, периметр 88=2(4x+7x) (так как противоположные стороны параллелограмма равны), следовательно, x=4.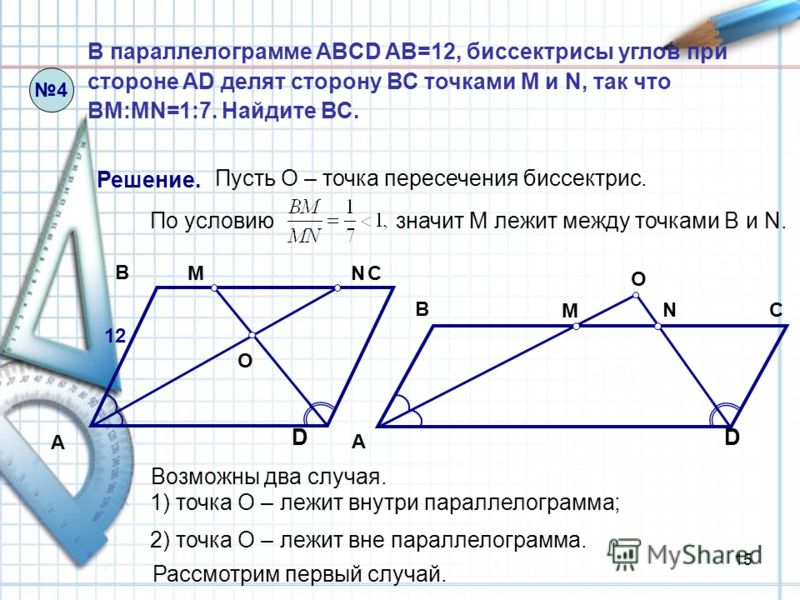
Значит, большая сторона параллелограмма равна 7x=28.
Ответ: 28
7(№ 24). Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.
1 случай: биссектрисы пересекаются вне параллелограмма.
Дано: ABCD – параллелограмм,
АК – биссектриса А,
DК – биссектриса D,
АВ=3 см, ВС=10 см
Найти: ВМ, МN, NC
D, то △DCN- равнобедренный
DC=CN= 3
Тогда, МN= 10 – (BM+NC) = 10 – (3+3)=4 см
2 случай: биссектрисы пересекаются внутри параллелограмма
Т.к. АN — биссектриса А, то △АВN – равнобедренный.
АВ=ВN= 3
Т.к. DM – биссектриса D, то △DCM- равнобедренный
DC=CM= 3
Тогда, BN=3 см, СN=10 – 3 = 7 см,
CM= 3 см, ВМ=10 – 3 =7 см, чего быть не может, т.к. ВC=10 см
2 случай не возможен.
Ответ: 3см, 4 см, 3 см
8 (№ 24). В параллелограмме ABCD: BC=2⋅AB, AN и CM – биссектрисы, AB=4. Найдите NM.
Дано: ABCD-параллелограмм, BC=2⋅AB,
AN и CM – биссектрисы, AB=4.
Найдите: NM.
РИС.20
Решение.
Внутренние накрест лежащие углы при параллельных прямых и секущей равны, тогда ∠BNA=∠NAD, но ∠NAD=∠BAN, тогда ∠BNA=∠BAN и треугольник BAN – равнобедренный, AB=BN. Обозначим AB=x. Аналогично треугольник MCD – равнобедренный, x=CD=MD. BC=2x=AD, тогда NC=x=AM, следовательно, BN=x=AM; AM∥BN, тогда ABNM – параллелограмм, откуда заключаем, что MN=AB=4.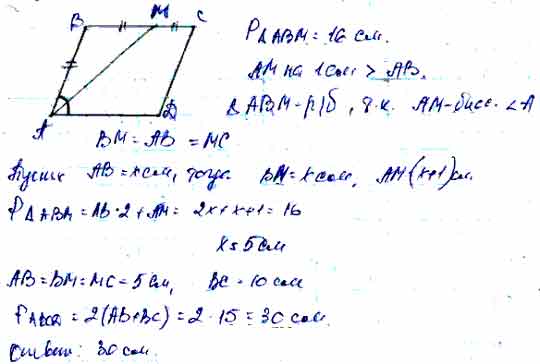
Ответ: 4
9. (№ 24 ОГЭ). В параллелограмме ABCD биссектрисы углов при стороне AD делят сторону ВС точками М и N так, что BM : MN = 1:5. Найдите ВС, если АВ =3
В этой задаче также возможны два случая: биссектрисы пересекаются вне параллелограмма и внутри параллелограмма.
1 случай: биссектрисы пересекаются вне параллелограмма
C
РИС.21
Дано: ABCD – параллелограмм, АМ – биссектриса А,
DN – биссектриса D, АВ=3 см, BM : MN = 1:5
Найти: BC
Решение
Т.к. АМ- биссектриса ⦟ А, то △АВМ – равнобедренный.
АВ=ВМ= 3 см
Т.к. DN – биссектриса D, то △DCN- равнобедренный
DC=CN= 3 см
Т. к. ВМ: МN=1:5, то на отрезок ВМ приходится 1 часть, а на отрезок MN – 5 частей,
Тогда, ВС= ВМ +МN+NC=3+15+3=21
2 случай: биссектрисы пересекаются внутри параллелограмма
Ответ: 21 см или 3,5 см
7.
Проверь себя!
Открытый банк заданий ОГЭ | |
Прототип заданий 18, 23. | Ответ |
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=7, CK=12. | |
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=5, CK=14. | |
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=8, CK=13. | |
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. | |
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=6, CK=10. | |
В параллелограмме ABCD: BK – биссектриса, BK=AK. Чему равен ∠D? Ответ дайте в градусах. | 120 |
В параллелограмме ABCD на стороне BC выбрана точка N так, что AB=BN, ∠B=150∘. Найдите ∠NAD. Ответ дайте в градусах. | 15 |
В параллелограмме ABCD проведены биссектрисы AN и BM, ∠ABM=58∘. Найдите ∠BAN. Ответ дайте в градусах. | 32 |
В параллелограмме ABCD проведена биссектриса AN, точка N лежит на стороне BC, причём NC=3, AB=5. | 26 |
24. В параллелограмме ABCD биссектрисы BK и AL пересекаются в точке O. Найдите периметр параллелограмма ABCD, если AD=10, а медиана OM в △AOB равна 4.. | 36 |
24. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону. | 10 |
ABCD –параллелограмм; KА – биссектриса; BK = 14 см; KC = 7 см. Найти: P ᴀᴃᴄᴅ | 70 |
Найдите периметр параллелограмма, если BK=3, CK=19.
Найдите периметр параллелограмма ABCD.8. Методические аспекты решения задачи № 23 2 части ОГЭ по математике
(Модуль «Геометрия»)
Задания второй части модуля «Геометрия» направлены на проверку владения таких качеств математической подготовки выпускников, как:
умение решить планиметрическую задачу, применяя различные теоретические знания курса геометрии;
умения математически грамотно и ясно записать решение, приводя при этом необходимые пояснения и обоснования;
владения широким спектром приёмов и способов рассуждений.
Основные проверяемые требования к математической подготовке при выполнении задания 23.
| Разделы элементов содержания | Разделы элементов требований | Максимальный балл за выполнение задания |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 7. Геометрия | 5. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 2 |
Задания второй части считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ.
В этом случае ему выставляется полный балл, соответствующий данному заданию. Ход решения верный, все его шаги выполнены правильно, но даны
неполные объяснения, или допущена одна вычислительная ошибка, то учащемуся засчитывается балл, на 1 меньше указанного.
9. Полезные советы учащимся для успешной подготовки к ОГЭ по математике.
1. Не секрет, что успешнее сдает экзамен тот, кто в полном объеме владеет материалом, хорошо знаком с процедурой проведения экзамена, психологически готов к экзамену и адекватно реагирует на нестандартные ситуации.
2. Хорошо знать документы, регламентирующие проведение экзамена по математике:
«Кодификатор требований к уровню подготовки обучающихся для проведения основного государственного экзамена по математике»
«Кодификатор элементов содержания для проведения основного государственного экзамена по математике»;
«Спецификация контрольных измерительных материалов для проведения основного государственного экзамена по математике»;
«Демонстрационный вариант контрольных измерительных материалов для проведения основного государственного экзамена по математике»;
Литературу для подготовки к ОГЭ.
Список сайтов, содержащих демоверсии и позволяющие онлайн-тестироваться.
3. На основании школьного плана подготовки к экзамену, составить личный план, включив в него консультации, которые проводит учитель, расписание «пробных» ОГЭ.
4. Тщательно анализировать пробные ОГЭ. По их итогам корректировать самостоятельную подготовку к экзамену.
5. Собирать свой портфолио-папку со всеми выполненными пробниками. Вести мониторинг выполнения всех заданий пробных экзаменов.
6. Серьезное внимание уделять устному счету, который проводит учитель на уроках. Эти упражнения активизируют мыслительную деятельность, требуют осознанного усвоения учебного материала. При их выполнении развивается память, речь, внимание, быстрота реакции. Устные упражнения позволяют корректировать знания, умения и навыки учащихся, а также автоматизировать навыки простейших вычислений и преобразований.
7. Научиться «читать» условие задачи до начала решения и после ее решения для того, чтобы верно ответить на поставленный вопрос (что нужно было найти?).
10. Заключение
Геометрия полна приключений, потому что за каждой задачей
скрывается приключение мысли. Решить задачу — это значит
пережить приключение…
(В.Произволов)
При рассмотрении данной темы меня постоянно мучил один вопрос: почему в учебниках геометрии так мало задач на применение свойств биссектрис параллелограмма, а в сборниках для подготовки к экзаменам их довольно много?
На экзаменах по математике задачи по геометрии являются самыми трудными заданиями. Задачи по геометрии требуют применения сведений из разных разделов курса планиметрии. Таким образом, для их решения нужно ориентироваться во всей совокупности знаний о свойствах рассматриваемой фигуры, которые могли изучаться в разных классах основной школы.
Решение задач требует комплексного применения 2 — 3 геометрических фактов, свойств из разных разделов курса.
Работая и изучая школьные учебники по геометрии авторов А.В. Погорелова, Л.С. Атанасяна, И.Ф. Шарыгина, можно сказать, что в них к теоретическим фактам (теоремам) отнесены в основном только те утверждения, которые необходимы для построения теории. При этом многие утверждения, весьма полезные для решения большого числа задач, даются как задачи на доказательство. К таким теоретическим фактам (не приведенным в учебниках) можно отнести, например, свойства биссектрисы угла параллелограмма.
Рассмотрение вопроса о свойствах биссектрис параллелограмма позволило мне приобрести новые знания. Я увидел необходимость этих свойств для решения большого количества задач. В своей работе я не только сам сформулировал, доказал свойства, но и попытался применить их к решению задач. Буду рад, если другие ребята воспользуются им.
Цель моей исследовательской работы выполнена.
11. Библиографический список
1. https://ru.wikipedia.org/wiki/
2. https://shkolkovo.net/catalog/planimetriya_chast_i/parallelogramm_svojstvo_ego_bissektrisy
3. http://www.fipi.ru/content/otkrytyy-bank-zadaniy-oge
4. ПогореловА.В. Геометрия 7-9: учебник для общеобразоват. учреждений-М.: Просвещение, 2019г
5.Л.С.Атанасян и др. Геометрия. Доп. Главы к учебнику 8 кл.: учеб. пособие для учащихся школ и классов с углубл. изуч. математики. – М.: Вита-пресс, 2018
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
01.19
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
В баллоне
объёмом 1,66^3 м находится 2 кг
азота при давлении 10^5 Па.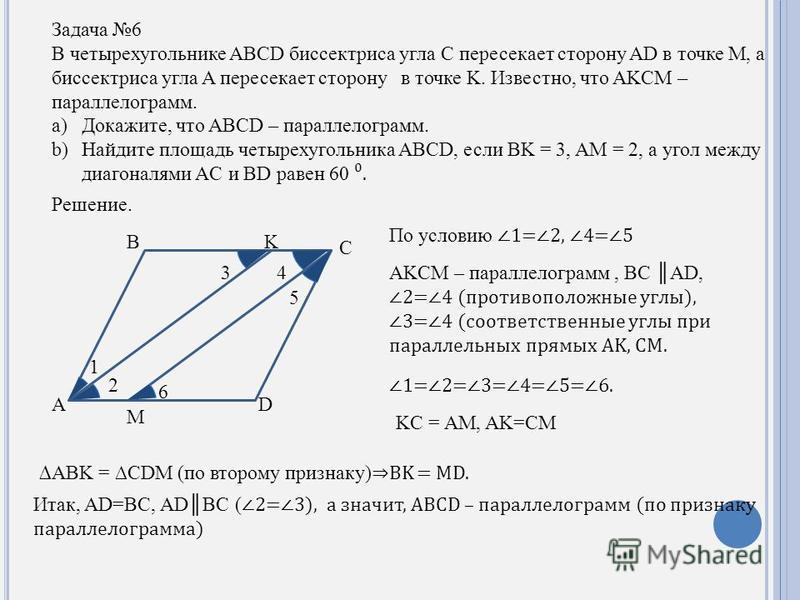
2-2x-3 Найдите: а) наименьшее значение функции; б) значения х, при которых значение функции равно 5; в) значения х, при которых функция принимает положительные
одна стрекоза летит со скоростью 12 м / с и догоняет другую , которая летит со скоростью 10 м /с . вначале расстояние между ними было 6 метров через сколько секунд первая стрекоза догонит вторую
Товарный поезд прошел 315 км.он был в пути до остановки 3 ч ипосле остановки 4 ч.сколько км прошел поезд до ипосле остановки,если он шел с одинаковой скоростью
AB//CD Mn=12 см Ac=4 см BD =6 см.найдите отрезок MB
Пользуйтесь нашим приложением
В параллелограмме $ ABCD $ биссектриса угла $ ABC $ пересекает $ AD $ в точке $ P. $ Если $ PD = 5, BP = 6 $ и $ CP = 6 $ , найдите $ AB $ (A) $ 5 $ (B) $ 4 $ (C) $ 6 $ (D) $ 8 $
Дата последнего обновления: 12 марта 2023
•
Всего просмотров: 264.
6k
•
Просмотров сегодня: 7.46k
3
Ответ
Проверено
264.6k+ просмотров
Подсказка : Используйте свойства параллелограмма и подобия треугольников, чтобы решить этот вопрос.
Полный пошаговый ответ :
Обратите внимание на схему
$ \Delta PBC $ равнобедренный треугольник.
$ \потому что PB = CP = 6 $ (Дано)
Кроме того, $\угол PBC = \угол APB $ (чередующиеся внутренние углы) . . . (1)
$ \угол PBC = \угол ABP $ (Поскольку PB — биссектриса угла) . . . (2)
Из уравнений (1) и (2) получаем
$ \angle APB = \angle ABP $
$ \Rightarrow \Delta APB $ — равнобедренный треугольник.
$ \Rightarrow AP = AB $ (Стороны, противоположные равным углам равнобедренного треугольника)
In $ \Delta PCB $ и $ \Delta APB $
$ \angle PBC = \angle PBA $ (Поскольку PB биссектриса угла) .
. . (3)
Из уравнения (3) и того факта, что треугольники $\Delta PCB$ и $\Delta APB$ равнобедренные. Можно сказать, что
$ \angle PCB = \angle APB $ (Поскольку их противоположные углы равны друг другу)
Так как два угла двух треугольников равны, то и третий угол должен быть равен.
$ \Rightarrow \angle CPB = \angle PAB $
Следовательно, по критериям подобия треугольников ААА можно записать соответствующие стороны двух треугольников равны
$ \Rightarrow \dfrac{{PC}}{{AP}} = \dfrac{{CB}}{{PB}} = \dfrac{{PB}}{{AB}} $
\[ \Rightarrow \dfrac{{CB}}{{PB}} = \dfrac{{PB}}{{AB}}\]
$ BC = AD $ (Противоположные стороны параллелограмма)
\[ \ Стрелка вправо \dfrac{{AD}}{{PB}} = \dfrac{{PB}}{{AB}}\] 92} + 9x — 4x — 36 = 0 $
$ \Стрелка вправо x(x + 9) — 4(x + 9) = 0 $
$ \Стрелка вправо (x + 9)(x — 4) = 0 $
$ \Rightarrow x = — 9,4 $
Но длина не может быть отрицательной.
Следовательно, $ x = 4 $
$ \ следовательно, AB = AP = 4 $
Следовательно, значение $ AB = 4 $
Итак, правильный ответ «Вариант Б».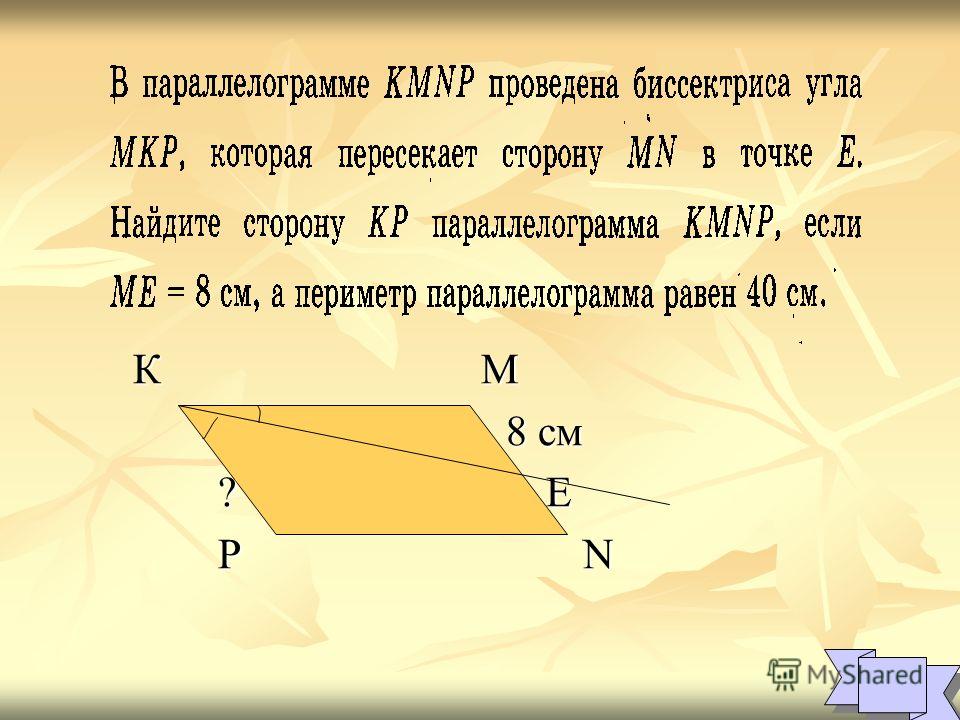
Примечание : В этом вопросе было дано меньше информации напрямую. Нам нужно было найти информацию, необходимую для решения этого вопроса, используя свойства параллелограмма, равнобедренного треугольника и подобия двух треугольников. Из этого вопроса мы понимаем, что свойства геометрических фигур очень важны.
Найдите длину отрезка между биссектрисами пересекающихся углов Средняя школа.
Дан параллелограмм ABCD, стороны AB и BC которого равны 6. 10 единиц соответственно. Биссектрисы углов А и В пересекаются в точки E, а биссектрисы углов C и D пересекаются в точке F. Найти длина отрезка EF.
Вид или опубликуйте решение
| Концепция | Определение | Теорема / Комментарий |
|---|---|---|
| Треугольник | Многоугольник с тремя сторонами и тремя углами. | Сумма углов треугольника равна 180 градусов. |
| Равнобедренный треугольник | Равнобедренный треугольник — это треугольник, у которого две стороны одинаковой длины. | В равнобедренном треугольнике высоты относительно конгруэнтных сторон конгруэнтны. |
| Параллелограмм | Параллелограмм – это четырехугольник, у которого обе пары противоположных сторон параллельны. | Противоположные стороны параллелограмма равны; противоположные углы равны; последовательные углы являются дополнительными; диагонали делят друг друга пополам. |
| Биссектриса угла | Линия или луч, делящий угол на два равных угла. | |
| Параллельные линии | Две прямые на плоскости, которые не пересекаются. | Если две параллельные прямые пересечены секущей, то смежные внутренние углы равны, соответственные углы равны, а последовательные внутренние углы дополнительные. |
| Конгруэнтность | Два треугольника называются конгруэнтными, если все соответствующие стороны и углы одного треугольника равны соответствующим сторонам и углам другого треугольника.. | Существует несколько способов доказать конгруэнтность двух треугольников, включая критерии сторона-сторона-сторона (SSS), сторона-угол-сторона (SAS), угол-сторона-угол (ASA) и гипотенуза-ног (HL) . |
| Вспомогательная линия | Вспомогательная линия — это линия, добавляемая к диаграмме для доказательства теоремы или решения проблемы. | Часто вспомогательная линия проводится для создания дополнительных конгруэнтных или подобных треугольников, для создания параллельных линий или для создания прямых углов. Использование вспомогательных прямых может упростить задачу или упростить доказательство. Однако важно следить за тем, чтобы вспомогательная линия не создавала новых пересечений или углов, которых не было на исходной схеме. |
Тематическая поэма:
Геометрический мир: формы и теоремы
В геометрии мы изучаем формы,
И теоремы для
укажи нам путь,
Имеет параллельные стороны, которые всегда остаются.
Противоположные стороны и углы, также конгруэнтные,
Последовательные углы, обязательно дополнительные,
Диагонали
делят друг друга пополам, это правда,
В параллелограмме мы
может обеспечить.
Биссектрисы угла делят угол пополам,
Создание
равные углы с обеих сторон,
Полезный инструмент для
решать проблемы заново,
В геометрии это весело.
Параллельные линии никогда не пересекаются,
В плоскости они
простираться далеко и широко,
Альтернативные внутренние углы
конгруэнтно,
Теорема, которую мы не можем скрыть.
Конгруэнтность — это такое великое понятие,
Все стороны и углы совпадают,
Доказать, что это может быть нашей целью.
Leave A Comment