Контрольная работа по геометрии 8 класс
ВАРИАНТ 1
1. Центральный угол AOB, равный 60°, опирается на хорду АВ длиной 3.Найдите радиус окружности.
2.В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 130°. Найдите вписанный угол ACB. Ответ дайте в градусах.
3. Треугольник ABC вписан в окружность с центром в точке О. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 123°.
4.На окружности с центром в точке отмечены точки и так, что . Длина меньшей дуги равна 61. Найдите длину большей дуги .
5.Точки A и B делят окружность на две дуги, длины которых относятся как 9:15 Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
6.Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC = 134° и ∠OAB = 75°. Найдите угол BCO. Ответ дайте в градусах.
Известно, что ∠ABC = 134° и ∠OAB = 75°. Найдите угол BCO. Ответ дайте в градусах.
7.Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 9°. Ответ дайте в градусах.
8.В угол C величиной 90° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
9.Сторона квадрата равна 26. Найдите радиус окружности, вписанной в этот квадрат.
10. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 24 , AO = 26 .
11.Длина хорды окружности равна 48, а расстояние от центра окружности до этой хорды равно . Найдите диаметр окружности.
12.Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 60°. Найдите величину угла OMK. Ответ дайте в градусах.
Точка O — центр окружности. Хорда KM образует с касательной угол, равный 60°. Найдите величину угла OMK. Ответ дайте в градусах.
13. Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 18, CD = 24, а расстояние от центра окружности до хорды AB равно 12.
14.Хорды AC и BD окружности пересекаются в точке P, BP = 8, CP = 24, DP = 18. Найдите AP.
ВАРИАНТ 2
1. Центральный угол AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
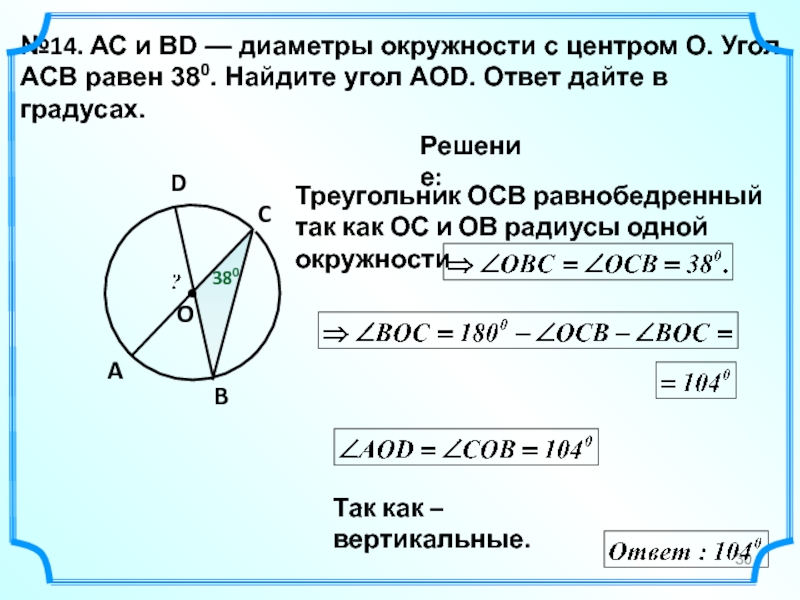
2.Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 23°. Найдите угол AOD. Ответ дайте в градусах
.3.Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB Найдите угол ACB, если угол AOB равен 153°. Ответ дайте в градусах
Точки O и C лежат в одной полуплоскости относительно прямой AB Найдите угол ACB, если угол AOB равен 153°. Ответ дайте в градусах
4.На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 98. Найдите длину большей дуги.
5.Точки A и B делят окружность на две дуги, длины которых относятся как 6:3 Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
6.Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC = 87° и ∠OAB = 75°. Найдите угол BCO. Ответ дайте в градусах.
7.Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 24°. Ответ дайте в градусах
8. В угол C величиной 62° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
Найдите угол AOB. Ответ дайте в градусах.
9.Сторона квадрата равна 34. Найдите радиус окружности, вписанной в этот квадрат.
10. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 14 , AO = 50 .
11.Длина хорды окружности равна 40, а расстояние от центра окружности до этой хорды равно . Найдите диаметр окружности.
12.Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 40°. Найдите величину угла KOM. Ответ дайте в градусах
13. Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 30, а расстояния от центра окружности до хорд AB и CD равны соответственно 20
центр, хорда, диаметр и радиус.
 {\circ}\), AB = 15 см, BC = 22 см. Найдите расстояние между прямой \(AB\) и прямой проходящей через точку \(C \) параллельно \(AB.\)
{\circ}\), AB = 15 см, BC = 22 см. Найдите расстояние между прямой \(AB\) и прямой проходящей через точку \(C \) параллельно \(AB.\)К окружности с центром в точке О проведены касательная AB и секущая АО. Найдите радиус окружности, если AB = 15, АО = 17.
В окружности с центром O отрезки AC и BD — диаметры. Вписанный угол ACB равен 38°. Найдите центральный угол AOD.
Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности.
Найдите центральный угол AOB, если он на 15° больше вписанного угла ACB, опирающегося на ту же дугу.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12 см. Найдите радиус описанной окружности этой трапеции.
В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 и 12 см. Найдите катеты треугольника.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 5, считая от вершины, противолежащей основанию.
Найдите площадь круга, длина окружности которого равна \(50\sqrt{\pi}\).
Площадь круга, вписанного в правильный шестиугольник, равна 60,75π см2. Найдите периметр шестиугольника.
Найдите диаметр основания юрты, если ее радиус равен 4,5 м.
Расстояние от центра окружности до касательной равно 13 дм. Найдите радиус данной окружности.
Найдите величину дуги АВ, на которую опирается угол АВС, вписанный в окружность.
В окружности с центром в точке О проведена хорда АС. Найдите угол АОС, если известно, что хорда равна радиусу (АО = АС)
Восемь шариков для настольного тенниса нужно уложить в коробку плотно друг к другу. Какова длина коробки, если радиус одного шарика 2,5 см?
Центральный угол и вписанный угол опираются на одну дугу. Найдите эти углы, если центральный угол на 20° больше вписанного.
Прямая АВ касается окружности с центром в точке О и радиусом, равным 7 см, в точке А. Найдите ОВ, если АВ = 24 дм.
АВ и СD – хорды. АВ и СD пересекаются в точке Е. АЕ = 0,7 см, ВЕ = 0,5 см, СЕ = 0,4 см. Найдите DЕ и DС.
АВ и СD пересекаются в точке Е. АЕ = 0,7 см, ВЕ = 0,5 см, СЕ = 0,4 см. Найдите DЕ и DС.
Вершины треугольника АВС делят описанную окружность в отношении 2: 3: 4. Найдите углы треугольника АВС.
Из точки А к окружности с центром в точке О проведена касательная АВ. Найдите радиус, если угол ОАВ равен 60°, АО =14\(\sqrt3\) см.
К окружности с центром в точке О проведены две касательные, угол между которыми равен 120°. АО = 24 см. Найдите СА и DА, если С и D – точки касания.
Два угла треугольника равны 60° и 80°.
В треугольнике даны две стороны: a = 12, b = 8. Угол между ними равен 60°. Найдите третью сторону.
Основание равнобедренного треугольника – a, боковая сторона – b. Найдите биссектрису, проведенную из вершины, противолежащей основанию.
В треугольнике ABC угол A = 45°, угол C = 15°, сторона BC = 4\(\sqrt6\). Найдите длину стороны AC.
В треугольнике ABC угол A = 30°, угол B = 30°. Найдите соотношение сторон \(\frac{BC}{AB}\)
Какому неравенству удовлетворяет точка C, принадлежащая кругу с центром в точке O и радиусом R?
Вписанный угол ABC равен 30°. Найдите радиус окружности, если длина хорды AC, на которую он опирается, равна 17.
Найдите радиус окружности, если длина хорды AC, на которую он опирается, равна 17.
АВ – диаметр окружности. Точки С и D лежат на окружности по одну сторону от диаметра. Угол СВD равен 21°, угол DВА равен 49°. Найдите угол СDВ.
Вершины треугольника АВС делят окружность, описанную около этого треугольника в отношении 1: 3 : 5. Найдите углы треугольника.
Радиус окружности равен 10 см, расстояние от точки А, лежащей на окружности, до точки В – конца диаметра – равно 16 см. Найдите АС, если точка С – второй конец диаметра.
Из точки А к окружности с центром в точке О проведена касательная АВ. Найдите АО, если радиус равен 12\(\sqrt2\) см, угол ОАВ равен 45°, точка В является точкой касания.
Найдите АО, если радиус равен 12\(\sqrt2\) см, угол ОАВ равен 45°, точка В является точкой касания.
АВ – диаметр окружности с центром в точке О. Точки С и К лежат на окружности по одну сторону от диаметра. Угол АВС равен 18°, угол СОК равен 46°. Найдите угол КАВ.
Точки А, В и С лежат на окружности с центром в точке О. Угол АОС равен 130°. Найдите угол АВС.
Прямая АВ касается в точке А окружности с центром в точке О. Найдите угол ОАВ.
Вершины четырехугольника АВСD делят описанную окружность в отношении 1: 2 : 7 : 8. Найдите градусную меру большей дуги.
Расстояние от точки А, лежащей на окружности, до концов диаметра ВD равно 9 см, 12 см. Найдите радиус.
Хорды СК и АВ пересекаются в точке Е. АЕ = 4 см, ВЕ = 6 см, КЕ меньше СЕ на 5 см. Найдите СЕ.
Дана окружность с центром в точке О, АВ – диаметр. Точки С и К лежат на окружности по одну сторону от диаметра. Угол СКА равен 12°, угол СОК равен 64°. Найдите угол КАВ.
Хорды АВ и СН пересекаются в точке М. СМ = 4 см, НМ = 15 см, АМ:МВ = 3 : 5. Найдите АВ.
Диагонали ромба равны 6 и 8. \circ\), АВ = 3\(\sqrt2\), АС = 1. Найдите ВС.
\circ\), АВ = 3\(\sqrt2\), АС = 1. Найдите ВС.
Сумма квадратов диагоналей прямоугольника равна 25. Найдите сумму квадратов его сторон.
Одна из сторон треугольника больше другой на 8 сантиметров, а угол между ними равен 120°. Найдите периметр треугольника, если длина третьей стороны равна 28 см.
Дан треугольник АВС. АВ = 15, ВС = 6, sin A = \(\frac15\). Найдите sin C.
В прямоугольной трапеции высота равна 12, большая боковая сторона равна 20, меньшее основание равно 5. Найдите большее основание.
Стороны треугольника равны 5\(\sqrt3\) см и 4 см, а угол между ними равен 30°. {\circ}\\
&9{\ круг} \\
\потому что \mathrm{OD} \| \mathrm{CB}
\end{array}
{\circ}\\
&9{\ круг} \\
\потому что \mathrm{OD} \| \mathrm{CB}
\end{array}
Следовательно,
∠AOD = ∠BCA (соответствующие углы)
∠AOD = 50
Но ∠AOD + ∠DOC = 180 (Линейная пара)
9000 2 50 + у = 180у = 180 – 50
Получаем,
y = 130
Следовательно, x = 50 и y = 130
(vi ) На рисунке
AC диаметр окружности с центр как O
BA = BC = CD
В △ABC,
∠ABC = 90 (Угол в полуокружности)
По свойству суммы углов треугольника получаем,
∠BAC + ∠BCA + ∠ABC = 180
∠BAC + ∠BCA + 90 = 180 9000 3
∠ВАЦ + ∠BCA = 90
Но при этом BA = BC
Следовательно, ∠BAC = ∠BCA = x
x + x = 90
2x = 90
x = 450 9000 3
В △BCD,
BC = CD
Следовательно,
∠CBD = ∠CDB = y и
Внешний ∠ACB = Сумма внутренних противоположных углов
9{1} \end{array}(vii) На рисунке
AB — диаметр окружности с центром O
ST — касательная в точке B
∠ASB = 65
In △ABS
∵ TS — касательная, а OB — радиус
OB перпендикулярен ST или
∠ABS = 90
Но в △ASB,
∠BAC + ∠ASB + ∠ABS = 180
900 02 х + 65 + 90 = 180х + 155 = 180
х = 180 — 155
Получаем,
x = 25
Следовательно, x = 25
( viii) На рисунке
AB — диаметр окружности с центром O
ST — касательная к окружности в точке B = BS
Следовательно,
ST — тангенс, а OB — радиус
OB ⊥ ST или ∠OBS = 90
In △ABS,
∠BAS + ∠BSA + ∠ABS = 180
По свойству суммы углов треугольника
∠BAS + ∠BSA + 90 = 180
∠BAS + ∠BSA = 9{\circ}
(ix) На рисунке
RS — диаметр окружности с центром при O
SR получается из Q
QT — касательная к окружности в точке P
OP соединена
∠Q = 36
QT — касательная, а OP — радиус окружности
Следовательно,
OP перпендикулярна QT
∠OPQ = 90
In △OP Q,
По свойству суммы углов треугольник, получаем,
∠OQP + ∠POQ + ∠OPQ = 180
∠OQP + ∠POQ + 90 = 180
Следовательно,
∠OQP + ∠POQ = 90
360 + x = 90
x = 90 — 360
Получаем,
х = 54
В △OPS
OP = OS (Радиусы окружности)
Следовательно,
∠OPS = ∠OSP = y и
Внешний угол ∠POQ = ∠OPS + ∠OSP
x = у + у
x = 2y = 54
404 — СТРАНИЦА НЕ НАЙДЕНА
Почему я вижу эту страницу?
404 означает, что файл не найден. Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Вы можете получить ошибку 404 для изображений, поскольку у вас включена защита от горячих ссылок, а домен отсутствует в списке авторизованных доменов.
Если вы перейдете по временному URL-адресу (http://ip/~username/) и получите эту ошибку, возможно, проблема связана с набором правил, хранящимся в файле .htaccess. Вы можете попробовать переименовать этот файл в .htaccess-backup и обновить сайт, чтобы посмотреть, решит ли это проблему.
Также возможно, что вы непреднамеренно удалили корневую папку документа или вам может потребоваться повторное создание вашей учетной записи. В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.
Вы используете WordPress? См. Раздел об ошибках 404 после перехода по ссылке в WordPress.
Как найти правильное написание и папку
Отсутствующие или поврежденные файлы Когда вы получаете ошибку 404, обязательно проверьте URL-адрес, который вы пытаетесь использовать в своем браузере. Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
http://example.com/example/Example/help.html
В этом примере файл должен находиться в public_html/example/Example/
Обратите внимание, что в этом примере важен CaSe . На платформах с учетом регистра e xample и E xample не совпадают.
Для дополнительных доменов файл должен находиться в папке public_html/addondomain.com/example/Example/, а имена чувствительны к регистру.
Неработающее изображениеЕсли на вашем сайте отсутствует изображение, вы можете увидеть на своей странице поле с красным размером X , где отсутствует изображение. Щелкните правой кнопкой мыши на X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Это зависит от браузера, если вы не видите на своей странице поле с красным X , попробуйте щелкнуть правой кнопкой мыши на странице, затем выберите «Просмотр информации о странице» и перейдите на вкладку «Мультимедиа».
http://example.com/cgi-sys/images/banner.PNG
В этом примере файл изображения должен находиться в папке public_html/cgi-sys/images/ пример. На платформах, которые обеспечивают чувствительность к регистру PNG и png — это разные местоположения.
404 Ошибки после перехода по ссылкам WordPress
При работе с WordPress ошибки 404 Page Not Found часто могут возникать, когда была активирована новая тема или когда были изменены правила перезаписи в файле .htaccess.
Когда вы сталкиваетесь с ошибкой 404 в WordPress, у вас есть два варианта ее исправления.
Вариант 1. Исправьте постоянные ссылки- Войдите в WordPress.
- В меню навигации слева в WordPress нажмите Настройки > Постоянные ссылки (Обратите внимание на текущую настройку. Если вы используете настраиваемую структуру, скопируйте или сохраните ее где-нибудь.)
- Выберите По умолчанию .

- Нажмите Сохранить настройки .
- Верните настройки к предыдущей конфигурации (до того, как вы выбрали «По умолчанию»). Верните пользовательскую структуру, если она у вас была.
- Нажмите Сохранить настройки .
Во многих случаях это сбросит постоянные ссылки и устранит проблему. Если это не сработает, вам может потребоваться отредактировать файл .htaccess напрямую.
Вариант 2. Измените файл .htaccessДобавьте следующий фрагмент кода в начало файла .htaccess:
# НАЧАЛО WordPress
RewriteEngine On
RewriteBase / 9index.php$ — [L]
RewriteCond %{REQUEST_FILENAME} !-f
RewriteCond %{REQUEST_FILENAME} !-d
RewriteRule . /index.php [L]
# Конец WordPress
Если ваш блог показывает неправильное доменное имя в ссылках, перенаправляет на другой сайт или отсутствуют изображения и стиль, все это обычно связано с одной и той же проблемой: в вашем блоге WordPress настроено неправильное доменное имя.
Как изменить файл .htaccess
Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.
Перенаправление и перезапись URL-адресов — это две очень распространенные директивы, которые можно найти в файле .htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
Возможно, вам потребуется отредактировать файл .htaccess в какой-то момент по разным причинам. В этом разделе рассказывается, как редактировать файл в cPanel, но не о том, что нужно изменить. статьи и ресурсы для этой информации.)
Существует множество способов редактирования файла .htaccess- Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
- Использовать режим редактирования программы FTP
- Используйте SSH и текстовый редактор
- Использовать файловый менеджер в cPanel
Самый простой способ отредактировать файл . htaccess для большинства людей — через диспетчер файлов в cPanel.
htaccess для большинства людей — через диспетчер файлов в cPanel.
Прежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.
Откройте файловый менеджер- Войдите в cPanel.
- В разделе «Файлы» щелкните значок «Диспетчер файлов ».
- Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.
- Убедитесь, что установлен флажок Показать скрытые файлы (точечные файлы) «.
- Нажмите Перейти . Файловый менеджер откроется в новой вкладке или окне.
- Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.
- Щелкните правой кнопкой мыши файл .



Leave A Comment