Прямоугольник, ромб, квадрат — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Прямоугольник
Четырехугольник, у которогоназывается прямоугольником.
все
углы
прямые,
Ясно, что прямоугольник является частным случаем
параллелограмма, следовательно, он обладает всеми
свойствами
параллелограмма.
В
частности,
в
прямоугольнике противоположные стороны попарно
равны и диагонали в точке пересечения делятся
пополам.

2. Упражнение 1
Докажите, что диагонали прямоугольника равны.Доказательство. Пусть ABCD – прямоугольник.
Прямоугольные треугольники ABC и BAD равны по
двум катетам. Следовательно, AC = BD, что и
требовалось доказать.
3. Признак прямоугольника
Теорема(Признак
прямоугольника.)
Если
в
параллелограмме
диагонали
равны,
то
этот
параллелограмм является прямоугольником.
Доказательство. Пусть ABCD – параллелограмм и AC = BD.
Треугольники ABC и BAD равны по третьему признаку равенства
треугольников (AB – общая, AC = BD, BC = AD). Следовательно,
угол ABC равен углу BAD. Но эти углы в сумме составляют 180о.
Значит, каждый из них равен 90о. Так как в параллелограмме
противоположные углы равны, то и остальные его углы также
равны 90о, т.е. ABCD – прямоугольник.
4. Ромб
Четырехугольник, уназывается ромбом.
Ромб
которого
все стороны
равны,
Из второго признака параллелограмма следует, что ромб
является частным случаем параллелограмма.
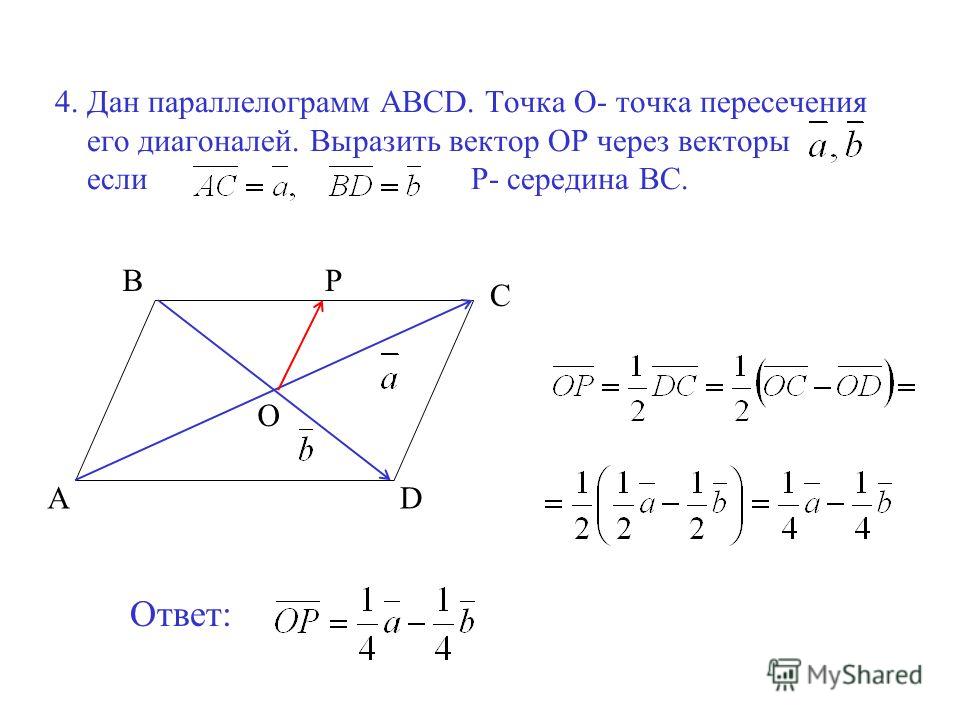
5. Упражнение 2
Докажите, что диагонали ромба перпендикулярны.Доказательство. Пусть ABCD – ромб, O – точка
пересечения
диагоналей.
Так
как
диагонали
параллелограмма в точке пересечения делятся пополам,
то BO = OD. Следовательно, AO – медиана
равнобедренного треугольника ABD (AB=AD). Так как
медиана равнобедренного треугольника, проведенная к
основанию, является высотой, то прямые AO и BD
перпендикулярны.
6. Признак ромба
Теорема. (Признак ромба.) Если в параллелограммедиагонали перпендикулярны, то этот параллелограмм
является ромбом.
Доказательство. Пусть ABCD – параллелограмм,
диагонали AC и BD перпендикулярны, O – точка их
пересечения. Прямоугольные треугольники AOB и AOD
равны (по двум катетам: AO – общий, OB = OD).
Следовательно, AB = AD. Так как в параллелограмме
противоположные стороны равны, то и остальные его
стороны равны, т.е. ABCD – ромб.
7. Квадрат
Прямоугольник, у которогоназывается квадратом.

все
стороны
равны,
Можно также сказать, что квадратом является ромб, у
которого все углы прямые.
8. Упражнение 3
Три угла четырехугольника равны 90о. Являетсяли этот четырехугольник прямоугольником?
Ответ: Да.
9. Упражнение 4
Верноли,
что
если
диагонали
четырехугольника
равны,
то
этот
четырехугольник – прямоугольник?
Ответ: Нет.
10. Упражнение 5
Верно ли, что если в четырехугольнике одинугол прямой, а диагонали равны, то он является
прямоугольником?
Ответ: Нет.
11. Упражнение 6
Изобразитепрямоугольник,
две
противоположные вершины которого даны на
рисунке, а оставшиеся вершины расположены в
узлах сетки. Сколько решений имеет задача?
Ответ: 3.
12. Упражнение 7
Изобразите ромб, две противоположныевершины которого даны на рисунке, а
оставшиеся вершины расположены в узлах
сетки. Сколько решений имеет задача?
Ответ: 3.

13. Упражнение 8
Изобразите квадрат, две противоположныевершины которого даны на рисунке, а
оставшиеся вершины расположены в узлах
сетки. Сколько решений имеет задача?
Ответ: 1.
14. Упражнение 9
Из точки D, принадлежащей гипотенузе ABпрямоугольного треугольника ABC, проведены
две прямые, параллельные катетам. Сумма
периметров получившихся треугольников AKD
и DLB равна 10 см. Найдите периметр данного
треугольника ABC.
Ответ: 10 см.
15. Упражнение 10
Два равных прямоугольных треугольникаприложили один к другому таким образом, что
их гипотенузы совпали, а неравные острые
углы приложились один к другому. Какой при
этом получился четырехугольник?
Ответ: Прямоугольник.
16. Упражнение 11
Меньшая сторона прямоугольника равна 5 см,диагонали пересекаются под углом 60о. Найдите
диагонали прямоугольника.
Ответ: 10 см.
17. Упражнение 12
В прямоугольнике диагональ делит угол вотношении 1:2, меньшая его сторона равна 5 см.

Найдите диагонали данного прямоугольника.
Ответ: 10 см.
18. Упражнение 13
Диагональ прямоугольника вдвое больше однойиз его сторон. Какие углы образуют диагонали
со сторонами прямоугольника?
Ответ: 30о и 60о.
19. Упражнение 14
Тупой угол между диагоналями прямоугольникаравен 120 . Чему при этом будет равно
отношение его меньшей стороны к диагонали?
Ответ: 1:2.
20. Упражнение 15
В прямоугольном треугольнике ABC из вершиныпрямого угла C опущена высота CH, равная 3
см. Из точки H опущены перпендикуляры HK и
HL на катеты треугольника. Найдите расстояние
между точками K и L.
Ответ: 3 см.
21. Упражнение 16
Найдите диагонали прямоугольника, если егопериметр равен 34 см, а периметр одного из
треугольников, на которые диагональ разделила
прямоугольник, равен 30 см.
Ответ: 13 см.
22. Упражнение 17
В прямоугольнике острый угол между егодиагоналями равен 50о. Найдите углы, которые
образуют диагонали со сторонами
прямоугольника.
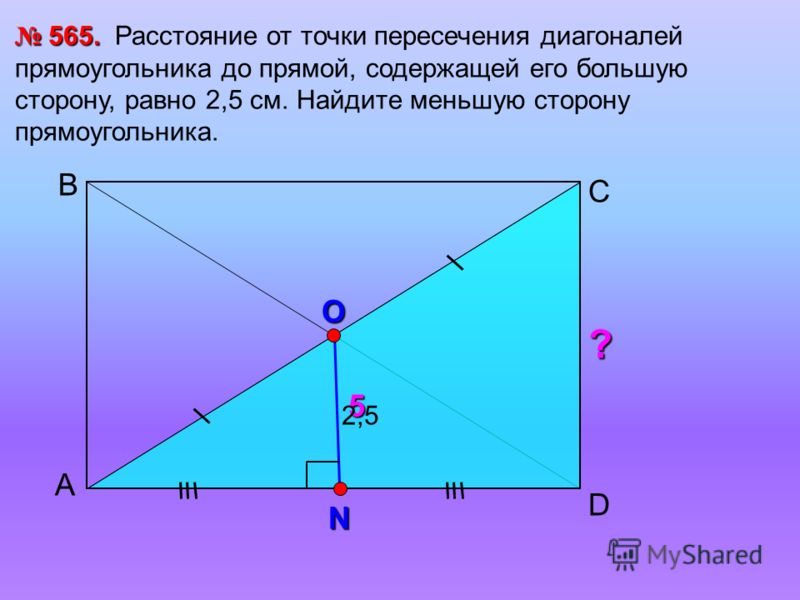
Ответ: 25о и 65о.
23. Упражнение 18
Перпендикуляр BH, опущенный из вершины Bпрямоугольника ABCD на его диагональ AC,
делит угол B в отношении 2:3. Найдите: а) углы,
которые
образуют
диагонали
данного
прямоугольника с его сторонами; б) угол между
перпендикуляром BH и диагональю BD.
Ответ: а) 36о и 54о; б) 18о.
24. Упражнение 19
Биссектриса одного из углов прямоугольникаделит пересекаемую ею сторону на отрезки 4 см
и 5 см. Найдите стороны
данного
прямоугольника.
Ответ: 4 см и 9 см.
25. Упражнение 20
Чему равна меньшая диагональ ромба состороной а и острым углом в 60о?
Ответ: a.
26. Упражнение 21
В ромбе одна из диагоналей равна его стороне.Найдите углы ромба.
Ответ: 60o, 120o, 60o, 120o.
27. Упражнение 22
Углы, образуемые диагоналями ромба с одной изего сторон, относятся как 4:5. Найдите углы
ромба.
Ответ: 80o, 100o, 80o, 100o.
28.
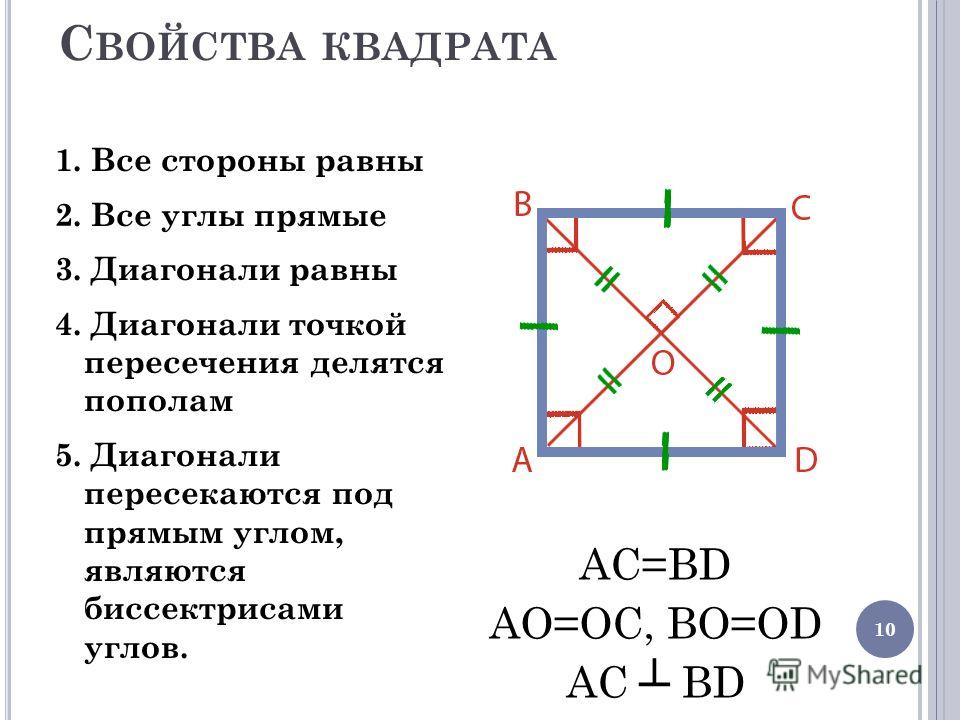 Упражнение 23Чему равен угол между: а) диагоналями
Упражнение 23Чему равен угол между: а) диагоналямиквадрата: б) диагональю и стороной квадрата?
Ответ: а) 90o;
б) 45o.
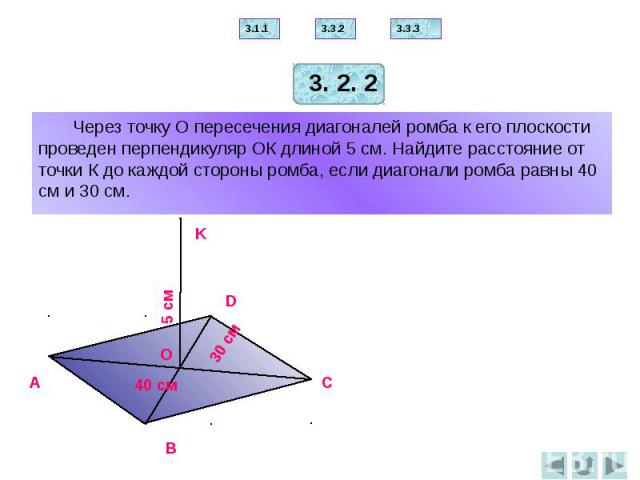
29. Упражнение 24
В квадрате расстояние от точки пересечениядиагоналей до одной из его сторон равно 5 см.
Найдите периметр этого квадрата.
Ответ: 40 см.
English Русский Правила
Презентация по теме «Четырёхугольники»
Упражнение 1
Сумма двух углов параллелограмма равна 80 о . Найдите один из оставшихся углов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 140 о .
Упражнение 2
Один угол параллелограмма больше другого на 40 о . Найдите больший угол.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 110 о .
Упражнение 3
Диагональ параллелограмма образует с двумя его сторонами углы 25 о и 35 о . Найдите больший угол параллелограмма.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 120 о .
Упражнение 4
Периметр параллелограмма равен 48. Одна сторона параллелограмма на 2 больше другой. Найдите большую сторону параллелограмма.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 13.
Упражнение 5
Боковая сторона равнобедренного треугольника равна 5. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10.
Упражнение 6
Из точки D , принадлежащей гипотенузе AB прямоугольного треугольника ABC , проведены две прямые, параллельные катетам. Сумма периметров получившихся треугольников

В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 12.
Упражнение 7
Меньшая сторона прямоугольника равна 5, диагонали пересекаются под углом 60 о . Найдите диагонали прямоугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10.
Упражнение 8
Диагональ прямоугольника вдвое больше одной из его сторон. Найдите меньший из углов, которые образует диагональ со сторонами прямоугольника?
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 30 о .
Упражнение 9
Найдите диагонали прямоугольника, если его периметр равен 34, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 30.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 13.
Упражнение 10
Биссектриса одного из углов прямоугольника делит пересекаемую ею сторону на отрезки длиной 4 и 5.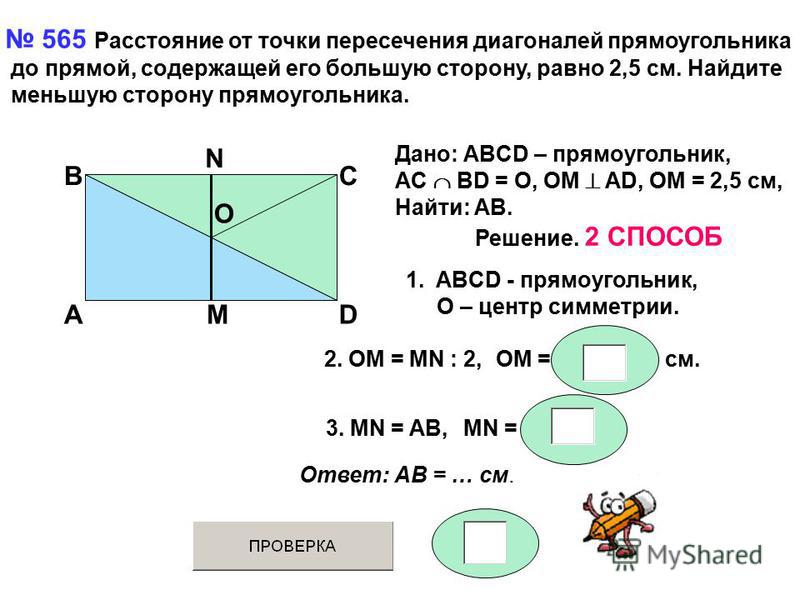 Найдите меньшую сторону данного прямоугольника.
Найдите меньшую сторону данного прямоугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 4.
Упражнение 11
В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 5. Найдите периметр этого квадрата.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 40.
Упражнение 12
Основания равнобедренной трапеции равны 6 и 4, один из углов равен 45 о . Найдите высоту трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 1.
Упражнение 13
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 5 и 2. Найдите среднюю линию этой трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 5.
Упражнение 14
Средняя линия трапеции равна 30, а меньшее основание равно 20.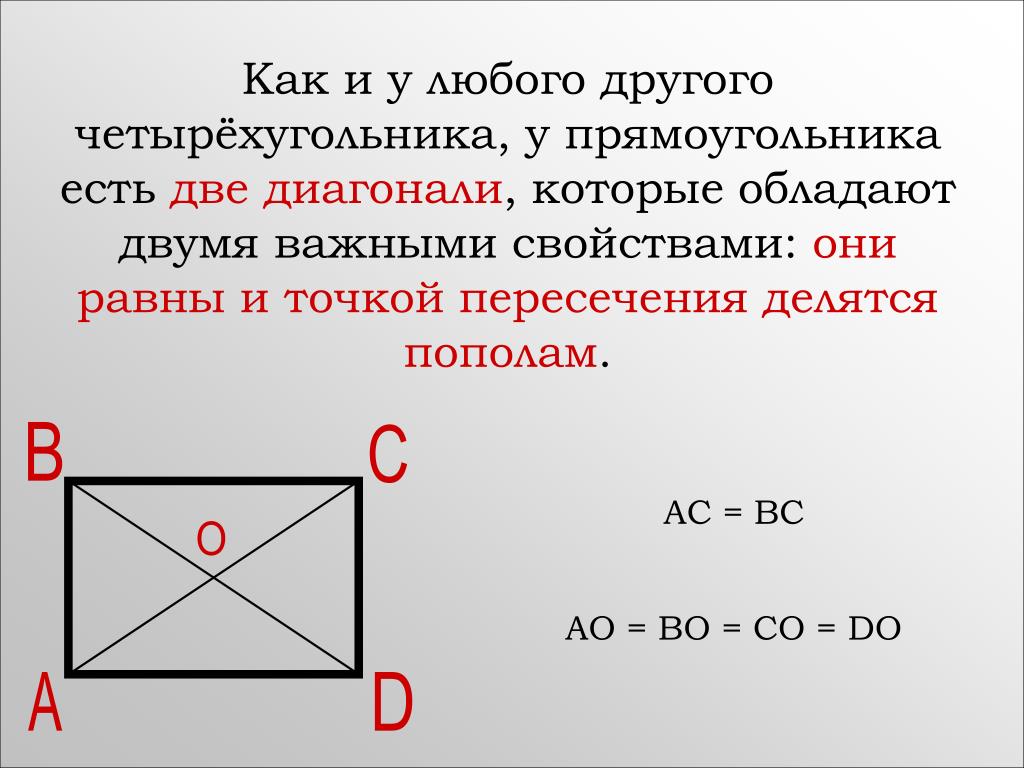 Найдите большее основание.
Найдите большее основание.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 40.
Упражнение 15
В равнобедренной трапеции большее основание равно 27, боковая сторона равна 1, угол между ними 60 о . Найдите меньшее основание.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 17.
Упражнение 16
В равнобедренной трапеции основания равны 13 и 28, острый угол равен 60. Найдите ее периметр.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 71.
Упражнение 17
В прямоугольной трапеции один из углов равен 45, средняя линия равна 24, основания относятся как 3:5. Найдите меньшую боковую сторону.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 12.
Упражнение 18
Периметр трапеции равен 50 см, а сумма непараллельных сторон равна 20 см. Найдите среднюю линию трапеции.
Найдите среднюю линию трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 15.
Упражнение 19
Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону данной трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 20.
Упражнение 20
Средняя линия трапеции равна 7 см, а одно из ее оснований больше другого на 4 см. Найдите большее основание трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 9.
Упражнение 21
Периметр прямоугольника
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 9.
Упражнение 22
Середины последовательных сторон прямоугольника, диагональ которого равна 10, соединены отрезками. Найдите периметр образовавшегося четырехугольника.
Найдите периметр образовавшегося четырехугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 20.
Упражнение 23
В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на 4 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 56. Найдите меньшую сторону.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10.
Упражнение 24
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника. Одна сторона этого прямоугольника вдвое меньше другой. Диагональ квадрата равна 36. Найдите меньшую сторону прямоугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 12.
Упражнение 25
В параллелограмме ABCD высота DH делит сторону
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2.
Упражнение 26
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 2:3, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 96.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 30.
Упражнение 27
Через точку O пересечения диагоналей параллелограмма
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 58.
Упражнение 28
Найдите диагональ прямоугольника, образованного биссектрисами углов параллелограмма, соседние стороны которого равны 3 см и 5 см.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2.
Упражнение 29
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите большую сторону.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10.
Упражнение 30
Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 48.
Упражнение 31
Меньшее основание равнобедренной трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне. Найдите больший угол трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 120 о .
Упражнение 32
Основания трапеции относятся как 5:2, а их разность равна 18 см. Найдите среднюю линию трапеции.
Найдите среднюю линию трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 21.
Упражнение 33
C редняя линия трапеции равна 10. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание этой трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 12.
Упражнение 34
Средняя линия трапеции делится ее диагоналями на части, которые относятся как 2:3:2. Найдите большее основание трапеции, если ее средняя линия равна 42.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 60.
Упражнение 35
Диагонали четырехугольника равны 3 и 4. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 7.
Упражнение 36
Основания трапеции равны 6 и 4. Найдите отрезок, соединяющий середины диагоналей трапеции.
Найдите отрезок, соединяющий середины диагоналей трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 1.
Упражнение 37
В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 10. Найдите среднюю линию.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10.
Упражнение 38
В прямоугольной трапеции ABCD ( AB || CD ) угол B равен 45 о и сторона AB равна 30. Через середину E стороны BC проведен к ней перпендикуляр, который пересекает продолжение стороны DA в точке F . Найдите DF .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 30.
Упражнение 39
Основания трапеции равны 14 см и 20 см. Одна из боковых сторон разделена на три равные части и через точки деления проведены прямые, параллельные основаниям трапеции.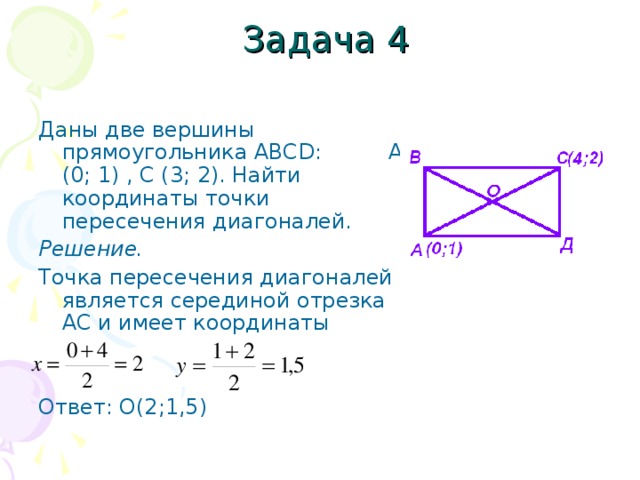 Найдите больший из отрезов этих прямых, заключенных внутри трапеции.
Найдите больший из отрезов этих прямых, заключенных внутри трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 18.
Упражнение 40
Каждая из сторон треугольника разделена на три равных отрезка и точки деления соединены отрезками. Найдите периметр образовавшейся при этом фигуры, если периметр исходного треугольника равен 15.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 15.
Упражнение 41
Найдите меньший угол параллелограмма, если два его угла относятся как 3:7.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 54.
Упражнение 42
Найдите угол между биссектрисами углов параллелограмма, прилежащими к одной стороне.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 90 о .
Упражнение 43
Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 40 о ?
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 110 о .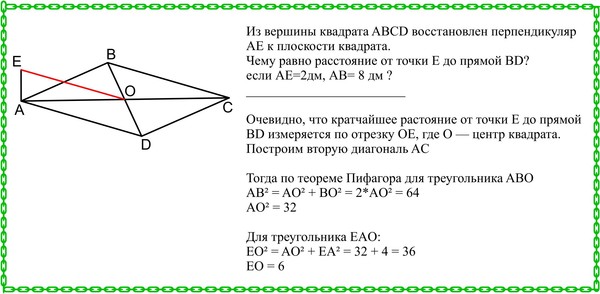
Упражнение 44
Две стороны параллелограмма относятся как 3 : 4, а периметр его равен 28. Найдите большую сторону параллелограмма.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 8.
Упражнение 45
В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 5. Найдите диагонали данного прямоугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10.
Упражнение 46
В прямоугольном треугольнике ABC из вершины прямого угла C опущена высота CH , равная 3. Из точки H опущены перпендикуляры HK и HL на катеты треугольника. Найдите расстояние между точками K и L .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 3.
Упражнение 47
Перпендикуляр BH , опущенный из вершины B прямоугольника ABCD на его диагональ AC , делит угол B в отношении 2:3. Найдите угол между перпендикуляром BH и диагональю BD .
Найдите угол между перпендикуляром BH и диагональю BD .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 18.
Упражнение 48
Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 3, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 21.
Упражнение 49
Основания трапеции относятся как 2 : 3, а средняя линия равна 5. Найдите меньшее основание.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 4.
Упражнение 50
Основания трапеции равны 4 и 10. Найдите меньший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2.
Математическая задача: Координаты пересечения диагоналей
В прямоугольной системе координат нарисован прямоугольник ABCD.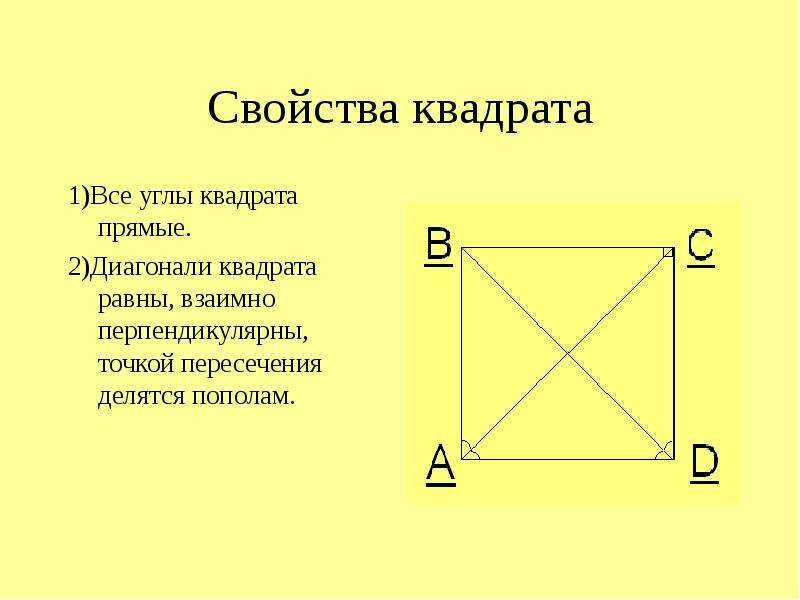 Эти координаты определяют вершины прямоугольника.
Эти координаты определяют вершины прямоугольника.
A = (2.2)
B = (8.2)
C = (8.6)
D = (2.6)
Найдите координаты пересечения диагоналей прямоугольника ABCD.
Правильный ответ:
x = 5y = 4
Пошаговое объяснение:
U = AC S = AC/2 A0 = 2; A1 = 2 C0 = 8; C1 =6 x=2A0+C0=22+8=5
y=2A1+C1=22+6=4
Нашли ошибку или неточность? Не стесняйтесь
напишите нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
Нужна помощь в вычислении среднего арифметического?
Ищете статистический калькулятор?
Для решения этой математической задачи вам необходимо знать следующие знания:
- статистика
- среднее
- геометрия
- аналитическая геометрия
- алгебра
- пересечение множеств
- планиметрия
- диагональ
- прямоугольник
- практика для 14-летних
- средняя школа
Рекомендуем посмотреть этот обучающий видеоролик по этой математической задаче: video1 video2
- Пересечение 3486
В прямоугольной системе координат есть точка A [-2; -4] и точку S [0; -2]. Определить координаты точек B, C и D так, чтобы ABCD был квадратом, а S — пересечением их диагоналей.
Определить координаты точек B, C и D так, чтобы ABCD был квадратом, а S — пересечением их диагоналей. - Прямоугольный 3478
Отрезок AB начерчен в прямоугольной системе координат с концами A [1;6] и B [5;2]. Центр симметрии является началом системы координат. Найдите координаты центра этого отрезка в этой проекции симметрии. - Координаты
Определить координаты вершин и площадь параллелограмма, две стороны которого лежат на прямых 8x + 3y + 1 = 0, 2x + y-1 = 0, а диагональ на прямой 3x + 2y + 3 = 0 - Определить
Определить, к какому типу относится четырехугольник ABCD, и найти его периметр, если известны координаты вершин: A/2,4/, B/-2,1/, C/-2,-2/, D/2,- 5 /. - Пересечение Q2 с линией
Уравнение кривой C равно y=2x² — 8x +9, а уравнение прямой L равно x + y=3. (1) Найдите x-координаты точек пересечения L и C. (ii) покажите, что одна из этих точек также является - Пересечение 19343
Какова сумма всех координат точек на пересечении прямой p: x = -1-2t, y = 5-4t, z = -3 + 6t, где t — действительное число, с координатными плоскостями xy и yz? - Кривая и линия
Уравнение кривой C равно y=2x² -8x+9, а уравнение прямой L равно x+ y=3 (1) Найдите координаты x точек пересечения L и C. (2) Показать, что одна из этих точек также является стационарной точкой C?
(2) Показать, что одна из этих точек также является стационарной точкой C? - Координаты 66474
Нарисуйте трапецию в системе координат с основаниями длиной 4 см, длиной 2 см и высотой 3 см. Пожалуйста, запишите координаты его вершин. - Координаты
Координаты (5, 2) и (-6, 2) являются вершинами шестиугольника. Объясните, как найти длину отрезка, образованного этими концами. Какова длина сегмента? - Координаты вершин квадрата
Квадрат ABCD имеет центр S [−3, −2] и вершину A [1, −3]. Найдите координаты остальных вершин квадрата. - Воздушный змей
ABCD — воздушный змей. Угол OBC = 20° и угол OCD = 35°. О — пересечение диагоналей. Найдите угол ABC, угол ADC и угол BAD. - Трапеция — пересечение диагоналей
В ABCD длина трапеции AB = 8 см, высота трапеции 6 см, расстояние от пересечения диагоналей до AB 4 см. Вычислите площадь трапеции. - Координаты вектора
Определить координату вектора u=CD, если C(19;-7) и D(-16;-5) - Диагонали трапеции
Дана трапеция ABCD с основаниями | АБ | = 12 см, |CD| = 8 см. Точка S — это пересечение диагоналей, для которых |AS| имеет длину 6 см. Вычислите длину полной диагонали АС.
Точка S — это пересечение диагоналей, для которых |AS| имеет длину 6 см. Вычислите длину полной диагонали АС. - Прямоугольная трапеция
В прямоугольной трапеции ABCD с прямыми углами при вершинах A и D со сторонами a = 12 см, b = 13 см, c = 7 см. Найдите углы бета и гамма и высоту v. - Вычислить 7
Вычислить высоту трапеции ABCD, где координаты вершин: A[2, 1], B[8, 5], C[5, 5] и D[2, 3] - X -coordinate 81737
В треугольнике ABC определите координаты точки B, если известно, что точки A и B лежат на прямой 3x-y-5=0, точки A и C лежат на прямой 2x+3y+4=0, точка C лежит на оси координат x, а угол при вершине C прямой.
Свойства прямоугольника и квадрата. Задача 2
Дан прямоугольник, нарисованный в координатной плоскости, можно найти точку пересечения диагоналей.
Сначала запишите вершины в терминах заданных длин сторон. Если нижняя левая вершина равна (0,0), а левая сторона имеет длину a , то верхняя левая вершина находится в координате (0,a). Тогда при заданной горизонтальной длине b + c правая верхняя вершина находится в точке (b + c, a), а при движении вниз по длине a нижняя правая вершина находится в точке (b + c, 0).
Тогда при заданной горизонтальной длине b + c правая верхняя вершина находится в точке (b + c, a), а при движении вниз по длине a нижняя правая вершина находится в точке (b + c, 0).
Тогда вспомните, что диагонали прямоугольника делят друг друга пополам. Итак, найдите середину одной из диагоналей, образованных в этом прямоугольнике (концы диагоналей — это координаты противоположных сторон).
равноугольный многоугольник конгруэнтные диагонали делить пополам правильный четырехугольник биссектрисы угла координатная геометрия
Иногда в геометрии нам нравится брать систему координат и применять ее к тому, что мы знаем. В этой задаче говорится, что четырехугольник является прямоугольником. Найдите точку пересечения диагоналей.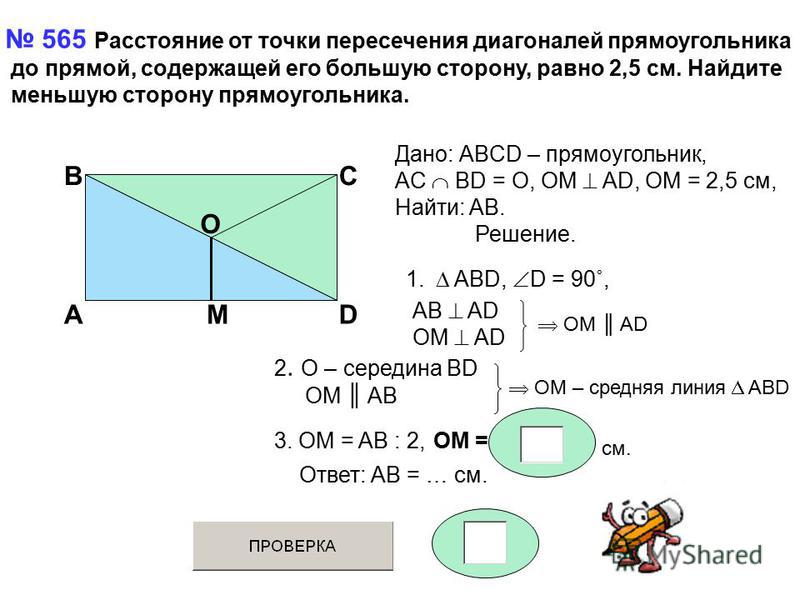
Итак, первое, что я собираюсь сделать, это нарисовать диагонали, чтобы дать нам представление о том, на что мы смотрим. А что я знаю о диагоналях прямоугольника? Что ж, если я посмотрю на эту диаграмму, мы увидим, что диагонали конгруэнтны и делят друг друга пополам. Так что эта ключевая часть о разделении друг друга пополам поможет нам найти эту точку пересечения.
Итак, давайте начнем с записи упорядоченных пар в каждой из четырех вершин. Что ж, мы знаем, что это точка (0,0), и если она имеет длину A, мы знаем, что это будет расстояние по вертикали, так что это будет точка (0,a), потому что мы не t перемещается влево или вправо по нашей оси X. Если я посмотрю на эту точку прямо здесь, мы преодолели расстояние b плюс c. Откуда я это знаю? Потому что в прямоугольнике противоположные стороны будут равны, потому что это параллелограмм.
Итак, мы собираемся переместить b плюс c вправо, поэтому я собираюсь написать b плюс c, но мы не двигались ни вверх, ни вниз, поэтому наша координата y останется прежней.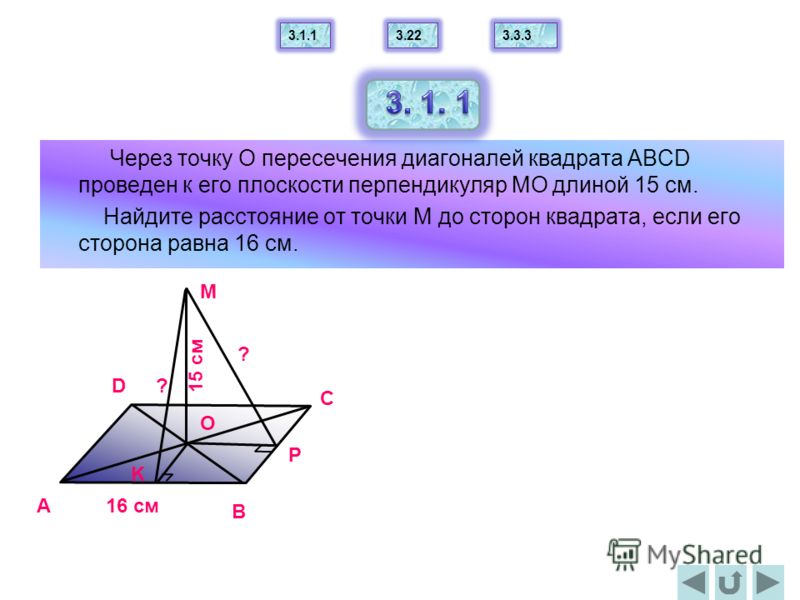

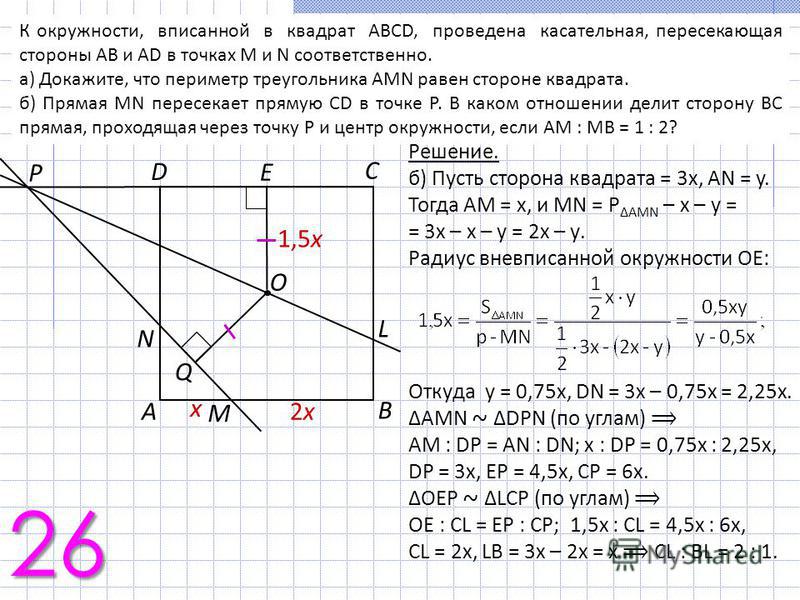 Определить координаты точек B, C и D так, чтобы ABCD был квадратом, а S — пересечением их диагоналей.
Определить координаты точек B, C и D так, чтобы ABCD был квадратом, а S — пересечением их диагоналей. (2) Показать, что одна из этих точек также является стационарной точкой C?
(2) Показать, что одна из этих точек также является стационарной точкой C? Точка S — это пересечение диагоналей, для которых |AS| имеет длину 6 см. Вычислите длину полной диагонали АС.
Точка S — это пересечение диагоналей, для которых |AS| имеет длину 6 см. Вычислите длину полной диагонали АС.
Leave A Comment