Подготовка к ЕГЭ по математике 2013. Решение задач типа С2 координатно-векторным методом. | Презентация к уроку по геометрии (11 класс) по теме:

При решении задач C2 и C4 единого государственного экзамена по математике полезным является использование координатного метода. Данный метод практически не используется в средней школе, но его использование существенно упрощает решение сложных геометрических задач, причем как из раздела планиметрия, так и стереометрия. В разработке продемонстрирован координатный метод решения стереометрических задач типа С2. Разбирается решение типичных задач на нахождение угла между плоскостями, встречающихся в задании С2 с помощью метода координат.

Скачать:

Подписи к слайдам:

ЕГЭ-2013. Задачи типа С2
Задание С2 ЕГЭ. Угол между плоскостями. Координатный метод решения стереометрических задач типа С2.Разработка учителя ГБОУ СОШ№618 Макаровой Т.П.
1. Уравнение плоскости имеет вид ax+by+cz+d=0
В этом уравнении плоскости коэффициенты – координаты вектора нормали к плоскости (то есть вектора, перпендикулярного плоскости).
Угол между плоскостями
Величина двугранного угла измеряется величиной соответствующего линейного угла.Чтобы построить линейный угол двугранного угла, нужно взять на линии пересечения плоскостей произвольную точку, и в каждой плоскости провести к этой точке луч перпендикулярно линии пересечения плоскостей. Угол, образованный этими лучами и есть линейный угол двугранного угла:
Величиной угла между плоскостями называется величина меньшего двугранного угла.Пусть плоскости и заданы уравнениями:Косинус угла между плоскостями находится по такой формуле:В ответе мы записываем , так как величиной угла между плоскостями называется величина меньшего двугранного угла.
Задача (ЕГЭ-2012).
В правильной четырехугольной призме со стороной основания 12 и высотой 21 на ребре взята точка М так, что AM=8 . На ребре взята точка K так, что . Найдите угол между плоскостью и плоскостью .
Решение.
Запишем координаты точек: М(0;0;13),К(12;0;8),
Подставим их в систему уравнений:
Отсюда:
С= -1/13, В= -1/12, А= -5/(12х13).
Подставим найденные коэффициенты в уравнение плоскости:
Подставим их в формулу для нахождения косинуса угла между плоскостями, и найдем угол:
Задача (ЕГЭ,2011). В единичном кубе АВСDA1В1С1D1 найдите угол между плоскостями АD1 Е и D1FC, где точки Е и F-середины ребер А1В1 и В1С1 соответственно.
Решение.Введём прямоугольную систему координат. Тогда А(0;0;0), С(1;1;0), D1(1;0;1), E(0;0,5;1), F(0,5;1;1).Решая систему составляем уравнение плоскости (АD1E): x+2y-z=0.2) плоскость CFD1: отсюда находим уравнение 2x+y+z-3=0. Найдём искомый угол как угол между нормалями плоскостей. , , откуда φ=60˚ Ответ: 60˚
Задача (ДР_2013).В правильной четырехугольной призме ABCDA1B1C1D1 стороны основания равны 1, а боковые ребра равны 5. На ребре АА1 отмечена точка Е так, что АЕ:ЕА1=2:3. Найдите угол между плоскостями АВС и ВЕD1.
Решение. Введем прямоугольную систему координат. Тогда В(1;0;0), Е(0;0;2), D1 (0;1;5). Решаем систему
Составляем уравнение плоскости (ВЕD1):-х+1,5у-0,5z+1=0, вектор нормали плоскости (ВЕD1)
Вектор нормали плоскости (ABC)
Найдем искомый угол как угол между нормалями плоскостей
Ответ:
Задача. Дан куб ABCDA1B1C1D1 с ребром 1. Точка М-середина ребра АВ, точка К – середина ребра DD1. Найти угол между плоскостями АКВ1 и КМС.
РЕШЕНИЕ. Введем прямоугольную систему координат, поместив начало координат в точку А. Составим уравнение плоскости АКВ1. Точка А (0;0;0) принадлежит этой плоскости, то d=0. Подставим координаты точек К(0;1; 0,5) и В1 (1;0;1)в уравнение плоскости, получим b+c/2=0, a+c=0. Таким образом имеем 2х+у — 2z=0. Составим уравнение плоскости КМС. Подставим координаты точек К(0;1; 0,5) и М (0,5;0;0),С(1;1;0) в уравнение плоскости, получим систему:
Уравнение плоскости (КМС) принимает вид
и угол между плоскостями АВК1 и КМС находим из
2х – у +4z=1. Итак,
Для самостоятельного решения
Задача (С2 ЕГЭ 2010). В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AB = 8 , AD = 6 , CC1 =6 . Найдите угол меду плоскостями CD1 B1 и AD1B1 .Задача (С2 ЕГЭ 2010). Все ребра пирамиды SABCD с вершиной S равны между собой. Найдите угол между плоскостями SBM и SCD , где точка M — середина ребра CD . Ответ:Задача. В единичном кубе АВСDA1В1С1D1 найдите угол между плоскостями АD1Е и D1FC, где точки Е и F-середины ребер А1В1 и В1С1 соответственно. Ответ: 600.Задача. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между плоскостями ACB1 и BA1C1.Задача. В правильной четырехугольной пирамиде SABCD с основанием ABCD сторона основания равна , а боковое ребро равно 10. Найти угол между плоскостями ABC и ACM, где точка M делит ребро BS так, что BM : MS = 2 : 1.
Источники:
http://ege-ok.ru/ http://nsportal.ru/

Координатный метод решения стереометрических задач типа С2 на ЕГЭ

1.

ЕГЭ-2013. Задачи типа С2Задание С2 ЕГЭ. Угол между плоскостями.
Координатный метод решения стереометрических задач типа С2.
Разработка Макаровой Татьяны Павловны,
учителя математики высшей категории
ГБОУ СОШ№618 г. Москвы

2. 1. Уравнение плоскости имеет вид ax+by+cz+d=0

• В этом уравнении плоскости
коэффициенты – координаты вектора
нормали к плоскости (то есть вектора,
перпендикулярного плоскости).
n ( a , b, c )

3. Угол между плоскостями

Величина двугранного угла
измеряется величиной
соответствующего линейного угла.
Чтобы построить линейный угол
двугранного угла, нужно взять на
линии пересечения плоскостей
произвольную точку, и в каждой
плоскости провести к этой точке луч
перпендикулярно линии пересечения
плоскостей. Угол, образованный
этими лучами и есть линейный
угол двугранного угла:
• Величиной угла между плоскостями
называется величина меньшего
двугранного угла.
• Пусть плоскости 1 и 2 заданы уравнениями:
1 : a1x b1 y c1z d 0
2 : a2 x b2 y c2 z d 0
• Косинус угла между плоскостями
находится по такой формуле:
cos
a1a2 b1b2 c1c2
a12 b12 c12 a22 b22 c22
• В ответе мы записываем cos
, так как
величиной угла между плоскостями называется
величина меньшего двугранного угла.

5. Задача (ЕГЭ-2012).

• В правильной
четырехугольной призме
ABCDA1B1C1D1 со стороной
основания 12 и высотой
21 на ребре АА1 взята
точка М так, что AM=8 .
На ребре ВВ1
взята
точка K так, что В1К 8 .
Найдите угол между
плоскостью D1MK
и
плоскостью СС1D1 .

6. Решение.

D1МК :
Запишем координаты точек:
М(0;0;13),К(12;0;8), D1 (0;12;0)
Подставим их в систему уравнений:
Отсюда:
С= -1/13, В= -1/12, А= -5/(12х13).
Подставим найденные коэффициенты в
уравнение плоскости:
Аналогично, С (12;12;21), С1 (12;12;0), D1 (0;12;0)
A 0,
12 A 12 B 1 0,
12 B 1 0,
C 0,
12 A 12 B 21C 1 0
1
B .
12
1
y 1 0, y 12 0.
12
Подставим их в формулу для нахождения косинуса угла
между плоскостями, и найдем угол:
сos
5 0 13 1 12 0
52 132 12 2 1
13
13 2
1
.
2
450

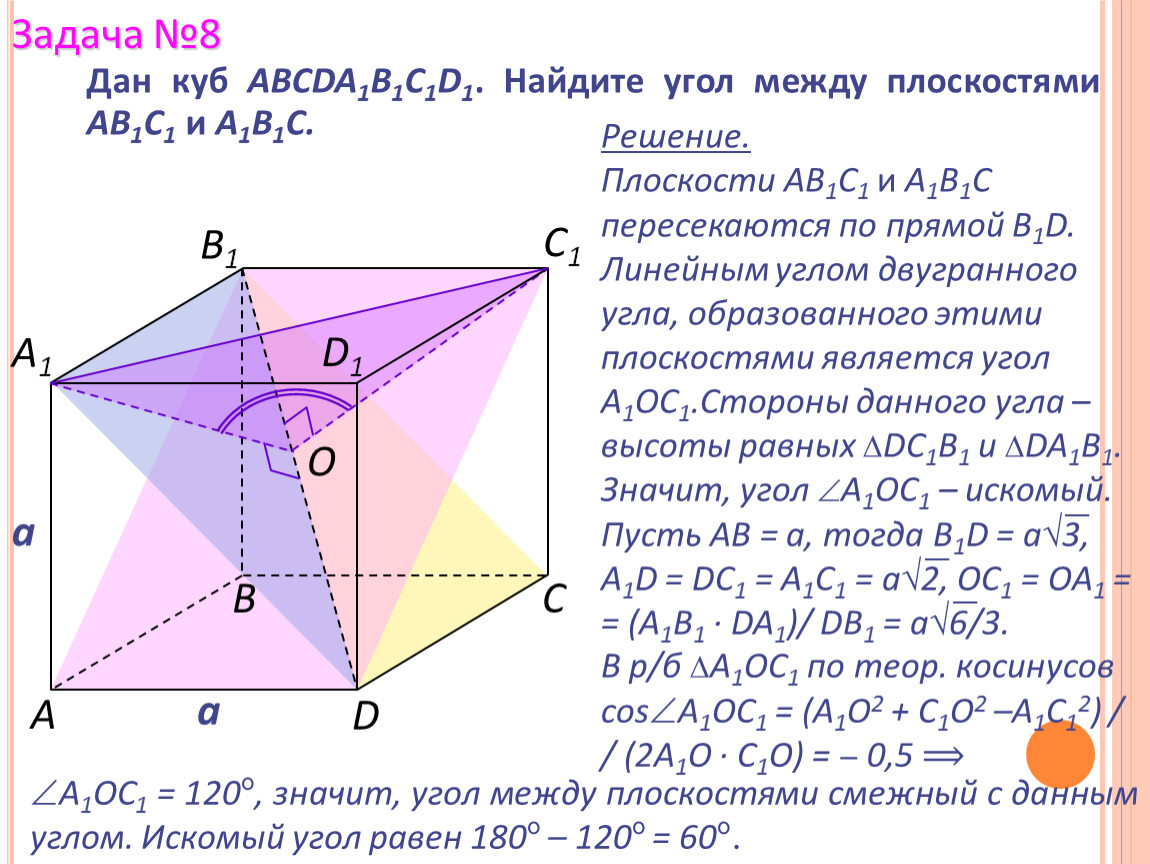
8. Задача (ЕГЭ,2011). В единичном кубе АВСDA1В1С1D1 найдите угол между плоскостями АD1 Е и D1FC, где точки Е и F-середины ребер А1В1 и В1С1 соответственно.

Задача (ЕГЭ,2011). В единичном кубе АВСDA1В1С1D1 найдите
угол между плоскостями АD1 Е и D1FC, где точки Е и Fсередины ребер А1В1 и В1С1 соответственно.
Решение.
Введём прямоугольную систему координат. Тогда
А(0;0;0), С(1;1;0), D1(1;0;1), E(0;0,5;1), F(0,5;1;1).
1) Решая систему 0 А 0 В 0 С D 0,
A C D 0,
0,5 B C D 0,
составляем уравнение плоскости (АD1E): x+2y-z=0.
2) плоскость CFD1: A C D 0,
0,5 A B C D 0,
A B D 0
отсюда находим уравнение 2x+y+z-3=0. Найдём
искомый угол как угол между нормалями плоскостей.
n 1;2; 1 , m 2;1;1 ,
n m 2 2 1 1
cos
n m
откуда φ=60˚ Ответ: 60˚
6 6
2

9. Задача (ДР_2013).В правильной четырехугольной призме ABCDA1B1C1D1 стороны основания равны 1, а боковые ребра равны 5. На ребре АА1 отмечена точка Е та

Задача (ДР_2013).В правильной четырехугольной призме ABCDA1B1C1D1
стороны основания равны 1, а боковые ребра равны 5. На ребре АА1 отмечена
точка Е так, что АЕ:ЕА1=2:3. 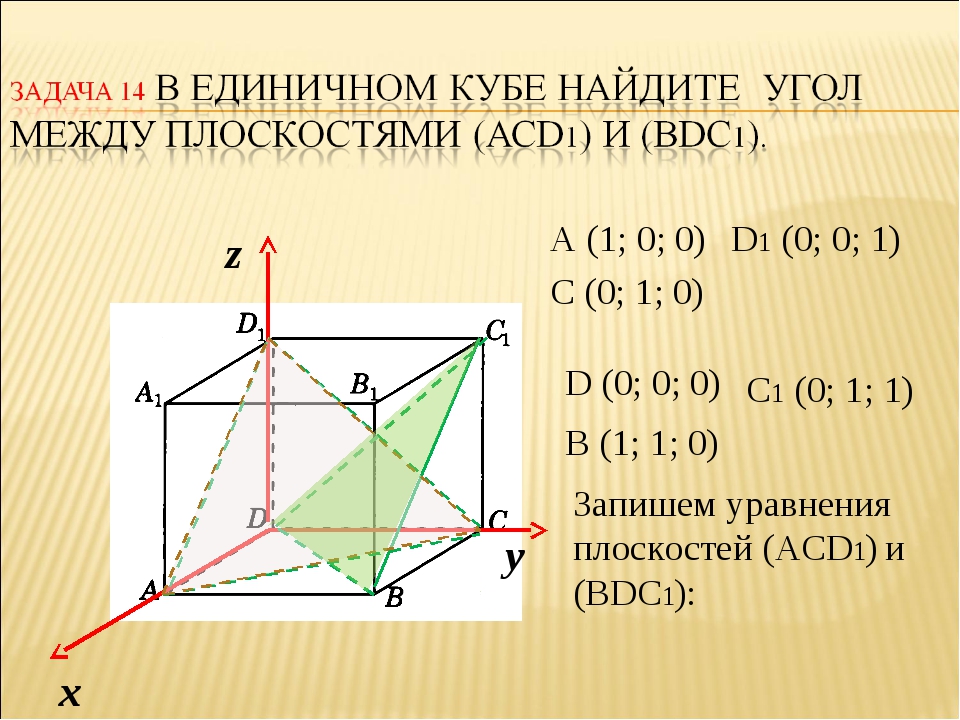Найдите угол между плоскостями АВС и ВЕD1.
Решение. Введем прямоугольную систему
координат. Тогда В(1;0;0), Е(0;0;2), D1 (0;1;5).
Решаем систему A 1 0,
A 1,
2C 1 0,
B 5C 1 0,
C 0,5;
B 1,5.
Составляем уравнение плоскости (ВЕD1):
-х+1,5у-0,5z+1=0, вектор нормали плоскости
(ВЕD1) n 1;1,5; 0,5
Вектор нормали плоскости (ABC) AA1 n2 0;0;5
1
Найдем искомый угол как угол между нормалями плоскостей
cos
Ответ:
0 ( 1) 0 1,5 5 ( 0,5)
0 0 52 12 (1,5) 2 ( 0,5) 2
1
arccos
.
14
1
1
, arccos
.
14
14

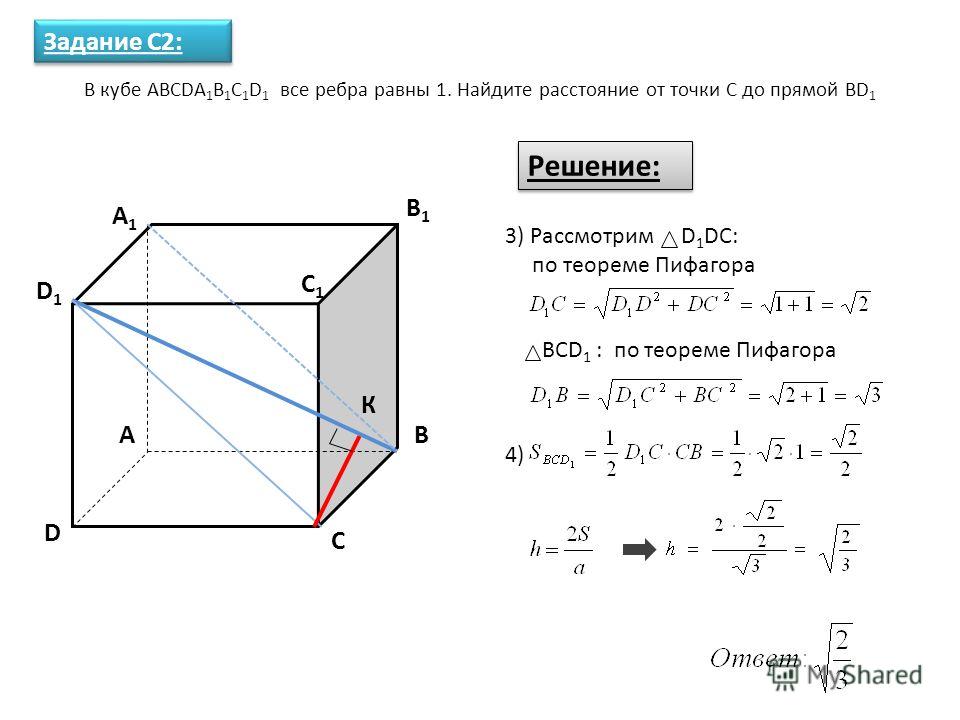
10. Задача. Дан куб ABCDA1B1C1D1 с ребром 1. Точка М-середина ребра АВ, точка К – середина ребра DD1. Найти угол между плоскостями АКВ1 и КМС.

РЕШЕНИЕ. Введем прямоугольную систему координат,
поместив начало координат в точку А. Составим уравнение
плоскости АКВ1. Точка А (0;0;0) принадлежит этой
плоскости, то d=0.
Подставим координаты точек К(0;1; 0,5) и В1 (1;0;1)
в уравнение плоскости, получим b+c/2=0, a+c=0.
Таким образом имеем 2х+у — 2z=0.
Составим уравнение плоскости КМС.
Подставим координаты точек К(0;1; 0,5) и М (0,5;0;0),
С(1;1;0) в уравнение плоскости, получим систему:
B 0,5C D 0, С 2 А,
0
/
5
A
D
0
,
В 0,5 А,
A B D 0. D 0,5 A.
Уравнение плоскости (КМС) принимает вид
2х – у +4z=1. Итак, n1 2;1; 2 , n1 3, n2 2; 1;4 , n2 21
и угол между плоскостями АВК1 и КМС находим из
соs
5
3 21
, arccos
5
.
3 21

13. Для самостоятельного решения

• Задача (С2 ЕГЭ 2010). В прямоугольном параллелепипеде ABCDA1B1C1D1
известны ребра AB = 8 , AD = 6 , CC1 =6 . Найдите угол меду плоскостями CD1 B1
и AD1B1 .
• Задача (С2 ЕГЭ 2010). Все ребра пирамиды SABCD с вершиной S равны между
собой. Найдите угол между плоскостями SBM и SCD , где точка M — середина
ребра CD . Ответ:
• Задача. В единичном кубе АВСDA1В1С1D1 найдите угол между плоскостями
АD1Е и D1FC, где точки Е и F-середины
ребер А1В1 и В1С1 соответственно.
3
arccos
Ответ: 600.
11
• Задача. В правильной треугольной призме ABCA1B1C1, все ребра которой
равны 1, найти косинус угла между плоскостями ACB1 и BA1C1.
• Задача. В правильной четырехугольной пирамиде SABCD с основанием
ABCD сторона основания равна , а боковое ребро равно 10. Найти угол
между плоскостями ABC и ACM, где точка M делит ребро BS так, что BM :
MS = 2 : 1.

14. Источники:

• http://ege-ok.ru/
• http://nsportal.ru/

геометрия — Угол между двумя плоскостями в кубе

Задавать вопрос

спросил

Изменено 1 год, 1 месяц назад

Просмотрено 136 раз

$\begingroup$

Найдите косинус угла между плоскостями $(A,B,C,D)$ и $(M,N,K)$ в кубе $ABCDA_1B_1C_1D_1$, где $M,N$ и $K$ — середины $BB_1,A_1B_1$ и $B_1C_1$ соответственно.

Как мы видим на диаграмме, линия пересечения $(A,B,C,D)$ и $(M,N,K)$ не находится внутри куба, и я не вижу, что характеризует его. Можете ли вы дать мне подсказку?

  • геометрия
  • 3d
$\endgroup$

6 9{-1}\left(\dfrac{1}{\sqrt{3}}\right)$

А это острый угол.

$\endgroup$

$\begingroup$

Угол между двумя плоскостями можно определить двумя эквивалентными способами: углом между нормалями (как в другом ответе) или углом между двумя прямыми, перпендикулярными на пересечении двух плоскостей. Эта вторая процедура немного дольше.

На вашем рисунке пересечение двух плоскостей представляет собой линию в плоскости $ABCD$, перпендикулярную $BD$. Назовем $T$ точку, где $BD$ встречается с пересечением плоскостей. Тогда в силу симметрии $TM$ пересечет $KN$ в точке $P$, где $P$ — середина между $K$ и $N$. Обратите внимание, что $\треугольник PMB_1$ и $\треугольник TMB$ конгруэнтны (прямоугольные треугольники, противоположные углы равны и $BM=B_1M$).