404 Cтраница не найдена
Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Педагогический (научно-педагогический) составИррациональные уравнения (8 класс) — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас.
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Мы урок сегодня с вами вместе проведем.Уравненья порешаем и ответ найдем.
Урок недлинный, но время растяжимо.
Оно зависит от того, какого рода
Содержимым вы наполните его.
Что ж, урок начнем сейчас!
Всем удачи, в добрый час!
НЕ ГОВОРИ: ИХ НЕТ, НО С ГОРДОСТЬЮ: БЫЛИ.
Эварист Галуа
(1811 – 1832)
Карл Гаусс
(1777 – 1855)
Франсуа Виет
(1540 – 1603)
ПОНЯТИЕ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ
?
Если в уравнении переменная содержится
под знаком квадратного корня, то
уравнение называют иррациональным.
Примеры:
2x 1 3
2x 5 4x 7
2 x 5x 2 x 6
2
ИЗУЧАЕМ НОВОЕ
Метод возведения в квадрат обеих частей
уравнения
2x 1 3
2x 1 3
2
2x 1 9
2x 8
x 4
Ответ: x 4
ИЗУЧАЕМ НОВОЕ
Метод возведения в квадрат обеих частей
уравнения
2x 5 4x 7
( 2x 5) ( 4x 7 )
2
2x 5 4x 7
x 1
Проверим!!!
2
ПРОВЕРКА
Подставим 1 вместо х в заданное
иррациональное уравнение, получим:
2 1 5 4 1 7
3 3
x 1 — посторонний корень
Ответ: иррациональное уравнение не
имеет корней
ЗАПОМНИ
Иррациональное уравнение решают методом
возведения обеих его частей в квадрат;
решив полученное в итоге рациональное
уравнение, надо обязательно сделать
проверку, отсеяв возможные посторонние
корни.
ТРЕНИРУЕМСЯ РЕШАТЬ
1)
х 2 3
х 2
2
32
х 2 9
х 7.
Проверка :
7 2 3
9 3
3 3 верно
2)
6 5х 2
2
6 5х 2
2
2
6 5х 4
2
2
х .
3
2
Корней нет
2
ТРЕНИРУЕМСЯ РЕШАТЬ
3) 2 х 3 1
Проверка : х 4
х 1
2х 3
1
х 1
2х 3 х 1
0
х 1
х 4 0;
х 1 0
х 4
х 1
2 ( 4 ) 3
1
4 1
1 1(верно)
ТРЕНИРУЕМСЯ РЕШАТЬ
Проверка : х1 7 п.к.
4) 15 3 х 1 х
15 3х 1 х
2
2
15 3 х 1 2 х х
2
х 5 х 14 0
2
х1 х2 5;
х1 х2 14
х1 7;
х2 2;
15 3 7 1 7
6 6(неверно)
х2 2;
15 3 ( 2) 1 ( 2)
3 3(верно)
Ответ : 2
ТРЕНИРУЕМСЯ РЕШАТЬ
Проверка : х1 5 п.к.
5) 34 5 х 7 2 х
34 5 х 49 28 х 4 х
4 х 23х 15 0
2
х1 5;
3
х2 ;
4
2
34 5 5 7 2 5
3 3(неверно)
3
х2 ;
4
3
3
34 5 7 2
4
4
11 11
(верно)
2 2
3
Ответ : .
4
РЕШЕНИЕ ТЕСТА
Упростите выражение 4с(с – 2) – (с – 4)2
1) 3с2;
2) 3с2 – 16;
3) 3с2 + 16;
4) 16.
Решите уравнение – х2 + 7х – 10 = 0
1) 2; 5;
2) – 2; -5;
3) нет корней;
4) 2.
Решите уравнение x 2
1) нет корней; 2) 9;
4) 11.
3
3) 7;
Решите уравнение 14+3x – 5×2 = 0 и найдите сумму его
корней.
1) 0,6;
2) 3,4;
3) – 3,4;
4) – 0,6.
3c2 – 16;
2;5;
11;
0,6;
ответ
САМОСТОЯТЕЛЬНАЯ РАБОТА
Вариант 1.
Вариант 2.
1) 6 х х;
1) 5 х 4 х;
2) 10 х 1 2 х;
2) 2 х 1 2 х;
3) х 3 1 х.
3) х х 2 4.
English Русский Правила
{2}-4ac}}{2a}. Квадратичная формула дает два решения: одно, когда ± является сложением, и одно, когда это вычитание.c=\frac{-\left(-10\right)±\sqrt{100-4\times 4\left(-6\right)}}{2\times 4}
Square -10.
c=\frac{-\left(-10\right)±\sqrt{100-16\left(-6\right)}}{2\times 4}
Умножить -4 раза 4.
c =\frac{-\left(-10\right)±\sqrt{100+96}}{2\times 4}
Умножить -16 на -6.
c=\frac{-\left(-10\right)±\sqrt{196}}{2\times 4}
Прибавьте 100 к 96.
c=\frac{-\left(-10\right)±14}{2\times 4}
Извлеките квадратный корень из 196.
c=\frac{10± 14}{2\times 4}
Противоположность -10 равна 10.
c=\frac{10±14}{8}
Умножить 2 раза на 4.
c=\frac{24}{8 }
Теперь решите уравнение c=\frac{10±14}{8}, если ± равно плюсу. Прибавьте 10 к 14.
c=3
Разделите 24 на 8.
c=\frac{-4}{8}
Теперь решите уравнение c=\frac{10±14}{8}, когда ± это минус. Вычтите 14 из 10. 92 = \frac{49}{16} u = \pm\sqrt{\frac{49}{16}} = \pm \frac{7}{4}
Упростите выражение, умножив -1 с обеих сторон и извлеките квадратный корень, чтобы получить значение неизвестной переменной u
r =\frac{5}{4} — \frac{7}{4} = -0,500 s = \frac{5}{4} + \frac{ 7}{4} = 3
Факторы r и s являются решениями квадратного уравнения. Подставьте значение u для вычисления r и s.
Оценка: оценка выражений и полиномов
Функции
Purplemath
Что такое «оценка» в математике?
«Оценка» в основном означает «упрощение выражения до одного числового значения».
Иногда вам будет дано числовое выражение, которое вам нужно будет только упростить; это скорее вопрос порядка операций. В этом уроке я сконцентрируюсь на аспекте оценки «подключи и пыхти»: подставляя значения для переменных и «пыхтя» мой путь к упрощенному ответу.
Содержание продолжается ниже
MathHelp.com
Вычисление выражений
(Кстати, да, «подключи и пыхни» — довольно стандартная терминология. Это не «технический» термин, поэтому вы, вероятно, не встретите его в своем учебнике, но вы наверняка услышите это от других студентов и, возможно, от своего преподавателя.)
Обычно единственной трудной частью оценки является отслеживание знаков «минус». Я настоятельно рекомендую вам широко использовать круглые скобки, особенно когда вы только начинаете.
Что является примером оценки?
Чтобы найти ответ, я просто подставляю заданные значения, стараясь использовать круглые скобки, особенно вокруг знаков «минус». Особенно, когда я только начинаю, может быть полезно сначала нарисовать круглые скобки:
a 2 b
( ) 2 ( )
908 3 (83) 2 901 03(4)(3)
12
Обратите внимание, как использование круглых скобок помогло мне отслеживать знак «минус» при значении и .
Это было важно, потому что в противном случае я мог бы возвести в квадрат только 2 и получить -4, что было бы неправильно.
Кстати, оказалось, что значения переменных c и d нам не нужны. Когда вам дается большой набор выражений для оценки, вы должны ожидать, что часто будет та или иная переменная, которая не будет включена ни в одно конкретное упражнение в наборе.
В этом упражнении мне дали дополнительную информацию. нет b в выражении, которое они хотят, чтобы я вычислил, поэтому я могу игнорировать это значение в своей работе: 16
16 − 2
14
Я должен позаботиться о том, чтобы не пытаться «распределить» показатель степени через круглые скобки. Показатели НЕ распределяются по сложению! Я никогда не должен пытаться сказать, что ( b + d ) 2 то же самое, что b 2 + d 2 . Это НЕ одно и то же! Я должен вычислить выражение в его нынешнем виде:
( (3) + (4) ) 2
( 7 ) 2
49
В этом выражении возведение в квадрат производится для каждой переменной отдельно.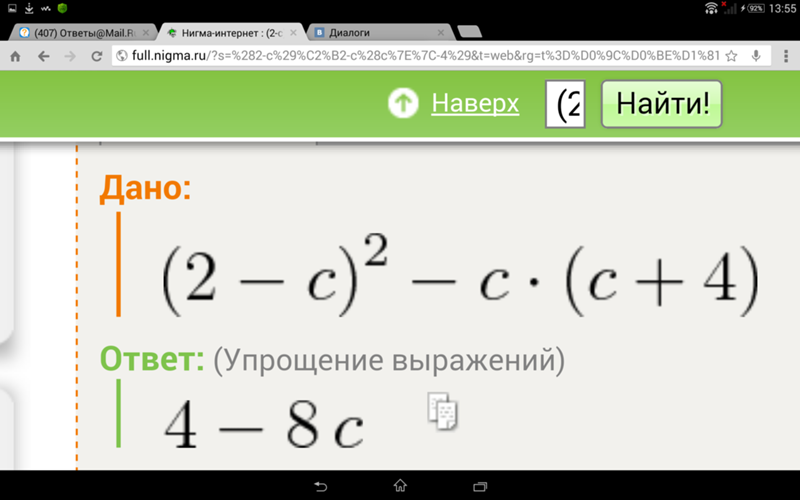
(3) 2 + (4) 2
9 + 16
25
Обратите внимание, что этот последний ответ выше не соответствует ответу на предыдущую оценку. Это прямо демонстрирует тот факт, что показатели степени не распределяются при сложении так, как это происходит при умножении.
На следующем тесте, а также на выпускном экзамене следует ожидать, по крайней мере, упражнения, аналогичные двум предыдущим. Эта склонность пытаться распределять показатель степени (а не умножение) над сложением является распространенной ошибкой учащихся, и ваш преподаватель почти наверняка захочет напоминать вам — и часто! — о разнице между возведением суммы в квадрат и суммированием двух квадратов. Не путайте их!
В этом упражнении мне нужно использовать значения всех четырех переменных. Но мне нужно быть осторожным в своем размещении, потому что это выражение не использует переменные в алфавитном порядке.
(3)(−4) 3 − (−2)(4)
(3)(−64) − (−8)
−192 + 8
−184
Наиболее общий тип «выражения», который вам, вероятно, потребуется оценить, будет полиномом.
Чтобы вычислить полином, вы берете этот полином и подставляете переменную (обычно x ) в любое число, которое они вам дали.
Что является примером вычисления многочлена?
Это мой первый многочлен для оценки, поэтому я снова начну с пустых скобок, показывающих, где нужно разместить значение переменной.
x 4 + 3 x 3 − x 2 + 6
( ) 8 1 + 9 9 83 3 − ( ) 2 + 6
( −3) 4 + 3(−3) 3 − (−3) 2 + 6
81 + 3(−27) − (9) + 6
81 − 81 − 9 + 6
−3
Я рад, что научился использовать круглые скобки, чтобы сделать свои замены понятными. В этом случае эти скобки помогут мне отслеживать знаки «минус».
3(−2) 2 − 12(−2) + 4
3(4) + 24 + 4
12 + 24 + 4
40
Это другое. Мне дали уравнение с двумя переменными, но дали значение только одной из переменных.
Я предполагаю, что они хотят, чтобы я подключил x и вычислил результирующее значение для y .
y = 4(−1) − 3
= −4 − 3 = −7
Тогда мой ответ будет уравнением:
y = −7
Примечание. В этом последнем упражнении выше мы подставляли значение одной из переменных и упрощали поиск значения другой переменной. Кроме того, часть, к которой мы подключались, была установлена равной имени, y . Из-за этого мы не просто вычисляли выражение; на самом деле мы оценивали полиномиальную функцию. Результат нашего plug-n-chug означает, что точка ( x , y ) = (−1, −7) находится на прямой y = 4 x — 3; то есть эта точка находится на графике полиномиальной функции.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении выражений для заданных значений переменных (или пропустите виджет и перейдите на следующую страницу). Попробуйте введенное упражнение или введите свое собственное упражнение.
Leave A Comment