Упрощение выражений с решением онлайн: Упрощение выражений · Калькулятор Онлайн

Упрощение Выражений — Mathcracker.Com

Инструкции: Используйте этот калькулятор упрощения выражений для сокращения любого действительного алгебраического выражения, которое вы предоставите, показывая все шаги. Пожалуйста, введите выражение, которое вы хотите упростить, используя правила PEMDAS.

Подробнее о калькулятор для упрощения выражений

Калькулятор упрощения с шагами позволяет упростить любое действительное выражение, включающее основные операции, в том числе сложение, вычитание, умножение, деление, дроби, радикалы и т.д.

Все, что вам нужно предоставить, это правильное выражение, включающее основные операции. Это может быть что-то простое, как «1/4 + 1/5», а может быть что-то более сложное, как «sqrt(3)/(3+2^3+5+1/6)».

После того как вы введете правильное выражение, вам нужно нажать на кнопку «Рассчитать», и вам будут показаны все этапы упрощения вычислений.

Калькулятор сделает все возможное, чтобы показать значимые шаги для вычислений, и он, безусловно, достигает этого для большинства простых выражений.

Как упростить выражения с помощью умножения

Этот вопрос связан с другим вопросом — как упрощать выражения с суммами, а еще интереснее, как упростить выражения, в которых смешаны суммы и умножения? Ответ прост: PEMDAS

PEMDAS обеспечивает четкое правило того, какие операции имеют приоритет для выполнения в первую очередь. Следуйте этим правилам PEMDAS:

• Первый: «P» (что соответствует «круглым скобкам»). В алгебраическом выражении круглые скобки имеют приоритет всегда.
• Следующий: «E» (экспоненты). После круглых скобок приоритет отдается экспонентам
• Следующий: «М» (умножение). После экспоненты приоритет отдается умножению
• Следующий: «D» (деление). После умножения приоритет отдается делению
• Следующий: «А» (дополнение). После делений приоритет отдается дополнениям
• Наконец: «S» (вычитание). После сложения приоритет отдается вычитанию

Эти правила позволят вам однозначно оценить составное выражение. Этот калькулятор покажет вам этапы упрощения, следуя правилам приоритета PEMDAS

Каковы шаги упрощения выражения

• Шаг 1: Оцените, хорошо ли определено выражение. Это может быть не прямое или простое определение, в зависимости от сложности передаваемого выражения
• Шаг 2: Если он недействителен, остановитесь, процесс завершается. Если он действителен, то вы используете PEMDAS для руководства процессом упрощения
• Шаг 3: Перейдите к упрощению по приоритетам, при необходимости сделайте много шагов, следя поочередно за приоритетами PEMDAS, пока выражение не будет невозможно упростить дальше

Как упростить выражения с дробями?

В целом, это легко упрощать дроби , потому что стратегию невозможно пропустить: нужно найти общие знаменатели. Например, в простейшем случае с 2 дробями, вы получите:

\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]

К сожалению, существуют выражения, которые намного сложнее простых дроби . Но все же, соблюдение правильной очередности операций, знание того, что нужно делать в первую очередь, а что потом, дает вам четкую дорожную карту для упрощения даже самых сложных выражений.

Это калькулятор для упрощения радикалов?

Да, это верно. Вычисление радикалов или корней — это форма применения экспоненты. {1/2}\), что означает, что квадратный корень из 3 равен возведению 3 в степень 1/2 (поэтому 1/2 — это экспонента).

Теперь этот калькулятор будет упрощать выражения, содержащие другие операции, чем просто a уменьшение количества радикалов . Таким образом, этот калькулятор хорош при упрощении алгебраических выражений в целом

Это калькулятор для упрощения экспоненты?

Да. Все элементарные операции, включенные в PEMDAS, поддерживаются этим калькулятором упрощения, включая экспоненты («E» в PEMDAS).

Теперь, когда у вас есть экспоненты, смешанные с выражениями, в которых нет экспонент, получаются сложные выражения, но это нормально.

В худшем случае выражение не будет иметь дальнейших упрощений.

Пример: вычисление упрощения выражения

Вычислите следующее: \( \displaystyle \frac{1}{3} + \frac{5}{4} — \frac{5}{6} \times \sqrt{8} \)

Отвечать: Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\cdot\sqrt{8}\).

Получается следующий расчет:

\( \displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\sqrt{8}\)

By simplifying the radical: \(\displaystyle \sqrt{8} = \sqrt{ 2^2 \cdot 2} = 2\sqrt{ 2}\)

\( = \,\,\)

\(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\cdot 2\sqrt{2}\)

Canceling 2 from the denominator of \(\displaystyle -\frac{ 5}{ 6} \)

\( = \,\,\)

\(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{3}\sqrt{2}\)

Amplifying in order to get the common denominator 12

\( = \,\,\)

\(\displaystyle \frac{1}{3}\cdot\frac{4}{4}+\frac{5}{4}\cdot\frac{3}{3}-\frac{5}{3}\sqrt{2}\)

We need to use the common denominator: 12

\( = \,\,\)

\(\displaystyle \frac{1\cdot 4+5\cdot 3}{12}-\frac{5}{3}\sqrt{2}\)

Expanding each term: \(4+5 \times 3 = 4+15\)

\( = \,\,\)

\(\displaystyle \frac{4+15}{12}-\frac{5}{3}\sqrt{2}\)

Adding up each term in the numerator

\( = \,\,\)

\(\displaystyle \frac{19}{12}-\frac{5}{3}\sqrt{2}\)

чем завершается расчет. 2 \cdot 2} = 2\sqrt{ 2}\)

\( = \,\,\)

\(\displaystyle \frac{\frac{1}{3}+\frac{5}{4}-\frac{5}{6}}{2+3\cdot 2\sqrt{2}}\)

Reducing the integers that can be multiplied together: \(\displaystyle 3\times2 = 6\)

\( = \,\,\)

\(\displaystyle \frac{\frac{1}{3}+\frac{5}{4}-\frac{5}{6}}{2+6\sqrt{2}}\)

Amplifying in order to get the common denominator 12

\( = \,\,\)

\(\displaystyle \frac{\frac{1}{3}\cdot \frac{4}{4}+\frac{5}{4}\cdot \frac{3}{3}-\frac{5}{6}\cdot \frac{2}{2}}{2+6\sqrt{2}}\)

Finding a common denominator: 12

\( = \,\,\)

\(\displaystyle \frac{\frac{1\cdot 4+5\cdot 3-5\cdot 2}{12}}{2+6\sqrt{2}}\)

Expanding each term in the numerator: \(4+5 \times 3-5 \times 2 = 4+15-10\)

\( = \,\,\)

\(\displaystyle \frac{\frac{4+15-10}{12}}{2+6\sqrt{2}}\)

Adding each term

\( = \,\,\)

\(\displaystyle \frac{\frac{9}{12}}{2+6\sqrt{2}}\)

We can factor out 3 for both the numerator and denominator.

\( = \,\,\)

\(\displaystyle \frac{\frac{3\cdot 3}{3\cdot 4}}{2+6\sqrt{2}}\)

Now we cancel 3 out from the numerator and denominator.

\( = \,\,\)

\(\displaystyle \frac{\frac{3}{4}}{2+6\sqrt{2}}\)

и на этом расчеты завершены.

Пример: еще одно упрощение выражения

Рассчитайте \( \displaystyle \frac{1}{\left(\frac{2}{3} \times \frac{6}{5} \right)} + \frac{2}{5} \).

Отвечать: Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \frac{1}{\frac{2}{3}\cdot\frac{6}{5}}+\frac{2}{5}\).

Получается следующий расчет:

\( \displaystyle \frac{1}{\frac{2}{3}\cdot\frac{6}{5}}+\frac{2}{5}\)

We can multiply the terms in the top and bottom, and we get \(\displaystyle\frac{ 2}{ 3} \times \frac{ 6}{ 5}= \frac{ 2 \times 6}{ 3 \times 5} \)

\( = \,\,\)

\(\displaystyle \frac{1}{\frac{2\cdot 6}{3\cdot 5}}+\frac{2}{5}\)

Factoring out the term \(\displaystyle 3\) in the numerator and denominator of \(\displaystyle \frac{ 2 \times 6}{ 3 \times 5}\)

\( = \,\,\)

\(\displaystyle \frac{1}{\frac{2\cdot 2}{5}}+\frac{2}{5}\)

After simplifying the common factors in the numerator and denominator

\( = \,\,\)

\(\displaystyle \frac{1}{\frac{4}{5}}+\frac{2}{5}\)

Multiplying by 1 preserves the value: \(\displaystyle 1 \times \frac{ 5}{ 4} = \frac{ 5}{ 4}\)

\( = \,\,\)

\(\displaystyle \frac{5}{4}+\frac{2}{5}\)

Amplifying in order to get the common denominator 20

\( = \,\,\)

\(\displaystyle \frac{5}{4}\cdot\frac{5}{5}+\frac{2}{5}\cdot\frac{4}{4}\)

Finding a common denominator: 20

\( = \,\,\)

\(\displaystyle \frac{5\cdot 5+2\cdot 4}{20}\)

Expanding each term: \(5 \times 5+2 \times 4 = 25+8\)

\( = \,\,\)

\(\displaystyle \frac{25+8}{20}\)

Operating the terms in the numerator

\( = \,\,\)

\(\displaystyle \frac{33}{20}\)

что завершает расчет.

Другие полезные калькуляторы по алгебре

Естественно, для упрощение дроби когда никакие другие операции не требуют более легкого подхода. Вы также можете использовать калькулятор выражений для получения числового значения выражения, что может пригодиться.

Что касается операций с дробями, вы также можете использовать следующее калькулятор смешанных дробей , который представляет собой простой калькулятор, не всегда доступный в других калькуляторах.

Калькулятор логических выражений

Программа предназначена для получения таблиц истинности логических функций с числом переменных от одной до пяти. Логической (булевой) функцией n переменных y = f(x₁, x₂, …, x_n) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.

A B C D

0 1

· + ¬

⊕ ⇒ ⇔

↓ |

( )

Решить!

Другой тип калькулятора для таблицы истинности

Шпаргалка по работе с калькулятором.

Переменные, которые могут принимать только два значения 0 и 1 называются логическими переменными (или просто переменными). Заметим, что логическая переменная х может подразумевать под числом 0 некоторое высказывание, которое ложно, и под числом 1 высказывание, которое истинно.

Из определения логической функции следует, что функция n переменных – это отображение Bⁿ в B, которое можно задать непосредственно таблицей, называемой таблицей истинности данной функции.

Основные функции логики – это функции двух переменных z = f(x,y).

Число этих функций равно 2⁴ = 16. Перенумеруем и расположим их в естественном порядке.

Рассмотрим более подробно эти функции. Две из них f₀ = 0 и f₁₅ = 1 являются константами. Функции f₃, f₅, f₁₀ и f₁₂ являются по существу функциями одной переменной.

Наиболее важные функции двух переменных имеют специальные названия и обозначения.

1) f₁ – конъюнкция (функция И)
Заметим, что конъюнкция – это фактически обычное умножение (нулей и единиц). Эту функцию обозначают x&y;

2) f₇ – дизъюнкция (функция или). Обозначается V.

3) f₁₃ – импликация (следование). Обозначается ->
Это очень важная функция, особенно в логике. Ее можно рассматривать следующим образом: если х = 0 (т. е. х “ложно”), то из этого факта можно вывести и “ложь”, и “истину” (и это будет правильно), если у = 1 (т. е. у “истинно”), то истина выводится и из “лжи” и из “истины”, и это тоже правильно. Только вывод “из истины ложь” является неверным. Заметим, что любая теорема всегда фактически содержит эту логическую функцию;

4) f₆ – сложение по модулю 2. Обозначается знаком “+” или знаком “+” в кружке.

5) f₉ – эквивалентность или подобие. Эта f₉ = 1 тогда и только тогда, когда х = у. Обозначается х ~ у.

6) f₁₄ – штрих Шеффера. Иногда эту функцию называют “не и” (так как она равна отрицанию конъюнкции). Обозначается x|y.

7) f₈ – стрелка Пирса (иногда эту функцию называют штрих Лукасевича).

Три оставшиеся функции, (f₂ , f₄ и f₁₁) особого обозначения не имеют.

Заметим, что часто в логике рассматриваются функции от функций, т.е. суперпозиции перечисленных выше функций. При этом последовательность действий указывается (как обычно) скобками.

Также можно скачать программу “Логический калькулятор” для Windows.

На данный момент логический калькулятор умеет выполнять следующее:

1. Ввод и проверка переменных на корректность. Под корректностью подразумевается правильное написание букв и операций над ними
2. Вывод таблицы истинности для выражения
3. СКНФ и СДНФ

Калькулятор логических выражений онлайн

Можно также попробовать работу калькулятора логики онлайн (это другая версия, а не та, которую можно скачать выше по ссылке). Правда, лучше считать в нем с PC, с телефона может работать не корректно. Пример ввода:

¬¬A & ¬A V A

Упрощение калькулятора — MathCracker.com

Инструкции: Используйте этот калькулятор упрощения, чтобы упростить любое допустимое алгебраическое выражение, числовое или символьное. Пожалуйста, введите выражение, которое вы хотите упростить, в поле формы ниже.

Калькулятор упрощенных выражений 92-1)(x-1)’, просто для примера.

После того, как вы укажете действительное выражение, все, что вам нужно сделать, это нажать кнопку «Рассчитать», которая находится прямо внизу, и вам будут показаны все соответствующие шаги процесса. тебе.

Некоторые упрощения выполнить легче, чем другие. Некоторые выражения легко поддаются упрощению, другие нет. Некоторые алгебраические выражения потребуют обширные и трудоемкие шаги следует упростить, а другие просто нельзя упростить.

Как упростить?

Упрощение — это не обязательно простой процесс, состоящий из группировки терминов с целью сокращения данного выражения. Процесс группировки, однако, не произвольным и следует некоторым строгим правилам и ограничениям, которые можно обобщить в 6 буквах: PEMDAS. Имеем:

P = Скобки

E = Возведение в степень

M = Умножение

D = Деление

A = Сложение

S = Вычитание

Итак, выражение состоит из таких элементов, как числа или неизвестные переменные, такие как ‘x’, которые представляют число, и различных операций, которые их комбинируют. ПЕМДАС показать нам, какие операции должны быть проведены в первую очередь. То есть сначала вы работаете со скобками, затем с показателями степени, затем умножаете и так далее.

Каковы шаги по упрощению выражений

• Шаг 1: Определите выражение, которое нужно упростить. Правильное выражение должно содержать числа и символы, такие как «x» (представляющие числа)
• Шаг 2: проверьте согласованность выражения. То есть убедитесь, что у любой открывающей скобки есть закрывающая, и что все операции завершены
• Шаг 3: Начните изнутри наружу, используя PEMDAS в качестве основного правила. Сначала упростите более простые термины.

Упомянув, что вы должны проверить, что операции «завершены», я имею в виду убедиться, что все операции имеют все свои компоненты. Например, при добавлении нужны две цифры и знак «+».

Таким образом, что-то вроде «3+4» является полной операцией, но что-то вроде «3+» или «+3» не содержит числа. Или что-то вроде «2 3» отсутствует «+», поэтому PEMDAS не могу сказать, какую операцию вы проводите.

Существуют некоторые паллиативные правила, такие как неявное умножение , которые учитывают, что в отсутствие операции пробел будет рассматриваться как «*», поэтому тогда «2 3» будет рассматриваться как «2 * 3»

В случае с нашим калькулятором упрощения, если выражение неполное или неверное, он сообщит вам, чтобы вы могли его исправить. 92 + 3х + 2\).

Как получить простейшую форму?

• Шаг 1: Сократите все простые операции, соблюдая PEMDAS
• Шаг 2. Расширьте условия
• Шаг 3: Упростите и сгруппируйте после расширения. Повторите при необходимости

Упростить общее выражение может быть сложно. Для специализированных структур мы можем разработать очень полный способ упрощения дробей. и упростить радикалы, например, которые являются одними из самых распространенных элементарных операций.

Зачем упрощать выражения?

Много магии в математике скрыто от глаз. Выражение может ничего вам не сказать, но после упрощения вы вдруг сможете все ясно увидеть. Кроме, упрощение похоже на устранение беспорядка, мы все хотим этого, верно?

Пример: Упростите выражение

Упростите следующее числовое выражение: \(\frac{2}{3} + \frac{5}{4} — \left(\frac{5}{6}\right) \cdot\left(\frac{8}{7}\right)\)

Решение. Нам нужно упростить следующее выражение: \(\displaystyle \frac{2}{3}+\frac{5}{4}-\frac{5}{6}\cdot\frac{8}{ 7}\).

Получен следующий расчет:

\( \displaystyle \frac{2}{3}+\frac{5}{4}-\frac{ 5}{ 6} \cdot \frac{ 8}{ 7} \)

Перемножив все числители и все знаменатели, мы получим \(\displaystyle-\frac{ 5}{ 6} \times \frac{ 8}{ 7}= \frac{ -5 \times 8} { 6 \times 7} \)

\( = \,\,\)

\(\displaystyle \frac{2}{3}+\frac{5}{4}+\frac{\left(\ влево(-5\вправо)\cdot 8\вправо)}{6\cdot 7}\)

Разложение числа \(\displaystyle 2\) в числителе и знаменателе \(\displaystyle \frac{ -5 \times 8}{ 6 \times 7}\)

\( = \,\,\ )

\(\displaystyle \frac{2}{3}+\frac{5}{4}-\frac{5\cdot 4}{3\cdot 7}\)

После исключения общих множителей из верх и низ

\( = \,\,\)

\(\displaystyle \frac{2}{3}+\frac{5}{4}-\frac{20}{21}\)

Умножение для получения общего знаменателя 84

\( = \,\,\)

\(\displaystyle \frac{2}{3}\cdot\frac{28}{28}+\frac{5}{4}\cdot\frac{21}{21}-\frac{20}{ 21}\cdot\frac{4}{4}\)

Нам нужно использовать общий знаменатель: 84

\( = \,\,\)

\(\displaystyle \frac{2\cdot 28+ 5\cdot 21-20\cdot 4}{84}\)

Разложение каждого члена в числителе: \(2 \times 28+5 \times 21-20 \times 4 = 56+105-80\)

\( = \,\,\)

\(\displaystyle \frac{56+105-80}{84}\)

Работа с членами в числителе

\( = \,\,\)

\(\displaystyle \frac{81}{84}\)

Мы можем вынести 3 из числителя и знаменателя.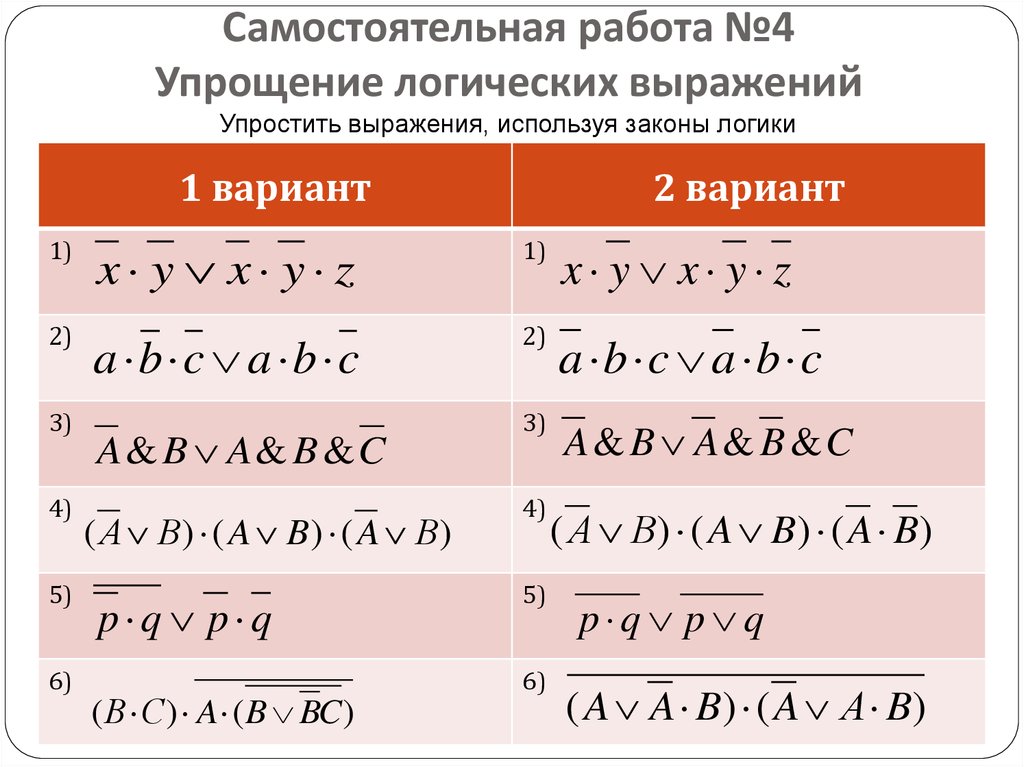

\( = \,\,\)

\(\displaystyle \frac{3\cdot 27}{3\cdot 28}\)

Теперь вычеркнем 3 из числителя и знаменателя.

\( = \,\,\)

\(\displaystyle \frac{27}{28}\)

что завершает процесс упрощения.

Пример: пример упрощенного калькулятора

Упростите следующее: \(\frac{x}{3} + \frac{x}{4} — \frac{x}{6}\)

Решение: Нам нужно упростить следующее выражение: \(\displaystyle \frac{x}{3}+\frac{x}{4}-\frac{x}{6}\).

Получается следующее вычисление:

\( \displaystyle \frac{x}{3}+\frac{x}{4}-\frac{x}{6}\)

Группировка членов с \( х\)

\( = \,\,\)

\(\displaystyle \left(\frac{1}{3}+\frac{1}{4}-\frac{1}{6}\ right)x\)

Упрощение терминов, сгруппированных с помощью \(x\)

\( = \,\,\)

\(\displaystyle \frac{5}{12}x\)

, который завершает процесс упрощения.

Пример: другой расчет упрощения

Вычислить \( \left(\frac{1}{3} \times \frac{6}{5} \right)+ \frac{2}{5} \).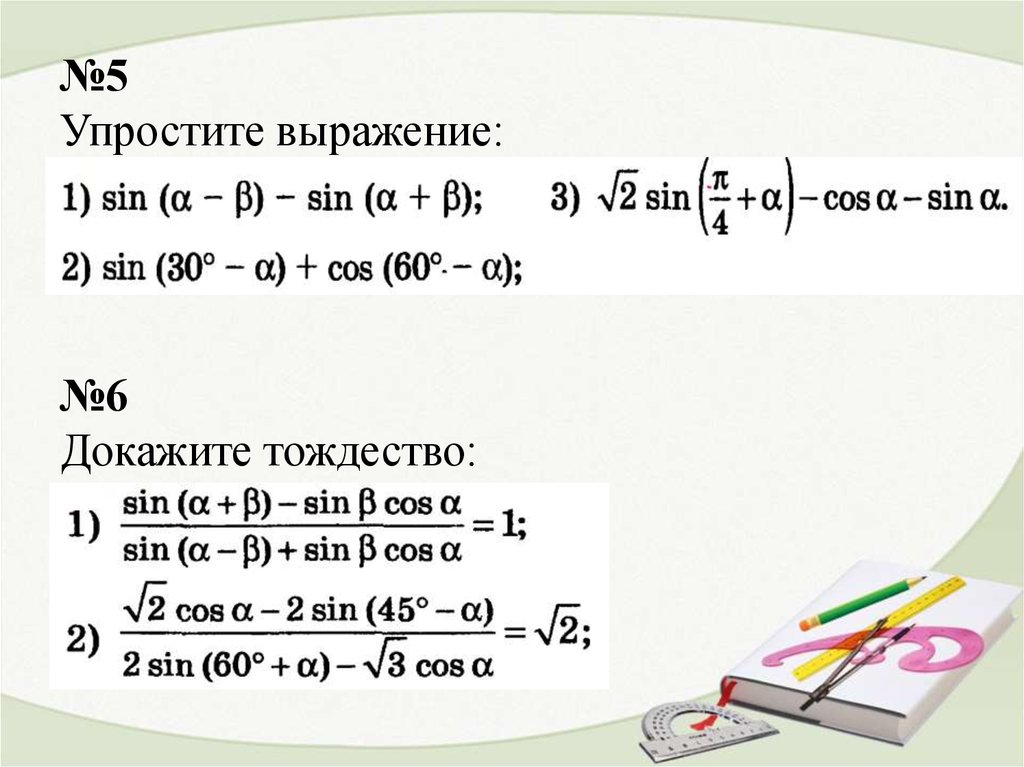

Решение. Нам нужно упростить следующее выражение: \(\displaystyle \frac{1}{3}\cdot\frac{6}{5}+\frac{2}{5}\).

Получен следующий расчет:

\( \displaystyle \frac{ 1}{ 3} \cdot \frac{ \left(6\right)}{ 5}+\frac{2}{5}\)

Путем умножения всех числителей и всех знаменателей: \(\displaystyle\frac{ 1}{ 3} \times \frac{ 6}{5}= \frac{ 6}{ 3 \times 5} \)

\( = \,\,\)

\(\displaystyle \frac{6}{3\cdot 5}+\frac{2}{5}\)

Мы можем вынести число \(\ displaystyle 3\) в числителе и знаменателе в \(\displaystyle \frac{ 6}{ 3 \times 5}\)

\( = \,\,\)

\(\displaystyle \frac{2}{ 5}+\frac{2}{5}\)

Нам нужно использовать общий знаменатель: 5

\( = \,\,\)

\(\displaystyle \frac{2+2}{5 }\)

Суммируя каждый член в числителе

\( = \,\,\)

\(\displaystyle \frac{4}{5}\)

завершает процесс упрощения.

Другие калькуляторы алгебры

Есть несколько интересных калькуляторов, которые группируют или сокращают выражения. Например, этот полный калькулятор квадратов занимает квадратичное и группирует его в определенную специфическую структуру. Или вы можете использовать этот калькулятор форм вершин, который аналогично пишет квадратичная функция как перевод из вершины ассоциированной параболы.

Другими специальными калькуляторами являются, например, этот калькулятор смешанных дробей, который очень полезен при работе с смешанные дроби в зависимости от вашей настройки обучения.

Упрощение калькулятора — Solumaths

Упрощение, расчет онлайн

Резюме:

Калькулятор, который может упростить алгебраическое выражение онлайн.

упростить онлайн

---

Описание:

Упростить выражение или отменить выражение означает сократить его путем группировки терминов. Калькулятор позволяет с этой функцией компьютерной алгебры сокращения алгебраического выражения. При использовании с функцией expand функция упрощения может расширять и сворачивать литеральное выражение.

С помощью этого алгебраического упрощения вы можете:
• Упростить алгебраическое выражение
• Упростить числовое выражение
• Упростить дроби
• Упростить комплексные числа
• Упрощение математических функций
• Упрощение тригонометрических выражений
• Упростить поверхность

Упростить алгебраическое выражение

Калькулятор может выполнять расчет с буквами (буквенный расчет), эта функция позволяет группировать, собирать члены выражения для получения сокращенной формы этого выражения.

К упростить выражение введите выражение , чтобы отменить и применить функцию упрощения. Таким образом, для упрощения выражения после a+2a, введите упрощение (`a+2a`) или напрямую a+2a, после вычисления возвращается сокращенная форма выражения 3a.

Возможности упрощения калькулятора применимы к буквенно-цифровым выражениям и, следовательно, также к чисто числовым выражениям.

Упростить числовое выражение

калькулятор symplify также применяется к числовым выражениям, он позволяет выполнять точные вычисления с числами:

• Например, калькулятор может упростить следующее выражение 1+2-5, чтобы получить результат этого вычисления, введите упростить(`1+2-5`), калькулятор возвращает -2
• Другой пример выражения, которое калькулятор может упростить `1+2-5/3`, чтобы сократить это выражение, введите упростить(`1+2-5/3`), после вычисления возвращается результат `4/3`.

Упростить дроби

Этот калькулятор предлагает возможность упростить дробь , сделать Расчет выражения , составленный из дробей и чтобы получить результат в виде несократимой дроби в виде специализированной калькулятор дроби делает. калькулятор дроби Однако особенность состоит в том, чтобы обеспечить этапы вычислений, позволяющие получить уменьшенная фракция . 9к`). Следует отметить, что в этой дроби показатель степени числителя и показатель степени знаменателя содержат буквы. Благодаря своим буквальным вычислительным возможностям калькулятор может легко упростить эту дробь.

Упрощение комплексных чисел

Калькулятор позволяет вам манипулировать комплексными числами в их алгебраической форме, он может упростить выражение, состоящее из комплексных чисел , как это делает сайт калькулятор комплексных чисел .

Упрощение функций благодаря их свойствам

Калькулятор использует различные методы для упрощения математических выражений: он использует четность функций для упрощения определенных результатов.

Например, чтобы упростить следующее выражение, simple(`cos(x)+cos(-x)`) , калькулятор использует четность функции косинуса.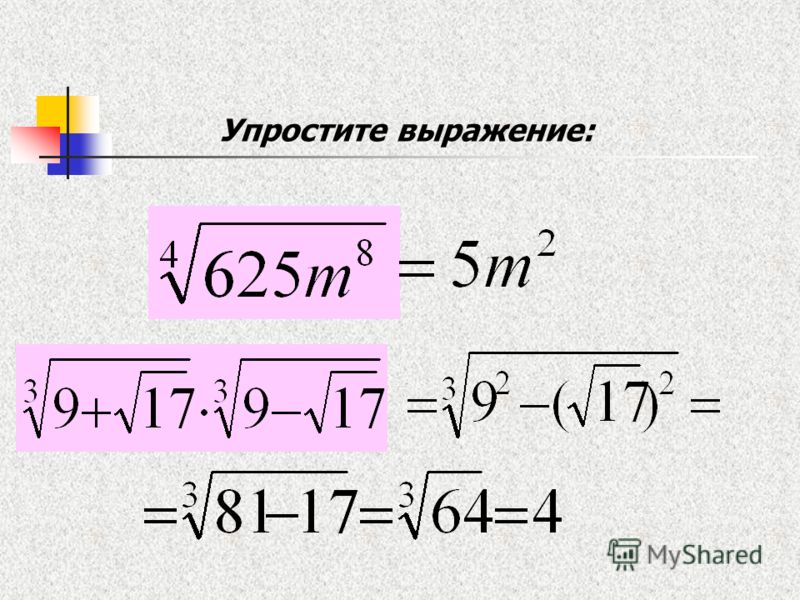 Для некоторых расчетов калькулятор указывает свойства, используемые для упрощения результатов, как показано в предыдущем примере.

Упростить тригонометрические выражения

Калькулятор также позволяет манипулировать тригонометрическими выражениями, он может упростить этот тип выражения, используя обычные тригонометрические формулы .

Таким образом, этот калькулятор можно использовать как тригонометрический калькулятор для упростить тригонометрические выражения , такие как следующие упростить(`cos(x+pi/2)+cos(-x)+sin(x+pi)`). Для некоторых расчетов калькулятор указывает свойства, используемые для уменьшения результатов, как показано в предыдущем примере.

Упрощение поверхностей

Калькулятор также позволяет упростить вычисление квадратного корня, используя свойства функции квадратного корня.

Упражнения, игры и викторины по упрощению алгебраических выражений.

2` 92`) = 2

Расчет онлайн с упрощением (Simplify Calculator)

См. также

Список связанных калькуляторов:

• Расчет ежемесячных платежей по страховке кредита : кредит_страхование. Калькулятор ежемесячных платежей по кредитному страхованию: кредит под залог недвижимости, потребительский кредит и другие виды кредита.
• Калькулятор алгебры: калькулятор. Калькулятор, позволяющий производить алгебраические вычисления, комбинируя операции с буквами и цифрами, а также указывать этапы вычислений.
• Калькулятор упрощения surds :simple_surd. Онлайн-калькулятор, который позволяет производить расчеты в точной форме с квадратными корнями: сумма, произведение, разность, отношение.
• Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
• Список вычислений, применимых к алгебраическому выражению: см._возможные_вычисления. Возвращает список вычислений, которые можно выполнить над алгебраическим выражением.
• Расчет биномиальных коэффициентов: binomial_coefficient. Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел.
• Калькулятор разложения на частичные дроби: partial_fraction_decomposition. Калькулятор позволяет разбить рациональную дробь на простые элементы.
• Калькулятор производных: производная. Калькулятор производной позволяет пошагово вычислить производную функции по переменной.
• Калькулятор расширения Тейлора: taylor_series_expansion. Калькулятор ряда Тейлора позволяет вычислить разложение Тейлора функции.
• Логарифмическое расширение: expand_log. Калькулятор позволяет получить логарифмическое расширение выражения.
• Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
• Расширить калькулятор: расширить. Калькулятор умеет расширять алгебраическое выражение онлайн и удалять ненужные скобки.
• Расширьте и упростите алгебраическое выражение онлайн: expand_and_simplify. Онлайн-калькулятор, позволяющий расширить и сократить алгебраическое выражение.
• Калькулятор факторинга: коэффициент. Калькулятор факторинга позволяет факторизовать алгебраическое выражение онлайн с шагом.
• Генератор решенных математических упражнений : Exercise_generator. Возвращает список утверждений математических упражнений и их решений, которые могут использоваться учителями для подготовки тестов и викторин.
• Интегральный калькулятор: интегральный. Калькулятор интегралов вычисляет онлайн интеграл функции между двумя значениями, результат выдается в точном или приближенном виде.
• Калькулятор неопределенных интегралов: первообразная. Калькулятор первообразной позволяет рассчитать первообразную онлайн с подробностями и шагами расчета.
• Калькулятор лимита: лимит. Калькулятор лимита позволяет рассчитать лимит функции с подробным описанием и шагами расчета.
• Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
• Расчет ежемесячных платежей по кредиту: month_loan. Калькулятор ежемесячного платежа по кредиту: жилищный кредит, потребительский кредит и другие виды кредита.