Рациональные неравенства — Алгебра — 9 класс
Просмотр содержимого документа
«Рациональные неравенства»
Рациональные неравенства
Задание 1
Вопрос:Укажите наибольшее отрицательное целое число, которое является решением неравенства .
Запишите число: ___________________________
Задание 2
Вопрос:Выберите целые неравенства
Выберите несколько из 4 вариантов ответа:
1) 2) 3) 4)
Задание 3
Вопрос:При решении неравенства получили следующие промежутки, на которых функция принимает значения одного знака (см. рисунок). Укажите промежутки, которые будут решениями неравенства:
Изображение:
1) 2) 3) 4) 5) 6)
Задание 4
Вопрос:При решении неравенства получили следующие промежутки, на которых функция принимает значения одного знака (см. рисунок). Укажите промежутки, которые будут решениями неравенства f(x)0:
рисунок). Укажите промежутки, которые будут решениями неравенства f(x)0:
Изображение:
Выберите несколько из 4 вариантов ответа:
1) 2) 3) 4)
Задание 5
Вопрос:Укажите те корни числителя и знаменателя, степень кратности которых не равна 1.
Выберите несколько из 5 вариантов ответа:
1) 1 2) -2 3) -0.5 4) 5 5) 4
Задание 6
Вопрос:Найдите сумму наибольшего целого отрицательного и наименьшего целого положительного решений неравенства: .
Запишите число: ___________________________
Задание 7
Вопрос:Укажите те корни числителя и знаменателя, степень кратности которых нечетная.
Выберите несколько из 5 вариантов ответа:
1) 1 2) -2 3) 5 4) 4 5) -0.5
Задание #8
Вопрос:Выберите дробно-рациональные неравенства
Выберите несколько из 4 вариантов ответа:
1) 2) 3) 4)
Задание 9
Вопрос:При решении неравенства получили следующие промежутки, на которых функция принимает значения одного знака (см.
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- x — 6
- — вычитание
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Логарифмические неравенства
Логарифмические неравенства
Часть А
Решите неравенства:
1) 3)
2) 4)
Найдите наибольшие целые значения , удовлетворяющие неравенствам:
5) 7)
6) 8)
Найдите наименьшее целое значение , удовлетворяющее неравенству:
9)
Часть В
Найдите наибольшее целое значение , удовлетворяющее неравенству:
10)
Найдите наименьшее целое значение , удовлетворяющее неравенству:
11)
Решениями неравенств являются:
12)
1) 3) 5)
2) 4)
13)
1) 3) 5)
2) 4)
14) Наибольшим целым решением неравенства является:
1) 2; 2) 3 3) 0 4) 1 5)
Решите неравенства:
15) 17)
16) 18)
Найдите наибольшие целые решения неравенств:
19) 22)
21) 24)
25) Решите неравенство
.
26) Наибольшее целое отрицательное решение неравенства равно:
1) 2) 3) 4) 5)
27) Решением неравенства является:
1) 3) 5)
2) 4)
28) Сумма целых решений неравенства равна:
1) 10 2) 9 3) 11 4) 7 5) 4
29) Решите неравенство
1) 2) 0 3) 1 4) 5) 7
31) Решите неравенство В ответе укажите наибольшее целое отрицательное решение.
32) Решением неравенства является:
1) 3) 5)
2) 4)
33) Наибольшим решением неравенства является:
1) 2 2) 1 3) 1,75 4) 5)
34) Решите неравенство .
35) Решите неравенство
36) Решите неравенство . В ответе укажите наименьшее целое неотрицательное решение.
1) 0 2) 1 3) 2 4) 3 5) 4
Решите неравенства:
37) 38)
39) Сумма наименьшего целого и наибольшего целого решений неравенства равна:
1) 46 2) 0 3) 45 4) 5) 12
40) 44)
41) 45)
42) 46)
43)
Найдите область определения функций:
47)
1) 3) 5)
2) 4)
48) 51)
49) 52)
50)
Часть С
Решите неравенства:
53) 56)
54) 57)
55)
58) Найдите все значения , для которых точки графика функции лежат не выше соответствующих точек графика функции
59) Найдите все значения , для которых точки графика функции лежат ниже соответствующих точек графика функции
60) Решением неравенства является:
1) 3) 5) нет правильного ответа
2) 4)
61) Решите неравенство
.
Логарифмические неравенства
ОТВЕТЫ
3
2
1
2
3
1
3
1
4
0
2
1
1
1
3
2
4
3
3
4
2
2
3
3
1
Решить неравенство методом интервалов — Документ
Задание № 1.
Решите неравенства:
а) 4х2 + 4х – 3 ≥ 0 б) 12х2 + х – 1 х2 + 2х – 1 ≥ 0
Решить неравенство методом интервалов:
а) (х + 2)(х + 3) > 0 б) х(х + 8)(х – 1,2) ≤ 0 в) х(х2 – 25) ≥ 0
Укажите наименьшее отрицательное решение неравенства
> 0
При каких значениях х неравенство будет верным
а) б) в)
Найдите область определения выражения:
а) б)
Решите неравенства:
а) б)
Найдите такое целое значение параметра р , при котором множество решений неравенства содержит:
а) два целых числа;
б) пять целых чисел.
Решайте! Готовьтесь! Кто хорошо учится, тот со спокойной совестью и с чувством выполненного долга отдыхает летом, и не дрожит перед каждой самостоятельной и контрольной работой.
Задание № 2.
Найдите произведение всех решений неравенства (х – 7)(х + 2)
Укажите сумму наибольшего целого отрицательного и наименьшего целого положительного решений неравенства (1 – 3х)(х2 – 9) > 0
Какие из данных неравенств выполняются при любых значениях х?
1) 2) 3) 2х2 – 4х + 5 > 0 4) х2 – 1
При каком наименьшем целом значении х выполняются оба неравенства: х2 + 4х – 21 х2 + 3х – 10 ≥ 0 ?
Сколько натуральных решений неравенства (х2 + )(х – 4) ?
Найдите наименьшее целое значение х, при котором функция
у = 3х2 – 2х – 5 принимает
отрицательное значение.
Сколько решений неравенства > 0, кратных 4, принадлежит промежутку ?
Укажите наибольшее целое решение неравенства .
Найдите область определения функции
Какое множество образуют абсциссы точек графика функции , расположенных не ниже соответствующих точек графика функции ?
При каких целых значениях р неравенство (х – р)(х – 6) р.
Репетитор по математике (Полоцк, Новополоцк): февраля 2018
Противоположные числа в сумме дают 0. Например, 2 и −2; −13 и 13. Произведение обратных чисел равно 1. Например, 10 и 1/10; −2/3 и −3/2.
Натуральные числа (ℕ) – это числа, которые используются при счете: 1;2;3;…
Натуральные числа, им противоположные и число 0 образуют множество целых чисел (ℤ): …; −2; −1; 0; 1; 2…
Рациональные числа (ℚ) – это числа, представимые в виде дроби 𝑝/𝑞, где 𝑝− целое число, 𝑞−натуральное число. Например, 1; −5; 0; −74; 514; 2,5, 13/8, 1,(3)…
Например, 1; −5; 0; −74; 514; 2,5, 13/8, 1,(3)…
Числа, которые не являются рациональными, называются иррациональными (𝕀): √5; −√19; π, e…
Иррациональные и рациональные числа вместе образуют множество действительных чисел (ℝ).
На множестве натуральны чисел существует понятие делимости
Делителем числа 𝑎 называется такое число, которое делится на 𝑎 без остатка. Число, для которого число 𝑏 является делителем, называется кратным числу 𝑏.
Натуральное число, имеющее только 2 делителя (единицу и само это число) называется простым. Например, 7 делится без остатка только на 1 и 7. Число, имеющее более двух делителей, называется составным. Например, 6 делится без остатка на 1, 2, 3 и 6. Значит, оно является составным. Число 1 не является ни простым, ни составным, т.к. имеет только 1 делитель – 1.
Простые числа первой двадцатки: 2;3;5;7;11;13;17;19.
Признаки делимости:
На 2 делятся четные числа (которые оканчиваются на 0;2;4;6;8)
На 3 делятся те числа, сумма цифр которых делится на 3. Например, 672⋮3 (6+7+2=15⋮3).
На 5 делятся числа, которые оканчиваются на 0 и 5.
НОК и НОД чисел
Наибольший общий делитель (НОД) двух чисел 𝑎 и 𝑏 – это наибольшее из всех натуральных чисел, на которое делятся и 𝑎 и 𝑏 без остатка.
Если НОД некоторых чисел равен 1, то такие числа называются взаимно простыми.
Наименьшее общее кратное (НОК) двух чисел 𝑎 и 𝑏 – это такое наименьшее из натуральное чисел, которое делится на 𝑎 и 𝑏 без остатка.
НОК двух взаимно простых чисел равен их произведению.
Для нахождения НОД числа раскладываются на простые множители, а затем выписывается общее из разложений.
Для нахождения НОК числа раскладываются на простые множители, затем выписывается одно (любое) разложение полностью и дописывается, чего не хватает из остальных разложений.
НОК и НОД двух чисел обладают следующим свойством: НОК (a, b) • НОД(a, b) = a • b
Тест. Решение неравенств методом интервалов
© 2020, ООО КОМПЭДУ, http://compedu.ru При поддержке проекта http://videouroki.net
Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!
Удачи!Список вопросов теста
Вопрос 1
Укажите порядок действий при решении неравенства методом интервалов.
Варианты ответов
- Перенести все слагаемые в левую часть неравенства и разложить её на множители.
- Рассмотреть соответствующую функцию и найти её нули.

- Изобразить нули функции на числовой прямой.
- На каждом промежутке, полученном в результате разбиения области определения нулями функции, определить знак функции.
- Записать ответ.
Вопрос 2
Сколько нулей имеет функция F(x), если известно, что они разбивают область определения на 7 промежутков.
Варианты ответов
Вопрос 3
Укажите целое число, которое является решением неравенства (x-3)(x-5)<0.
Вопрос 4
Укажите целое число, которое является решением неравенства
Вопрос 5
Используя график функции y=F(x), укажите промежутки, являющиеся решением неравенства F(x)<0.
Варианты ответов
- (-2;0)
- (0;3)
- (3;7)
Вопрос 6
Решите неравенство
Варианты ответов
Вопрос 7
Множеством решений неравенства (x-10)(5x+25)(x-4)>0 является . .. .
.. .
Варианты ответов
Вопрос 8
Решите неравенство (x+5)(3-2x)>0. Запись промежутка не должна содержать пробелы. Например: (-6,3;9].
Вопрос 9
Решите неравенство (x2-49)(x2+1)<0.
Варианты ответов
- (-7;7)
- [-7;7]
- (-7;-1)U(1;7)
- [-7;-1]U[1;7]
Вопрос 10
Найдите, при каких значениях x произведение (x-6)(21-x) неотрицательно. Запись промежутка не должна содержать пробелы. Например: (-6,3;9].
Запись промежутка не должна содержать пробелы. Например: (-6,3;9].
Тест на тему «Неравенства»
Тест на тему
«Неравенства»
1. Найдите наибольшее целое число x , удовлетворяющее неравенству х < 4.
1) 4; 2) 3; 3) 5; 4) 0.
2. Найдите наименьшее целое число у , удовлетворяющее неравенству у > -2.
1) -3; 2) 0; 3) -2; 4) -1.
3. Найдите наибольшее целое число m , удовлетворяющее неравенству .
1) -13; 2) -14; 3) -12; 4) 0.
4. Найдите наименьшее целое число у , удовлетворяющее неравенству .
1) 6; 2) 4; 3) 5; 4) 10.
5. Найдите наибольшее целое число x , удовлетворяющее неравенству .
1) 3; 2) 2; 3) 1; 4) 4.
6. Найдите наибольшее целое число x , удовлетворяющее неравенству .
Найдите наибольшее целое число x , удовлетворяющее неравенству .
1) 3; 2) 2; 3) 1; 4) 4.
7. Решите неравенство .
1) ; 2) ; 3) ; 4) .
8. Решите неравенство .
1) ; 2) ; 3) ; 4) .
9. Решите неравенство . В ответе укажите наибольшее целое число.
1) 4; 2) 5; 3) 10; 4) 9.
10. Решите неравенство . В ответе укажите наибольшее целое число.
1) 4; 2) 5; 3) 6; 4) -5.
11. Решите систему неравенств
1) ; 2) ; 3) ; 4) .
12. Множество чисел, изображенных на рисунке запишите в виде неравенства
1) ; 2) ;
3) ; 4) .
Тест 1
«Неравенства»
Вариант 2
1. Найдите наибольшее целое число x , удовлетворяющее неравенству х < -5.
1) -4; 2) -3; 3) -5; 4) 0.
2. Найдите наименьшее целое число у , удовлетворяющее неравенству у > 2.
1) 3; 2) 0; 3) 2; 4) 1.
3. Найдите наибольшее целое число m , удовлетворяющее неравенству .
1) 13; 2) 14; 3) 15; 4) 0.
4. Найдите наименьшее целое число у , удовлетворяющее неравенству .
1) 1; 2) 2; 3) 0; 4) 3.
5. Найдите наибольшее целое число x , удовлетворяющее неравенству .
1) 12; 2) 11; 3) 1; 4) 13.
6. Найдите наибольшее целое число x , удовлетворяющее неравенству .
1) -3; 2) -2; 3) -1; 4) -4.
7. Решите неравенство .
1) ; 2) ; 3) ; 4) .
8. Решите неравенство .
1) ; 2) ; 3) ; 4) .
9. Решите неравенство . В ответе укажите наибольшее целое число.
1) 6; 2) 7; 3) 10; 4) 8.
10. Решите неравенство . В ответе укажите наибольшее целое число.
1) 2; 2) 3; 3) 4; 4) 5.
11. Решите систему неравенств
1) ; 2) ; 3) ; 4) .
12. Множество чисел, изображенных на рисунке запишите в виде неравенства
1) ; 2) ;3) ; 4) .
Ответы:
В-т | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
1 | 1 | 2 | 4 | 1 | 3 | 1 | 4 | 3 | 1 | 1 | 2 | 2 | 2 |
2 | 4 | 3 | 1 | 3 | 1 | 2 | 3 | 1 | 4 | 1 | 2 | 4 |
Прочтите: Опишите решения проблемы неравенства
Цели обучения
- Изобразите неравенства на числовой прямой
- Изобразите неравенства, используя обозначение интервалов
Изобразите неравенства на числовой прямой
Во-первых, давайте определимся с важной терминологией. Неравенство — это математическое утверждение, которое сравнивает два выражения, используя идеи больше или меньше чем. В этих утверждениях используются специальные символы.Когда вы читаете неравенство, читайте его слева направо — как если бы вы читали текст на странице. В алгебре неравенства используются для описания больших наборов решений. Иногда существует бесконечное количество чисел, которые удовлетворяют неравенству, поэтому вместо того, чтобы пытаться перечислить бесконечное количество чисел, мы разработали несколько способов краткого описания очень больших списков.
Неравенство — это математическое утверждение, которое сравнивает два выражения, используя идеи больше или меньше чем. В этих утверждениях используются специальные символы.Когда вы читаете неравенство, читайте его слева направо — как если бы вы читали текст на странице. В алгебре неравенства используются для описания больших наборов решений. Иногда существует бесконечное количество чисел, которые удовлетворяют неравенству, поэтому вместо того, чтобы пытаться перечислить бесконечное количество чисел, мы разработали несколько способов краткого описания очень больших списков.
Первый способ, с которым вы, вероятно, знакомы, — основное неравенство. Например:
- [латекс] {x} \ lt {9} [/ latex] указывает список чисел, которые меньше [latex] 9 [/ latex].Вы бы предпочли написать [latex] {x} \ lt {9} [/ latex] или попытаться перечислить все возможные числа, которые меньше [latex] 9 [/ latex]? (Большинство людей ответят первым)
- [латекс] -5 \ le {t} [/ latex] указывает все числа, которые больше или равны [латекс] -5 [/ латекс].

Обратите внимание, как размещение переменной слева или справа от знака неравенства может изменить, ищете ли вы больше или меньше.
Например:
- [латекс] x \ lt5 [/ latex] означает все действительные числа, которые меньше 5, тогда как;
- [latex] 5 \ lt {x} [/ latex] означает, что 5 меньше x, или мы могли бы переписать это с x слева: [latex] x \ gt {5} [/ latex] обратите внимание, как неравенство по-прежнему указывает в том же направлении относительно x.Этот оператор представляет все действительные числа, которые больше 5, что легче интерпретировать, чем 5 меньше x.
Второй способ — график с использованием числовой прямой:
И третий способ — с интервалом.
В этом разделе мы подробно рассмотрим второй и третий способы. Опять же, эти три способа написать решения неравенства:
- неравенство
- интервал
- график
Признаки неравенства
В поле ниже показаны символ, значение и пример для каждого знака неравенства. Иногда легко запутаться в неравенствах, просто не забывайте читать их слева направо.
Иногда легко запутаться в неравенствах, просто не забывайте читать их слева направо.
| Символ | слов | Пример |
|---|---|---|
| [латекс] \ neq [/ латекс] | не равно | [латекс] {2} \ neq {8} [/ latex], 2 равно не равно –8 . |
| [латекс] \ gt [/ латекс] | больше | [латекс] {5} \ gt {1} [/ latex], 5 больше, чем 1 |
| [латекс] \ lt [/ латекс] | менее | [латекс] {2} \ lt {11} [/ латекс], 2 меньше 11 |
| [латекс] \ geq [/ латекс] | больше или равно | [латекс] {4} \ geq {4} [/ latex], 4 больше или равно 4 |
| [латекс] \ leq [/ латекс] | меньше или равно | [латекс] {7} \ leq {9} [/ latex], 7 меньше или равно 9 |
Неравенство [latex] x> y [/ latex] также можно записать как [latex] {y} <{x} [/ latex]. Стороны любого неравенства могут быть поменяны местами, если символ неравенства между ними также перевернут.
Стороны любого неравенства могут быть поменяны местами, если символ неравенства между ними также перевернут.
Графическое изображение неравенства
Неравенства также можно изобразить на числовой прямой. Ниже приведены три примера неравенств и их графики. Графики — очень полезный способ визуализировать информацию, особенно когда эта информация представляет собой бесконечный список чисел!
[латекс] х \ leq -4 [/ латекс]. Это переводится во все действительные числа в числовой строке, которые меньше или равны [латекс] 4 [/ латекс].
[латекс] {x} \ geq {-3} [/ латекс]. Это переводится во все действительные числа в числовой строке, которые больше или равны -3.
Каждый из этих графиков начинается с круга — открытого или закрытого (закрашенного) круга. Эту точку часто называют конечной точкой решения. Замкнутый или заштрихованный круг используется для обозначения неравенств , которые больше или равны [latex] \ displaystyle \ left (\ geq \ right) [/ latex] или меньше или равно [latex] \ displaystyle. \ left (\ leq \ right) [/ латекс].Дело в том, что это часть решения. Открытый кружок используется для значений больше (>) или меньше (<). Дело в , а не в части решения.
\ left (\ leq \ right) [/ латекс].Дело в том, что это часть решения. Открытый кружок используется для значений больше (>) или меньше (<). Дело в , а не в части решения.
Затем график бесконечно продолжается в одном направлении. Это показано линией со стрелкой в конце. Например, обратите внимание, что для графа [latex] \ displaystyle x \ geq -3 [/ latex], показанного выше, конечной точкой является [latex] −3 [/ latex], представленная замкнутым кружком, поскольку неравенство составляет больше или равно [латекс] -3 [/ латекс].Синяя линия проведена справа от числовой, потому что значения в этой области больше, чем [latex] −3 [/ latex]. Стрелка в конце указывает, что решения продолжаются бесконечно.
Пример
Построить график неравенства [латекс] x \ ge 4 [/ латекс]
Показать решение Мы можем использовать числовую линию, как показано. Поскольку значения [latex] x [/ latex] включают [latex] 4 [/ latex], мы помещаем сплошную точку на числовой строке в [latex] 4 [/ latex].
Затем мы рисуем линию, которая начинается с [latex] x = 4 [/ latex] и, как указано стрелкой, продолжается до положительной бесконечности, что показывает, что набор решений включает в себя все действительные числа, большие или равные [latex] 4 [/ латекс].
В этом видео показан пример построения графика неравенства.
Пример
Напишите неравенство, описывающее все действительные числа в числовой строке, которые меньше [latex] 2 [/ latex], затем нарисуйте соответствующий график.
Показать решениеНам нужно начать слева и работать вправо, поэтому мы начнем с отрицательной бесконечности и закончим на [latex] 2 [/ latex]. Мы не будем включать ни то, ни другое, потому что бесконечность не является числом, и неравенство не включает [латекс] 2 [/ латекс].
Неравенство: [латекс] x \ lt2 [/ латекс]
Чтобы нарисовать график, сначала поместите открытую точку на числовой прямой, а затем проведите линию, идущую влево. Нарисуйте стрелку в самой левой точке линии, чтобы указать, что она продолжается до бесконечности.
Нарисуйте стрелку в самой левой точке линии, чтобы указать, что она продолжается до бесконечности.
Изобразите неравенства, используя обозначение интервала
Другой широко используемый и, возможно, наиболее краткий метод описания неравенств и решений неравенств называется интервальной нотацией . Согласно этому соглашению, наборы строятся с использованием круглых или квадратных скобок, каждая из которых имеет свое значение.Решения для [latex] x \ geq 4 [/ latex] представлены как [latex] \ left [4, \ infty \ right) [/ latex]. Этот метод широко используется и будет присутствовать в других курсах математики, которые вы, возможно, пройдете.
Основная концепция, которую следует запомнить, заключается в том, что круглые скобки представляют решения больше или меньше числа, а скобки представляют решения, которые больше или равны или меньше или равны числу. Используйте круглые скобки для обозначения бесконечности или отрицательной бесконечности, поскольку положительная и отрицательная бесконечность не являются числами в обычном смысле слова и, следовательно, не могут быть «равны». ”Несколько примеров интервала или набора чисел, в который попадает решение: [latex] \ left [-2,6 \ right) [/ latex] или все числа между [latex] -2 [ / латекс] и [латекс] 6 [/ латекс], включая [латекс] -2 [/ латекс], но не включая [латекс] 6 [/ латекс]; [latex] \ left (-1,0 \ right) [/ latex], все действительные числа между, но не включая [latex] -1 [/ latex] и [latex] 0 [/ latex]; и [latex] \ left (- \ infty, 1 \ right] [/ latex], все действительные числа меньше [latex] 1 [/ latex] включительно. В таблице ниже представлены возможные варианты.Не забывайте читать неравенства слева направо, как текст.
”Несколько примеров интервала или набора чисел, в который попадает решение: [latex] \ left [-2,6 \ right) [/ latex] или все числа между [latex] -2 [ / латекс] и [латекс] 6 [/ латекс], включая [латекс] -2 [/ латекс], но не включая [латекс] 6 [/ латекс]; [latex] \ left (-1,0 \ right) [/ latex], все действительные числа между, но не включая [latex] -1 [/ latex] и [latex] 0 [/ latex]; и [latex] \ left (- \ infty, 1 \ right] [/ latex], все действительные числа меньше [latex] 1 [/ latex] включительно. В таблице ниже представлены возможные варианты.Не забывайте читать неравенства слева направо, как текст.
В таблице ниже описаны все возможные неравенства, которые могут возникнуть, и способы их записи с использованием интервальной записи, где a и b — действительные числа.
 «>
«>Пример
Опишите неравенство [латекс] x \ ge 4 [/ latex], используя обозначение интервала
Показать решение Решения для [latex] x \ ge 4 [/ latex] представлены как [latex] \ left [4, \ infty \ right) [/ latex].
Обратите внимание на использование кронштейна слева, потому что 4 включены в набор решений.
Пример
Используйте обозначение интервала, чтобы указать все действительные числа, большие или равные [latex] -2 [/ latex].
Показать решениеИспользуйте скобку слева от [latex] -2 [/ latex] и скобки после бесконечности: [latex] \ left [-2, \ infty \ right) [/ latex]. Скобка указывает, что [latex] -2 [/ latex] включен в набор со всеми действительными числами, большими, чем [latex] -2 [/ latex], до бесконечности.
Подумай об этом
В предыдущих примерах вам давали неравенство или описание одного со словами и просили нарисовать соответствующий график и записать интервал. В этом примере вам дается интервал и предлагается написать неравенство и нарисовать график.
Дано [latex] \ left (- \ infty, 10 \ right) [/ latex], запишите соответствующее неравенство и нарисуйте график.
В поле ниже укажите, считаете ли вы, что сначала будет проще нарисовать график или сначала записать неравенство.
Сначала нарисуем график.
Интервал читается как «все действительные числа меньше 10», поэтому мы начнем с размещения открытой точки на 10 и рисования линии слева со стрелкой, указывающей, что решение продолжается до отрицательной бесконечности.
Чтобы записать неравенство, мы будем использовать <, поскольку круглые скобки указывают, что 10 не включено. [латекс] x <10 [/ латекс]
В следующем видео вы увидите примеры того, как записывать неравенства тремя представленными здесь способами: в виде неравенства, в интервальной нотации и с помощью графика.
Решить неравенства | Начальная алгебра
Результаты обучения
- Опишите решения проблемы неравенства
- Изобразите неравенства на числовой прямой
- Изобразите неравенства, используя обозначение интервалов
- Решите пошаговые неравенства
- Используйте свойства сложения и умножения, чтобы решать алгебраические неравенства и выражать их решения графически и с интервальной нотацией
- Решите неравенства, содержащие абсолютное значение
- Решите многоступенчатые неравенства
- Комбинирование свойств неравенства для выделения переменных, решения алгебраических неравенств и графического представления их решений
- Упростите и решите алгебраические неравенства, используя свойство распределенности, чтобы очистить круглые скобки и дроби
Изобразите неравенства на числовой прямой
Во-первых, давайте определимся с важной терминологией. Неравенство — это математическое утверждение, которое сравнивает два выражения, используя идеи больше или меньше чем. В этих утверждениях используются специальные символы. Когда вы читаете неравенство, читайте его слева направо — как если бы вы читали текст на странице. В алгебре неравенства используются для описания больших наборов решений. Иногда существует бесконечное количество чисел, которые удовлетворяют неравенству, поэтому вместо того, чтобы пытаться перечислить бесконечное количество чисел, мы разработали несколько способов краткого описания очень больших списков.
Неравенство — это математическое утверждение, которое сравнивает два выражения, используя идеи больше или меньше чем. В этих утверждениях используются специальные символы. Когда вы читаете неравенство, читайте его слева направо — как если бы вы читали текст на странице. В алгебре неравенства используются для описания больших наборов решений. Иногда существует бесконечное количество чисел, которые удовлетворяют неравенству, поэтому вместо того, чтобы пытаться перечислить бесконечное количество чисел, мы разработали несколько способов краткого описания очень больших списков.
Первый способ, с которым вы, вероятно, знакомы, — основное неравенство. Например:
- [latex] {x} \ lt {9} [/ latex] указывает список чисел, которые меньше 9. Вы бы предпочли написать [latex] {x} \ lt {9} [/ latex] или попробовать перечислить все возможные числа меньше 9? (надеюсь, ваш ответ отрицательный)
- [латекс] -5 \ le {t} [/ latex] указывает все числа, которые больше или равны [латекс] -5 [/ латекс].

Обратите внимание, как размещение переменной слева или справа от знака неравенства может изменить, ищете ли вы больше или меньше.
Например:
- [латекс] x \ lt5 [/ latex] означает все действительные числа, которые меньше 5, тогда как;
- [latex] 5 \ lt {x} [/ latex] означает, что 5 меньше x, или мы могли бы переписать это с x слева: [latex] x \ gt {5} [/ latex] обратите внимание, как неравенство по-прежнему указывает в том же направлении относительно x. Этот оператор представляет все действительные числа, которые больше 5, что легче интерпретировать, чем 5 меньше x.
Второй способ — график с использованием числовой прямой:
И третий способ — с интервалом.
В этом разделе мы подробно рассмотрим второй и третий способы. Опять же, эти три способа написать решения неравенства:
- неравенство
- интервал
- график
Признаки неравенства
В поле ниже показаны символ, значение и пример для каждого знака неравенства. Иногда легко запутаться в неравенствах, просто не забывайте читать их слева направо.
Иногда легко запутаться в неравенствах, просто не забывайте читать их слева направо.
| Символ | слов | Пример |
|---|---|---|
| [латекс] \ neq [/ латекс] | не равно | [латекс] {2} \ neq {8} [/ latex], 2 равно не равно –8 . |
| [латекс] \ gt [/ латекс] | больше | [латекс] {5} \ gt {1} [/ latex], 5 больше, чем 1 |
| [латекс] \ lt [/ латекс] | менее | [латекс] {2} \ lt {11} [/ латекс], 2 меньше 11 |
| [латекс] \ geq [/ латекс] | больше или равно | [латекс] {4} \ geq {4} [/ latex], 4 больше или равно 4 |
| [латекс] \ leq [/ латекс] | меньше или равно | [латекс] {7} \ leq {9} [/ latex], 7 меньше или равно 9 |
Неравенство [latex] x> y [/ latex] также можно записать как [latex] {y} <{x} [/ latex]. Стороны любого неравенства могут быть поменяны местами, если символ неравенства между ними также перевернут.
Стороны любого неравенства могут быть поменяны местами, если символ неравенства между ними также перевернут.
Графическое изображение неравенства
Неравенства также можно изобразить на числовой прямой. Ниже приведены три примера неравенств и их графики. Графики — очень полезный способ визуализировать информацию, особенно когда эта информация представляет собой бесконечный список чисел!
[латекс] х \ leq -4 [/ латекс]. Это переводится во все действительные числа в числовой строке, которые меньше или равны 4.
[латекс] {x} \ geq {-3} [/ латекс]. Это переводится во все действительные числа в числовой строке, которые больше или равны -3.
Каждый из этих графиков начинается с круга — открытого или закрытого (закрашенного) круга. Эту точку часто называют конечной точкой решения. Замкнутый или заштрихованный круг используется для обозначения неравенств , которые больше или равны [latex] \ displaystyle \ left (\ geq \ right) [/ latex] или меньше или равно [latex] \ displaystyle. \ left (\ leq \ right) [/ латекс].Дело в том, что это часть решения. Открытый кружок используется для значений больше (>) или меньше (<). Дело в , а не в части решения.
\ left (\ leq \ right) [/ латекс].Дело в том, что это часть решения. Открытый кружок используется для значений больше (>) или меньше (<). Дело в , а не в части решения.
Затем график бесконечно продолжается в одном направлении. Это показано линией со стрелкой в конце. Например, обратите внимание, что для графа [latex] \ displaystyle x \ geq -3 [/ latex], показанного выше, конечной точкой является [latex] −3 [/ latex], представленная замкнутым кружком, поскольку неравенство составляет больше или равно [латекс] -3 [/ латекс].Синяя линия проведена справа от числовой, потому что значения в этой области больше, чем [latex] −3 [/ latex]. Стрелка в конце указывает, что решения продолжаются бесконечно.
Пример
Построить график неравенства [латекс] x \ ge 4 [/ латекс]
Показать решение Мы можем использовать числовую линию, как показано. Поскольку значения x включают 4, мы помещаем сплошную точку на числовой прямой в позиции 4.
Затем мы рисуем линию, которая начинается с [latex] x = 4 [/ latex] и, как указано стрелкой, продолжается до положительной бесконечности, что показывает, что набор решений включает в себя все действительные числа, большие или равные 4.
В этом видео показан пример построения графика неравенства.
Пример
Напишите неравенство, описывающее все действительные числа на числовой прямой, которые меньше 2, а затем нарисуйте соответствующий график.
Показать решениеНам нужно начать слева и работать вправо, поэтому мы начнем с отрицательной бесконечности и закончим на [latex] -2 [/ latex]. Мы не будем включать ни то, ни другое, потому что бесконечность не является числом, и неравенство не включает [латекс] -2 [/ латекс].
Неравенство: [латекс] x <2 [/ латекс]
Чтобы нарисовать график, сначала поместите открытую точку на числовой прямой, а затем проведите линию, идущую влево. Нарисуйте стрелку в самой левой точке линии, чтобы указать, что она продолжается до бесконечности.
Нарисуйте стрелку в самой левой точке линии, чтобы указать, что она продолжается до бесконечности.
В следующем видео показано, как математически написать неравенство, если оно выражается словами. Затем мы построим график.
Изобразите неравенства, используя обозначение интервала
Другой широко используемый и, возможно, наиболее краткий метод описания неравенств и решений неравенств называется интервальной нотацией . Согласно этому соглашению, наборы строятся с использованием круглых или квадратных скобок, каждая из которых имеет свое значение. Решения для [latex] x \ geq 4 [/ latex] представлены как [latex] \ left [4, \ infty \ right) [/ latex]. Этот метод широко используется и будет присутствовать в других курсах математики, которые вы, возможно, пройдете.
Основная концепция, которую следует запомнить, заключается в том, что круглые скобки представляют решения больше или меньше числа, а скобки представляют решения, которые больше или равны или меньше или равны числу. Используйте круглые скобки для обозначения бесконечности или отрицательной бесконечности, поскольку положительная и отрицательная бесконечность не являются числами в обычном смысле этого слова и, следовательно, не могут быть «равны». Несколько примеров интервала или набора чисел, в который попадает решение: [latex] \ left [-2,6 \ right) [/ latex] или все числа между [latex] -2 [/ латекс] и [латекс] 6 [/ латекс], включая [латекс] -2 [/ латекс], но не включая [латекс] 6 [/ латекс]; [latex] \ left (-1,0 \ right) [/ latex], все действительные числа между, но не включая [latex] -1 [/ latex] и [latex] 0 [/ latex]; и [latex] \ left (- \ infty, 1 \ right] [/ latex], все действительные числа меньше, чем [latex] 1 [/ latex] включительно.В таблице ниже представлены возможные варианты. Не забывайте читать неравенства слева направо, как текст.
Используйте круглые скобки для обозначения бесконечности или отрицательной бесконечности, поскольку положительная и отрицательная бесконечность не являются числами в обычном смысле этого слова и, следовательно, не могут быть «равны». Несколько примеров интервала или набора чисел, в который попадает решение: [latex] \ left [-2,6 \ right) [/ latex] или все числа между [latex] -2 [/ латекс] и [латекс] 6 [/ латекс], включая [латекс] -2 [/ латекс], но не включая [латекс] 6 [/ латекс]; [latex] \ left (-1,0 \ right) [/ latex], все действительные числа между, но не включая [latex] -1 [/ latex] и [latex] 0 [/ latex]; и [latex] \ left (- \ infty, 1 \ right] [/ latex], все действительные числа меньше, чем [latex] 1 [/ latex] включительно.В таблице ниже представлены возможные варианты. Не забывайте читать неравенства слева направо, как текст.
В таблице ниже описаны все возможные неравенства, которые могут возникнуть, и способы их записи с использованием интервальной записи, где a и b — действительные числа.
Пример
Опишите неравенство [латекс] x \ ge 4 [/ latex], используя обозначение интервала
Показать решение Решения для [latex] x \ ge 4 [/ latex] представлены как [latex] \ left [4, \ infty \ right) [/ latex].
Обратите внимание на использование кронштейна слева, потому что 4 включены в набор решений.
В следующем видео мы показываем еще один пример использования обозначения интервалов для описания неравенства.
Пример
Используйте обозначение интервала, чтобы указать все действительные числа, большие или равные [latex] -2 [/ latex].
Показать решениеИспользуйте скобку слева от [latex] -2 [/ latex] и скобки после бесконечности: [latex] \ left [-2, \ infty \ right) [/ latex].Скобка указывает, что [latex] -2 [/ latex] включен в набор со всеми действительными числами, большими, чем [latex] -2 [/ latex], до бесконечности.
В следующем видео мы показываем еще один пример преобразования слов в неравенство и записи его в интервальной нотации, а также рисование графика.
youtube.com/embed/OYkQ-McI2qg?feature=oembed» frameborder=»0″ gesture=»media» allow=»encrypted-media» allowfullscreen=»»/>
Подумай об этом
В предыдущих примерах вам давали неравенство или описание одного со словами и просили нарисовать соответствующий график и записать интервал.В этом примере вам дается интервал и предлагается написать неравенство и нарисовать график.
Дано [latex] \ left (- \ infty, 10 \ right) [/ latex], запишите соответствующее неравенство и нарисуйте график.
В поле ниже укажите, считаете ли вы, что сначала будет проще нарисовать график или сначала записать неравенство.
Показать решениеСначала нарисуем график.
Интервал читается как «все действительные числа меньше 10», поэтому мы начнем с размещения открытой точки на 10 и рисования линии слева со стрелкой, указывающей, что решение продолжается до отрицательной бесконечности.
Чтобы записать неравенство, мы будем использовать <, поскольку круглые скобки указывают, что 10 не включено.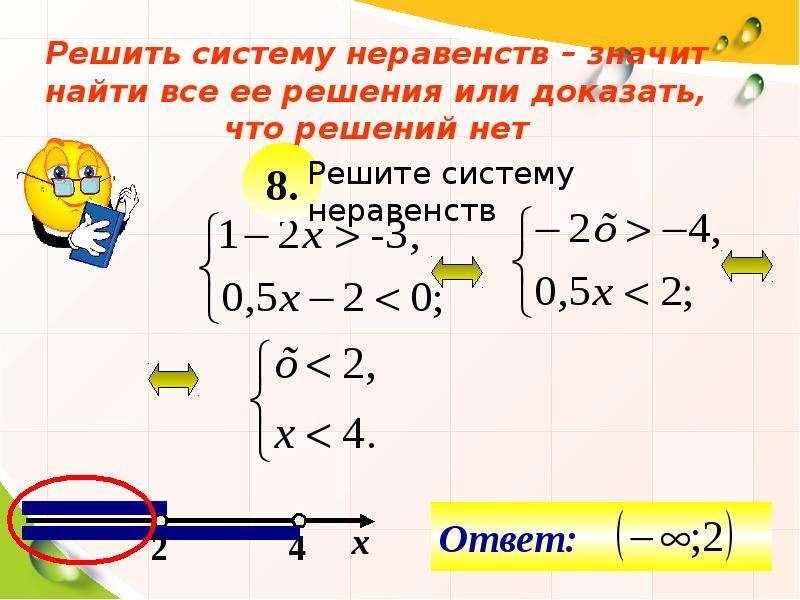 [латекс] x <10 [/ латекс]
[латекс] x <10 [/ латекс]
В следующем видео вы увидите примеры того, как нарисовать график с учетом неравенства в обозначении интервалов.
И, наконец, последнее видео, в котором показано, как записывать неравенства с помощью графика, с обозначением интервалов и в виде неравенства.
Решите пошаговые неравенства
Решите неравенства сложением и вычитанием
Вы можете решить большинство неравенств, используя обратные операции, как при решении уравнений.Это потому, что когда вы добавляете или вычитаете одно и то же значение из обеих сторон неравенства, вы сохраняете неравенство. Эти свойства указаны в поле ниже.
Сложение и вычитание свойств неравенства
Если [латекс] a> b [/ латекс], , то [латекс] a + c> b + c [/ латекс].
Если [латекс] a> b [/ latex] , , то [латекс] a-c> b-c [/ latex].
Поскольку неравенства имеют несколько возможных решений, графическое представление решений дает полезное визуальное представление ситуации, как мы видели в последнем разделе.В приведенном ниже примере показаны шаги для решения и графического представления неравенства и выражения решения с использованием интервальной записи.
Пример
Решите относительно x.
[латекс] {x} +3 \ lt {5} [/ латекс]
Показать решениеПолезно думать об этом неравенстве как о том, что вам предлагается найти все значения для x , включая отрицательные числа, так что при сложении трех вы получите число меньше 5.
[латекс] \ displaystyle \ begin {array} {l} x + 3 <\, \, \, \, 5 \\\ подчеркивание {\, \, \, \, \, - 3 \, \, \, \, - 3} \\ x \, \, \, \, \, \, \, \, <\, \, \, \, 2 \, \, \ end {array} [/ latex]
Выделите переменную, вычтя 3 из обеих частей неравенства.
Ответ
Неравенство: [латекс] x <2 [/ латекс]
Интервал: [латекс] \ влево (- \ infty, 2 \ вправо) [/ латекс]
График:
Линия представляет всех чисел, к которым можно сложить 3 и получить число меньше 5. Есть много чисел, которые разрешают это неравенство!
Так же, как вы можете проверить решение уравнения, вы можете проверить решение неравенства. Сначала вы проверяете конечную точку, подставляя ее в соответствующее уравнение.Затем вы проверяете, верно ли неравенство, подставляя любое другое решение, чтобы увидеть, является ли оно одним из решений. Поскольку существует несколько решений, рекомендуется проверять более одного из возможных решений. Это также может помочь вам проверить правильность вашего графика.
В приведенном ниже примере показано, как проверить, что [latex] x <2 [/ latex] является решением для [latex] x + 3 <5 [/ latex] .
Пример
Убедитесь, что [latex] x <2 [/ latex] является решением для [latex] x + 3 <5 [/ latex].
Подставьте конечную точку 2 в соответствующее уравнение [латекс] x + 3 = 5 [/ латекс].
[латекс] \ begin {array} {r} x + 3 = 5 \\ 2 + 3 = 5 \\ 5 = 5 \ end {array} [/ latex]
Выберите значение меньше 2, например 0, чтобы проверить неравенство. (Это значение будет на затененной части графика.)
[латекс] \ displaystyle \ begin {array} {r} x + 3 <5 \\ 0 + 3 <5 \\ 3 <5 \ end {array} [/ latex]
Проверяет!
[латекс] x <2 [/ latex] - это решение для [latex] x + 3 <5 [/ latex].
В следующих примерах показаны проблемы неравенства, которые включают операции с отрицательными числами. Также показан график решения неравенства. Не забудьте проверить решение. Это хорошая привычка!
Пример
Решить для x : [латекс] x-10 \ leq-12 [/ латекс]
Показать решениеВыделите переменную, добавив 10 к обеим сторонам неравенства.
[латекс] \ displaystyle \ begin {array} {r} x-10 \ le -12 \\\ underline {\, \, \, + 10 \, \, \, \, \, + 10} \\ x \, \, \, \, \, \, \, \, \, \, \ le \, \, \, — 2 \ end {array} [/ latex]
Ответ
Неравенство: [латекс] x \ leq-2 [/ latex]
Интервал: [latex] \ left (- \ infty, -2 \ right] [/ latex]
График: Обратите внимание, что используется замкнутый круг, поскольку неравенство «меньше или равно» [латекс] \ left (\ leq \ right) [/ latex]. Синяя стрелка нарисована слева от точки [латекс] -2 [/ латекс], потому что это значения меньше, чем [латекс] -2 [/ латекс].
Синяя стрелка нарисована слева от точки [латекс] -2 [/ латекс], потому что это значения меньше, чем [латекс] -2 [/ латекс].
Проверьте раствор [латекс] x-10 \ leq -12 [/ latex]
Показать решениеПодставьте конечную точку [латекс] -2 [/ латекс] в соответствующее уравнение [латекс] x-10 = -12 [/ латекс]
[латекс] \ displaystyle \ begin {array} {r} x-10 = -12 \, \, \, \\\ text {Does} \, \, \, — 2-10 = -12? \\ — 12 = -12 \, \, \, \ end {array} [/ latex]
Выберите значение меньше [латекс] -2 [/ латекс], например [латекс] -5 [/ латекс], чтобы проверить неравенство.(Это значение будет на затененной части графика.)
[латекс] \ displaystyle \ begin {array} {r} x-10 \ le -12 \, \, \, \\\ text {} \, \ text {Is} \, \, — 5-10 \ le -12? \\ — 15 \ le -12 \, \, \, \\\ text {It} \, \ text {проверяет!} \ End {array} [/ latex]
[латекс] x \ leq -2 [/ latex] — это решение [латекса] x-10 \ leq -12 [/ latex]
Пример
Решите относительно и . [латекс] a-17> -17 [/ латекс]
[латекс] a-17> -17 [/ латекс]
Выделите переменную, добавив 17 к обеим сторонам неравенства.
[латекс] \ displaystyle \ begin {array} {r} a-17> -17 \\\ подчеркивание {\, \, \, + 17 \, \, \, \, \, + 17} \\ a \ , \, \, \, \, \, \, \, \, \, \,> \, \, \, \, \, \, 0 \ end {array} [/ latex]
Ответ
Неравенство: [латекс] \ displaystyle a \, \,> \, 0 [/ latex]
Интервал: [latex] \ left (0, \ infty \ right) [/ latex] Обратите внимание, как мы используем скобки слева, чтобы показать, что решение не включает 0.
График: обратите внимание на пустой кружок, чтобы показать, что решение не включает 0.
Проверьте раствор [латекс] a-17> -17 [/ latex]
Показать решение[latex] \ displaystyle a \, \,> \, 0 [/ latex] — правильное решение для [latex] a-17> -17 [/ latex]?
Подставьте конечную точку 0 в соответствующее уравнение.
[латекс] \ displaystyle \ begin {array} {r} a-17 = -17 \, \, \, \\\ text {Does} \, \, \, 0-17 = -17? \\ — 17 = -17 \, \, \, \ end {array} [/ latex]
Выберите значение больше 0, например 20, чтобы проверить неравенство. (Это значение будет на затененной части графика.)
(Это значение будет на затененной части графика.)
[латекс] \ displaystyle \ begin {array} {r} a-17> -17 \, \, \, \\\ text {Is} \, \, 20-17> -17? \\ 3> -17 \, \, \, \\\\\ text {Проверяет!} \, \, \, \, \ end {array} [/ latex]
[latex] \ displaystyle a \,> \, 0 [/ latex] является решением для [latex] a-17> -17 [/ latex]
Предыдущие примеры показали вам, как решить одношаговое неравенство с переменной в левой части.В следующем видео представлены примеры того, как разрешить однотипное неравенство.
Что бы вы сделали, если бы переменная находилась в правой части неравенства? В следующем примере вы увидите, как справиться с этим сценарием.
Пример
Решите для x : [латекс] 4 \ geq {x} +5 [/ латекс]
Показать решение Выделите переменную, добавив 10 к обеим сторонам неравенства.
[латекс] \ displaystyle \ begin {array} {r} 4 \ geq {x} +5 \\\ подчеркивание {\, \, \, — 5 \, \, \, \, \, — 5} \\ -1 \, \, \, \, \, \, \, \, \, \, \ ge \, \, \, x \ end {array} [/ latex]
Перепишите неравенство с переменной слева — это упростит запись интервала и построение графика.
[латекс] x \ le {-1} [/ латекс]
Обратите внимание на то, что острая часть неравенства по-прежнему направлена на переменную, поэтому вместо того, чтобы читать, как отрицательное значение больше или равно x, теперь оно читается как x меньше или равно отрицательному.
Ответ
Неравенство: [латекс] x \ le {-1} [/ latex] Это также можно записать как
Интервал: [латекс] \ left (- \ infty, -1 \ right] [/ latex]
График: Обратите внимание, что замкнутый кружок используется потому, что неравенство «меньше или равно».Синяя стрелка нарисована слева от точки [латекс] -1 [/ латекс], потому что это значения меньше, чем [латекс] -1 [/ латекс].
Проверьте решение [latex] 4 \ geq {x} +5 [/ latex]
Показать решениеПодставьте конечную точку [латекс] -1 [/ латекс] в соответствующее уравнение [латекс] 4 = x + 5 [/ latex]
[латекс] \ displaystyle \ begin {array} {r} 4 = x + 5 \, \, \, \\\ text {Does} \, \, \, 4 = -1 + 5? \\ — 1 = -1 \, \, \, \ end {array} [/ latex]
Выберите значение меньше [латекс] -1 [/ латекс], например [латекс] -5 [/ латекс], чтобы проверить неравенство. (Это значение будет на затененной части графика.)
(Это значение будет на затененной части графика.)
[латекс] \ displaystyle \ begin {array} {r} 4 \ geq {-5} +5 \, \, \, \\\ text {} \, \ text {Is} \, \, 4 \ ge 0 ? \\\ text {It} \, \ text {проверяет!} \ end {array} [/ latex]
[latex] x \ le {-1} [/ latex] — это решение [latex] 4 \ geq {x} +5 [/ latex]
В следующем видео показаны примеры решения неравенств с переменной справа.
Решите неравенства с умножением и делением
Решение неравенства с переменной, коэффициент которой отличается от 1, обычно включает умножение или деление.Эти шаги подобны решению одношаговых уравнений, включающих умножение или деление, ЗА ИСКЛЮЧЕНИЕМ знака неравенства. Давайте посмотрим, что происходит с неравенством, когда вы умножаете или делите каждую сторону на одно и то же число.
| Начнем с истинного утверждения: [латекс] 10> 5 [/ латекс] | Давайте попробуем еще раз, начав с того же истинного утверждения: [латекс] 10> 5 [/ латекс] |
| Затем умножьте обе стороны на одинаковое положительное число: [латекс] 10 \ cdot 2> 5 \ cdot 2 [/ латекс] | На этот раз умножьте обе стороны на одинаковое отрицательное число: [латекс] 10 \ cdot-2> 5 \\ \, \, \, \, \, \ cdot -2 \, \ cdot-2 [/ латекс] |
| 20 больше 10, так что истинное неравенство сохраняется: [латекс] 20> 10 [/ латекс] | Погодите! [latex] −20 [/ latex] не на , а на больше, чем [latex] −10 [/ latex], так что ваше утверждение неверно. [латекс] -20> -10 [/ латекс] |
| При умножении на положительное число оставьте знак неравенства как есть! | Вы должны «перевернуть» знак неравенства, чтобы утверждение стало верным: [латекс] -20 <-10 [/ латекс] |
Внимание! Когда вы умножаете или делите на отрицательное число, «переверните» знак неравенства. Всякий раз, когда вы умножаете или делите обе стороны неравенства на отрицательное число, знак неравенства должен быть перевернут, чтобы утверждение оставалось верным.Эти правила кратко изложены во вставке ниже.
Свойства неравенства умножения и деления
| Начать с | Умножить на | Окончательное неравенство |
| [латекс] a> b [/ латекс] | [латекс] c [/ латекс] | [латекс] ac> bc [/ латекс] |
| [латекс] a> b [/ латекс] | [латекс] -c [/ латекс] | [латекс] ac |
| Начать с | Разделить на | Окончательное неравенство |
| [латекс] a> b [/ латекс] | [латекс] c [/ латекс] | [латекс] \ displaystyle \ frac {a} {c}> \ frac {b} {c} [/ latex] |
| [латекс] a> b [/ латекс] | [латекс] -c [/ латекс] | [латекс] \ displaystyle \ frac {a} {c} <\ frac {b} {c} [/ latex] |
Имейте в виду, что вы меняете знак только при умножении и делении на отрицательное число . Если вы добавите или вычтете на отрицательное число, неравенство останется прежним.
Если вы добавите или вычтете на отрицательное число, неравенство останется прежним.
Пример
Решите относительно x. [латекс] 3x> 12 [/ латекс]
Показать решение Разделите обе части на 3, чтобы изолировать переменную.[латекс] \ displaystyle \ begin {array} {r} \ underline {3x}> \ underline {12} \\ 3 \, \, \, \, \, \, \, \, \, \, \, \, 3 \\ x> 4 \, \, \, \ end {array} [/ latex]
Проверьте свое решение, сначала проверив конечную точку 4, а затем проверив другое решение на предмет неравенства.
[латекс] \ begin {array} {r} 3 \ cdot4 = 12 \\ 12 = 12 \\ 3 \ cdot10> 12 \\ 30> 12 \\\ text {Проверяет!} \ End {array} [/ латекс]
Ответ
Неравенство: [латекс] \ displaystyle x> 4 [/ latex]
Интервал: [латекс] \ left (4, \ infty \ right) [/ latex]
График:
Не было необходимости вносить какие-либо изменения в знак неравенства, потому что обе части неравенства были разделены на положительное 3. В следующем примере есть деление на отрицательное число, поэтому есть дополнительный шаг в решении!
В следующем примере есть деление на отрицательное число, поэтому есть дополнительный шаг в решении!
Пример
Решите для x .[латекс] -2x> 6 [/ латекс]
Показать решение Разделите каждую сторону неравенства на [латекс] −2 [/ латекс], чтобы изолировать переменную, и измените направление знака неравенства из-за деления на отрицательное число.[латекс] \ displaystyle \ begin {array} {r} \ underline {-2x} <\ underline {\, 6 \,} \\ - 2 \, \, \, \, - 2 \, \\ x < -3 \ end {array} [/ latex]
Проверьте свое решение, сначала проверив конечную точку [latex] −3 [/ latex], а затем проверив другое решение на предмет неравенства.
[латекс] \ begin {array} {r} -2 \ left (-3 \ right) = 6 \\ 6 = 6 \ -2 \ left (-6 \ right)> 6 \\ 12> 6 \ end {array} [/ latex]
Проверяет!
Ответ
Неравенство: [латекс] \ displaystyle x <-3 [/ latex]
Интервал: [латекс] \ left (- \ infty, -3 \ right) [/ latex]
График:
Поскольку обе стороны неравенства были разделены отрицательным числом, [латекс] -2 [/ latex], символ неравенства был изменен с> на <.
В следующем видео показаны примеры решения одношаговых неравенств с использованием свойства равенства умножения, где переменная находится в левой части.
Подумай об этом
Прежде чем вы прочитаете решение следующего примера, подумайте, какие свойства неравенств вам, возможно, потребуется использовать для решения неравенства. Чем этот пример отличается от предыдущего? Напишите свои идеи в поле ниже.
Решите для x .[латекс] — \ frac {1} {2}> — 12x [/ латекс]
Показать решениеЭто неравенство имеет переменную в правой части, которая отличается от предыдущих примеров. Начните процесс решения, как раньше, а в конце вы можете переместить переменную влево, чтобы записать окончательное решение.
Разделите обе стороны на [латекс] -12 [/ латекс], чтобы изолировать переменную. Поскольку вы делите на отрицательное число, вам нужно изменить направление знака неравенства.
Поскольку вы делите на отрицательное число, вам нужно изменить направление знака неравенства.
[латекс] \ displaystyle \ begin {array} {l} — \ frac {1} {2} \ gt {-12x} \\\\\ frac {- \ frac {1} {2}} {- 12} \ gt \ frac {-12x} {- 12} \\\ end {array} [/ latex]
Для деления дроби на целое число необходимо умножить на обратную величину, а обратная величина [latex] -12 [/ latex] будет [latex] \ frac {1} {- 12} [/ latex]
[латекс] \ displaystyle \ begin {array} {r} \ left (- \ frac {1} {12} \ right) \ left (- \ frac {1} {2} \ right) \ lt \ frac {- 12x} {- 12} \, \, \\\\ \ frac {1} {24} \ lt \ frac {\ cancel {-12} x} {\ cancel {-12}} \\\\ \ frac { 1} {24} \ lt {x} \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
Ответ
Неравенство: [latex] \ frac {1} {24} \ lt {x} [/ latex] Это также можно записать с переменной слева как [latex] x \ gt \ frac {1} {24} [ /латекс].Чтобы записать неравенство с переменной слева, нужно немного подумать, но это поможет вам записать интервал и правильно нарисовать график.
Интервал: [латекс] \ left (\ frac {1} {24}, \ infty \ right) [/ latex]
График:
В следующем видео приводятся примеры того, как решить неравенство со свойством умножения равенства, где переменная находится справа.
Объединить свойства неравенства для решения алгебраических неравенств
Популярная стратегия решения уравнений с выделением переменной также применима к решению неравенств.Путем сложения, вычитания, умножения и / или деления вы можете переписать неравенство так, чтобы переменная находилась с одной стороны, а все остальное — с другой. Как и в случае одношаговых неравенств, решения многоступенчатых неравенств можно изобразить на числовой прямой.
Пример
Решите относительно p. . [латекс] 4p + 5 <29 [/ латекс]
Показать решение Начните изолировать переменную, вычтя 5 из обеих частей неравенства.
[латекс] \ displaystyle \ begin {array} {l} 4p + 5 <\, \, \, 29 \\\ подчеркивание {\, \, \, \, \, \, \, \, \, - 5 \, \, \, \, \, - 5} \\ 4p \, \, \, \, \, \, \, \, \, <\, \, 24 \, \, \ end {array} [ / латекс]
Разделите обе части неравенства на 4, чтобы выразить переменную с коэффициентом 1.
[латекс] \ begin {array} {l} \ underline {4p} \, <\, \, \ underline {24} \, \, \\\, 4 \, \, \, \, <\, \ , 4 \\\, \, \, \, \, p <6 \ end {array} [/ latex]
Ответ
Неравенство: [латекс] p <6 [/ латекс]
Интервал: [латекс] \ влево (- \ infty, 6 \ вправо) [/ латекс]
График: обратите внимание на белый кружок в конечной точке 6, чтобы показать, что решения неравенства не включают 6. Значения, где p меньше 6, находятся вдоль числовой линии слева от 6.
Проверить решение.
Показать решениеПроверьте конечную точку 6 в соответствующем уравнении.
[латекс] \ displaystyle \ begin {array} {r} 4p + 5 = 29 \, \, \, \\\ text {Does} \, \, \, 4 (6) + 5 = 29? \\ 24 + 5 = 29 \, \, \, \\ 29 = 29 \, \, \, \\\ текст {Да!} \, \, \, \, \, \, \ End {array} [/ latex]
Попробуйте другое значение, чтобы проверить неравенство. Давайте использовать [latex] p = 0 [/ latex].
Давайте использовать [latex] p = 0 [/ latex].
[латекс] \ displaystyle \ begin {array} {r} 4p + 5 <29 \, \, \, \\\ text {Is} \, \, \, 4 (0) +5 <29? \\ 0 +5 <29 \, \, \, \\ 5 <29 \, \, \, \\\ text {Да!} \, \, \, \, \, \ End {array} [/ latex]
[латекс] p <6 [/ латекс] - это решение [латекс] 4p + 5 <29 [/ латекс]
Пример
Решить для x : [латекс] 3x – 7 \ ge 41 [/ латекс]
Показать решениеНачните изолировать переменную, прибавив 7 к обеим сторонам неравенства, затем разделите обе стороны неравенства на 3, чтобы выразить переменную с коэффициентом 1.
[латекс] \ displaystyle \ begin {array} {l} 3x-7 \ ge 41 \\\ подчеркивание {\, \, \, \, \, \, \, + 7 \, \, \, \, + 7} \\\ frac {3x} {3} \, \, \, \, \, \, \, \, \ ge \ frac {48} {3} \\\, \, \, \, \, \, \, \, \, \, x \ ge 16 \ end {array} [/ latex]
Ответ
Неравенство: [латекс] x \ ge 16 [/ латекс]
Интервал: [латекс] \ left [16, \ infty \ right) [/ latex]
График: Чтобы изобразить это неравенство, вы рисуете замкнутый круг в конечной точке 16 числовой линии, чтобы показать, что решения включают значение 16. Линия продолжается вправо от 16, потому что все числа больше 16 также будут составлять неравенство [латекс] 3x – 7 \ ge 41 [/ латекс] верно.
Линия продолжается вправо от 16, потому что все числа больше 16 также будут составлять неравенство [латекс] 3x – 7 \ ge 41 [/ латекс] верно.
Проверить решение.
Показать решениеСначала проверьте конечную точку 16 в соответствующем уравнении.
[латекс] \ displaystyle \ begin {array} {r} 3x-7 = 41 \, \, \, \\\ text {Does} \, \, \, 3 (16) -7 = 41? \\ 48 -7 = 41 \, \, \, \\ 41 = 41 \, \, \, \\\ текст {Да!} \, \, \, \, \, \ End {array} [/ latex]
Затем попробуйте другое значение, чтобы проверить неравенство. Давайте использовать [латекс] x = 20 [/ латекс].
[латекс] \ displaystyle \ begin {array} {r} \, \, \, \, 3x-7 \ ge 41 \, \, \, \\\ текст {Is} \, \, \, \, \ , 3 (20) -7 \ ge 41? \\ 60-7 \ ge 41 \, \, \, \\ 53 \ ge 41 \, \, \, \\\ текст {Да!} \, \, \ , \, \, \ end {array} [/ latex]
При решении многоступенчатых уравнений обратите внимание на ситуации, в которых вы умножаете или делите на отрицательное число.В этих случаях необходимо перевернуть знак неравенства.
Пример
Решите относительно p. . [латекс] −58> 14−6p [/ латекс]
Показать решениеОбратите внимание, как переменная находится в правой части неравенства, метод решения в этом случае не меняется.
Начните изолировать переменную, вычтя 14 из обеих частей неравенства.
[латекс] \ displaystyle \ begin {array} {l} −58 \, \,> 14−6p \\\ подчеркивание {\, \, \, \, \, \, \, \, \, \, \ , \, — 14 \, \, \, \, \, \, \, — 14} \\ — 72 \, \, \, \, \, \, \, \, \, \, \,> — 6p \ end {array} [/ latex]
Разделите обе части неравенства на [латекс] −6 [/ латекс], чтобы выразить переменную с коэффициентом 1.При делении на отрицательное число знак неравенства меняется на противоположный.
[латекс] \ begin {array} {l} \ underline {-72}> \ underline {-6p} \\ — 6 \, \, \, \, \, \, \, \, \, \, — 6 \\\, \, \, \, \, \, 12 \ lt {p} \ end {array} [/ latex]
Мы также можем записать это как [latex] p> 12 [/ latex]. Обратите внимание, как знак неравенства все еще открывается в сторону переменной p.
Ответ
Неравенство: [латекс] p> 12 [/ latex]
Интервал: [latex] \ left (12, \ infty \ right) [/ latex]
График: График неравенства p > 12 имеет открытый кружок на 12 со стрелкой, уходящей вправо.
Проверить решение.
Показать решениеСначала проверьте конечную точку 12 в соответствующем уравнении.
[латекс] \ begin {array} {r} -58 = 14-6p \\ — 58 = 14-6 \ left (12 \ right) \\ — 58 = 14-72 \\ — 58 = -58 \ end {array} [/ latex]
Затем попробуйте другое значение, чтобы проверить неравенство. Попробуйте 100.
[латекс] \ begin {array} {r} -58> 14-6p \\ — 58> 14-6 \ left (100 \ right) \\ — 58> 14-600 \\ — 58> -586 \ end {array} [/ latex]
В следующем видео вы увидите пример решения линейного неравенства с переменной в левой части неравенства и пример переключения направления неравенства после деления на отрицательное число.
В следующем видео вы увидите пример решения линейного неравенства с переменной в правой части неравенства и пример переключения направления неравенства после деления на отрицательное число.
Упростите и решите алгебраические неравенства, используя свойство распределения
Как и в случае с уравнениями, свойство распределения можно применять для упрощения выражений, являющихся частью неравенства.Как только скобки будут убраны, устранение неравенства будет несложным.
Пример
Решите для x . [латекс] 2 \ влево (3x – 5 \ вправо) \ leq 4x + 6 [/ латекс]
Показать решениеРаздать, чтобы убрать скобки.
[латекс] \ displaystyle \ begin {array} {r} \, 2 (3x-5) \ leq 4x + 6 \\\, \, \, \, 6x-10 \ leq 4x + 6 \ end {array} [/ латекс]
Вычтите 4 x с обеих сторон, чтобы получить переменный член только с одной стороны.
[латекс] \ begin {array} {r} 6x-10 \ le 4x + 6 \\\ подчеркивание {-4x \, \, \, \, \, \, \, \, \, \, \, \ , \, \, — 4x} \, \, \, \, \, \, \, \, \, \\\, \, \, 2x-10 \, \, \ leq \, \, \, \ , \, \, \, \, \, \, \, \, 6 \ end {array} [/ latex]
Добавьте 10 к обеим сторонам, чтобы изолировать переменную.
[латекс] \ begin {array} {r} \\\, \, \, 2x-10 \, \, \ le \, \, \, \, \, \, \, \, 6 \, \, \, \\\ подчеркивание {\, \, \, \, \, \, + 10 \, \, \, \, \, \, \, \, \, + 10} \\\, \, \, 2x \, \, \, \, \, \, \, \, \, \, \, \ le \, \, \, \, \, 16 \, \, \, \ end {array} [/ latex ]
Разделите обе части на 2, чтобы выразить переменную с коэффициентом 1.
[латекс] \ begin {array} {r} \ underline {2x} \ le \, \, \, \ underline {16} \\\, \, \, 2 \, \, \, \, \, \ , \, \, \, \, \, \, \, 2 \, \, \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, x \, \, \, \ le \, \, \, \, \, 8 \ end {array} [/ latex]
Ответ
Неравенство: [latex] x \ le8 [/ latex]
Интервал: [latex] \ left (- \ infty, 8 \ right] [/ latex]
График: График этого набора решений включает 8 и все, что слева от 8 в числовой строке.
Проверить решение.
Показать решениеСначала проверьте конечную точку 8 в соответствующем уравнении.
[латекс] \ displaystyle \ begin {array} {r} 2 (3x-5) = 4x + 6 \, \, \, \, \, \, \\ 2 (3 \, \ cdot \, 8-5 ) = 4 \, \ cdot \, 8 + 6 \\\, \, \, \, \, \, \, \, \, \, \, 2 (24-5) = 32 + 6 \, \, \, \, \, \, \\ 2 (19) = 38 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \\ 38 = 38 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
Затем выберите другое решение и оцените неравенство для этого значения, чтобы убедиться, что это истинное утверждение. Попробуйте 0.
Попробуйте 0.
[латекс] \ displaystyle \ begin {array} {l} 2 (3 \, \ cdot \, 0-5) \ le 4 \, \ cdot \, 0 + 6? \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, 2 (-5) \ le 6 \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, — 10 \ le 6 \, \, \ end {array} [/ latex]
[latex] x \ le8 [/ latex] — это решение для [latex] \ left (- \ infty, 8 \ right] [/ latex]
В следующем видео вам дается пример того, как решить многоступенчатое неравенство, которое требует использования свойства распределения.
Подумай об этом
В следующем примере вам дано неравенство с термином, который выглядит сложным.Если вы остановитесь и подумаете о том, как использовать порядок операций для устранения неравенства, мы надеемся, что это покажется простой проблемой. Используйте текстовое поле, чтобы записать, что вы считаете лучшим первым шагом.
Найдите файл. [латекс] \ displaystyle \ frac {{2} {a} — {4}} {{6}} {<2} [/ latex]
Показать решениеОчистите дробь, умножив обе части уравнения на 6.
[латекс] \ displaystyle \ begin {array} {r} \ frac {{2} {a} — {4}} {{6}} {<2} \, \, \, \, \, \, \ , \, \\\\ 6 \, \ cdot \, \ frac {2a-4} {6} <2 \, \ cdot \, 6 \\\\ {2a-4} <12 \, \, \, \, \, \, \ end {array} [/ latex]
Добавьте 4 к обеим сторонам, чтобы изолировать переменную.
[латекс] \ displaystyle \ begin {array} {r} 2a-4 <12 \\\ underline {\, \, \, + 4 \, \, \, \, + 4} \\ 2a <16 \ end {array} [/ latex]
Разделите обе части на 2, чтобы выразить переменную с коэффициентом 1.
[латекс] \ displaystyle \ begin {array} {c} \ frac {2a} {2} <\, \ frac {16} {2} \\\\ a <8 \ end {array} [/ latex]
Ответ
Неравенство: [латекс] a <8 [/ латекс]
Интервал: [латекс] \ left (- \ infty, 8 \ right) [/ latex]
График: График этого решения содержит сплошную точку у 8, чтобы показать, что 8 входит в набор решений. Линия продолжается влево, показывая, что значения менее 8 также включены в набор решений.
Линия продолжается влево, показывая, что значения менее 8 также включены в набор решений.
Проверить решение.
Показать решение Сначала проверьте конечную точку 8 в соответствующем уравнении.[латекс] \ displaystyle \ begin {array} {r} \ frac {2a-4} {6} = 2 \, \, \, \, \\\\\ text {Does} \, \, \, \ frac {2 (8) -4} {6} = 2? \\\\\ frac {16-4} {6} = 2 \, \, \, \, \\\\\ frac {12} {6 } = 2 \, \, \, \, \\\\ 2 = 2 \, \, \, \, \\\\\ text {Да!} \, \, \, \, \, \ End {массив } [/ латекс]
Затем выберите другое решение и оцените неравенство для этого значения, чтобы убедиться, что это истинное утверждение.Попробуйте 5.
[латекс] \ displaystyle \ begin {array} {r} \ text {Is} \, \, \, \ frac {2 (5) -4} {6} <2? \\\\\ frac {10- 4} {6} <2 \, \, \, \\\\\, \, \, \, \ frac {6} {6} <2 \, \, \, \\\\ 1 <2 \, \, \, \\\\\ text {Да!} \, \, \, \, \, \ end {array} [/ latex]
Сводка
Решение неравенств очень похоже на решение уравнений, за исключением того, что вы должны перевернуть символы неравенства, когда вы умножаете или делите обе стороны неравенства на отрицательное число. Решения неравенств можно представить тремя способами: интервал, график и неравенство.Поскольку обычно существует более одного решения неравенства, когда вы проверяете свой ответ, вы должны проверить конечную точку и еще одно значение, чтобы проверить направление неравенства.
Решения неравенств можно представить тремя способами: интервал, график и неравенство.Поскольку обычно существует более одного решения неравенства, когда вы проверяете свой ответ, вы должны проверить конечную точку и еще одно значение, чтобы проверить направление неравенства.
Неравенства могут иметь ряд ответов. Решения часто изображаются на числовой линии, чтобы визуализировать все решения. Многоступенчатые неравенства решаются с использованием тех же процессов, которые работают для решения уравнений, за одним исключением. Когда вы умножаете или делите обе стороны неравенства на отрицательное число, вы должны перевернуть символ неравенства.Символы неравенства остаются неизменными при добавлении или вычитании положительных или отрицательных чисел к обеим сторонам неравенства.
Устранение неравенств — объяснения и примеры
Что такое неравенство в математике?
Слово неравенство означает просто математическое выражение, в котором стороны не равны друг другу. По сути, неравенство сравнивает любые два значения и показывает, что одно значение меньше, больше или равно значению на другой стороне уравнения.
По сути, неравенство сравнивает любые два значения и показывает, что одно значение меньше, больше или равно значению на другой стороне уравнения.
В основном, для представления уравнений неравенства используются пять символов неравенства.
Символы неравенства
Эти символы неравенства: меньше ( <), больше (> ), меньше или равно ( ≤ ), больше или равно ( ≥ ) и символ неравенства ( ≠ ) .Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной.
Операции с неравенствами
Операции с линейными неравенствами включают сложение, вычитание, умножение и деление. Общие правила этих операций показаны ниже.
Хотя мы использовали символ <для иллюстрации, следует отметить, что те же правила применяются к>, ≤ и ≥.
- Символ неравенства не меняется при добавлении одного и того же числа к обеим сторонам неравенства.
 Например, если a
Например, если a - Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства.Например, если a
- Умножение обеих частей неравенства на положительное число не меняет знака неравенства. Например, если a
- Разделение обеих сторон неравенства на положительное число не меняет знака неравенства. Если a
- Умножение обеих сторон уравнения неравенства на отрицательное число изменяет направление символа неравенства.Например, если a b *
- Аналогичным образом, разделение обеих сторон уравнения неравенства на отрицательное число изменяет символ неравенства. Если a b / c
- Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства.Например, если a
Как устранить неравенства?
Так же, как и линейные уравнения, неравенства можно решить, применяя аналогичные правила и шаги за некоторыми исключениями. Единственная разница при решении линейных уравнений — это операция умножения или деления на отрицательное число.Умножение или деление неравенства на отрицательное число изменяет символ неравенства.
Единственная разница при решении линейных уравнений — это операция умножения или деления на отрицательное число.Умножение или деление неравенства на отрицательное число изменяет символ неравенства.
Линейные неравенства могут быть решены с помощью следующих операций:
- Сложение
- Вычитание
- Умножение
- Деление
- Распределение собственности
Решение линейных неравенств с добавлением
Давайте разберемся с несколькими примерами ниже. это понятие.
Пример 1
Решите 3x — 5 ≤ 3 — x.
Решение
Начнем с добавления обеих сторон неравенства на 5
3x — 5 + 5 ≤ 3 + 5 — x
3x ≤ 8 — x
Затем сложим обе стороны на x.
3x + x ≤ 8 — x + x
4x ≤ 8
Наконец, разделите обе части неравенства на 4, чтобы получить;
x ≤ 2
Пример 2
Вычислите диапазон значений y, который удовлетворяет неравенству: y — 4 <2y + 5.
Решение
Сложите обе части неравенства на 4.
y — 4 + 4 <2y + 5 + 4
y <2y + 9
Вычтите обе части на 2y.
y — 2y <2y - 2y + 9
−y <9 Умножьте обе части неравенства на −1 и измените направление символа неравенства. y> — 9
Решение линейных неравенств с вычитанием
Чтобы понять эту концепцию, рассмотрим несколько примеров ниже.
Пример 3
Решите x + 8> 5.
Решение
Выделите переменную x, вычтя 8 из обеих сторон неравенства.
x + 8-8> 5-8 => x> −3
Следовательно, x> −3.
Пример 4
Решите 5x + 10> 3x + 24.
Решение
Вычтите 10 с обеих сторон неравенства.
5x + 10-10> 3x + 24-10
5x> 3x + 14.
Теперь вычтем обе части неравенства на 3x.
5x — 3x> 3x — 3x + 14
2x> 14
x> 7
Решение линейных неравенств с умножением
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 5
Решить x / 4> 5
Решение:
Умножить обе стороны неравенства на знаменатель дроби
4 (x / 4)> 5 x 4
x > 20
Пример 6
Решите -x / 4 ≥ 10
Решение:
Умножьте обе стороны неравенства на 4.
4 (-x / 4) ≥ 10 x 4
-x ≥ 40
Умножьте обе стороны неравенства на -1 и измените направление символа неравенства на противоположное.
x ≤ — 40
Решение линейных неравенств с делением
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 7
Решите неравенство: 8x — 2> 0.
Решение
Прежде всего, сложите обе стороны неравенства на 2
8x — 2 + 2> 0 + 2
8x> 2
Теперь решите, разделив обе части неравенства на 8, чтобы получить;
x> 2/8
x> 1/4
Пример 8
Решите следующее неравенство:
−5x> 100
Решение
Разделите оба сторон неравенства на -5 и измените направление символа неравенства
= −5x / -5 <100 / -5
= x <- 20
Решение линейных неравенств с использованием распределительного свойства
Давайте см. несколько примеров ниже, чтобы понять эту концепцию.
Пример 9
Решить: 2 (x — 4) ≥ 3x — 5
Решение
2 (x — 4) ≥ 3x — 5
Примените свойство распределения для удаления скобок.
⟹ 2x — 8 ≥ 3x — 5
Сложить обе стороны на 8.
⟹ 2x — 8 + 8 ≥ 3x — 5 + 8
⟹ 2x ≥ 3x + 3
Вычесть обе стороны на 3.
⟹ 2x — 3x ≥ 3x + 3 — 3x
⟹ -x ≥ 3
⟹ x ≤ — 3
Пример 10
Студент набрал 60 баллов за первый тест и 45 баллов во втором тесте заключительного экзамена.Сколько минимальных баллов должен набрать ученик в третьем тесте, чтобы получить в среднем 62 балла.
Решение
Пусть в третьем тесте будет набрано x баллов.
(60 + 45 + x) / 3 ≥ 62
105 + x ≥ 196
x ≥ 93
Следовательно, учащийся должен набрать 93 балла, чтобы поддерживать среднее значение не менее 62 баллов.
Пример 11
Джастину требуется не менее 500 долларов для празднования своего дня рождения.Если он уже накопил 150 долларов, до этой даты осталось 7 месяцев. Какую минимальную сумму он должен откладывать ежемесячно?
Решение
Пусть минимальная ежемесячная экономия = x
150 + 7x ≥ 500
Решите для x
150-150 + 7x ≥ 500-150
x ≥ 50
Следовательно, Джастин должен экономить 50 долларов и более
Пример 12
Найдите два последовательных нечетных числа, которые больше 10 и имеют сумму меньше 40.
Решение
Пусть меньшее нечетное число = x
Следовательно, следующее число будет x + 2
x> 10 ………. больше 10
x + (x + 2) <40 …… сумма меньше 40
Решите уравнения.
2x + 2 <40
x + 1 <20
x <19
Объедините два выражения.
10 Следовательно, последовательные нечетные числа следующие: 11 и 13, 13 и 15, 15 и 17, 17 и 19. Числовая прямая — лучший инструмент для представления и визуализации чисел. Числовая линия определяется как прямая горизонтальная линия с числами, расположенными на равных отрезках или интервалах. У числовой прямой есть нейтральная точка в середине, известная как начало координат. Справа от начала координат на числовой прямой находятся положительные числа, а слева от начала координат — отрицательные числа. Линейные уравнения также можно решить графическим методом с использованием числовой прямой. Пример 13 Если символ неравенства больше или равен или меньше или равен знаку (≥ или ≤), нарисуйте круг над числовым числом и заполните или заштрихуйте круг.Наконец, проведите линию, идущую от заштрихованного круга в направлении чисел, которые удовлетворяют уравнению неравенства. Пример 14 x ≥ 1 Та же процедура используется для решения уравнений, включающих интервалы. Пример 15 –2 < x <2 Пример 16 –1 ≤ x ≤ 2 Пример 17 –1 < x ≤ 2 Решите следующие неравенства и представьте свой ответ в числовой строке. Ответы Большинство правил или методов, используемых при решении многошаговых уравнений, должны легко применяться к решению неравенств. Единственная большая разница заключается в том, как символ неравенства переключает направление , когда отрицательное число умножается или делится на обе части уравнения. В этом уроке я рассмотрю семь (7) рабочих примеров с различные уровни сложности, чтобы обеспечить достаточно практики. БОЛЬШЕ, ЧЕМ БОЛЬШЕ ИЛИ РАВНО МЕНЬШЕ, ЧЕМ МЕНЬШЕ ИЛИ РАВНО Пример 1: Решить и построить график решения неравенства Чтобы решить это неравенство, мы хотим найти всех значений x, которые могут ему удовлетворить. Проверьте значения x = 0, x = 1, x = 2, x = 3, x = 5, x = 6 и x = 7. Какое из этих значений x соответствует истинному утверждению? После выполнения некоторых обратных замен вы должны согласиться, что работают только 5, 6 и 7; а остальные терпят неудачу. Но вопрос в том, есть ли больше значений x, кроме упомянутых? Ответ положительный! Теперь давайте решим неравенство, чтобы выяснить весь набор значений, которые могут сделать его истинным. Пример 2: Решите и изобразите решение неравенства В этом примере показано, что происходит с символом неравенства при делении на отрицательное число. ВСЕГДА переключайте направление неравенства всякий раз, когда вы делите или умножаете отрицательное число на обе стороны неравенства. Используйте закрытое или закрашенное отверстие , чтобы указать, что 7 является частью решения. Решение неравенства x \ le 7 включает 7 и все, что находится слева от него. Пример 3: Решите и изобразите решение неравенства В этой задаче у меня есть переменные по обе стороны неравенства. Однако, если вы попытаетесь сохранить переменную справа, убедитесь, что вы знаете об их тонкостях. Например, ответ на эту проблему: x <- \, 6, что совпадает с - \, 6> x. Они эквивалентны, потому что начало неравенства также указывает на — \, 6. Следовательно, это означает, что если я переключаю переменную и константу в своем окончательном ответе, я также должен изменить направление символа, чтобы значение оставалось неизменным. Обратите внимание, что I не изменил направление неравенства потому что я разделил обе стороны на положительное число. Пример 4: Решите и изобразите решение неравенства Я построил эту задачу, чтобы подчеркнуть шаг, необходимый для работы с символом скобки . Я знаю, что это вас не смутит, потому что вы уже видели это раньше, когда решали линейные уравнения, верно? Шаг, необходимый для того, чтобы избавиться от скобок, — применить распределительное свойство умножения над сложением.Однако я должен предостеречь вас, чтобы вы были осторожны со знаками в процессе умножения. Помните, что произведение двух членов с одинаковыми знаками является положительным, а если знаки не совпадают, произведение отрицательное. Пример 5: Решите и изобразите решение неравенства Мой общий подход заключается в том, чтобы немедленно удалить скобки, используя свойство распределения, объединить одинаковые термины с обеих сторон и, наконец, оставить x слева, а постоянная в противоположную сторону. Что касается правой стороны, это похожие термины, поэтому я просто объединю их. Пример 6: Решите и изобразите решение неравенства «Сложность» этой задачи не должна вас беспокоить. Ключ к успешному решению этой проблемы — применение всех техник, которые вы уже изучили из наших предыдущих примеров. Если вам нужен обзор, пожалуйста, оглядывайтесь назад. Попробуйте решить эту проблему, не просматривая подробное решение. Каждый раз, когда вы думаете, что закончили, сравните то, что у вас есть на бумаге, с ответом ниже. Пример 7: Решите и изобразите решение неравенства Давайте закончим, выполнив один последний пример мастерства! Опять же, сначала сделайте это самостоятельно на бумаге, а затем сравните свое решение с ответом ниже. Затем упростите правую часть, объединив похожие термины, появившиеся после распространения. Возможно, вас также заинтересует: Шаги по построению графиков линейных неравенств Примеры построения графиков линейных неравенств Графические системы линейных неравенств1 Устранение неравенств В этом разделе вы узнаете, как решить проблему неравенства. Вот пример: Рассмотрим неравенство Когда мы подставляем 8 вместо x, неравенство становится 8-2> 5.
Таким образом, x = 8 — это решение неравенства.
С другой стороны, замена -2 на x дает ложное утверждение.
(-2) -2> 5.
Таким образом, x = -2 НЕ является решением неравенства.Неравенства
обычно есть много решений. Как и в случае с решением уравнений, есть определенные манипуляции
неравенства, не меняющие решений. Вот список
«допустимых» манипуляций: Пример: Неравенство x -2> 5 имеет те же решения, что и
неравенство x > 7. (Второе неравенство было получено из
первый, добавив 2 с обеих сторон.) Пример: Неравенство 5- x > 4 имеет те же решения, что и
неравенство 4 <5 - x . (Мы перешли на другую сторону и повернули «> »
в « <''). И последнее, но не менее важное: операция, лежащая в основе всех
проблемы с неравенством: Примеры: Звучит достаточно безобидно. Неравенство имеет те же решения, что и неравенство. (Мы разделили на +2 с обеих сторон). Неравенство -2 x > 4 имеет те же решения, что и
неравенство x <-2. (Мы разделили на (-2) с обеих сторон и поменяли местами
"> » на» <''.) Но Правило 3 запрещает более причудливые ходы: неравенство ДЕЙСТВИТЕЛЬНО.
НЕ имеет тех же решений, что и неравенство x > 1.(Мы были
планируем разделить обе стороны на x , но мы не можем, потому что не
теперь знайте, будет ли x положительным или отрицательным!)
легко проверить, что x = -2 решает первое неравенство, но делает
не решить второе неравенство. С помощью этих трех правил решаются только « простые » неравенства; наиболее
неравенство устраняется с помощью различных методов. Решим некоторые неравенства: Основная стратегия для неравенств и уравнений та же самая: изолировать x с одной стороны и поместить «другие вещи» с другой стороны.Следуя этой стратегии, переместим +5 вправо. Мы достигаем этого путем вычитания 5 с обеих сторон (Правило 1), чтобы получить после упрощения получаем После того, как мы разделим на +2 с обеих сторон (Правило 3a), нам удалось выделить x слева: или упрощенно, Все действительные числа меньше единицы решают неравенство. Мы говорим, что
«множество решений» неравенства состоит из всех действительных чисел за вычетом
чем 1.В обозначении интервала набором решений является интервал. Начнем с перемещения цифры 5 вправо путем вычитания 5 с обеих сторон (Правило 1): или упрощенно, Как избавиться от знака « — » перед размером x ?
Просто умножьте на (-1) с обеих сторон (Правило 3b), по ходу меняя «» на «»: или упрощенное Все действительные числа больше или равные
-1 удовлетворяют неравенству. Давайте сначала упростим: Есть несколько маршрутов; возьмем это: вычтем 2 x с обеих сторон (Правило 1). и упростить: Затем вычтите 9 с обеих сторон (Правило 1): упростить, чтобы получить Затем разделите на 4 (Правило 3а): и еще раз упростим: Приятнее смотрится, если поменяться стороной (Правило 2). В интервальной записи набор решений выглядит так:
. Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard. К концу этого раздела вы сможете: Будьте готовы 2.18 Перед тем, как начать, пройдите тест на готовность. Перевести с алгебры на английский язык: 15> x15> x. Будьте готовы 2.19 Решите: n − 9 = −42.n − 9 = −42. Будьте готовы 2.20 Решите: −5p = −23. − 5p = −23. Будьте готовы 2.21 Решите: 3a − 12 = 7a − 20.3a − 12 = 7a − 20. Вы помните, что означает число, являющееся решением уравнения? Решение уравнения — это значение переменной, которое делает истинное утверждение при подстановке в уравнение. А как насчет решения неравенства? Какое число сделало бы неравенство x> 3x> 3 истинным? Вы думаете, « x может быть 4»? Это правильно, но x тоже может быть 5, 20 или даже 3.001. Любое число больше 3 является решением неравенства x> 3x> 3. Мы показываем решения неравенства x> 3x> 3 на числовой прямой, закрашивая все числа справа от 3, чтобы показать, что все числа больше 3 являются решениями. Поскольку число 3 само по себе не является решением, мы помещаем открывающую скобку в 3. График x> 3x> 3 показан на рисунке 2.7. Обратите внимание, что используется следующее соглашение: голубые стрелки указывают в положительном направлении, а синие стрелки указывают в отрицательном направлении. График неравенства x≥3x≥3 очень похож на график x> 3x> 3, но теперь нам нужно показать, что 3 также является решением. Мы делаем это, помещая скобку в положение x = 3x = 3, как показано на рисунке 2.8. Обратите внимание, что символ открытых скобок (, показывает, что конечная точка неравенства не включена. Символ открытой скобки, [, показывает, что конечная точка включена. График на числовой прямой: ⓐ x≤1x≤1 ⓑ x <5x <5 ⓒ x> −1x> −1 Решение Попробовать 2.131 График на числовой прямой: ⓐ x≤ − 1x≤ − 1 ⓑ x> 2x> 2 ⓒ x <3x <3 Попробовать 2.132 График на числовой прямой: ⓐ x> −2x> −2 ⓑ x <−3x <−3 ⓒ x≥ − 1x≥ − 1 Мы также можем представить неравенства, используя обозначение интервалов . Неравенство x≤1x≤1 означает все числа, меньшие или равные 1.У этих чисел нет нижнего предела. Мы пишем x≤1x≤1 в обозначении интервала как (−∞, 1] (- ∞, 1]. Символ −∞ − ∞ читается как «отрицательная бесконечность». На рисунке 2.10 показаны как числовая строка, так и обозначение интервала. Вы заметили, как скобка или скобка в обозначении интервала соответствует символу в конце стрелки? Эти отношения показаны на рисунке 2. Рисунок 2.11 Обозначение неравенств на числовой прямой и в обозначении интервалов использует аналогичные символы для обозначения конечных точек интервалов. График в числовой строке и запись в интервале. ⓐ x≥ − 3x≥ − 3 ⓑ x <2,5x <2,5 ⓒ x≤ − 35x≤ − 35 Попробуй 2,133 График на числовой прямой и запись в интервале обозначений: ⓐ x> 2x> 2 ⓑ x≤ − 1,5x≤ − 1,5 ⓒ x≥34x≥34 Попробуй 2.134 График на числовой прямой и запись в интервале обозначений: ⓐ x≤ − 4x≤ − 4 ⓑ x≥0,5x≥0,5 ⓒ x <−23x <−23 Свойства равенства вычитания и сложения утверждают, что если две величины равны, когда мы добавляем или вычитаем одинаковую сумму из обеих величин, результаты будут равными. Аналогичные свойства верны и для неравенств. Аналогичным образом мы можем показать, что неравенство остается неизменным и для сложения. Это приводит нас к свойствам неравенства на вычитание и сложение. Мы используем эти свойства для решения неравенств, выполняя те же действия, что и при решении уравнений. Решая неравенство x + 5> 9x + 5> 9, шаги будут выглядеть так: Таблица 2.6 Любое число больше 4 является решением этого неравенства. Решите неравенство n − 12≤58n − 12≤58, обозначьте решение на числовой прямой и запишите решение в интервальной записи. Попробовать 2.135 Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. p-34≥16p-34≥16 Попробуйте 2.136 Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. r − 13≤712r − 13≤712 Свойства равенства деления и умножения утверждают, что если две величины равны, когда мы делим или умножаем обе величины на одинаковую величину, результаты также будут равны (при условии, что не делить на 0). Существуют ли аналогичные свойства для неравенств? Что происходит с неравенством, когда мы делим или умножаем обе части на константу? Рассмотрим числовые примеры. Неравенство сохраняется, когда мы делим или умножаем на отрицательное число? Когда мы делим или умножаем неравенство на положительное число, знак неравенства остается прежним. Когда мы делим или умножаем неравенство на отрицательное число, знак неравенства меняется на противоположный. Вот свойства неравенства деления и умножения для удобства. Неравенства и числовая линия
 Например, чтобы построить x> 1 на числовой прямой, вы просто обведите цифру 1 на числовой прямой и проведете линию, идущую от круга в направлении чисел, которые удовлетворяют утверждению о неравенстве.
Например, чтобы построить x> 1 на числовой прямой, вы просто обведите цифру 1 на числовой прямой и проведете линию, идущую от круга в направлении чисел, которые удовлетворяют утверждению о неравенстве.
Предыдущий урок | Главная страница | Следующий урок Решение линейных неравенств — ChiliMath
Символы неравенства с примерами и иллюстрациями на числовых линиях
Примеры решения и график линейных неравенств
 Это означает, что существует почти бесконечное количество значений x, которые при подстановке дают истинные утверждения.
Это означает, что существует почти бесконечное количество значений x, которые при подстановке дают истинные утверждения. Теперь вы понимаете, почему все числа больше 3 являются решениями?
Теперь вы понимаете, почему все числа больше 3 являются решениями? Хотя не имеет значения, где мы храним переменную, слева или справа, имеет смысл всегда быть последовательным, изолировав ее на левой стороне. Думаю, это просто «стандартный» способ.
Хотя не имеет значения, где мы храним переменную, слева или справа, имеет смысл всегда быть последовательным, изолировав ее на левой стороне. Думаю, это просто «стандартный» способ.





Практика с рабочими листами
1300000 Устранение неравенств Неравенства
 «Решение»
неравенство означает нахождение всех его решений. «Решение»
неравенство — это число, которое при замене переменной делает
неравенство истинное утверждение.
«Решение»
неравенство означает нахождение всех его решений. «Решение»
неравенство — это число, которое при замене переменной делает
неравенство истинное утверждение.

Пример 1:
Рассмотрим неравенство Пример 2:
Найти все решения неравенства Множество решений неравенства — интервал.
Множество решений неравенства — интервал. Пример 3:
Решите неравенство Упражнение 1:
Найти все решения неравенства Ответить.
Упражнение 2:
Решите неравенство Ответ.
Упражнение 3:
Решите неравенство Ответ.
Упражнение 4:
Найти все решения неравенства Ответить.
[Назад]
[Следующий] [Алгебра]
[Тригонометрия]
[Комплексные переменные]
[Исчисление]
[Дифференциальные уравнения]
[Матричная алгебра] С. Домашняя страница O.S MATHematics
Домашняя страница O.S MATHematics
Copyright 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователя онлайн за последний час 2.7 Решение линейных неравенств — элементарная алгебра 2e
Задачи обучения
Если вы пропустили эту проблему, просмотрите Пример 1. 12.
12.
Если вы пропустили эту проблему, просмотрите Пример 2.3.
Если вы пропустили эту проблему, просмотрите Пример 2.13.
Если вы пропустили эту проблему, просмотрите Пример 2.34. Неравенства в графике на числовой прямой

Пример 2.
 66
66
Это означает, что все числа меньше или равны 1. Мы закрашиваем все числа в числовой строке слева от 1 и помещаем скобку в x = 1x = 1, чтобы показать, что оно включено.
Это означает, что все числа меньше 5, но не включая 5. Мы закрашиваем все числа в числовой строке слева от 5 и помещаем круглые скобки в x = 5x = 5, чтобы показать, что они не включены.
Это означает, что все числа больше -1-1, но не включая -1-1. Мы закрашиваем все числа в числовой строке справа от −1−1, затем помещаем скобки в x = −1x = −1, чтобы показать, что он не включен.  Как мы видели выше, неравенство x> 3x> 3 означает все числа больше 3. У решения этого неравенства нет верхнего конца. В обозначениях интервалов мы выразим x> 3x> 3 как (3, ∞). (3, ∞). Символ ∞∞ читается как «бесконечность». Это не настоящее число. На рис. 2.9 показаны числовая линия и обозначения интервалов.
Как мы видели выше, неравенство x> 3x> 3 означает все числа больше 3. У решения этого неравенства нет верхнего конца. В обозначениях интервалов мы выразим x> 3x> 3 как (3, ∞). (3, ∞). Символ ∞∞ читается как «бесконечность». Это не настоящее число. На рис. 2.9 показаны числовая линия и обозначения интервалов. Неравенства, числовые линии и обозначение интервалов
 11.
11. Пример 2.67
Решите неравенства, используя свойства неравенства вычитания и сложения
Свойства равенства
Свойство вычитания равенства Сложение Свойство равенства Для любых чисел a, b и c, для любых чисел a, b и c, если a = b, то a − c = b − c. если a = b, то a + c = b + c. Свойство вычитания равенства Сложение Свойство равенства Для любых чисел a, b и c, для любых чисел a, b и c, если a = b, то a − c = b − c. ifa = b, тогда a + c = b + c.
если a = b, то a + c = b + c. Свойство вычитания равенства Сложение Свойство равенства Для любых чисел a, b и c, для любых чисел a, b и c, если a = b, то a − c = b − c. ifa = b, тогда a + c = b + c. Например, мы знаем, что −4 меньше 2. Если мы вычтем 5 из обеих величин, будет ли левая часть
все еще меньше правой? Мы получаем −9 слева и −3 справа. И мы знаем, что −9 меньше −3. Знак неравенства остался прежним. 
Свойства неравенства
Свойство вычитания неравенстваСвойство неравенства сложения Для любых чисел a, b и c, для любых чисел a, b и c, если a x + 5> 9x + 5> 9 Вычтите 5 с обеих сторон, чтобы выделить xx. x + 5−5> 9−5x + 5−5> 9−5 Упростить. x> 4x> 4 
Пример 2.68
Решайте неравенства, используя свойства неравенства деления и умножения
Свойства равенства
Свойство деления равноправия Свойство умножения равенства Для любых чисел a, b, c и c For 0, для любых действительных чисел a, b, c, ifa = b, thenac = bc. ifa = b, thenac = bc. любые числа a, b, c и c ≠ 0, для любых действительных чисел a, b, c, если a = b, то ac = bc. ifa = b, thenac = bc.
ifa = b, thenac = bc. любые числа a, b, c и c ≠ 0, для любых действительных чисел a, b, c, если a = b, то ac = bc. ifa = b, thenac = bc. Свойства неравенства
деления и умножения
Для любых действительных чисел a, b, cifa
- положительное число , неравенство остается таким же .
- отрицательное число , неравенство отменяет .
Пример 2.69
Решите неравенство 7y <427y <42, нанесите решение на числовой прямой и запишите решение в интервальной записи.
Попробуй 2,137
Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
(8, ∞) (8, ∞)
Попробовать 2. 138
138
Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
12d≤ 6012d≤ 60
Пример 2,70
Решите неравенство −10a≥50−10a≥50, обозначьте решение на числовой прямой и запишите решение в интервальной записи.
Попробовать 2.139
Решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
−8q <32−8q <32
Попробуйте 2.140
Решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
−7r≤ −70−7r≤ −70
Устранение неравенств
Иногда при решении неравенства переменная оказывается справа. Мы можем переписать неравенство в обратном порядке, чтобы переменная оказалась слева.
x> a имеет то же значение, что и a
Пример 2.71
Решите неравенство −20 <45u − 20 <45u, нанесите решение на числовой прямой и запишите решение в интервальной записи.
Попробовать 2.141
Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
24≤38м24≤38м
Попробовать 2.142
Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
−24 <43n − 24 <43n
Пример 2.72
Решите неравенство t − 2≥8t − 2≥8, обозначьте решение на числовой прямой и запишите решение в интервальной записи.
Попробовать 2.143
Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
к − 12≤15 к − 12≤15
Попробуй 2.144
Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
u − 4≥ − 16u − 4≥ − 16
Устранение неравенств, требующих упрощения
Для устранения большинства неравенств потребуется более одного шага. Мы следуем тем же шагам, что и в общей стратегии решения линейных уравнений, но обязательно обращаем особое внимание во время умножения или деления.
Мы следуем тем же шагам, что и в общей стратегии решения линейных уравнений, но обязательно обращаем особое внимание во время умножения или деления.
Пример 2.73
Решите неравенство 4m≤9m + 174m≤9m + 17, обозначьте решение на числовой прямой и запишите решение в интервальной записи.
Попробовать 2.145
Решите неравенство 3q ≥ 7q — 233q ≥ 7q — 23, обозначьте решение на числовой прямой и запишите решение в интервальной записи.
Попробовать 2.146
Решите неравенство 6x <10x + 196x <10x + 19, обозначьте решение на числовой прямой и запишите решение в интервальной записи.
Пример 2.74
Решите неравенство 8p + 3 (p − 12)> 7p − 288p + 3 (p − 12)> 7p − 28, обозначьте решение на числовой прямой и запишите решение в интервальной записи.
Решение
| Максимально упростите каждую сторону. | 8p + 3 (p − 12)> 7p − 288p + 3 (p − 12)> 7p − 28 |
Распространить. | 8p + 3p − 36> 7p − 288p + 3p − 36> 7p − 28 |
| Объедините похожие термины. | 11p-36> 7p-2811p-36> 7p-28 |
| Вычтите 7p7p с обеих сторон, чтобы собрать переменные слева. | 11п − 36−7p> 7p − 28−7p11p − 36−7p> 7p − 28−7p |
| Упростить. | 4p − 36> −284p − 36> −28 |
| Добавьте 36 с обеих сторон, чтобы собрать константы справа. | 4p − 36 + 36> −28 + 364p − 36 + 36> −28 + 36 |
| Упростить. | 4p> 84p> 8 |
| Разделим обе части неравенства на 4; неравенство остается прежним. | 4p4> 844p4> 84 |
| Упростить. | p> 2p> 2 |
Изобразите решение на числовой прямой. | |
| Запишите решение во внутренних обозначениях. | (2, ∞) (2, ∞) |
Попробовать 2.147
Решите неравенство 9y + 2 (y + 6)> 5y − 249y + 2 (y + 6)> 5y − 24, обозначьте решение на числовой прямой и запишите решение в интервальной записи.
Попробуйте 2.148
Решите неравенство 6u + 8 (u − 1)> 10u + 326u + 8 (u − 1)> 10u + 32, обозначьте решение на числовой прямой и запишите решение в интервальной записи.
Подобно тому, как некоторые уравнения являются тождествами, а некоторые — противоречиями, неравенства могут быть тождествами или противоречиями. Мы узнаем эти формы, когда у нас остаются только константы при решении неравенства. Если результатом является истинное утверждение, у нас есть личность. Если результатом является ложное утверждение, мы получаем противоречие.
Пример 2.75
Решите неравенство 8x − 2 (5 − x) <4 (x + 9) + 6x8x − 2 (5 − x) <4 (x + 9) + 6x, отобразите решение на числовой прямой и запишите решение. в интервальной записи.
в интервальной записи.
Решение
| Максимально упростите каждую сторону. | 8x − 2 (5 − x) <4 (x + 9) + 6x8x − 2 (5 − x) <4 (x + 9) + 6x |
| Распространить. | 8x − 10 + 2x <4x + 36 + 6x8x − 10 + 2x <4x + 36 + 6x |
| Объедините похожие термины. | 10x − 10 <10x + 36 10x − 10 <10x + 36 |
| Вычтите 10x10x с обеих сторон, чтобы собрать переменные слева. | 10x − 10−10x <10x + 36−10x10x − 10−10x <10x + 36−10x |
| Упростить. | −10 <36−10 <36 |
| Хх больше нет, и у нас есть верное утверждение. | Неравенство — это тождество. Решение — все действительные числа. |
Изобразите решение на числовой прямой. | |
| Запишите решение в интервальной записи. | (−∞, ∞) (- ∞, ∞) |
Попробовать 2.149
Решите неравенство 4b − 3 (3 − b)> 5 (b − 6) + 2b4b − 3 (3 − b)> 5 (b − 6) + 2b, отобразите решение на числовой прямой и запишите решение. в интервальной записи.
Попробуй 2.150
Решите неравенство 9h − 7 (2 − h) <8 (h + 11) + 8h9h − 7 (2 − h) <8 (h + 11) + 8h, отобразите решение на числовой прямой и запишите решение. в интервальной записи.
Пример 2.76
Решите неравенство 13a − 18a> 524a + 3413a − 18a> 524a +34, нанесите решение на числовой прямой и запишите решение в интервальной записи.
Попробуй 2.151
Решите неравенство 14x − 112x> 16x + 7814x − 112x> 16x + 78, обозначьте решение на числовой прямой и запишите решение в интервальной записи.
Попробуй 2.152
Решите неравенство 25z − 13z <115z −3525z − 13z <115z −35, обозначьте решение на числовой прямой и запишите решение в интервальной записи.
Переведите на неравенство и решите
Чтобы перевести английские предложения в выражения неравенства, нам нужно распознавать фразы, указывающие на неравенство. Некоторые слова просты, например «больше чем» и «меньше чем». Но другие не так очевидны.
Подумайте о фразе «по крайней мере» — что значит быть «не моложе 21 года»? Значит 21 или больше. Фраза «по крайней мере» означает «больше или равно».
В таблице 2.7 приведены некоторые общие фразы, указывающие на неравенство.
| >> | ≥ ≥ | << | ≤≤ |
|---|---|---|---|
| больше | больше или равно | меньше | меньше или равно |
| больше | не менее | меньше | — максимум |
| больше | не менее | имеет менее | не более |
| превышает | — это минимум | ниже | это максимальное |
Таблица 2. 7
7
Пример 2.77
Перевести и решить. Затем запишите решение в интервальной записи и нанесите график на числовой прямой.
Двенадцать раз c не более 96.
Попробовать 2.153
Перевести и решить. Затем запишите решение в интервальной записи и нанесите график на числовой прямой.
Двадцать раз y не более 100
Попробуй 2.154
Перевести и решить. Затем запишите решение в интервальной записи и нанесите график на числовой прямой.
Девять раз z не меньше 135
Пример 2.78
Перевести и решить. Затем запишите решение в интервальной записи и нанесите график на числовой прямой.
Тридцать меньше x не меньше 45.
Попробуй 2.155
Перевести и решить. Затем запишите решение в интервальной записи и нанесите график на числовой прямой.
Девятнадцать меньше p не меньше 47
Попробуй 2.156
Перевести и решить. Затем запишите решение в интервальной записи и нанесите график на числовой прямой.
Четыре больше чем максимум 15.
Раздел 2.7 Упражнения
Практика ведет к совершенству
Неравенства графика на числовой прямой
В следующих упражнениях нарисуйте каждое неравенство на числовой прямой.
430.
ⓐ x≤ − 2x≤ − 2
ⓑ x> −1x> −1ⓒ x <0x <0
x> 1x> 1ⓑ x <−2x <−2
ⓒ x≥ − 3x≥ − 3
x≥ − 3x≥ − 3ⓑ x <4x <4ⓒ x≤ − 2x≤ − 2
ⓐ x≤0x≤0ⓑ x> −4x> −4ⓒ x≥ − 1x≥ − 1
В следующих упражнениях нарисуйте каждое неравенство на числовой прямой и запишите в интервальной нотации.
434.
ⓐ х <−2x <−2ⓑ x≥ − 3,5x≥ − 3,5ⓒ x≤23x≤23

ⓐ x> 3x> 3ⓑ x≤ − 0,5x≤ − 0,5ⓒ x≥13x≥13
x≥ − 4x≥ − 4ⓑ x <2,5x <2,5ⓒ x> −32x> −32
ⓐ x≤5x≤5ⓑ x≥ − 1,5x≥ − 1,5ⓒ x <−73x <−73
Решите неравенства, используя свойства неравенства вычитания и сложения
В следующих упражнениях решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
444.f − 1320 <−512f − 1320 <−512
445.г − 1112 <−518 г − 1112 <−518
Решите неравенства, используя свойства неравенства деления и умножения
В следующих упражнениях решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
Устранение неравенств, требующих упрощения
В следующих упражнениях решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
12x + 3 (x + 7)> 10x − 2412x + 3 (x + 7)> 10x − 24
471.9y + 5 (y + 3) <4y − 359y + 5 (y + 3) <4y − 35
472.6h − 4 (час − 1) ≤7h − 116h − 4 (час − 1) ≤7h − 11
473.4k− (k − 2) ≥7k − 264k- (k − 2) ≥7k − 26
474.8 м − 2 (14 − м) ≥ 7 (м − 4) + 3 м 8 м − 2 (14 − м) ≥ 7 (м − 4) + 3 м
475.6n − 12 (3 − n) ≤9 (n − 4) + 9n6n − 12 (3 − n) ≤9 (n − 4) + 9n
476.34b-13b <512b-1234b-13b <512b-12
477.9u + 5 (2u − 5) ≥12 (u − 1) + 7u9u + 5 (2u − 5) ≥12 (u − 1) + 7u
478.23 г-12 (г-14) ≤16 (г + 42) 23 г-12 (г-14) ≤16 (г + 42)
479.56a − 14a> 712a + 2356a − 14a> 712a + 23
480.45h − 23 (h − 9) ≥115 (2h + 90) 45h − 23 (h − 9) ≥115 (2h + 90)
481.12v + 3 (4v − 1) ≤19 (v − 2) + 5v12v + 3 (4v − 1) ≤19 (v − 2) + 5v
Смешанная практика
В следующих упражнениях решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи.
23p − 2 (6−5p)> 3 (11p − 4) 23p − 2 (6−5p)> 3 (11p − 4)
485.18q − 4 (10−3q) <5 (6q − 8) 18q − 4 (10−3q) <5 (6q − 8)
486.−94x≥ − 512−94x≥ − 512
487.−218y≤ − 1528−218y≤ − 1528
Переведите на неравенство и решите
В следующих упражнениях переведите и решите. Затем запишите решение в виде интервалов и нанесите график на числовой прямой.
492.Четырнадцать раз d больше 56.
493.Девяносто раз c меньше 450.
494.В восемь раз z меньше −40−40.
495.Десять раз y не больше −110−110.
496.Три больше х не меньше 25.
497.Шесть больше k больше 25.
498.10 меньше w не менее 39
499.
Двенадцать меньше x не меньше 21.
500.Отрицательный пять раз r не более 95.
501.Дважды отрицательное значение с меньше 56.
502.Девятнадцать меньше b не больше −22−22.
503.Пятнадцать меньше, чем , а не меньше −7−7.
Повседневная математика
504.Безопасность Рост ребенка h должен быть не менее 57 дюймов, чтобы ребенок мог безопасно ездить на переднем сиденье автомобиля. Запишите это как неравенство.
505.Пилоты-истребители Максимальная высота пилота-истребителя h составляет 77 дюймов. Запишите это как неравенство.
506. Лифты Общий вес пассажиров лифта w не может превышать 1 200 фунтов. Запишите это как неравенство.
Запишите это как неравенство.
Покупки Количество товаров, n , которые покупатель может иметь в полосе экспресс-оформления, не превышает 8. Запишите это как неравенство.
Письменные упражнения
508.Приведите пример из своей жизни, используя фразу «хотя бы».
509.Приведите пример из своей жизни, используя фразу «максимум».
510.Объясните, почему необходимо обратить неравенство при решении −5x> 10−5x> 10.
511.Объясните, почему необходимо изменить неравенство при решении n − 3 <12n − 3 <12.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
неравенств | Энциклопедия.
 com
comНеравенство — это математическое утверждение, которое выглядит в точности как уравнение, за исключением того, что знак равенства заменяется одним из пяти символов неравенства.
≠ не равно
<меньше
≤ меньше или равно
> больше
≥ больше или равно
Представьте себе двух друзей в возрасте 9 и 12 лет. Каждый из пяти символов неравенства может использоваться для написания заявления об их возрасте, в зависимости от того, какой аспект их возраста следует подчеркнуть.
9 ≠ 12 говорит, что 9 не равно 12
9 <12 говорит, что 9 меньше 12
9 ≤ 12 говорит, что 9 меньше или равно 12
12> 9 говорит, что 12 больше чем 9
12 ≥ 9 означает, что 12 больше или равно 9
Обратите внимание, что 9 <12 и 12> 9 — это два способа представления одного и того же отношения; когда 9 и 12 меняются местами, неравенство также меняется на противоположное.
Разница в значениях «больше чем» и «больше или равно» незначительна. Например, пусть a представляют возраст человека. Как можно было бы написать равенство, чтобы показать, что возрастной ценз для голосования составляет 18 лет?
Например, пусть a представляют возраст человека. Как можно было бы написать равенство, чтобы показать, что возрастной ценз для голосования составляет 18 лет?
Выражение a > 18 означает, что возраст должен быть больше 18 лет. Выражение a ≥ 18 означает, что возраст может быть больше 18 или равным 18 лет. Ровно 18 лет имеет право голосовать, неравенство a ≥ 18 является правильным для этой ситуации.
Различные ограничения в обществе могут быть выражены с помощью неравенства.Вот лишь несколько примеров: ограничения скорости, минимальное и максимальное снятие средств с банка, минимальный и максимальный уровни жидкости, требования к оценке для поступления в колледж и минимальные продажи для достижения цели сбора средств. Некоторые общие фразы, которые указывают на неравенство в словесных проблемах, — это «минимум», «максимум», «максимум», «минимум» и превосходные степени, такие как «самый старый» и «самый маленький».
Устранение неравенств
Каждое возможное уравнение может быть преобразовано в неравенство. Кроме того, неравенства решаются так же, как и уравнения, за одним исключением; а именно, когда неравенство умножается или делится на отрицательное число по обе стороны от знака неравенства.
Кроме того, неравенства решаются так же, как и уравнения, за одним исключением; а именно, когда неравенство умножается или делится на отрицательное число по обе стороны от знака неравенства.
Например, начните с истинного утверждения 5 <6. Когда обе части умножаются на -2, утверждение становится -10 <-12. Это результирующее утверждение неверно, потому что -10 больше, чем -12. Так как умножение (или деление) неравенства на отрицательное число приводит к ложному утверждению, символ неравенства должен быть перевернут, чтобы поддерживать истинное утверждение. В этом примере правильный ответ -10> -12. В качестве другого примера, чтобы решить −4 x > 12, разделите обе части на −4, а затем измените неравенство на противоположное, чтобы получить x <−3.
Практический пример. Рассмотрим следующую проблему. Студент сэкономил 40 долларов и хочет сэкономить не менее 300 долларов на покупку нового велосипеда и велосипедного снаряжения. Его работа платит 7,25 доллара в час. Найдите, сколько часов ему нужно работать, чтобы сэкономить не менее 300 долларов.
Найдите, сколько часов ему нужно работать, чтобы сэкономить не менее 300 долларов.
Чтобы решить эту проблему, пусть h будет количеством часов, которое ему нужно для работы. Слова «как минимум» означают, что сумма сбережений и оплаты должна быть больше или равна 300 долларам. Приведенное ниже решение показывает, что студент должен работать 36 или более часов, чтобы достичь своей цели — сэкономить 300 долларов.
40 $ + 7,25 ч ≤ 300 $
7,25 ч ≤ 260: Вычтем 40 с каждой стороны.
h ≥ 35,9: Разделите каждую сторону на 7,25.
Графическое изображение неравенств
Числовые линии в пяти верхних рядах рисунка в рамке иллюстрируют каждый случай, который может возникнуть при графическом отображении неравенств по одной переменной, x . Закрашенный кружок на номере указывает, что он включен в набор решений, а белый кружок указывает, что он не включен в набор решений.Затенение слева с затемненной стрелкой на конце указывает, что все числа меньшего значения включены в набор решений; затенение справа с затемненной стрелкой на конце указывает, что все числа большего значения включены в набор решений.
Графические составные неравенства. Сложные неравенства — это два неравенства, разделенные словами «и» или «или». Решение, заданное составным неравенством, разделенным словом «и», представляет собой область, в которой два графика перекрываются.Это называется перекрестком.
Подумайте, как написать составное неравенство, которое представляет возможный возраст подростка, а затем как построить график этого набора решений. Чтобы записать это неравенство, пусть a представляют возраст. Итак, a ≥ 13 и a <20. График пересечения показан в шестой числовой строке на рисунке в рамке.
Составные неравенства, которые представляют собой решения, попадающие между двумя числами, часто записываются в сокращенной записи с переменной в середине.Следовательно, описанное выше неравенство также может быть записано как 13 ≤ a <20.
Решение, заданное составным неравенством, которое разделяется словом «или», представляет собой комбинацию всех точек на обоих графиках. Это называется союзом.
Это называется союзом.
Подумайте, как написать составное неравенство, чтобы представить возможный возраст брата или сестры, не являющегося подростком, а затем как построить график этого набора решений.
Чтобы записать это неравенство, пусть a представляют возраст. Итак, a <13 или a ≥ 20.График объединения показан в седьмой числовой строке на рисунке в рамке.
Следствием сложных неравенств по одной переменной является система неравенств по двум переменным. Решение системы неравенств — это пересечение двух графиков, как и решение системы уравнений. Однако пересечение системы неравенств обычно состоит из целой области точек. Это особенно полезно, поскольку реальные проблемы часто включают выбор из нескольких возможных решений.
Неравенства в двух переменных
На приведенном ниже графике показано, как изобразить линейное неравенство по двум переменным. Графики двух переменных рисуются сплошной или пунктирной линией. Сплошная линия указывает, что точки на линии включены в набор решений, а пунктирная линия указывает, что точки на линии не включены в набор решений.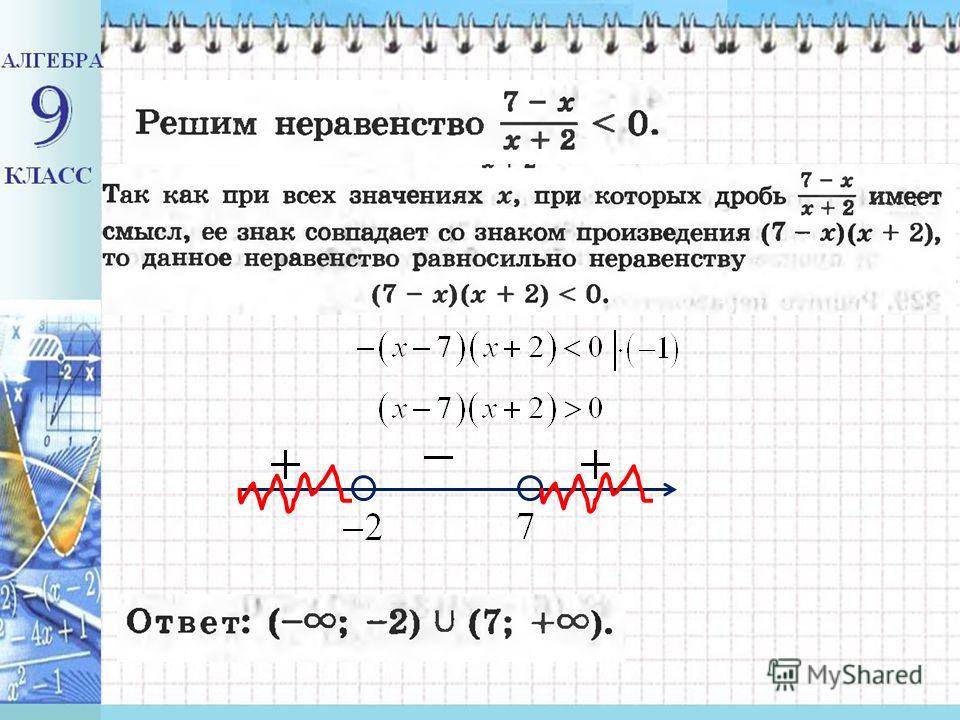 Для линейного графика сплошная или пунктирная линия делит плоскость на две области, только одна из которых будет набором решений.
Для линейного графика сплошная или пунктирная линия делит плоскость на две области, только одна из которых будет набором решений.
Подумайте, как решить и изобразите y + 7> 3 x + 8. Сначала вычтите 7 из обеих сторон, чтобы получить y > 3 x 1. Изобразите уравнение y = 3 x + 1 пунктирной линией. Пунктирная линия делит плоскость на две области. Выберите по одному баллу из каждого региона, который будет легко подставить в неравенство. Ниже выбраны точки (0, 0) и (0, 2). Только одна из двух точек будет решением неравенства, указывая, в какой области находится набор решений.
Сначала подставьте (0, 0).
y > 3 x 1
0> (3 × 0) + 1
0> 1 (FALSE)
Далее подставляем (0, 2).
y > 3 x + 1
2> (3 × 0) + 1
2> 1 (ИСТИНА)
Следовательно, точка (0, 2) является решением неравенства. Если будет протестировано больше точек в том же регионе, они также будут решениями.

 3
3 14159..
14159..


 Например, если a
Например, если a
Leave A Comment