Центростремительное ускорение луны вокруг земли: № 5. Луна движется вокруг Земли на расстоянии 380 000 км от нее, совершая один оборот за 27,3 сут. Вычислите центростремительное ускорение Луны.

7 фактов, которые вы должны знать

Центростремительное ускорение определяется как равноправие движения гаджета, пересекающего круговой путь. Любое устройство, движущееся по кругу с пиком вектора ускорения относительно центра этого круга, называется центростремительным ускорением.

Центростремительное ускорение на Луне описывается как «Луна должна двигаться быстрее в направлении Земли через диаметр от Земли до Луны. Ускорение, необходимое для того, чтобы устройство (здесь Луна) продолжало движение по окружности, называется центростремительным ускорением. Центростремительное ускорение всегда находится под прямым углом к ​​ходу гаджета».

Существует ли центростремительное ускорение на Луне?

Да, на Луне существует центростремительное ускорение. Гравитационное притяжение между Землей и Луной удерживает Луну в петле относительно Земли. В этом случае мы можем применить к силе притяжения центростремительную силу, но центростремительная сила не является абстрактной силой, удерживающей гаджеты, движущиеся по кругу.

Луна, вращающаяся вокруг Земли по круговой петле, захватывается гравитационной силой Земли, действующей на Луну. Гравитационная сила никогда не действует на Луне, потому что центростремительная сила каждый раз направлена ​​вертикально к наблюдению за движением. Следовательно, работа не выполняется.

 Предположим, что масса Луны составляет около 1.2% массы Земли. В отличие от силы гравитации, действующей на Луну, сила тяготения, которую Земля применяет к Луне, идентична силе тяготения Луны, действующей на Землю.

F_{тяготение}=GMм/R² выражает гравитационную силу. Где М и М — массы небесных тел, а R — расстояние между ними. На две массы действует одинаковая сила M и m, F=гм/R²

Центростремительное ускорение на изображении Луны: pixabay

Почему на Луне существует центростремительное ускорение?

Центростремительное ускорение существует на Луне из-за гравитационной силы, действующей на Луну со стороны Земли. Луна вращается вокруг Земли относительно равномерным круговым движением. Это движение Луны достижимо, потому что гравитационная сила на Луне обеспечивает необходимое центростремительное ускорение, чтобы оставаться на орбите.

Луна вращается вокруг Земли под действием центростремительной силы. Каждое круговое движение усиливает центростремительную силу. В случае Луны притяжение или гравитация является центростремительной силой. Если бы у нас был вращающийся волчок, то внутреннее давление молекулярных связей создавало бы центростремительную силу.

Луна не просто заходит, потому что сила тяжести каждый раз поперечна скорости, поэтому она меняет свое наблюдение. Однако это оценка, поскольку предполагалось, что Земля и Луна являются точечными массами, а орбита полностью сферической. Гравитация заставляет и Землю, и Луну умеренно деформироваться.Вращение Луны вокруг Земли. Кредит на изображение: pixabay

У Луны и Земли одинаковое ускорение?

Нет, Луна и Земля не имеют одинакового ускорения.  

Луна ускоряется больше, чем Земля, потому что гравитация Земли удерживает Луну вокруг нас. Он сохраняет различное наблюдение за скоростью Луны. Это означает, что гравитация заставляет Луну постоянно ускоряться. Однако его скорость оставалась неизменной.

Внешняя гравитация Луны составляет примерно 1/6 силы или около 1.6 метра в секунду. Внешняя гравитация Луны устойчива, потому что она намного легче Земли. Внешняя гравитация тела соответствует его массе, но обратно соответствует квадрату его радиуса.

Луна прибывает, чтобы в одно и то же время двигаться значительно быстрее, чем Земля, поэтому она должна двигаться быстрее. Та же самая сила, действующая на разнородные массы, создаст ускорение, обратно пропорциональное массе, поэтому земля, масса которой в 80 раз больше, ускоряется в 80 раз меньше, чем Луна, и должна двигаться по пути.Внешняя гравитация Луны значительно больше, чем кредит изображения Земли: pixabay

Чем центростремительное ускорение на Луне отличается от земного?

Центростремительное ускорение представлено как a= v²/r, и это выражение основано на скорости Луны, которая нильпотентна a_m — центростремительное ускорение Луны из-за гравитационного притяжения Земли, ω — лучевая скорость, R_m является бифуркацией между Землей и Луной, которая составляет 60 активов диаметра Земли.  

Позвольте мне взять пример центростремительного ускорения на Луне; чтобы узнать центростремительное ускорение Луны при ее обращении вокруг Земли, мы должны определить частоту обращения. Затем мы можем использовать частоту для перечисления величины скорости. Примером центростремительного ускорения на Земле является то, что если мы управляем автомобилем по кругу, наш автомобиль испытывает центростремительное ускорение.

Центростремительное ускорение Луны v²/r = 2.725 *10^-3м/с².Принимая во внимание, что центростремительное ускорение Земли составляет около 0.03м/с² . Земной период вращения составляет астрономический день, а тропический радиус Земли составляет около 6378 км.Центростремительное ускорение Луны при ее обращении вокруг Земли кредит изображения: pixabay

Рассчитать величину центростремительного ускорения на Луне?

Чтобы гаджет оставался в круге, центростремительное ускорение должно притягивать гаджет к центру круга.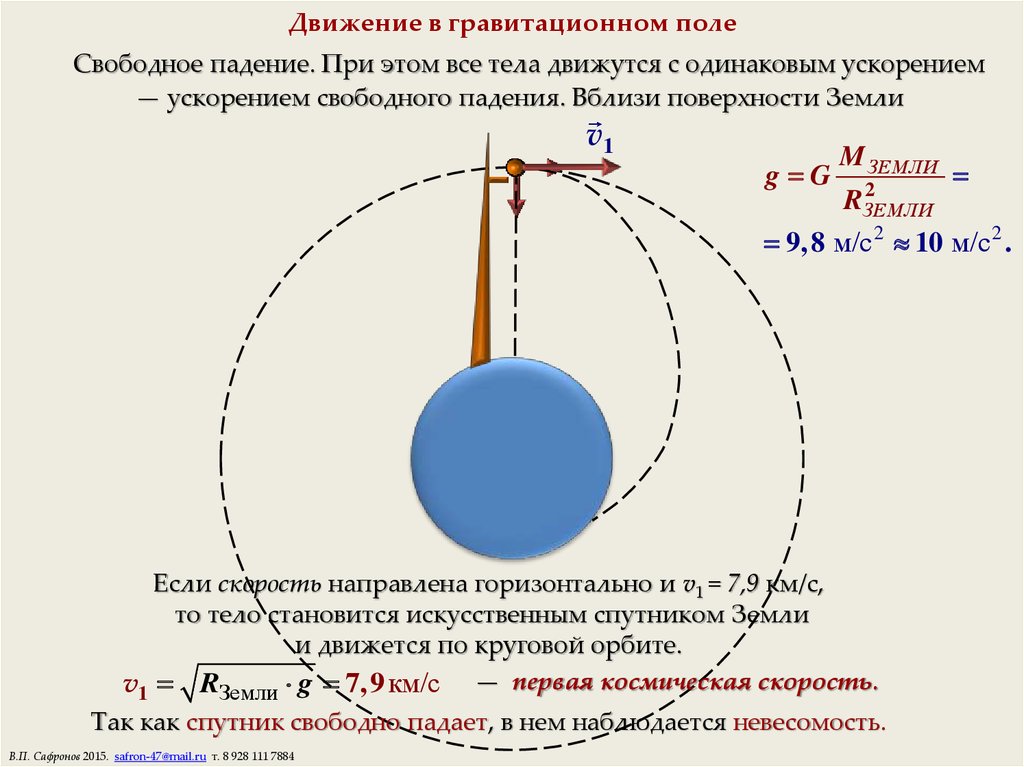 Посмотрите на Луну, вращающуюся вокруг Земли, на следующем рисунке. Луна ускоряется относительно Земли по радиусу от Земли до Луны.Луна кружит Земля

Центростремительное ускорение всегда перпендикулярно движению гаджета, и его ускорение достигло максимума относительно центра круга. Центростремительное ускорение ас имеет величину, равную квадрату скорости тела v через разбиение орбиты бифуркацией r от окружности, имеющей центр, к движущемуся телу; который,

a_c= V²/r

 Горизонтальная скорость v устройства, движущегося близко к кругу, прямо связана с радиальной скоростью. т.е. v = ω×r. Таким образом, мы также можем записать приведенное выше уравнение как

a_c = v²/r= (ωr)²/ г = ш²r

Пример вопроса

Учитывая, что Луна совершает оборот вокруг Земли примерно каждые 27.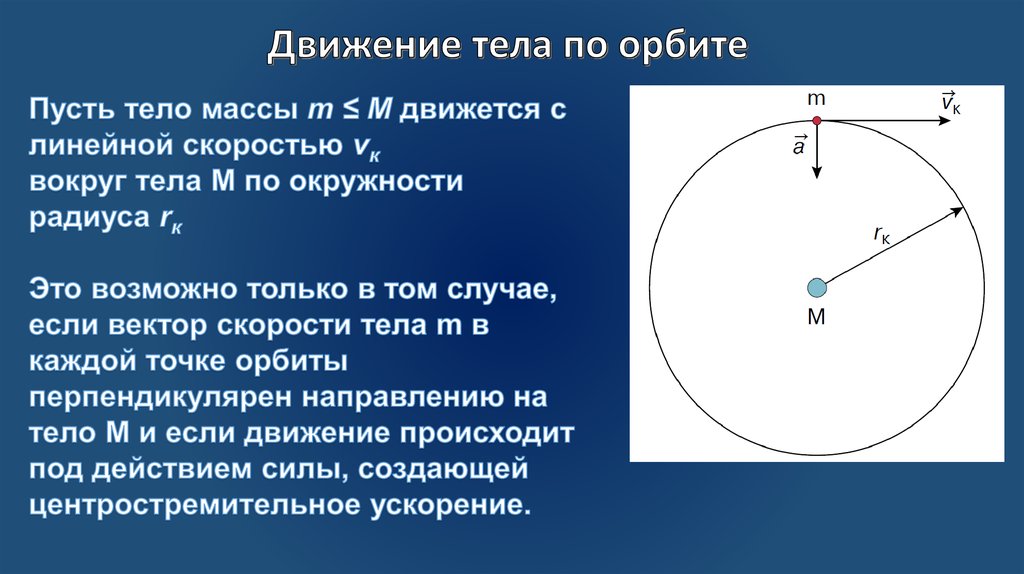 3 дня, а ее расстояние от центра Земли составляет 3.85 × 108 м, какова длина Луны? центростремительное ускорение?

Величина центростремительного ускорения определяется выражением

a_c=v²/r

Расстояние, которое Луна проходит за 27.3 дня, составляет d = 2πr = 2.41 * 109 м.

Нам нужно найти скорость Луны, поэтому переведите 27.3 в секунды.

v = д / (27.3 дня) = (д / (2.36 * 106 с))

Следовательно, скорость Луны 

Центростремительное ускорение Луны равно v²/r=

Вычислите центростремительное ускорение Луны относительно Земли?

а = v²/r дает центростремительное ускорение.

Это выражение основано на скорости Луны, которая разрешима. Поработаем с формулой

Ɛ Р_m = a_m

a_m это центростремительное ускорение Луны под действием силы тяжести земли.

R_m = 604 = 60× 6.4× 106

= 384 × 106 м

Как известно, угловая скорость

И T = 27.3 дня = 27.3 × 24 × 60 × 60 секунд = 2.358 × 106 с.

Подставив указанные выше значения в формулу для ускорения 

a_m =

a_m = 0.00272 м / с²

Компания центростремительное ускорение Луны по направлению к Земле = 0.00272 м/с.

Что было бы, если бы на Луне не было центростремительного ускорения?

  Более того, Луна вращается вокруг Земли по косой из-за центростремительное ускорение перевернулся. В отсутствие центростремительной силы Луна не сможет двигаться по круговой траектории и будет двигаться по прямой, расходящейся к орбите Луны.

Если на Луну не действует центростремительная сила, то Луна будет двигаться линейно, а не вращаться вокруг Земли. Без центростремительной силы Луна никогда не должна изменять свое наблюдение. Наличие центростремительной силы обязательно для сохранения кругового движения.

Следовательно, это противоположно наблюдению за гравитацией на экваторе; в лучах Земли он равен нулю. Центростремительная сила — это обязательная внутренняя сила, которая удерживает массу от движения по прямой; по величине она аналогична центробежной силе, но с обратным знаком.

Заключение

Из прочтения вышеупомянутого факта мы, наконец, пришли к выводу, что когда Луна сталкивается с равномерным круговым движением, ускорение Луны и сила, необходимая для управления движением, имеют определенные связи. Центростремительное ускорение имеет прямую связь с квадратом ускорения Луны.

РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ И СТАТИКИ

(Окончание. Начало см. «Наука и жизнь» № 4, 2001 г.)

Рис. 5.

Рис. 6.

Рис. 7.

Рис. 8.

‹

›

Открыть в полном размере

Продолжаем публиковать разбор конкурсных задач по физике, которые в последние годы предлагались поступающим на физический факультет МГУ.

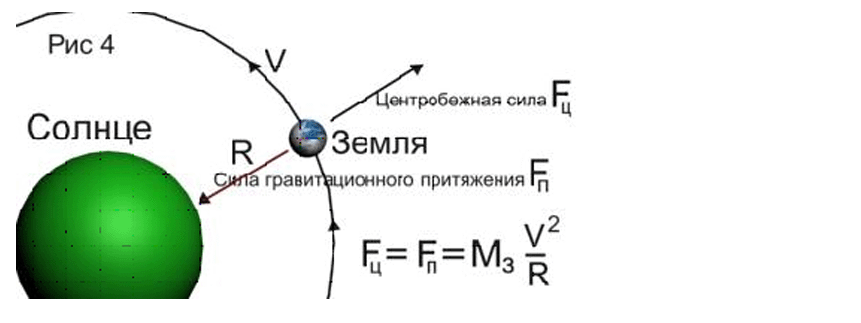
Задача 3 (1998 г.). Космический корабль движется по круговой орбите вокруг Земли так, что все время находится на прямой, соединяющей Землю и Луну, на таком расстоянии, что действие их гравитационных сил на корабль уравновешено. Найти вес космонавта в корабле, если масса космонавта равна m, отношение масс Земли и Луны равно k, радиус орбиты Луны в n раз больше радиуса Земли, а ускорение свободного падения у поверхности Земли равно g.

Решение. Будем решать задачу, используя геоцентрическую систему отсчета, считая ее инерциальной, то есть не станем учитывать орбитального движения Земли. Одновременно пренебрежем влиянием всех остальных небесных тел на движение Луны и космического корабля. По условию задачи орбиту Луны следует считать круговой. Поэтому на основании второго закона Кеплера можно утверждать, что Луна по своей орбите движется равномерно. Следовательно, согласно законам кинематики, ее ускорение направлено к центру Земли и равно а

n = ω R_л, где ω — угловая скорость, а R_л — радиус орбиты Луны. При сделанных предположениях можно утверждать, что ускорение Луны обусловлено действием на нее только гравитационных сил со стороны Земли (массой космического корабля можно пренебречь). Тогда, согласно закону всемирного тяготения и второму закону Ньютона, пренебрегая размерами Луны, получим

,

где G — гравитационная постоянная, а m_л и m_з — массы Луны и Земли соответственно.

Учитывая, что ускорение свободного падения на полюсе вблизи поверхности Земли

,

из написанных соотношений следует, что угловая скорость движения Луны, а следовательно, и космического корабля (так как он все время остается на прямой, соединяющей Землю и Луну) равна

.

Здесь учтено, что по условию задачи

.

По условию задачи космический корабль находится на таком расстоянии r от Земли, что гравитационные силы, действующие на него со стороны Земли и Луны, уравновешивают друг друга. Это, согласно закону всемирного тяготения, возможно только в том случае, если с учетом ранее сделанных предположений выполняется соотношение

.

Поскольку по условию задачи

,

то радиус орбиты корабля

.

Следовательно, центростремительное ускорение корабля определяется соотношением

.

Поскольку действия Земли и Луны на корабль скомпенсированы, а действием всех других небесных тел мы пренебрегаем и считаем геоцентрическую систему отсчета инерциальной, вычисленное ускорение может быть обеспечено только за счет работы двигателей самого корабля. Пренебрегая размерами корабля по сравнению с радиусом его орбиты, следует считать, что такое же ускорение относительно инерциальной системы отсчета имеет и космонавт. Поэтому на основании второго закона Ньютона получаем, что на космонавта корабль должен действовать с силой F=ma_кn . Следовательно, согласно третьему закону Ньютона, вес космонавта в системе отсчета, связанной с кораблем, равен

.

Задача 4 (2000 г.). На горизонтальном диске на расстоянии R от его оси лежит маленькая шайба. Диск медленно раскручивают так, что его угловая скорость равномерно возрастает со временем. Через время τ после начала раскручивания шайба стала скользить по диску. Найти коэффициент трения шайбы о диск, если за время τ диск сделал n оборотов.

Решение. Поскольку диск первоначально покоился и его угловую скорость увеличивают с постоянным угловым ускорением ε, по аналогии с законами изменения проекции скорости и координаты точки при прямолинейном равнопеременном движении можно утверждать, что к моменту времени τ угловая скорость диска должна стать равной ω(τ)=ετ и диск должен повернуться на угол φ(τ) = ετ

2/2. За один оборот диск поворачивается на угол 2, по условию задачи он за время τ совершил n оборотов, поэтому из написанных выше выражений следует, что диск раскручивали с угловым ускорением ε=4ν/τ.

По определению, длина дуги окружности радиуса R, заключенная между радиусами, образующими угол φ, равна Rφ. Следовательно, тангенциальная составляющая ускорения точки диска, находящейся на расстоянии R от оси вращения, равна α_φ=εR. Вспоминая, что нормальная составляющая ускорения точки, движущейся с угловой скоростью со по дуге с радиусом кривизны R, равна

,

можно утверждать, что ускорение шайбы к моменту времени τ относительно лабораторной системы отсчета, в которой ось диска неподвижна, должно стать равным

.

Считая, как обычно, указанную систему отсчета инерциальной и пренебрегая действием воздуха на шайбу, можно утверждать, что ускорение шайбы обусловлено действием на нее только тангенциальной составляющей силы реакции диска (плоскость диска по условию задачи горизонтальна). Поэтому, согласно второму закону Ньютона, максимальное значение тангенциальной составляющей силы реакции диска — силы сухого трения — должно быть равно

.

Учитывая, что при выполнении сделанных ранее предположений шайба прижимается к диску только за счет действия на нее силы тяжести, нормальная составляющая силы реакции диска должна быть равна N=mg, где g — ускорение свободного падения. Поэтому, вспоминая закон Кулона—Амона для сил сухого трения, можно утверждать, что μ= F_τmax /N. Подставив в это выражение ранее полученные соотношения, определим искомый коэффициент трения шайбы о диск

.

Задача 5 (1997 г.). Из тонкого резинового шнура массой m жесткостью k изготовили кольцо радиусом r. Каким стал бы радиус кольца, если бы оно вращалось равномерно с угловой скоростью ω вокруг своей оси?

Решение. Из кинематики известно, что ускорение движущейся по криволинейной траектории точки в общем случае можно представить в виде суммы двух компонент: нормальной а_n, направленной по радиусу кривизны траектории, и тангенциальной а_τ, направленной по касательной к траектории в сторону возрастания траекторной координаты и характеризующей быстроту изменения проекции скорости на это направление. Требуется определить радиус кольца при заданной угловой скорости вращения, то есть когда все точки кольца движутся равномерно, а

τ равно нулю. В условии задачи не указано, какие тела действуют на кольцо и как расположена его ось. Выбрав из всех возможных случаев простейший, будем считать, что ось кольца неподвижна относительно инерциальной системы отсчета, и так как вращение кольца происходит с постоянной скоростью, действие окружающих тел на любую из точек кольца скомпенсировано. Кольцо сделано из тонкого шнура, все точки которого находятся на одинаковом расстоянии от его оси и их ускорение равно α_n=ω²R, где R — искомый радиус кольца.

Это ускорение при сделанных предположениях могут обеспечить лишь силы натяжения, возникающие за счет упругой деформации шнура. На рис. 5 показаны участок вращающегося кольца, ограниченный радиусами R, образующими малый угол ∆α, и силы, действующие на него со стороны соседних участков. Поскольку эти силы направлены по касательным к оси кольца в соответствующих точках и тангенциальная составляющая ускорения точек кольца равна нулю, модули этих сил — сил натяжения — должны быть равны.

Считая, что при заданной угловой скорости применим закон Гука, величина силы натяжения

.

Силы натяжения, действующие на концы рассматриваемого участка, направлены перпендикулярно соответствующим радиусам, их результирующая равна и направлена к оси вращения. Поэтому на основании второго закона Ньютона можно утверждать, что

,

так как рассматриваемый участок кольца можно в силу малости угла ∆α принять за материальную точку массой

.

Из написанных уравнений следует, что при сделанных предположениях радиус кольца при заданной угловой скорости вращения должен быть равен

.

Из этого выражения видно, что при увеличении угловой скорости вращения до

радиус кольца должен неограниченно возрастать, то есть кольцо разорвется. В действительности разрушение кольца произойдет при несколько меньшей угловой скорости ω

п, когда силы натяжения кольца достигнут величины F_max, при которой нарушается закон Гука. Таким образом, если угловая скорость вращения кольца

,

то искомый радиус кольца равен

.

При попытке заставить кольцо вращаться с угловой скоростью ω>ω_п кольцо должно разорваться.

Задача 6 (2000 г.). В узкую прямоугольную кювету налили воду и положили два гладких одинаковых цилиндра так, что их оси оказались горизонтальны и параллельны длинным стенкам кюветы. При этом цилиндры касались стенок кюветы только своими образующими, верхний цилиндр погрузился в воду наполовину, а нижний — касался ее поверхности своими верхними точками. Найти силы, действующие со стороны цилиндров на стенки кюветы, если объем каждого из них равен V=20 см³.

Решение. Будем решать задачу, полагая, что торцы цилиндров находятся на одинаковом расстоянии от параллельных им стенок кюветы, кювета с ее содержимым покоится относительно ЛСО и эту систему можно считать инерциальной. Верхний цилиндр погружен в воду наполовину, поэтому можно утверждать, что равнодействующая F₁ сил гидростатического давления на верхний цилиндр должна быть равна -ρVg/2, где g~9,8 м/с² — ускорение свободного падения, а ρ~1 г/см³ — плотность воды. Действующая же со стороны воды на полностью погруженный нижний цилиндр сила будет в два раза больше и равна F₂=-ρVg. Из соображений симметрии ясно, что линии действия сил F₁ и F₂ должны пересекать середины осей цилиндров под прямым углом. Поскольку по условию задачи цилиндры гладкие, силы их взаимодействия должны лежать в плоскости, проходящей через оси цилиндров, и быть перпендикулярными этим осям. Перпендикулярными осям цилиндров, но направленными горизонтально будут и силы реакции со стороны стенок кюветы, так как эти стенки вертикальны. Вспомнив, что при равновесии сумма моментов действующих на твердое тело сил должна быть равна нулю, можно утверждать, что равнодействующие сил тяжести, действующих на цилиндры, должны лежать в вертикальных плоскостях, проходящих через их оси. Более того, опираясь на сказанное, можно доказать, что при заданном расположении цилиндров и выполнении сделанных предположений равнодействующие всех рассмотренных сил должны лежать в вертикальной плоскости, проходящей через середины этих цилиндров.

На рис. 6 показаны сечение кюветы вертикальной плоскостью, равнодействующие сил реакции стенок F_cl и F_c2, сил гидростатического давления F₁ и F₂, сил взаимодействия цилиндров N₁ и N₂ и сил тяжести. Буквами D и С обозначены точки приложения сил F₁ и F₂, а буквой m — масса цилиндра. Поскольку цилиндры находятся в равновесии, сумма всех сил, действующих на каждый из них, должна быть равна нулю и, следовательно, должны выполняться соотношения:

,

причем, согласно третьему закону Ньютона, N₁=N₂.

Решая полученную систему уравнений с учетом того, что F₂ = 2F₁ = ρgV, силы взаимодействия двух тел равны по величине и треугольник ABC является прямоугольным, а потому sin α = ВС/AC = 0,5, определим искомые силы действия цилиндров на стенки кюветы:

.

Задача 7 (2000 г.). Горизонтальная штанга длиной r, на конце которой закреплен груз массой m, вращается на подшипнике с угловой скоростью ω вокруг вертикальной стойки штатива высотой h (рис. 7). При какой угловой скорости основание штатива — тонкий диск массой М и радиусом R (R >r — перестанет касаться всей плоскостью горизонтальной поверхности стола? Массой штанги и стойки пренебречь. Считать, что диск не скользит по столу, а размеры груза существенно меньше r.

Решение. Все тела, указанные в условии, будем считать твердыми. Поскольку вращение груза по условию задачи происходит с неизменной угловой скоростью ω, то действием сил сопротивления движению штанги и груза следует пренебречь. Кроме того, как обычно, лабораторную систему отсчета, относительно которой штатив при достаточно малой угловой скорости вращения покоится, будем считать инерциальной. Тогда на основании второго закона Ньютона можно утверждать, что со стороны штанги на груз действует сила, горизонтальная составляющая которой обеспечивает грузу центростремительное ускорение —ω²r, а вертикальная составляющая уравновешивает действие на груз силы тяжести mg, где g — ускорение свободного падения.

Основываясь на сказанном и на третьем законе Ньютона, можно утверждать, что на штангу со стороны груза действует сила F_r, горизонтальная и вертикальная составляющие которой показаны на рис. 8. Кроме этих сил на штатив действуют еще сила тяжести и сила реакции стола. По условию задачи масса штанги со стойкой достаточно мала, а основанием штатива является тонкий однородный диск. Следовательно, равнодействующая всех действующих на штатив сил тяжести Mg приложена к центру диска, как и показано на рисунке. При критической скорости вращения со стороны стола на штатив может действовать лишь сила, точка приложения которой совпадает с точкой О на краю диска, лежащей в вертикальной плоскости, в которой располагаются оси стойки и штанги штатива в данный момент времени (см. рис. 8). При этом положение штатива становится неустойчивым. Однако, как и при меньших угловых скоростях вращения, сумма всех действующих на штатив сил и сумма моментов этих сил относительно произвольной оси должны быть равны нулю, так как штатив все еще остается неподвижным. Отсюда следует, что алгебраическая сумма моментов силы тяжести Mg и силы F_r относительно горизонтальной оси, проходящей через точку О перпендикулярно указанной вертикальной плоскости, должна быть равна нулю, то есть

,

поскольку плечо силы реакции стола относительно точки О равно нулю. Отметим, что из равенства нулю суммы всех действующих на штатив сил и моментов этих сил относительно указанной оси следует равенство нулю их моментов относительно любой параллельной ей оси. Так как линии действия всех приложенных к штативу сил лежат в указанной выше вертикальной плоскости, можно утверждать, что при выполнении последнего соотношения алгебраическая сумма моментов всех действующих на штатив сил относительно любой другой оси также будет равна нулю. Таким образом, искомая угловая скорость вращения груза, при которой основание штатива перестанет касаться всей плоскостью горизонтальной поверхности стола, равна

.

Центростремительное ускорение — манекены ies with Online Practice

Physics I Workbook For Dummies with Online Практика

Исследуйте книгу Купить на Amazon

Чтобы объект продолжал вращаться по кругу, этот объект необходимо тянуть к центру круга. Взгляните на Луну, вращающуюся вокруг Земли, на следующем рисунке. Луна ускоряется к Земле по радиусу от Земли до Луны.

Ускорение, необходимое для того, чтобы объект (здесь это Луна) двигался по кругу, называется центростремительным ускорением, и оно всегда перпендикулярно движению объекта. Центростремительное ускорение направлено к центру окружности.

Если вам известна линейная скорость объекта, движущегося по кругу, и радиус круга, вы можете рассчитать центростремительное ускорение, a _c , например:

Это уравнение дает вам ускорение, необходимое для того, чтобы объект двигался по кругу. Вы можете думать об этом ускорении как о постоянном изменении направления движения объекта, чтобы он продолжал двигаться по кругу.

Линейная скорость v объекта, движущегося по окружности, напрямую связана с угловой скоростью omega и радиусом окружности: v = omega x r . Таким образом, вы также можете записать это уравнение как

Пример вопроса

1. Учитывая, что Луна обращается вокруг Земли примерно каждые 27,3 дня и что ее расстояние от центра Земли составляет 3,85 x 10 ⁸ м, каково центростремительное ускорение Луны?

   Правильный ответ: 2,7 x 10 ^–3 м/с ² .

   1. Начните с этого уравнения:

   2. Найдите скорость Луны. Он проходит 2ð r за 27,3 дня, поэтому преобразуйте 27,3 в секунды:

   3. Следовательно, скорость Луны равна

   4. Подставьте числа:

Практические вопросы

1. Кончики лопастей вертолета движутся со скоростью 300 м/с и имеют радиус 7,0 м. Каково центростремительное ускорение этих наконечников?

2. Ваш шарик на веревочке вращается по кругу. Если он движется со скоростью 60 миль в час в радиусе 2,0 м, каково его центростремительное ускорение?

Ниже приведены ответы на практические вопросы:

1. 1,3 x 10 ⁴ м/с ²

   1. Используйте это уравнение:

   2. Подставьте числа:

2. 360 м/с ²

   1. Используйте это уравнение:

   2. Преобразование скорости 60 миль/ч в м/с:

   3. Подставьте числа:

Об этой статье

Эта статья из книги:

• Рабочая тетрадь по физике I для чайников с онлайн-практикой,

Об авторе книги:

Эту статью можно найти в категории:

• Физика,

90 000 Равномерное круговое движение Равномерное круговое движение

Объект, движущийся по окружности радиусом r с постоянной скоростью v ускоряется. направление вектора его скорости все время меняется, но величина вектор скорости остается постоянным. Вектор ускорения не может иметь компонента в направлении вектора скорости, так как такая компонента вызвать изменение скорости. Поэтому вектор ускорения должен быть перпендикулярно вектору скорости в любой точке окружности. Этот ускорение называется радиальное ускорение или центростремительное ускорение , и это указывает к центру круга. Величина центростремительной вектор ускорения равен a _c = v ² /r. (Мы пропускаем производное этого выражения.)

Внешняя ссылка: Равномерное круговое движение

Проблема:

Орбита Луны вокруг Земля приблизительно круглая, со средним радиусом 3,85*10 ⁸ м. Луне требуется 27,3 дня, чтобы совершить один оборот вокруг Земли. земля. Найти
(а) средняя орбитальная скорость Луны и
б) его центростремительное ускорение.

Решение:

• Обоснование:
  Расстояние, которое Луна проходит за один орбитальный период T, равно d = 2πr.
  Его скорость равна v = расстояние/время = d/T.
  Центростремительное ускорение Луны v ² /r.
• Детали расчета:
  (a) Расстояние, которое Луна проходит за 27,3 дня, равно d = 2πr = 2,41*10 ⁹ м.
  Его скорость равна v = d/(27,3 дня) = (d/(2,36*10 ⁶ с)) = 1023 м/с.
  (b) Центростремительное ускорение Луны равно v ² /r = 2,725*10 ^-3 м/с ² .

Объект, движущийся по кругу с постоянной или неравномерной скоростью, ускорение. Поскольку он ускоряется, на него должна действовать сила. Такой сила называется центростремительная сила .

Какая сила при других обстоятельствах?

Пусть мы решим некоторые задачи, исследуя этот вопрос.

Проблема:

Груз массой 3 кг, прикрепленный к легкой нити, вращается по горизонтальной стол без трения. Радиус окружности равен 0,8 м, а струна может выдержать массу 25 кг до разрыва. В каком диапазоне скоростей может двигаться масса есть до разрыва струны?

Решение:

• Обоснование:
  Масса, прикрепленная к нити, вращается по горизонтали, стол без трения.
  Предположим, что масса вращается с постоянной скоростью. Это ускорение. Направление ускорения в сторону центр круга, а его величина v ² /r. В струне есть напряжение. Нить натягивает массу с силой F, направленной к центру окружности. Этот сила F отвечает за центростремительное ускорение, F = мв ² /р.
  Струна может выдержать до разрыва массу 25 кг, т.е. может позволить массе до 25 кг висеть на веревке рядом с поверхность земли. Максимальное натяжение струны поэтому F _max = mg = (25 кг)(9,8 м/с ² ) ^{= 245 Н.
  Учитывая F _max = 245 Н и F = mv 2 /r, мы можем найти v _max .}
• Детали расчета:
  v _max ² = F _макс. об/мин = (245 Н)(0,8 м)/(3кг). v _max = 8,1 м/с.

Проблема:

Монета, помещенная на расстоянии 30 см от центра вращающегося горизонтального поворотный стол проскальзывает, когда его скорость составляет 50 см/с.
а) Какая сила обеспечивает центростремительное ускорение, когда монета неподвижен относительно поворотного стола?
б) Чему равен коэффициент статического трения между монетой и Проигрыватель?

Решение:

• Обоснование:
  Когда монета покоится относительно вращающегося поворотного стола, сила статическое трение между монетой и поворотным столом обеспечивает центростремительное ускорение.
  Сила трения покоя имеет максимальное значение f _с = μ _с Н = μ _с мг.
  Настройка μ _с мг = mv ² /r, мы можем решить для μ _s .
• Детали расчета:
  (а) Сила трения покоя между монетой и поворотным столом обеспечивает центростремительное ускорение.