Вписанные и описанные углы в окружности
Browse from millions of quizzesQUIZ
Mathematics
60%accuracy
2plays
Семенова Варвара3 months
Mathematics
Семенова Варвара
2plays
10 questions
No student devices needed. Know more
10 questions
See Preview
1.
 Multiple-choice
Multiple-choice30 seconds
1 pt
Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.
2. Fill-in-the-Blank
1 minute
1 pt
В окружности с центром в точке О проведены диаметры
3. Multiple-choice
30 seconds
1 pt
Найдите градусную меру центрального ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.
4.
 Multiple-choice
Multiple-choice30 seconds
Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
5. Multiple-choice
30 seconds
1 pt
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 48°.
6. Multiple-choice
30 seconds
1 pt
Точка
7. Fill-in-the-Blank
1 minute
1 pt
На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 63.
 Найдите длину большей дуги.
Найдите длину большей дуги.8. Multiple-choice
1 pt
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC = 15° и ∠OAB = 8°. Найдите угол BCO. Ответ дайте в градусах.
9. Multiple-choice
30 seconds
1 pt
Сторона AC треугольника ABC содержит центр описанной около него окружности. Найдите угол С , если А=75 градусов. Ответ дайте в градусах.
10. Multiple-choice
1 pt
AC и BD — диаметры окружности с центром O.
 Угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах.
Угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах.Expore all questions with a free account
Already have an account?
Вычисление углов II. Задачи для ОГЭ. Вычисление углов II Угол с величиной 107 вписана окружность
Вопрос № 1
Вписанный в окружность угол равен 71°. Найдите центральный угол, опирающийся на ту же самую дугу.
142 152 132
Вопрос № 2
Вписанный угол ABC равен 30°. Найдите длину хорды AC, на которую он опирается, если радиус окружности равен 12.
Вопрос № 3
Центральный угол AOC равен 60°. Найдите длину хорды AC, на которую он опирается, если радиус окружности равен 25.
24 25 35 34
Вопрос № 4
Найдите центральный угол, который опирается на дугу в 97°.
97 194 48,5
Вопрос № 5
Вписанный угол ABC равен 30°. Найдите радиус окружности, если длина хорды AC, на которую он опирается, равна 27.
26 27 60
Вопрос № 6
Центральный угол окружности равен 106°.
 Найдите вписанный угол, опирающийся на ту же самую дугу.
Найдите вписанный угол, опирающийся на ту же самую дугу.53 212 16
Вопрос № 7
39 90 180
Вопрос № 8
Вписанный угол ABC равен 30°. Найдите радиус окружности, если длина хорды AC, на которую он опирается, равна 17.
16 17 15 60
ВАРИАНТ 1
2. Дана окружность. Центральный угол АОВ равен 110°. Найдите вписанный угол ВСА, если отрезки АВ и ОС пересекаются.
1) 55° 2) 90° 3) 110° 4) 125° 5) 70°
Ответ: 4.
4. Хорды АВ и CD окружности пересекаются в точке К, причем АВ = 8, СК = 3, DK = 4. Найти АК, если известно, что АК > ВК.
1) 3 2) 4 3) 5 4) 6
Ответ: 4.
5. Хорда АВ окружности с центром О перпендикулярна ее радиусу ОС и делит его на отрезки ОК = 1,5 и СК = 1. Найдите длину хорды АВ.
6. Найдите больший из углов, образованных касательной к окружности в точке А и хордой АВ, равной радиусу окружности.
Ответ: 150°.
7. Точка А лежит вне круга, ограниченного окружностью w. Угол с вершиной А высекает на окружности w дуги градусной меры 40° и 88°. Найдите величину угла А.
Угол с вершиной А высекает на окружности w дуги градусной меры 40° и 88°. Найдите величину угла А.
Ответ: 24°.
8. Хорды АВ и CD окружности пересекаются в точке К. Найдите угол AKD, если сумма градусных мер дуг AD и ВС равна сумме градусных мер дуг DB и АС.
Ответ: 90°.
Тест-контроль
Работа по карточкам
Точка О – центр окружности. Найдите значение x.
А) 600; Б) 400; В) 800.А) 600; Б) 1400; В) 800.А) 600; Б) 400; В) 1250.
А) 1600; Б) 1400; В) 800.А) 1200; Б) 1400; В) 800.А) 550; Б) 450; В) 650. А) 600; Б) 400; В) 500.А) 600; Б) 400; В) 800.ТЕСТ №11.
-762000609601В угол C величиной 107° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
lefttop
2Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60° . Найдите длину хорды АВ, если радиус окружности равен 8.
Ответ: 8
-9188451854203. В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
4. Центральный угол AOB, равный 60° , опирается на хорду АВ длиной 4. Найдите радиус окружности.
5. Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
6. Найдите ∠KOM, если градусные меры дуг KO и OM равны 112° и 170° соответственно.
7 В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину углаOAB.
8. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
9. Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.
10. Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?
11. Точка О — центр окружности, ∠ACB = 24° (см. рисунок). Найдите величину угла AOB (в градусах).
рисунок). Найдите величину угла AOB (в градусах).
12.. На окружности с центром O отмечены точки A и B так, что ∠AOB = 66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
13. В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 112°. Найдите вписанный угол ACB. Ответ дайте в градусах.
14. На окружности по разные стороны от диаметра ABвзяты точки M и N. Известно, что ∠NBA = 38°. Найдите угол NMB. Ответ дайте в градусах.
15.. AC и BD — диаметры окружности с центром O. Угол ACBравен 79°. Найдите угол AOD. Ответ дайте в градусах.
- Угол А четырехугольника ABCD, вписанного в окружность, равен 126 o . Найдите угол С этого четырехугольника. Ответ дайте в градусах.
- Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 63 o , 62 o , 90 o и 145 o . Найдите угол В этого четырехугольника. Ответ дайте в градусах.
- Точки A, B, C и D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 1: 4: 12: 19.
 Найдите угол А четырехугольника ABCD. Ответ дайте в градусах.
Найдите угол А четырехугольника ABCD. Ответ дайте в градусах. - Точки A, B, C и D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 1: 5: 10: 20. Найдите угол А четырехугольника ABCD. Ответ дайте в градусах.
- Четырехугольник ABCD вписан в окружность. Угол АВС равен 58 o , угол CAD равен 43 o . Найдите угол ABD. Ответ дайте в градусах.
- Два угла вписанного в окружность четырехугольника равны 25 o и 51 o . Найдите больший из оставшихся углов. Ответ дайте в градусах.
- Углы А, В и С четырехугольника АВСD относятся как 1: 13: 17. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
- Центральный угол на 45 o больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
- Центральный угол на 47 o больше острого вписанного угла, опирающегося на ту же дугу окружности.
 Найдите вписанный угол. Ответ дайте в градусах.
Найдите вписанный угол. Ответ дайте в градусах. - Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
- Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах.
- Найдите вписанный угол, опирающийся на дугу, которая составляет 10% окружности. Ответ дайте в градусах.
- Дуга окружности АС, не содержащая точки В, составляет 180 o . А дуга окружности ВС, не содержащая точки А, составляет 45 o . Найдите вписанный угол АСВ. Ответ дайте в градусах.
- Точки А, В и С, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1: 4: 13. Найдите больший угол треугольника АВС. Ответ дайте в градусах.
- АС и BD — диаметры окружности с центром О. Угол АСВ равен 35 o . Найдите угол АОD. Ответ дайте в градусах.
- AС и BD — диаметры окружности с центром О. Угол АСВ равен 39 o . Найдите угол АОD. Ответ дайте в градусах.
- Хорда АВ стягивает дугу окружности в 6 o .
 Найдите острый угол АВС между этой хордой и касательной к окружности, проведенной через точку В. Ответ дайте в градусах.
Найдите острый угол АВС между этой хордой и касательной к окружности, проведенной через точку В. Ответ дайте в градусах. - Хорда АВ стягивает дугу окружности в 114 o . Найдите острый угол АВС между этой хордой и касательной к окружности, проведенной через точку В. Ответ дайте в градусах.
- В угол С величиной 107 o вписана окружность, которая касается сторон угла в точках А и В. Найдите угол АОВ, где точка О — центр окружности. Ответ дайте в градусах.
- Касательные в точка А и В к окружности с центром О пересекаются под углом 2 o . Найдите угол АВО. Ответ дайте в градусах.
- Найдите угол CDB, если вписанные углы ADB и ADC опираются на дуги окружности, градусные величины которых равны соответственно 67 o и 25 o . Ответ дайте в градусах.
- Угол между стороной правильного -угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 75 o . Найдите .
- Угол между стороной правильного -угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 54 o .
 Найдите .
Найдите . - Угол между стороной правильного -угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 30 o . Найдите .
Как найти длину хорды
Все ресурсы по промежуточной геометрии
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
Справка по геометрии среднего уровня » Плоская геометрия » Круги » Аккорды » Как найти длину хорды
Радиус футов и . Найдите длину хорды.
Возможные ответы: Правильный ответ: Объяснение:Начнем с трех радиусов: один к , один к и один перпендикулярно к с конечной точкой на нашей окружности.
Мы также должны помнить, что наш центральный угол имеет меру, равную дуге, на которую он опирается. Поэтому, . Наш перпендикулярный радиус фактически делится на два конгруэнтных треугольника. Следовательно, она также делит пополам наш центральный угол, а это означает, что
Поэтому, . Наш перпендикулярный радиус фактически делится на два конгруэнтных треугольника. Следовательно, она также делит пополам наш центральный угол, а это означает, что
Следовательно, каждый из этих треугольников является треугольником 30-60-90, а это означает, что каждая половина нашей хорды равна половине длины гипотенузы (наш радиус равен 6). Следовательно, каждая половина равна 3, а вся хорда равна 6 футам.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы: Правильный ответ: Объяснение:Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 9,798.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы: Правильный ответ: Объяснение:Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 16.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы: Правильный ответ: Объяснение: Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 7,937.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы: Правильный ответ: Объяснение:Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 3,606.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы: Правильный ответ: Объяснение: Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше или в 6 раз больше.
Сообщить об ошибке
, какова длина этой хорды?
Возможные ответы: Правильный ответ: Объяснение:Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 13,266.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы: Правильный ответ: Объяснение: Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 4,472.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы: Правильный ответ: Объяснение:Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 7,746.
Сообщить об ошибке
Если хорда удалена от центра круга на единиц, а радиус равен , какова длина этой хорды?
Возможные ответы: Правильный ответ: Объяснение: Проведите из центра отрезок, перпендикулярный хорде, и эта линия разделит хорду пополам. Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Установив теорему Пифагора с радиусом в качестве гипотенузы и расстоянием в качестве одного из катетов, мы найдем другой катет.
Поскольку этот отрезок составляет половину хорды, общая длина хорды в 2 раза больше, или 9,592.
Сообщить об ошибке
← Назад 1 2 3 4 Далее →
Уведомление об авторских правах
Все промежуточные ресурсы по геометрии
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept
геометрия — Найдите длину окружности по хорде и длине остальной части окружности
спросил
Изменено 6 лет, 7 месяцев назад
Просмотрено 7к раз
$\begingroup$Если вы знаете длину хорды в окружности, а также длину окружности за вычетом отрезка, отсекаемого хордой, можете ли вы найти длину окружности?
Например, учитывая рисунок ниже, предположим, что мы знаем $d$, длину синей дуги, а также $b$, длину красной хорды. Мы хотели бы вычислить угол $\theta$, радиус $r$ или полную длину окружности.
Мы хотели бы вычислить угол $\theta$, радиус $r$ или полную длину окружности.
Из рисунка можно вывести следующие уравнения:
$\cos\,\theta=\frac{b}{2\,r}$
$d=c\,\frac{\pi -\theta}{\pi}=2\pi\,r\frac{\pi-\theta}{\pi}=2r(\pi-\theta) \quad \textrm{где c – длина окружности}$ 9c$ и r радиус.
Используя информацию о дуге, мы можем получить уравнение с двумя неизвестными, r и $\theta$.
Из уравнения хорды мы можем получить другое уравнение относительно r и $\sin\theta$.
Следующим шагом является объединение этих двух (предполагаемых независимыми) одновременных уравнений в одно путем исключения r (или $\theta$).
В первом случае результирующее комбинированное уравнение будет иметь множитель в виде $\dfrac {\sin \theta}{2\pi — \theta}$ (более или менее). Это уравнение относится к типу, называемому трансцендентным уравнением, которое не может быть решено обычным математическим методом. Мы можем получить только приблизительный ответ, используя численные методы.

 Multiple-choice
Multiple-choice Multiple-choice
Multiple-choice Найдите длину большей дуги.
Найдите длину большей дуги. Угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах.
Угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах. Найдите угол А четырехугольника ABCD. Ответ дайте в градусах.
Найдите угол А четырехугольника ABCD. Ответ дайте в градусах. Найдите вписанный угол. Ответ дайте в градусах.
Найдите вписанный угол. Ответ дайте в градусах.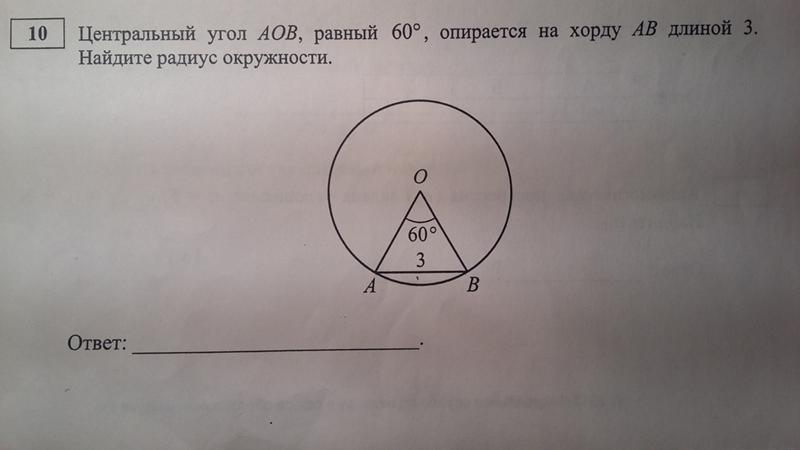 Найдите острый угол АВС между этой хордой и касательной к окружности, проведенной через точку В. Ответ дайте в градусах.
Найдите острый угол АВС между этой хордой и касательной к окружности, проведенной через точку В. Ответ дайте в градусах. Найдите .
Найдите .
Leave A Comment