Центр стремительного ускорения формула: Формула центростремительного ускорения в физике

Центростремительное ускорение – формула через угловую скорость, частота при движении кратко (9 класс)

4.7

Средняя оценка: 4.7

Всего получено оценок: 146.

4.7

Средняя оценка: 4.7

Всего получено оценок: 146.

Важнейшим кинематическим параметром неравномерного движения является ускорение. Если движение материальной точки происходит по окружности, то в этом движении всегда есть ускорение, называемое центростремительным. Получим формулу центростремительного ускорения.

Движение с ускорением

В 9 классе известно, что ускорение — это величина, которая характеризует, как быстро изменяется скорость. Оно равно отношению изменения скорости ко времени, за которое это изменение произошло:

$$\overrightarrow a={Δ \overrightarrow v \over Δt}$$

Если ускорение точки равно нулю, то точка движется равномерно и прямолинейно. В случае если вектор скорости изменяется, в движении присутствует ускорение.

Рис. 1. Движение с ускорением.

Ускорение при движении по окружности

Подчеркнем: ускорение характеризует любое изменение вектора скорости, не только по модулю, но и по направлению.

Даже при движении с постоянным модулем скорости, если направление вектора скорости меняется, ускорение в таком движении не равно нулю. Следовательно, криволинейное движение (даже равномерное) — это всегда движение с ускорением.

Рис. 2. Криволинейное движение.

Наиболее частым случаем криволинейного равномерного движения является движение по окружности. В таком движении модуль скорости материальной точки не меняется, а траектория движения представляет собой окружность. Найдем ускорение такого движения.

Если рассмотреть вектор перемещения точки по окружности за малое время $Δt$, то относительное изменение вектора скорости будет равно отношению вектора перемещения к радиусу поворота:

$${|Δ\overrightarrow v| \over v}={|Δ \overrightarrow r |\over R}$$

Разделив это соотношение на $Δt$, получим:

$${1\over v}{|Δ\overrightarrow v| \over Δt}={1\over R}{|Δ \overrightarrow r |\over Δt}$$

Откуда:

$${|Δ\overrightarrow v| \over Δt}={v\over R}{|Δ \overrightarrow r |\over Δt}$$

Отношение изменения вектора скорости ко времени в левой части по определению равно ускорению.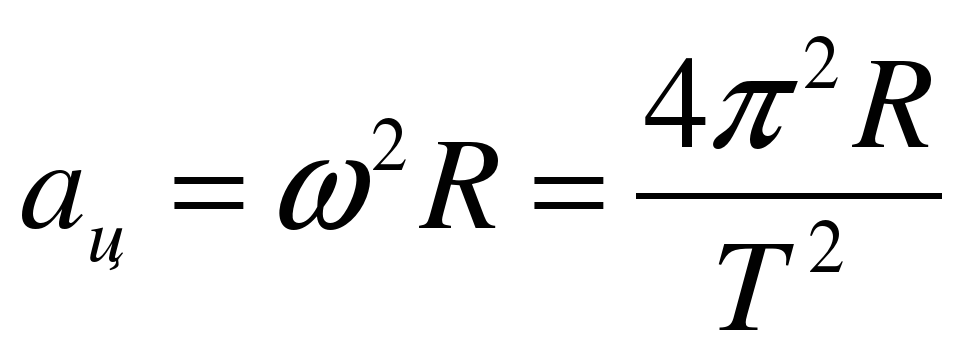 2 R}$$

Что мы узнали?

Криволинейное движение, даже если оно равномерно, — это всегда движение с ускорением. При равномерном движении по окружности ускорение всегда направлено в центр окружности, и поэтому называется центростремительным. Его модуль постоянен, а направление всегда перпендикулярно вектору скорости.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 146.

---

А какая ваша оценка?

Центростремительное ускорение. Вывод формулы. | by maxim | dx/dy

Движение по окружности часто встречается в природе и в деятельности человека. По окружности движутся спутники вокруг Земли (при упрощенном рассмотрении, на самом деле по эллиптической орбите), по окружности двигаются детали механизмов, ободы колес, шестерен, движение по окружности возникает при движении машин по закруглению дороги и так далее.

Рассмотрим равномерное движение тела по окружности.

Вектор скорости в таком случае направлен по касательной к окружности, и при движении не меняется по модулю, но, очевидно, изменяется по направлению.

Изобразим такое движение на схеме:

На схеме видно, как точка движется по окружности, из начального положения M переходит последовательно в положения М₁, М₂, М₃. Очевидно, что модуль вектора скорости в этих положениях не изменяется, а вектор всегда направлен по касательной окружности в этой точке.

Рассмотрим внимательнее перемещение точки из положения М в положение М₁ за интервал времени 𝛥t.

Отметим на рисунке векторы скоростей:

скорость точки в положении Мскорость точки в положении М₁

Эти скорости по модулю равны:

вектор изменения скорости.

Найдем изменение скорости. Для этого надо из конечного вектора скорости вычесть вектор скорости в начальной точке:

Среднее ускорение за время 𝛥t по определению (ускорение есть изменение скорости за промежуток времени) будет равно:

Найдем модуль и направление вектора ускорения.

Снова рассмотрим схему:

На схеме отмечены векторы:

вектор перемещения

И с помощью векторного вычитания отметим разность векторов скорости:

разность векторов (М₁АВ)

Для того, чтобы определить модуль среднего ускорения нам необходимо углубиться в геометрию.

Рассмотрим треугольники ОММ₁ и М₁АВ.

Это подобные треугольники. Докажем это:

во-первых, треугольники ОММ₁ и М₁АВ равнобедренные:

У треугольника ОММ₁ стороны ОМ = ОМ₁ (т.к. это радиусы окружности, по которой движется точка).

У треугольника М₁АВ стороны М₁А = АВ — так как это векторы скорости, их длина (модуль) не меняется во время движения.

Во-вторых, у треугольников ОММ₁ и М₁АВ равные углы при вершинах.

Докажем и это:

Эти углы равны, т.к. сторона ОМ треугольника ОММ₁ перпендикулярна стороне АВ треугольника М₁АВ, а сторона ОМ₁ треугольника ОММ₁ перпендикулярна стороне М₁А треугольника М₁АВ

(ведь ОМ и ОМ₁ — это радиусы окружности, а АВ и М₁А — это векторы скорости, направленные по касательной к окружности, а значит перпендикулярно радиусу).

Из курса геометрии вспомним теорему об углах с соответственно перпендикулярными сторонами: стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 180º.

В нашем случае очевидно что оба угла острые, соответственно они равны.

Снова вспоминаем курс геометрии, а именно теорему о подобии треугольников: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

В нашем случае эти условия выполняются, стало быть треугольники ОММ₁ и М₁АВ подобны.

Для подобных треугольников мы можем составить пропорцию:

Вернемся из геометрии к физическому смыслу сторон наших треугольников, и запишем пропорцию в виде:

Разделим обе части равенства на промежуток времени 𝛥t:

Умножим обе части равенства на модуль скорости v:

Но ведь отношение разности скоростей к промежутку времени — это среднее ускорение:

а отношение вектора перемещения к промежутку времени — это средняя скорость:

Но нам необходимо найти модуль мгновенного ускорения.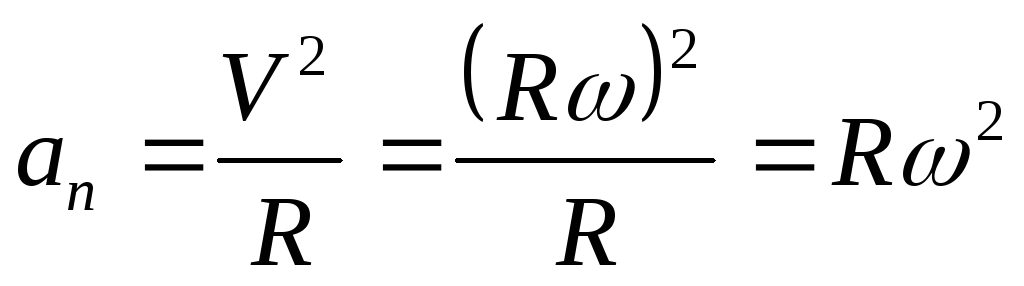 Для этого мы должны взять предельный случай, когда промежуток времени 𝛥t стремится к нулю.

В этом случае,

модуль ускорения точки в момент времени t

и

модуль вектора мгновенной скорости в момент времени t

Значит равенство:

мы можем записать в виде:

или:

Вот мы и вывели формулу вычисления центростремительного ускорения.

А так как в равномерном движении по окружности — радиус окружности и модуль скорости остаются постоянными, то и модуль центростремительного ускорения тоже остается постоянным.

Далее, определим направление вектора ускорения.

Из названия центростремительного ускорения очевидно, что вектор ускорения направлен к центру окружности, по которой движется точка. Но, докажем это. Снова рассмотрим схему:

Вектор ускорения будет направлен так, как направлен вектор

при приближении промежутка времени к нулю.

Если

то точка М₁ приближается к точке М, а угол 𝜑 стремится к нулю.

Это значит, что угол ВМ₁А стремится к 90°.

А это значит, что угол между вектором изменения скорости и радиусом окружности при приближении промежутка времени к нулю тоже стремится к нулю. Таким образом, вектор мгновенного ускорения стремится к центру окружности.

Для наглядности, изобразим это на схеме:

мы видим как при уменьшении промежутка времени 𝛥t направление разности векторов 𝛥v все ближе и ближе приближается к радиусу (отмечен пунктирной линией), и в конце концов совпадает с радиусом и в предельном случае, вектор изменения скорости направлен строго к центру. Соответственно, строго к центру направлен и вектор мгновенного ускорения.

Изобразим векторы ускорения на схеме:

Резюмируем: при равномерном движении точки по окружности (т.е. с постоянной линейной скоростью), модули скорости и ускорения остаются неизменными, вектор скорости постоянно направлен по касательной к окружности, а вектор центростремительного ускорения — к центру окружности.

Формула для определения центростремительного ускорения:

3 формулы, которые вам нужны

«Вау, вы действительно перешли от нуля к шестидесяти!»

Вы когда-нибудь слышали, чтобы кто-то использовал идиому «от нуля до шестидесяти», как это сделал я в приведенном выше примере? Когда кто-то говорит, что что-то изменилось с «ноля до шестидесяти», на самом деле он имеет в виду, что все ускорилось очень быстро. Ускорение — это величина, на которую изменяется скорость чего-либо за установленный период времени.

В этой статье мы поговорим об ускорении: что это такое и как его рассчитать. Пристегнитесь!

 

Что такое ускорение?

Ускорение — это скорость изменения скорости за заданный период времени. Для расчета ускорения необходимо знать скорость и время.

Многие путают ускорение со скоростью (или скоростью). Во-первых, скорость — это просто скорость с указанием направления, поэтому эти два понятия часто используются взаимозаменяемо, даже если между ними есть небольшие различия.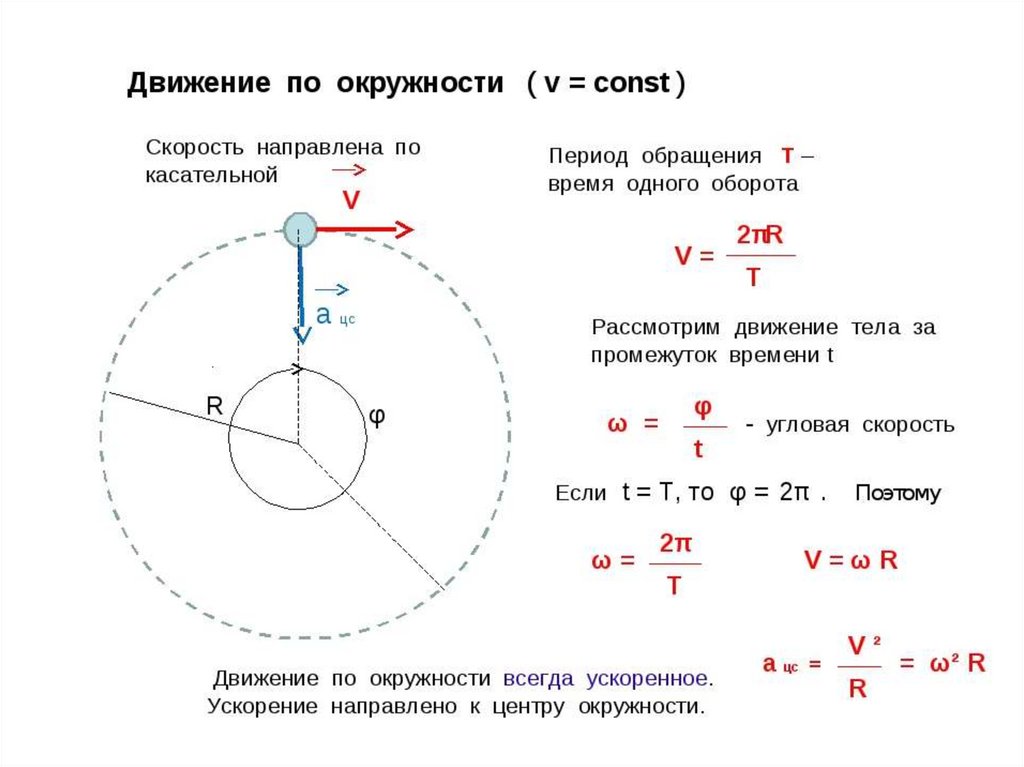 Ускорение — это скорость изменения скорости, означающая, что что-то становится быстрее или медленнее.

 

Что такое формула ускорения?

Вы можете использовать уравнение ускорения для расчета ускорения. Вот наиболее распространенная формула ускорения:

$$a = {Δv}/{Δt}$$

, где $Δv$ — изменение скорости, а $Δt$ — изменение времени.

Вы также можете записать уравнение ускорения следующим образом:

$$a = {v(f) — v(i)}/{t(f) — t(i)}$$

В этом уравнении ускорения $v(f)$ — конечная скорость, а $v(i)$ — начальная скорость. $T(f)$ — конечное время, а $t(i)$ — начальное время.

Некоторые другие вещи, которые следует учитывать при использовании уравнения ускорения:

• Вам нужно вычесть начальную скорость из конечной скорости. Если вы поменяете их местами, вы неправильно поймете направление ускорения.

• Если у вас нет времени начала, вы можете использовать «0».

• Если конечная скорость меньше начальной скорости, ускорение будет отрицательным, что означает, что объект замедлился.

Теперь давайте разберем уравнение ускорения шаг за шагом на реальном примере.

 

 

Как рассчитать ускорение: пошаговая разбивка

Теперь мы шаг за шагом разберем формулу ускорения на реальном примере.

Гоночный автомобиль разгоняется с 15 м/с до 35 м/с за 3 секунды. Каково его среднее ускорение?

Сначала напишите уравнение ускорения.

$$a = {v(f) — v(i)}/{t(f) — t(i)}$$

Затем определите свои переменные. 92$$

Давайте попробуем другой пример.

Велосипедист, движущийся со скоростью 23,2 м/с, полностью останавливается через 1,5 $s$. Каково было ее замедление?

Сначала напишите уравнение ускорения.

$$a = (v(f) — v(i)) ÷ (t(f) — t(i))$$

Затем определите свои переменные.

a = то, что мы решаем для

$$V(f) = 0 м/с$$

$$V(i) = 23,2 м/с$$

$$T(f) = 1,4 с $$

$$T(i) = 0 s$$

Теперь подставьте свои переменные в уравнение и решите: 92}$$

 

2 Другие распространенные формулы ускорения

Хотите узнать, как рассчитать ускорение по другой формуле? Есть несколько других распространенных формул ускорения.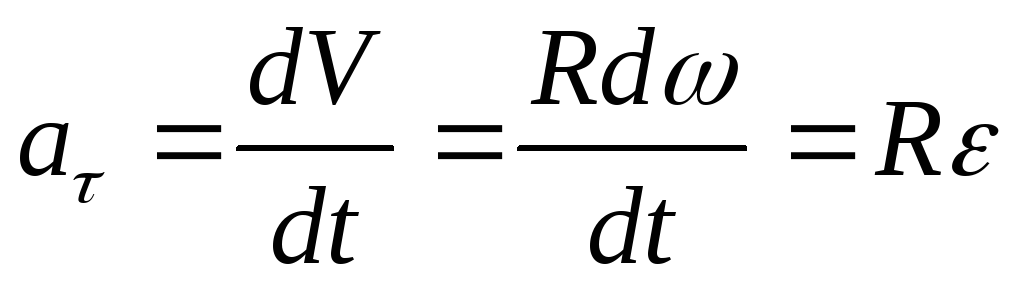

 

Формула углового ускорения

Угловое ускорение — это скорость изменения углового ускорения вращающегося объекта во времени.

Вот уравнение углового ускорения:

$$a = {\change \in\угловая\скорость}/{\change\in\time}$$ 92}/r$$

$a(c) $= ускорение, центростремительное

$v$ = скорость

$r$ = радиус

 

Ключевые выводы

Ускорение – это скорость изменения скорости в течение установить период времени.

Ускорение рассчитывается путем деления изменения скорости на изменение времени.

 

Что дальше?

Ищете другие научные объяснения? Разбираем электрическую энергию и как определить различных типов облаков с нашими опытными гидами.

Работаете над исследовательской работой, но не знаете, с чего начать? Тогда ознакомьтесь с нашим руководством, в котором мы собрали множество высококачественных тем для исследований, которые вы можете использовать бесплатно.

Нужна помощь в изучении английского языка — особенно в определении литературных приемов в текстах, которые вы читаете? Тогда вам определенно стоит взглянуть на наше исчерпывающее объяснение самых важных литературных приемов 9.0177 и как они используются.

 

Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!

Наша база данных проверенных преподавателей включает в себя ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.

{{cta(‘21006efe-96ea-47ea-9553-204221f7f333’)}}

 

Есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!

Хейли Миллиман

Об авторе

Хейли Миллиман — бывшая учительница, ставшая писателем и ведущая блоги об образовании, истории и технологиях. Когда она была учителем, ученики Хейли регулярно набирали 99-й процентиль благодаря ее страсти к тому, чтобы делать темы удобоваримыми и доступными. В дополнение к своей работе для PrepScholar, Хейли является автором Путеводителя Museum Hack по самым свирепым женщинам в истории.

Ускорение

Последняя математическая величина, обсуждавшаяся в Уроке 1, — это ускорение. Ускорение, которое часто путают, имеет значение, сильно отличающееся от того, которое связывают с ним спортивные дикторы и другие лица. Определение ускорения:

• Ускорение — это векторная величина, определяемая как скорость, с которой объект изменяет свою скорость. Объект ускоряется, если он меняет свою скорость.

Спортивные комментаторы иногда говорят, что человек ускоряется, если он/она движется быстро. Однако ускорение не имеет ничего общего с быстрой ездой. Человек может двигаться очень быстро и при этом не ускоряться. Ускорение связано с изменением скорости движения объекта.

Если объект не меняет свою скорость, то он не ускоряется. Данные справа представляют объект, движущийся на север с ускорением. Скорость меняется с течением времени. Фактически скорость изменяется на постоянную величину — 10 м/с — в каждую секунду времени. Когда скорость объекта изменяется, говорят, что объект ускоряется; у него есть ускорение.

Значение постоянного ускорения

Иногда ускоряющийся объект меняет свою скорость на одну и ту же величину каждую секунду. Как упоминалось в предыдущем абзаце, приведенная выше таблица данных показывает, что скорость объекта изменяется на 10 м/с каждую последующую секунду. Это называется постоянным ускорением, поскольку скорость изменяется на постоянную величину каждую секунду. Объект с постоянным ускорением не следует путать с объектом с постоянной скоростью. Не дайте себя обмануть! Если объект меняет свою скорость — на постоянную или переменную величину — тогда это ускоряющийся объект. А объект с постоянной скоростью не ускоряется.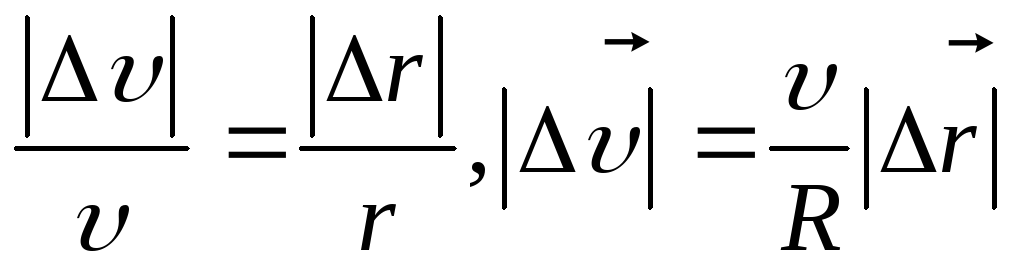

В приведенных ниже таблицах данных показано движение объектов с постоянным ускорением и изменяющимся ускорением. Обратите внимание, что каждый объект имеет изменяющуюся скорость.

Поскольку ускоряющиеся объекты постоянно меняют свою скорость, можно сказать, что пройденное расстояние/время не является постоянной величиной. Например, падающий объект обычно ускоряется при падении. Если бы мы наблюдали за движением свободно падающего объекта (движение свободного падения будет подробно рассмотрено позже), мы бы заметили, что средняя скорость объекта составляет примерно 5 м/с в первую секунду, примерно 15 м/с. во вторую секунду, примерно 25 м/с в третью секунду, примерно 35 м/с в четвертую секунду и т. д. Наш свободно падающий объект будет постоянно ускоряться. Учитывая эти средние значения скорости в течение каждого последовательного 1-секундного интервала времени, мы могли бы сказать, что объект упадет на 5 метров в первую секунду, на 15 метров во вторую секунду (при общем расстоянии 20 метров), на 25 метров в третью секунду.

секунда (на общую дистанцию ​​45 метров), 35 метров на четвертую секунду (на общую дистанцию ​​80 метров через четыре секунды). Эти цифры приведены в таблице ниже.

Время Интервал	Изменение скорости Во время перерыва	пр. Скорость Во время перерыва	Пройденное расстояние Во время перерыва	Общее пройденное расстояние от 0 с до конца интервала
0 – 1,0 с	от 0 до ~10 м/с	~5 м/с	~5 м	~5 м
1,0–2,0 с	~10…20 м/с	~15 м/с	~15 м	~20 м
2,0 – 3,0 с	~от 20 до 30 м/с	~25 м/с	~25 м	~45 м
3,0 – 4,0 с	~от 30 до 40 м/с	~35 м/с	~35 м	~80 м

Примечание.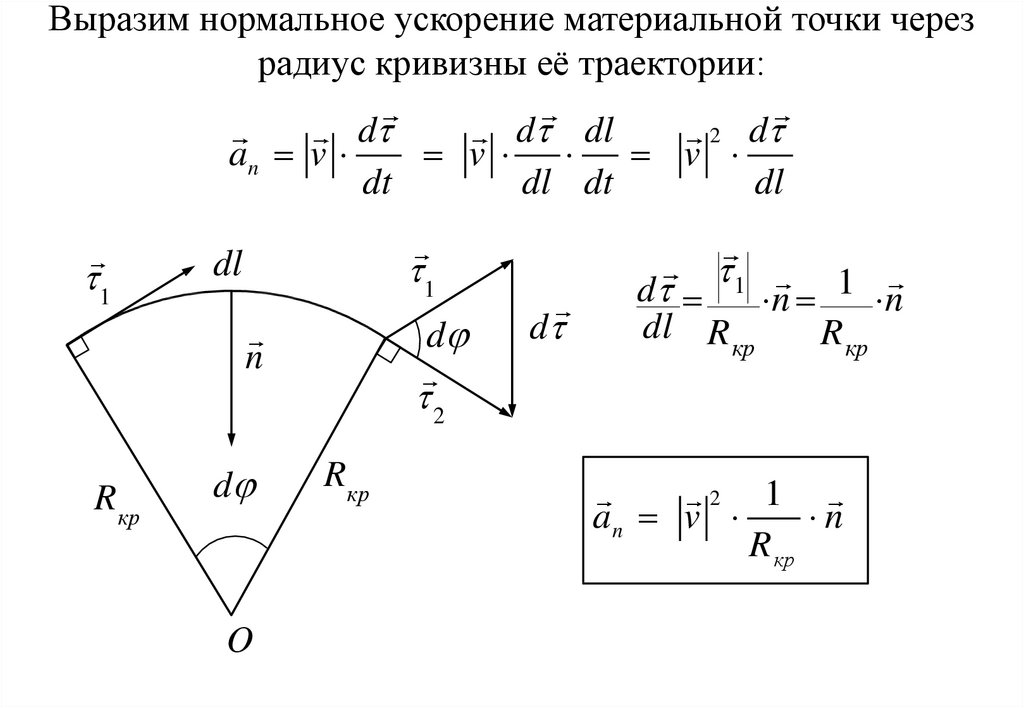 2); расстояние, пройденное за четыре секунды, в 16 раз больше расстояния, пройденного за одну секунду. Для объектов с постоянным ускорением расстояние перемещения прямо пропорционально квадрату времени перемещения.

 

Расчет среднего ускорения

Среднее ускорение (a) любого объекта за заданный интервал времени (t) можно рассчитать с помощью уравнения

Это уравнение можно использовать для расчета ускорения объекта, движение которого изображено приведенной выше таблицей данных скорость-время. Данные скорости-времени в таблице показывают, что ускорение объекта составляет 10 м/с/с. Расчет показан ниже.

Значения ускорения выражаются в единицах скорости/времени. Типичные единицы ускорения включают следующее:

м/с/с
миль/ч/с
км/ч/с
м/с ²

Эти единицы могут показаться немного неудобными начинающему студенту-физику. Тем не менее, это очень разумные единицы, когда вы начинаете рассматривать определение и уравнение для ускорения.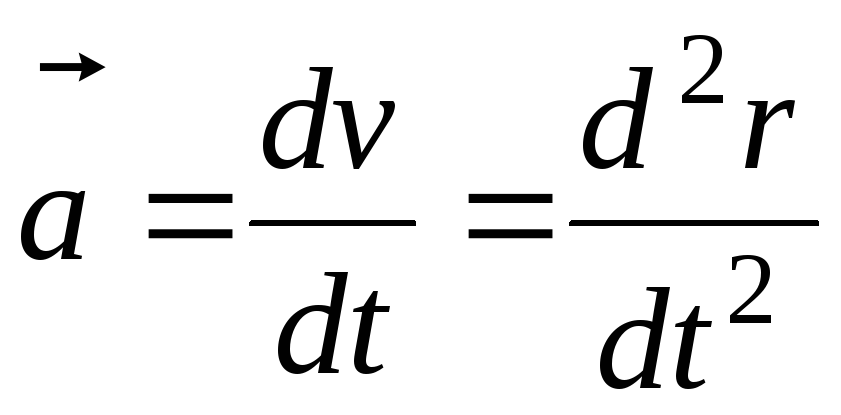 Причина единиц становится очевидной при рассмотрении уравнения ускорения.

Поскольку ускорение — это изменение скорости во времени, единицы измерения ускорения — это единицы скорости, разделенные на единицы времени, то есть (м/с)/с или (ми/ч)/с. Единица (м/с)/с может быть математически упрощена до м/с ² .

 

Направление вектора ускорения

Поскольку ускорение является векторной величиной, с ним связано направление. Направление вектора ускорения зависит от двух вещей:

• ускоряется или замедляется объект
• движется ли объект в направлении + или —

Общий принцип определения ускорения:

Если объект замедляется, то его ускорение направлено в сторону, противоположную его движению.

Этот общий принцип можно применять для определения того, является ли знак ускорения объекта положительным или отрицательным, правым или левым, верхним или нижним и т. д. Рассмотрим две приведенные ниже таблицы данных. В каждом случае ускорение объекта находится в положительном направлении. В примере А объект движется в положительном направлении (т. е. имеет положительную скорость) и ускоряется. Когда объект ускоряется, ускорение идет в том же направлении, что и скорость. Таким образом, этот объект имеет положительное ускорение. В примере B объект движется в отрицательное направление (т. е. имеет отрицательную скорость) и замедляется. Согласно нашему общему принципу, когда объект замедляется, ускорение идет в направлении, противоположном скорости. Таким образом, этот объект также имеет положительное ускорение.

Этот же общий принцип можно применить к движению объектов, представленных в двух таблицах данных ниже. В каждом случае ускорение объекта находится в отрицательном направлении. В примере C объект движется в положительное направление (т. е. имеет положительную скорость) и замедляется. Согласно нашему принципу, когда объект замедляется, ускорение идет в направлении, противоположном скорости.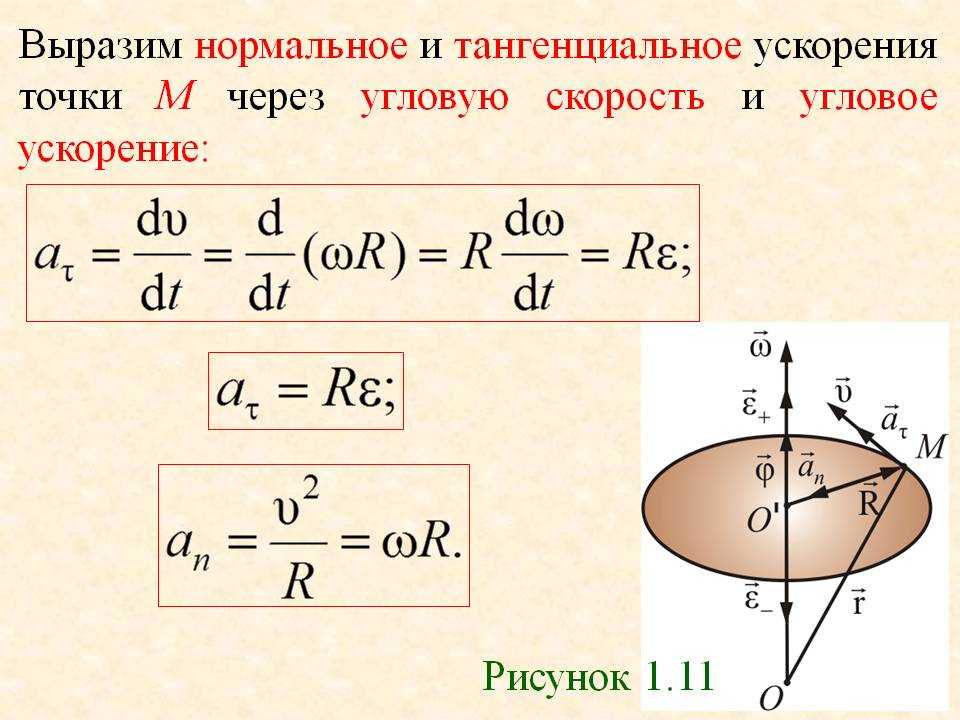 Таким образом, этот объект имеет отрицательное ускорение. В примере D объект движется в отрицательном направлении (т. е. имеет отрицательную скорость) и ускоряется. Когда объект ускоряется, ускорение идет в том же направлении, что и скорость. Таким образом, этот объект также имеет отрицательное ускорение.

Обратите внимание на использование положительных и отрицательных слов, использованных в обсуждении выше (примеры A — D). В физике использование положительного и отрицательного всегда имеет физический смысл. Это больше, чем просто математический символ. Как используется здесь для описания скорости и ускорения движущегося объекта, положительное и отрицательное описывают направление. И скорость, и ускорение являются векторными величинами, и полное описание величины требует использования прилагательного, направленного по направлению. Север, юг, восток, запад, право, лево, вверх и вниз — все прилагательные, указывающие направление. Физика часто заимствует из математики и использует символы + и — как прилагательные, указывающие направление. В соответствии с математическим соглашением, используемым на числовых линиях и графиках, положительное часто означает вправо или вверх, а отрицательное часто означает влево или вниз. Таким образом, сказать, что объект имеет отрицательное ускорение, как в примерах C и D, означает просто сказать, что его ускорение направлено влево или вниз (или в любом другом направлении, которое было определено как отрицательное). Отрицательные ускорения не относятся к значениям ускорения, меньшим 0. Ускорение -2 м/с/с — это ускорение величиной 2 м/с/с, направленное в отрицательном направлении.

Мы хотели бы предложить …

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактива Name That Motion. Он находится в разделе «Интерактивная физика» и позволяет учащемуся применять понятия скорости, скорости и ускорения.