Тетраэдр. Правильный тетраэдр. Ребра тетраэдра. Грани тетраэдра.
Дарим в подарок бесплатный вводный урок!
Что такое тетраэдр
Тетраэдр является частным случаем пирамиды т. е. все его грани являются треугольниками, включая основание пирамиды. Как и все пирамиды, тетраэдр представляет собой многогранник — трехмерную геометрическую форму с плоскими гранями и прямыми ребрами. Слово «tetra» берет свое начало в греческом языке и означает четыре, так как у тетраэдра 4 грани.
Тетраэдр имеет:
- четыре грани;
- шесть ребер;
- четыре вершины.
Свойства тетраэдра
Как видно из рисунка выше, тетраэдр всегда имеет треугольное основание, любая из четырех граней тетраэдра может быть обозначена как основание, если он правильный.
Все грани тетраэдра являются треугольниками, включая основание. Правильный тетраэдр является частным случаем тетраэдра, для которого все четыре треугольные грани равны, а все внутренние углы равны \(60°\).
На рисунке ниже показан равнобедренный тетраэдр.
Грани равнобедренного тетраэдра равны.
Поскольку все грани правильного тетраэдра являются равносторонними треугольниками, все внутренние углы тетраэдра будут составлять шестьдесят градусов 60°, а сумма углов граней, встречающихся в любой вершине, будет равно 180°. Оси симметрии имеют особое значение, когда мы имеем дело с правильным тетраэдрами. Ось симметрии, которая соединяет вершину правильного тетраэдра с центроидом противоположной грани. По определению, линия, проходящая через любую вершину тетраэдра и центром грани, противоположной этой вершине, называется медианой. Таким образом, тетраэдр имеет четыре 4 медианы.
У правильного тетраэдра каждая медиана совпадает с осью симметрии. Аналогичная ситуация возникает, когда мы рассматриваем ось симметрии, которая соединяет среднюю точку двух противоположных ребер правильного тетраэдра.
Виды тетраэдров
В зависимости от расположения граней и углов между ними существует несколько видов тетраэдров.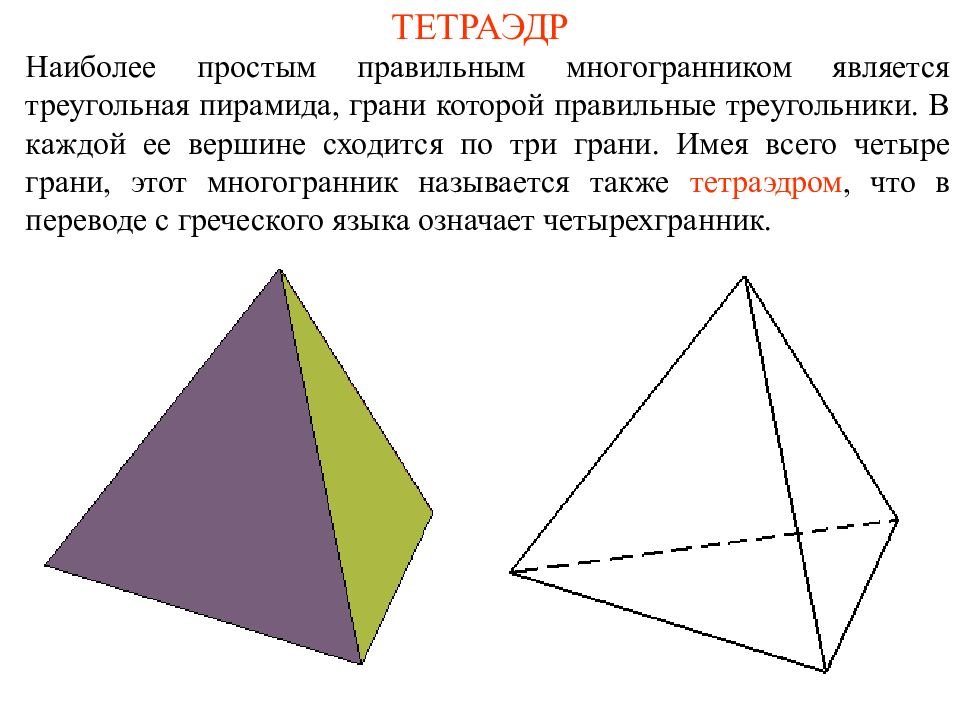
-
Равносторонний тетраэдр — это тетраэдр, у которого все грани равносторонние треугольники, а все углы между ними равны 60 градусам.
-
Равнобедренный тетраэдр — это тетраэдр, у которого все грани являются равнобедренными треугольниками, то есть имеют две равные стороны, а третья сторона может быть разной длины.
-
Прямоугольный тетраэдр — это тетраэдр, у которого три грани являются прямоугольными треугольниками, а четвертая грань может быть либо прямоугольным треугольником, либо равносторонним треугольником.
-
Неправильный тетраэдр — это тетраэдр, у которого все грани имеют разные размеры и формы.
Кроме того, в математике существует понятие расширенного тетраэдра, который состоит из обычного тетраэдра и сферы, которая описывает его грани. Расширенный тетраэдр имеет несколько интересных свойств и применений в различных областях науки.
Часто задаваемые вопросы:
✅
org/Answer»>↪ Тетраэдр — это геометрическая фигура, состоящая из четырех треугольных граней, которые соединены в одной общей вершине.✅ Какие виды тетраэдров существуют?
↪ Существует несколько видов тетраэдров: равносторонний, равнобедренный, прямоугольный и неправильный тетраэдр.
✅ В каких областях науки используются тетраэдры?
↪ Тетраэдры используются в различных областях науки, включая математику, физику, химию и геометрию. Например, тетраэдры могут использоваться для моделирования молекул в химии или для аппроксимации трехмерных объектов в компьютерной графике.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Тетраэдр по клеточкам — 75 фото
Тетраэдр на клетчатой бумаге
Схема октаэдра BP rktxtnjq ,evfub
Рисование объемных фигур по клеточкам
Тригональная бипирамида
Тетраэдр и правильная треугольная пирамида
Наклонный параллелепипед на плоскости
Платоновы тела Метатрон
Сложные геометрические фигуры по клеточкам
Треугольник Эшера
Как рисовать тетраэдр по клеточкам
Трехмерные фигуры по клеткам
Ребра тетраэдра
Многогранник октаэдр
Икосаэдр Лабана
Узоры по клеточкам в тетради
Десятиугольная пирамида
Точки m и n являются серединами рёбе
Изобразите правильную четырехугольную пирамиду
Рисунки по клеточкам ручкой
ГЕОГЕБРА тетраэдр
Сечение тетраэдра перпендикулярно ребру
Пирамида Серпинского
Тетраэдр и правильная треугольная пирамида
Самая сложная фигура
Граф додекаэдра планарный
Звездочный октаэдр
Симплекс 4
Настенный тетраэдр аппарат Delta
Бимедиана тетраэдра
Правильная пятиугольная пирамида
Рисунки по клеткам в тетради
Барицентрические координаты
Треугольник в пространстве
Правильный тетраэдр и правильная треугольная пирамида
Октаэдр вписанный в тетраэдр
Тетраэдр это правильная пирамида
Тетраэдр это правильная пирамида
Развертка правильного октаэдра
Элементы симметрии правильного октаэдра
Распечатка икосаэдра
Правильная четырехугольная пирамида фигура
Каркасный тетраэдр рисунок
Три оси симметрии тетраэдра
Правильный икосаэдр
Правильный октаэдр развертка для склеивания
Икосаэдр Эшера
Равносторонний треугольник пирамида
Тетраэдр оригами
Правильный икосаэдр
Плоскость симметрии правильного тетраэдра
Развертка правильного октаэдра
Фигуры на клеточках
Звёздчатый октаэдр (звезда Кеплера)
Кубогемиоктаэдр развертка
Пирамида геометрия
Неправильная пятиугольная пирамида
Тетраэдр из двух полосок бумаги
Тригональная пирамида развертка
Полный Граф k6
Тригон тритетраэдр развертка
Дельтоидальный икоситетраэдр
Кубооктоусеченный Кубоктаэдр
Оси симметрии тетраэдра
Октаэдр в Кубе
Рисунки по клеточкам Гарри Поттер
Меркаба звездчатый октаэдр
Тетраэдр из пластика
Объемные фигуры в клетку
Крыша шестиугольник в плане
Пирамида для дошкольников Геометрическая фигура
Треугольная и четырехугольная пирамида
Объемный крест
Многогранник октаэдр
Тетраэдр Меркаба
Правильный икосаэдр 20 граней
Комментарии (0)
Написать
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.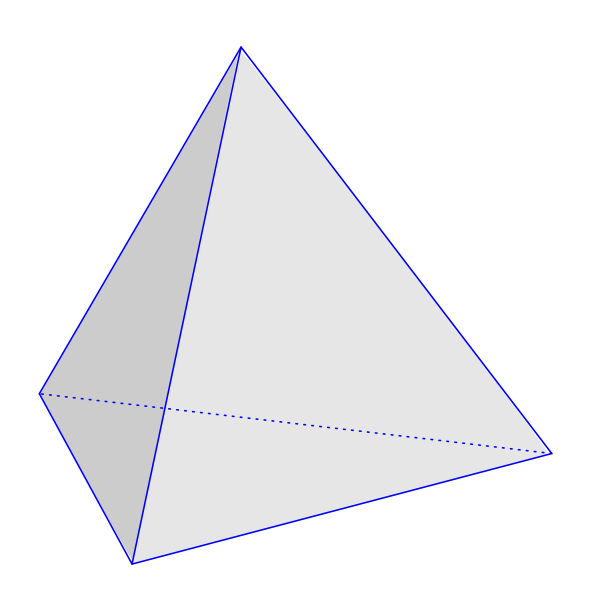
Тетраэдр — определение, свойства, формулы, примеры
Тетраэдр — это трехмерная фигура, имеющая четыре треугольные грани. Один из треугольников считается основанием, а остальные три треугольника вместе образуют пирамиду. Тетраэдр — разновидность пирамиды, представляющая собой многогранник с треугольными гранями, соединяющими основание с общей точкой, и плоское многоугольное основание. Он имеет треугольное основание, поэтому его также называют треугольной пирамидой.
| 1. | Определение тетраэдра |
| 2. | Сеть тетраэдра |
| 3. | Свойства тетраэдра |
| 4. | Площадь поверхности тетраэдра |
| 5. | Объем тетраэдра |
| 6. | Часто задаваемые вопросы о тетраэдре |
Определение тетраэдра
Тетраэдр — это многогранник с 4 гранями, 6 ребрами и 4 вершинами, у которого все грани — треугольники.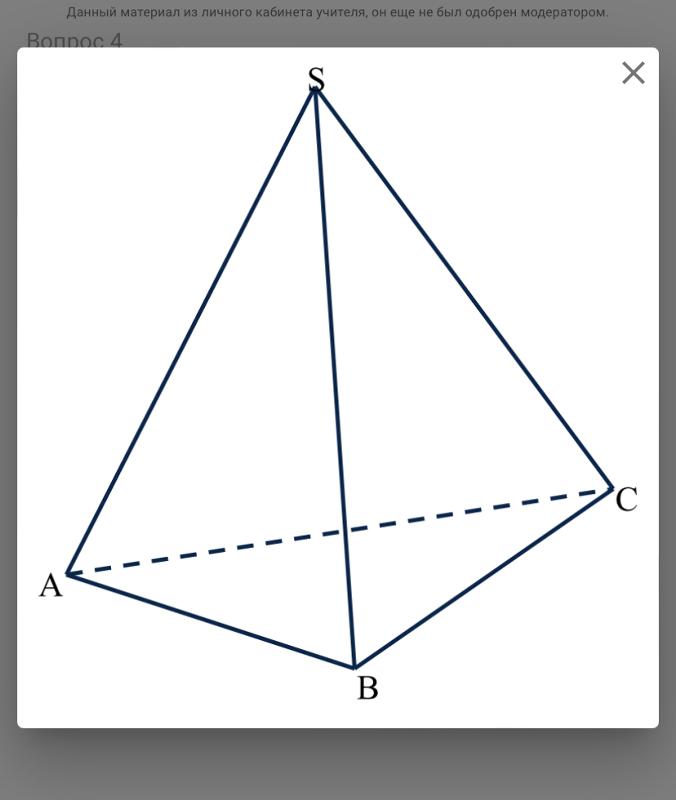
Сеть тетраэдра
В геометрии сетку можно определить как двухмерную форму, которая при складывании определенным образом дает трехмерную форму. Тетраэдр — это трехмерная фигура, которую можно сформировать с помощью геометрической сетки. Возьмите лист бумаги. Обратите внимание на две различные сети тетраэдров, показанные ниже. Скопируйте это на лист бумаги. Разрежьте его по краю и сложите, как указано на рисунке. Сложенная бумага образует тетраэдр.
Свойства тетраэдра
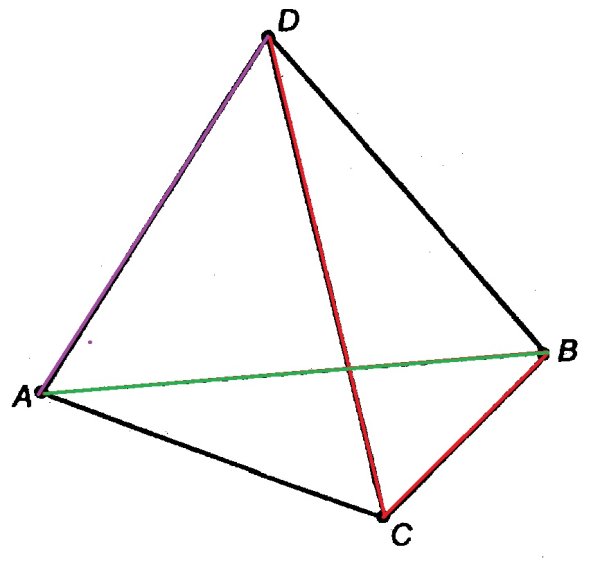
Тетраэдр представляет собой трехмерную форму, которая характеризуется некоторыми отличительными свойствами. На приведенном ниже рисунке показаны грани, ребра и вершины тетраэдра.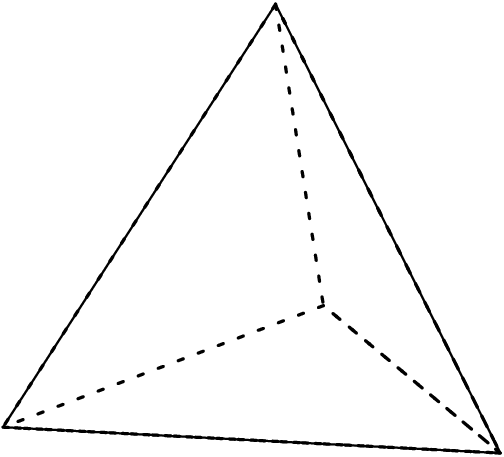
Ниже приведены свойства тетраэдра, которые помогают нам легко идентифицировать форму.
- Имеет 4 грани, 6 ребер и 4 вершины (угла).
- В правильном тетраэдре все четыре вершины равноудалены друг от друга.
- Имеет 6 плоскостей симметрии.
- В отличие от других платоновых тел у него нет параллельных граней.
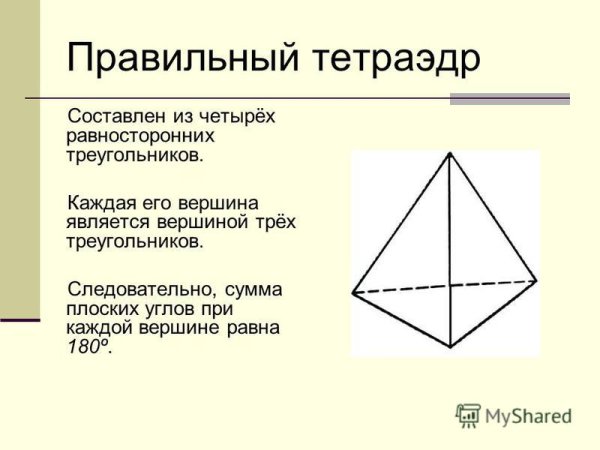
- Правильный тетраэдр имеет четыре равносторонних треугольника своими гранями.
Площадь поверхности тетраэдра
Площадь поверхности тетраэдра определяется как общая площадь или область, покрытая всеми гранями формы. Он выражается в квадратных единицах, например, в м 2 , в см 2 , в 2 , в футах 2 , в ярдах 2 и т. д. Тетраэдр может иметь два типа площадей поверхности:
- Площадь боковой поверхности тетраэдра
- Общая площадь поверхности тетраэдра
Площадь боковой поверхности тетраэдра
Площадь боковой поверхности тетраэдра определяется как площадь поверхности боковых или наклонных граней тетраэдра.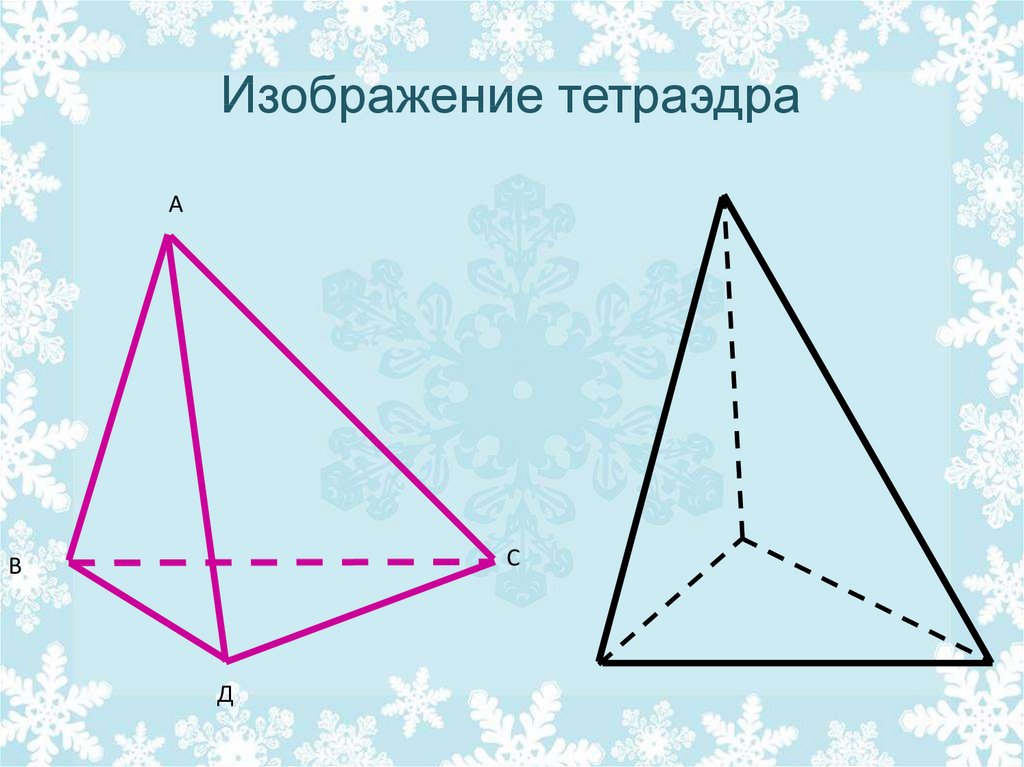
Формула для расчета площади боковой поверхности правильного тетраэдра имеет вид
.
LSA правильного тетраэдра = сумма 3 конгруэнтных равносторонних треугольников (т.е. боковых граней)
= 3 × (√3)/4 a 2 квадратных единиц
где а — длина стороны правильного тетраэдра.
Общая площадь поверхности тетраэдра
Общая площадь поверхности тетраэдра определяется как площадь поверхности всех граней тетраэдра. Формула для расчета общей площади поверхности правильного тетраэдра имеет вид
.
TSA правильного тетраэдра = сумма 4 конгруэнтных равносторонних треугольников (т.е. боковых граней)
= 4 × (√3)/4 a 2 = √3 a 2 квадратных единиц
где а — длина стороны правильного тетраэдра.
Объем тетраэдра
Объем тетраэдра определяется как общее пространство, занимаемое им в трехмерной плоскости. Формула для расчета объема тетраэдра дается как,
Объем правильного тетраэдра = (1/3) × площадь основания × высота = (1/3) ∙ (√3)/4 ∙ a 2 × (√2)/(√3) a
= (√2/12) a 3 кубических единиц
где а — длина стороны правильного тетраэдра.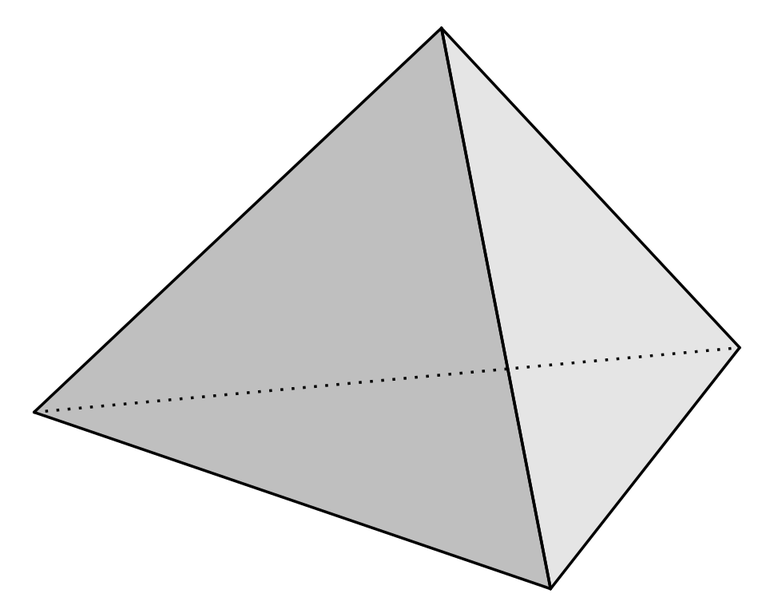
Темы, относящиеся к тетраэдру:
Ознакомьтесь с этими интересными статьями, связанными с тетраэдром.
- Многогранник
- Платоновые тела
- Формы
- Твердые формы
- 3D-фигуры
Важные примечания по тетраэдру:
- 5 платоновых тел могут быть перечислены как тетраэдр, куб, октаэдр, икосаэдр и додекаэдр.
- Тетраэдр — это треугольная пирамида, у которой все 4 грани — треугольники.
- Тетраэдр имеет 4 грани, 6 ребер и 4 угла.
Примеры тетраэдра
Пример 1. Два конгруэнтных тетраэдра склеиваются вдоль основания, образуя треугольную бипирамиду. Сколько граней, ребер и вершин у этой бипирамиды?
Решение:
Если мы откроем треугольную бипирамиду, чтобы увидеть ее сеть, она будет похожа на то, что показано на следующем рисунке:
Это показывает, что треугольная бипирамида имеет 6 треугольных граней, 9 ребер и 5 вершин.
Пример 2: Найдите объем правильного тетраэдра с длиной стороны, равной 5 единицам. (Округлите ответ до 2 знаков после запятой)
Решение:
Мы знаем, что объем тетраэдра равен (1/6√2) с 3 кубических единиц, где s = длина стороны.
Подставив ‘s’ вместо 5, получим:
Объем = 5 3 /6√2
= 125/8,485
≈ 14,73
Следовательно, объем тетраэдра равен 14,73 кубических единиц.Пример 3: Каждое ребро правильного тетраэдра равно 6 единицам. Найдите площадь его полной поверхности.
Решение:
Общая площадь поверхности правильного тетраэдра:
Общая площадь поверхности = √3s 2
Подставив ‘s’ = 6, получим:
Общая площадь поверхности = √3 × 6 2
= √3 × 6 × 6= 62,35
Таким образом, общая площадь поверхности тетраэдра составляет 62,35 квадратных единиц.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Забронировать бесплатный пробный урок
Практические вопросы по тетраэдру
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о тетраэдре
Что такое тетраэдр?
Тетраэдр — это платоническое тело, имеющее 4 треугольные грани, 6 ребер и 4 угла. Его также называют «треугольной пирамидой», потому что основанием тетраэдра является треугольник. Тетраэдр отличается от квадратной пирамиды тем, что имеет квадратное основание.
Каковы свойства тетраэдра?
Свойства тетраэдра:
- У него 4 грани, 6 ребер и 4 угла.
- В правильном тетраэдре все четыре вершины равноудалены друг от друга.
- В отличие от других платоновых тел у него нет параллельных граней.
- У правильного тетраэдра все грани равнобедренные треугольники.
- Имеет 6 плоскостей симметрии.
Является ли тетраэдр пирамидой?
Да, тетраэдр — это тип пирамиды, потому что пирамида — это многогранник, у которого основание всегда многоугольник, а остальные боковые грани — треугольники. Поскольку тетраэдр имеет треугольное основание и все его грани — треугольники, он известен как треугольная пирамида.
В чем разница между тетраэдром и пирамидой с треугольным основанием?
Треугольная пирамида имеет основание в виде треугольника, который не обязательно может быть равносторонним треугольником, тогда как тетраэдр является уникальным случаем треугольной пирамиды, в которой все грани являются равносторонними треугольниками.
Является ли пирамида с квадратным основанием тетраэдром?
Пирамида с квадратным основанием имеет квадратное основание, а все остальные ее грани — треугольники, тогда как тетраэдр имеет треугольное основание, а все его грани — равносторонние треугольники.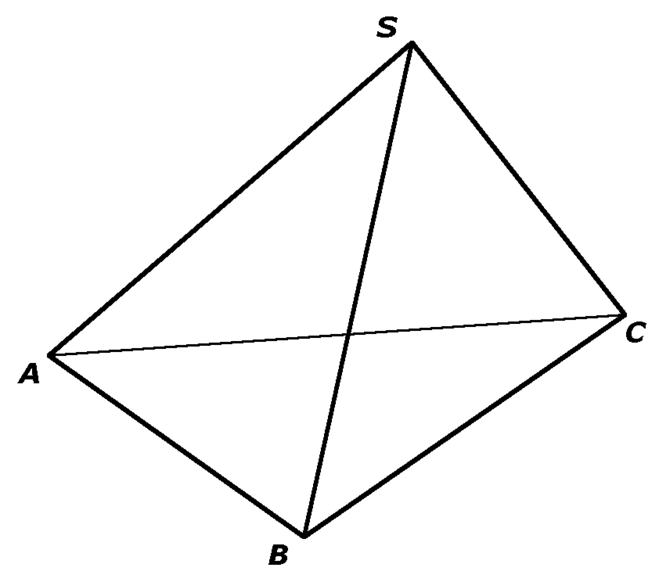
Таким образом, пирамида с квадратным основанием не является тетраэдром.
Что такое основание тетраэдра?
Тетраэдр — фигура с 4 треугольными гранями, следовательно, основание тетраэдра — тоже треугольник.
Как найти объем тетраэдра?
Объем тетраэдра можно рассчитать по формуле (1/6√2) s 3 кубических единиц, где s — длина стороны тетраэдра. Измеряется в кубических единицах.
Как сделать тетраэдр
Тема: учебники
Описание: Как нарисовать сетку тетраэдра, используя только линейку и циркуль, и сделать модель
Автор: David Caldwell 15/04/20 в 10:59
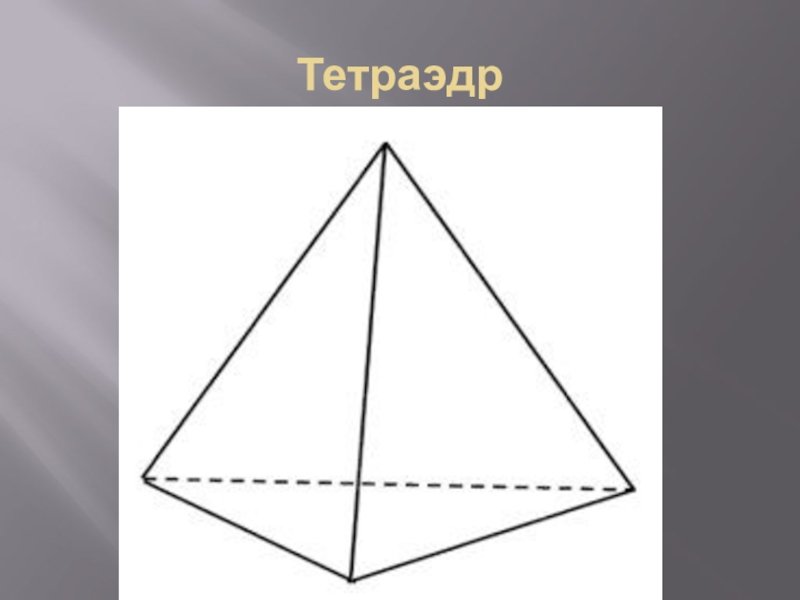
ТетраэдрТетраэдр – это четырехгранный правильный многогранник. У него четыре угла, четыре грани и шесть ребер. Его также называют треугольной пирамидой.
Что означает тетраэдр?
Тетраэдр — это греческое слово, буквально означающее «четырехсторонний». «Тетра» означает «четыре», а «эдр» — многоликость.
Четыре на латыни — это «Квадрат», как в «Четырехугольнике» или «Квадроцикле».
Тетра по-гречески означает четыре.
Платоново тело
Тетраэдр является одним из пяти Платоновых тел и представляет элемент Огня.
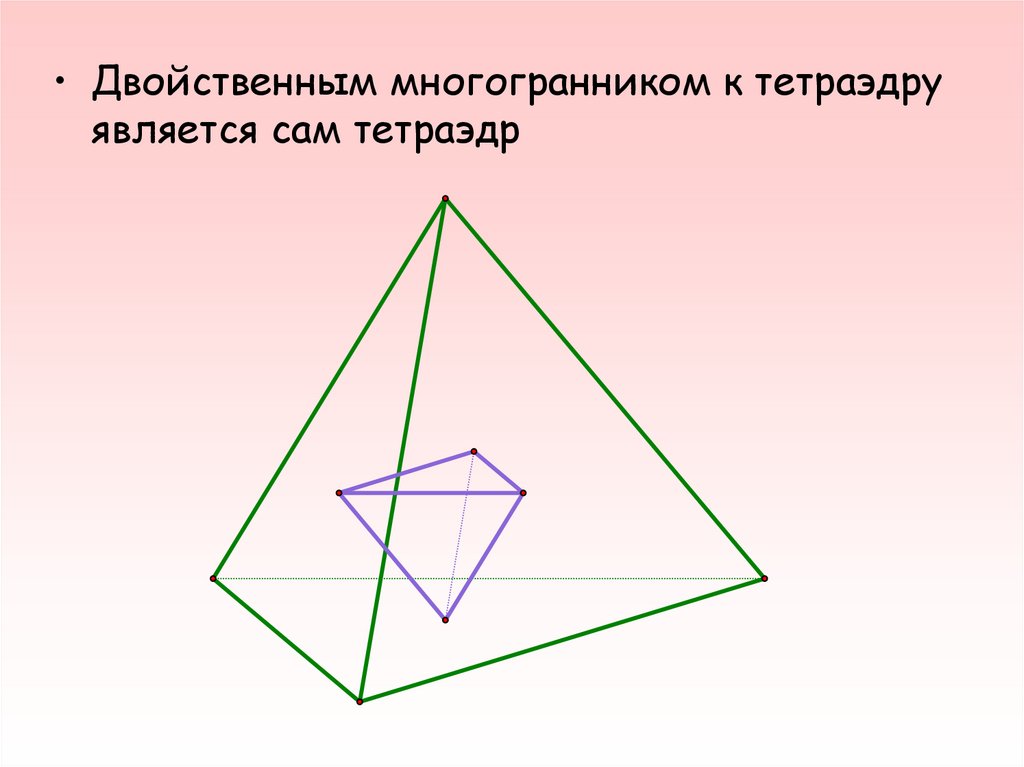
Тетраэдр уникален среди Платоновых Тел тем, что он дуален только самому себе. Если бы вы соединили точку в центре каждой грани внутри, это создало бы еще один тетраэдр.
Tetrahedron DualityВы можете посмотреть видео этого урока на YouTube.
Пошаговое руководство по созданию модели тетраэдра
Рисование сетки тетраэдра
Шаг первый
- Используйте лист светового картона.
- Проведите горизонтальную линию поперек страницы с помощью линейки или линейки.
- Поместите острие компаса на линию немного смещенным от центра и нарисуйте круг.
- Переместите точку компаса на пересечение линии и окружности и нарисуйте вторую окружность, перекрывающую первую.
Шаг второй
- Поместите компас на пересечение линии и круга слева и начертите дугу внутри левого круга.
- Поместите компас на пересечение линии и круга слева и начертите дугу внутри правого круга.
Шаг третий
- С помощью линейки нарисуйте три стороны равностороннего треугольника, который получается путем соединения точки пересечения двух окружностей вверху и пересечения левой и правой дуг, созданных на втором шаге. центральные точки двух окружностей.
Шаг четвертый
- Проведите две линии от центральных точек кругов до точки пересечения двух кругов внизу.
Шаг пятый
- Обведите сетку тонким карандашом и сотрите вспомогательные линии.
- Нарисуйте три язычка для склейки вашей модели.
Шаг шестой
- С помощью канцелярского ножа или ножниц аккуратно вырежьте сетку.
- Сделайте надрезы по внутренним линиям и выступам, чтобы их можно было согнуть, чтобы получился аккуратный прямой край.
Шаг седьмой
- Сложите выступы и внутренние складки сетки тетраэдра.
- Нанесите прозрачный клей ПВА на выступы сетки.
Шаг восьмой
- Аккуратно прижмите язычок к противоположной стороне и удерживайте, пока он не начнет прилипать. Вы можете использовать малярный скотч, пока он сохнет.
- Повторяйте, пока все выступы не будут приклеены.
- Удерживайте модель пальцами, резинкой или малярным скотчем, пока все стороны не будут склеены.
Ваша модель тетраэдра завершена
Ключевые слова: тетраэдр, тетраэдрическая сетка, модельный тетраэдр, что означает тетраэдр
04.20 
11.15 
Leave A Comment