Карточки «Подобие треугольников. Средняя линия треугольника»
Просмотр содержимого документа
«Карточки «Подобие треугольников. Средняя линия треугольника»»
1 | Точки M и N являются серединами сторон AB и |
2 | В треугольнике ABC отмечены середины M и N |
3 | Точки M и N являются серединами сторон AB и CM пересекаются в точке O, AN=24, CM=9. Найдите AO. |
4 | Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA = 1:4 , KM = 13 |
5 | Прямая, параллельная стороне AC треугольника |
1 | Точки M и N являются серединами сторон AB и |
2 | В треугольнике ABC отмечены середины M и N |
3 | Точки M и N являются серединами сторон AB и |
4 | Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA = 1:4 , KM = 13 |
5 | Прямая, параллельная стороне AC треугольника |
Домашнее задание |
1. |
2. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA= 3:7, KM =12. |
3. Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH =8, AC =32. |
Домашнее задание |
1. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM. |
2. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA= 3:7, KM =12. |
3. Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH =8, AC =32. |
Домашнее задание |
1. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM. |
2. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA= 3:7, KM =12. |
3. Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH =8, AC =32. |
Домашнее задание |
1. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. |
2. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA= 3:7, KM =12. |
3. Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH =8, AC =32. |
Домашнее задание |
1. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM. |
2. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA= 3:7, KM =12. |
3. Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH =8, AC =32. |
Задание №15 ОГЭ по математике
треугольники, четырехугольники, многоугольники и их элементы
Первичный бал: 1 Сложность (от 1 до 3): 1 Среднее время выполнения: 2 мин.
В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.
Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.
Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу.
Теория к заданию №15
Так как задания №16 основаны на теории по теме “треугольники”, рассмотрим базовые понятия, определения и формулы.
Вначале предлагаю рассмотреть углы на плоскости:
Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
- Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
- Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.

- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
Медиана: Теперь вспомним основные формулы нахождения площади треугольника: Во многих задачах встречается понятие
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
- Средняя линия параллельна третьей стороне и равна её половине.
- Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
Теперь рассмотрим частные случаи треугольников – равнобедренный, равносторонний, прямоугольный. Перейдем к рассмотрению равнобедренного треугольника:
Равнобедренный треугольник – треугольник, у которого две стороны равны.
Свойства равнобедренного треугольника:
- Углы, при основании треугольника, равны.

- Высота, проведенная из вершины, является биссектрисой и медианой.
Рассмотрим равносторонний треугольник:
Равносторонний треугольник – треугольник, у которого все стороны равны.
- Все углы равны 60°.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
Прямоугольный треугольник:
Задание 15OM21RВ треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1611o В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ВАС. Ответ дайте в градусах.
Найдите величину угла ВАС. Ответ дайте в градусах.Для решения этого задания нужно помнить два факта:
- Внутренний угол с внешним углом дают в сумме 180°
- Углы при основании равнобедренного треугольника равны.
Из первого пункта следует, что угол BCA = 180 – 123 = 57°
Из второго – что ∠BCA = ∠BAC = 57°
Ответ: 57pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1610o Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:
m = ( a • √3 )/ 2
Здесь же нам необходимо решить обратную задачу, найти a, если известно m.
Выразим a:
a = ( 2 • m ) / √3
Подставим значение:
a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22
Ответ: 22pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1609o Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Найдите гипотенузу этого треугольника.Воспользуемся теоремой Пифагора:
c² = 12² + 16² = 144 + 256 = 400
c = √400 = 20
Ответ: 20pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1608o Сторона равностороннего треугольника равна 12√3. Найдите его высоту.Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( a • √3 )/ 2
Подставим значение:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18
Ответ: 18pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1607o Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
AM = ½ AC = ½ 56 = 28
Ответ: 28pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1605o Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно, второй острый угол равен:
90 – 23 = 67°
Ответ: 67pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1604o Сторона равностороннего треугольника равна 10√3. Найдите его медиану.Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
m = ( a • √3 )/ 2
Где m – медиана в равностороннем треугольнике, а a – сторона. Таким образом, для решения данной задачи подставим значение в формулу:
m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15
Ответ: 15pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1603o В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.Если в треугольнике две стороны равны – значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:
180 – 122 = 58°
Так как углы при основании равны, значит угол BCA равен углу BAC:
∠BCA = ∠BAC
58° = ∠BCA + ∠BAC = 2 ∠BCA
∠BCA = 58 / 2 = 29°
Ответ: 29pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1602o Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64.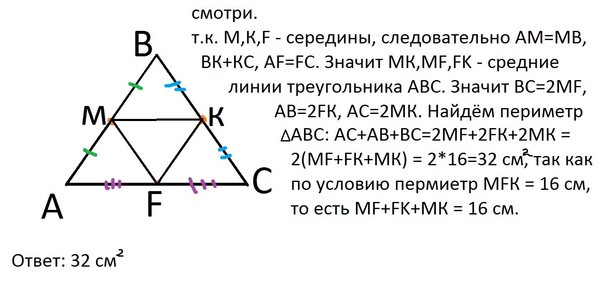 Найдите MN.
Найдите MN.Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.
Средняя линия – это линия соединяющая середины сторон и параллельная основанию.
Средняя линия равна половине основания, которому она параллельна.
Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC – третьей стороне. А это в свою очередь означает, что она равна половине AC:
MN =½ • AC = 64 / 2 = 32
Ответ: 32pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1601o В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.Для решения этого задания достаточно знать правило – сумма углов в треугольнике равна 180°.
Нам известны два угла, значит можем найти третий:
180 – 73 – 48 = 59
Ответ: 59pазбирался: Даниил Романович | обсудить разбор | оценить
👀 28.
 2k |
2k |геометрия — В треугольнике ABC пусть L, M — середины сторон BC, CA соответственно. Докажите, что AL = BM тогда и только тогда, когда AC = BC
. спросил
Изменено 2 года, 8 месяцев назад
Просмотрено 120 раз
$\begingroup$
Мне удалось доказать, что если AC = BC, то AL = BM, заметив, что для треугольников ABL и ABM, поскольку AB является общим, а AM = BL и $\angle$ BAM = $\angle$ ABL, поскольку треугольник ABC равнобедренный, по аксиоме конгруэнтности SAS треугольники ABL и ABM конгруэнтны, поэтому AL = BM. У меня проблемы с доказательством обратного утверждения. Будем признательны за любую помощь
- геометрия
$\endgroup$
1
$\begingroup$
Пусть $G$ пересечение $AL$ и $BM$. Точка $G$ является центром тяжести треугольника, поэтому $AG=2GL$ и $BG=2GM$. Теперь, используя $AL=BM$, действуйте следующим образом:
Точка $G$ является центром тяжести треугольника, поэтому $AG=2GL$ и $BG=2GM$. Теперь, используя $AL=BM$, действуйте следующим образом:
- Докажите, что $\triangle AGM \cong \triangle BGL$;
- Тогда этот $\треугольник BGC\cong\triangle AGC$.
Из второго сравнения следует, что $AC=BC$.
$\endgroup$
1 92) =0 ,\\ 3(б+а)(б-а)&=0 \end{align}
и $a=b$ следует.
$\endgroup$
$\begingroup$
$$\overrightarrow{CL}=\frac{1}{2}
\overrightarrow{CB},\quad
\overrightarrow{CM}=\frac{1}{2}
\overrightarrow{CA},$$
$$\overrightarrow{BM}=\overrightarrow{CM}-\overrightarrow{CB}=
\frac{1}{2}\overrightarrow{CA}-\overrightarrow{CB},\quad
\overrightarrow{AL}=\overrightarrow{CL}-\overrightarrow{CA}=
\frac{1}{2}\overrightarrow{CB}-\overrightarrow{CA},$$
$$|\overrightarrow{AL}|=|\overrightarrow{BM}|\Leftrightarrow
|\overrightarrow{AL}|^2=|\overrightarrow{BM}|^2\Leftrightarrow
\overrightarrow{AL}^2=\overrightarrow{BM}^2\Leftrightarrow
$$
$$
\левый(
\frac{1}{2}\overrightarrow{CB}-\overrightarrow{CA}
\справа)^2=
\левый(
\frac{1}{2}\overrightarrow{CA}-\overrightarrow{CB}
\право)^2\стрелка влево\тег{1}
$$
$$
\frac{1}{4}\overrightarrow{CB}^2
-\overrightarrow{CB}\cdot\overrightarrow{CA}
+\overrightarrow{CA}^2=
\frac{1}{4}\overrightarrow{CA}^2
-\overrightarrow{CA}\cdot\overrightarrow{CB}
+\overrightarrow{CB}^2\Leftrightarrow\тег{2}
$$
$$
\frac{3}{4}\overrightarrow{CA}^2=
\frac{3}{4}\overrightarrow{CB}^2\Leftrightarrow\tag{3}$$ $$
\overrightarrow{CA}^2=\overrightarrow{CB}^2\Leftrightarrow
|\overrightarrow{CA}|^2=|\overrightarrow{CB}|^2\Leftrightarrow
|\overrightarrow{CA}|=|\overrightarrow{CB}|,\hbox{ QED. 2$$
и мы закончили. 92)=
2$$
и мы закончили. 92)=
ПУБЛИКАЦИЯ DIPTI (AP EAMET)-СИСТЕМА КООРДИНАЦИИ (3D)-УПРАЖНЕНИЕ 1
20 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Pro и dekho sari видео бина kisi ad ki ke!
Обновлено: 27-06-2022
Текст Решение
Ответ
Правильный ответ C 9(2)) равно
показывают, что определитель
∣∣
∣
∣∣a2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2∣∣
∣
∣∣
всегда неотрицательно.
69047050
В △ABC середины сторон AB,BC и CA равны соответственно (l,0,0),(0,m,0) и (0,0,n) . Тогда AB2+BC2+CA2l2+m2+n2 равно
308529676
Текст Решение
В треугольнике ABC , если середины сторон AB, BC, CA равны (3,0,0),(0, 4,0),(0,0,5) соответственно, то AB2+BC2+CA2=
376682046
Текст Решение
यदि a,b,c ∈ R तब सारणिक △∣∣ ∣ ∣∣a2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2∣∣ ∣ ∣ अऋणांत्मक होगा पुनः सारणिक के शून्य होने के स स000 बताये
618430505
Покажите, что определитель
∣
∣
∣∣a2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2∣∣
∣
∣∣
всегда неотрицательно.


 Площадь треугольника
Площадь треугольника Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
 Найдите AM.
Найдите AM.


Leave A Comment