Задание 3 ЕГЭ по математике (профиль) часть 9
Тренажер задания 3 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 3 — задачи на поиск элементов в треугольнике, параллелограмме, ромбе, трапеции и прямоугольнике. Это задание на планиметрию. Номер заданий соответствует номеру заданий в базе mathege.ru.
27792. В треугольнике ABC Найдите высоту CH.
27793. В равностороннем треугольнике ABC высота CH равна Найдите AB.
27826. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
27827. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
27809. Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма.
27824. Две стороны параллелограмма относятся как 3 : 4, а периметр его равен 70. Найдите большую сторону параллелограмма.
27829. Диагонали ромба относятся как 3 : 4. Периметр ромба равен 200. Найдите высоту ромба.
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
27601. Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.
27603. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1 : 2.
27604. Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
27606. Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.
27843. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
27835. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
27845. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
27821. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Понравилось это:
Нравится Загрузка…
Дайте определение параллелограмма и выполнить рисунок. Свойство диагоналей параллелограмма
1. Определение параллелограмма.
Если пару параллельных прямых пересечём другой парой параллельных прямых, то получим четырёхугольник, у которого противоположные стороны попарно параллельны.
В четырёхугольниках ABDС и ЕFNМ (рис. 224) ВD || АС и AB || СD;
ЕF || МN и ЕМ || FN.
Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
2. Свойства параллелограмма.
Теорема . Диагональ параллелограмма делит его на два равных треугольника.
Пусть имеется параллелограмм ABDС (рис. 225), в котором AB || СD и АС || ВD.
Требуется доказать, что диагональ делит его на два равных треугольника.
Проведём в параллелограмме ABDС диагональ СВ.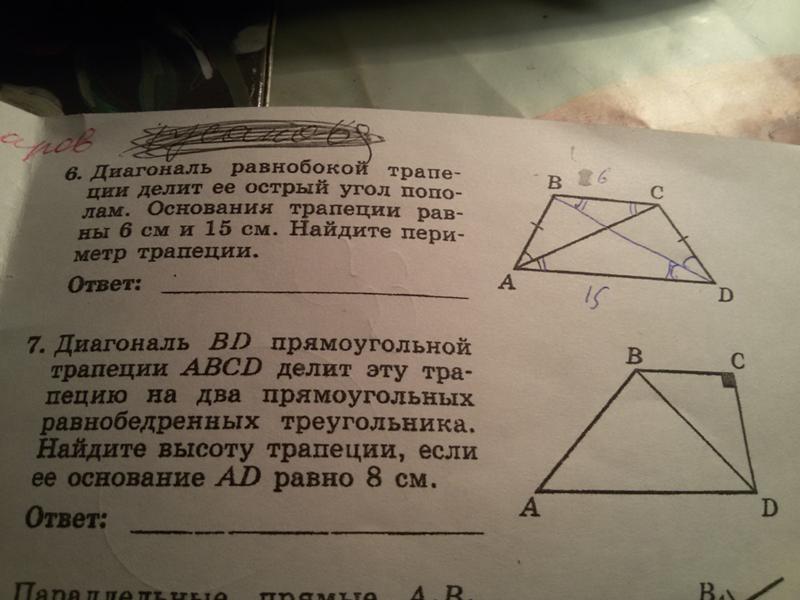 Докажем, что \(\Delta\)CAB = \(\Delta\)СDВ.
Докажем, что \(\Delta\)CAB = \(\Delta\)СDВ.
Сторона СВ общая для этих треугольников; ∠ABC = ∠BCD, как внутренние накрест лежащие углы при параллельных AB и СD и секущей СВ; ∠ACB = ∠СВD, тоже как внутренние накрест лежащие углы при параллельных АС и ВD и секущей CB.
Отсюда \(\Delta\)CAB = \(\Delta\)СDВ.
Таким же путём можно доказать, что диагональ AD разделит параллелограмм на два равных треугольника АСD и ABD.
Следствия:
1 . Противоположные углы параллелограмма равны между собой.
∠А = ∠D, это следует из равенства треугольников CAB и СDВ.
Аналогично и ∠С = ∠В.
2. Противоположные стороны параллелограмма равны между собой.
AB = СD и АС = ВD, так как это стороны равных треугольников и лежат против равных углов.
Теорема 2.
Пусть BC и AD — диагонали параллелограмма AВDС (рис. 226). Докажем, что АО = OD и СО = OB.
Для этого сравним какую-нибудь пару противоположно расположенных треугольников, например \(\Delta\)AOB и \(\Delta\)СОD.
В этих треугольниках AB = СD, как противоположные стороны параллелограмма;
∠1 = ∠2, как углы внутренние накрест лежащие при параллельных AB и СD и секущей AD;
∠3 = ∠4 по той же причине, так как AB || СD и СВ — их секущая.
Отсюда следует, что \(\Delta\)AOB = \(\Delta\)СОD. А в равных треугольниках против равных углов лежат равные стороны. Следовательно, АО = OD и СО = OB.
Теорема 3. Сумма углов, прилежащих к одной стороне параллелограмма, равна 180° .
В параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC.
Треугольники равны, так как ∠1 = ∠4, ∠2 = ∠3 (накрест лежащие углы при параллельных прямых), а сторона АС общая.
Из равенства \(\Delta\)ABC = \(\Delta\)ADC следует, что AB = CD, BC = AD, ∠B = ∠D.
Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых.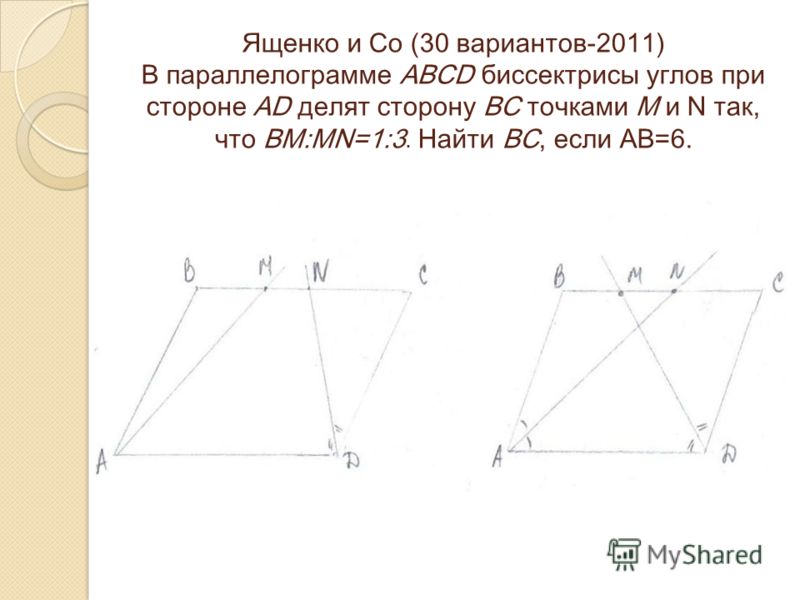
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Муниципальное бюджетное общеобразовательное учреждение
Савинская средняя общеобразовательная школа
Исследовательская работа
Параллелограмм и его новые свойства
Выполнила: ученица 8Б класса
МБОУ Савинская СОШ
Кузнецова Светлана,14 лет
Руководитель: учитель математики
Тульчевская Н.А.
п. Савино
Ивановская область, Россия
2016г.
I . Введение __________________________________________________стр 3
II . Из истории параллелограмма ___________________________________стр 4
III Дополнительные свойства параллелограмма ______________________стр 4
IV
. Доказательство свойств _____________________________________ стр 5
Доказательство свойств _____________________________________ стр 5
V . Решение задач с использованием дополнительных свойств __________стр 8
VI . Применение свойств параллелограмма в жизни ___________________стр 11
VII . Заключение _________________________________________________стр 12
VIII . Литература _________________________________________________стр 13
Введение
«Среди равных умов
при одинаковости прочих условий
превосходит тот, кто знает геометрию»
(Блез Паскаль).
Во время изучения темы «Параллелограмм» на уроках геометрии мы рассмотрели два свойства параллелограмма и три признака, но когда мы начали решать задачи, то оказалось, что этого недостаточно.
У меня возник вопрос, а есть ли у параллелограмма еще свойства, и как они помогут при решении задач.
И я решила изучить дополнительные свойства параллелограмма и показать, как их можно применить для решения задач.
Предмет исследования : параллелограмм
Объект исследования : свойства параллелограмма
Цель работы:
формулировка и доказательство дополнительных свойств параллелограмма, которые не изучаются в школе;
применение этих свойств для решения задач.
Задачи:
Найти дополнительную литературу по исследуемому вопросу;
Изучить дополнительные свойства параллелограмма и доказать их;
Показать применение этих свойств для решения задач;
Рассмотреть применение свойств параллелограмма в жизни.
Методы исследования:
Работа с учебной и научно – популярной литературой, ресурсами сети Интернет;
Изучение теоретического материала;
Выделение круга задач, которые можно решать с использованием дополнительных свойств параллелограмма;
Наблюдение, сравнение, анализ, аналогия.
Продолжительность исследования : 3 месяца: январь-март 2016г
Из истории параллелограмма
В учебнике геометрии мы читаем следующее определение параллелограмма: параллелограмм – это такой четырехугольник, у которого противоположные стороны попарно параллельны
Слово «параллелограмм» переводится как «параллельные линии» (от греческих слов Parallelos — параллельный и gramme — линия), этот термин был введен Евклидом. В своей книге «Начала» Евклид доказал следующие свойства параллелограмма: противоположные стороны и углы параллелограмма равны, а диагональ делит его пополам.
В своей книге «Начала» Евклид доказал следующие свойства параллелограмма: противоположные стороны и углы параллелограмма равны, а диагональ делит его пополам.
III Дополнительные свойства параллелограмма
В учебнике по геометрии даны только 2 свойства параллелограмма:
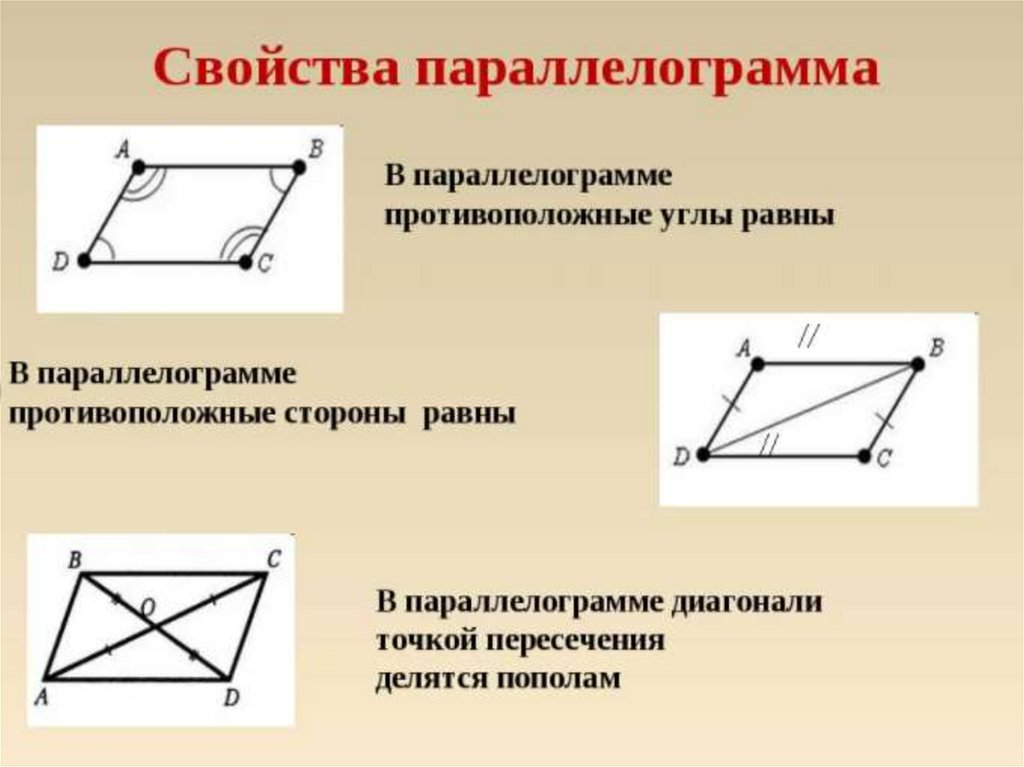
Противоположные углы и стороны равны
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
В различных источниках по геометрии можно встретить следующие дополнительные свойства:
Сумма соседних углов параллелограмма равна 180 0
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник;
Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых;
Биссектрисы соседних углов параллелограмма пересекаются под прямым углом;
Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник;
Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.
Если в параллелограмме соединить противоположные вершины с серединами противоположных сторон, то получится еще один параллелограмм.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.
Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.
IV Доказательство свойств параллелограмма
Сумма соседних углов параллелограмма равна 180 0
Дано :
ABCD – параллелограмм
Доказать:
A
+
B
=
Доказательство:
А и
B
–внутренние односторонние углы при параллельных прямых ВС АD
и секущей АВ, значит,
A
+
B
=
2
Дано: АBCD — параллелограмм,
АК -биссектриса
А.
Доказать: АВК – равнобедренный
Доказательство:
1)
1=
3 (накрест лежащие при ВСAD
и секущей AK
),
2)
2=
3 т.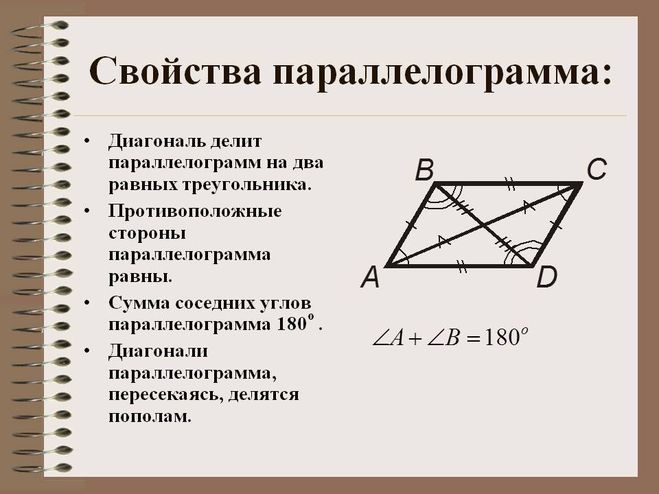 к. АК – биссектриса,
к. АК – биссектриса,
значит 1=
2.
3) АВК – равнобедренный т. к. 2 угла треугольника равны
. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник
3
Дано: АВСD – параллелограмм,
АК – биссектриса A,
СР — биссектриса C.
Доказать: АК ║ СР
Доказательство:
1) 1=2 т. к. АК-биссектриса
2) 4=5 т.к. СР – биссектриса
3) 3=1 (накрест лежащие углы при
ВС ║ АD и АК-секущей),
4) A =C (по свойству параллелограмма), значит2=3=4=5.
4) Из п. 3 и 4 следует, что 1=4, а эти углы соответственные при прямых АК и СР и секущей ВС,
значит, АК ║ СР (по признаку параллельности прямых)
. Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых
Биссектрисы соседних углов параллелограмма пересекаются под прямым углом
Дано: АВСD — параллелограмм,
АК-биссектриса A,
DР-биссектриса D
Доказать: DР АК.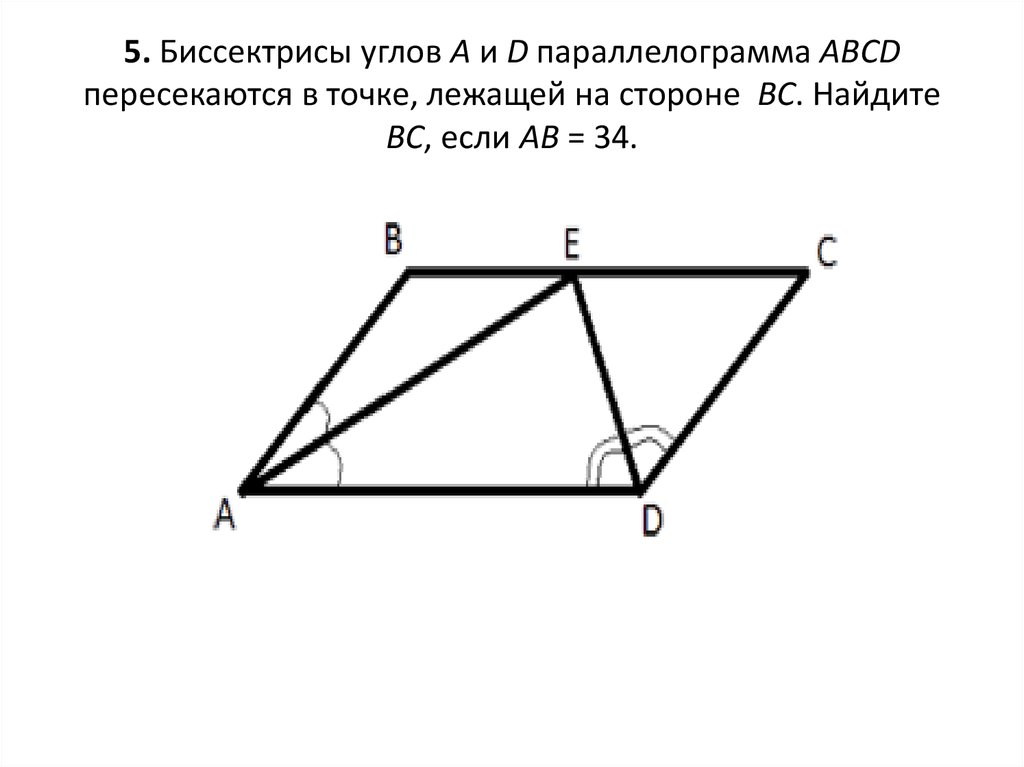
Доказательство:
1) 1=2, т.к. АК — биссектриса
Пусть, 1=2=x, тогда А=2x,
2) 3=4, т.к. D Р – биссектриса
Пусть, 3=4= у, тогда D =2y
3) A +D =180 0 , т.к. сумма соседних углов параллелограмма равна 180
2) Рассмотрим A ОD
1+3=90 0 , тогда
5. Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник
Дано: АВСD — параллелограмм, АК-биссектриса A,
DР-биссектриса D,
CM -биссектриса C ,
BF -биссектриса B .
Доказать : KRNS -прямоугольник
Доказательство:
Исходя из предыдущего свойства 8=7=6=5=90 0 ,
значит KRNS -прямоугольник.
Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.
Дано: ABCD-параллелограмм, АС-диагональ.
ВК АС, DPAC
Доказать: BК=DР
Доказательство: 1)DCР=КAB, как внутренние накрест лежащие при АВ ║ СD и секущей АС.
2) AКB=CDР (по стороне и двум прилежащим к ней углам АВ=СD CD Р=AB К).
А в равных треугольниках соответственные стороны равны, значит DР=BК.
Если в параллелограмме соединить противоположные вершины с серединами противоположных сторон, то получится еще один параллелограмм.
Дано: ABCD-параллелограмм.
Доказать: ВКDР – параллелограмм.
Доказательство:
1) BР=КD (AD=BC, точки К и Р
делят эти стороны пополам)
2) ВР ║ КD (лежат на АD BC)
Если в четырехугольнике противоположные стороны равны и параллельны, значит, этот четырехугольник -параллелограмм.
Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.
Дано: ABCD – параллелограмм. BD и AC — диагонали.
Доказать: АС 2 +ВD 2 =2(AB 2 + AD 2 )
Доказательство: 1)АСК: AC ²=
+
2)B Р D : BD 2 = B Р 2 + Р D 2 (по теореме Пифагора)
3) AC ²+ BD ²=СК²+ A К²+ B Р²+Р D ²
4) СК = ВР = Н (высота)
5) АС 2 +В D 2 = H 2 + A К 2 + H 2 +Р D 2
6) Пусть D К= A Р=х , тогда C К D : H 2 = CD 2 – х 2 по теореме Пифагора)
7) АС²+В D ² = С D 2 — х²+ АК 1 ²+ CD 2 -х 2 +Р D 2 ,
АС²+В D ²=2С D 2 -2х 2 + A К 2 +Р D 2
8) A К =AD+ х , Р D=AD- х ,
АС²+В D ² =2 CD 2 -2х 2 +(AD +х) 2 +(AD -х) 2 ,
АС ²+ В D²=2 С D²-2 х ² +AD 2 +2AD х + х 2 +AD 2 -2AD х + х 2 ,
АС ²+ В D²=2CD 2 +2AD 2 =2(CD 2 +AD 2 ).
V . Решение задач с использованием этих свойств
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5 . Найдите его большую сторону.
Дано: ABCD – параллелограмм,
АК – биссектриса
А,
D
К – биссектриса
D
, АВ=5
Найти : ВС
ешение
Решение
Т.к. АК — биссектриса
А, то АВК – равнобедренный.
Т.к. D
К – биссектриса
D
, то DCK
— равнобедренный
DC =C К= 5
Тогда, ВС=ВК+СК=5+5 = 10
Ответ: 10
2. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
1 случай
Дано:
А,
ВК=14 см, КС=7 см
Найти: Р параллелограмма
Решение
ВС=ВК+КС=14+7=21 (см)
Т. к. АК – биссектриса
к. АК – биссектриса
А, то АВК – равнобедренный.
АВ=ВК= 14 см
Тогда Р=2 (14+21) =70 (см)
случай
Дано: ABCD – параллелограмм,
D
К – биссектриса
D
,
ВК=14 см, КС=7 см
Найти : Р параллелограмма
Решение
ВС=ВК+КС=14+7=21 (см)
Т.к. D
К – биссектриса
D
, то DCK
— равнобедренный
DC =C К= 7
Тогда, Р= 2 (21+7) = 56 (см)
Ответ: 70см или 56 см
3.Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.
1 случай: биссектрисы пересекаются вне параллелограмма
Дано: ABCD
– параллелограмм, АК – биссектриса
А,
D
К – биссектриса
D
, АВ=3 см, ВС=10 см
Найти : ВМ, МN , NC
Решение
Т.к. АМ — биссектриса
А, то АВМ – равнобедренный.
Т.к. DN
– биссектриса
D
, то DCN
— равнобедренный
DC =CN = 3
Тогда, МN = 10 – (BM +NC ) = 10 – (3+3)=4 см
2 случай: биссектрисы пересекаются внутри параллелограмма
Т.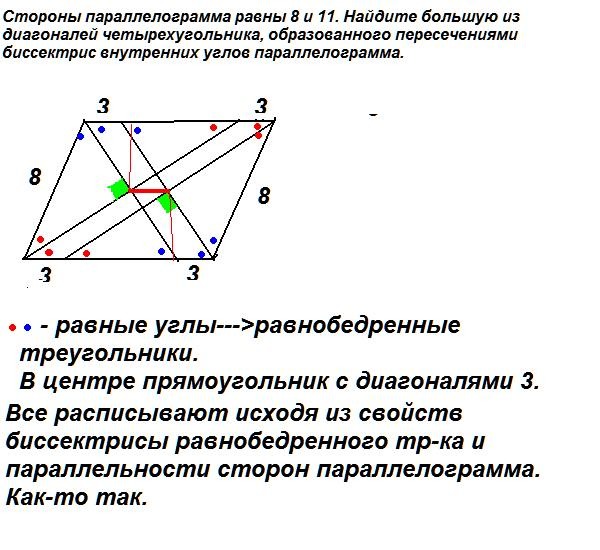 к. АN
— биссектриса
к. АN
— биссектриса
А, то АВN
– равнобедренный.
АВ=В N = 3 D
А раздвижную решетку – отодвигать на необходимое расстояние в дверном проеме
Параллелограммный механизм — четырёхзвенный механизм, звенья которого составляют параллелограмм. Применяется для реализации поступательного движения шарнирными механизмами.
Параллелограмм с неподвижным звеном — одно звено неподвижно, противоположное совершает качательное движение, оставаясь параллельным неподвижному. Два параллелограмма, соединённых друг за другом, дают конечному звену две степени свободы, оставляя его параллельным неподвижному.
Примеры: стеклоочистители автобусов, погрузчики, штативы, подвесы, автомобильные подвески.
Параллелограмм с неподвижным шарниром — используется свойство параллелограмма сохранять постоянное соотношение расстояний между тремя точками. Пример: чертёжный пантограф — прибор для масштабирования чертежей.
Ромб — все звенья одинаковой длины, приближение (стягивание) пары противоположных шарниров приводит к раздвиганию двух других шарниров.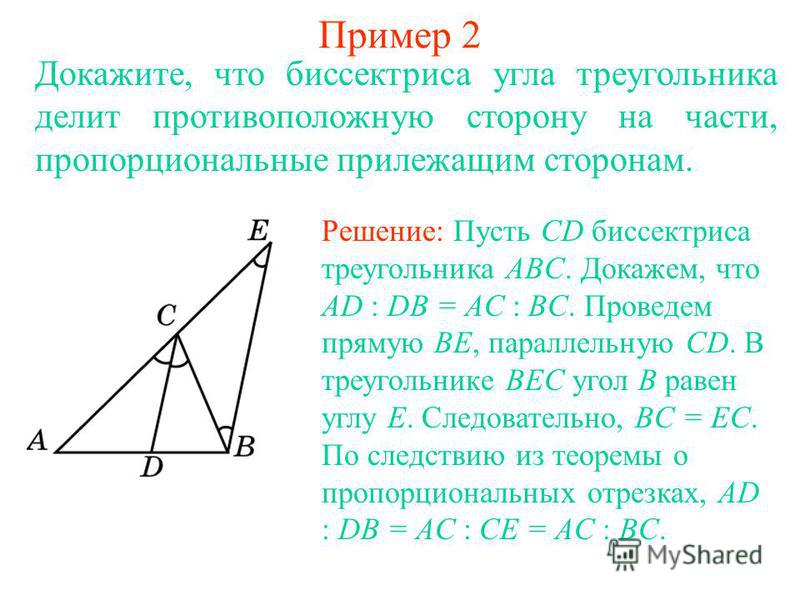 Все звенья работают на сжатие.
Все звенья работают на сжатие.
Примеры — автомобильный ромбовидный домкрат, трамвайный пантограф.
Ножничный или X-образный механизм , также известный как Нюрнбергские ножницы — вариант ромба — два звена, соединённые посередине шарниром. Достоинства механизма — компактность и простота, недостаток — наличие двух пар скольжения. Два (и более) таких механизма, соединённые последовательно, образуют в середине ромб(ы). Применяется в подъёмниках, детских игрушках.
VII Заключение
Кто с детских лет занимается математикой,
тот развивает внимание, тренирует свой мозг,
свою волю, воспитывает в себе настойчивость
и упорство в достижении цели
А. Маркушевич
В ходе работы я доказала дополнительные свойства параллелограмма.
Я убедилась, что применяя эти свойства, можно решать задачи быстрее.
Я показала, как применяются эти свойства на примерах решения конкретных задач.
Я узнала много нового о параллелограмме, чего нет в нашем учебнике геометрии
Я убедилась в том, что знания геометрии очень важны в жизни на примерах применения свойств параллелограмма.
Цель моей исследовательской работы выполнена.
О том, насколько важны математические знания, говорит тот факт, что была учреждена премия тому, кто издаст книгу о человеке, который всю жизнь прожил без помощи математики. Эту премию до сих пор не получил ни один человек.
VIII Литература
ПогореловА.В. Геометрия 7-9: учебник для общеобразоват. учреждений-М.: Просвещение, 2014г
Л.С.Атанасян и др. Геометрия. Доп. Главы к учебнику 8 кл.: учеб. пособие для учащихся школ и классов с углубл. изуч.математики. – М.: Вита-пресс, 2003
Ресурсы сети Интернет
материалы Википедии
Доказательство
Первым делом проведем диагональ AC . Получаются два треугольника: ABC и ADC .
Так как ABCD — параллелограмм, то справедливо следующее:
AD || BC \Rightarrow \angle 1 = \angle 2
как лежащие накрест.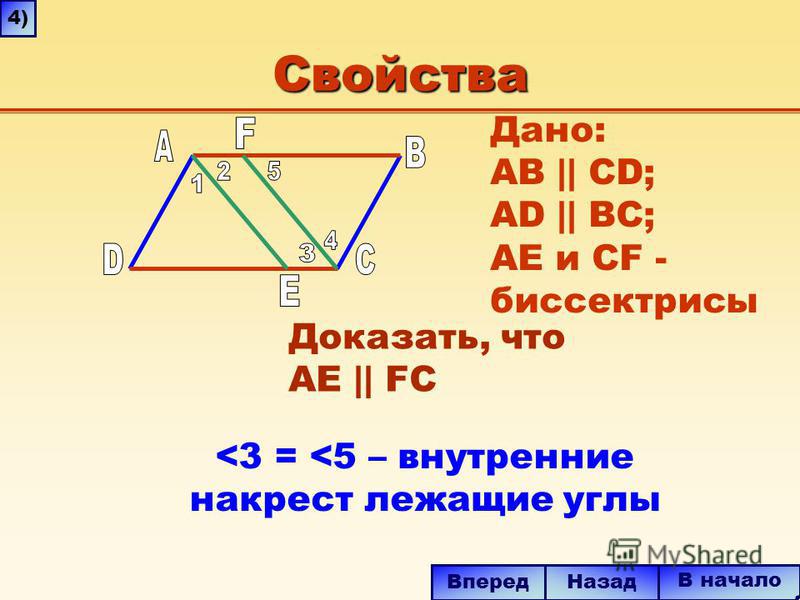
AB || CD \Rightarrow \angle3 = \angle 4 как лежащие накрест.
Следовательно, \triangle ABC = \triangle ADC (по второму признаку: и AC — общая).
И, значит, \triangle ABC = \triangle ADC , то AB = CD и AD = BC .
Доказано!
2. Противоположные углы тождественны.
Доказательство
Согласно доказательству свойства 1 мы знаем, что \angle 1 = \angle 2, \angle 3 = \angle 4 . Таким образом сумма противоположных углов равна: \angle 1 + \angle 3 = \angle 2 + \angle 4 . Учитывая, что \triangle ABC = \triangle ADC получаем \angle A = \angle C , \angle B = \angle D .
Доказано!
3. Диагонали разделены пополам точкой пересечения.
Доказательство
Проведем еще одну диагональ.
По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD . Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что \triangle AOB = \triangle COD
по второму признаку равенства треугольников (два угла и сторона между ними).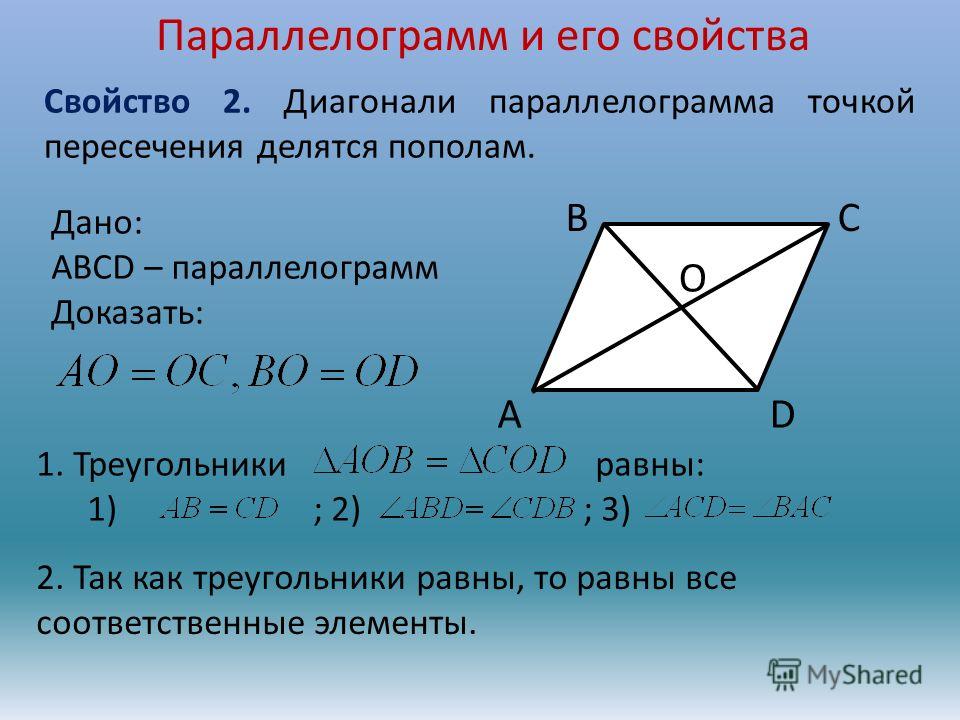 То есть, BO = OD
(напротив углов \angle 2
и \angle 1
) и AO = OC
(напротив углов \angle 3
и \angle 4
соответственно).
То есть, BO = OD
(напротив углов \angle 2
и \angle 1
) и AO = OC
(напротив углов \angle 3
и \angle 4
соответственно).
Доказано!
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?» . То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.
AB = CD ; AB || CD \Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим подробнее. Почему AD || BC ?
\triangle ABC = \triangle ADC по свойству 1 : AB = CD , AC — общая и \angle 1 = \angle 2 как накрест лежащие при параллельных AB и CD и секущей AC .
Но если \triangle ABC = \triangle ADC
, то \angle 3 = \angle 4
(лежат напротив AB
и CD
соответственно). {\circ}
говорит и о том, что AD || BC
.
{\circ}
говорит и о том, что AD || BC
.
При этом \alpha и \beta — внутренние односторонние при секущей AD . И это значит AB || CD .
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.
AO = OC ; BO = OD \Rightarrow параллелограмм.
Доказательство
BO = OD ; AO = OC , \angle 1 = \angle 2 как вертикальные \Rightarrow \triangle AOB = \triangle COD , \Rightarrow \angle 3 = \angle 4 , и \Rightarrow AB || CD .
Аналогично BO = OD ; AO = OC , \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 , и \Rightarrow AD || BC .
Четвертый признак верен.
Биссектриса угла — определение, свойства, конструкция, факт
Что такое биссектриса угла?
Биссектриса угла – это луч или прямая, которая делит угол на две равные части . Слово «биссектриса» подразумевает деление на две равные части.
На следующем изображении $\angle\; \text{ABC}$ делится на две равные части биссектрисой угла BD.
Можете ли вы привести примеры биссектрис угла в реальной жизни? Ну, для начала взгляните на большой кусок пиццы, разрезанный на равные кусочки. Здесь нож выступал в роли биссектрисы угла. Вы также можете найти биссектрису угла в часах, когда угол составляет минутная стрелка, а часовая стрелка делится пополам секундной стрелкой! Продолжайте искать больше таких примеров биссектрисы угла вокруг вас! 9{\circ}$ каждый. Она делит угол на два равных угла.
Родственные игры
Биссектриса треугольника
Каждый треугольник имеет три вершины и три угла. Значит, есть и биссектрисы с тремя углами — по одной на каждую вершину. Точка пересечения этих трех биссектрис угла называется «входящим центром», который равноудален от всех вершин.
В $\Delta\;\text{ABC}$ отрезки AF, BD и CE являются биссектрисами углов, а G является центром вписанной окружности.
Похожие рабочие листы
Свойства биссектрисы угла
- Биссектриса делит угол на два равных угла.

- Любая заданная точка, лежащая на биссектрисе угла, находится на равном расстоянии от плеч или сторон угла.
- Биссектриса угла треугольника делит противолежащую сторону в отношении, равном отношению двух других сторон
Как построить биссектрису угла?
Для построения биссектрисы угла требуются линейка и циркуль . Давайте разберемся, как построить биссектрису угла для угла.
Разделим данный $\angle\;\text{XYZ}$.
Этапы построения биссектрисы угла
- С помощью циркуля поместите указатель в точку Y и начертите дугу, пересекающую два плеча угла, XY и YZ, в двух разных точках.
- Затем поместите указатель компаса там, где дуга пересекает линию XY, и нарисуйте другую дугу внутри угла.
- Не изменяя радиус компаса, поместите указатель в точку пересечения дуги с плечом YZ и нарисуйте аналогичную дугу внутри угла так, чтобы она пересекала дугу, нарисованную на предыдущем шаге.

- Теперь используйте линейку, чтобы провести линию от точки Y до точки, где две дуги пересекаются внутри угла.
Вот как построить биссектрису угла. Линия, проведенная на шаге 5, является биссектрисой угла $\angle\;\text{XYZ}$.
Теорема о биссектрисе угла
Теорема о биссектрисе угла утверждает, что биссектриса угла треугольника делит противоположную сторону на два отрезка, которые пропорциональны двум другим сторонам треугольника.
Таким образом, когда биссектриса угла, проведенная из одной вершины треугольника, падает на одну сторону такого треугольника, она делит эту сторону в том же отношении, что и отношение двух других сторон. Мы можем искать «доказательство теоремы о биссектрисе угла», построив такую биссектрису в треугольнике.
Следующее изображение демонстрирует теорему для справки.
Заключение
Существует множество практических примеров биссектрисы угла, включая архитектурные инсталляции и многое другое. Для построения биссектрисы угла в реальной жизни понадобится линейка и циркуль. Мы также можем доказать теорему о биссектрисе угла, построив ее в реальной жизни.
Для построения биссектрисы угла в реальной жизни понадобится линейка и циркуль. Мы также можем доказать теорему о биссектрисе угла, построив ее в реальной жизни.
Увлекательные практические задачи и решенные примеры помогут вам понять все о биссектрисах углов в мельчайших деталях. В SplashLearn обучение становится проще благодаря подробному объяснению всех концепций. Присоединяйтесь к нам в путешествии по миру математики. 9{\circ}$.
2. Для изображения, приведенного ниже, найдите x, если луч OM является биссектрисой угла.
Решение: Значение x равно 8.
Поскольку OM — биссектриса угла, мы знаем, что $\text{m}\;\angle\text{AOM} = \text{m}\angle\ ;\text{МОБ}$.
$4x + 5 = 37$
$4x = 32$
$x = \frac{32}{4}$
$x = 8$
3. Для изображения, приведенного ниже, m $\угол$ AOC $=$ м $\угол$ BOC. Что вы можете сказать о луче ОС?
Решение: На изображении m$\angle$AOC $=$ m$\angle$BOC. {\ circ} $ 9{\circ}$.
{\ circ} $ 9{\circ}$.
4
Красная линия представляет собой биссектрису угла ____.
Прямой угол
Острый угол
Прямой угол
Рефлекторный угол
Правильный ответ: Прямой угол
Луч делит прямой угол пополам на два прямых угла.
5
Определите значение x.
18
17
14
9
Правильный ответ: 9
Согласно теореме о биссектрисе угла, биссектриса треугольника делит противоположную сторону на два отрезка, которые пропорциональны двум другим сторонам треугольника. треугольник.
Таким образом, $\frac{\text{PS}{\text{RS}} = \frac{\text{PQ}}{\text{RQ}}$
$\Rightarrow \frac{6}{x} = \frac{12}{18}$
\Rightarrow x = \frac{18 \times 6}{12}$
$\Rightarrow x = 9$
Часто задаваемые вопросы о биссектрисе угла
Сколько биссектрис может быть угол есть?
У данного угла может быть только одна биссектриса угла.
Сколько биссектрис может быть у треугольника?
Треугольник может иметь только три биссектрисы угла, так как в треугольнике только три угла.
Что такое инцентр?
Инцентр — это точка в треугольнике, где все три биссектрисы треугольника пересекаются друг с другом.
Какое значение имеет биссектриса угла?
Когда дело доходит до определения соответствующих частей подобных треугольников, биссектрисы углов могут оказаться очень полезными. Они помогают определить доказательства, связанные с треугольниками.
Видео-урок: Геометрические построения: Биссектрисы угла
Стенограмма видео
Геометрические конструкции: угол Биссектрисы
В этом уроке мы узнаем о биссектриса угла и как построить биссектрису любого заданного угла с помощью циркуля и линейки.
Мы можем начать с описания того, что мы
значит биссектриса угла. Биссектриса угла это прямая
через вершину угла, делящего его на два равных угла. Можно сказать, что угол
разделен пополам, так как он разделен пополам. Мы можем распространить эту идею на угол
трисекторы, которые представляют собой линии, делящие угол на трети, и мы можем расширить это
идея еще дальше. Однако мы остановимся только на
биссектрисы в этом видео.
Биссектриса угла это прямая
через вершину угла, делящего его на два равных угла. Можно сказать, что угол
разделен пополам, так как он разделен пополам. Мы можем распространить эту идею на угол
трисекторы, которые представляют собой линии, делящие угол на трети, и мы можем расширить это
идея еще дальше. Однако мы остановимся только на
биссектрисы в этом видео.
Мы можем видеть много примеров углов
биссектрисы, рассматривая угловые меры. Например, допустим, что мы
угол измерения 60 градусов, как показано. Мы знаем, что биссектриса угла
линия, проходящая через вершину угла, делящего угол измерения на 60 градусов
на два равных угла. Так как половина 60 это 30, мы знаем
что мера двух углов после разделения пополам должна быть 30 градусов. Это дает нам следующую строку
то есть биссектриса угла. Стоит отметить, что мы обычно
только нарисуйте линию как луч, начинающийся в вершине на той же стороне, что и
угол. Однако мы можем нарисовать это как линию
также.
Однако мы можем нарисовать это как линию
также.
Здесь стоит повторить Дело в том, что мы не хотим полагаться на меру угла, чтобы найти биссектрису угла. Например, с помощью транспортира разделить угол пополам будет иметь ошибки измерения. Вместо этого мы хотим найти метод точно разделить пополам любой заданный угол. Для этого сначала нужно вспомнить свойство воздушных змеев, которые представляют собой четырехугольники с парами конгруэнтных смежных стороны, как показано. Если построить диагональ между парами конгруэнтных сторон, в данном случае это линия 𝐴𝐶, то образуем два треугольника: 𝐴𝐵𝐶 и 𝐴𝐷𝐶. Тогда мы можем отметить, что эти два треугольники имеют одинаковые длины сторон. Значит, они конгруэнтны по Критерий согласованности стороны-стороны-стороны.
Используя это соответствие, мы можем
сделать вывод, что соответствующие углы также равны.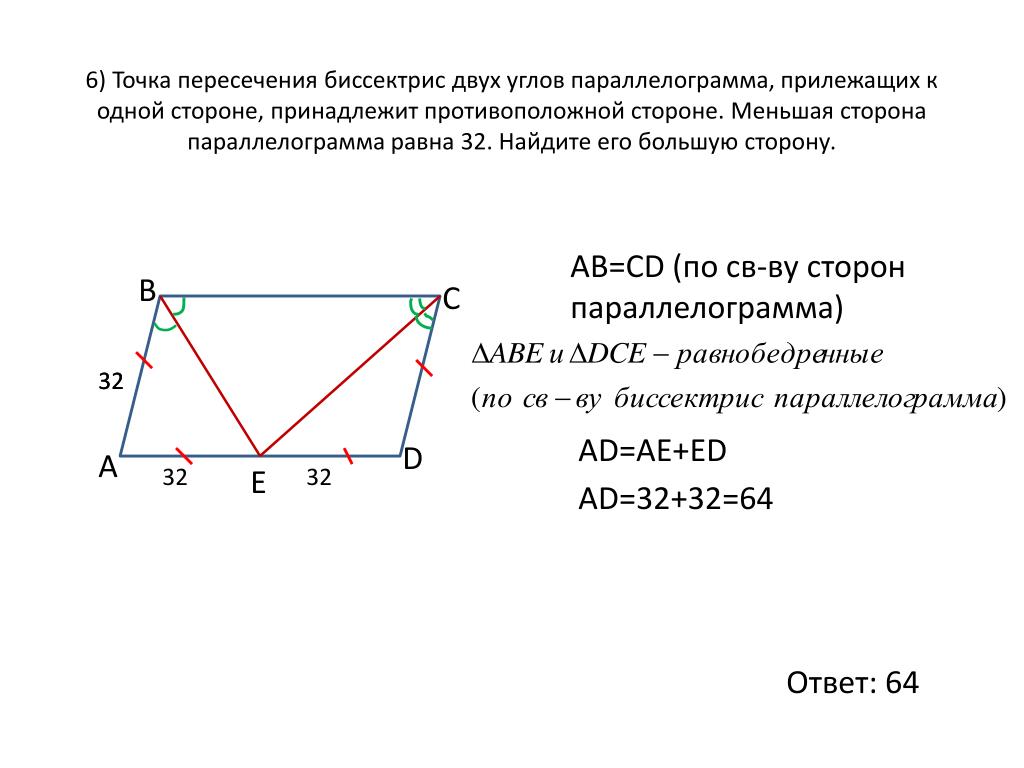 В частности, мы можем видеть, что
угол 𝐶𝐴𝐵 и угол 𝐶𝐴𝐷 имеют одинаковую меру. Следовательно, диагональ — это биссектриса
этого угла.
В частности, мы можем видеть, что
угол 𝐶𝐴𝐵 и угол 𝐶𝐴𝐷 имеют одинаковую меру. Следовательно, диагональ — это биссектриса
этого угла.
Стоит отметить, что этот результат и доказательство работает и для ромба, то есть четырехугольника, у которого все стороны одинаковы длина. В самом деле, обе диагонали ромб делит свои внутренние углы пополам.
Мы можем использовать эту идею, чтобы разделить любое угол с помощью циркуля и линейки. Нам нужно построить воздушного змея или ромба в вершине угла, используя стороны угла, а затем используйте диагональ фигуры, делящая угол пополам.
Чтобы увидеть, как мы можем это сделать, давайте
делит заданный острый угол 𝐶𝐴𝐵 пополам. Мы можем построить ромб, используя
стороны угла, используя свойства окружностей. Сначала начертим круг
с центром в 𝐴, который пересекает стороны угла в двух точках 𝐷 и 𝐸 как
показано. Поскольку отрезки 𝐴𝐸 и 𝐴𝐷
являются радиусами одной и той же окружности, мы можем заметить, что они имеют одинаковую длину. Мы хотим составить четырехугольник
со всеми четырьмя сторонами одинаковой длины. Поэтому нам нужно найти другую точку
на таком же расстоянии от 𝐷 и 𝐸. Мы можем сделать это, проследив конгруэнтные
круги в 𝐷 и 𝐸 и обозначение точек пересечения между кругами 𝐹
как показано.
Поскольку отрезки 𝐴𝐸 и 𝐴𝐷
являются радиусами одной и той же окружности, мы можем заметить, что они имеют одинаковую длину. Мы хотим составить четырехугольник
со всеми четырьмя сторонами одинаковой длины. Поэтому нам нужно найти другую точку
на таком же расстоянии от 𝐷 и 𝐸. Мы можем сделать это, проследив конгруэнтные
круги в 𝐷 и 𝐸 и обозначение точек пересечения между кругами 𝐹
как показано.
Теперь мы можем отметить, что четырехугольник 𝐴𝐸𝐹𝐷 является ромбом, так как все его стороны имеют одинаковую длину. Мы знаем, что они одинаковы длины, так как все они являются радиусами конгруэнтных окружностей.
Наконец, напомним, что диагональ ромба делит его внутренние углы пополам. Таким образом, мы можем сделать вывод, что линия между 𝐴 и 𝐹 должна быть биссектриса угла 𝐶𝐴𝐵.
Прежде чем мы рассмотрим это
построение для неострых углов, запишем шаги, которые мы предприняли для
построить биссектрису угла 𝐵𝐴𝐶 с помощью циркуля и
прямая грань. Сначала мы обводим окружность с центром
в вершине угла 𝐴, пересекающего стороны угла 𝐴𝐵 и 𝐴𝐶
в двух различных точках мы помечаем 𝐷 и 𝐸 соответственно. Во-вторых, мы хотим проследить конгруэнтные
окружности с центрами в точках 𝐷 и 𝐸. Затем мы обозначаем точку
пересечение этих двух окружностей, лежащее на той же стороне, что и угол, который мы
хочу разделить пополам 𝐹. Наконец, мы можем нарисовать линию,
луч или отрезок между 𝐴 и 𝐹 и обратите внимание, что это диагональ
ромба со сторонами угла в качестве его сторон, поэтому он должен разделить угол пополам.
Сначала мы обводим окружность с центром
в вершине угла 𝐴, пересекающего стороны угла 𝐴𝐵 и 𝐴𝐶
в двух различных точках мы помечаем 𝐷 и 𝐸 соответственно. Во-вторых, мы хотим проследить конгруэнтные
окружности с центрами в точках 𝐷 и 𝐸. Затем мы обозначаем точку
пересечение этих двух окружностей, лежащее на той же стороне, что и угол, который мы
хочу разделить пополам 𝐹. Наконец, мы можем нарисовать линию,
луч или отрезок между 𝐴 и 𝐹 и обратите внимание, что это диагональ
ромба со сторонами угла в качестве его сторон, поэтому он должен разделить угол пополам.
Это построение и доказательство
построение более или менее одинаково для тупых, рефлекторных и прямых
углы. Чтобы убедиться в этом, давайте пройдем
Показан пример использования этого процесса для разделения пополам угла рефлекса 𝐶𝐴𝐵. Начнем с обведения круга
с центром в вершине угла 𝐴, который пересекает стороны угла в двух
различные точки 𝐷 и 𝐸, как показано. Во-вторых, нам нужно проследить конгруэнтность
окружности с центрами 𝐷 и 𝐸, которые пересекаются в точке на той же стороне, что и
угол. Для этого нам нужно увеличить
радиус нашей пары компасов. Делая это, мы получаем точку вида
𝐹 как показано.
Во-вторых, нам нужно проследить конгруэнтность
окружности с центрами 𝐷 и 𝐸, которые пересекаются в точке на той же стороне, что и
угол. Для этого нам нужно увеличить
радиус нашей пары компасов. Делая это, мы получаем точку вида
𝐹 как показано.
Стоит отметить, что поскольку мы увеличил радиус нашего компаса, у нас больше нет ромба. Однако мы можем отметить, что четырехугольник 𝐹𝐸𝐴𝐷 — воздушный змей, поэтому доказательство остается прежним.
Наконец, мы рисуем линию между
𝐴 и 𝐹 и обратите внимание, что это диагональ воздушного змея между его парой конгруэнтных
стороны. Значит, это биссектриса рефлекса.
угол 𝐵𝐴𝐶. Другой способ понять, почему это
верно, это нарисовать линии между 𝐸 и 𝐹 и 𝐷 и 𝐹. Затем мы можем увидеть этот треугольник
𝐴𝐹𝐸 сравним с треугольником 𝐴𝐹𝐷 по конгруэнтности сторон
критерий. Давайте теперь посмотрим на пример
применение этого процесса для идентификации данной геометрической конструкции.
Давайте теперь посмотрим на пример
применение этого процесса для идентификации данной геометрической конструкции.
Что означает следующий рисунок проиллюстрировать? Вариант (А) биссектриса угол. Вариант (Б) перпендикуляр из точка, лежащая вне прямой. Вариант (С) биссектриса прямой сегмент. Вариант (D) прямая линия параллельно другой линии. Или это вариант (Е) угол равны другому углу?
В этом вопросе нам дается
пять вариантов, и нам нужно определить, какой из вариантов иллюстрируется
фигура. Мы можем прямо ответить на это
вопрос, вспомнив построение биссектрисы угла. Однако мы также можем сделать это с помощью
используя фигуру. Прежде всего заметим, что круг
прослеживается в вершине угла. Итак, радиусы этой окружности
должны иметь одинаковую длину. Тогда мы можем отметить, что конгруэнтное
окружности чертят с центрами в точках пересечения сторон
угол и исходный круг. Это означает, что мы можем отметить
что радиусы этих окружностей имеют одинаковую длину. Это дает нам следующее
летающий змей.
Тогда мы можем отметить, что конгруэнтное
окружности чертят с центрами в точках пересечения сторон
угол и исходный круг. Это означает, что мы можем отметить
что радиусы этих окружностей имеют одинаковую длину. Это дает нам следующее
летающий змей.
Наконец, либо с помощью тот факт, что диагональ воздушного змея между парой его конгруэнтных сторон делит его пополам. внутренних углов или используя конгруэнтность двух треугольников, мы можем заключить что на рисунке изображена биссектриса угла.
В нашем следующем примере мы построить биссектрису внутреннего угла треугольника, чтобы найти точку на стороне треугольника, так что мы можем сравнить отношение длин стороны делится на.
Учитывая, что 𝐴𝐵𝐶 является
треугольник, используйте линейку и циркуль, чтобы нарисовать треугольник и биссектрису
угол 𝐶 через биссектрису луча из 𝐶 через 𝐷, который пересекает луч из
𝐴 через 𝐵 в 𝐷.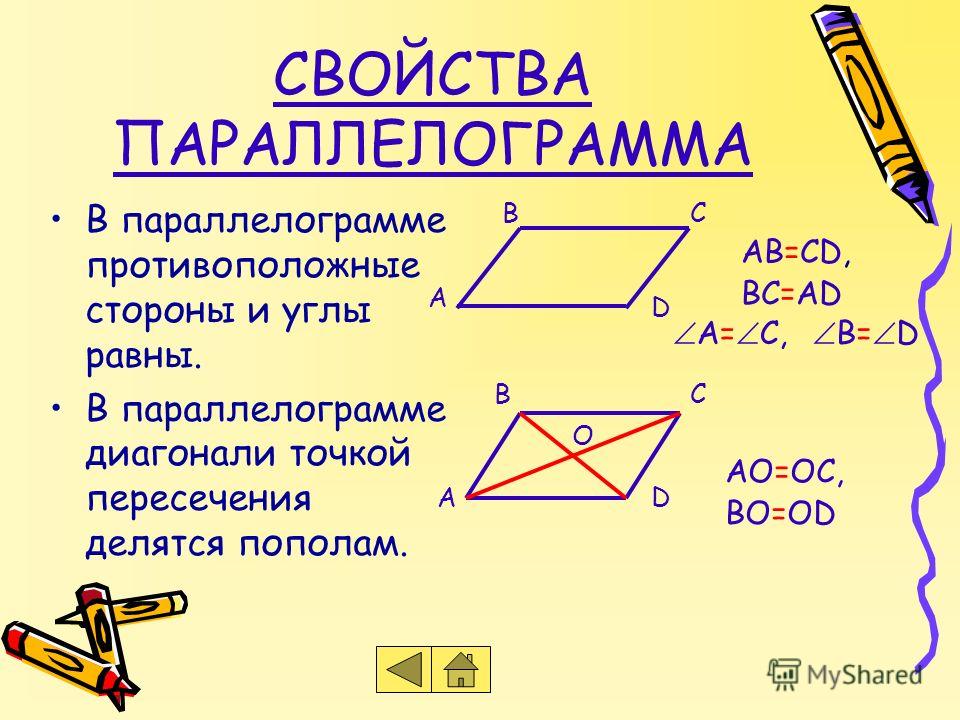 Используйте линейку, чтобы измерить
длина отрезка 𝐴𝐷 до ближайшего десятичного знака. Вариант (А) 4,2 см,
вариант (В) 3,2 см, вариант (С) 4,7 см, вариант (Г) 3,7
сантиметры. Или это вариант (Е) 5.2
сантиметры?
Используйте линейку, чтобы измерить
длина отрезка 𝐴𝐷 до ближайшего десятичного знака. Вариант (А) 4,2 см,
вариант (В) 3,2 см, вариант (С) 4,7 см, вариант (Г) 3,7
сантиметры. Или это вариант (Е) 5.2
сантиметры?
В этом вопросе нас спрашивают начертить треугольник заданной длины с помощью линейки и циркуля, разделите угол 𝐶 пополам, чтобы найти точку 𝐷, а затем измерьте длину отрезка 𝐴𝐷 с точностью до десятых долей сантиметра.
Начнем с первой части
вопроса. Нас просят нарисовать
треугольник с заданными длинами. У нас может возникнуть соблазн пропустить
этот шаг и используйте данную схему. Однако это не всегда
точный. Так что это хорошая идея
сами построим треугольник, хотя в этом случае диаграмма
точный.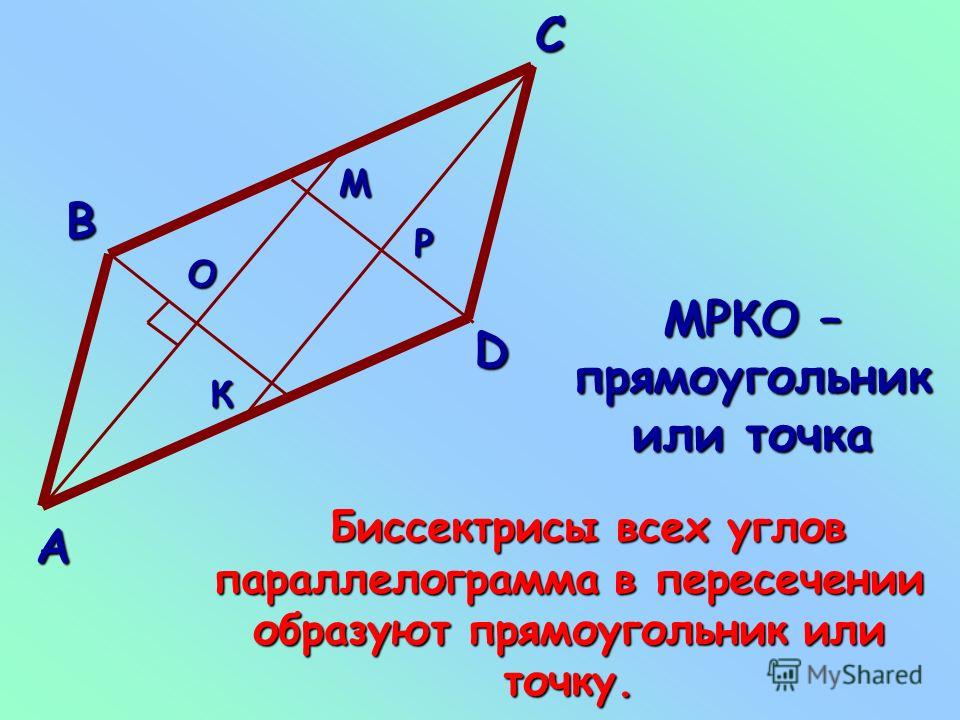
Чтобы построить треугольник с циркуль и линейка, нам нужно начать с построения одной стороны треугольник. Допустим, мы начинаем с 𝐵𝐶, который имеет длину пять сантиметров. Затем мы можем проследить круг радиус семь сантиметров с центром в 𝐶 и круг радиусом восемь сантиметров с центром в 𝐵 и обозначьте любую точку пересечения кругов 𝐴. Затем мы можем использовать радиус каждый круг, чтобы отметить, что треугольник 𝐴𝐵𝐶 имеет желаемые длины сторон.
Вторая часть этого
вопрос просит нас разделить пополам угол при 𝐶, то есть внутренний угол
треугольник. Напомним, что биссектриса
разделит этот угол на два равных угла. Мы также можем отметить, что это
биссектриса будет лежать внутри треугольника, поэтому точка 𝐷 будет лежать на отрезке
𝐴𝐵. Нам не нужно расширять это
сторона. Затем мы вспоминаем, что можем
делит углы пополам построением. Сначала обводим круг
с центром в вершине угла, который мы хотим разделить пополам и обозначить точки
пересечение между кругом и сторонами 𝐴 простое, 𝐵 простое, как показано. Затем мы можем сделать набросок конгруэнтных
окружности с центрами в 𝐴 простом и 𝐵 простом числах, которые пересекаются в одной точке
сторона как угол, который мы хотим разделить пополам. Мы будем называть эту точку
перекресток 𝐸.
Нам не нужно расширять это
сторона. Затем мы вспоминаем, что можем
делит углы пополам построением. Сначала обводим круг
с центром в вершине угла, который мы хотим разделить пополам и обозначить точки
пересечение между кругом и сторонами 𝐴 простое, 𝐵 простое, как показано. Затем мы можем сделать набросок конгруэнтных
окружности с центрами в 𝐴 простом и 𝐵 простом числах, которые пересекаются в одной точке
сторона как угол, который мы хотим разделить пополам. Мы будем называть эту точку
перекресток 𝐸.
Тогда мы можем сделать вывод, что
линия между 𝐶 и 𝐸 делит пополам угол при 𝐶. Мы можем продолжить эту биссектрису до
пересечь противоположную сторону и обозначить точку пересечения 𝐷, как показано на рисунке. Тогда мы можем измерить длину
отрезка 𝐴𝐷 с нашей линейкой. И если мы это сделаем, мы получим 4,7
сантиметров с точностью до десятых долей сантиметра, что является вариантом (C).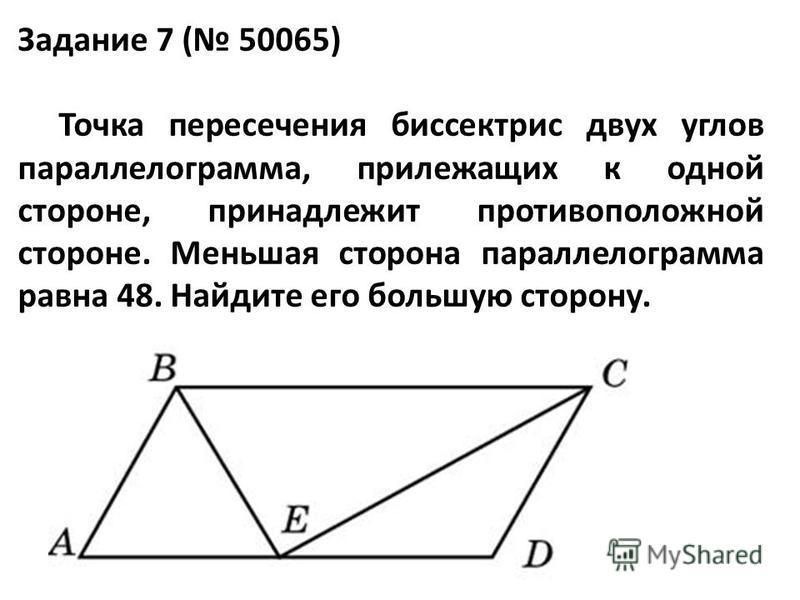
Стоит отметить, что это показывает что биссектриса треугольника не обязательно делит противоположный угол пополам сторона. Еще одно полезное приложение биссектриса углов состоит в рассмотрении бисекции прямого угла, скажем 𝐵𝐴𝐶. Мы рисуем окружность с центром в 𝐴 и обозначьте точки пересечения 𝐷 и 𝐸, а затем нарисуйте конгруэнтные окружности. с центром в точках 𝐷 и 𝐸 и обозначьте точку пересечения 𝐹, как показано на рисунке. Тогда мы знаем, что 𝐴𝐹 — это биссектриса прямого угла, поэтому она должна разделить угол на две прямые углы. Это означает, что мы можем использовать это конструкция для построения прямых углов с помощью циркуля и прямая грань. Мы можем даже применить этот процесс второй раз разделить прямой угол пополам, давая нам процесс построения Угол 45 градусов с компасом и линейкой.
В нашем следующем примере мы
вычислить периметр треугольника, построенного с помощью биссектрис.
Учитывая, что 𝐴𝐵𝐶 является треугольник, используйте линейку и циркуль, чтобы нарисовать показанный треугольник и делят пополам угол 𝐶 и угол 𝐵 биссектрисами луча из 𝐶 через 𝐷 и луч из 𝐵 через 𝐷, пересекающийся в 𝐷. Используйте линейку, чтобы измерить периметр треугольника 𝐷𝐵𝐶 до ближайшего десятичного знака. Вариант (А) 17,6 см, вариант (Б) 17,9см, вариант (С) 16,9 см, вариант (Г) 18,4 сантиметры. Или это вариант (Е) 19.1 сантиметры?
В этом вопросе нам говорят
построить треугольник 𝐴𝐵𝐶 заданных длин, а затем построить угол
биссектрисы двух его углов. Мы знаем, что эти будут
пересекаются в точке, и мы можем обозначить эту точку 𝐷. Нам нужно найти эту точку и
затем измерьте периметр треугольника 𝐷𝐵𝐶 с точностью до десятых
сантиметр.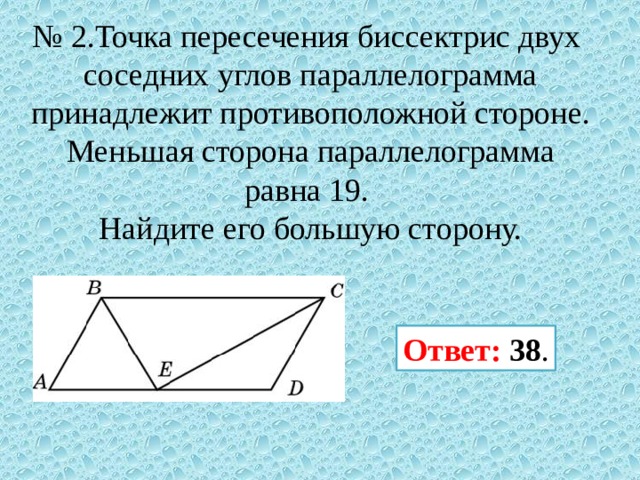
Для начала у нас может возникнуть соблазн пользоваться приведенной схемой. Однако может быть неточности в схеме. Вместо этого мы должны построить треугольник сами, чтобы минимизировать ошибки. Для этого нам нужно начать с зарисовкой любой стороны треугольника. Допустим, мы рисуем линию длина девять сантиметров, как показано на рисунке. Затем мы можем проследить круг радиусом шесть сантиметров с центром в 𝐶 и окружностью радиусом пять сантиметров с центром в 𝐵 и обозначьте точку пересечения 𝐴. Если мы соединим вершины с стороны, как показано, то мы построили треугольник с данной стороной длины.
Теперь нам нужно разделить пополам
углы при 𝐶 и 𝐵. Мы можем сделать это, вспомнив
метод построения биссектрисы с помощью циркуля и
линейка. Мы можем начать с разделения пополам
угол в 𝐶. Сначала нам нужно обвести круг
с центром в точке 𝐶, которая пересекает обе стороны угла. Мы будем называть эти точки 𝐸
и 𝐹, как показано. Далее прослеживаем конгруэнтность
окружности с центрами 𝐸 и 𝐹, которые пересекаются в точке на той же стороне, что и
угол, который мы хотим разделить пополам. Мы будем называть эту точку 𝐺 как
показано. Наконец, мы можем заключить, что
прямая между 𝐶 и 𝐺 является биссектрисой угла. Мы продолжим эту биссектрису до
противоположная сторона треугольника.
Мы можем начать с разделения пополам
угол в 𝐶. Сначала нам нужно обвести круг
с центром в точке 𝐶, которая пересекает обе стороны угла. Мы будем называть эти точки 𝐸
и 𝐹, как показано. Далее прослеживаем конгруэнтность
окружности с центрами 𝐸 и 𝐹, которые пересекаются в точке на той же стороне, что и
угол, который мы хотим разделить пополам. Мы будем называть эту точку 𝐺 как
показано. Наконец, мы можем заключить, что
прямая между 𝐶 и 𝐺 является биссектрисой угла. Мы продолжим эту биссектрису до
противоположная сторона треугольника.
Теперь нам нужно следовать этому же
процесс, чтобы разделить пополам угол в 𝐵. Начнем с того, что обведем круг в
𝐵 и обозначив точки пересечения окружности со сторонами
угол 𝐼 и 𝐻 как показано. Далее прослеживаем конгруэнтность
круги в 𝐼 и 𝐻 и обозначьте точку пересечения между кругами
𝐽.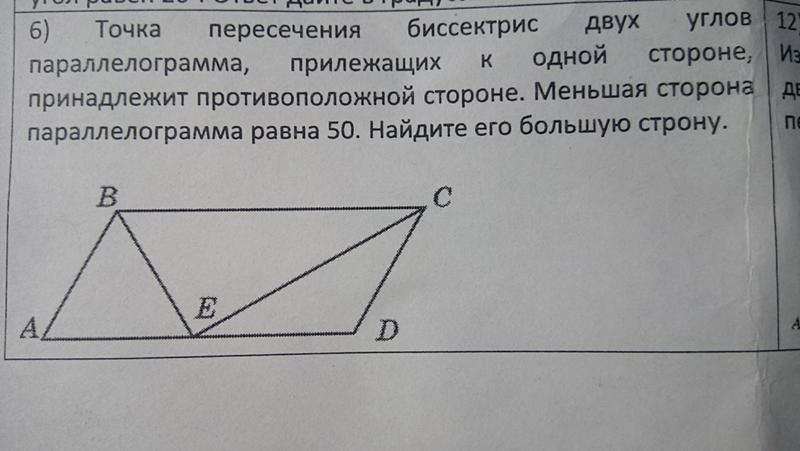 Тогда мы можем сделать вывод, что
прямая между 𝐽 и 𝐵 является биссектрисой угла при 𝐵. Мы можем расширить эту линию до
противоположная сторона треугольника. Теперь мы можем обозначить точку
пересечение биссектрис 𝐷.
Тогда мы можем сделать вывод, что
прямая между 𝐽 и 𝐵 является биссектрисой угла при 𝐵. Мы можем расширить эту линию до
противоположная сторона треугольника. Теперь мы можем обозначить точку
пересечение биссектрис 𝐷.
Теперь мы хотим оценить периметр треугольника 𝐷𝐵𝐶, то есть сумма длин сторон. Если мы измерим два неизвестных длины сторон этого треугольника с помощью линейки, мы можем оценить, что 𝐶𝐷 равно примерно 5,2 сантиметра в длину и 𝐵𝐷 примерно 4,2 сантиметра длинный. Складываем эти длины вместе дает нам периметр 18,4 сантиметра с точностью до десятых долей сантиметра, что, как мы видим, согласуется с вариантом (D).
Есть еще одно полезное свойство
биссектрисы, которые мы можем отметить, используя этот пример. Построим биссектрису
угол 𝐴 так же, как мы делали для углов 𝐵 и 𝐶. Следуя этому процессу, мы можем отметить
что биссектриса 𝐴 также пересекает другие биссектрисы в точке 𝐷. Этот результат справедлив для любого
треугольник. В общем имеем, что
биссектрисы внутренних углов любого треугольника пересекаются в одной точке. Другими словами, они
одновременно. В нашем последнем примере мы будем
построить прямую трапецию, а затем использовать биссектрисы угла, чтобы оценить длину
сегмента линии.
Следуя этому процессу, мы можем отметить
что биссектриса 𝐴 также пересекает другие биссектрисы в точке 𝐷. Этот результат справедлив для любого
треугольник. В общем имеем, что
биссектрисы внутренних углов любого треугольника пересекаются в одной точке. Другими словами, они
одновременно. В нашем последнем примере мы будем
построить прямую трапецию, а затем использовать биссектрисы угла, чтобы оценить длину
сегмента линии.
Учитывая, что 𝐴𝐵𝐶𝐷 — трапеция, с помощью линейки и циркуля начертите трапецию и биссектрису 𝐴 по биссектриса луча от 𝐴 до 𝐷, который пересекает луч от 𝐶 до 𝐵 в 𝑀. Используйте линейку для измерения длины отрезка 𝐴𝑀 до ближайшего десятичного знака. Вариант (А) 12,0 см, вариант (Б) 10,9 см, вариант (С) 14,1 см, вариант (Г) 11,6 см. Или это вариант (Е) 13.0 сантиметры?
В этом вопросе нам дается
правильной трапеции 𝐴𝐵𝐶𝐷 и попросил построить точную версию этой трапеции
с помощью линейки и циркуля. Затем нам нужно найти точку 𝑀 по
разделив пополам угол в 𝐴, а затем измерьте длину отрезка между 𝐴
и 𝑀 с точностью до десятых долей сантиметра. Начнем с построения
точная версия трапеции с помощью линейки и циркуля. Мы можем начать с измерения линии
отрезок длиной 10 сантиметров и обозначив конечные точки 𝐴 и 𝐵, как показано на рисунке.
Затем нам нужно найти точку 𝑀 по
разделив пополам угол в 𝐴, а затем измерьте длину отрезка между 𝐴
и 𝑀 с точностью до десятых долей сантиметра. Начнем с построения
точная версия трапеции с помощью линейки и циркуля. Мы можем начать с измерения линии
отрезок длиной 10 сантиметров и обозначив конечные точки 𝐴 и 𝐵, как показано на рисунке.
Далее нам нужно построить правильный
угол в 𝐵. И мы можем сделать это, разделив пополам
прямой угол в 𝐵. Начнем с расширения линии
сегмент за 𝐵, а затем проследить окружность с центром в 𝐵, которая пересекает линию
в 𝐸 и 𝐹, как показано. Затем мы рисуем конгруэнтные окружности
с центром в 𝐸 и 𝐹, которые пересекаются в точке над 𝐵, как показано. Тогда мы можем заметить, что линия
через 𝐵 и эта точка пересечения делит прямой угол пополам, поэтому будет
прямой угол. Если мы нарисуем отрезок прямой
длиной 12 сантиметров, то мы можем обозначить другой конец 𝐶.
Если мы нарисуем отрезок прямой
длиной 12 сантиметров, то мы можем обозначить другой конец 𝐶.
Мы могли бы повторить этот процесс снова построить прямой угол при 𝐶. Однако мы также можем отметить, что 𝐴𝐶𝐷 — треугольник. И мы можем построить этот треугольник с помощью линейки и линейки. Очерчиваем круг радиусом 13 сантиметров с центром в 𝐴 и круг радиусом пять сантиметров с центром в 𝐶 и обозначьте показанную точку пересечения 𝐷, чтобы построить трапецию.
Теперь нам нужно разделить угол пополам
𝐴. Мы делаем это, обводя круг
с центром в 𝐴, который пересекает стороны угла в двух точках, которые мы будем
метка 𝐺 и 𝐻. Затем мы рисуем конгруэнтные окружности
с центром в 𝐺 и 𝐻 и обозначьте точку пересечения на той же стороне, что и угол
𝐴 𝐼. Тогда мы можем сделать вывод, что линия
между 𝐴 и 𝐼 делит пополам угол при 𝐴. Мы продолжаем эту линию, чтобы пересечь
линию между 𝐵 и 𝐶 и обозначьте точку пересечения 𝑀. Если мы затем измерим длину
этот отрезок с точностью до миллиметра, мы получаем 12,0 сантиметров, которые мы можем
см. вариант (А).
Мы продолжаем эту линию, чтобы пересечь
линию между 𝐵 и 𝐶 и обозначьте точку пересечения 𝑀. Если мы затем измерим длину
этот отрезок с точностью до миллиметра, мы получаем 12,0 сантиметров, которые мы можем
см. вариант (А).
Давайте теперь пройдемся по ключевым моментам с этого урока. Мы начали с определения биссектрисы угла — это линия, проходящая через вершину угла, которая делит угол на наполовину, или, другими словами, на два равных угла. Далее мы доказали, что диагональ воздушного змея, лежащего между конгруэнтными сторонами, делит пополам два внутренних угла воздушного змея. Точно так же мы можем расширить это к обеим диагоналям ромба.
Затем мы используем это свойство, чтобы найти
конструкция для деления любого угла пополам с помощью циркуля и
прямая грань. Сначала мы обводим окружность с центром
в вершине угла мы хотим разделить пополам то, что пересекает стороны угла
в различных точках, которые мы обозначаем 𝐷 и 𝐸 соответственно.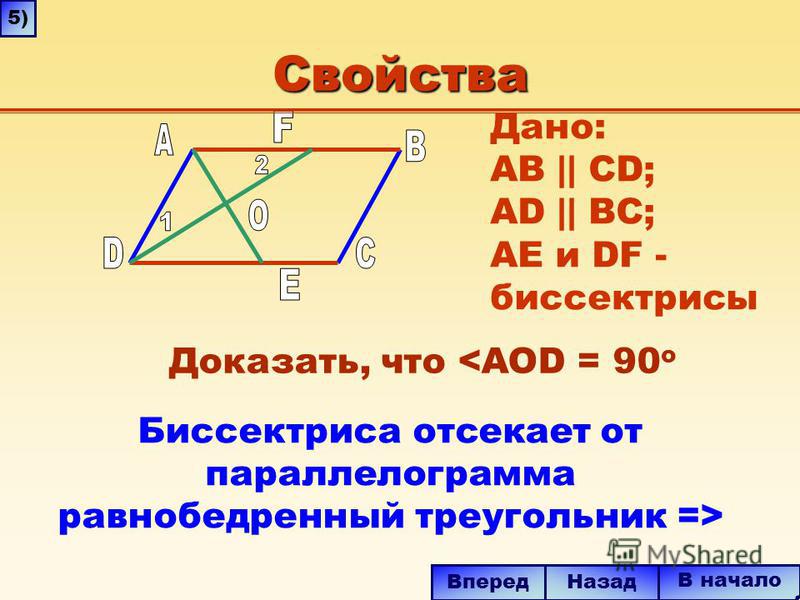


Leave A Comment