6.2.2. Точка максимума и минимума
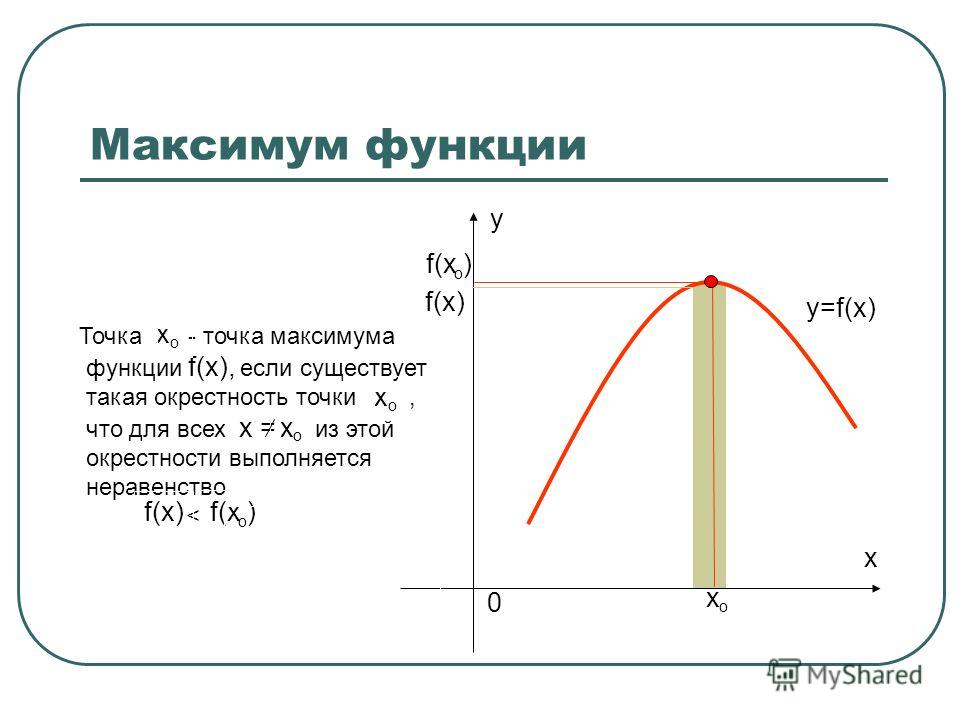
Точка х=х1 называется точкой максимума функции у=f(x), если для всех точек некоторого интервала, содержащего точку х1, будет выполняться равенство при любых достаточно малых или .
Точка х=х2 называется точкой минимума функции у=f(x), если для всех точек некоторого интервала, содержащего точку х2, будет выполняться неравенство , где или .
Точка максимума и минимума называются точками экстремума функции. Рассмотрим методы нахождения экстремумов.
6.2.3. Необходимое условие экстремума
Теорема.
Если дифференцируемая функция у=f(x) имеет в точке х=х0 экстремум,
то её производная в точке обращается в
нуль, то есть ,
или не существует.
Пусть для определённости точка х0 является точкой максимума. Тогда из определения максимума следует, что или . Составим и оценим знаки отношения приращений , а именно: , если и , если .
По условию теоремы функция дифференцируема в точке х0, значит существует предел , и он не зависит от того, как стремится к нулю. Беря пределы от обеих приведённых выше неравенств, получаем с одной стороны , если >0, с другой , если <0. но так как есть определённое число, то два последних неравенства совместимы, только если .
Точки,
в которых производная обращается в нуль
или не существует, называются критическими
точками первого рода или точками подозрительными
на экстремум. Условия существования
критических точек, в которых производная
равна нулю, описываются условием теоремы
Ролля, которую мы приведём без
доказательств.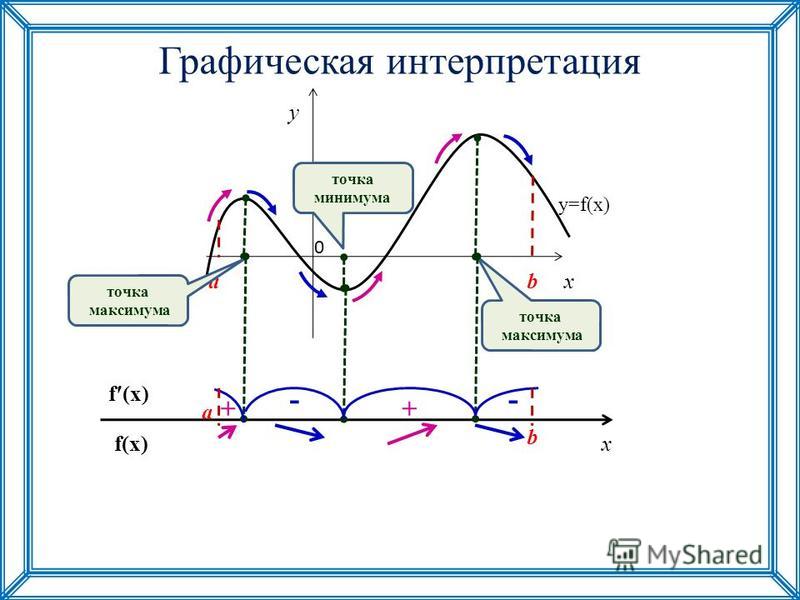 Если
функция у=f(x) непрерывна на отрезке и дифференцируема в каждой его точке,
а не на концах отрезка имеем значения f
Если
функция у=f(x) непрерывна на отрезке и дифференцируема в каждой его точке,
а не на концах отрезка имеем значения f
Геометрически это значит, что найдётся хотя бы одна точка a<c<b, в которой касательная параллельна оси Ох.
Для того, чтобы найти точку экстремума функции у=f(x) необходимо найти её производную, приравнять её нулю и решить полученное уравнение. Корни этого уравнения, а также точки разрыва производной будут критическими точками.
Пример 6.1
Р
ешение. Найдём производную .
Решим уравнение 6х2-12х=0,
его корни х1=0,
х2=2 – критические точки.
Найдём производную .
Решим уравнение 6х2-12х=0,
его корни х1=0,
х2=2 – критические точки.
Пример 6.2. Найти критические точки функции у=х3.
Решение. — критическая точка.
Легко
увидеть (рис.6.3.), что х=0 для функции у=х
6.2.4. Достаточные признаки существования экстремума
Первый достаточный признак экстремума формулируется на основе изменения знака первой производной при переходе через критическую точку. О втором признаке экстремума речь пойдёт ниже в § 6.4.
Теорема
(первый признак экстремума): Если х0 –
критическая точка функции у=f(x) и в некоторой окрестности точки х0,
переходя через неё слева направо,
производная меняет знак на противоположный, то х0 является точкой экстремума.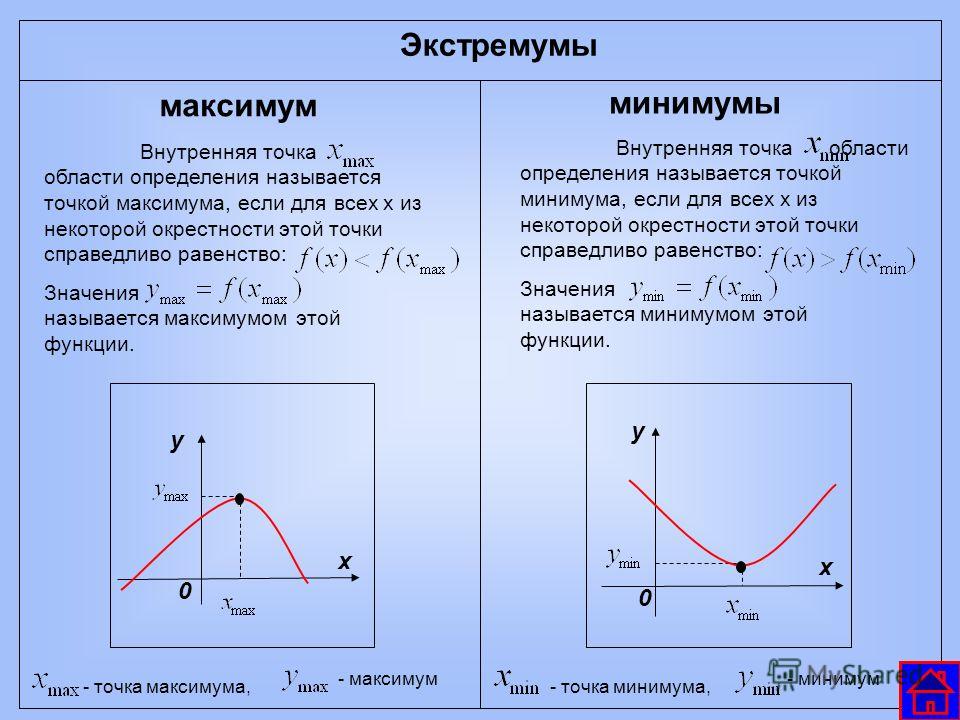
Рассмотренный экстремум носит локальный (местный) характер и касается некоторой малой окрестности критической точки.
Точки экстремума и точки разрыва делят область определения функции на интервалы монотонности.
Пример 6.3. В примере 6.1. мы нашли критические точки х1=0 и х2=2.
Выясним,
действительно ли в этих точках функция у=2х3-6х2+1 имеет экстремум. Подставим в её производную
значения х,
взятые слева и справа от точки х1=0 в достаточно близкой окрестности,
например, х=-1и х=1. получим .
Так как производная меняет знак с «+»
на «-», то х1
получим .
Так как производная меняет знак с «+»
на «-», то х1
Чтобы найти наибольшее и наименьшее значение функции непрерывной на отрезке нужно вычислить её значение во всех критических точках и на концах отрезка, а затем выбрать из них наибольшее и наименьшее.
обнаружение максимума и минимума OTUS
Математики и Data Science-специалисты должны хорошо разбираться в функциях. Предлагаем попрактиковаться в решении задач на обнаружение максимальных и минимальных значений у заданных функций.
Максимум
Задумываясь над тем, как найти максимальное значение функции, нужно четко понимать, с чем предстоит иметь дело.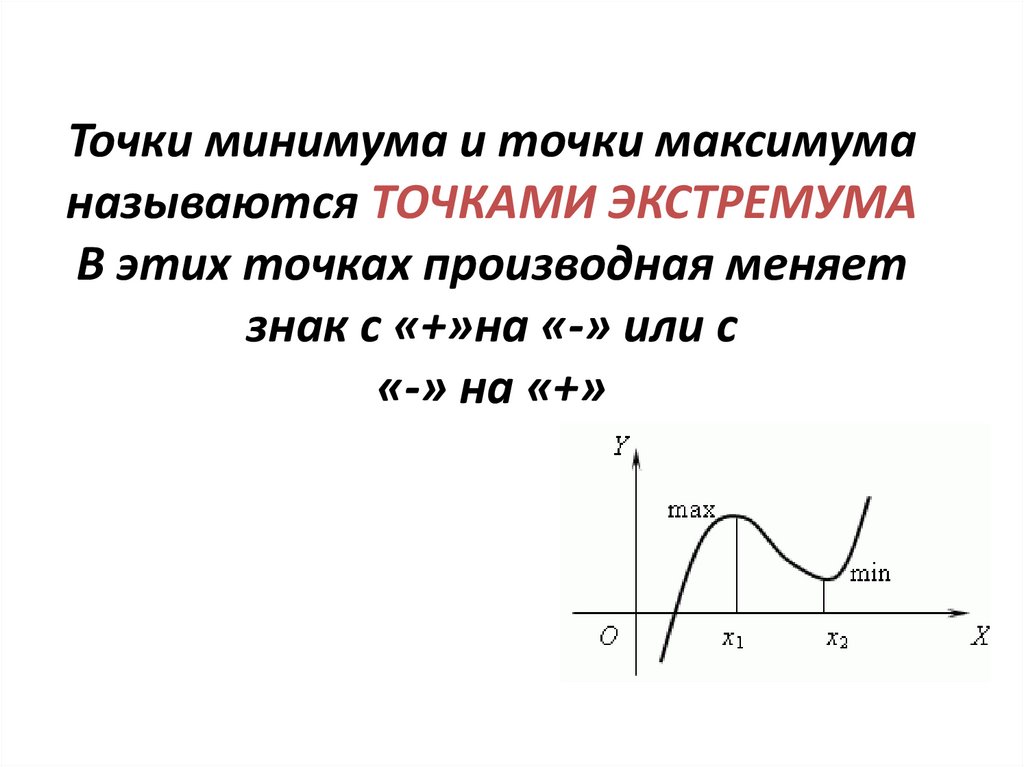 Для этого нужно запомнить такое определение:
Для этого нужно запомнить такое определение:
Наибольшее значение функции y = f(x) на промежутке x – это max y = f(x0). Оно будет при любом значении x€ X, x≠x0 делает справедливым неравенство: f(x)≤f(x0).
Максимальное значение (максимум) – это точка на функции, в которой значение функции больше, чем в соседних «отметках».
Минимум
Наименьшее значение функции находить так же легко, как и наибольшее. Но сначала нужно понимать, что это такое.
Значение функции на отрезке будет считаться минимумом, если оно меньше, чем в соседних «отметках». Здесь действует такое определение:
Наименьшее значение функции y=f(x) на промежутке x – это miny=f(x0), которое при любом значении x€ X, x≠x0 делает справедливым неравенство f(x)≥f(x0).
Соответствующие определения являются достаточными и очевидными. Если говорить простыми словами, то максимум функции – это ее самое большое значение на заданном промежутке (участке) при абсциссе x0, а минимум – самое маленькое.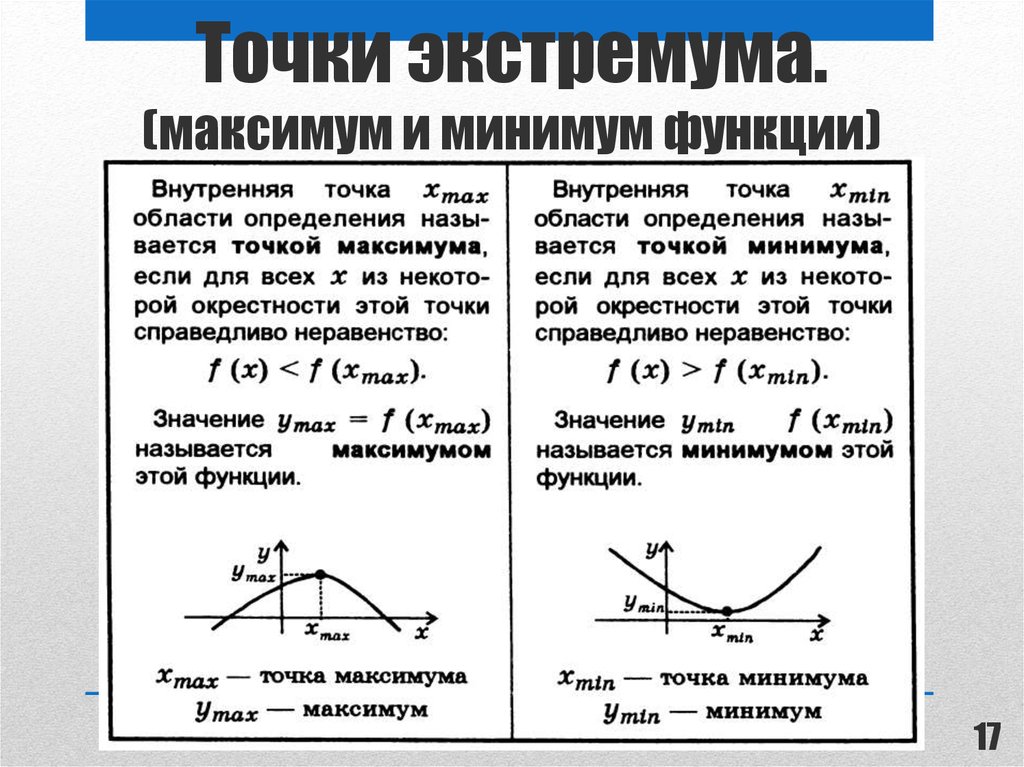
Стационарные точки
При решении вопроса о том, как найти наибольшее или наименьшее значение функции, стоит обратить внимание на так называемые «стационарные точки». Это – значения аргумента функции, при которых ее производная будет равняться нулю.
Стационарная точка – это «отметка», в которой расположен экстремум дифференцируемой функции. А именно – локальный минимум или максимум. В одной из таких «отметок» записанное выражение будет достигать своих предельных параметров.
Здесь рекомендуется запомнить следующее:
- Экстремум функции – это минимумы и максимумы.
- Если определить производную в точках экстремумов, она будет равно 0.
- Когда говорят «экстремумы», подразумевается значение функции. Если же речь идет об «отметках» экстремумов, рассматривать стоит x, в которых достигаются соответствующие пределы.
Этого достаточно для того, чтобы разобраться, как найти наибольшее на заданном отрезке у выражения. Для реализации поставленной задачи вовсе не обязательно составлять график. Поэтому сначала воспользуемся записями формул и вычислений.
Поэтому сначала воспользуемся записями формул и вычислений.
План действий
Пример – дана функция f(x) на отрезке [a, b]. Наибольшее и наименьшее значение такой непрерывной функции достигаются в определенных местах. Это – критические точки. Там, где производная записанного выражения будет равно нулю.
Для того, чтобы найти наибольшие значения уравнения, потребуется придерживаться следующего алгоритма:
- Узнайте, какая перед вами функция. Для этого нужно проверить ее на непрерывность. В расчет обязательно берется заданный отрезок.
- Если запись непрерывная – ищем производную.
- После того, как найдем производную, приравниваем ее к нулю. Это поможет найти точки экстремумов. В результате получаются корни.
- Образовавшиеся корни – это критические точки. Нужно выбрать те «параметры», что относятся к промежутку [a, b].
- Вычислить значения функции на концах отрезка [a, b].
- Определить значения имеющегося выражения в критических «отметках».

Теперь понятно, как найти наибольшие функции на заданном отрезке. После произведенных подсчетов остается выбрать из результатов M (максимум) и m (минимум).
На отрезке
Разобравшись в тем, как найти наибольшие «параметры» выражения «на бумаге», стоит рассмотреть соответствующий процесс на графиках. Определять максимумы/минимумы в данном случае будет проще.
Первый график указывает на выражение, у которого точка минимума и максимума находятся в стационарных точках на промежутке [-6;6]. Соответствующие «пределы» обозначены жирным.
Второй график указывает на изменение отрезка. Теперь он будет [1;6]. Минимальное значение останется прежним. А вот максимальное – изменится. Оно образуется в правой части в точке с абсциссой. Поиск минимального «параметра» окажется в критической точке.
Задумываясь, как найти наименьшие или «самые крупные» параметры выражения на графике, можно также рассмотреть третий рисунок. Здесь функция принадлежала промежутку [-3;2].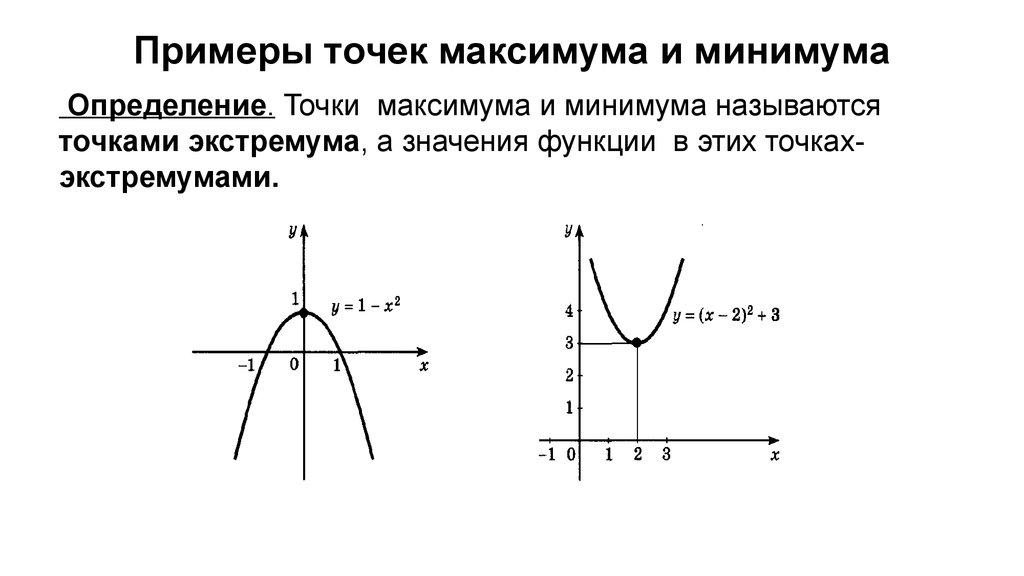 Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы.
Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы.
Открытый интервал
Если промежуток задан конкретным числом, определить экстремумы будет не так сложно. Иначе происходит, если интервал открыт.
Здесь:
- Функция будет принимать максимум/минимум по значению в стационарных точках на открытом интервале от -6 до 6. Ответ – на 4 рисунке.
- Если взять отрезок [1;6), минимум будет достигнут в стационарной точке. А вот максимум – неизвестен. Связано это с тем, что 6 не принадлежит к заданному интервалу. Если бы «шестерка» относилась к соответствующему промежутку, ответ на вопрос относительно определения максимума оказался понятным. Максимальный параметр был бы в точке с абсциссой 6.
- На рисунке 6, задумываясь, как найти наименьшие «параметры», нужно обратить внимание на заданный интервал. Он равен (-3;2]. Минимум будет достигнут в правой границе. А вот максимум – не определен.
Найти значения на графиках обычно проще, чем «в чистых формулах». Соответствующие задания можно отыскать тут.
Соответствующие задания можно отыскать тут.
Бесконечность
Иногда значения функций нужно найти на бесконечном промежутке. Графически возможны такие ситуации:
На 7 рисунке функция достигает максимума в стационарной точке с абсциссой 1. Минимум окажется на границе интервала справа. На минус бесконечности значения приближаются к y=3 асимптотически.
Если взять интервал от 2-х до «плюс бесконечности», заданная функция не будет иметь ни максимумов, ни минимумов. Значения здесь стремятся к бесконечности. Связано это с тем, что x=2 является вертикальной асимптотой. Если абсцисса стремится к плюс бесконечности, значения будут асимптотически подходить к y=3. Соответствующий пример показан на рисунке 8.
Чтобы не приходилось долго разбираться с тем, как найти наименьшее у заданной функции, не путаться с тем, какие знаки производной использовать, а также легко строить графики, можно воспользоваться специальными онлайн калькуляторами. А еще – закончить тематические дистанционные онлайн курсы.
Страница не найдена — Фонд Наффилда
Страница не найдена — Фонд НаффилдаСтраница, которую вы ищете, не может быть найдена. Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.
Поиск проектов, новостей, влияния, событий
Поиск
Образование 655Когнитивные и некогнитивные навыки 33Учебная программа и выбор предметов 31Ранние годы 166Персонал образования 75Оценка образования 29Высшее образование 92Язык и грамотность Места58Обучение на протяжении всей жизни 79Пожизненное обучение 1ments аренда 75Педагогика 20Пост-16 образование и навыки 95Начальное образование 134Q-Step 26Эффективность школы 45Среднее образование 156Специальные образовательные потребности и инвалидность 57Системные проблемы образования 98Правосудие 235Доступ к правосудию 39Административное правосудие 26Гражданское правосудие 22Судебный опыт и доказательства 21Уголовное правосудие 24Домашнее насилие 5Равенство и права человека 771Искусственный интеллект 3Вспомогательная смерть 1Дополненная реальность 0Преимущества 52Обязанности по уходу 27Сообщества и социальная сплоченность 63Стоимость жизни 21Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 29Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 48Инвалидность 14Экономика, государственные расходы и услуги 182Этническая принадлежность 48Семья и семейная динамика 117Гендер 43Глобальное неравенство в отношении здоровья дети и нуждающиеся дети 74Психическое здоровье 91Нарушения опорно-двигательного аппарата 18Пенсии 16Физическое здоровье 50Бедность и уровень жизни 109Продуктивность и инновации 7Общественное здравоохранение 149Социальные медиа 2Социоэкономика старения 25Социоэкономика раннего взросления 42Спортивная наука 1Злоупотребление психоактивными веществами 11Налоги 48Доверие к демократии 65Оценка данных 5
166Персонал образования 75Оценка образования 29Высшее образование 92Язык и грамотность 79На протяжении всей жизни обучение 15Nuffield Research Placement 23Числа 84Воспитание детей 75Педагогика 20Образование и навыки после 16 лет 95Начальное образование 134Q-Step 26Эффективность школы 45Среднее образование 156Специальные образовательные потребности и инвалидность 57Системные проблемы образования 98Правосудие 235Доступ к правосудию 39Административное правосудие 26Гражданское правосудие 22Судебный опыт и доказательства 21Уголовное правосудие 24Домашнее насилие 5Равенство и права человека 771Искусственный интеллект 3Вспомогательная смерть 1Дополненная реальность 0Преимущества 52Обязанности по уходу 27Сообщества и социальная сплоченность 63Стоимость жизни 21Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 29Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 48Инвалидность 14Экономика, государственные расходы и услуги 182Этническая принадлежность 48Семья и семейная динамика 117Гендер 43Глобальное неравенство в отношении здоровья дети и нуждающиеся дети 74Психическое здоровье 91Нарушения опорно-двигательного аппарата 18Пенсии 16Физическое здоровье 50Бедность и уровень жизни 109Производительность и инновации 7Общественное здравоохранение 149Социальные сети 2Социоэкономика старения 25Социоэкономика раннего взросления 42Спортивная наука 1Злоупотребление психоактивными веществами 11Налоги 48Доверие к демократии 65Оценка данных 5
Ознакомьтесь с нашими проектами
В процессе
Образование | 2023 – 2025
Целенаправленная и эффективная практическая работа по естествознанию начальных классов
Посмотреть проект
Благосостояние | 2023 – 2026
Широкие плечи: повышение налогов в топ-
Посмотреть проект
Новый
Благосостояние | 2023 – 2024
Подтверждение аутсорсинга оказания социальной помощи в Англии
Посмотреть проект
Новый
Образование | 2023 – 2024
Оптимизация и осуществимость родительской программы Triple P для дистанционного обучения
Посмотреть проект
Новый
Благосостояние | 2023 – 2026
Продление трудовой жизни людям с заболеваниями опорно-двигательного аппарата
Посмотреть проект
Новый
Благосостояние | 2023 – 2025
Ювенильные ревматические заболевания: образование, профессиональная подготовка и трудоустройство
Посмотреть проект
Новый
Правосудие | 2023 – 2023
Создание и использование более качественных данных о правосудии
Посмотреть проект
Новый
Благосостояние | 2023 – 2025
Испытание PAW: осуществимость и приемлемость инструментария Pain-at-Work Toolkit
Посмотреть проект
Новый
Образование | 2023 – 2024
Приоритеты образования на следующих всеобщих выборах
Посмотреть проект
Новый
Образование | 2023 – 2023
Кризис стоимости жизни: влияние на школы
Посмотреть проект
Благосостояние | 2023 – 2026
Широкие плечи: повышение налогов наверху
Посмотреть проект
Новый
Образование | 2023 – 2024
Приоритеты образования на следующих всеобщих выборах
Посмотреть проект
Новый
Правосудие | 2023 – 2025
Физические наказания и последствия для детей в Великобритании
Посмотреть проект
Новый
Образование | 2023 – 2024
Оптимизация и осуществимость родительской программы Triple P для дистанционного обучения
Посмотреть проект
Новый
Образование | 2022 – 2024
Понимание использования прав на дошкольное образование
Посмотреть проект
Новый
Образование | 2023 – 2026
Переосмысление особых образовательных потребностей
Посмотреть проект
Новый
Благосостояние | 2023 – 2026
Артрит, работа и благополучие: исследование смешанных методов с рекомендациями по политике
Посмотреть проект
Новый
Благосостояние | 2023 – 2025
Испытание PAW: осуществимость и приемлемость инструментария Pain-at-Work Toolkit
Посмотреть проект
В процессе
Образование | 2022 – 2024
Работа или учеба? Пол и переход от учебы к работе
Посмотреть проект
В процессе
Благосостояние | 2023 – 2025
Региональный индекс регенерации для отслеживания социально-экономического «повышения уровня»
Посмотреть проект
В процессе
Образование | 2019 – 2024
Пути развития после 16 лет: роль сверстников, семейное положение и ожидания
Посмотреть проект
В процессе
Благосостояние | 2023 – 2024
Проектирование инклюзивной удаленной и гибридной работы для поддержки работников с ограниченными возможностями
Посмотреть проект
В процессе
Образование | 2023 – 2024
Влияние выявления потребностей в дополнительном обучении в Уэльсе
Посмотреть проект
В процессе
Образование | 2022 – 2024
Сравнение неравенства и результатов в системе образования после 16 лет в Великобритании
Посмотреть проект
В процессе
Правосудие | 2022 – 2025
Изучение расового неравенства при отвлечении от системы ювенальной юстиции
Посмотреть проект
В процессе
Благосостояние | 2022 – 2024
Жизнь детей в переменчивых местах
Посмотреть проект
В процессе
Правосудие | 2022 – 2024
Административная справедливость в цифровом государстве всеобщего благосостояния
Посмотреть проект
Новый
Благосостояние | 2023 – 2025
Дистанционное наставничество по остеоартрозу для малообеспеченных людей
Посмотреть проект
Новый
Благосостояние | 2023 – 2025
Ювенильные ревматические заболевания: образование, профессиональная подготовка и трудоустройство
Посмотреть проект
Новый
Благосостояние | 2023 – 2026
Продление трудовой жизни людям с заболеваниями опорно-двигательного аппарата
Посмотреть проект
Новый
Образование | Благосостояние | 2022 – 2024
Изменение выбора школы для более справедливого обучения в Англии
Посмотреть проект
Новый
Образование | 2022 – 2023
Среднесрочное влияние пандемии COVID-19 на учащихся с SEND
Посмотреть проект
Сообщено
Правосудие | 2019 – 2021
Личное представление свидетельских показаний адвокатами и сторонами в процессе
Посмотреть проект
Сообщено
Образование | 2020 – 2022
COVID-19 и уход за детьми: местные последствия в Англии
Посмотреть проект
Сообщено
Правосудие | 2020 – 2022
Когда свадьба не брак? Изучение не имеющих юридической силы церемоний
Посмотреть проект
Сообщено
Образование | 2020 – 2022
Этические принципы, лежащие в основе совместного производства с молодежью
Посмотреть проект
Сообщено
Образование | 2020 – 2021
Меры по смягчению последствий COVID-19: предоставление образования и доступ к специальным школам
Посмотреть проект
Сообщено
Образование | 2020 – 2022
Могут ли математические приложения повысить ценность обучения?
Посмотреть проект
Сообщено
Благосостояние | 2020 – 2021
Как кризис COVID-19 влияет на продовольственную безопасность
Посмотреть проект
Сообщено
Образование | 2020 – 2021
Влияние COVID-19 на общеобразовательные школы Англии
Посмотреть проект
Сообщено
Образование | Благосостояние | 2020 – 2022
Взросление в условиях COVID-19
Посмотреть проект
Увидеть всеПоследние
Последние
Как найти максимальную и минимальную точки с помощью дифференцирования
Следующие шаги были бы полезны для нахождения максимального и минимального значения функции с использованием первой и второй производной.
Шаг 1:
Пусть f(x) f(x) — функция. Найдите первую производную от f(x), которая равна f'(x).
Шаг 2 :
Приравняйте первую производную f'(x) к нулю и найдите x, которые называются критическими числами.
Шаг 3:
Найдите вторую производную f(x), которая равна f»(x).
Шаг 4:
Подставьте критические числа, найденные на шаге 2, во вторую производную f»(x).
Шаг 5:
Если f»(x) < 0 для некоторого значения x, скажем, x = a, то функция f(x) максимальна при x = a.
Если f»(x) > 0 для некоторого значения x, скажем, x = b, то функция f(x) минимальна при x = b.
Шаг 6:
Чтобы получить максимальное и минимальное значения замена функции x = a и x = b в f(x).
Максимальное значение = f(a)
Минимальное значение = f(b)
Шаг 7:
Максимальная точка: (a, f(a) )
Минимальная точка: (b, f(b))
Найдите максимальную и минимальную точки следующих функций:
Пример 1:
2x 3 — 3x 2 — 12x + 5
Решение:
Пусть f(x) = 2x 3 9039 397 — 12x + 5.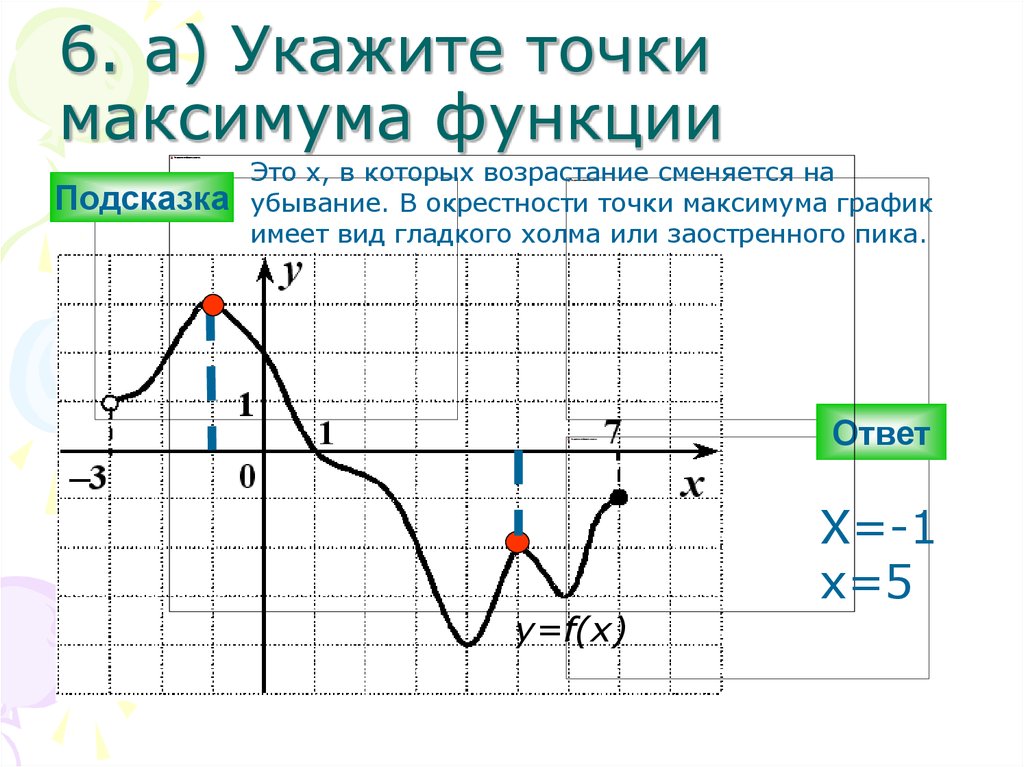
ф ‘(x) = 2(3x 2 ) — 3(2x) — 12(1) + 0
f'(x) = 6x 2 — 6x — 12
Приравнивание f'(x) к нулю ,
f'(x) = 0
6x 2 — 6x — 12 = 0
Разделите обе части на 6.
x 2 — x — 2 = 0
3 (
3 (х + 1) = 0
x — 2 = 0 или x + 1 = 0
x = 2 или x = -1
Найдите вторую производную «(x) = 6(2x) — 6(1) — 0
f»(x) = 12 x — 6
Подставим x = 2 в f»(x).
f»(2) = 12(2) — 6
= 24 — 6
f»(2) = 18 > 0 Минимум
Чтобы найти минимальное значение, подставьте x = 2 в f(x).
f(x) ) = 2 х 3 — 3 х 2 — 12 х + 5
f (2) = 2(2) 3 — 3(2) 2 — 12(2) + 5
= 2(8) — 3(4) — 24 + 5
= 16 — 12 — 24 + 5
= 21 — 36
= -15
Подставить x = -1 в f»(x). 90′-29 90’0’29 90 1) = 12(-1) -6
= -12 — 6
f»(-1) = -18 > 0 Максимум
Чтобы найти максимальное значение, подставьте x = -1 в f(x
f(x) = 2x 3 — 3x 2 — 12 х + 5
f(-1) = 2(-1) 3 — 3(-1) 2 — 12(-1) + 5
= 2(-1) — 3(1) + 12 + 5
= -2 — 3 + 12 + 5
= -5 + 17
= 12
Следовательно,
, максимальная точка = 1 ((1)
точка минимума = (2, 15)
Пример 2 :
Найдите максимальное и минимальное значение функции
Решение:
Пусть f(x) = x 3 — 3x 2 — 9 x + 12.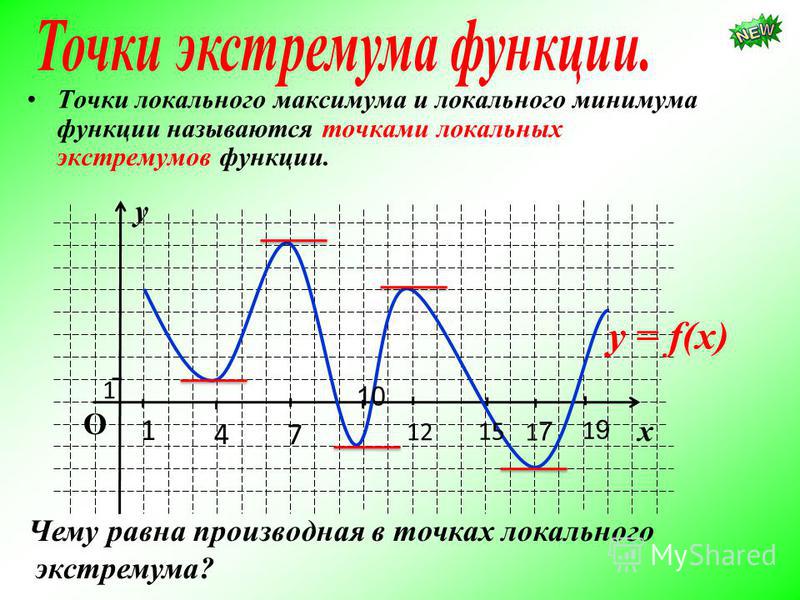

Leave A Comment