Равномерное движение по окружности | Физика
1. Основные характеристики равномерного движения по окружности
Движение по окружности часто встречается в природе и технике: по траекториям, близким к окружностям, движутся планеты вокруг Солнца, Луна и искусственные спутники Земли, точки колес и вращающихся деталей механизмов.
Мы ограничимся в нашем курсе равномерным движением по окружности. Напомним, что равномерным называют движение, при котором тело за любые равные промежутки времени проходит одинаковые пути.
Каковы же основные характеристики равномерного движения по окружности?
Прежде всего, это радиус окружности r и модуль скорости тела v (рис. 8.1). Далее мы увидим, что мгновенная скорость в каждой точке траектории направлена по касательной к траектории.
Следующей характеристикой равномерного движения по окружности является период обращения T. Он равен промежутку времени, в течение которого тело совершает один оборот.
? 1. Во сколько раз период обращения секундной стрелки меньше периода обращения часовой стрелки?
? 2.
T = 2πr/v. (1)
Частотой обращения ν называют число оборотов за единицу времени (секунду). Значение частоты не всегда целое число: например, если тело совершает 10 оборотов в секунду, то ν = 10 с-1, а если оно совершает пол-оборота в секунду, то ν = 0,5 с-1.
Чем больше частота обращения, тем меньше период.
? 3. Докажите, что период T и частота обращения ν связаны соотношением
ν = 1/T (2).
? 4. Чему равна частота обращения секундной стрелки, ми- К. нутной стрелки, часовой стрелки, Земли при ее суточном вращении и при ее движении вокруг Солнца?
2. Направление мгновенной скорости при движении по окружности
Поставим опыт
Затачивая инструмент с по: мощью точильного круга, можно заметить, что искры летят по касательной к кругу в точке, которой касается инструмент (рис. 8.2). Это раскаленные кусочки, оторвавшиеся от круга, поэтому их скорость в момент отрыва равна (по модулю и направлению) скорости точек диска, соприкасающихся с инструментом.
Этот опыт показывает, что при движении по окружности мгновенная скорость тела v_vec направлена по касательной к окружности в точке, где в данный момент находится тело.
Чтобы лучше осознать это, рассмотрим движение тела в течение времени Δt, малого по сравнению с периодом T. Пройденная за это время дуга окружности почти сливается с участком касательной к окружности (эта касательная показана голубой линией на рис. 8.3). А это как раз и означает, что мгновенная скорость тела направлена по касательной.
Заметим, что касательная к окружности в некоторой точке перпендикулярна радиусу окружности, проведенному в эту точку. Следовательно,
при движении по окружности мгновенная скорость тела v_vec направлена перпендикулярно радиусу, проведенному в точку, где находится тело в данный момент (см. рис. 8.1).
? 5. На рисунке 8.4 изображена траектория тела, движущегося по окружности. Перенесите рисунок в тетрадь и отметьте на нем:
б) точку С, в которой скорость тела составляет угол 45º со скоростью тела в момент, когда оно находится в точке А.

3. Ускорение при равномерном движении по окружности
Поскольку мгновенная скорость тела направлена по касательной в каждой точке траектории, направление скорости тела при его движении по окружности изменяется. А если скорость тела изменяется любым образом (пусть даже только по направлению), то это тело движется с ускорением. Итак, при равномерном движении по окружности тело движется с ускорением.
Докажем, что
при равномерном движении тела со скоростью v по окружности радиуса r:
а) ускорение тела в каждый момент времени направлено по радиусу к центру окружности,
б) модуль ускорения a = v2/r.
Направление ускорения
Поскольку
направление вектора ускорения совпадает с направлением вектора изменения скорости Δ.
Найдем изменение скорости Δ за промежуток времени Δt, малый по сравнению с периодом T.
Обозначим 1 скорость тела в момент времени t, а 2 скорость тела в момент времени t + Δt. Тогда
Тогда
Δ =2 – 1.
Обозначим Δα угол, на который повернется за время Δt радиус, проведенный в точку, где находится тело (рис. 8.5, а). Угол Δα мал, если Δt мало по сравнению с T.
На такой же угол Δα повернется за время Δt и вектор скорости тела (скорость остается все время перпендикулярной радиусу).
На рисунке 8.5, б показано, как найти изменение скорости Δ.
Векторы 1, 2 и Δ образуют равнобедренный треугольник с основанием Δ и малым углом Δα при вершине. Поэтому углы при основании этого треугольника близки к прямым углам (это следует из того, что сумма углов треугольника 180º).
Значит, изменение скорости Δ за очень малое время Δt направлено перпендикулярно скорости, то есть по радиусу, причем к центру окружности, как показано на рисунке 8.5, в. Ускорение направлено так же, как изменение скорости Δ, следовательно, ускорение тела направлено к центру окружности.
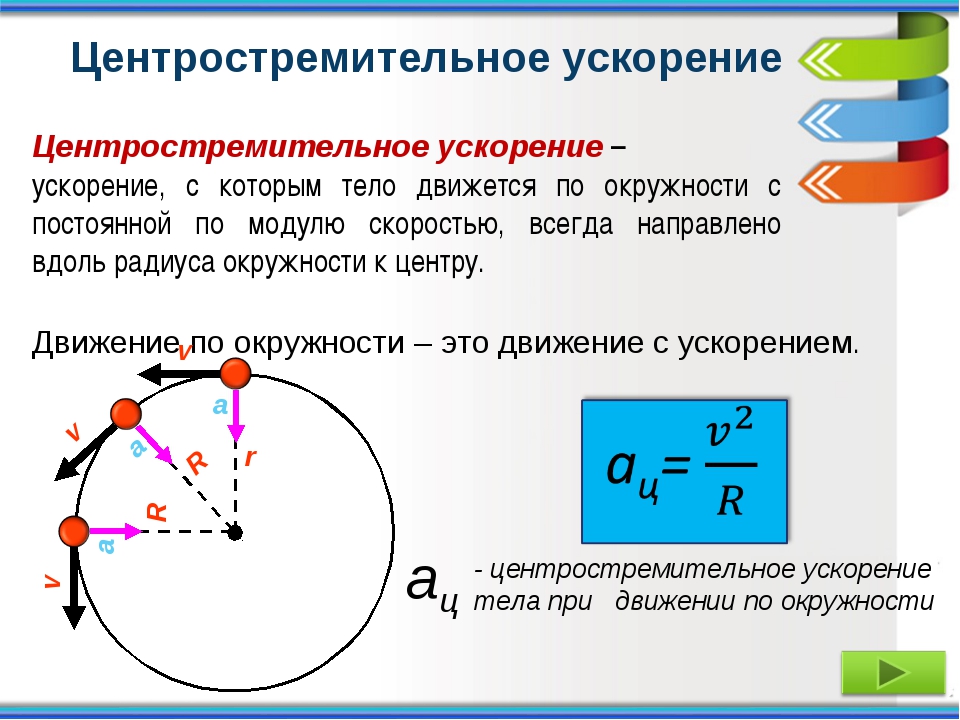
По этой причине ускорение тела при его движении по окружности часто называют центростремительным.
Из курса физики основной школы вы уже знаете, что ускорение тела обусловлено действующими на него силами. Например, при движении Земли вокруг Солнца силой, вызывающей центростремительное ускорение Земли, является сила тяготения со стороны Солнца.
? 6. Автомобиль поворачивает на 90º по дуге окружности. Изобразите на чертеже в тетради векторы скорости и ускорения автомобиля в середине дуги поворота.
Модуль ускорения
За промежуток времени Δt тело, движущееся со скоростью v, проходит по дуге окружности путь Δl = v * Δt (это красная сплошная линия на рисунке 8.6, а).
Если Δt мало по сравнению с T, эта дуга почти не отличается от отрезка прямой. Поэтому фигура, образованная двумя радиусами r и этим отрезком, представляет собой равнобедренный треугольник с основанием Δl = v * Δt.
Этот треугольник подобен равнобедренному треугольнику, образованному скоростями Δ1, Δ2 и изменением скорости Δ = * Δt (он изображен на рисунке 8.
(a * Δt) / (v * Δt) = v/r,
откуда получаем:
a = v2/r, (4)
Центростремительное ускорение можно выразить также через ν и r или через T и r.
? 7. Докажите, что центростремительное ускорение выражается также формулами
Подсказка. Воспользуйтесь формулами (4), (1), (2).
Можно подумать, что центростремительное ускорение, обусловленное изменением только направления скорости, не может быть значительным. Убедимся, что это не всегда так.
? 8. Чтобы космонавты без вреда для здоровья переносили большие перегрузки во время старта и посадки космического корабля, их тренируют с помощью специального аппарата – огромной центрифуги (рис. 8.7). Во время тренировки в Центре подготовки космонавтов им. Ю. А. Гагарина космонавт движется в капсуле (она изображена в левой части фотографии) по окружности радиусом 18 м.
а) С каким ускорением движется космонавт, когда центрифуга делает шесть оборотов в минуту?
б) При какой частоте обращения космонавт движется с ускорением, превышающим ускорение свободного падения в 10 раз? Чему равна при этом его линейная скорость?
? 9. Радиус колеса аттракциона 10 м. Чему равен период его обращения, когда пассажиры движутся с ускорением, в 2,5 раза превышающим ускорение свободного падения?
4. Угловая скорость
Иногда используют еще одну характеристику равномерного движения по окружности – угловую скорость ω. Ее определяют соотношением
ω = Δα/t,
где Δα – угол, на который за время t поворачивается радиус, проведенный к телу из центра окружности (рис. 8.9).
При атом угол измеряют в радианах, то есть одному полному обороту соответствует поворот на угол 2π.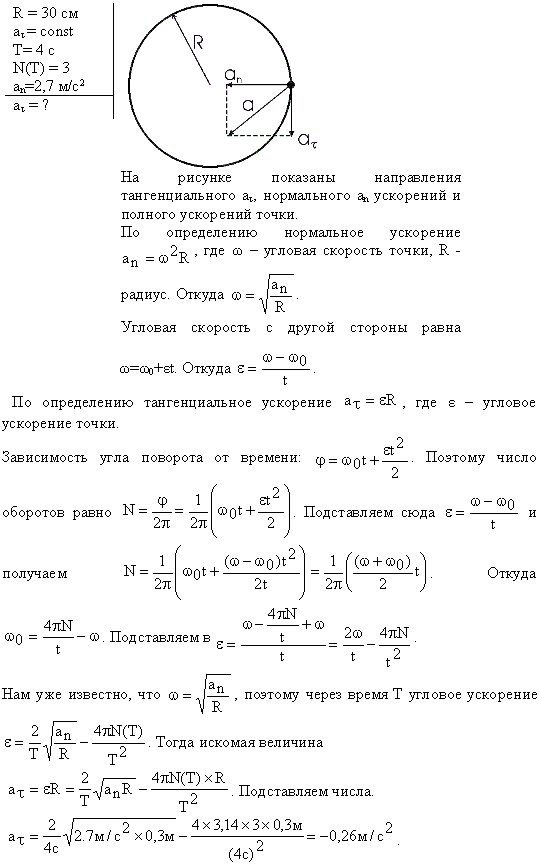
? 10. Какая скорость одинакова для всех точек минутной стрелки – линейная или угловая?
? 11. Во сколько раз угловая скорость секундной стрелки больше угловой скорости минутной стрелки?
? 12. Докажите, что угловая скорость связана с периодом обращения, частотой, радиусом окружности и скоростью соотношениями
ω = 2π/T, (7)
ω = 2πν, (8)
v = ωr. (9)
? 13.Чему равна угловая скорость движения точки поверхности Земли, обусловленная суточным вращением? Одинакова ли эта скорость для всех точек земной поверхности, находящихся: а) на одной параллели; б) на одном меридиане; в) на различных параллелях и меридианах?
? 14. Докажите, что центростремительное ускорение выражается через угловую скорость и радиус окружности формулой
a = ω2r. (10)
5.
 Катящееся колесо
Катящееся колесоРассмотрим движение различных точек колеса автомобиля.
Пусть автомобиль едет со скоростью (рис. 8.10), причем его колеса катятся без проскальзывания.
Что означают слова «без проскальзывания»? Это значит, что нижняя точка колеса А покоится относительно земли (при этом шины оставляют четкие следы). Этот факт – отправная точка для нахождения скорости всех других точек колеса – например, точек В, С, D на рисунке 8.10.
Чтобы найти скорость этих точек, удобно перейти в систему отсчета, связанную с автомобилем, а потом вернуться в систему отсчета, связанную с дорогой.
В системе отсчета, связанной с автомобилем, все точки обода колеса движутся по окружности с равными по модулю скоростями. Обозначим vвр модуль этой скорости, обусловленной вращением колеса вокруг своей оси. Выясним: как связаны скорость автомобиля v и скорость вращения vвр точек его колеса? Именно тут нам и поможет тот факт, что нижняя точка колеса А покоится относительно земли.
Заметим, что скорость Aвр вращения нижней точки А направлена противоположно скорости автомобиля (рис. 8.11).
Выразим через v и vвр скорость vА точки А в системе отсчета, связанной с дорогой. Согласно правилу сложения скоростей скорость точки А относительно дороги
A = Aвр + .
Итак, скорости Aвр и направлены противоположно, а их сумма A = 0. Следовательно,
vвр = v,
то есть скорость движения точек обода колеса в системе отсчета, связанной с автомобилем, равна но модулю скорости автомобиля.
? 15.Докажите, что скорость точки С (см. рис. 8.10) относительно дороги равна 2v.
? 16. Найдите направление и модуль скорости точек В и D (см. рис. 8.10) относительно земли.
? 17. Катушка с ниткой (рис. 8.12) может катиться по горизонтальному столу без проскальзывания. Конец нити тянут в горизонтальном направлении со скоростью, равной по модулю u (рис. 8.13). Внутренний радиус катушки r, а внешний R. Докажите, что катушка будет двигаться вправо со скоростью v = u(R/(R+r)).
Внутренний радиус катушки r, а внешний R. Докажите, что катушка будет двигаться вправо со скоростью v = u(R/(R+r)).
Подсказка. Рассмотрите движение точки А, воспользовавшись сложением скоростей, а также тем фактом, что точка катушки, касающаяся стола, покоится относительно стола.
? 18.С какой скоростью v и в каком направлении будет двигаться катушка в случае, изображенном на рисунке 8.14?
Если вы выполнили это задание правильно, ответ может показаться вам неправдоподобным. Попробуйте проверить его на опыте, проследив за тем, чтобы катушка катилась без проскальзывания.
? 19. С какой скоростью едет велосипедист, если сорвавшаяся с колеса в точке А (рис. 8.15) капелька попала снова в эту же точку? Радиус колеса 30 см.
Подсказка. Перейдите в систему отсчета, связанную с велосипедистом.
Дополнительные вопросы и задания
Необходимые для решения задач справочные данные, не приведенные в условии задачи, вы можете найти в конце учебника (под обложкой).
20. Длина минутной стрелки настенных часов 15 см, а часовой стрелки – 10 см. Какие величины можно определить из этого условия? Чему они равны?
21. Чему равна обусловленная суточным вращением скорость точек поверхности Земли, расположенных на экваторе? Длину экватора примите равной 40000 км.
22. Две шестеренки сцеплены, как показано на рисунке 8.16. Радиусы шестеренок 60 см и 30 см. Большая шестеренка вращается с частотой 2 с-1.
а) С какой скоростью движутся зубцы большой шестеренки?
б) По часовой стрелке или против нее движутся зубцы маленькой шестеренки? С какой скоростью они движутся?
в) Чему равна частота обращения маленькой шестеренки?
23. Диск радиусом 2 м равномерно вращается вокруг своей оси с периодом 0,5 с. Начертите графики зависимости скорости v и ускорения a точки диска от расстояния r до центра диска.
24. Наблюдения колец Сатурна (рис. 8.17) показали, что чем дальше от планеты находится участок кольца, тем меньше его скорость. Могут ли кольца Сатурна быть сплошными? Обоснуйте свой ответ.
Могут ли кольца Сатурна быть сплошными? Обоснуйте свой ответ.
Самолет летит вдоль 60-й параллели. Во время всего полета его пассажиры наблюдают Солнце в одной и той же точке небосвода. Длину экватора примите равной 40000 км.
а) В каком направлении летит самолет?
б) За какое время он совершит полный круг?
в) Какой путь самолет пролетит за это время?
г) С какой скоростью летит самолет?
26. Два тела равномерно движутся по окружностям радиусом 10 см и 1 м соответственно. У какого тела ускорение больше и во сколько раз, если:
а) скорости тел равны?
б) периоды обращения тел равны?
27. Во сколько раз ускорение точек земной поверхности на экваторе меньше ускорения свободного падения g? Во сколько раз надо было бы уменьшить продолжительность суток, чтобы оно стало равным g?
1) 2) 3) 4) 1) увеличить в 4 раза 2) уменьшить в 4 раза 3) уменьшить в 2 раза 4) увеличить в 2 раза
2,5 2,5.
 a x, м/с 2 2,5
a x, м/с 2 2,5Часть 1 Ответами к заданиям 1 4 являются цифра, число или последовательность цифр. Запишите ответ в поле ответа в тексте работы, а затем перенесите в БЛАНК ОТВЕТОВ 1 справа от номера соответствующего задания,
ПодробнееФизика ЕГЭ 2015 Тренировочный вариант 2
Часть 1 1. После толчка брусок скользит вверх по наклонной плоскости. В системе отсчета, связанной с плоскостью, направление оси 0x показано на рисунке. Направления векторов скорости бруска, его ускорения
ПодробнееВариант Задание 1
Параграфы 88-93 повторить выполнить упражнение 12. Выполнить тест Вариант 3679536 1. Задание 1 На рисунке изображены графики зависимости модуля скорости движения четырёх автомобилей от времени. Один из
ПодробнееОтвет: 35. Ответ: 21.

Задачи по теме «Электродинамика» (тексты Демидовой М.Ю. ЕГЭ-2017) Вариант 1 Задание 14. Пять одинаковых резисторов с сопротивлением 1 Ом соединены в электрическую цепь, через которую течёт ток I = 2 А
ПодробнееФизика ЕГЭ 2015 Тренировочный вариант 1
Часть 1 1. Тело начинает двигаться из начала координат вдоль оси Ох, причем проекция скорости v x меняется с течением времени по закону, приведенному на графике. Через 2 с ускорение тела равно 1) 0 м/с
ПодробнееОбразовательный портал «РЕШУ ЕГЭ» (
Вариант 2593766 1. Тело, брошенное вертикально вверх со скоростью через некоторое время упало на поверхность Земли. Какой график соответствует зависимости проекции скорости на ось ОХ от времени? Ось ОХ
ПодробнееОткрытая олимпиада Физтех-лицея 2015
И. В. Яковлев Материалы по физике MathUs.ru Открытая олимпиада Физтех-лицея 2015 Физика, 11 класс 1. На тонком прозрачном горизонтальном столе лежит тонкая собирающая линза с фокусным расстоянием F = 70
В. Яковлев Материалы по физике MathUs.ru Открытая олимпиада Физтех-лицея 2015 Физика, 11 класс 1. На тонком прозрачном горизонтальном столе лежит тонкая собирающая линза с фокусным расстоянием F = 70
Тренировочный вариант Часть 1
Тренировочный вариант 00 Часть А. На рисунке представлен график зависимости модуля скорости v автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 30
ПодробнееПовторить параграфы Выполнить работу
Повторить параграфы 76-93 Выполнить работу Выполнить вариант ЕГЭ РЕШЕНИЯ РПАСПИСАТЬ!!! Вариант 3697168 1. Задание 1 Точечное тело Т начинает двигаться по окружности с центром в точке О. В момент начала
ПодробнееОЛИМПИАДА ПО ФИЗИКЕ Вариант А
ОЛИМПИАДА ПО ФИЗИКЕ 7 Вариант А. С какой горизонтальной скоростью нужно бросить камень с вершины горы, склон которой образует угол с горизонтом, чтобы он упал на склон горы на расстоянии L от вершины?
С какой горизонтальной скоростью нужно бросить камень с вершины горы, склон которой образует угол с горизонтом, чтобы он упал на склон горы на расстоянии L от вершины?
Отложенные задания (25)
Отложенные задания (25) В области пространства, где находится частица с массой 1 мг и зарядом 2 10 11 Кл, создано однородное горизонтальное электрическое поле. Какова напряжённость этого поля, если из
Подробнее«Академика»
Комплексная олимпиада школьников «Академика» [email protected] 1. Начальная скорость камня, брошенного под некоторым углом к горизонту, равна 10 м/с, а спустя время 0,5 с скорость камня равна 7 м/с. На
ПодробнееЗадания 1. Физические величины
Задания 1. Физические величины 1. Задание 1 46. Для каждого физического понятия из первого столбца подберите соответствующий пример из второго столбца. Запишите в таблицу выбранные цифры под соответствующими
Запишите в таблицу выбранные цифры под соответствующими
ID_969 1/8 neznaika.pro
Вариант 1 Часть 1 Ответами к заданиям 1 23 являются слово, число или последовательность цифр или чисел. Запишите ответ в соответствующее поле справа. Каждый символ пишите без пробелов. Единицы измерения
ПодробнееОткрытый банк заданий ЕГЭ
Воздушный шар объемом 2500 м 3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Какова максимальная масса груза, который может поднять шар, если воздух
ПодробнееОбразец возможного решения
Физика. 11 класс. Вариант 1 1 Критерии оценивания заданий с развёрнутым ответом C1 Медный стержень укреплен на штативе в горизонтальном положении. К нижней поверхности стержня на равных расстояниях друг
ПодробнееИнструкция по выполнению работы
Класс Фамилия, имя (полностью) Дата 014 г. Инструкция по выполнению работы На выполнение экзаменационной работы по физике отводится 60 минут. Работа состоит из 3 частей, включающих в себя 17 заданий. Часть
Инструкция по выполнению работы На выполнение экзаменационной работы по физике отводится 60 минут. Работа состоит из 3 частей, включающих в себя 17 заданий. Часть
Олимпиада «Физтех» по физике 2017
Олимпиада «Физтех» по физике 217 Класс 11 Билет 11-3 Шифр 1. На наклоненной под углом ( cos 3/ 4 ) к горизонту поверхности лежит брусок, прикрепленный к упругой невесомой и достаточно длинной пружине (см.
Подробнее/ /13
Вариант 3580642 1. Задание 27 1926 На входе в электрическую цепь квартиры стоит предохранитель, размыкающий цепь при силе тока 20 А. Подаваемое в цепь напряжение равно 220 В. Какое максимальное количество
Подробнее1) 10 м 2) 15 м 3) 25 м 4) 45 м
Часть 1 При выполнении заданий части 1 в бланке ответов 1 под номером выполняемого вами задания (А1-А25) поставьте знак «х» в клеточке, номер которой соответствует номеру выбранного вами ответа. А1. Тело
А1. Тело
Олимпиада «Физтех» по физике
И. В. Яковлев Материалы по физике MathUs.ru Олимпиада «Физтех» по физике 11 класс, онлайн-этап, 2013/14 год 1. Камень, брошенный с крыши сарая почти вертикально вверх со скоростью 15 м/с, упал на землю
ПодробнееОбразовательный портал «РЕШУ ЕГЭ» (
Вариант 2593761 1. Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах
Подробнее/6 A Б В Г Д
Вариант 3366482 1. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 45 с? Ответ выразите в м/с 2. 2. На брусок массой 5 кг,
ПодробнееТренировочные задания.
 Часть А. Движение тела по окружности
Часть А. Движение тела по окружностиДвижение тела по окружности. Часть А.
Любое криволинейное движение можно представить
как движение по отрезкам прямых и дугам окружностей,
с радиусами R1, R2, R3 R1 R2 R3
А
В φ – угол поворота радиуса вектора
ω = Угловая скорость — физическая величина,
показывающая угловое перемещение за единицу времени.
Линейная скорость – физическая величина, показывающая путь,
пройденный телом за единицу времени.
V = где l – длина дуги АВ, R — радиус
Период – время одного оборота. Т = Единица измерения – 1 сек.
Частота
– число оборотов за единицу времени. ν = Единица измерения – 1 Гц.
ν = Единица измерения – 1 Гц.
Связь линейной и угловой скорости: V = ω R;
При движении тела по окружности вектор перемещения направлен по хорде, вектор скорости – по касательной, а ускорение – к центру.
А
B а =
·O a
VB
Тренировочные задания. Часть А. Движение тела по окружности.
1(6-2006) Кубик массой 100г лежит без скольжения на вращающемся горизонтальном диске на расстоянии 50 см от оси вращения, при этом относительно модуль скорости кубика равен 2 м/с. Центростремительное ускорение кубика равно: 1) 12, 5м/с2; 2) 0,08м/с2; 3) 8м/с2; 4) 25м/с2;
2.(ЕГЭ-07.Тр). Материальная точка, двигаясь равномерно А
по окружности против часовой стрелки, через 3 с
первый раз попала из точки А в точку В.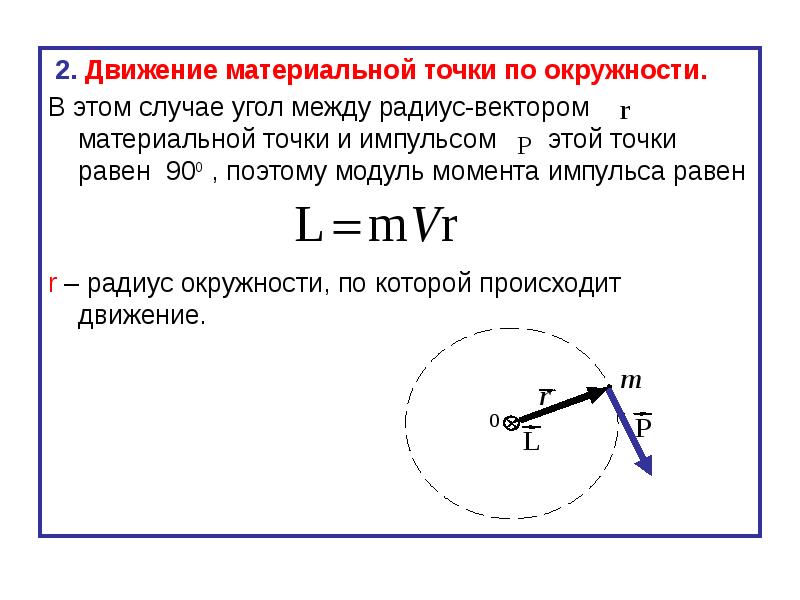
Частота обращения точки равна …
1); 2) ;3) ; 4) ; В
3.(ЕГЭ-07) Автомобиль движется с постоянной 1
по модулю скоростью по траектории,
представленной на рисунке. В какой из 2
указанных точек траектории центростремительное
ускорение максимально? 3
1) 1; 2) 2; 3) 3; 4) Во всех точках одинаково.
4.(1-07 ТР) Две материальные точки движутся по окружностям радиусами R1 и R2 = 2R1 с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением 1) Т1 = 0,5 Т2 ; 2) Т1 = Т2; 3) Т1 = 2Т2; 4) Т1 = 4Т1;
5.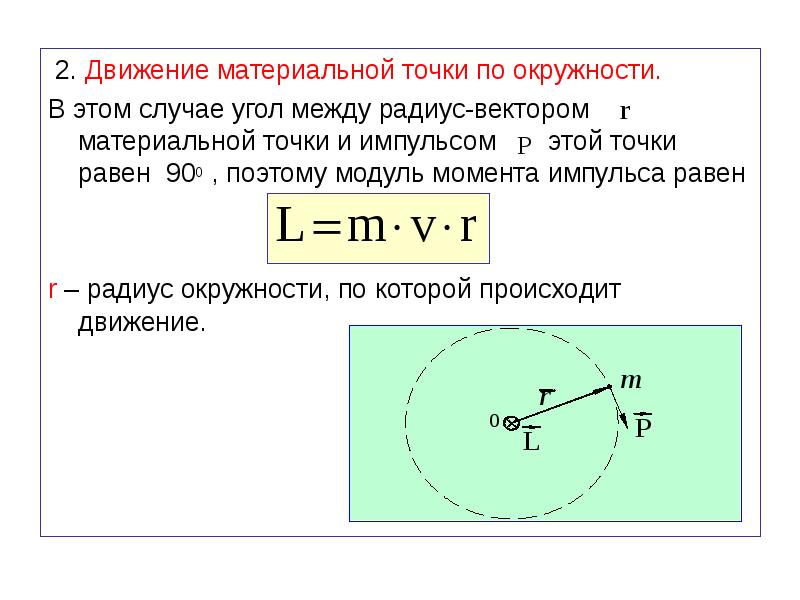 (Дем. Вар 07). Две материальные точки
движутся по окружностям радиусами R1 и R2 = 2R1.
При условии равенства линейных скоростей
точек их центростремительные ускорения
связаны соотношением 1) а1 = 2 а2; 2) а1 =
а2; 3) а1 =
0,5 а2; 4) а1 =
4 а2;
(Дем. Вар 07). Две материальные точки
движутся по окружностям радиусами R1 и R2 = 2R1.
При условии равенства линейных скоростей
точек их центростремительные ускорения
связаны соотношением 1) а1 = 2 а2; 2) а1 =
а2; 3) а1 =
0,5 а2; 4) а1 =
4 а2;
6.(62-06) Материальная точка движется по окружности. Как изменится величина ее центростремительного ускорения, если скорость увеличить в 2 раза, а радиус окружности в 2 раза уменьшить?
1) увеличится в 2 раза; 2) уменьшится в 2 раза; 3) увеличится в 4 раза; 4) уменьшится в 4 раза;
7.(254-05) Точка движется по окружности радиуса R со скоростью V. Как нужно изменить радиус окружности, сохранив скорость точки прежней, чтобы ее центростремительное ускорение при этом увеличилось вдвое? 1) увеличить в 2 раза; 2) увеличить в 4 раза; 3) уменьшить в 2 раза; 4) уменьшить в 4 раза;
8 (134-05) Самолет
движется с постоянной по модулю скоростью
по горизонтальной окружности. Как
направлен вектор ускорения самолета
при таком движении? 1) в плоскости
окружности от ее центра. 2) в направлении
вектора скорости. 3) противоположно
вектору скорости.
Как
направлен вектор ускорения самолета
при таком движении? 1) в плоскости
окружности от ее центра. 2) в направлении
вектора скорости. 3) противоположно
вектору скорости.
4) в плоскости окружности к ее центру.
9. Материальная точка движется по окружности. Ее скорость увеличивают в 2 раза. Как нужно изменить радиус окружности, чтобы величина центростремительного ускорения точки не изменилась? 1) увеличить в 4 раза; 2) увеличить в 2 раза; 3) уменьшить в 2 раза; 4) уменьшить в 4 раза;
10. Автомобиль движется по окружности радиусом 100 м со скоростью 10 м/с. Центростремительное ускорение автомобиля равно 1) 1 м/с2; 2) 5 м/с2 3) 10 м/с2 4) 0,1 м/с2.
11. При равномерном движении тела по окружности остается постоянной6 1) линейная скорость. 2) угловая скорость. 3) период обращения. 4) частота обращения.
12. Тело движется равномерно по окружности
в направлении 2
Тело движется равномерно по окружности
в направлении 2
против часовой стрелки. Какая стрелка (рис) указывает направление 2
вектора скорости при таком движении? 1
А)1; б) 2; в) 3; г) 4; д) 5; 5
13. . Тело движется равномерно по окружности в направлении 2
против часовой стрелки. Какая стрелка (рис) указывает направление 2
вектора ускорения при таком движении? 1
А)1; б) 2; в) 3; г) 4; д) 5; 5
14. Автомобиль массой 1000 кг движется по выпуклому мосту радиус кривизны которого равен 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали состояние невесомости?1) 0,05 м/с 2) 20 м/с 3) 25 м/с 4) 400 м/с
15. Чему
равна линейная скорость верхней точки
протектора колеса автомобиля относительно
земли, если скорость движения автомобиля
15 м/с?
Чему
равна линейная скорость верхней точки
протектора колеса автомобиля относительно
земли, если скорость движения автомобиля
15 м/с?
1) 0; 2) 15 м/с; 3) 30 м/с 4) 60 м/с;
16. Тело совершает 50 оборотов за π секунд. На каком расстоянии от оси вращения находится точка, движущаяся со скоростью 10 м/с
1) 0,1 м; 2) 1 м; 3) 0,2π м; 4) 0,1π м
17. Круглый диск радиусом R катится без проскальзывания по горизонтальной плоскости, вращаясь с угловой скоростью ω. Чему равны скорости точек А, В, С (рис. ) относительно земли? 1) 0, ; 2ωR.2) ωR, ωR,ωR. 3) ; 2ωR.4) 0;2ωR ;/2;5) ) 0; 4ωR ;; 5
18. Циркулярная пила имеет диаметр D = 600 мм. На ось пилы насажен шкив диаметром d1 = 300 мм, который приводится во вращение посредством ременной передачи от шкива диаметром d2 = 120 мм, насаженного на вал электродвигателя (рис. 41). Какова скорость пилы, если вал двигателя совершает 1200 об/мин? ( Ответ: 15 м/с)
19. Шарик
на стержне равномерно вращается в
горизонтальной плоскости. На графике
(рис. 42) представлена зависимость
центростремительного ускорения шарика
от его линейной скорости. Какова длина
стержня? (Размеры шарика много меньше
длины стержня.)
Шарик
на стержне равномерно вращается в
горизонтальной плоскости. На графике
(рис. 42) представлена зависимость
центростремительного ускорения шарика
от его линейной скорости. Какова длина
стержня? (Размеры шарика много меньше
длины стержня.)
1) 1 м. 2)1,5 м. 3)З м. 4)9 м. 5)27м.
20. За 10 с точка прошла равномерно половину окружности, радиус которой 100 см. Определить линейную скорость.1)0,314м/с; 2) 0,1 м/с; 3)10 м/с; 4) 6,28 м/с;
21(136). Каков период вращения секундной, минутной и часовой стрелки часов? Какова частота вращения?
22(141). Скорость поезда 72 км/ч. Сколько оборотов в минуту делают колеса локомотива, радиус которых 1,2 м?1)2,65 об; 2)159об; 3) 38,2об; 4)60 об.
23(144). Обтачиваемый на токарном станке вал диаметром 80 мм вращается с частотой 600 об/мин. Определить скорость резания.
24.(254) Точка движется по окружности радиуса R со скоростью V. Как нужно изменить радиус окружности, сохранив скорость точки прежней, чтобы ее центростремительное ускорение при этом увеличилось вдвое? 1) увеличить в 2 раза; 2) увеличить в 4 раза; 3) уменьшить в 2 раза; 4) уменьшить в 4 раза;
25 (134) Самолет движется
с постоянной по модулю скоростью по
горизонтальной окружности. Как направлен
вектор ускорения самолета при таком
движении? 1) в плоскости окружности от
ее центра. 2) в направлении вектора
скорости. 3) противоположно вектору
скорости.
Как направлен
вектор ускорения самолета при таком
движении? 1) в плоскости окружности от
ее центра. 2) в направлении вектора
скорости. 3) противоположно вектору
скорости.
4) в плоскости окружности к ее центру.
26. Материальная точка движется по окружности. Ее скорость увеличивают в 2 раза. Как нужно изменить радиус окружности, чтобы величина центростремительного ускорения точки не изменилась? 1) увеличить в 4 раза; 2) увеличить в 2 раза; 3) уменьшить в 2 раза; 4) уменьшить в 4 раза;
27. Автомобиль движется по окружности радиусом 100 м со скоростью 10 м/с. Центростремительное ускорение автомобиля равно 1) 1 м/с2; 2) 5 м/с2 3) 10 м/с2 4) 0,1 м/с2.
150. Какова частота, и угловая скорость вращения колеса ветродвигателя, если за 2 мин (точно) колесо сделало 500 оборотов?
151. Во сколько раз угловая скорость минутной стрелки часов больше угловой скорости часовой стрелки?
152. На
вал плотно насажены два шкива; диаметр
первого 10 см, а второго 20см (сравнить
угловые скорости шкивов.
На
вал плотно насажены два шкива; диаметр
первого 10 см, а второго 20см (сравнить
угловые скорости шкивов.
154. Ветряное колесо радиусом 2,0 м делает 40,0 об/мин. Каково центростремительное ускорение концевых точек лопастей колеса? При какой частоте вращения центростремительное ускорение будет в 2 раза больше?
155. Какова линейная скорость тела, движущегося равномерно по окружности радиусом 3,0 м, если центростремительное ускорение равно 12 см/с2?
156. При постоянной скорости 900 км/ч самолет описывает вертикальную петлю. При каком радиусе петли центростремительное ускорение не превысит 5g?
157. Шкив вращается с угловой скоростью 50 рад/с. Определить центростремительные ускорения точек, находящихся на расстоянии 20 и 80 мм от оси вращения.
24(148). Определить угловые, скорости валов, Вращающихся с периодами Т1 = 10 с, Т2 = 0,050 с, Т3 = 1,00∙10 с.
25(149).
Определить угловые скорости валов,
частоты, вращения которых 24, 60, 1800 об/мин.
Равномерное движение точки по окружности
Равномерное движение по окружности – это простейший пример криволинейного движения. Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость.
При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть \(v = const,\) а изменяется только направление вектора скорости. Тангенциальное ускорение в этом случае отсутствует \( (a_r = 0),\) а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительным ускорением (нормальное ускорение) \(a_n\), или \(a_{цс}\). В каждой точке траектории вектор центростремительного ускорения направлен к центру окружности по радиусу.
Модуль центростремительного ускорения равен \(a_{цс}=\frac{υ_2}{ R},\) где \(υ\) – линейная скорость, \(R\) – радиус окружности. \circ18\)’ . Угловая скорость равномерного движения тела по окружности – это величина \(\omega\), равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершен этот поворот: \(ω = \frac φ t \). Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени \(t: υ= \frac l t \). Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина \(l\) дуги окружности, пройденной точкой, связана с углом поворота φ выражением \(l = Rφ\), где \(R\) – радиус окружности.
\circ18\)’ . Угловая скорость равномерного движения тела по окружности – это величина \(\omega\), равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершен этот поворот: \(ω = \frac φ t \). Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени \(t: υ= \frac l t \). Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина \(l\) дуги окружности, пройденной точкой, связана с углом поворота φ выражением \(l = Rφ\), где \(R\) – радиус окружности.
Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:
\(υ = \frac l t =\frac{ Rφ} t = Rω\), или \(υ = Rω\).
Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности. 2\).
2\).
4.4 Равномерное круговое движение | University Physics Volume 1
Частица, совершающая круговое движение, может быть описана ее вектором положения [latex] \ overset {\ to} {r} (t). [/ latex] (Рисунок) показывает частицу, совершающую круговое движение против часовой стрелки. Когда частица движется по кругу, ее вектор положения сметает угол [латекс] \ тета [/ латекс] с осью x —. Вектор [латекс] \ overset {\ to} {r} (t) [/ latex], образующий угол [латекс] \ theta [/ latex] с осью x- , показан с его компонентами вдоль оси x — и y — оси.Величина вектора положения [латекс] A = | \ overset {\ to} {r} (t) | [/ latex] и также является радиусом круга, так что с точки зрения его компонентов,
Здесь [latex] \ omega [/ latex] — это постоянная, называемая угловой частотой частицы. Угловая частота измеряется в радианах (рад) в секунду и представляет собой просто количество радианов угловой меры, через которую проходит частица за секунду. {2} \ overset {\ to} {r} (t).{-7} \ text {s} = 200 \, \ text {ns} \ text {.} [/ Latex] Показана траектория протона. Угол, под которым протон движется по окружности, составляет 5,712 рад, что немного меньше одного полного оборота.
{2} \ overset {\ to} {r} (t).{-7} \ text {s} = 200 \, \ text {ns} \ text {.} [/ Latex] Показана траектория протона. Угол, под которым протон движется по окружности, составляет 5,712 рад, что немного меньше одного полного оборота.
Значение
Мы выбрали начальное положение частицы на оси x —. Это было совершенно произвольно. Если бы была задана другая начальная позиция, у нас было бы другое конечное положение при t = 200 нс.
Равномерное круговое движение
Введение
Равномерное круговое движение — это движение объекта, движущегося с постоянной (равномерной) скоростью по круговой траектории.Помимо скорости, есть несколько других переменных, которые используются для характеристики движения. Это радиус движения r , угловая скорость ω , период T и частота вращения f . Период — это время, необходимое для того, чтобы объект совершил один оборот движения.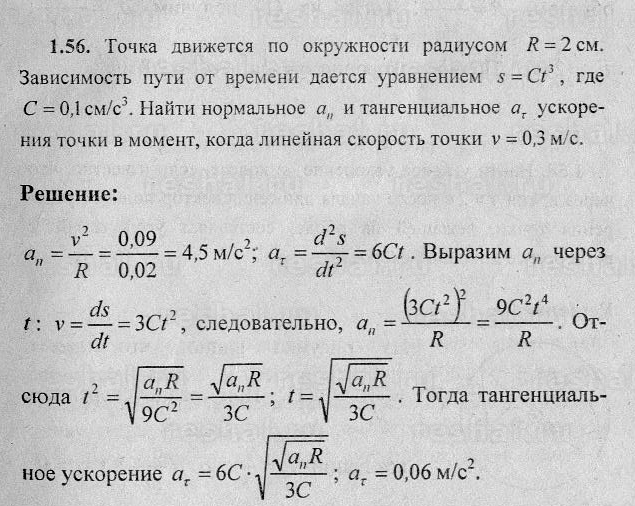 Угловая скорость — это угловое смещение в секунду, которое связано с частотой следующим образом: с ω в рад / с.Частота вращения — это количество оборотов в секунду и определяется как: с f в Гц или сек -1 . Скорость объекта является касательной к окружности с величиной v = rω . Ускорение , a направлено к центру круга (центростремительное) с величиной, определяемой следующим образом: с и в м / с 2 . Чтобы объект массой м мог двигаться по окружности с постоянной скоростью, на объект должна действовать чистая центростремительная сила.Величина результирующей силы F должна быть постоянной и связана с центростремительным ускорением вторым законом Ньютона: с F в N. Эта центростремительная сила может быть обеспечена за счет натяжения (как в этой лаборатории), трения (как для автомобиля, движущегося по кривой), нормальной силы (как в петлеобразных американских горках) или гравитации (как для движения спутника).
Угловая скорость — это угловое смещение в секунду, которое связано с частотой следующим образом: с ω в рад / с.Частота вращения — это количество оборотов в секунду и определяется как: с f в Гц или сек -1 . Скорость объекта является касательной к окружности с величиной v = rω . Ускорение , a направлено к центру круга (центростремительное) с величиной, определяемой следующим образом: с и в м / с 2 . Чтобы объект массой м мог двигаться по окружности с постоянной скоростью, на объект должна действовать чистая центростремительная сила.Величина результирующей силы F должна быть постоянной и связана с центростремительным ускорением вторым законом Ньютона: с F в N. Эта центростремительная сила может быть обеспечена за счет натяжения (как в этой лаборатории), трения (как для автомобиля, движущегося по кривой), нормальной силы (как в петлеобразных американских горках) или гравитации (как для движения спутника). В этом эксперименте вы будете измерять период объекта, совершающего равномерное круговое движение с фиксированным радиусом, но с различными значениями F .По периоду можно рассчитать угловую скорость. Используя эти известные значения и приведенные выше уравнения, вы можете найти эмпирическую массу вращающегося объекта и сравнить его со значением массы, полученным путем непосредственного взвешивания его на весах.
В этом эксперименте вы будете измерять период объекта, совершающего равномерное круговое движение с фиксированным радиусом, но с различными значениями F .По периоду можно рассчитать угловую скорость. Используя эти известные значения и приведенные выше уравнения, вы можете найти эмпирическую массу вращающегося объекта и сравнить его со значением массы, полученным путем непосредственного взвешивания его на весах.Аппарат UCM
Аппарат UCM состоит из платформы с регулируемой скоростью вращения . На расстоянии х от центра вращения находится узел боковой стойки , на котором висит объект массой м , называемый вращающейся массой (не путать со статической массой ).Вращающаяся масса прикреплена к пружине на центральной стойке с помощью струны и небольшого шкива. Когда платформа вращается, вращающаяся масса будет перемещаться по круговому пути из-за силы, прилагаемой к ней струной (посредством натяжения пружины). Поскольку невозможно получить мгновенное считывание этой силы натяжения во время вращения платформы, будет производиться косвенное измерение этой силы с использованием веса статической массы, как показано и объяснено ниже.
Поскольку невозможно получить мгновенное считывание этой силы натяжения во время вращения платформы, будет производиться косвенное измерение этой силы с использованием веса статической массы, как показано и объяснено ниже.Рисунок 1
Когда платформа не вращается, вращающаяся масса не свисает вертикально с боковой стойки, а, скорее, втягивается внутрь за счет натяжения струны и пружины. При проведении эксперимента вы будете регулировать скорость вращения платформы до тех пор, пока вращающаяся масса не будет висеть вертикально на радиусе r . Оранжевый индикаторный диск поможет вам определить, когда вращающаяся масса достигла этого положения.Рисунок 2
Период вращения измеряется секундомером .Платформу можно вращать, поворачивая вручную стержень с накаткой.Процедура
Выравнивание прибора
Если платформа неровная, это отрицательно скажется на ваших результатах. Студенты в первой лаборатории недели должны были уже выровнять прибор. Будем надеяться, что с тех пор аппарат не перемещали, и его не нужно будет снова выравнивать. Проверьте, выровнено ли ваше устройство, включив двигатель регулировки скорости и наблюдая за оранжевым индикаторным диском, чтобы увидеть, качается ли он вверх и вниз при вращении платформы.Если ваше устройство необходимо выровнять, выполните следующие действия.
Студенты в первой лаборатории недели должны были уже выровнять прибор. Будем надеяться, что с тех пор аппарат не перемещали, и его не нужно будет снова выравнивать. Проверьте, выровнено ли ваше устройство, включив двигатель регулировки скорости и наблюдая за оранжевым индикаторным диском, чтобы увидеть, качается ли он вверх и вниз при вращении платформы.Если ваше устройство необходимо выровнять, выполните следующие действия.1
Чтобы примерно выровнять платформу, поместите пузырьковый уровень в середину платформы и отрегулируйте два регулировочных винта на основании устройства, пока пузырь не будет отцентрирован.2
Поместите дополнительную массу (~ 500 г) на тот же конец вращающейся платформы, что и вращающаяся масса. Если платформа неровная, тяжелый конец будет качаться в низкую сторону.3
Отрегулируйте регулировочные винты на ножках основания до тех пор, пока конец платформы не будет качаться равномерно при легком вращении рукой.
Установка радиуса
1
Осторожно отсоедините вращающуюся массу от струн. Используйте весы, чтобы взвесить его, и запишите значение массы.2
Подвесьте вращающуюся гирю к боковой стойке и подсоедините шнур от пружины к гири.Убедитесь, что эта струна проходит под (а не за) маленьким шкивом на центральной стойке.3
Переместите кронштейн индикатора на центральной стойке в самое нижнее положение.4
Потяните вращающуюся массу в сторону от центральной стойки, пока оранжевый индикатор не окажется в центре кронштейна. Если струна, поддерживающая вращающийся груз, не является вертикальной, когда индикатор совмещен с кронштейном, боковую стойку следует перемещать внутрь или наружу, пока струна не станет вертикальной.Используйте вертикальную линию на боковой стойке, чтобы облегчить это выравнивание. При затягивании боковой стойки, нажмите на платформу, чтобы убедиться, что она надежно удерживается в вертикальном положении, и избегайте чрезмерного затягивания и поломки пластикового винта с накатанной головкой!5
Измерьте и запишите радиус вместе с оценкой погрешности на основании центровки.
6
Теперь ваш аппарат должен быть готов к работе в максимально широком диапазоне центростремительных сил.(Почему это важно?) Центростремительную силу можно изменять, перемещая опору пружины вверх и вниз, при этом другие части устройства остаются на месте. Этот диапазон движение по центральной стойке должно составлять не менее 5 см, что соответствует диапазону натяжения пружины примерно 1,2 Н.
Установка величины центростремительной силы
В этой первой части процедуры вы будете использовать метод static (без вращения) для настройки прибора на известное значение центростремительной силы.1
Прикрепите фиксирующий шкив к концу платформы, ближайшему к вращающейся массе. Прикрепите шнур к вращающейся массе и навесьте известную массу (начиная с 20 г) над зажимным роликом. Отрегулируйте прижимной шкив вверх или вниз по мере необходимости так, чтобы шнур между шкивом и вращающаяся масса расположена горизонтально. (Почему это важно?)
(Почему это важно?)2
Запишите значение этой статической массы , которая будет определять центростремительную силу.3
Отрегулируйте опору пружины по вертикали, пока оранжевый индикаторный диск не окажется в центре держателя индикатора. Теперь устройство должно быть выровнено, чтобы точно знать радиус движения вращающейся массы, когда платформа вращается.
КПП 1:
Прежде чем продолжить, попросите ТА проверить ваше устройство.
Измерение периода
1
Снимите статическую массу и струну с вращающейся массы. (Зачем?)2
Поверните устройство, равномерно повернув стержень с накаткой по часовой стрелке. Уделите минуту, чтобы прочувствовать поворот платформы с постоянной скоростью. Увеличивайте скорость до тех пор, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора на центральной стойке.Это указывает на то, что струна, поддерживающая вращающуюся массу, вертикальна и, следовательно, масса находится на желаемом радиусе.
Уделите минуту, чтобы прочувствовать поворот платформы с постоянной скоростью. Увеличивайте скорость до тех пор, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора на центральной стойке.Это указывает на то, что струна, поддерживающая вращающуюся массу, вертикальна и, следовательно, масса находится на желаемом радиусе.3
Когда один партнер по лаборатории вращает платформу, другой должен использовать секундомер для измерения времени, необходимого для совершения одного оборота. Сделайте десять таких измерений.4
Альтернативный метод измерения среднего периода заключается в использовании секундомера для измерения времени для N (например, 10) оборотов и деления на N, чтобы получить T .Сделайте это хотя бы для одного испытания и сравните со значением, полученным с помощью процедуры, приведенной в шаге 3. Какой метод, по вашему мнению, более точен?5
Прежде чем продолжить, проверьте свои результаты для этой единственной точки данных и подтвердите, что ваше эмпирическое значение для вращающейся массы является разумным. Если ваш результат не имеет смысла, проанализируйте свою процедуру и исправьте все ошибки, прежде чем брать дополнительные данные.
Если ваш результат не имеет смысла, проанализируйте свою процедуру и исправьте все ошибки, прежде чем брать дополнительные данные.
КПП 2:
Перед тем, как продолжить, ваш технический специалист должен проверить ваши данные и результаты расчетов.
Изменение центростремительной силы
Повторите описанную выше процедуру как минимум с пятью различными статическими массами (и, следовательно, с пятью различными силами), которые охватывают максимально широкий диапазон значений (обычно от 40 до 150 г).Анализ
1
Вес статической массы, висящей на шкиве, равен центростремительной силе F , приложенной пружиной. Вычислите эту силу для каждого из пяти испытаний, умножив статическую массу на г , и запишите результаты.2
Для каждой центростремительной силы F вычислите средний период вращения T и его стандартную ошибку.
3
Для каждого значения F рассчитайте ω 2 и его неопределенность из4
Постройте график ω 2 против F (с планками ошибок) и выполните аппроксимацию методом наименьших квадратов.5
Определите экспериментальное значение вращающейся массы, м , исходя из наклона графика и уравнения центростремительной силы.Определите пересечение и линейного соответствия вашим данным. Это то, чего вы ожидаете?
Обсуждение
Сравните значение м , полученное при подборе кривой, с измеренными значениями вращающейся массы м и радиуса движения r . Есть согласие в пределах неопределенностей? Если вы проведете этот эксперимент осторожно, вы сможете получить результаты с ошибкой менее 3%. Сравните значение интерцепта y с ожидаемым значением.Они согласны? Почему для этого (и большинства других) экспериментов важно получить данные в самом широком диапазоне значений? Каковы потенциальные последствия близкого расположения точек данных? Объясните, как вы собираете данные с помощью этого устройства, чтобы проверить следующую гипотезу: для данного значения центростремительной силы F радиус движения r обратно пропорционален квадрату угловой скорости ω .
Copyright © 2011 Advanced Instructional Systems, Inc. и Университет Северной Каролины | Кредиты
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследование
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что Вы ищете? Увидеть больше результатов
Предложения или отзывы?
Веб-сайт класса физики
Круговое движение и гравитация: обзор набора задач
Этот набор из 27 задач нацелен на вашу способность комбинировать законы Ньютона и уравнения кругового движения и гравитации, чтобы анализировать движение объектов, движущихся по кругу, включая орбитальные спутники. Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи обозначены цветом , синие задачи .
Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи обозначены цветом , синие задачи .
Характеристики движения объектов, движущихся по кругам
Объекты, движущиеся по кругу, имеют скорость, равную пройденному за время пути расстоянию. Расстояние по окружности эквивалентно длине окружности и рассчитывается как 2 • pi • R, где R — радиус.Время на один оборот по окружности называется периодом и обозначается символом T. Таким образом, средняя скорость объекта, движущегося по кругу, определяется выражением 2 • pi • R / T. Часто в постановке задачи указывается частота вращения в оборотах в минуту или в оборотах в секунду. Каждый оборот по окружности эквивалентен длине окружности. Таким образом, умножение частоты вращения на длину окружности позволяет определить среднюю скорость объекта.
Ускорение объектов, движущихся по кругу, в первую очередь основано на изменении направления.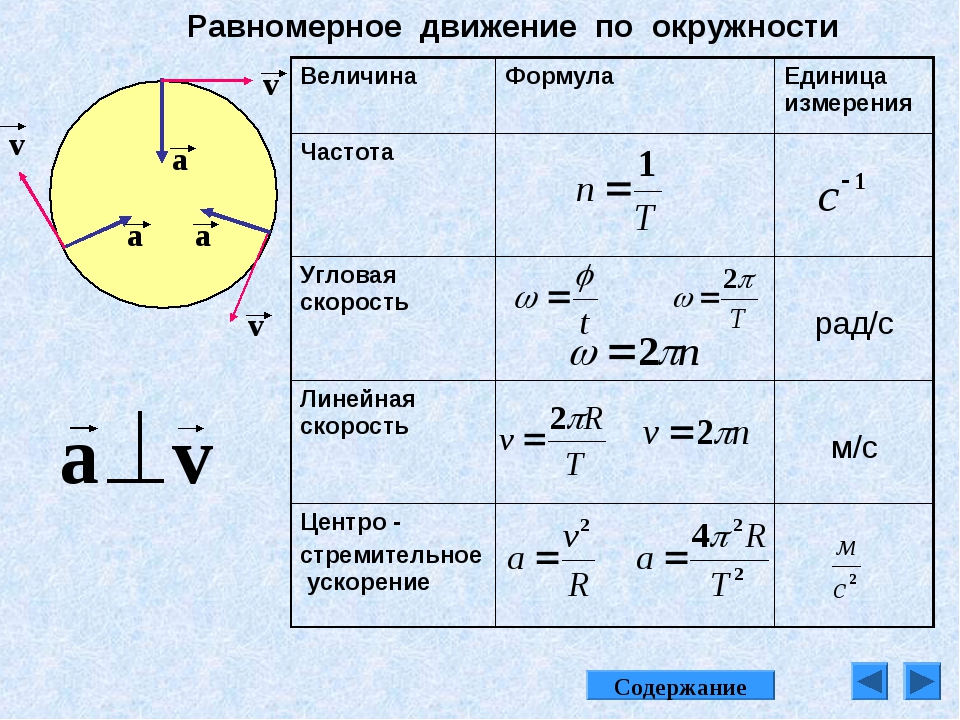 Фактическая скорость ускорения зависит от того, насколько быстро меняется направление, и напрямую связана со скоростью, и обратно пропорциональна радиусу поворота. В итоге ускорение определяется выражением v 2 / R, где v — скорость, а R — радиус окружности.
Фактическая скорость ускорения зависит от того, насколько быстро меняется направление, и напрямую связана со скоростью, и обратно пропорциональна радиусу поворота. В итоге ускорение определяется выражением v 2 / R, где v — скорость, а R — радиус окружности.
Уравнения для средней скорости (v) и среднего ускорения (a) приведены ниже.
v = d / t = 2 • pi • R / T = частота • 2 • pi • R
а = v 2 / R
Направленные величины для объектов, движущихся по кругам
Успешный математический анализ объектов, движущихся по кругу, во многом зависит от концептуального понимания направления вектора ускорения и результирующей силы. Движение по круговой траектории требует чистой силы, направленной к центру круга.В каждой точке пути результирующая сила должна быть направлена внутрь. Хотя может существовать отдельная сила, направленная наружу, должна быть внутренняя сила, которая подавляет ее по величине и удовлетворяет требованию для внутренней чистой силы. Поскольку чистая сила и ускорение всегда в одном направлении, ускорение объектов, движущихся по кругу, также должно быть направлено внутрь.
Поскольку чистая сила и ускорение всегда в одном направлении, ускорение объектов, движущихся по кругу, также должно быть направлено внутрь.
Диаграммы свободного тела и второй закон Ньютона
Часто силовой анализ необходимо проводить для объекта, движущегося по кругу.Цель анализа — определить величину отдельной силы, действующей на объект, или использовать значения отдельных сил для определения ускорения. Как и любая задача анализа сил, эти задачи должны начинаться с построения диаграммы свободного тела, показывающей тип и направление всех сил, действующих на объект. Из диаграммы F net = m • можно написать уравнение. При написании уравнения помните, что сеть F представляет собой векторную сумму всех индивидуальных сил.Лучше всего это записывать, складывая все силы, действующие в направлении ускорения (внутрь), и вычитая те, которые ему противостоят. Два примера показаны на рисунке ниже.
Закон всемирного тяготения Ньютона
Орбитальные спутники — это просто снаряды — объекты, на которые действует только сила тяжести. Сила, управляющая их движением, — это сила гравитационного притяжения к объекту, который находится в центре их орбиты.Планеты вращаются вокруг Солнца в результате гравитационной силы притяжения к Солнцу. Естественные луны вращаются вокруг планет в результате гравитационной силы притяжения к планете. Гравитация — это сила, которая действует на больших расстояниях таким образом, что любые два объекта с массой будут притягиваться. Ньютон был первым, кто предложил теорию, чтобы описать это универсальное массовое притяжение и выразить его математически. Закон, известный как закон всемирного тяготения, гласит, что сила гравитационного притяжения прямо пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между их центрами. В форме уравнения
В форме уравнения
F grav = G • m 1 • m 2 / d 2
где m 1 и m 2 — массы притягивающих объектов (в кг), d — расстояние разделения, измеренное от центра объекта до центра объекта (в метрах), а G — константа пропорциональности (иногда называемая всемирная гравитационная постоянная). Значение G составляет 6,673 x 10 -11 Н • м 2 / кг 2 .
Ускорение свободного падения
Поскольку на орбитальные спутники действует только сила тяжести, их ускорение является ускорением силы тяжести (g). На земной поверхности это значение составило 9,8 м / с 2 . Для местоположений, отличных от поверхности Земли, необходимо уравнение, которое выражает g через соответствующие переменные. Ускорение свободного падения зависит от массы объекта, который находится в центре орбиты (M центральный ) и расстояния разделения от этого объекта (d). Уравнение, связывающее эти две переменные с ускорением свободного падения, выводится из закона всемирного тяготения Ньютона. Уравнение
Уравнение, связывающее эти две переменные с ускорением свободного падения, выводится из закона всемирного тяготения Ньютона. Уравнение
g = G • M центральный / d 2
где G составляет 6,673 x 10 -11 Н • м 2 / кг 2 .
Орбитальная скорость
Скорость, необходимая для того, чтобы спутник оставался на орбите вокруг центрального тела (планеты, солнца, другой звезды и т. Д.).) зависит от радиуса орбиты и массы центрального тела. Уравнение, выражающее связь между этими переменными, получается путем объединения определений ускорения кругового движения с законом всемирного тяготения Ньютона. Уравнение
v = SQRT (G • M центральный / R)
где M central — это масса центрального тела, вокруг которого вращается спутник, R — радиус орбиты, а G — 6,673 x 10 -11 Н • м 2 / кг 2 .
Орбитальный период
Для общего движения объекта по кругу период связан с радиусом круга и скоростью объекта уравнением v = 2 • pi • R / T. В случае орбитального спутника это уравнение для скорости можно приравнять к уравнению для орбитальной скорости, полученной из всемирного тяготения, чтобы получить новое уравнение для орбитального периода. Результат вывода —
T 2 / R 3 = 4 • pi 2 / (G • M центральный )
где M central — масса центрального тела, вокруг которого вращается спутник, R — радиус орбиты, а G — 6.673 x 10 -11 Н • м 2 / кг 2 . Выраженное таким образом уравнение показывает, что отношение квадрата периода к радиусу в кубе для любого спутника, вращающегося вокруг центрального тела, одинаково независимо от природы спутника или радиуса его орбиты. Это соотношение зависит только от массы объекта, который втягивает орбитальный спутник внутрь. Этот принцип согласуется с третьим законом движения планет Кеплера.
Этот принцип согласуется с третьим законом движения планет Кеплера.
Резюме математических формул
Одна из трудностей, с которыми студент может столкнуться в этом наборе задач, — это путаница относительно того, какую формулу использовать.В приведенной ниже таблице приводится полезное резюме формул, относящихся к круговому движению и движению спутника. В таблице многие формулы получены из других уравнений. Таким образом, часто будет несколько способов определения неизвестной величины. Подходя к этим проблемам, рекомендуется практиковать обычные привычки эффективного решателя проблем; определить известные и неизвестные величины в виде символов физических формул, наметить стратегию использования известных для решения неизвестного, а затем, наконец, выполнить необходимые алгебраические шаги и замены, необходимые для решения.
| Для расчета … | … используйте уравнение (а): |
|---|---|
| Скорость (v) | v = 2 • pi • R / T v = SQRT (G • M центральный / R) только для спутников |
| Разгон (а) | a = v 2 / R или a = F нетто / м a = g = G • M центральный / d 2 только для спутников |
| Чистая сила (F net ) | F net = m • a или F net = m • v 2 / R F net = F grav = G • m sat • M central / d 2 только для спутников |
| Период (Т) | T = 2 • pi • R / v T 2 = 4 • pi 2 / (G • M центральный ) • R 3 только для спутников |
Привычки эффективного решателя проблем
Эффективный решатель проблем по привычке подходит к физической проблеме таким образом, чтобы отражать набор дисциплинированных привычек.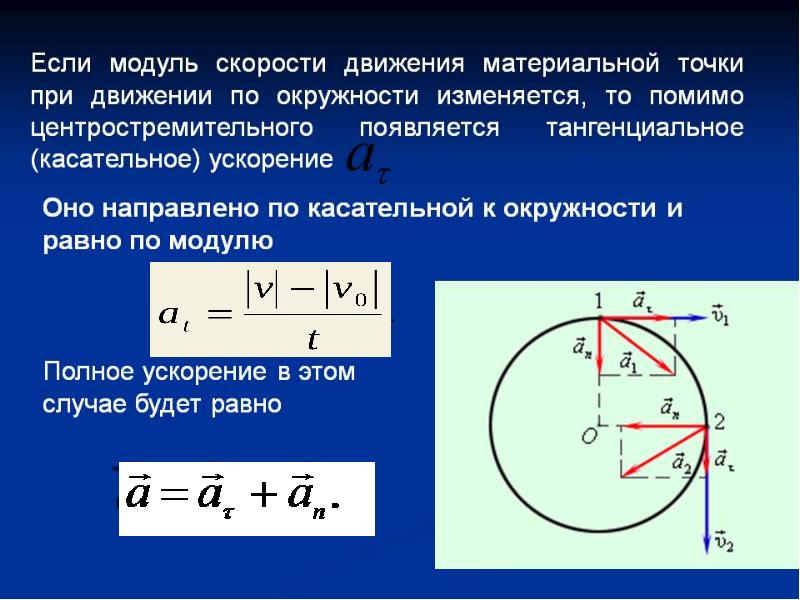 Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем …
Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем …
- … внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
- … определяет известные и неизвестные величины в организованном порядке, часто записывая их на диаграмме.Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например, m = 61,7 кг, v = 18,5 м / с, R = 30,9 м, F norm = ???).
- … строит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания физических принципов.
- … определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.

- … выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.
Подробнее …
Дополнительная литература / Учебные пособия:
Следующие страницы учебного пособия по физике могут быть полезны для понимания концепций и математики, связанных с этими проблемами.
Набор задач кругового движения и гравитации
Просмотреть набор задач
Решения с аудиогидом для кругового движения и гравитации
Просмотрите решение проблемы с аудиогидом:1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27
6.3 Центростремительная сила — Университетская физика, том 1
Цели обучения
К концу раздела вы сможете:
- Объясните уравнение центростремительного ускорения
- Примените второй закон Ньютона, чтобы получить уравнение для центростремительной силы
- Используйте концепции кругового движения при решении задач, связанных с законами движения Ньютона
В «Движении в двух и трех измерениях» мы рассмотрели основные концепции кругового движения. Объект, совершающий круговое движение, как одна из гоночных машин, показанных в начале этой главы, должен ускоряться, потому что он меняет направление своей скорости. Мы доказали, что это центрально направленное ускорение, называемое центростремительным ускорением , задается формулой
Объект, совершающий круговое движение, как одна из гоночных машин, показанных в начале этой главы, должен ускоряться, потому что он меняет направление своей скорости. Мы доказали, что это центрально направленное ускорение, называемое центростремительным ускорением , задается формулой
где v — скорость объекта, направленная по касательной к кривой в любой момент времени. Если мы знаем угловую скорость
, тогда мы можем использовать
Угловая скорость показывает скорость, с которой объект поворачивает кривую, в рад / с.Это ускорение действует по радиусу криволинейной траектории и поэтому также называется радиальным ускорением.
Ускорение должно производиться силой. Любая сила или комбинация сил могут вызвать центростремительное или радиальное ускорение. Вот лишь несколько примеров: натяжение веревки на тросе, сила притяжения Земли на Луне, трение между роликовыми коньками и полом катка, сила наклона проезжей части, действующая на автомобиль, и силы, действующие на трубу вращающейся центрифуги. . Любая чистая сила, вызывающая равномерное круговое движение, называется центростремительной силой .Направление центростремительной силы — к центру кривизны, то же самое, что и направление центростремительного ускорения. Согласно второму закону движения Ньютона, чистая сила равна массе, умноженной на ускорение:
. Любая чистая сила, вызывающая равномерное круговое движение, называется центростремительной силой .Направление центростремительной силы — к центру кривизны, то же самое, что и направление центростремительного ускорения. Согласно второму закону движения Ньютона, чистая сила равна массе, умноженной на ускорение:
Для равномерного кругового движения ускорением является центростремительное ускорение: .
Таким образом, величина центростремительной силы
это
Подставляя выражения для центростремительного ускорения
получаем два выражения для центростремительной силы
по массе, скорости, угловой скорости и радиусу кривизны:
Вы можете использовать любое более удобное выражение для центростремительной силы.Центростремительная сила
всегда перпендикулярно траектории и указывает на центр кривизны, потому что
перпендикулярно скорости и указывает на центр кривизны. Обратите внимание, что если вы решите первое выражение для r , вы получите
Обратите внимание, что если вы решите первое выражение для r , вы получите
Это означает, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть резкую кривую, как на (Рисунок).
Рисунок 6.20 Сила трения обеспечивает центростремительную силу и численно равна ей. Центростремительная сила перпендикулярна скорости и вызывает равномерное круговое движение. Чем больше, тем меньше радиус кривизны r и круче кривая. У второй кривой такой же v, но больше
дает меньшее r ‘.
Пример
Какой коэффициент трения нужен автомобилям на плоской кривой?
(a) Рассчитайте центростремительную силу, действующую на 900.Автомобиль весом 0 кг, который преодолевает поворот радиусом 500,0 м со скоростью 25,00 м / с. (b) Предполагая, что кривая без кренована, найдите минимальный статический коэффициент трения между шинами и дорогой, поскольку статическое трение является причиной, по которой автомобиль не скользит ((Рисунок)).
Стратегия
- Мы знаем, что
Таким образом,
- (рисунок) показывает силы, действующие на автомобиль на кривой без наклона (ровной поверхности). Трение направлено влево, предотвращая скольжение автомобиля, и поскольку это единственная горизонтальная сила, действующая на автомобиль, трение в данном случае является центростремительной силой. Мы знаем, что максимальное статическое трение (при котором шины катятся, но не скользят) составляет
где
— статический коэффициент трения, а Н, — нормальная сила.
 Нормальная сила равна массе автомобиля на ровной поверхности, поэтому
Нормальная сила равна массе автомобиля на ровной поверхности, поэтомуТаким образом, центростремительная сила в данной ситуации равна
Теперь у нас есть связь между центростремительной силой и коэффициентом трения. Используя уравнение
получаем
Решаем это для
, отмечая, что масса отменяется, и получаем
Замена известных,
(Поскольку коэффициенты трения являются приблизительными, ответ дается только двумя цифрами.)
Значение
Коэффициент трения, указанный на (Рисунок) (b), намного меньше, чем обычно наблюдается между шинами и дорогой. Автомобиль все еще движется по кривой, если коэффициент больше 0,13, потому что трение покоя — это сила реакции, которая может принимать значение меньше, но не больше
Более высокий коэффициент также позволит автомобилю преодолевать поворот на более высокой скорости, но если коэффициент трения меньше, безопасная скорость будет меньше 25 м / с.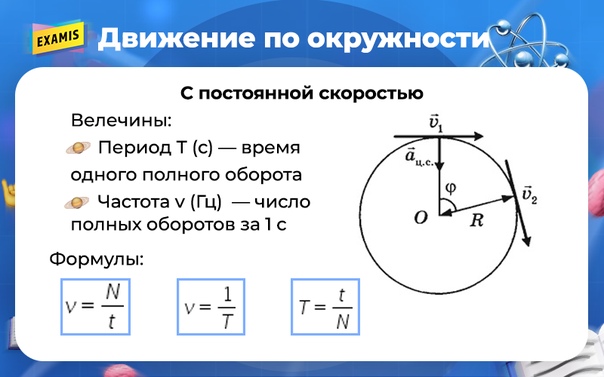 Обратите внимание, что масса отменяется, что означает, что в этом примере не имеет значения, насколько сильно загружена машина для прохождения поворота. Масса сокращается, потому что трение считается пропорциональным нормальной силе, которая, в свою очередь, пропорциональна массе. Если бы поверхность дороги была наклонной, нормальная сила была бы меньше, как обсуждается далее.
Обратите внимание, что масса отменяется, что означает, что в этом примере не имеет значения, насколько сильно загружена машина для прохождения поворота. Масса сокращается, потому что трение считается пропорциональным нормальной силе, которая, в свою очередь, пропорциональна массе. Если бы поверхность дороги была наклонной, нормальная сила была бы меньше, как обсуждается далее.
Проверьте свое понимание
Автомобиль, движущийся со скоростью 96,8 км / ч, движется по круговой кривой радиусом 182,9 м по ровной проселочной дороге. Какой должен быть минимальный коэффициент статического трения, чтобы автомобиль не скользил?
[показать-ответ q = ”694795 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 694795 ″] 0.40 [/ hidden-answer]
Кривые с наклоном
Давайте теперь рассмотрим кривых с наклоном , где наклон дороги помогает вам преодолевать кривую ((Рисунок)). Чем больше угол
, тем быстрее вы сможете пройти кривую. Например, гоночные трассы для велосипедов и автомобилей часто имеют крутые повороты. На «кривой с идеальным наклоном» угол
Например, гоночные трассы для велосипедов и автомобилей часто имеют крутые повороты. На «кривой с идеальным наклоном» угол
такова, что вы можете преодолевать поворот на определенной скорости без трения между шинами и дорогой.Получим выражение для
для кривой с идеальным наклоном и рассмотрим связанный с ней пример.
Рисунок 6.22 Автомобиль на этой кривой с наклоном удаляется и поворачивает налево.Для с идеальным креном чистая внешняя сила равна горизонтальной центростремительной силе в отсутствие трения. Составляющие нормальной силы Н в горизонтальном и вертикальном направлениях должны равняться центростремительной силе и массе автомобиля соответственно.В случаях, когда силы не параллельны, удобнее всего рассматривать компоненты вдоль перпендикулярных осей — в данном случае вертикального и горизонтального направлений.
(рисунок) показывает диаграмму свободного тела для автомобиля на кривой без трения с наклоном. Если угол
Если угол
идеально подходит для скорости и радиуса, тогда чистая внешняя сила равна необходимой центростремительной силе. На автомобиль действуют только две внешние силы — это его вес
г.и нормальная сила дороги
(Поверхность без трения может оказывать только силу, перпендикулярную поверхности, то есть нормальную силу.Эти две силы должны складываться, чтобы получить чистую внешнюю силу, горизонтальную по направлению к центру кривизны и имеющую величину
.Поскольку это решающая сила и она горизонтальна, мы используем систему координат с вертикальной и горизонтальной осями. Только нормальная сила имеет горизонтальную составляющую, поэтому она должна равняться центростремительной силе, то есть
Поскольку автомобиль не отрывается от поверхности дороги, чистая вертикальная сила должна быть равна нулю, что означает, что вертикальные компоненты двух внешних сил должны быть равными по величине и противоположными по направлению. Из (Рисунок) мы видим, что вертикальная составляющая нормальной силы равна
Из (Рисунок) мы видим, что вертикальная составляющая нормальной силы равна
, а единственная другая вертикальная сила — это вес автомобиля. Они должны быть равными по величине; таким образом,
Теперь мы можем объединить эти два уравнения, чтобы исключить N и получить выражение для
, по желанию. Решение второго уравнения для
и подставив его в первое, получим
Взяв арктангенс, получаем
Это выражение можно понять, рассмотрев, как
зависит от v и r .Большой
получается для большого v и маленького r. То есть дороги должны иметь крутой уклон для высоких скоростей и крутых поворотов. Трение помогает, потому что оно позволяет вам двигаться по кривой с большей или меньшей скоростью, чем если бы по кривой не было трения. Обратите внимание, что
не зависит от массы автомобиля.
Пример
Какая идеальная скорость для прохождения крутой крутой кривой?
Кривые на некоторых испытательных треках и гоночных трассах, таких как Международная гоночная трасса Дейтона во Флориде, имеют очень крутой наклон.Этот вираж с помощью трения шин и очень стабильной конфигурации автомобиля позволяет преодолевать повороты на очень высокой скорости. Чтобы проиллюстрировать это, вычислите скорость, с которой кривая радиусом 100,0 м выходит на угол
Наследует ездить, если на дороге нет трения.
Стратегия
Прежде всего отметим, что все члены в выражении для идеального угла кривой с наклоном, кроме скорости, известны; таким образом, нам нужно только переставить его так, чтобы скорость отображалась слева, а затем подставить известные величины.
Решение
Начиная с
получаем
Отметив, что
получаем
Значение
Это примерно 165 км / ч, что соответствует очень крутому и довольно крутому повороту. Трение шин позволяет автомобилю двигаться по кривой на значительно более высоких скоростях.
Трение шин позволяет автомобилю двигаться по кривой на значительно более высоких скоростях.
Самолеты также совершают развороты по крену. Подъемная сила, создаваемая силой воздуха, воздействующего на крыло, действует под прямым углом к крылу.Когда самолет кренится, пилот получает большую подъемную силу, чем необходимо для горизонтального полета. Вертикальная составляющая подъемной силы уравновешивает вес самолета, а горизонтальная составляющая ускоряет самолет. Угол крена, показанный на (Рисунок), равен
. Мы анализируем силы так же, как и в случае поворота автомобиля по кривой.
Рис. 6.23 В крене горизонтальный компонент подъемной силы неуравновешен и ускоряет самолет.Обычная составляющая подъемной силы уравновешивает вес самолета. Угол крена определяется как. Сравните векторную диаграмму с диаграммой, показанной на (Рисунок).
Силы инерции и неинерциальные (ускоренные) кадры: сила Кориолиса
Что общего между взлетом на реактивном самолете, поворотом на машине, катанием на карусели и круговым движением тропического циклона? Каждый из них демонстрирует силы инерции — силы, которые кажутся просто возникающими в результате движения, потому что система отсчета наблюдателя ускоряется или вращается. Большинство людей согласятся, что при взлете на реактивном самолете создается ощущение, будто вас толкают обратно в кресло, когда самолет ускоряется по взлетно-посадочной полосе. Однако физик сказал бы, что вы, , склонны оставаться неподвижными, в то время как сиденье толкает вас вперед. Еще более распространенный опыт происходит, когда вы делаете крутой поворот на своей машине, скажем, вправо ((рисунок)). Вы чувствуете, как будто вас отбрасывает (то есть форсированный ) влево относительно машины. Опять же, физик сказал бы, что вы, , движетесь по прямой (вспомните первый закон Ньютона), но автомобиль движется вправо, а не то, что вы испытываете силу слева.
Большинство людей согласятся, что при взлете на реактивном самолете создается ощущение, будто вас толкают обратно в кресло, когда самолет ускоряется по взлетно-посадочной полосе. Однако физик сказал бы, что вы, , склонны оставаться неподвижными, в то время как сиденье толкает вас вперед. Еще более распространенный опыт происходит, когда вы делаете крутой поворот на своей машине, скажем, вправо ((рисунок)). Вы чувствуете, как будто вас отбрасывает (то есть форсированный ) влево относительно машины. Опять же, физик сказал бы, что вы, , движетесь по прямой (вспомните первый закон Ньютона), но автомобиль движется вправо, а не то, что вы испытываете силу слева.
 Слева от водителя относительно Земли нет силы. Вместо этого справа на машине есть сила, заставляющая ее повернуть.
Слева от водителя относительно Земли нет силы. Вместо этого справа на машине есть сила, заставляющая ее повернуть. Мы можем согласовать эти точки зрения, исследуя используемые системы координат.Давайте сконцентрируемся на людях в машине. Пассажиры инстинктивно используют автомобиль в качестве ориентира, тогда как физик может использовать Землю. Физик мог бы сделать этот выбор, потому что Земля является почти инерциальной системой отсчета, в которой все силы имеют идентифицируемое физическое происхождение. В такой системе отсчета законы движения Ньютона принимают форму, данную в Законах Ньютона. Автомобиль представляет собой неинерциальную систему отсчета , потому что он ускоряется в сторону. Сила слева, воспринимаемая пассажирами автомобиля, — это сила инерции , не имеющая физического происхождения (она возникает исключительно из-за инерции пассажира, а не из-за какой-либо физической причины, такой как напряжение, трение или гравитация).Автомобиль, как и водитель, действительно ускоряется вправо. Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, например гравитации.
Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, например гравитации.
Физик выберет ту систему отсчета, которая наиболее удобна для анализируемой ситуации. Для физика, как обычно, нет проблем с включением сил инерции и второго закона Ньютона, если это удобнее, например, на карусели или на вращающейся планете. Неинерционные (ускоренные) системы отсчета используются, когда это полезно.При обсуждении движения космонавта в космическом корабле, движущемся со скоростью, близкой к скорости света, необходимо учитывать различные системы отсчета, как вы это поймете при изучении специальной теории относительности.
Давайте теперь мысленно прокатимся на карусели — а именно, на быстро вращающейся игровой площадке ((Рисунок)). Вы берете карусель в качестве системы отсчета, потому что вы вращаетесь вместе. Вращаясь в этой неинерциальной системе отсчета, вы чувствуете инерционную силу, которая имеет тенденцию сбивать вас с толку; это часто называют центробежной силой (не путать с центростремительной силой). Центробежная сила — это широко используемый термин, но на самом деле его не существует. Вы должны держаться крепче, чтобы противодействовать своей инерции (которую люди часто называют центробежной силой). В системе отсчета Земли нет силы, пытающейся сбить вас с толку; мы подчеркиваем, что центробежная сила — это фикция. Вы должны держаться, чтобы заставить себя двигаться по кругу, потому что в противном случае вы бы пошли по прямой, прямо с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прилагаете, действует к центру круга.
Центробежная сила — это широко используемый термин, но на самом деле его не существует. Вы должны держаться крепче, чтобы противодействовать своей инерции (которую люди часто называют центробежной силой). В системе отсчета Земли нет силы, пытающейся сбить вас с толку; мы подчеркиваем, что центробежная сила — это фикция. Вы должны держаться, чтобы заставить себя двигаться по кругу, потому что в противном случае вы бы пошли по прямой, прямо с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прилагаете, действует к центру круга.
и голов по прямой). Сила,
, необходим для создания кругового пути.
Этот инерционный эффект, уносящий вас от центра вращения, если нет центростремительной силы, вызывающей круговое движение, хорошо используется в центрифугах ((Рисунок)). Центрифуга вращает образец очень быстро, как упоминалось ранее в этой главе. Если смотреть из вращающейся системы координат, сила инерции выбрасывает частицы наружу, ускоряя их осаждение. Чем больше угловая скорость, тем больше центробежная сила. Но на самом деле происходит то, что инерция частиц уносит их по линии, касательной к окружности, в то время как пробирка движется по круговой траектории центростремительной силой.
Рис. 6.26. Центрифуги выполняют свою задачу по инерции. Частицы в жидком осадке осаждаются, потому что их инерция уносит их от центра вращения. Большая угловая скорость центрифуги ускоряет осаждение. В конце концов, частицы вступают в контакт со стенками пробирки, которые затем создают центростремительную силу, необходимую для их движения по кругу постоянного радиуса.
Давайте теперь рассмотрим, что происходит, если что-то движется во вращающейся системе отсчета.Например, что, если вы сдвинете мяч прямо от центра карусели, как показано на (Рисунок)? Мяч движется по прямой относительно Земли (при незначительном трении) и по изогнутой вправо траектории на поверхности карусели. Человек, стоящий рядом с каруселью, видит, как мяч движется прямо, а под ним вращается карусель. В системе отсчета карусели мы объясняем кажущуюся кривую вправо с помощью силы инерции, называемой силой Кориолиса , которая заставляет мяч изгибаться вправо.Сила Кориолиса может быть использована любым человеком в этой системе отсчета, чтобы объяснить, почему объекты следуют изогнутыми путями, и позволяет нам применять законы Ньютона в неинерциальных системах отсчета.
Рис. 6.27. Посмотрев вниз на вращение карусели против часовой стрелки, мы видим, что шар, скользящий прямо к краю, следует по кривой, изогнутой вправо. Человек перемещает мяч к точке B, начиная с точки A. Обе точки поворачиваются в затемненные положения (A ‘и B’), показанные в то время, когда мяч следует по изогнутой траектории во вращающейся рамке и по прямой траектории в системе координат Земли. .
Обе точки поворачиваются в затемненные положения (A ‘и B’), показанные в то время, когда мяч следует по изогнутой траектории во вращающейся рамке и по прямой траектории в системе координат Земли. .До сих пор мы считали Землю инерциальной системой отсчета, почти не беспокоясь о эффектах, возникающих из-за ее вращения, или совсем не волновались. Однако такие эффекты и существуют — например, во вращении погодных систем. Большинство последствий вращения Земли качественно можно понять по аналогии с каруселью. Если смотреть сверху на Северный полюс, Земля вращается против часовой стрелки, как и карусель на (Рисунок). Как и в случае с каруселью, любое движение в Северном полушарии Земли испытывает силу Кориолиса вправо.Прямо противоположное происходит в Южном полушарии; там сила слева. Поскольку угловая скорость Земли мала, сила Кориолиса обычно незначительна, но для крупномасштабных движений, таких как характер ветра, она оказывает существенное влияние.
Сила Кориолиса заставляет ураганы в северном полушарии вращаться против часовой стрелки, тогда как тропические циклоны в южном полушарии вращаются по часовой стрелке. (Термины ураган, тайфун и тропический шторм являются региональными названиями циклонов, которые представляют собой штормовые системы, характеризующиеся центрами низкого давления, сильными ветрами и проливными дождями.) (Рисунок) помогает показать, как происходят эти вращения. Воздух течет в любую область низкого давления, а тропические циклоны имеют особенно низкое давление. Таким образом, ветры движутся к центру тропического циклона или погодной системы низкого давления на поверхности. В Северном полушарии эти внутренние ветры отклоняются вправо, как показано на рисунке, создавая циркуляцию против часовой стрелки на поверхности для зон низкого давления любого типа. Низкое давление у поверхности связано с поднимающимся воздухом, который также вызывает охлаждение и образование облаков, что делает картины низкого давления вполне заметными из космоса.И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но она менее заметна, потому что высокое давление связано с опусканием воздуха, обеспечивающим чистое небо.
(Термины ураган, тайфун и тропический шторм являются региональными названиями циклонов, которые представляют собой штормовые системы, характеризующиеся центрами низкого давления, сильными ветрами и проливными дождями.) (Рисунок) помогает показать, как происходят эти вращения. Воздух течет в любую область низкого давления, а тропические циклоны имеют особенно низкое давление. Таким образом, ветры движутся к центру тропического циклона или погодной системы низкого давления на поверхности. В Северном полушарии эти внутренние ветры отклоняются вправо, как показано на рисунке, создавая циркуляцию против часовой стрелки на поверхности для зон низкого давления любого типа. Низкое давление у поверхности связано с поднимающимся воздухом, который также вызывает охлаждение и образование облаков, что делает картины низкого давления вполне заметными из космоса.И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но она менее заметна, потому что высокое давление связано с опусканием воздуха, обеспечивающим чистое небо.
Вращение тропических циклонов и траектория шара на карусели также могут быть объяснены инерцией и вращением системы под ним. Когда используются неинерциальные системы отсчета, для объяснения искривленной траектории должны быть изобретены силы инерции, такие как сила Кориолиса.Физического источника этих сил инерции нет. В инерциальной системе отсчета инерция объясняет путь, и не обнаруживается силы без идентифицируемого источника. Любая точка зрения позволяет нам описывать природу, но взгляд в инерциальной системе отсчета является самым простым в том смысле, что все силы имеют истоки и объяснения.
Любая точка зрения позволяет нам описывать природу, но взгляд в инерциальной системе отсчета является самым простым в том смысле, что все силы имеют истоки и объяснения.
Концептуальные вопросы
Если вы хотите уменьшить нагрузку (которая связана с центростремительной силой) на высокоскоростные шины, вы бы использовали шины большого или малого диаметра? Объясни.
Определите центростремительную силу. Может ли сила любого типа (например, натяжение, сила тяжести, трение и т. Д.) Быть центростремительной силой? Может ли любое сочетание сил быть центростремительной силой?
[показывать-ответ q = ”fs-id1165039453744 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165039453744 ″]
Центростремительная сила определяется как любая чистая сила, вызывающая равномерное круговое движение. Центростремительная сила — это не новый вид силы. Метка «центростремительная» относится к любой силе , которая заставляет что-то вращаться по кругу. Эта сила может быть напряжением, гравитацией, трением, электрическим притяжением, нормальной силой или любой другой силой. Любая их комбинация может быть источником центростремительной силы, например, центростремительная сила в верхней части траектории троса, проходящего через вертикальный круг, является результатом как натяжения, так и силы тяжести.
Эта сила может быть напряжением, гравитацией, трением, электрическим притяжением, нормальной силой или любой другой силой. Любая их комбинация может быть источником центростремительной силы, например, центростремительная сила в верхней части траектории троса, проходящего через вертикальный круг, является результатом как натяжения, так и силы тяжести.
[/ hidden-answer]
Если центростремительная сила направлена к центру, почему вы чувствуете, что вас «отбрасывает» от центра, когда машина движется по кривой? Объясни.
Водители гоночных автомобилей обычно срезают углы, как показано ниже (Путь 2). Объясните, как это позволяет снимать кривую с максимальной скоростью.
[раскрыть-ответ q = «329939 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =» 329939 ″] Водитель, который срезает угол (на пути 2), имеет более плавную кривую с большей радиус. Это будет лучшая гоночная трасса. Если водитель слишком быстро завернет за угол, используя гоночную трассу, он все равно соскользнет с трассы; Ключевым моментом является максимальное значение статического трения.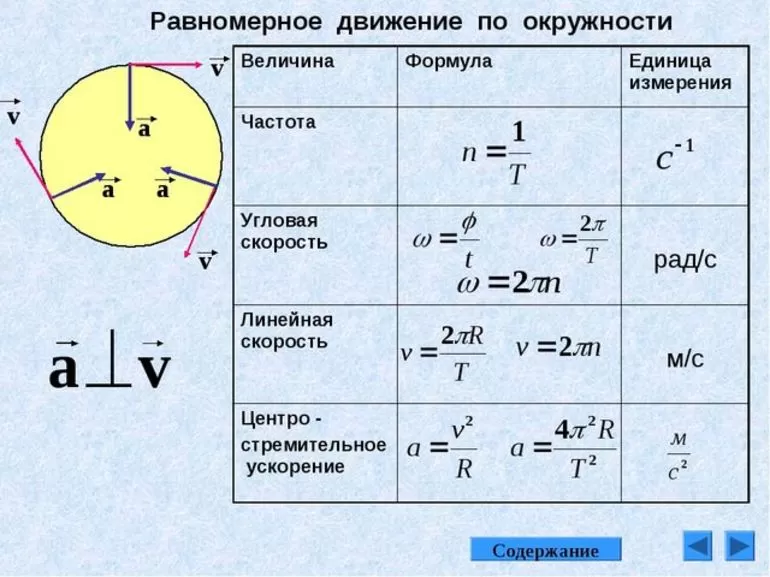 Итак, водитель хочет максимально возможной скорости и максимального трения. Рассмотрим уравнение для центростремительной силы:
Итак, водитель хочет максимально возможной скорости и максимального трения. Рассмотрим уравнение для центростремительной силы:
где v — скорость, а r — радиус кривизны. Таким образом, уменьшая кривизну (1 / r) пути, по которому движется автомобиль, мы уменьшаем силу, которую шины должны оказывать на дорогу, что означает, что теперь мы можем увеличить скорость v. Глядя на это с точки зрения вид водителя на Пути 1, мы можем рассуждать так: чем круче поворот, тем меньше радиус поворота; чем меньше диаметр поворота, тем больше требуется центростремительная сила.Если эта центростремительная сила не действует, результатом будет занос. [/ Hidden-answer]
Во многих парках развлечений есть аттракционы с вертикальными петлями, как показано ниже. В целях безопасности вагоны прикреплены к рельсам таким образом, чтобы они не могли упасть. Если автомобиль преодолевает вершину с правильной скоростью, только сила тяжести будет обеспечивать центростремительную силу. Какая еще сила действует и в каком направлении, если:
(a) Автомобиль переезжает через вершину быстрее этой скорости?
(b) Автомобиль переезжает через вершину со скоростью ниже этой?
Что заставляет воду удаляться с одежды в центрифуге?
[show-answer q = ”fs-id1165039477270 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165039477270 ″]
Цилиндр сушилки создает центростремительную силу на одежде (включая капли воды), заставляя ее двигаться по круговой траектории.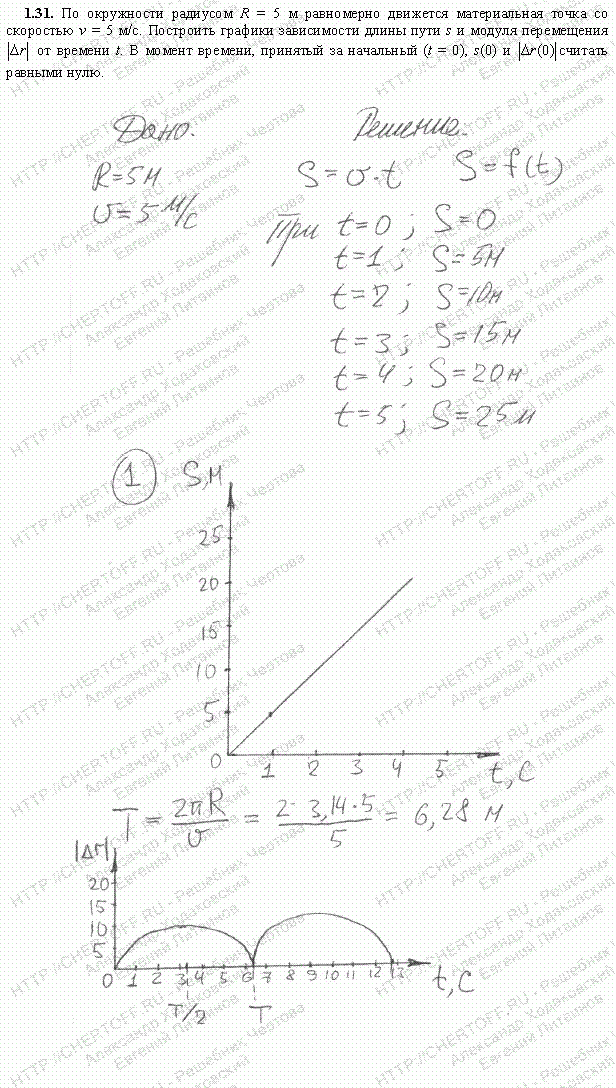 Когда капля воды попадает в одно из отверстий бочки, она перемещается по касательной к окружности.
Когда капля воды попадает в одно из отверстий бочки, она перемещается по касательной к окружности.
[/ hidden-answer]
Когда фигурист образует круг, какая сила отвечает за его поворот? Используйте в своем ответе диаграмму свободного тела.
Предположим, что ребенок едет на карусели на расстоянии примерно посередине между ее центром и краем. У нее есть коробка для завтрака, стоящая на вощеной бумаге, так что между ней и каруселью очень мало трения.По какому пути, показанному ниже, пойдет коробка для завтрака, когда она отпустит? Ланч-бокс оставляет след в пыли на карусели. Эта тропа прямая, изогнута влево или вправо? Поясните свой ответ.
[раскрыть-ответ q = ”60053 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 60053 ″] Если нет трения, значит и центростремительной силы нет. Это означает, что коробка для завтрака будет двигаться по касательной к кругу и, таким образом, будет следовать по пути B. След пыли будет прямым. Это результат первого закона движения Ньютона. [/ Hidden-answer]
Это результат первого закона движения Ньютона. [/ Hidden-answer]
Чувствуете ли вы, что вас бросает в любую сторону, когда вы проезжаете поворот, идеально подходящий для скорости вашего автомобиля? В каком направлении на вас действует автокресло?
Предположим, что масса движется по круговой траектории на столе без трения, как показано ниже. В земной системе координат центробежная сила, оттягивающая массу от центра вращения, отсутствует, но есть сила, растягивающая нить, прикрепляющую массу к гвоздю.Используя концепции, связанные с центростремительной силой и третьим законом Ньютона, объясните, какая сила натягивает струну, указав ее физическое происхождение.
[показать-ответ q = ”965193 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 965193 ″] Для поддержания кругового движения необходима центростремительная сила; это обеспечивается гвоздем в центре. Третий закон Ньютона объясняет это явление. Сила воздействия — это сила струны, действующая на массу; сила реакции — это сила массы на струне. Эта сила реакции заставляет струну растягиваться. [/ Hidden-answer]
Эта сила реакции заставляет струну растягиваться. [/ Hidden-answer]
Когда сливают унитаз или слив из раковины, вода (и другие материалы) по пути вниз начинает вращаться вокруг слива. Предполагая, что начального вращения нет и поток изначально направлен прямо к водостоку, объясните, что вызывает вращение и какое направление оно имеет в Северном полушарии. (Обратите внимание, что это небольшой эффект, и в большинстве туалетов вращение вызывается направленными струями воды.) Будет ли направление вращения измениться на противоположное, если вода будет вытесняться в канализацию?
Автомобиль объезжает поворот и наталкивается на кусок льда с очень низким коэффициентом кинетической фиксации.Автомобиль съезжает с дороги. Опишите путь, по которому машина съезжает с дороги.
[Показать-ответ q = ”fs-id116503
62 ″] Показать решение [/ Показать-ответ][скрытый-ответ a = ”fs-id116503
62 ″] Поскольку радиальное трение с шинами обеспечивает центростремительную силу, а трение почти равно нулю, когда автомобиль сталкивается со льдом, автомобиль подчиняется первому закону Ньютона и съезжает с дороги по прямой линии, касательной к кривой. Распространенное заблуждение состоит в том, что автомобиль будет двигаться по извилистой дороге за пределами дороги.
Распространенное заблуждение состоит в том, что автомобиль будет двигаться по извилистой дороге за пределами дороги.
[/ hidden-answer]
Во время одной поездки в парке развлечений всадники входят в большую вертикальную бочку и становятся у стены на ее горизонтальном полу. Бочка раскручивается, и пол падает. Всадники чувствуют себя так, как будто они прижаты к стене силой, похожей на силу гравитации. Это сила инерции, которую всадники воспринимают и используют для объяснения событий во вращающейся системе отсчета ствола. Объясните в инерциальной системе отсчета (Земля почти что одна), что прижимает всадников к стене, и определите все силы, действующие на них.
Два друга разговаривают. Анна говорит, что спутник на орбите находится в свободном падении, потому что спутник продолжает падать на Землю. Том говорит, что спутник на орбите не находится в свободном падении, потому что ускорение свободного падения не равно
.. С кем вы согласны и почему?
[show-answer q = ”fs-id116503
36 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116503
36 ″]
Анна права.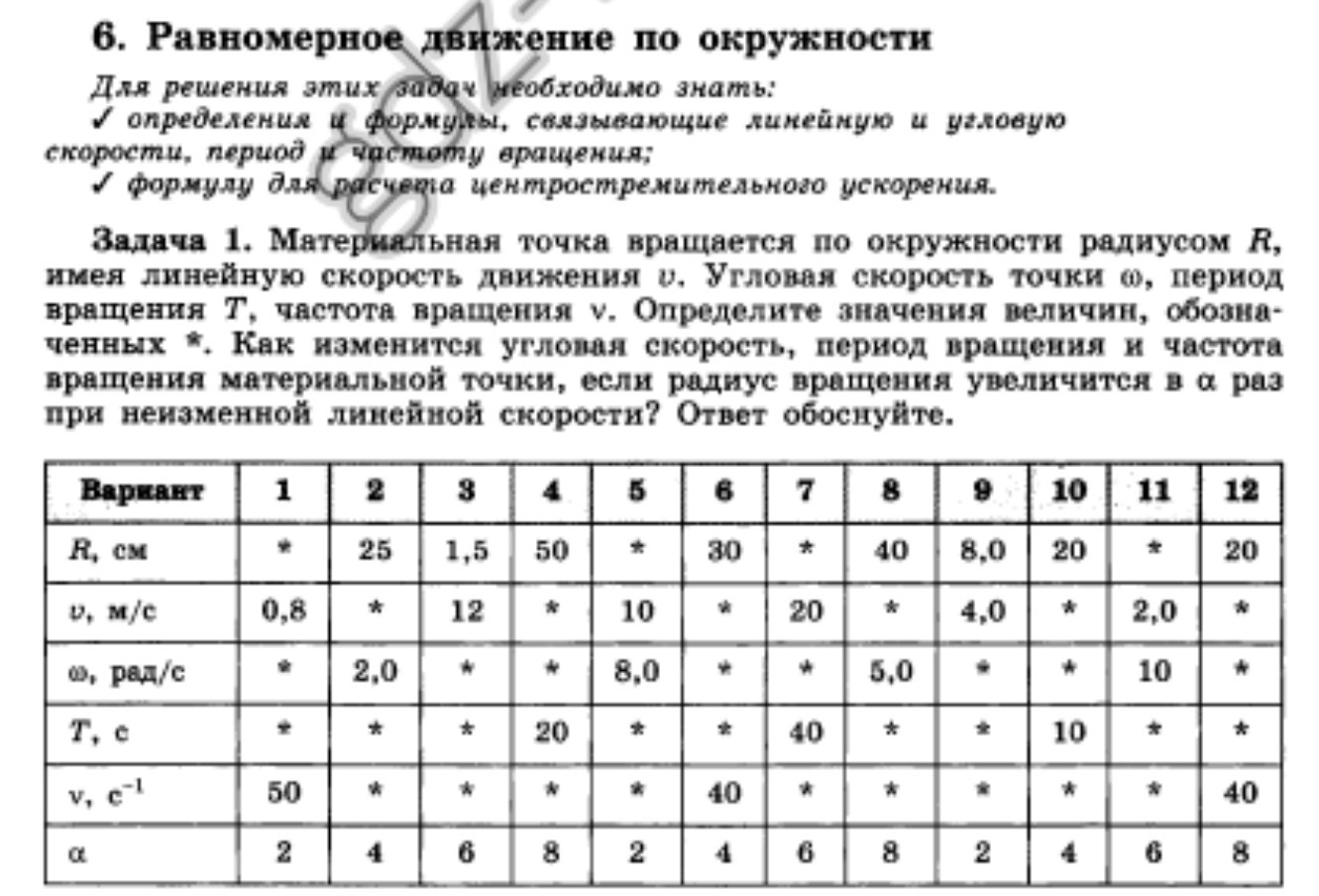 Спутник свободно падает на Землю из-за силы тяжести, хотя сила тяжести на высоте спутника слабее, и g — это не
Спутник свободно падает на Землю из-за силы тяжести, хотя сила тяжести на высоте спутника слабее, и g — это не
.Свободное падение не зависит от стоимости г ; то есть вы можете испытать свободное падение на Марсе, если спрыгнете с Олимпа (самого высокого вулкана в Солнечной системе).
[/ hidden-answer]
Невращающаяся система отсчета, помещенная в центр Солнца, очень близка к инерциальной. Почему это не совсем инерциальная система отсчета?
Проблемы
(a) Ребенок весом 22,0 кг катается на детской карусели, которая вращается со скоростью 40,0 об / мин. Какая центростремительная сила действует, если он равен 1.25 м от центра? (b) Какая центростремительная сила действует, если карусель вращается со скоростью 3,00 об / мин и находится на расстоянии 8,00 м от ее центра? (c) Сравните каждую силу с его весом.
[show-answer q = ”fs-id116503
11 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116503
11 ″]
а.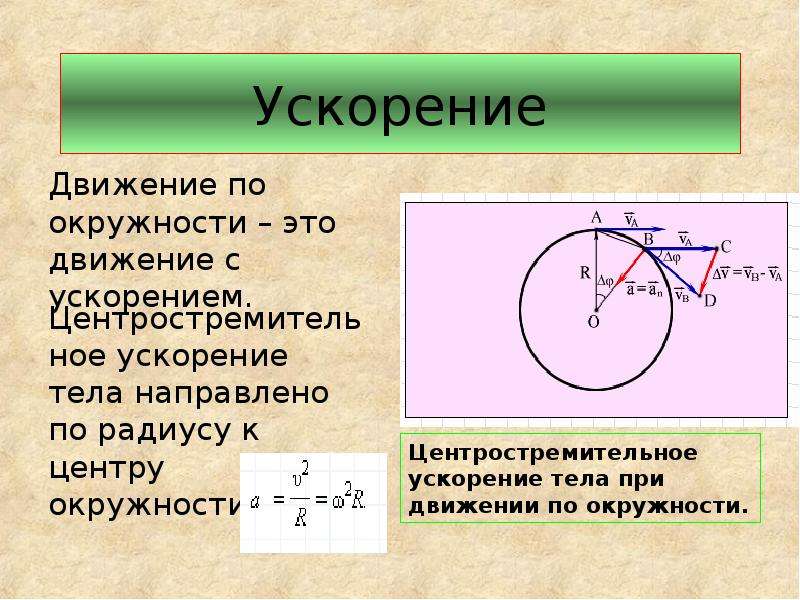 483 Н; б. 17,4 Н; c. 2,24, 0,0807
483 Н; б. 17,4 Н; c. 2,24, 0,0807
[/ hidden-answer]
Рассчитайте центростремительную силу на конце лопасти ветряной турбины радиусом 100 м, которая вращается на 0.5 об / с. Предположим, что масса 4 кг.
Каков идеальный угол крена для пологого поворота радиусом 1,20 км на шоссе с ограничением скорости 105 км / ч (около 65 миль / ч), если все едут на пределе?
[show-answer q = ”fs-id1165039344901 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165039344901 ″]
[/ hidden-answer]
Какова идеальная скорость для прохождения кривой радиусом 100,0 м с наклоном на
угол?
(а) Каков радиус бобслейного поворота с креном
?и взято в 30.0 м / с при условии идеального наклона? (b) Рассчитайте центростремительное ускорение. (c) Вам кажется это ускорение большим?
[show-answer q = ”fs-id116503
09 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116503
09 ″]
а. 24,6 м; б.
24,6 м; б.
г. 3,73 раза г
[/ hidden-answer]
Часть езды на велосипеде включает наклон под правильным углом при повороте, как показано ниже. Чтобы быть стабильным, сила, действующая на землю, должна быть на линии, проходящей через центр тяжести.Сила, действующая на колесо велосипеда, может быть разделена на две перпендикулярные составляющие: трение параллельно дороге (оно должно обеспечивать центростремительную силу) и вертикальную нормальную силу (которая должна равняться весу системы). а) Покажите, что
(как показано) относится к скорости v и радиусу кривизны r поворота так же, как и для проезжей части с идеальным уклоном, то есть
(б) Вычислить
за 12.0-м / с разворот радиусом 30,0 м (как в гонке).
Если автомобиль движется по крутому повороту со скоростью ниже идеальной, необходимо трение, чтобы не допустить скольжения внутрь поворота (проблема на обледенелых горных дорогах).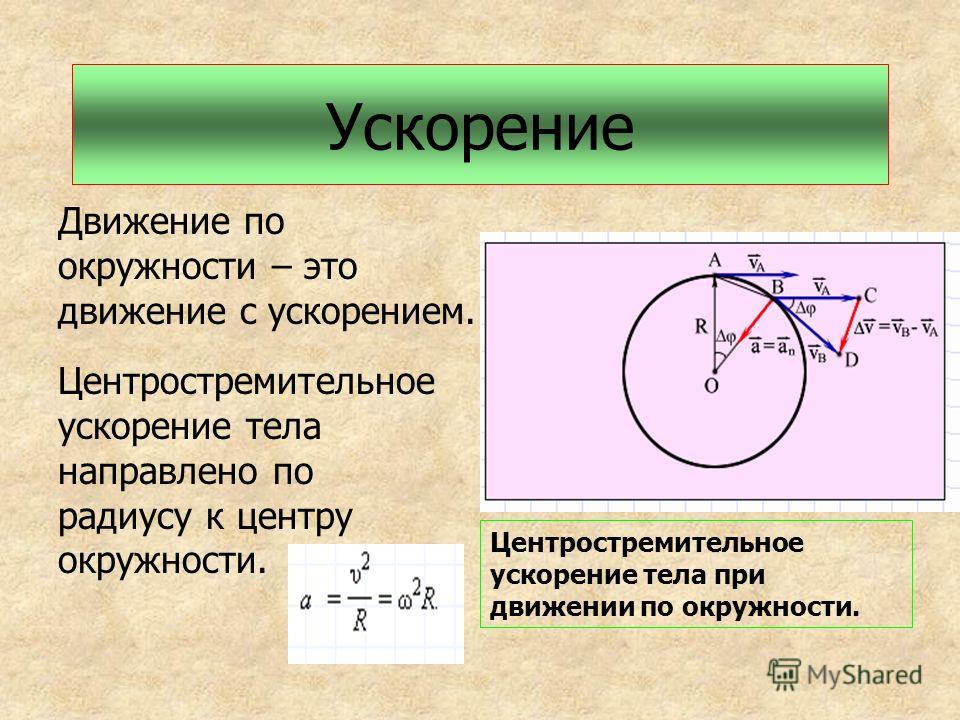 (a) Рассчитайте идеальную скорость, чтобы взять кривую радиусом 100,0 м с наклоном
(a) Рассчитайте идеальную скорость, чтобы взять кривую радиусом 100,0 м с наклоном
. (b) Какой минимальный коэффициент трения нужен для того, чтобы напуганный водитель проехал по той же кривой на скорости 20,0 км / ч?
[show-answer q = ”fs-id1165038980331 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165038980331 ″]
а.16,2 м / с; б. 0,234
[/ hidden-answer]
Современные американские горки имеют вертикальные петли, подобные показанной здесь. Радиус кривизны вверху меньше, чем по бокам, поэтому центростремительное ускорение вниз вверху будет больше, чем ускорение свободного падения, удерживая пассажиров плотно прижатыми к своим сиденьям. (a) Какова скорость американских горок в верхней части петли, если радиус кривизны там 15,0 м, а ускорение машины вниз равно 1.50 г ? (b) На какой высоте над вершиной петли американские горки должны начинаться из состояния покоя, если трение пренебрежимо мало? (c) Если он действительно начинается на 5,00 м выше, чем ваш ответ на вопрос (b), сколько энергии он потерял на трение? Его масса
.
Ребенок массой 40,0 кг находится в машине с американскими горками, которая движется по петле радиусом 7,00 м. В точке А скорость автомобиля составляет 10,0 м / с, а в точке B — 10,5 м / с. Предположим, что ребенок не держится и не пристегнут ремнем безопасности.(а) Какое усилие автомобильного кресла действует на ребенка в точке А? (b) Какое усилие автомобильного кресла действует на ребенка в точке B? (c) Какая минимальная скорость требуется, чтобы удерживать ребенка на сиденье в точке A?
[показать-ответ q = ”484990 ″] Показать решение [/ показать-ответ]
[скрытый-ответ a =” 484990 ″] a. 179 Н; б. 290 Н; c. 8,3 м / с [/ hidden-answer]
В простой модели Бора основного состояния атома водорода электрон движется по круговой орбите вокруг фиксированного протона.Радиус орбиты
, а скорость электрона —
Масса электрона
. Какая сила действует на электрон?
Железнодорожные пути следуют круговой кривой радиусом 500,0 м и имеют крен под углом
. Для поездов какой скорости предназначены эти пути?
Для поездов какой скорости предназначены эти пути?
[show-answer q = ”fs-id116503
32 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116503
32 ″]
20.7 м / с
[/ hidden-answer]
Ускоритель частиц в ЦЕРНе имеет форму окружности 7,0 км. (а) Какое ускорение протонов
, которые вращаются вокруг ускорителя на
скорости света? (Скорость света
) (б) Какая сила действует на протоны?
Автомобиль объезжает кривую без кренов радиусом 65 м. Если коэффициент статического трения между дорогой и автомобилем равен 0.70, какова максимальная скорость, с которой автомобиль преодолевает поворот без скольжения?
[показывать-ответ q = ”fs-id1165039269152 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165039269152 ″]
21 м / с
[/ hidden-answer]
Трасса с наклоном предназначена для движения со скоростью 90,0 км / ч. Радиус поворота 310 м. Какой угол крена шоссе?
Радиус поворота 310 м. Какой угол крена шоссе?
Глоссарий
- наклонная кривая
- поворот на дороге с уклоном, который помогает транспортному средству преодолевать поворот
- центростремительная сила
- любая чистая сила, вызывающая равномерное круговое движение
- Сила Кориолиса
- Сила инерции, вызывающая кажущееся отклонение движущихся объектов при просмотре во вращающейся системе отсчета
- Идеальное банковское дело
- уклон кривой дороги, где угол наклона позволяет транспортному средству преодолевать поворот с определенной скоростью без помощи трения между шинами и дорогой; чистая внешняя сила на транспортном средстве равна горизонтальной центростремительной силе при отсутствии трения
- инерционная сила
- сила, не имеющая физического происхождения
- неинерциальная система отсчета
- ускоренная система отсчета
Эта страница поддерживает мультимедийные учебные пособия «Вес, контактные силы и вращение».
Теперь предположим, что колесо катится по земле — представим его как колесо велосипеда — и мы настаиваем на том, чтобы оно катилось, а не буксовало.Вид, который мы представили выше слева, — это вид велосипедиста, который в этом случае едет вправо. По отношению к гонщику положение оси фиксировано, верхняя часть колеса движется вперед в точке v, а нижняя часть колеса движется назад в точке v, как указано выше.
|



 (Почему это важно?)
(Почему это важно?) Уделите минуту, чтобы прочувствовать поворот платформы с постоянной скоростью. Увеличивайте скорость до тех пор, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора на центральной стойке.Это указывает на то, что струна, поддерживающая вращающуюся массу, вертикальна и, следовательно, масса находится на желаемом радиусе.
Уделите минуту, чтобы прочувствовать поворот платформы с постоянной скоростью. Увеличивайте скорость до тех пор, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора на центральной стойке.Это указывает на то, что струна, поддерживающая вращающуюся массу, вертикальна и, следовательно, масса находится на желаемом радиусе. Если ваш результат не имеет смысла, проанализируйте свою процедуру и исправьте все ошибки, прежде чем брать дополнительные данные.
Если ваш результат не имеет смысла, проанализируйте свою процедуру и исправьте все ошибки, прежде чем брать дополнительные данные.

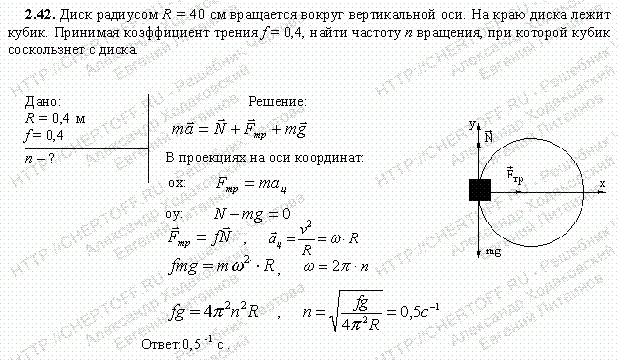 Нормальная сила равна массе автомобиля на ровной поверхности, поэтому
Нормальная сила равна массе автомобиля на ровной поверхности, поэтому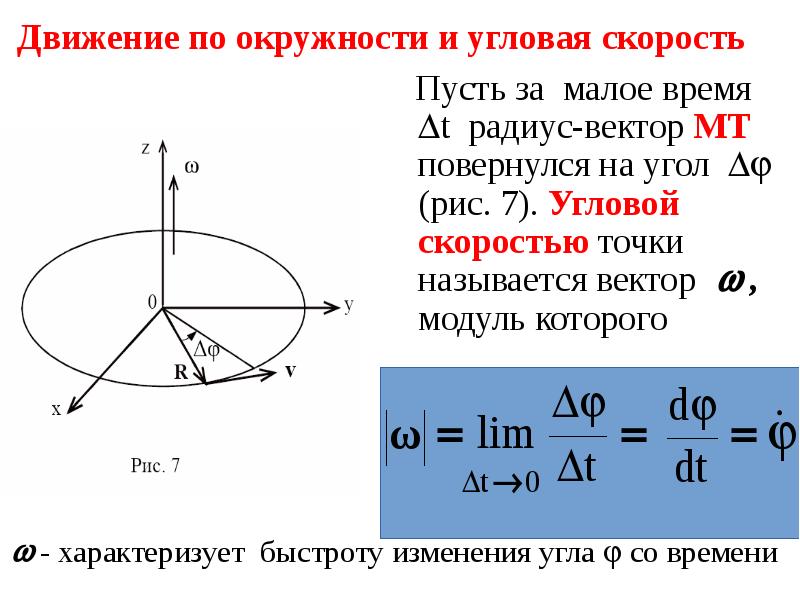
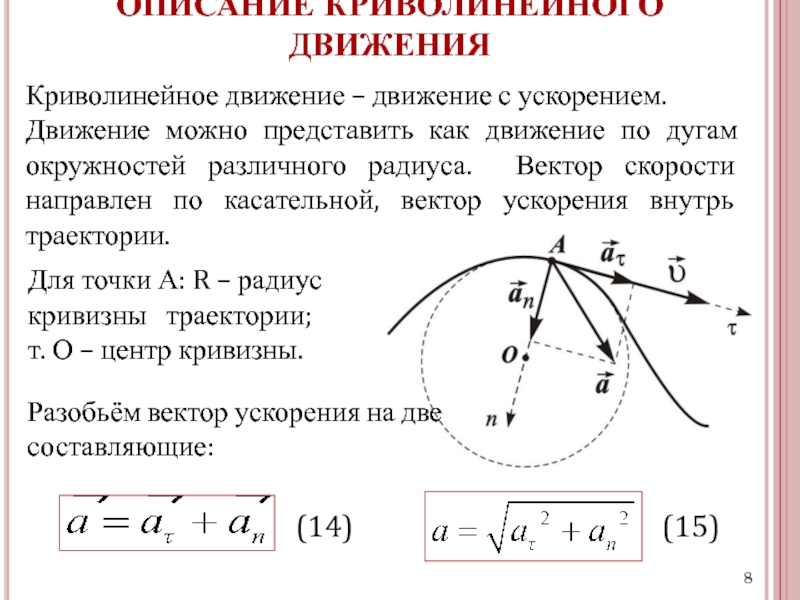 Из определения угла ds = rdθ получаем
Из определения угла ds = rdθ получаем Затем проведите им по руке. В первом случае нет (горизонтального) относительного движения между контактом бутылки и вашей кожей, тогда как во втором случае вы чувствуете, как бутылка скользит по коже.
Затем проведите им по руке. В первом случае нет (горизонтального) относительного движения между контактом бутылки и вашей кожей, тогда как во втором случае вы чувствуете, как бутылка скользит по коже. Снова посмотрев на анимированный график, мы можем наблюдать изменение положения и скорости точки на ободе колеса. В клипе кусок белой ленты на задней шине обозначает такую точку. В частности, обратите внимание на горизонтальные (и вертикальные) компоненты смещения от одного кадра к другому. Давайте будем количественными. Для точки, вращающейся по часовой стрелке по окружности радиуса r с угловой частотой ω, начиная с вершины круга, координаты равны
Снова посмотрев на анимированный график, мы можем наблюдать изменение положения и скорости точки на ободе колеса. В клипе кусок белой ленты на задней шине обозначает такую точку. В частности, обратите внимание на горизонтальные (и вертикальные) компоненты смещения от одного кадра к другому. Давайте будем количественными. Для точки, вращающейся по часовой стрелке по окружности радиуса r с угловой частотой ω, начиная с вершины круга, координаты равны Таким образом, dx / dt для этой точки, горизонтальная составляющая скорости, имеет максимальное значение 2r ω = 2v, когда она находится наверху колеса — вершина колеса обгоняет ось с удвоенной скоростью. Он имеет минимальное значение, равное нулю, когда его значение мгновенно равно нулю, когда он касается земли.
Таким образом, dx / dt для этой точки, горизонтальная составляющая скорости, имеет максимальное значение 2r ω = 2v, когда она находится наверху колеса — вершина колеса обгоняет ось с удвоенной скоростью. Он имеет минимальное значение, равное нулю, когда его значение мгновенно равно нулю, когда он касается земли.
 Задача согласования требуется для правильной передачи сигнала и энергии от «источника» к «нагрузке».
Задача согласования требуется для правильной передачи сигнала и энергии от «источника» к «нагрузке». Им также нужен опыт, чтобы найти полезные данные среди множества получаемых результатов. Кроме того, программное обеспечение для моделирования схем не устанавливается на компьютеры заранее, если они не предназначены для такого приложения.
Им также нужен опыт, чтобы найти полезные данные среди множества получаемых результатов. Кроме того, программное обеспечение для моделирования схем не устанавливается на компьютеры заранее, если они не предназначены для такого приложения. Они также могут помочь проектировщику в таких задачах, как оптимизация для достижения наилучших показателей шума, обеспечение влияния фактора качества и оценка анализа устойчивости.
Они также могут помочь проектировщику в таких задачах, как оптимизация для достижения наилучших показателей шума, обеспечение влияния фактора качества и оценка анализа устойчивости.
 Вместо того, чтобы напрямую рассматривать его импеданс, вы выражаете его коэффициент отражения Γ L , который используется для характеристики нагрузки (например, проводимости, усиления и крутизны). Γ L более полезен при работе с радиочастотами.
Вместо того, чтобы напрямую рассматривать его импеданс, вы выражаете его коэффициент отражения Γ L , который используется для характеристики нагрузки (например, проводимости, усиления и крутизны). Γ L более полезен при работе с радиочастотами.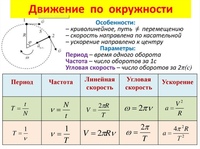 Затем мы можем определить нормализованный импеданс нагрузки следующим образом:
Затем мы можем определить нормализованный импеданс нагрузки следующим образом:
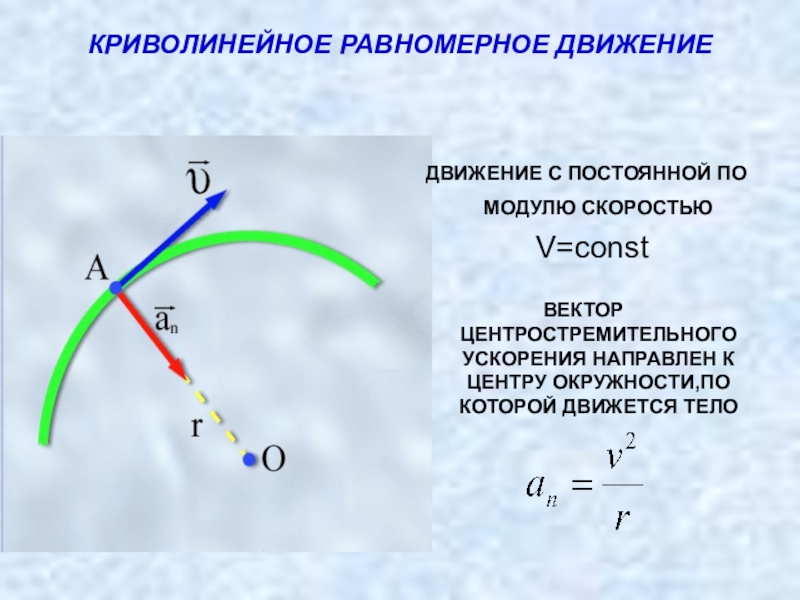
 Все круги (постоянный x) включают точку (1, 0). В отличие от кругов действительной части, × может быть положительным или отрицательным. Это объясняет повторяющиеся зеркальные круги в нижней части комплексной плоскости.Все центры окружностей расположены на вертикальной оси, пересекающей точку 1.
Все круги (постоянный x) включают точку (1, 0). В отличие от кругов действительной части, × может быть положительным или отрицательным. Это объясняет повторяющиеся зеркальные круги в нижней части комплексной плоскости.Все центры окружностей расположены на вертикальной оси, пересекающей точку 1. 
 Рисунок 5 ).Точки расположены следующим образом:
Рисунок 5 ).Точки расположены следующим образом: Номера:
Номера: Часто в мире допуска проще работать с параллельными элементами.
Часто в мире допуска проще работать с параллельными элементами.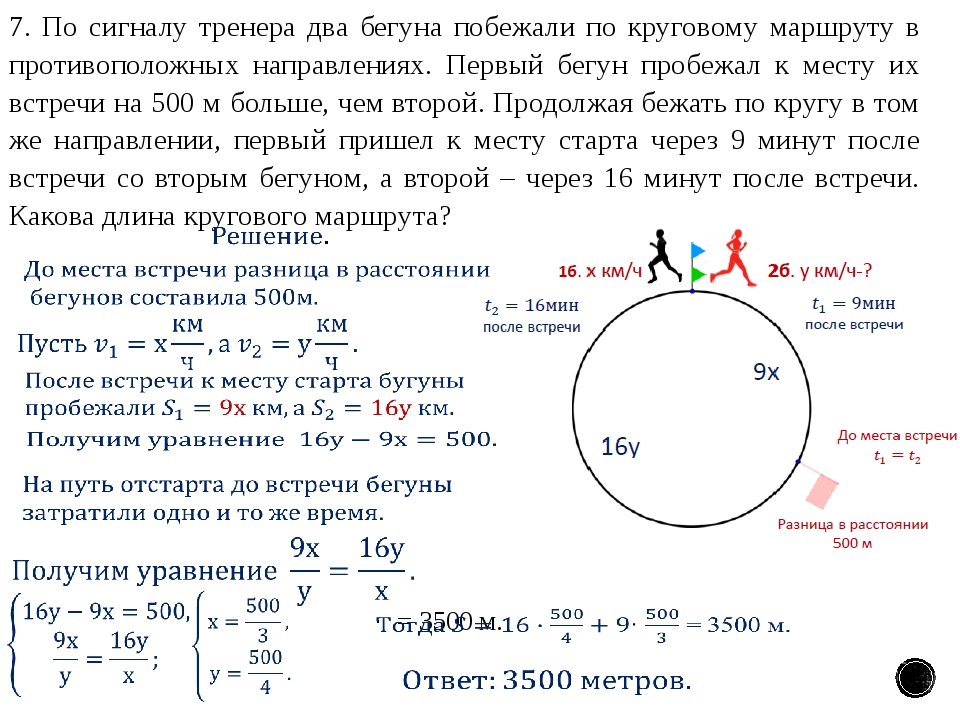 Тот же результат может быть получен путем поворота на угол 180 ° вокруг центральной точки (см. Рисунок 7).
Тот же результат может быть получен путем поворота на угол 180 ° вокруг центральной точки (см. Рисунок 7). Это очень удобно, так как избавляет от необходимости строить еще одну диаграмму. Точка пересечения всех окружностей (постоянная проводимость и постоянная проводимость) автоматически находится в точке (-1, 0). С этим сюжетом также становится проще добавлять элементы параллельно. Математически диаграмма Смита строится следующим образом:
Это очень удобно, так как избавляет от необходимости строить еще одну диаграмму. Точка пересечения всех окружностей (постоянная проводимость и постоянная проводимость) автоматически находится в точке (-1, 0). С этим сюжетом также становится проще добавлять элементы параллельно. Математически диаграмма Смита строится следующим образом: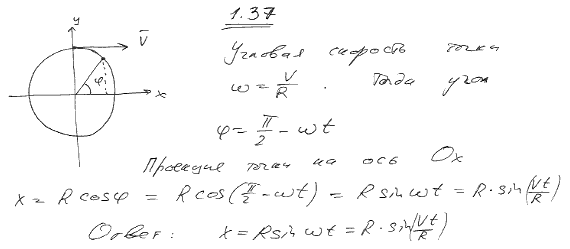
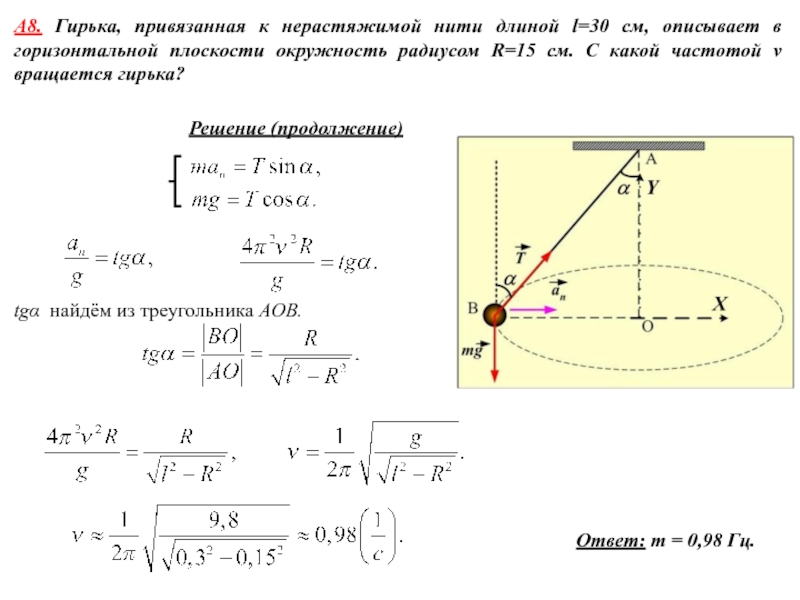 Затем у нас есть еще один элемент серии. Мы снова переключаемся обратно на диаграмму Смита импеданса.
Затем у нас есть еще один элемент серии. Мы снова переключаемся обратно на диаграмму Смита импеданса. Затем мы определяем требуемое значение z, расположенное на пересечении круга резистора 0,2 и круга реактивного сопротивления 0,5. Таким образом, z определено равным 0,2 + j0,5. Если характеристическое сопротивление системы составляет 50 Ом, тогда Z = 10 + j25 Ом (см. , рисунок 10 ).
Затем мы определяем требуемое значение z, расположенное на пересечении круга резистора 0,2 и круга реактивного сопротивления 0,5. Таким образом, z определено равным 0,2 + j0,5. Если характеристическое сопротивление системы составляет 50 Ом, тогда Z = 10 + j25 Ом (см. , рисунок 10 ). Но проблема в том, что может существовать бесконечное количество подходящих комбинаций компонентов сети, которые дают аналогичные результаты. И другие входные данные, возможно, также должны быть рассмотрены (например, структура типа фильтра, коэффициент качества и ограниченный выбор компонентов).
Но проблема в том, что может существовать бесконечное количество подходящих комбинаций компонентов сети, которые дают аналогичные результаты. И другие входные данные, возможно, также должны быть рассмотрены (например, структура типа фильтра, коэффициент качества и ограниченный выбор компонентов). Вот как находится решение.
Вот как находится решение. Это будет точка B (вход). Поскольку следующий элемент является последовательным элементом, точка B должна быть преобразована в плоскость импеданса. Тогда можно получить точку B ‘.Точка B ‘должна быть расположена на той же окружности резистора, что и D. Графически существует только одно решение от A’ до D, но промежуточная точка B (и, следовательно, B ‘) должна быть проверена с помощью «теста и -попробовать «setup. Найдя точки B и B ‘, мы можем измерить длины дуги A’ через B и дуги B ‘через D. Первая дает нормированное значение проводимости C. Вторая дает нормированное значение реактивного сопротивления L. Дуга A ‘через B измеряет b = 0,78 и, следовательно, B = 0,78 × Y 0 = 0.0156S. Поскольку ωC = B, тогда C = B / ω = B / (2πf) = 0,0156 / [2π (60 × 10 6 )] = 41,4 пФ.
Это будет точка B (вход). Поскольку следующий элемент является последовательным элементом, точка B должна быть преобразована в плоскость импеданса. Тогда можно получить точку B ‘.Точка B ‘должна быть расположена на той же окружности резистора, что и D. Графически существует только одно решение от A’ до D, но промежуточная точка B (и, следовательно, B ‘) должна быть проверена с помощью «теста и -попробовать «setup. Найдя точки B и B ‘, мы можем измерить длины дуги A’ через B и дуги B ‘через D. Первая дает нормированное значение проводимости C. Вторая дает нормированное значение реактивного сопротивления L. Дуга A ‘через B измеряет b = 0,78 и, следовательно, B = 0,78 × Y 0 = 0.0156S. Поскольку ωC = B, тогда C = B / ω = B / (2πf) = 0,0156 / [2π (60 × 10 6 )] = 41,4 пФ. 13. Типовая рабочая схема MAX2472.
13. Типовая рабочая схема MAX2472.  Это дает нам точку А ‘.
Это дает нам точку А ‘. Второй дает нормированное значение реактивного сопротивления C MATCH . Дуга от A ‘до B имеет размер b = -0,575 и, следовательно, B = -0,575 × Y 0 = 0,0115S. Поскольку 1 / ωL = B, то L MATCH = 1 / Bω = 1 / (B2πf) = 1 / (0,01156 × 2 × π × 900 × 10 6 ) = 15.38nH, что округляется до 15nH. Дуга от B ‘до D имеет размер × = -2,81, таким образом, X = -2,81 × Z 0 = -140,5 Ом. Поскольку -1 / ωC = X, тогда C MATCH = -1 / Xω = -1 / (X2πf) = -1 / (- 140,5 × 2 × π × 900 × 10 6 ) = 1,259 пФ, что округляет до 1 пФ. Хотя эти рассчитанные значения не учитывают паразитные индуктивности и емкости компонентов, они дают значения, близкие к значениям, указанным в технических данных: L MATCH = 12 нГн и C MATCH = 1 пФ.
Второй дает нормированное значение реактивного сопротивления C MATCH . Дуга от A ‘до B имеет размер b = -0,575 и, следовательно, B = -0,575 × Y 0 = 0,0115S. Поскольку 1 / ωL = B, то L MATCH = 1 / Bω = 1 / (B2πf) = 1 / (0,01156 × 2 × π × 900 × 10 6 ) = 15.38nH, что округляется до 15nH. Дуга от B ‘до D имеет размер × = -2,81, таким образом, X = -2,81 × Z 0 = -140,5 Ом. Поскольку -1 / ωC = X, тогда C MATCH = -1 / Xω = -1 / (X2πf) = -1 / (- 140,5 × 2 × π × 900 × 10 6 ) = 1,259 пФ, что округляет до 1 пФ. Хотя эти рассчитанные значения не учитывают паразитные индуктивности и емкости компонентов, они дают значения, близкие к значениям, указанным в технических данных: L MATCH = 12 нГн и C MATCH = 1 пФ.
Leave A Comment