2+x) $$ log(a,x) Логарифм x по основанию a log(3,cos(x)) $$ log_3(cos(x)) $$ sh(x) Гиперболический синус sh(x-1) $$ sh(x-1) $$ ch(x) Гиперболический косинус ch(x) $$ ch(x) $$ th(x) Гиперболический тангенс th(x) $$ th(x) $$ cth(x) Гиперболический котангенс cth(x) $$ cth(x) $$

При решении этой задачи используется большой и дорогой модуль одного «забугорного» сервиса. Решение он выдает в виде изображения и только на английском языке. Изменить это, к сожалению, нельзя. Ничего лучше мы найти не смогли. Зато он выводит подробное и очень качественное решение в том виде в котором оно принято в высших учебных заведениях. Единственное неудобство — на английском языке, но это не большая цена за качество.

ВыводПеревод, пояснениеSolve for x over the real numbersРешить относительно х в действительных числах (бывают ещё комплексные)Multiply both sides by …Умножаем обе части на …Equate exponents of … on both sidesПриравниваем степени … в обоих частях (с обоих сторон)Simplify and substitute …Упрощаем и делаем подстановку …Bring … together using the commom denominator …Приводим … к общему знаменателю …The left hand side factors into a product with two terms
Левая часть разбивается на множители как два многочленаSplit into two equationsРазделяем на два уравненияTake the square root of both sidesИзвлекаем квадратный корень из обоих частейSubtract . {-x}} \)\(coth(x)\)Гиперболический котангенс. У нас пишут \(cth(x) = \frac{1}{th(x)} \)

Если вам что-то осталось не понятно обязательно напишите об этом в Обранной связи и мы дополним эту таблицу.

tgx корень из 3 log13 2 sin 2x log31 корень из 2 cosx

Вы искали tgx корень из 3 log13 2 sin 2x log31 корень из 2 cosx? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и решите уравнение tgx корень из 3 log13 2sin 2x log31 корень из 2 cosx, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «tgx корень из 3 log13 2 sin 2x log31 корень из 2 cosx».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как tgx корень из 3 log13 2 sin 2x log31 корень из 2 cosx,решите уравнение tgx корень из 3 log13 2sin 2x log31 корень из 2 cosx. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и tgx корень из 3 log13 2 sin 2x log31 корень из 2 cosx. Просто введите задачу в окошко и нажмите «решить» здесь (например, tgx корень из 3 log13 2 sin 2x log31 корень из 2 cosx).

Где можно решить любую задачу по математике, а так же tgx корень из 3 log13 2 sin 2x log31 корень из 2 cosx Онлайн?

Решить задачу tgx корень из 3 log13 2 sin 2x log31 корень из 2 cosx вы можете на нашем сайте https://pocketteacher. 2 4x-1)-2cos4x=0`, `2cos4x(cos4x-1)=0 iff` $$ \iff \left[\begin{array}{l}\mathrm{cos}4x=1.\\ \mathrm{cos}4x=0.\end{array}\right.$$

Если  `cos4x=1`, то `4x=2pin,x=(pin)/2,ninZ`.

1. Изображаем точки

`x=(pin)/2,ninZ`,                                                           (3)

на тригонометрическом круге  (рис. 4а). Геометрически их `4` штуки (для `n=0,1,2,3` – далее они повторяются).

2. Изображаем точки

`x=(pim)/3,m inZ`                                                         (4)

которые не удовлетворяют ОДЗ на тригонометрическом круге (4б). Их `6` штук (для `m=0,1,2,3,4,5` – далее они повторяются).

   

Видно, что совпадения точек в `(3)` и `(4)` будут при `x=pin,ninZ`. Эти значения надо исключить из решения, т. е. в ответ пойдут точки       

`x=pi/2+pin,ninZ`.

С решениями уравнения

`cos4x=0`, `4x=pi/2+pin,ninZ`,

или `x=pi/8+(pin)/4,ninZ`, можно поступить аналогично, сделав отбор на тригонометрическом круге. Но когда точек–решений на тригонометрическом круге много, и много точек, не входящих в ОДЗ, то удобнее воспользоваться аналитическим способом отбора решений. В данном случае точек — решений на тригонометрическом круге в серии `x=pi/8+(pin)/4,ninZ`, будет `8` штук (различные при `n=0, 1, 2, 3, 4, 5, 6, 7` –  далее они повторяются), а точек, не входящих в ОДЗ на тригонометрическом круге `6`. Посмотрим, есть ли совпадения, т. е. существуют ли целые `m`  и  `n` такие, что

`pi/8+(pin)/4=(pim)/3 iff 1/8+n/4=m/3 iff`

`iff 3+6n=8m iff 3=2(4m-3n)`.

Последнее равенство невозможно, т. к. слева стоит нечётное число, а справа чётное.

Отметим, что и для решений уравнения `cos4x=1` отбор можно было сделать аналитически. А именно смотрим, существуют ли целые `m`  и  `n` такие, что `(pin)/2=(pim)/3 iff 3n=2m`.  Видим, что  `n` делится на `2`. Тогда `n=2k` и `m=3k,kinZ`. Т.  е. из решения уравнения `cos4x=1` надо исключить `x=(pin)/2`, где `n=2k`, т. е. оставить `x=(pin)/2` с `n=2k+1,kinZ`.

2-t-3=0`.  Его решение `t_1=-1` и `t_2=3/2`.

1) `»tg»x=-1`.  Следовательно, `x=-pi/4+pin,ninZ`.

2)  `»tg»x=2/3`. Тогда `x=»arctg»2/3+pin,ninZ`.

б) Сделаем отбор корней, принадлежащих отрезку `[-(3pi)/2; -pi/2]`.

1) Решаем неравенство `-(3pi)/2<=-pi/4+pin<=-pi/2`. Оно равносильно неравенству `-5/4<=n<=-1/4`. Т. к. `ninZ`, то последнему неравенству удовлетворяет только `n=-1`. Итак, из серии решений `x=-pi/4+pin,ninZ`, только корень `x=-(5pi)/4 in [-(3pi)/2; -pi/2]`.

2) Аналогично решаем неравенство

`-(3pi)/2<=»arctg»2/3+pin<=-pi/2`.                                                              (5)

Т. к. `ninZ`,  то в силу правого неравенства `n<0`. Число `n=-1` подходит, т. к. неравенство (5) в этом случае преобразуется в неравенство `-pi/2<=»arctg»2/3<=pi/2`,  что верно, `n=-2`  не удовлетворяет  (5), т. к. в этом случае получим `pi/2<=»arctg»2/3`, что неверно. Аналогично не подходит `n< -2`. Итак, из серии решений `x=»arctg»2/3+pin,ninZ`, только корень `(«arctg»2/3-pi)in[-(3pi)/2; -pi/2]`.

а)   `x=-pi/4+pin,ninZ`;  `x=»arctg»2/3+pin,ninZ`.

б)   `x=-(5pi)/4` и `x=»arctg»2/3-pi`.

Найти наименьший корень уравнения `»ctg»6x-«tg»5x=1/(cos5x)`,

принадлежащий отрезку `[(8pi)/17; (40pi)/17]`.

Преобразуем данное уравнение

`(cos6x)/(sin6x)-(sin5x)/(cos5x)=1/(cos5x)`, 

`(cos6x*cos5x-sin6x*sin5x)/(sin6x*cos5x)=1/(cos5x)`,

`(cos11x)/(sin6x*cos5x)=1/(cos5x)`.

Последнее уравнение равносильно `cos11x=sin6x` при условии  `sin6x*cos5x!=0`.

Решаем  уравнение  `cos11x-sin6x=0`. Преобразуем его:

`cos11x-cos(6x-pi/2)=0`   или  `-2sin((17x)/2-pi/4)sin((5x)/2+pi/4)=0`.

1) Если `sin((5x)/2+pi/4)=0` то `(5x)/2+pi/4=pin,ninZ`, откуда `5x=-pi/2+2pin,ninZ`.

Эти числа не являются корнями исходного уравнения, т. к. нарушается условие `cos5x!=0`.

2) Если `sin((17x)/2-pi/4)=0`, то `x=(pi(1+4n))/(34),ninZ`. Находим, при каких `ninZ`, эти числа лежат на отрезке  `[(8pi)/17;(40pi)/17]`. 2x)=0`  или  `sin2x+cos2x=0`.

Это однородное уравнение 1-го порядка. Оно эквивалентно уравнению   `»tg»2x=-1`.

Отсюда `2x=-pi/4+pin,ninZ`, или `x=-pi/8+(pin)/2,ninZ`.

Изобразим решения на тригонометрическом круге (рис. 6). Это `4` точки (`n=0,1,2,3` — далее они повторяются).

Для этих точек надо проверить неравенство `cosx-3sinx>=0`. Ясно, что точка `x_1` удовлетворяет этому неравенству, т. к. `cosx_1>0` и `sinx_1<0`. Для точки `x_3`, диаметрально противоположной точке `x_1`, `sinx` и `cosx` меняют знак, меняет знак и выражение `(cosx-3sinx)`, и, следовательно, для `x_3` неравенство не выполняется. Точка `x_2` не удовлетворяет неравенству, т. к. `sinx_2>0`, `cosx_2>0`, но `sinx_2>cosx_2` в виду того, что `pi/4<x_2<pi/2`, так что выражение `cosx_2-3sinx_2<0`. Точка `x_4` диаметрально противоположна `x_2`. Следовательно, 

`cosx_4-3sinx_4=-(cosx_2-3sinx_2)>0`,

и, значит, это решение. Учитывая, что решения имеют период `2pi`, получаем

`x=-pi/8+2pin,ninZ`;  `x=11/8pi+2pin,ninZ`.

VII. Уравнения с модулем

Решить уравнение `sin3x+|sinx|=sin2x`.

Решение уравнения сводится к объединению решений двух систем.

1) $$ \left\{\begin{array}{l}\mathrm{sin}x\ge 0,\\ \mathrm{sin}3x+\mathrm{sin}x=\mathrm{sin}2x.\end{array}\right.$$

2) sinx0,sin3x-sinx=sin2x.\left\{\begin{array}{l}\sin x

Решаем первую систему. Уравнение  `sin3x+sinx=sin2x` преобразуем:

`2sin2xcosx=sin2x` или `sin2x(2cosx-1)=0`. 

Значит,

$$ \left[\begin{array}{l}\mathrm{sin}2x=0,\\ \mathrm{cos}x=\frac{1}{2}.\end{array}\right.$$

Изображаем решения уравнения `sin2x=0` на тригонометрическом круге: `x=(pin)/2,ninZ`, (рис. 7). В силу неравенства `sinx>=0` не подходит нижняя точка, т. е. в решения системы входят

`x=pin,ninZ`, и `x=pi/2+2pin,ninZ`.   

   

Аналогично, изображаем на тригонометрическом круге (рис. 2x-cosx-1=0`.

Отсюда `cosx=1` или `cosx=-1/2`. На тригонометрическом круге этим уравнениям удовлетворяют соответственно точки (рис. 9 и рис. 10). Неравенству `sinx<0` удовлетворяет только одна из этих трёх точек, находящаяся в нижней полуплоскости, а именно       

`x=pi/3+pi+2pin,ninZ`.

   

В ответе две серии решений

  `x=pi/3+2pin,ninZ`  и  `x=pi/3+pi+2pin,ninZ`,   

соответствующие двум диаметрально противоположным точкам тригонометрического круга, можно задать одной формулой:

`x=pi/3+pin,ninZ` (но это не обязательно).

`x=pin`;  `x=pi/2+2pin`;  `x=pi/3+pin,ninZ`.

Примеры решения простейших тригонометрических неравенств

Часть 2.

Начало здесь.

Если вы беретесь за изучение темы «Простейшие тригонометрические неравенства», то должны прежде знать, где находятся оси тангенса и котангенса и уметь решать простейшие тригонометрические уравнения (часть III).

Кстати, для сдающих ЕГЭ по математике, –   умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.

Примеры решения простейших тригонометрических  неравенств

Пример 1. 

Решить неравенство:

Решение: 

Отмечаем на оси тангенсов 1. Указываем все значения тангенса, меньшие 1 – ниже 1.

Далее, отмечаем все точки тригонометрического круга, значение тангенса в которых будет меньше 1.  Для этого мы мысленно соединяем каждую точку оси тангенсов ниже 1 с началом координат; тогда каждая проведенная прямая пересечет дважды тригонометрический круг. Вот эти-то точки круга нас и интересуют! Они выстраиваются в две дуги (точнее в две серии дуг). Значения тангенса в них – меньше 1.

Заметим, кстати, что дуга повторяет дугу равно через пол круга, то есть через (период функции – это ).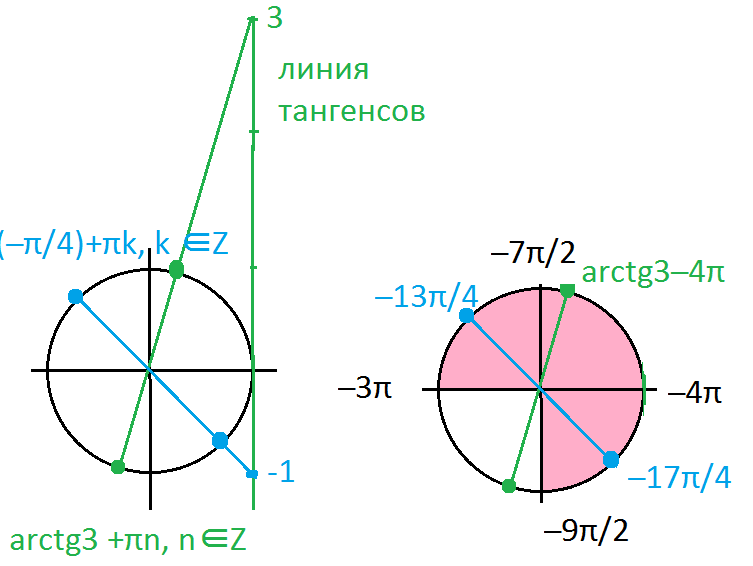

Все подходящие значения можно записать в виде следующего двойного неравенства:

или так

Пример 2. 

Решить неравенство:

Решение: 

Отмечаем на оси тангенсов . Указываем все значения тангенса, большие или равные  – выше   (включая саму точку).

«Транслируем» отмеченные точки оси тангенсов  на тригонометрический круг.

 

Все подходящие значения можно записать в виде следующего двойного неравенства:

или такого (разницы – никакой):

 

Пример 3.

Решить неравенство:

Решение: 

Отмечаем на оси котангенсов . Указываем все значения котангенса, большие или равные  – правее  (включая саму точку).

«Транслируем» отмеченные точки оси котангенсов  на тригонометрический круг:

Все подходящие значения можно записать в виде следующего двойного неравенства:

Вы обратили внимание, решая тригонометрическое неравенство с тангенсом,  – мы не включаем в ответ точки (значение тангенса в этих точках не определено)?

А, решая тригонометрическое неравенство с котангенсом,  – мы не включаем в ответ точки  (значение котангенса в этих точках не определено).

Пример 4.

Решить неравенство:

Решение: 

Проверьте себя

Помните,  решения (ответы)  к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. (См., например,  задание 2).

 1. Решить неравенство:

Ответ: + показать

2. Решить неравенство:

Ответ: + показать

3. Решить неравенство:

Ответ: + показать

Если у вас  есть  вопросы, – пожалуйста, – пишите в комментариях!

3 2 тригонометрия. Решение тригонометрических уравнений. Как решить тригонометрическое уравнение. Приведение к однородному уравнению

Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.

Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).

Примеры.

1. Уравнения, сводящиеся к простейшим.

1) Решить уравнение

Решение:

Ответ:

2) Найти корни уравнения

(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .

Решение:

Ответ:

2. Уравнения, сводящиеся к квадратным.

1) Решить уравнение 2 sin 2 x – cosx –1 = 0.

Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем

Ответ:

2) Решить уравнение cos 2x = 1 + 4 cosx.

Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем

Ответ:

3) Решить уравнение tgx – 2ctgx + 1 = 0

Решение:

Ответ:

3. Однородные уравнения

1) Решить уравнение 2sinx – 3cosx = 0

Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим

Ответ:

2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x

Решение:

Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим

sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0

Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получим

tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .

Ответ: arctg4 + 2 k , arctg2 + 2 k, k

4. Уравнения вида a sinx + b cosx = с, с ≠ 0.

1) Решить уравнение .

Решение:

Ответ:

5. Уравнения, решаемые разложением на множители.

1) Решить уравнение sin2x – sinx = 0.

Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. Проверим это:

cos 0 = 0 + 1 – равенство верно.

Число 0 единственный корень данного уравнения.

Ответ: 0.

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Концепция решения тригонометрических уравнений.

  • Для решения тригонометрического уравнения преобразуйте его в одно или несколько основных тригонометрических уравнений. Решение тригонометрического уравнения в конечном итоге сводится к решению четырех основных тригонометрических уравнений.

  • Решение основных тригонометрических уравнений.

    • Существуют 4 вида основных тригонометрических уравнений:
    • sin x = a; cos x = a
    • tg x = a; ctg x = a
    • Решение основных тригонометрических уравнений подразумевает рассмотрение различных положений «х» на единичной окружности, а также использование таблицы преобразования (или калькулятора).
    • Пример 1. sin x = 0,866. Используя таблицу преобразования (или калькулятор), вы получите ответ: х = π/3. Единичная окружность дает еще один ответ: 2π/3. Запомните: все тригонометрические функции являются периодическими, то есть их значения повторяются. Например, периодичность sin x и cos x равна 2πn, а периодичность tg x и ctg x равна πn. Поэтому ответ записывается следующим образом:
    • x1 = π/3 + 2πn; x2 = 2π/3 + 2πn.
    • Пример 2. соs х = -1/2. Используя таблицу преобразования (или калькулятор), вы получите ответ: х = 2π/3. Единичная окружность дает еще один ответ: -2π/3.
    • x1 = 2π/3 + 2π; х2 = -2π/3 + 2π.
    • Пример 3. tg (x — π/4) = 0.
    • Ответ: х = π/4 + πn.
    • Пример 4. ctg 2x = 1,732.
    • Ответ: х = π/12 + πn.

  • Преобразования, используемые при решении тригонометрических уравнений.

    • Для преобразования тригонометрических уравнений используются алгебраические преобразования (разложение на множители, приведение однородных членов и т.д.) и тригонометрические тождества.
    • Пример 5. Используя тригонометрические тождества, уравнение sin x + sin 2x + sin 3x = 0 преобразуется в уравнение 4cos x*sin (3x/2)*cos (x/2) = 0. Таким образом, нужно решить следующие основные тригонометрические уравнения: cos x = 0; sin (3x/2) = 0; cos (x/2) = 0.

    • Нахождение углов по известным значениям функций.

      • Перед изучением методов решения тригонометрических уравнений вам необходимо научиться находить углы по известным значениям функций. Это можно сделать при помощи таблицы преобразования или калькулятора.
      • Пример: соs х = 0,732. Калькулятор даст ответ х = 42,95 градусов. Единичная окружность даст дополнительные углы, косинус которых также равен 0,732.

    • Отложите решение на единичной окружности.

      • Вы можете отложить решения тригонометрического уравнения на единичной окружности. Решения тригонометрического уравнения на единичной окружности представляют собой вершины правильного многоугольника.
      • Пример: Решения x = π/3 + πn/2 на единичной окружности представляют собой вершины квадрата.
      • Пример: Решения x = π/4 + πn/3 на единичной окружности представляют собой вершины правильного шестиугольника.

    • Методы решения тригонометрических уравнений.

      • Если данное тригонометрическое уравнение содержит только одну тригонометрическую функцию, решите это уравнение как основное тригонометрическое уравнение. Если данное уравнение включает две или более тригонометрические функции, то существуют 2 метода решения такого уравнения (в зависимости от возможности его преобразования).
      • Преобразуйте данное уравнение в уравнение вида: f(x)*g(x)*h(x) = 0, где f(x), g(x), h(x) — основные тригонометрические уравнения.
      • Пример 6. 2cos x + sin 2x = 0. (0
      • Решение. Используя формулу двойного угла sin 2x = 2*sin х*соs х, замените sin 2x.
      • 2соs х + 2*sin х*соs х = 2cos х*(sin х + 1) = 0. Теперь решите два основных тригонометрических уравнения: соs х = 0 и (sin х + 1) = 0.
      • Пример 7. cos x + cos 2x + cos 3x = 0. (0
      • Решение: Используя тригонометрические тождества, преобразуйте данное уравнение в уравнение вида: cos 2x(2cos x + 1) = 0. Теперь решите два основных тригонометрических уравнения: cos 2x = 0 и (2cos x + 1) = 0.
      • Пример 8. sin x — sin 3x = cos 2x . (0
      • Решение: Используя тригонометрические тождества, преобразуйте данное уравнение в уравнение вида: -cos 2x*(2sin x + 1) = 0. Теперь решите два основных тригонометрических уравнения: cos 2x = 0 и (2sin x + 1) = 0. n – минус один в степени n.

        Ещё примеры тригонометрических уравнений.

        Решить уравнения: а) cos(x/5)=1 б)tg(3x- π/3)= √3

        Решение:

        А) В этот раз перейдем непосредственно к вычислению корней уравнения сразу:

        X/5= ± arccos(1) + 2πk. Тогда x/5= πk => x=5πk

        Ответ: x=5πk, где k – целое число.

        Б) Запишем в виде: 3x- π/3=arctg(√3)+ πk. Мы знаем что: arctg(√3)= π/3

        3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3

        Ответ: x=2π/9 + πk/3, где k – целое число.

        Решить уравнения: cos(4x)= √2/2. И найти все корни на отрезке .

        Решение:

        Решим в общем виде наше уравнение: 4x= ± arccos(√2/2) + 2πk

        4x= ± π/4 + 2πk;

        X= ± π/16+ πk/2;

        Теперь давайте посмотрим какие корни попадут на наш отрезок. При k При k=0, x= π/16, мы попали в заданный отрезок .
        При к=1, x= π/16+ π/2=9π/16, опять попали.
        При k=2, x= π/16+ π=17π/16, а тут вот уже не попали, а значит при больших k тоже заведомо не будем попадать.

        Ответ: x= π/16, x= 9π/16

        Два основных метода решения.

        Мы рассмотрели простейшие тригонометрические уравнения, но существуют и более сложные. Для их решения применяют метод ввода новой переменной и метод разложения на множители. Давайте рассмотрим примеры.

        Решим уравнение:

        Решение:
        Для решения нашего уравнения воспользуемся методом ввода новой переменной, обозначим: t=tg(x).

        В результате замены получим: t 2 + 2t -1 = 0

        Найдем корни квадратного уравнения: t=-1 и t=1/3

        Тогда tg(x)=-1 и tg(x)=1/3, получили простейшее тригонометрическое уравнение, найдем его корни.

        X=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.

        Ответ: x= -π/4+πk; x=arctg(1/3) + πk.

        Пример решения уравнения

        Решить уравнений: 2sin 2 (x) + 3 cos(x) = 0

        Решение:

        Воспользуемся тождеством: sin 2 (x) + cos 2 (x)=1

        Наше уравнение примет вид:2-2cos 2 (x) + 3 cos (x) = 0

        2 cos 2 (x) — 3 cos(x) -2 = 0

        Введем замену t=cos(x): 2t 2 -3t — 2 = 0

        Решением нашего квадратного уравнения являются корни: t=2 и t=-1/2

        Тогда cos(x)=2 и cos(x)=-1/2.

        Т.к. косинус не может принимать значения больше единицы, то cos(x)=2 не имеет корней.

        Для cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk

        Ответ: x= ±2π/3 + 2πk

        Однородные тригонометрические уравнения.

        Определение: Уравнение вида a sin(x)+b cos(x) называются однородными тригонометрическими уравнениями первой степени.

        Уравнения вида

        однородными тригонометрическими уравнениями второй степени.

        Для решения однородного тригонометрического уравнения первой степени разделим его на cos(x): Делить на косинус нельзя если он равен нулю, давайте убедимся что это не так:
        Пусть cos(x)=0, тогда asin(x)+0=0 => sin(x)=0, но синус и косинус одновременно не равны нулю, получили противоречие, поэтому можно смело делить на ноль.

        Решить уравнение:
        Пример: cos 2 (x) + sin(x) cos(x) = 0

        Решение:

        Вынесем общий множитель: cos(x)(c0s(x) + sin (x)) = 0

        Тогда нам надо решить два уравнения:

        Cos(x)=0 и cos(x)+sin(x)=0

        Cos(x)=0 при x= π/2 + πk;

        Рассмотрим уравнение cos(x)+sin(x)=0 Разделим наше уравнение на cos(x):

        1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk

        Ответ: x= π/2 + πk и x= -π/4+πk

        Как решать однородные тригонометрические уравнения второй степени?
        Ребята, придерживайтесь этих правил всегда!

        1. Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде

        2. Если a≠0, то нужно поделить обе части уравнения на косинус в квадрате, получим:


        Делаем замену переменной t=tg(x) получаем уравнение:

        Решить пример №:3

        Решить уравнение:
        Решение:

        Разделим обе части уравнения на косинус квадрат:

        Делаем замену переменной t=tg(x): t 2 + 2 t — 3 = 0

        Найдем корни квадратного уравнения: t=-3 и t=1

        Тогда: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk

        Tg(x)=1 => x= π/4+ πk

        Ответ: x=-arctg(3) + πk и x= π/4+ πk

        Решить пример №:4

        Решить уравнение:

        Решение:
        Преобразуем наше выражение:


        Решать такие уравнение мы умеем: x= — π/4 + 2πk и x=5π/4 + 2πk

        Ответ: x= — π/4 + 2πk и x=5π/4 + 2πk

        Решить пример №:5

        Решить уравнение:

        Решение:
        Преобразуем наше выражение:


        Введем замену tg(2x)=t:2 2 — 5t + 2 = 0

        Решением нашего квадратного уравнения будут корни: t=-2 и t=1/2

        Тогда получаем: tg(2x)=-2 и tg(2x)=1/2
        2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2

        2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2

        Ответ: x=-arctg(2)/2 + πk/2 и x=arctg(1/2)/2+ πk/2

        Задачи для самостоятельного решения.

        1) Решить уравнение

        А) sin(7x)= 1/2 б) cos(3x)= √3/2 в) cos(-x) = -1 г) tg(4x) = √3 д) ctg(0.5x) = -1.7

        2) Решить уравнения: sin(3x)= √3/2. И найти все корни на отрезке [π/2; π ].

        3) Решить уравнение: ctg 2 (x) + 2ctg(x) + 1 =0

        4) Решить уравнение: 3 sin 2 (x) + √3sin (x) cos(x) = 0

        5) Решить уравнение:3sin 2 (3x) + 10 sin(3x)cos(3x) + 3 cos 2 (3x) =0

        6)Решить уравнение:cos 2 (2x) -1 — cos(x) =√3/2 -sin 2 (2x)

        Требует знания основных формул тригонометрии — сумму квадратов синуса и косинуса, выражение тангенса через синус и косинус и другие. Для тех, кто их забыл или не знает рекомендуем прочитать статью » «.
        Итак, основные тригонометрические формулы мы знаем, пришло время использовать их на практике. Решение тригонометрических уравнений при правильном подходе – довольно увлекательное занятие, как, например, собрать кубик Рубика.

        Исходя из самого названия видно, что тригонометрическое уравнение – это уравнение, в котором неизвестное находится под знаком тригонометрической функции.
        Существуют так называемые простейшие тригонометрические уравнения. Вот как они выглядят: sinх = а, cos x = a, tg x = a. Рассмотрим, как решить такие тригонометрические уравнения , для наглядности будем использовать уже знакомый тригонометрический круг.

        sinх = а
        cos x = a

        tg x = a

        cot x = a

        Любое тригонометрическое уравнение решается в два этапа: приводим уравнение к простейшему виду и далее решаем его, как простейшее тригонометрическое уравнение.
        Существует 7 основных методов, с помощью которых решаются тригонометрические уравнения.

        1. Метод замены переменной и подстановки

          2. Решить уравнение 2cos 2 (x + /6) – 3sin( /3 – x) +1 = 0

          Используя формулы приведения получим:

          2cos 2 (x + /6) – 3cos(x + /6) +1 = 0

          Заменим cos(x + /6) на y для упрощения и получаем обычное квадратное уравнение:

          2y 2 – 3y + 1 + 0

          Корни которого y 1 = 1, y 2 = 1/2

          Теперь идем в обратном порядке

          Подставляем найденные значения y и получаем два варианта ответа:

        2. Решение тригонометрических уравнений через разложение на множители

          3. Как решить уравнение sin x + cos x = 1 ?

          Перенесем все влево, чтобы справа остался 0:

          sin x + cos x – 1 = 0

          Воспользуемся вышерассмотренными тождествами для упрощения уравнения:

          sin x — 2 sin 2 (x/2) = 0

          Делаем разложение на множители:

          2sin(x/2) * cos(x/2) — 2 sin 2 (x/2) = 0

          2sin(x/2) * = 0

          Получаем два уравнения

        3. Приведение к однородному уравнению

          4. Уравнение является однородным относительно синуса и косинуса, если все его члены относительно синуса и косинуса одной и той же степени одного и того же угла. Для решения однородного уравнения, поступают следующим образом:

          а) переносят все его члены в левую часть;

          б) выносят все общие множители за скобки;

          в) приравнивают все множители и скобки к 0;

          г) в скобках получено однородное уравнение меньшей степени, его в свою очередь делят на синус или косинус в старшей степени;

          д) решают полученное уравнение относительно tg.

          Решить уравнение 3sin 2 x + 4 sin x cos x + 5 cos 2 x = 2

          Воспользуемся формулой sin 2 x + cos 2 x = 1 и избавимся от открытой двойки справа:

          3sin 2 x + 4 sin x cos x + 5 cos x = 2sin 2 x + 2cos 2 x

          sin 2 x + 4 sin x cos x + 3 cos 2 x = 0

          Делим на cos x:

          tg 2 x + 4 tg x + 3 = 0

          Заменяем tg x на y и получаем квадратное уравнение:

          y 2 + 4y +3 = 0, корни которого y 1 =1, y 2 = 3

          Отсюда находим два решения исходного уравнения:

          x 2 = arctg 3 + k

        4. Решение уравнений, через переход к половинному углу

          5. Решить уравнение 3sin x – 5cos x = 7

          Переходим к x/2:

          6sin(x/2) * cos(x/2) – 5cos 2 (x/2) + 5sin 2 (x/2) = 7sin 2 (x/2) + 7cos 2 (x/2)

          Пререносим все влево:

          2sin 2 (x/2) – 6sin(x/2) * cos(x/2) + 12cos 2 (x/2) = 0

          Делим на cos(x/2):

          tg 2 (x/2) – 3tg(x/2) + 6 = 0

        5. Введение вспомогательного угла

          6. Для рассмотрения возьмем уравнение вида: a sin x + b cos x = c ,

          где a, b, c – некоторые произвольные коэффициенты, а x – неизвестное.

          Обе части уравнения разделим на :

          Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают свойствами sin и cos, а именно: их модуль не более 1 и сумма квадратов = 1. Обозначим их соответственно как cos и sin , где – это и есть так называемый вспомогательный угол. Тогда уравнение примет вид:

          cos * sin x + sin * cos x = С

          или sin(x + ) = C

          Решением этого простейшего тригонометрического уравнения будет

          х = (-1) k * arcsin С — + k, где

          Следует отметить, что обозначения cos и sin взаимозаменяемые.

          Решить уравнение sin 3x – cos 3x = 1

          В этом уравнении коэффициенты:

          а = , b = -1, поэтому делим обе части на = 2

        Mathway | Популярные задачи

        1 Найти точное значение sin(30)
        2 Найти точное значение sin(45)
        3 Найти точное значение sin(30 град. )
        4 Найти точное значение sin(60 град. )
        5 Найти точное значение tan(30 град. )
        6 Найти точное значение arcsin(-1)
        7 Найти точное значение sin(pi/6)
        8 Найти точное значение cos(pi/4)
        9 Найти точное значение sin(45 град. )
        10 Найти точное значение sin(pi/3)
        11 Найти точное значение arctan(-1)
        12 Найти точное значение cos(45 град. )
        13 Найти точное значение cos(30 град. )
        14 Найти точное значение tan(60)
        15 Найти точное значение csc(45 град. )
        16 Найти точное значение tan(60 град. )
        17 Найти точное значение sec(30 град. )
        18 Найти точное значение cos(60 град. )
        19 Найти точное значение cos(150)
        20 Найти точное значение sin(60)
        21 Найти точное значение cos(pi/2)
        22 Найти точное значение tan(45 град. )
        23 Найти точное значение arctan(- квадратный корень 3)
        24 Найти точное значение csc(60 град. )
        25 Найти точное значение sec(45 град. )
        26 Найти точное значение csc(30 град. )
        27 Найти точное значение sin(0)
        28 Найти точное значение sin(120)
        29 Найти точное значение cos(90)
        30 Преобразовать из радианов в градусы pi/3
        31 Найти точное значение tan(30)
        32 Преобразовать из градусов в радианы 45
        33 Найти точное значение cos(45)
        34 Упростить sin(theta)^2+cos(theta)^2
        35 Преобразовать из радианов в градусы pi/6
        36 Найти точное значение cot(30 град. )
        37 Найти точное значение arccos(-1)
        38 Найти точное значение arctan(0)
        39 Найти точное значение cot(60 град. )
        40 Преобразовать из градусов в радианы 30
        41 Преобразовать из радианов в градусы (2pi)/3
        42 Найти точное значение sin((5pi)/3)
        43 Найти точное значение sin((3pi)/4)
        44 Найти точное значение tan(pi/2)
        45 Найти точное значение sin(300)
        46 Найти точное значение cos(30)
        47 Найти точное значение cos(60)
        48 Найти точное значение cos(0)
        49 Найти точное значение cos(135)
        50 Найти точное значение cos((5pi)/3)
        51 Найти точное значение cos(210)
        52 Найти точное значение sec(60 град. )
        53 Найти точное значение sin(300 град. )
        54 Преобразовать из градусов в радианы 135
        55 Преобразовать из градусов в радианы 150
        56 Преобразовать из радианов в градусы (5pi)/6
        57 Преобразовать из радианов в градусы (5pi)/3
        58 Преобразовать из градусов в радианы 89 град.
        59 Преобразовать из градусов в радианы 60
        60 Найти точное значение sin(135 град. )
        61 Найти точное значение sin(150)
        62 Найти точное значение sin(240 град. )
        63 Найти точное значение cot(45 град. )
        64 Преобразовать из радианов в градусы (5pi)/4
        65 Найти точное значение sin(225)
        66 Найти точное значение sin(240)
        67 Найти точное значение cos(150 град. )
        68 Найти точное значение tan(45)
        69 Вычислить sin(30 град. )
        70 Найти точное значение sec(0)
        71 Найти точное значение cos((5pi)/6)
        72 Найти точное значение csc(30)
        73 Найти точное значение arcsin(( квадратный корень 2)/2)
        74 Найти точное значение tan((5pi)/3)
        75 Найти точное значение tan(0)
        76 Вычислить sin(60 град. )
        77 Найти точное значение arctan(-( квадратный корень 3)/3)
        78 Преобразовать из радианов в градусы (3pi)/4
        79 Найти точное значение sin((7pi)/4)
        80 Найти точное значение arcsin(-1/2)
        81 Найти точное значение sin((4pi)/3)
        82 Найти точное значение csc(45)
        83 Упростить arctan( квадратный корень 3)
        84 Найти точное значение sin(135)
        85 Найти точное значение sin(105)
        86 Найти точное значение sin(150 град. )
        87 Найти точное значение sin((2pi)/3)
        88 Найти точное значение tan((2pi)/3)
        89 Преобразовать из радианов в градусы pi/4
        90 Найти точное значение sin(pi/2)
        91 Найти точное значение sec(45)
        92 Найти точное значение cos((5pi)/4)
        93 Найти точное значение cos((7pi)/6)
        94 Найти точное значение arcsin(0)
        95 Найти точное значение sin(120 град. )
        96 Найти точное значение tan((7pi)/6)
        97 Найти точное значение cos(270)
        98 Найти точное значение sin((7pi)/6)
        99 Найти точное значение arcsin(-( квадратный корень 2)/2)
        100 Преобразовать из градусов в радианы 88 град. 2 + n-72) = 1 / (n + 9)

        # НАЗВАНИЕ № || КОБЕЛКО — КОБЕ СТАЛЬ, ООО.-

        Технические особенности, том 6

        Порошковая проволока Kobelco для нержавеющих сталей: удовлетворение разнообразных потребностей рынка с помощью широкого ассортимента продукции


        1. Мировой спрос на нержавеющую сталь и сопутствующие сварочные материалы

        Рисунок 1: Мировое производство нержавеющей стали
        Примечание: Китай был включен в Азию до 2007 года.

        За годы, прошедшие после финансового кризиса 2008 года, мировое производство нержавеющей стали плавно восстановилось благодаря значительному увеличению потребления в Китае, достигнув уровня 30 миллионов тонн в 2011 году (см. Диаграмму 1).По прогнозам, он вырастет до 40 миллионов тонн в 2014 году и до 45 миллионов тонн в 2020 году, поскольку ожидается постоянный рост мирового спроса.

        Если проанализировать мировой спрос по странам, то на долю Китая приходится самая большая сумма с 2008 года и около 40% в 2011 году, что намного превышает спрос со стороны Японии (чуть более 10%) и США (чуть менее 10%). Прогнозы будущего спроса предполагают увеличение потребления на развивающихся рынках, таких как Индия и Турция, в дополнение к Китаю.

        Что касается того, какие виды нержавеющей стали будут востребованы в 2020 году, то ожидается небольшое снижение количества аустенитных сталей. с нынешних 60% от общего спроса до примерно 50%, в то время как ферритная, а также дуплексная сталь будет увеличиваться.

        В отличие от этого, хотя данные о мировом спросе на сварочные материалы для нержавеющих сталей отсутствуют, его можно рассчитать на основе данных по нержавеющим сталям. Информация о сварочных материалах для нержавеющих сталей в Японии данные Японской ассоциации сварочных материалов, которая сообщает, что внутреннее потребление сварочных материалов для нержавеющих сталей в 2011 году составило около 7500 тонн. Соответственно, соотношение сварочных материалов и нержавеющих сталей (удельное соотношение) рассчитывается как примерно 0.2%. Следовательно, при том же соотношении единиц 0,2% мировой спрос на сварочные материалы для нержавеющих сталей прогнозируется на уровне немногим более 60 000 тонн в 2011 году, увеличиваясь до 80 000 тонн в 2014 году и 90 000 тонн в 2020 году.

        2. Характеристики порошковой проволоки Kobelco для нержавеющих сталей

        Рисунок 2: Схема поперечного сечения
        Kobe Steel FCW
        для нержавеющей стали

        Порошковая проволока

        (FCW) обеспечивает высокую скорость наплавки, а также отличную свариваемость в целом.Высота скорость наплавки помогает сократить общее время сварки, улучшить свариваемость и минимизировать время, затрачиваемое на обработка после сварки, такая как удаление брызг и дыма, прилипающих к стальным пластинам. FCW, особенно при использовании с аустенитной нержавеющей сталью, придает сварным участкам красивый внешний вид и высокую коррозионную стойкость: важные факторы для конструкций из аустенитной нержавеющей стали.

        На рис. 2 показано схематическое поперечное сечение Kobe Steel FCW для аустенитных нержавеющих сталей.Наружная оболочка должен стать как можно более тонким, чтобы обеспечить высокую плотность тока, что, в свою очередь, увеличивает эффективность за счет увеличение количества свариваемого металла в единицу времени даже при одинаковом сварочном токе.


        Рисунок 3: Сравнение образования брызг

        FCW

        Kobelco для нержавеющих сталей также имеют хорошую репутацию за стабильную дугу со 100% CO 2 и Ar-CO 2 смешанными защитными газами, что приводит к очень небольшому разбрызгиванию, как показано на Рисунке 3.Эта особенность достигается не только за счет соответствующей конструкции флюса (и отличного контроля качества на производственных предприятиях Kobelco в Японии и Нидерланды), а также специальную обработку поверхности проволоки, которая обеспечивает стабильную подачу проволоки. Еще одна особенность FCW для нержавеющих сталей, таких как PREMIARCTM DW-308L, PREMIARCTM DW-316L (для плоского положения и угловой сварки), — это то, как они предназначены для борьбы с образованием шлака: шлак можно легко снять в оптимальное время после сварки, что предотвращает образование темного цвета на поверхности валика (см. рисунок 4).

        Рисунок 4: Удаление шлака и внешний вид валика сразу после сварки (DW-308L)

        Когда на сварных швах, требующих эстетичного внешнего вида и чистоты, образуется цвет отпуска, в качестве меры противодействия требуется обработка травлением, кислотная обработка для удаления цвета с поверхности металла шва. Избегая образования Темперированного цвета сокращается время, затрачиваемое на кислотную обработку, что увеличивает производительность.


        4. Современные станки Kobelco FCW для нержавеющих сталей

        Технологически продвинутые FCW Kobelco для нержавеющих сталей — это единичные продукты, разработанные исключительно Kobe Steel; им доверяют и предпочитают пользователи по всему миру.В Таблице 1 (на стр. 4) представлен широкий спектр FCW для нержавеющих сталей.

        3-1. FCW с низким содержанием Cr (VI) для нержавеющих сталей: «серия XR»

        Рисунок 5: Взаимосвязь между компонентами флюса и Cr (VI) в сварочном дыме

        Сварочные сварочные аппараты

        могут выделять больше дыма, чем другие традиционные сварочные процессы, что увеличивает риски для безопасности. Сварочный дым представляет собой оксид, который образуется при охлаждении и затвердевании паров металла, генерируемых дугой, на воздухе.В случае сварки нержавеющей стали дым содержит от 5 до 20% оксида Cr, часть которого существует в виде вредного Cr6 +, обозначенного как Cr (VI).

        Токсичность Cr (VI) недавно была переоценена в соответствии с шагами по более строгому регулированию ее на рабочем месте. Например, в 2010 году Американское управление по безопасности и гигиене труда (OSHA) снизить допустимое количество Cr (VI) в воздухе на рабочем месте на 90%. Само собой разумеется, что самый эффективный метод для снижения содержания Cr (VI), связанного со сваркой нержавеющей стали, необходимо установить более мощные системы вентиляции для удаления пары.С другой стороны, если бы сварочный дым изначально содержал меньше Cr (VI), потребовалось бы меньше усилий для его удаления за счет лучшей вентиляции, такой как местная вентиляция.

        Рисунок 6: Рекомендуемый диапазон параметров сварки DW-308LP-XR

        Эффективно снижает содержание Cr (VI) в сварочном дыме. Kobe Steel разработала новую серию FCW, «серию XR» для плоской / горизонтальной угловой сварки, а также для сварки во всех положениях, которые резко снижают содержание Cr (VI) в сварочном дыме.Универсальные FCW серии XR предназначены для трех типов нержавеющих сталей, а именно 308L, 316L и 309L.

        Как показано на Рисунке 5, контроль содержания Na и K, добавленных во флюс в качестве стабилизаторов дуги, может снизить содержание Cr (VI) в сварочном дыме. Однако для поддержания стабильной свариваемости может потребоваться корректировка содержания других добавок, таких как фториды, а также Na и K.

        Рисунок 7: Интенсивность выбросов Cr (VI) DW-308LP-XR

        Одним из новых FCW серии XR является универсальный PREMIARCTM DW-308LP-XR.Он предназначен для применения как 100% CO 2 , так и смешанный защитный газ Ar-CO 2 . На рисунке 6 показан рекомендуемый диапазон параметров сварки и На рисунке 7 показан уровень выбросов Cr (VI) (измеренный в соответствии с ISO 15011-1 и ISO 16740) соответственно. Это показывает, что Серия XR выделяет Cr (VI) в размере всего 1/6 от обычного DW-308LP. Для получения дополнительной информации о PREMIARCTM DW-308L-XR и PREMIARCTM DW-316L-XR, пожалуйста, обратитесь к колонке Product Spotlight в KOBELCO WELDING TODAY, Vol.14, №3 от 2011г.

        Рисунок 8: Внешний вид валика и макроструктура стыкового соединения, сварка в положении 3G с DW-308LP-XR

        Стыковое соединение было сварено в вертикальном положении вверх (3G) с помощью DW-308LP-XR в условиях, перечисленных в таблице 2; На рис. 8 показан вид валика и макроструктура соответственно.

        3-2. FCW для дуплексных нержавеющих сталей

        Рисунок 9: Гофрированные элементы перегородки в танкере-химовозе
        Рис. 10: Мост Стоункуттерс в Гонконге

        Дуплексная нержавеющая сталь имеет двухфазную микроструктуру: 50% ферритной и 50% аустенитной.Преимущества включают высокую прочность, превосходную стойкость к точечной коррозии, щелевой коррозии, а также коррозионному растрескиванию под напряжением (SCC).

        На рынке доступны три различных дуплексных нержавеющей стали: (1) стандартные дуплексные нержавеющие стали, обычно ASTM S31803, S32205 и JIS SUS329J3L; (2) бедные дуплексные нержавеющие стали, которые, хотя и уступают другим дуплексным нержавеющим сталям, почти эквивалентны 304L и 316L по коррозионной стойкости и более дешевы из-за пониженного содержания Ni и Mo, и (3) супердуплексные нержавеющие стали, которые содержат большее количество Cr, Mo и N, чтобы выдерживать более агрессивные среды.Благодаря своей превосходной стойкости к точечной коррозии они широко применяются в опреснительных установках, при бурении и переработке нефти и природного газа, в системах обессеривания дымовых газов и гофрированных перегородках в танкерах-химовозах (рис. 9). Дуплексная нержавеющая сталь распространяется даже на более общие конструкции, такие как мост Stonecutters в Гонконге (рис. 10) и крышу международного аэропорта Нью-Доха в Катаре.

        FCW

        для дуплексной нержавеющей стали включает недавно разработанный PREMIARC TM DW-2209 для стандартной дуплексной нержавеющей стали, PREMIARC TM DW-2307 для бедной дуплексной нержавеющей стали и PREMIARC TM DW-2594 для супер-дуплексной нержавеющей стали.В Таблице 3 показан химический состав всех металлов сварного шва, а в Таблице 4 — механические свойства DW-2307 и DW-2594, соответственно.

        Рисунок 11: Внешний вид валика и макроструктура DW-2594 в позиции 3G.
        (80% Ar-20% CO 2 экранирование, 160A-26V)

        Одной из особенностей дуплексных нержавеющих сталей и связанных с ними сварочных материалов является высокое содержание азота, которые могут вызвать выбоины в металле сварного шва или ямки и червячные отверстия на поверхности металла сварного шва, когда высокое содержание азота, растворенного в расплавленном металле, не остается в затвердевающем металле сварного шва в состоянии твердого раствора.В машинах Kobelco FCW для дуплексных нержавеющих сталей компоненты флюса оптимизированы так, чтобы противостоять газовым полостям, несмотря на высокое содержание азота. На рисунке 11 показан внешний вид борта и макроструктура стыкового соединения DW-2594 в позиции 3G. Никаких дефектов, таких как червоточина или ямка, не видно.

        3-3. Стержень для сварки TIG с флюсовым сердечником «Серия TGX»

        Рисунок 12: Задний валик при сварке заднего валика трубы проволокой TGX
        Рисунок 13: Задний валик (слева) и поверхностный валик (справа)

        При сварке корневого прохода труб из нержавеющей стали с помощью прутка TIG обычно требуется задний экран из чистого газа Ar, чтобы предотвратить окисление заднего валика, которое может сделать его несостоятельным.Существует два распространенных метода задней защиты: защита всей трубы и защита зоны сварного шва. Однако при использовании любого из этих методов количество времени и газа Ar, необходимого для защиты, огромно и дорого.

        Еще один пример ведущей технологии проектирования FCW от Kobe Steel — присадочные стержни серии TGX для сварки TIG. Сварка корневого прохода устраняет необходимость в дорогостоящей задней защите. Еще одним важным моментом является то, как они позволяют операторам безопасно работать внутри труб без опасности дефицита кислорода.

        Рисунок 14: Как сохранить отверстие под ключ

        Флюс внутри присадочного стержня TGX образует соответствующее количество шлака, который полностью покрывает как задняя и поверхностная стороны борта, защищая их от воздействия воздуха и предотвращая окисление даже без заднего экрана. Шлак, покрывающий обе стороны валика, легко удаляется легким постукиванием и оставляет красивый валик, как показано на рисунках 12 и 13.

        Поскольку FCW серии TGX бесшовные, с ними обращаются почти так же, как со сплошными TIG-стержнями.

        Чтобы закрепить прочный задний борт с помощью присадочного прутка TGX, необходимо во время сварки сформировать шпоночное отверстие, чтобы что достаточное количество расплавленного шлака потечет к задней стороне канавки и покроет заднюю сторону валика (Рисунок 14).

        Таблица 5 показывает рекомендуемые формы канавок в зависимости от толщины стенки и корневого зазора.

        Скорость подачи присадочного прутка TGX немного отличается от скорости подачи обычного присадочного прутка TIG. Его нужно кормить быстро и понемногу, уделяя внимание тому, чтобы не кормить слишком много за один раз.

        С тех пор, как серия TGX была запущена в середине 1980-х годов, они считаются одними из эталонов Kobelco. продукты из-за их надежности и за то, чего они достигли. Чтобы удовлетворить новые потребности рынка, серия была расширена за счет PREMIARCTM TG-X2209 для дуплексной нержавеющей стали, а также PREMIARCTM TG-X308L, TG-X316L, TG-X309L и TG-X347.

        3-4. Серия DW-T, подходит для тонких листов нержавеющей стали

        Рисунок 15: Зависимость между скоростью сварки и длиной плеча по серии DW-T

        Потому что толщина тонких листов, применяемых для конструкций из нержавеющей стали, намного выше, чем для углеродистых. Для стальных конструкций сварка слабым током более важна для нержавеющих сталей, чем для углеродистых сталей.В прошлом диаметр 0,9 мм. В основном использовались FCW или сплошные провода. Однако диаметром 1,2 мм. FCW давно востребованы из-за их разумной стоимости и большей доступности. Серия DW-T была разработана в этих условиях и сейчас высоко ценится на рынках.


        Рис.16: Оптимальный диапазон параметров сварки для серии DW-T

        Серия DW-T, диам. 1,2 мм. предлагает следующее:
        (1) Пригоден для использования при небольшой длине ножек, как показано на рис. 15, а также при сварке слабым током, как показано на рис. 16.Возможна даже сварка на 100А.
        (2) Возможна сварка тонких листов толщиной от 1,0 до 2,0 мм, тогда как с обычным диаметром 1,2 мм это было затруднительно. провода.
        (3) Превосходный повторный запуск дуги, устраняющий необходимость обрезки края проволоки при повторном запуске дуги во время прихваточной сварки.


        4. Постскриптум

        Как один из наиболее эффективных сварочных процессов, FCW, как ожидается, получит все более широкое распространение. поля; соответственно, для удовлетворения будущих потребностей необходимо будет разработать новые типы FCW.

        FCW

        Kobe Steel для нержавеющей стали являются одними из самых надежных сварочных материалов в мире и имеют были высоко оценены и поддержаны рынками. Разработанные до сих пор технологии проектирования и производства использовались для разработки не только FCW для нержавеющих сталей, но и для никелевых сплавов, как показано в таблице 1.

        В недавно разработанном процессе сварки FCW для нержавеющих сталей в качестве защитного газа используется чистый аргон. В Чрезвычайно низкий уровень разбрызгивания и низкое содержание углерода, характерные для этого недавно разработанного процесса, будут представлены в следующем выпуске KOBELCO WELDING TODAY.

        Ссылки:
        【1】 Международный форум по нержавеющей стали (ISSF), домашняя страница

        Начало страницы

        Wolfram | Примеры альфа: тригонометрия

        Тригонометрические расчеты

        Вычисляйте тригонометрические функции или более крупные выражения, включающие тригонометрические функции с разными входными значениями.

        Вычислить значения тригонометрических функций:

        Вычислить значения обратных тригонометрических функций:

        Другие примеры

        Тригонометрические функции

        Узнавайте и выполняйте вычисления с использованием тригонометрических функций и их обратных функций над действительными или комплексными числами.

        Вычислить свойства тригонометрической функции:

        Вычислить свойства обратной тригонометрической функции:

        Постройте тригонометрическую функцию:

        Проанализируйте тригонометрическую функцию комплексной переменной:

        Проанализируйте тригонометрический полином:

        Сгенерируйте таблицу специальных значений функции:

        Вычислить среднеквадратическое значение периодической функции:

        Другие примеры

        Тригонометрические идентичности

        Узнайте и примените известные тригонометрические тождества.

        Найдите формулы для нескольких углов:

        Найдите другие триггерные идентичности:

        Другие примеры

        Тригонометрические уравнения

        Решите уравнения, содержащие тригонометрические функции.

        Решите тригонометрическое уравнение:

        Другие примеры

        Тригонометрические теоремы

        Узнайте и примените известные тригонометрические теоремы.

        Примените тригонометрическую теорему:

        Примените теорему Пифагора:

        Другие примеры

        Сферическая тригонометрия

        Изучите отношения между длинами сторон и углами треугольников, когда эти треугольники нарисованы на сферической поверхности.

        Примените теорему сферической тригонометрии:

        Другие примеры

        Эффект Fusarium oxysporum f.sp. glycines и Sclerotium rolfsii о патогенности Meloidogyne incognita race 2 для сои по JSTOR

        Abstract

        Были проведены специальные исследования для изучения эффектов Fusarium oxysporum f. sp. glycines и Sclerotium rolfsii на патогенность Meloidogyne incognita race 2 на сою и влияние нематод на частоту увядания и рост сои. Взаимодействие каждого гриба с нематодой привело к снижению роста побегов и корней.Конечная популяция нематод также уменьшалась за счет одновременной инокуляции нематод и грибка или инокуляции грибка перед нематодой. В то время как M. incognita подавляла частоту увядания у двух чувствительных к нематодам сортов сои (TGX 1485-2D и TGX 1440-IE), она оказывала ограниченное влияние на частоту увядания у устойчивого к нематодам сорта сои (TGX 1448-2E). Когда F. oxysporum инокулировали нематодой, среднее количество нематод, проникших в корни соевых бобов, уменьшилось на 75% в TGX 1448-2E, на 68% в TGX 1485-1D и на 65% в TGX 1440-1E.Аналогичным образом, когда почва была обработана S. rolfsii, количество уменьшилось на 78% в TGX 1448-2E, на 77% в TGX 1485-1D и на 68% в TGX 1440-1E. В TGX-1448-2E нематода не развивалась дальше второй стадии молоди.

        Информация журнала

        Plant and Soil публикует оригинальные статьи и обзорные статьи, исследующие взаимодействие биологии растений и почвоведения и предлагающие четкий механистический компонент. Это включает как фундаментальные, так и прикладные аспекты минерального питания, взаимоотношений растений и воды, симбиотических и патогенных взаимодействий растений и микробов, анатомии и морфологии корней, биологии почвы, экологии, агрохимии и агрофизики.Статьи, в которых обсуждается важная молекулярная или математическая составляющая, также попадают в рамки журнала.

        Информация об издателе

        Springer — одна из ведущих международных научных издательских компаний, издающая более 1200 журналов и более 3000 новых книг ежегодно, охватывающих широкий круг предметов, включая биомедицину и науки о жизни, клиническую медицину, физика, инженерия, математика, компьютерные науки и экономика.

        Проект последовательности генома биологической N2-фиксирующей бактерии Rhizobium tropici A12, выделенной из корневого клубенька тропической сои (Glycine max), сорт TGx-1148

        РЕФЕРАТ

        Здесь мы представляем последовательность генома и аннотированные характеристики штамма Rhizobium tropici12 , который способен клубеньков тропического Glycine max (соя).Черновой геном штамма состоит из 107 контигов общим размером 6,5 Мбит / с. В аннотации выявлено 6 204 гена, кодирующих белок, 52 тРНК и 7 рРНК.

        ОБЪЯВЛЕНИЕ

        Род Rhizobium включает несколько видов почвенных бактерий, способных фиксировать атмосферный азот (N 2 ) посредством эндосимбиотической ассоциации с корнями бобовых (1). Эти бактерии несут гены, ответственные за превращение атмосферного N 2 в органические азотистые соединения (аммоний [NH 4 + ]), способные усваиваться растениями.Благодаря процессу азотфиксации бобовые играют жизненно важную роль в сельскохозяйственных циклах за счет восстановления плодородия почвы, а также служат источником пищи и доходов для мелких фермеров (2). Вид Rhizobium tropici считается наиболее эффективным симбионтом Phaseolus vulgaris (фасоль обыкновенная) в тропических кислых почвах; он также очень беспорядочный и способен устанавливать симбиотические ассоциации с различными бобовыми (3–5). Здесь мы представляем проект последовательности генома штамма R. tropici A12, который был выделен из тропических растений Glycine max в условиях африканской почвы.

        Ризобии выделяли из корневых клубеньков растений сои, выращенных в течение 8 недель в тепличных условиях. Штаммы были идентифицированы морфологически, а свежие чистые культуры сохранены в генбанке Международного института тропического сельского хозяйства (IITA). Штамм R. tropici A12 культивировали на среде дрожжевой экстракт-маннит-бульон (YMB) (дрожжевой экстракт, 1 г / л; маннит, 10 г / л; дикалий фосфат, 0,5 г / л; сульфат магния, 0,2 г / л; хлорид натрия, 0,1 г / литр; карбонат кальция, 1 г / литр) при 28 ° C, и 2 мл свежей культуры использовали для инокуляции проростков сои, проросших через 5 дней, сорта TGx-1148.План эксперимента включает четыре обработки: (i) внесение эталонного азота в количестве 120 кг N га -1 , (ii) контроль без инокуляции, (iii) инокуляция R. tropici A12 и (iv) инокуляция R. tropici A12 плюс Нанесение P при 20 кг P га −1 (рис. 1).

        Рис. 1

        Рост и развитие сорта сои TGx-1148 через 8 недель после посева, с внесением контрольного азота (120 кг N га -1 ) (a), без инокуляции ризобиями (b), инокуляцией R. tropici A12 ( в), или Р.tropici A12 плюс внесение P в количестве 20 кг P га -1 в виде тройного суперфосфата (d).

        Экстракцию геномной ДНК проводили из ночной культуры отдельной колонии на среде YMB с использованием набора для очистки ДНК Qiagen. Количественное определение и контроль качества ДНК были выполнены с использованием прибора NanoDrop ND1000 и электрофореза в 1,0% агарозном геле соответственно. Геномная ДНК была подвергнута технологии секвенирования нового поколения. Библиотеку с парными концами сконструировали с использованием набора для подготовки библиотеки ДНК NEBNext Ultra для Illumina (New England Biolabs, Великобритания) и секвенировали в системе MiSeq (Illumina, Сан-Диего, Калифорния, США) с использованием модуля PE-250, получив 1871 679 читает (Биологические науки Восточной и Центральной Африки — Международный научно-исследовательский институт животноводства, Найроби, Кения).После качественной обрезки последовательности ДНК и удаления адаптера с помощью пакета BBMap (https://github.com/BioInfoTools/BBMap) было получено 1 648 214 чистых считываний, что соответствует 289 620 715 основаниям. Сборка De novo была выполнена с использованием программного обеспечения SPAdes (v3.11.1) с параметрами по умолчанию (6). Сборка сгенерировала 107 контигов (> 2000 п.н.) на общую сумму 6 590 945 п.о. со средним покрытием 44 ×. Средняя длина контигов составила 61 597 п.н., а самый большой контиг — 391 517 п.н., с содержанием GC 59.55% и контиг N 50 стоимостью 119,397 п.н. Последовательность генома R. tropici A12 была аннотирована с помощью NCBI Prokaryotic Genome Annotation Pipeline (PGAP) (7), в результате чего было получено 6204 гена, кодирующих белок, 52 тРНК и 7 рРНК.

        Доступность данных. Этот проект с полным геномом был депонирован в DDBJ / ENA / GenBank под номером доступа JAADZA000000000. Версия, описанная в этом документе, является первой версией, JAADZA010000000. Считывания Illumina доступны в SRA под инвентарным номером SRX7775460.

        ПОДТВЕРЖДЕНИЕ

        Это исследование было поддержано грантом Фонда Билла и Мелинды Гейтс для IITA.

        СНОСКИ

          • Получено 24 февраля 2020 г.
          • Принято 19 апреля 2020 г.
          • Опубликовано 14 мая 2020 г.
        • Авторские права © 2020 Khayi et al.

        (PDF) Оценка генетической согласованности, разнообразия и ассоциации признаков в селекционных линиях позднеспелых сои

        EJPB

        616

        https: // doi.org / 10.37992 / 2020.1102.100

        Lawal et al.,

        переводят на большую общую биомассу и, возможно, урожай зерна

        (White et al., 1992). Корневая нодуляция генотипов

        не сильно отличается (P≤0,5) друг от друга, TGX

        2006 — 3F имеет самую высокую клубеньчатость корня (5,3), а TGX

        1448 -2E имеет самую низкую клубеньку корня. . Высокая нодуляция

        подразумевает высокий потенциал генотипа для x азота в почве

        , а затем обогащает почву и, следовательно, увеличивает урожай

        (Karikari et al., 2015). Генотип (TGX 2006 -3F)

        со значительно высокой нодуляцией, однако, был среди

        наименее урожайных с точки зрения экономической урожайности, общей биомассы растения

        и низкого индекса урожая. Возможно, эффективность фиксации азота

        TGX 2006 — 3F могла быть низкой, или зафиксированный ею азот

        , скорее всего, был недоступен в течение того посевного сезона

        . Генотип с наивысшим урожаем (улучшенная проверка

        ) имел клубеньки, которые были значительно сопоставимы с генотипом

        и TGX 2006-3F.Однако генотипы (TGX 1448 -2E

        и местная проверка) с наименьшей нодуляцией также были генотипами

        с наименьшей урожайностью. Следовательно, согласуясь с

        , отчет Karikari et al. (2015), которые утверждали, что нодуляция корня

        помогает закрепить N и, следовательно, повысить урожайность.

        Общая биомасса растений колеблется от 1143,30 г для TGX 2010

        -12F и до 106,70 г для TGX-1448 2E. TGX 2010-12F

        имеет самый высокий биологический урожай (2,858.30 г), а у TGX

        1448 -2E самый низкий (266,70 г). В TGX 2010-12F

        ассимилятов и фотосинтатов были направлены на производство

        биомассы. Следовательно, это хороший кандидат

        , где производство кормов имеет первостепенное значение, особенно

        при кормлении скота. Что касается экономической урожайности, урожай зерна улучшенного сорта

        (TGX 1448) имеет самый высокий (512,33

        кг / га) урожай зерна, а у TGX1448-2E — самый низкий

        (87.92 кг / га) вес семян (Таблица 4). Очевидно, TGX 1448

        передал ассимиляты и фотосинтаты в производство семян

        . Индекс урожая может предоставить средства

        для идентификации генотипов с высокой биомассой и количеством семян

        (экономическая урожайность) для двойного назначения кормов и семян.

        Следовательно, генотип, такой как улучшенная проверка (TGX 1448)

        , не может быть успешным.

        Обобщенная матрица фенотипического корреляционного анализа для

        агрономических признаков и компонентов урожайности представлена ​​

        в таблице 5.Были выявлены значимые отрицательные корреляции

        между днями посадки и массой семян со стручками, соотношением стручков

        , массой семян, экономической урожайностью и индексом урожая

        . Также между количеством ветвей

        10 WAS и общей биомассой с одной стороны и между

        биологическим урожаем и соотношением стручков с другой стороны.

        Отрицательная взаимосвязь между днями до 50% -ного роста

        и параметрами, связанными с урожаем, такими как вес семян на стручок

        , соотношение стручков и экономическая урожайность, показала, что

        длиннее дней до 50% -ного роста и, следовательно, зрелости ,

        за вычетом количества семян на стручок, веса семян на стручок

        и, следовательно, экономической урожайности.Это означает, что

        генотип с более длительным вегетационным периодом был менее урожайным

        , возможно, из-за фотосинтата / ассимиляций

        Таблица 5. Корреляция вегетативных и связанных с урожайностью признаков сои

        FWR NLV6 PH6 NB6 NLV10 Ph20 NB10 RTNODT HI SCR

        FWR 1 -0,19 0,04 -0,11 -0,03 0,13 0,2 -0,06 0,1 0,1 -0,3 * -0,33 * -0,40 * -0,30 * -0,09

        NLV6 0,31 * 0,45 * 0,59 * -0,04 0,25 -0,13 -0,42 * -0,42 * -0,11 0.15 -0,02 0,21 -0,04

        PH6 0,25 -0,01 0,23 -0,07 -0,11 0,04 0,04 0,09 -0,15 0,11 -0,09 -0,02

        NB6 0,23 -0,04 0,11 -0,02 -0,16 -0,16 -0,2 -0,05 0,04 0,11 0,37 *

        NLV10 0,03 0,50 * -0,15 -0,30 * -0,30 * -0,27 -0,01 -0,14 0,15 0,07

        Ph20 0,23 0 -0,02 -0,02 -0,18 -0,13 -0,30 * -0,18 -0,12

        NB10 -0,22 -0,40 * -0,40 * -0,3 0,25 -0,13 0,40 * 0,17

        RTNODT 0,28 0,28 0,13 -0,26 0,1 -0,28 -0,04

        TBIOM 0,05 0,48 * -0,42 * 0,13 -0,56 * -0.34 *

        BYLD 0,48 * -0,42 * 0,13 -0,56 * -0,34 *

        WTSP 0,36 * 0,74 * 0,06 -0,25

        PPR 0,41 * 0,83 * 0,12

        EYLD 0,45 * 0,35 *

        HI 0,54 * SC 909 1

        FWR = дни до 50% включения; количество листьев, количество веток; высота растений вся через 6 и 10 недель после посева;

        клубеньков корня; общая биомасса; биологический урожай; вес стручка; соотношение стручковых растений; экономическая доходность; индекс урожая и семена

        cha ratio

        , которые были преобразованы в семена и стручки на раннем этапе роста.

        генотипов (улучшенная проверка, TGX 2009-12F, TGX 2007-

        11F) были использованы для обильного роста в конце посадки

        Генотип

        (TGX 2004-10F, TGX 2006-11F и TGX

        2006-3F).В качестве альтернативы, это может быть результат окончательной

        засухи в начале засушливого сезона, из-за которой уцелели

        ранних генотипов. Это подтверждает

        выводы Шаврукова и др. (2017), что преждевременность

        — это стратегия, позволяющая избежать засухи и гарантировать хороший урожай

        , а также возможность посадки в два сезона в пределах

        года (Bindu et al., 2011). Однако была положительная корреляция

        между признаками, повышающими корм или биомассу

        , такими как количество листьев 6 WAS и высота растения,

        количество ветвей при 6 WAS и биологическая урожайность;

        количество листьев на 10 WAS и количество

        веток на 10 WAS, биологический урожай и индекс урожая.

        Вес семян влияет на рост побегов и корней среди генотипов сои и внутри них за пределами стадии проростков: значение для скрининга на устойчивость к низкому фосфору

      • Beebe S, Lynch J, Galwey N, Tohme J, Ochoa I (1997) Географический подход к идентификации фосфор-эффективные генотипы местных сортов и диких предков фасоли. Euphytica 95: 325–336

        Статья Google Scholar

      • Деррик Дж. У., Райан М. Х. (1998) Влияние содержания фосфора в семенах на рост проростков пшеницы: последствия для органического и традиционного управления фермой в Юго-Восточной Австралии.Biol Agric Hortic 16: 223–237

        Статья Google Scholar

      • Hanley ME, Cordier PK, May O, Kelly CK (2007) Размер семян и рост рассады: дифференциальная реакция австралийских и британских Fabaceae на ограничение питательных веществ. Новый Фитол 174: 381–388

        CAS Статья PubMed Google Scholar

      • Колаволе Г.О., Канг Б.Т. (1997) Влияние размера семян и внесения фосфорных удобрений на рост выбранных бобовых культур.Commun Soil Sci Plant Anal 28: 1223–1235

        CAS Статья Google Scholar

      • Liao H, Yan X (1999) Размер семян тесно связан с эффективностью использования фосфора и эффективностью использования фотосинтетического фосфора в фасоли обыкновенной. J Plant Nutr 22: 877–888

        CAS Статья Google Scholar

      • Марко Д. (1990) Влияние веса семян, а также концентрации фосфора и азота в семенах на ранний рост проростков пшеницы.Aust J Exp Agric 30: 545–549

      • McPhee K (2005) Вариация архитектуры корня проростков в основной коллекции зародышевой плазмы гороха. Crop Sci 45: 1758–1763

        Статья Google Scholar

      • Милберг П., Ламонт Б. Б. (1997) Размер семян / семядолей и содержание питательных веществ играют важную роль в ранней продуктивности видов на бедных питательными веществами почвах. New Phytol 137: 665–672

        Артикул Google Scholar

      • Надим М., Молье А., Морель С., Вивес А., Прюдом Л., Пеллерин С. (2011) Относительный вклад запасов фосфора семян и экзогенного поглощения фосфора кукурузой (Zea mays L.) питание на ранних стадиях роста. Растительная почва 346: 231–244

        CAS Статья Google Scholar

      • Надим М., Молье А., Морель С., Вивес А. (2013) Фосфорное питание проростков кукурузы: распределение ремобилизованных запасов фосфора семян и внешнее поглощение фосфора корнями и побегами проростков на ранних стадиях роста. Растительная почва 371: 327–338

        CAS Статья Google Scholar

      • Osborne L, Rengel Z (2002) Скрининг зерновых на предмет генотипических вариаций эффективности поглощения и использования фосфора.Aust J Agric Res 53: 295–303

        Статья Google Scholar

      • Ozturk L, Eker S, Torun B, Cakmak I (2005) Различия в эффективности фосфора среди 73 генотипов хлебной и твердой пшеницы, выращенных на известковой почве с дефицитом фосфора. Почва растений 269: 69–80

        CAS Статья Google Scholar

      • Pypers P (2006) Изотопные подходы для характеристики наличия и накопления фосфора кукурузой и бобовыми культурами в сильно выветренных почвах.Katholieke Universiteit leuven, Бельгия

        Google Scholar

      • Рос С., Белл Р., Уайт П. (1997) Влияние внесения фосфора в семена и почвенного фосфора на ранний рост риса ( Oryza sativa L.) cv IR66. Soil Sci Plant Nutr 43: 499–509

        CAS Статья Google Scholar

      • Rose TJ, Pariasca-Tanaka J, Rose MT, Mori A, Wissuwa M (2012) Семена сомнения: переоценка влияния концентрации P в зерне на жизнеспособность проростков.J Plant Nutr Soil Sci 175: 799–804

        CAS Статья Google Scholar

      • SAS Institute Inc (2012) Руководство пользователя SAS / STAT 9.3, 2-е изд. SAS Institute Inc, Кэри

        Google Scholar

      • Schwertmann US, Cornell RM (1991) Оксиды железа в лаборатории: получение и характеристика. VCH, Вайнхайм

        Google Scholar

      • White PJ, Veneklaas EJ (2012) Природа и воспитание: важность содержания фосфора в семенах.Почва растений 357: 1–8

        CAS Статья Google Scholar

      • Ян X, Линч JP, Beebe SE (1995) Генетическая изменчивость фосфорной эффективности фасоли обыкновенной в контрастных типах почв I. Вегетативная реакция. Crop Sci 35: 1086–1093

        Статья Google Scholar

      • Захран Х. Х. (1999) Симбиоз ризобий-бобовых и азотфиксация в суровых условиях и в засушливом климате.Microbiol Mol Biol Rev 63: 968–989

        CAS PubMed PubMed Central Google Scholar

      • Zhang M, Nyborg M, Mcgill WB (1990) Концентрация фосфора в семенах ячменя ( Hordeum vulgare L.): влияние на рост проростков и производство сухого вещества. Растительная почва 122: 79–83

        CAS Статья Google Scholar

      • Zhu Y-G, Smith SE (2001) Содержание фосфора (P) в семенах влияет на рост и поглощение P растениями пшеницы и их связь с грибами арбускулярной микоризы (AM).