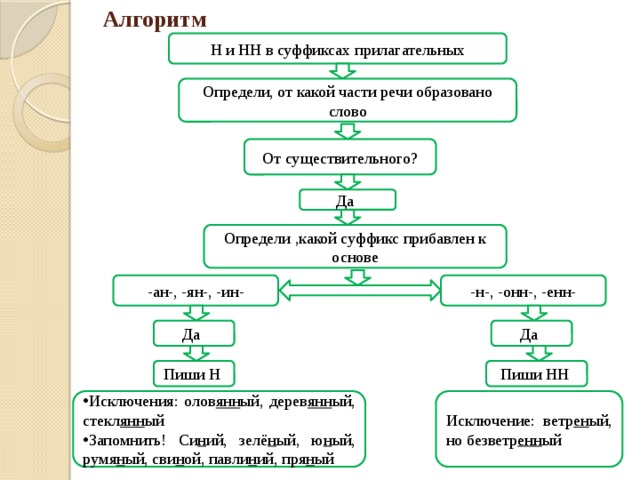
Тест “Н” и “нн” в разных частях речи” с ответами: самостоятельная работа
Последний раз тест пройден 27 минут назад.
Для учителя
Материал подготовлен совместно с учителем высшей категории Кучминой Надеждой Владимировной.
Опыт работы учителем русского языка и литературы — 27 лет.
Вопрос 1 из 12
В каком слове пишется одна Н?
Закопчен…ые стены
Трава подстрижен…а
Неждан…ый
Услышан…ая мною история
Правильный ответ
Неправильный ответ
Пояснение к правильному ответу
Подстрижена — краткое причастие. Причастия в краткой форме всегда пишутся с одной «н» в суффиксе.

В вопросе ошибка?
Вопрос 2 из 12
В каком слове пишется одна Н?
Свежезаморожен…ые овощи
Швы отстрочен…ы
Перевязан…ая рука
Вязан…ые бабушкой носки
Правильный ответ
Неправильный ответ
Пояснение к правильному ответу
Отстрочены — краткое причастие. Оно всегда пишется с одной «н» в суффиксе.
В вопросе ошибка?
Вопрос 3 из 12
В каком слове пишется одна Н?
Общепризнан…ое мнение
Сушен…ые в печи грибы
Стилизован…ый интерьер
Морожен…ая рыба
Правильный ответ
Неправильный ответ
Пояснение к правильному ответу
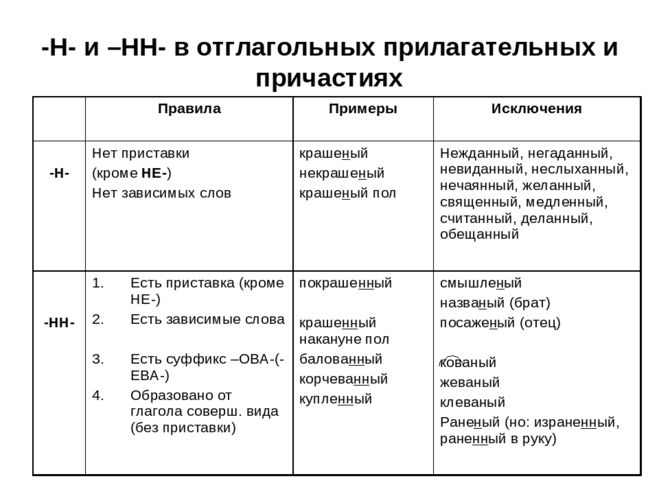
Отглагольное прилагательное, образованное от бесприставочного глагола несовершенного вида, пишется с одной
«н».
. Отглагольное прилагательное «мороженая» образовано от глагола «морозить», поэтому пишется с одной «н»
Отглагольное прилагательное «мороженая» образовано от глагола «морозить», поэтому пишется с одной «н»В вопросе ошибка?
Вопрос 4 из 12
В каком слове пишется одна Н?
Обоснован…ый вывод
Избалован…ый ребенок
Площадь оцеплен…а
Асфальтирован…ая улица
Правильный ответ
Неправильный ответ
Пояснение к правильному ответу
Причастие
«оцеплена» употреблено в краткой форме, поэтому его следует писать с одной «н»
.В вопросе ошибка?
Вопрос 5 из 12
В каком слове пишется НН?
ПодсказкаНеправильный ответ
Пояснение к правильному ответу
Слово
«воспитанный» можно отнести как к прилагательному, так и к причастию, все зависит от контекста.
(вне зависимости от того, к какой части речи относится). Оно употреблено в полной форме, поэтому пишется с «нн»
Оно употреблено в полной форме, поэтому пишется с «нн»В вопросе ошибка?
Вопрос 6 из 12
В каком предложении содержится слово с двумя НН?
Работа выполнен…а безупречно.
Задача решен…а правильно.
Девушка хорошо воспитан…а родителями.
Учительница строга и сдержан…а
Правильный ответ
Неправильный ответ
Пояснение к правильному ответу
Сдержанна — прилагательное. Если перед ним поставить слово
«более», то смысл предложения не исказится. В прилагательном в краткой форме пишется столько «н»
, сколько и в полной форме: сдержанная — сдержанна.В вопросе ошибка?
Вопрос 7 из 12
В каком предложении содержится слово с двумя НН?
Участки застроен.
 ..ы.
..ы.У работников предприятия ненормирован…ый рабочий день.
Во двор въехала гружен…ая машина.
Поля засеян…ы пшеницей
Правильный ответ
Неправильный ответ
Пояснение к правильному ответу
Если в слове есть суффиксы
«-ова-», «-ева-», «-ирова-», нужно писать «нн». В слове «ненормированный» есть суффикс «-ирова-», поэтому пишутся удвоенные согласные «нн»
В вопросе ошибка?
Вопрос 8 из 12
В каком ряду есть «третье лишнее»?
Куплен…ые книги, избалован…ый ребенок, сушен…ые на солнце яблоки
Нехожен…ые тропы, незван…ые гости, трава скоше…а
Подписан…ый договор, решен…ая задача, желан…ый ребенок
Исключен…ый из школы, коротко стрижен.
 ..а, бешен…ая скорость
..а, бешен…ая скорость
Правильный ответ
Неправильный ответ
Слово
«бешеная» образовано от бесприставочного глагола несовершенного вида (бесить), у него нет зависимых слов, поэтому пишется оно с одной «н». Стрижена — причастие в краткой форме, пишется с одной «н». Исключенный — страдательное причастие, образовано от глагола совершенного вида (исключить), пишется с «нн»
— лишнее слово.В вопросе ошибка?
Вопрос 9 из 12
На месте каких цифр пишется НН? В конце XIX века Александром Паншиным были сконструирова(1)ы невида(2)ые, удлине(3)ые коньки, которые и позволили ему победить фи(4)ского и норвежского скороходов.
1,2
2
2,3
3,4
Неправильный ответ
Пояснение к правильному ответу
Сконструированы — причастие в краткой форме, пишется с одной
«н».
. Отглагольное прилагательное «невиданные» является словарным и пишется с «нн». Отглагольное прилагательное «удлиненные» образовано от глагола совершенного вида «удлинить», поэтому в нем пишется «нн». Следует запомнить, что прилагательное «финский» пишется с одной «н», хотя образовано оно от слова «финн»
Отглагольное прилагательное «невиданные» является словарным и пишется с «нн». Отглагольное прилагательное «удлиненные» образовано от глагола совершенного вида «удлинить», поэтому в нем пишется «нн». Следует запомнить, что прилагательное «финский» пишется с одной «н», хотя образовано оно от слова «финн»В вопросе ошибка?
Вопрос 10 из 12
На месте каких цифр пишется НН? Может быть, коньки назва(1)ы коньками именно потому, что в старину делали деревя(2)ые коньки, украше(3)ые завитком в виде лошади(4)ой головы.
1,2
2,3
1, 2, 3
3, 4
Правильный ответ
Неправильный ответ
Пояснение к правильному ответу
Названы — краткое причастие, пишется с одной
«н». Деревянные — прилагательное-исключение, пишется с «нн».
 Украшенные — полное страдательное причастие, образованное от приставочного глагола совершенного вида (украсить), пишется с «нн». Лошадиной — прилагательное, образовано от существительного «лошадь» при помощи суффикса «-ин-». Пишется с одной «н»
Украшенные — полное страдательное причастие, образованное от приставочного глагола совершенного вида (украсить), пишется с «нн». Лошадиной — прилагательное, образовано от существительного «лошадь» при помощи суффикса «-ин-». Пишется с одной «н»В вопросе ошибка?
Вопрос 11 из 12
В каком слове на месте пропуска пишется две буквы НН?
Ути…ые истории
Чище…ая морская рыба
Проштампова…ое письмо
Колено раздробле.о
Правильный ответ
Неправильный ответ
Пояснение к правильному ответу
Слово
«проштампованное» образовано от приставочного глагола совершенного вида «проштамповать», поэтому пишется с двумя «нн»
В вопросе ошибка?
Вопрос 12 из 12
В каком ряду во всех словах пропущено НН?
Оловя.
 ..ый солдатик, сено высуше…о, нежда…ые гости
..ый солдатик, сено высуше…о, нежда…ые гостиЖела…ый подарок, общепризна…ое превосходство, суко…ая скатерть
Веществе…ое доказательство, овчи…ый тулуп, лицо заплака…о
Кова…ое железо, линова…ая бумага, некоше…ый луг
Правильный ответ
Неправильный ответ
Пояснение к правильному ответу
Хотя отглагольное прилагательное
«желанный» и образовано от бесприставочного глагола несовершенного вида, оно относится к исключениям и пишется с «нн». Прилагательное «общепризнанный» образовано от глагола совершенного вида (признать), поэтому в нем пишется «нн». Прилагательное «суконный» образовано от существительного «сукно» при помощи суффикса «-н»
, поэтому в нем тоже удваиваются согласные.В вопросе ошибка?
Доска почёта
Чтобы попасть сюда — пройдите тест.
Галина Данилова
12/12
Наталия Семушкина
12/12
Наталья Садовская
0/12
Зифа Шарафутдинова
11/12
Хусрав Власов
11/12
Алиса Достоевская
12/12
Даша Вощенко
10/12
Валентина Валентина
12/12
Наталья Дорофеева
12/12
Екатерина Потехина
12/12
Тест «Н и НН в разных частях речи» – эффективный способ проверки уровня своих знаний.
Вопросы в заданиях охватывают все пройденные правила написания данной орфограммы. Упражнения составлены в соответствии с программными требованиями по русскому языку. Ученики на практике тренируются находить правильные варианты написания слов, вставлять нужное буквосочетание. С помощью этих заданий можно подготовиться к написанию самостоятельных работ по разным частям речи.
Тест на одну и две буквы н в разных частях речи с ответами поможет наверстать упущенный материал и закрепить полученные знания.
Рейтинг теста
3.9
Средняя оценка: 3.9
Всего получено оценок: 15439.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Онлайн тест по Русскому языку по теме Н и НН в разных частях речи
Н и НН в разных частях речи – одно из основных правило в школьной программе по русскому языку, которое очень часто встречается в выпускных экзаменах. Выполните тест и проверьте свои знания!
Вам предложено 12 заданий, схожих по формату с вопросами ЕГЭ. Каждый пункт подразумевает выбор Н или НН. Такое однообразие – отличная возможность натренировать руку, чтобы в дальнейшем автоматически справляться с таким типом упражнений.
Благодаря этому тесту вы сможете определить ваши сильные и слабые стороны. Вопросы касаются всех случаев употребления Н и НН. Вам встретятся краткие прилагательные и причастные, зависимые слова и, конечно, исключения. При подготовке сделайте акцент на морфемах: как пишется слова, в зависимости от наличия суффикса -ОВА-, -ЕВА- или приставки.
Задания в тесте сформированы по уровню сложности. Сначала вам предстоит рассмотреть только одно словосочетание и дать ответ. Затем будут проверяться ваши знания в контексте предложений: насколько успешно вы определяете части речи, выявляете зависимые слова. Далее наполнение вопросов только увеличивается. В финальной части теста вам нужно будет выбрать «третье лишнее», а также определить в каких местах будет стоять Н или НН. Таким образом, для правильного ответа вы должны будете поработать не с одним словосочетанием, как в начале, а с несколькими.
Пройти тест онлайн
1. В каком слове пишется одна Н?
закопчен…ые стены
трава подстрижен…а
неждан…ый
услышан…ая мною история
2. В каком слове пишется одна Н?
В каком слове пишется одна Н?
свежезаморожен…ые овощи
швы отстрочен…ы
перевязан…ая рука
вязан…ые бабушкой носки
3. В каком слове пишется одна Н?
общепризнан…ое мнение
сушен…ые в печи грибы
стилизован…ый интерьер
морожен…ая рыба
4. В каком слове пишется одна Н?
обоснован…ый вывод
избалован…ый ребенок
площадь оцеплен. ..а
..а
асфальтирован…ая улица
5. В каком слове пишется НН?
ранен…ый боец
кожан…ое кресло
юн…ый возраст
воспитан…ый человек
6. В каком предложении содержится слово с двумя НН?
Работа выполнен…а безупречно.
Задача решен…а правильно.
Девушка хорошо воспитан…а родителями.
Учительница строга и сдержан…а
7. В каком предложении содержится слово с двумя НН?
В каком предложении содержится слово с двумя НН?
Участки застроен…ы.
У работников предприятия ненормирован…ый рабочий день.
Во двор въехала гружен…ая машина.
Поля засеян…ы пшеницей
8. В каком ряду есть «третье лишнее»?
куплен…ые книги, избалован…ый ребенок, сушен…ые на солнце яблоки
нехожен…ые тропы, незван…ые гости, трава скоше…а
подписан…ый договор, решен…ая задача, желан…ый ребенок
исключен…ый из школы, коротко стрижен…а, бешен…ая скорость
9. На месте каких цифр пишется НН? В конце 19 века Александром Паншиным были сконструирова(1)ы невида(2)ые, удлине(3)ые коньки, которые и позволили ему победить фи(4)ского и норвежского скороходов.
На месте каких цифр пишется НН? В конце 19 века Александром Паншиным были сконструирова(1)ы невида(2)ые, удлине(3)ые коньки, которые и позволили ему победить фи(4)ского и норвежского скороходов.
1,2;
2;
2,3;
3,4
10. На месте каких цифр пишется НН? Может быть, коньки назва(1)ы коньками именно потому, что в старину делали деревя(2)ые коньки, украше(3)ые завитком в виде лошади(4)ой головы.
1,2;
2,3;
1, 2, 3;
3, 4
11. В каком слове на месте пропуска пишется две буквы НН?
ути. ..ые истории
..ые истории
чище…ая морская рыба
проштампова…ое письмо
колено раздробле.о
12. В каком ряду во всех словах пропущено НН?
оловя…ый солдатик, сено высуше…о, нежда…ые гости
жела…ый подарок, общепризна…ое превосходство, суко…ая скатерть
веществе…ое доказательство, овчи…ый тулуп, лицо заплака…о
кова…ое железо, линова…ая бумага, некоше…ый луг
Может быть интересно
Ещё никто не оставил комментария, вы будете первым.
Написать комментарий
Исчисление II — Проверка соотношения
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 10.10: Проверка отношения
В этом разделе мы рассмотрим тест, который мы можем использовать, чтобы увидеть, является ли ряд абсолютно сходящимся или нет. Напомним, что если ряд абсолютно сходится, то мы также будем знать, что он сходится, и поэтому мы будем часто использовать его, чтобы просто определить сходимость ряда.
Прежде чем приступить к тесту, давайте быстро напомним о факториалах. Этот тест будет особенно полезен для рядов, содержащих факториалы (и мы увидим некоторые из них в приложениях), поэтому давайте убедимся, что можем с ними справиться, прежде чем столкнемся с ними в примере.
Если \(n\) является целым числом таким, что \(n \ge 0\), то \(n\) факториал определяется как
\[\begin{выравнивание*}n! & = n\left( {n — 1} \right)\left( {n — 2} \right) \cdots \left( 3 \right)\left( 2 \right)\left( 1 \right) & \ hspace{0.15in} & {\mbox{if}}n \ge 1\\ 0! & = 1 & \hspace{0,15 дюйма} & {\mbox{по определению}}\end{align*}\]
Давайте быстро посчитаем пару.
\[\begin{выравнивание*}& 1! = 1\\ & 2! = 2\влево( 1\вправо) = 2\\ & 3! = 3\влево(2\вправо)\влево(1\вправо) = 6\\ & 4! = 4\влево(3\вправо)\влево(2\вправо)\влево(1\вправо) = 24\\ & 5! = 5\влево(4\вправо)\влево(3\вправо)\влево(2\вправо)\влево(1\вправо) = 120\конец{выравнивание*}\]
Обратите внимание, что в последнем вычислении выше мы можем переписать факториал несколькими способами. Например,
\[\begin{выравнивание*}5! & = 5 \ подкос {\ влево ( 4 \ вправо) \ влево ( 3 \ вправо) \ влево ( 2 \ вправо) \ влево ( 1 \ вправо)} _ {4!} = 5 \ cdot 4! \\ 5! & = 5 \ влево ( 4 \ вправо) \ подкос {\ влево ( 3 \ вправо) \ влево ( 2 \ вправо) \ влево ( 1 \ вправо)} _ {3!} = 5 \ влево ( 4 \ вправо) \ cdot 3!\end{выравнивание*}\]
В общем случае мы всегда можем «вырезать» члены из факториала следующим образом.
\[\begin{выравнивание*}n! & = n\left( {n — 1} \right)\left( {n — 2} \right) \cdots \left( {n — k} \right)\left( {n — \left( {k + 1} \right)} \right) \cdots \left( 3 \right)\left( 2 \right)\left( 1 \right)\\ & = n\left( {n — 1} \right)\left ( {n — 2} \right) \cdots \left( {n — k} \right) \cdot \left( {n — \left( {k + 1} \right)} \right)!\\ & = n\left( {n — 1} \right)\left( {n — 2} \right) \cdots \left( {n — k} \right) \cdot \left( {n — k — 1} \right )!\конец{выравнивание*}\]
Нам нужно будет делать это время от времени, так что не забывайте об этом.
Кроме того, при работе с факториалами нужно быть очень осторожным со скобками. Например, \(\left( {2n} \right)! \ne 2\,\,n!\), как мы увидим, выписав каждый из следующих факториалов.
\[\begin{align*}\left( {2n} \right)! & = \left( {2n} \right)\left( {2n — 1} \right)\left( {2n — 2} \right) \cdots \left( 3 \right)\left( 2 \right)\ влево( 1 \вправо)\\ 2\,\,n! & знак равно 2 \ влево [ {\ влево ( п \ вправо) \ влево ( {п — 1} \ вправо) \ влево ( {п — 2} \ вправо) \ cdots \ влево ( 3 \ вправо) \ влево ( 2 \ вправо)\влево( 1 \вправо)} \вправо]\конец{выравнивание*}\]
Опять же, мы столкнемся с факториалами со скобками, так что не опускайте их.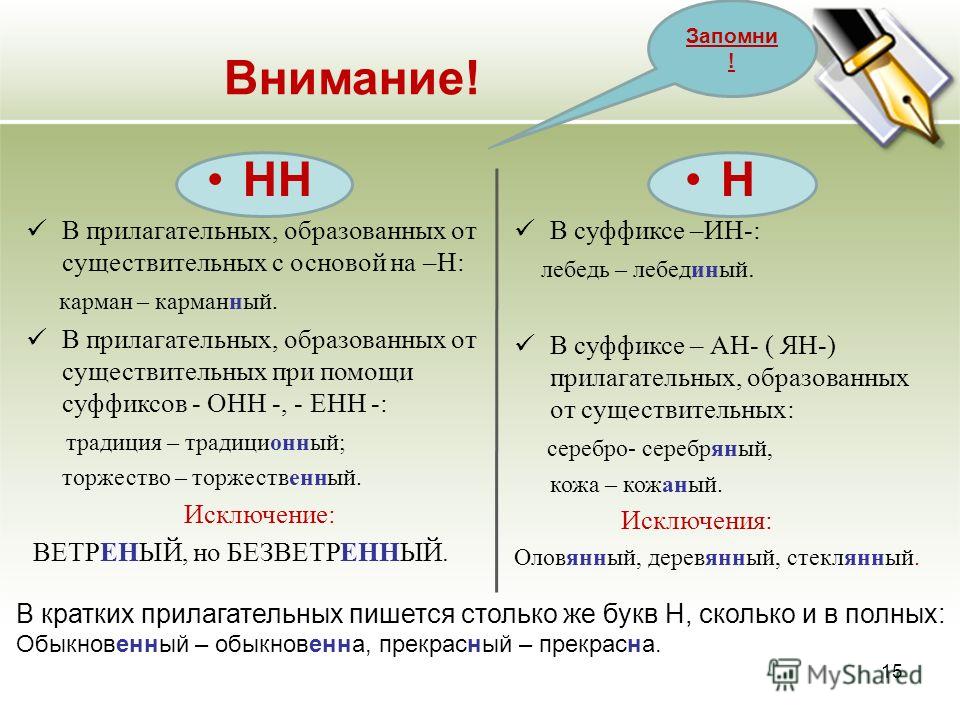 Часто это одна из самых распространенных ошибок, которую допускают учащиеся, когда впервые сталкиваются с факториалами.
Часто это одна из самых распространенных ошибок, которую допускают учащиеся, когда впервые сталкиваются с факториалами.
Итак, мы готовы к тесту.
Проверка соотношения
Предположим, у нас есть ряд \(\displaystyle \sum {{a_n}} \). Определить,
\[L = \mathop {\lim}\limits_{n \to \infty} \left| {\ frac {{{a_{n + 1}}}}{{{a_n}}}} \right|\]
Тогда
- , если \(L < 1\) ряд абсолютно сходится (и, следовательно, сходится).
- , если \(L > 1\) ряд расходится.
- , если \(L = 1\) ряд может быть расходящимся, условно сходящимся или абсолютно сходящимся.
Доказательство этого теста находится в конце раздела.
Обратите внимание, что в случае \(L = 1\) критерий соотношения практически бесполезен, и нам пришлось бы прибегнуть к другому критерию, чтобы определить сходимость ряда. 9{2n + 3}}\влево( {n + 2} \вправо)}}\]
Теперь для определения \(L\) мы будем использовать
\[L = \mathop {\lim}\limits_{n \to \infty} \left| {{a_{n + 1}} \cdot \frac{1}{{{a_n}}}} \right|\]
, так как это будет немного проще при работе с дробями, как здесь. 2} \ left ( {n + 2} \ right)}}} \ right | \\ & = \ frac {{10}}{{16}}\mathop {\lim}\limits_{n \to \infty} \frac{{n + 1}}{{n + 2}}\\ & = \frac{{10 }}{{16}} < 1\end{align*}\]
9n}}}{{n!}}} \right| = \mathop {\lim }\limits_{n \to \infty} \frac{{\left({n + 1} \right)!}}{{5\,\,n!}}\]
2} \ left ( {n + 2} \ right)}}} \ right | \\ & = \ frac {{10}}{{16}}\mathop {\lim}\limits_{n \to \infty} \frac{{n + 1}}{{n + 2}}\\ & = \frac{{10 }}{{16}} < 1\end{align*}\]
9n}}}{{n!}}} \right| = \mathop {\lim }\limits_{n \to \infty} \frac{{\left({n + 1} \right)!}}{{5\,\,n!}}\]
Чтобы выполнить этот предел, нам нужно исключить факториалы. Мы просто не можем сделать предел с факториалами в нем. Чтобы исключить факториалы, мы вспомним из нашего обсуждения факториалов выше, что мы всегда можем «вырезать» термины из факториала. Если мы проделаем это с числителем (в данном случае потому, что он больший из двух), мы получим
\[L = \mathop {\lim}\limits_{n \to \infty} \frac{{\left({n + 1} \right)\,\,n!}}{{5\,\,n !}}\]
после чего мы можем отменить \(n\)! для числителя знаменатель получить,
\[L = \mathop {\lim}\limits_{n \to \infty} \frac{{\left({n + 1} \right)}}{5} = \infty > 1\]
Итак, по тесту отношений этот ряд расходится. 2}}}{{\left({2n — 1} \right)!}}} \]
9n}}}} \right|\\ & = \mathop {\lim }\limits_{n \to \infty} \left| {\ frac {{9 \, n}} {{\ left ({ — 2} \ right) \, \ left ( {n + 1} \ right)}}} \ right | \\ & = \ frac {9 {2}\mathop {\lim }\limits_{n \to \infty} \frac{n}{{n + 1}}\\ & = \frac{9}{2} > 1\end{align* }\]
2}}}{{\left({2n — 1} \right)!}}} \]
9n}}}} \right|\\ & = \mathop {\lim }\limits_{n \to \infty} \left| {\ frac {{9 \, n}} {{\ left ({ — 2} \ right) \, \ left ( {n + 1} \ right)}}} \ right | \\ & = \ frac {9 {2}\mathop {\lim }\limits_{n \to \infty} \frac{n}{{n + 1}}\\ & = \frac{9}{2} > 1\end{align* }\]
Следовательно, по тесту отношений этот ряд расходится.
В предыдущем примере для получения правильного ответа требовались полосы абсолютного значения. Если бы мы их не использовали, то получили бы \(L = — \frac{9{2} < 1\), что подразумевало бы сходящийся ряд!
Теперь давайте рассмотрим пару примеров, чтобы увидеть, что происходит, когда мы получаем \(L = 1\). Напомним, что тест отношения ничего не скажет нам о сходимости этих рядов. В обоих этих примерах мы сначала проверим, что получаем \(L = 1\), а затем используем другие тесты для определения сходимости.
Пример 5 Определите, является ли следующий ряд сходящимся или расходящимся. 2} + 1}}} \ ]
9\ infty {\ гидроразрыва {{n + 2}} {{2n + 7}}} \]
2} + 1}}} \ ]
9\ infty {\ гидроразрыва {{n + 2}} {{2n + 7}}} \]
Показать решение
Вот предел.
\[L = \mathop {\lim}\limits_{n \to \infty} \left| {\ frac {{n + 3}} {{2 \ left ( {n + 1} \ right) + 7}} \, \, \ frac {{2n + 7}} {{n + 2}}} \ правильно| знак равно \ mathop {\ lim} \ limit_ {n \ to \ infty} \ frac {{\ left ({n + 3} \ right) \ left ({2n + 7} \ right)}} {{\ left ({ 2n + 9} \right)\left( {n + 2} \right)}} = 1\]
Опять же, тест отношения ничего нам не говорит. Однако мы можем быстро использовать для этого тест на дивергенцию. На самом деле, это, вероятно, должно было быть нашим первым выбором в любом случае.
\[\ mathop {\lim }\limits_{n \to \infty} \frac{{n + 2}}{{2n + 7}} = \frac{1}{2} \ne 0\]
По критерию расходимости этот ряд расходится.
Итак, как мы видели в предыдущих двух примерах, если мы получаем \(L = 1\) из проверки отношений, ряд может быть либо сходящимся, либо расходящимся.
Прежде чем мы перейдем к следующему разделу, мы должны отметить еще одну вещь, связанную с тестом отношения. Последняя серия представляла собой полином, деленный на полином, и мы увидели, что получили \(L = 1\) из теста отношения. Это всегда будет происходить с рациональным выражением, включающим только полиномы или полиномы под радикалами. Таким образом, в будущем не стоит даже пробовать тест отношения для таких задач, поскольку теперь мы знаем, что получим \(L = 1\).
Кроме того, в предпоследнем примере мы видели пример знакопеременного ряда, в котором положительный член был рациональным выражением, включающим многочлены, и снова мы всегда будем получать \(L = 1\) в этих случаях.
Давайте закончим этот раздел доказательством теста соотношения.
Доказательство соотношения
Во-первых, обратите внимание, что мы можем предположить без ограничения общности, что ряд будет начинаться с \(n = 1\), как мы делали для всех наших тестовых доказательств.
Давайте начнем доказательство здесь, предположив, что \(L < 1\), и нам нужно показать, что \(\sum {{a_n}} \) абсолютно сходится. Для этого сначала заметим, что, поскольку \(L < 1\), существует некоторое число \(r\) такое, что \(L < r < 1\).
Вспомните,
\[L = \mathop {\lim}\limits_{n \to \infty} \left| {\ frac {{{a_{n + 1}}}}{{{a_n}}}} \right|\]
и поскольку мы также выбрали \(r\) так, что \(L < r\) существует некоторое \(N\) такое, что если \(n \ge N\) мы будем иметь,
\[\слева| {\ frac {{{a_{n + 1}}}}{{{a_n}}}} \right| < r\hspace{0,5 дюйма} \Rightarrow \hspace{0,5 дюйма}\left| {{a_{n + 1}}} \right| < г \ влево | {{a_n}} \право|\] 9\infty {{a_n}} \) абсолютно сходится.
Далее нам нужно предположить, что \(L > 1\) и показать, что \(\sum {{a_n}} \) расходится. Напоминая,
\[L = \mathop {\lim}\limits_{n \to \infty} \left| {\ frac {{{a_{n + 1}}}}{{{a_n}}}} \right|\]
и поскольку \(L > 1\) мы знаем, что должно быть некоторое \(N\) такое, что если \(n \ge N\) мы будем иметь,
\[\слева| {\ frac {{{a_{n + 1}}}}{{{a_n}}}} \right| > 1\hspace{0,5 дюйма} \Rightarrow \hspace{0,5 дюйма}\left| {{a_{n + 1}}} \right| > \влево| {{a_n}} \право|\]
Однако если \(\left| {{a_{n + 1}}} \right| > \left| {{a_n}} \right|\) для всех \(n \ge N\), то мы знаем то,
\[\ mathop {\lim }\limits_{n \to \infty} \left| {{a_n}} \право| \ne 0\]
, потому что члены становятся больше и гарантированно не будут отрицательными. Это, в свою очередь, означает, что
Это, в свою очередь, означает, что
\[\ mathop {\lim }\limits_{n \to \infty} {a_n} \ne 0\]
Следовательно, по критерию расходимости \(\sum {{a_n}} \) расходится. 9\ infty {\ frac {1} {n}} & \ hspace {0,5 дюйма} & {\ mbox {расходящийся}} \ end {align *} \]
Исчисление II — Корневой тест
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. {\ frac{1}{n}}}\]
{\ frac{1}{n}}}\]
Тогда
- , если \(L < 1\) ряд абсолютно сходится (и, следовательно, сходится).
- , если \(L > 1\) ряд расходится.
- , если \(L = 1\) ряд может быть расходящимся, условно сходящимся или абсолютно сходящимся.
Доказательство этого теста находится в конце раздела.
Как и в случае теста отношения, если мы получим \(L = 1\), корневой тест ничего нам не скажет, и нам нужно будет использовать другой тест, чтобы определить сходимость ряда. Также обратите внимание, что, как правило, для серий, с которыми мы будем иметь дело в этом классе, если \(L = 1\) в тесте на отношение, то корневой тест также даст \(L = 1\). 9{\ frac {1} {n}}}}} = \ frac {{12}} {1} = 12 > 1 \]
После использования приведенного выше факта мы видим, что корневой тест говорит нам, что этот ряд расходится.
Доказательство корневого теста
Во-первых, обратите внимание, что мы можем предположить без ограничения общности, что ряд будет начинаться с \(n = 1\), как мы делали для всех наших тестовых доказательств серии.


 Отглагольное прилагательное «мороженая» образовано от глагола «морозить», поэтому пишется с одной «н»
Отглагольное прилагательное «мороженая» образовано от глагола «морозить», поэтому пишется с одной «н» Оно употреблено в полной форме, поэтому пишется с «нн»
Оно употреблено в полной форме, поэтому пишется с «нн» ..ы.
..ы.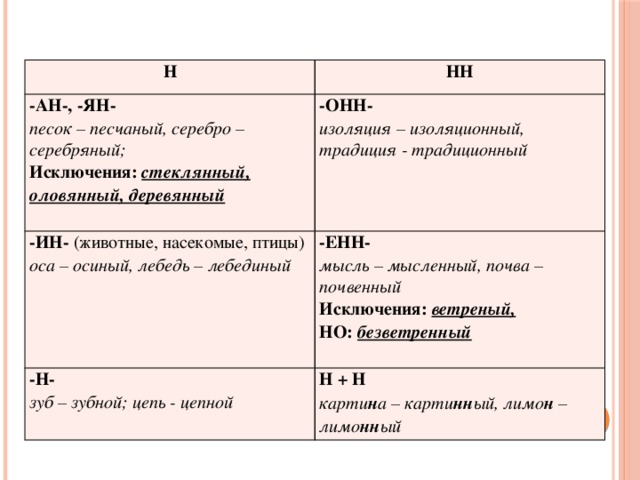 ..а, бешен…ая скорость
..а, бешен…ая скорость Отглагольное прилагательное «невиданные» является словарным и пишется с «нн». Отглагольное прилагательное «удлиненные» образовано от глагола совершенного вида «удлинить», поэтому в нем пишется «нн». Следует запомнить, что прилагательное «финский» пишется с одной «н», хотя образовано оно от слова «финн»
Отглагольное прилагательное «невиданные» является словарным и пишется с «нн». Отглагольное прилагательное «удлиненные» образовано от глагола совершенного вида «удлинить», поэтому в нем пишется «нн». Следует запомнить, что прилагательное «финский» пишется с одной «н», хотя образовано оно от слова «финн» Украшенные — полное страдательное причастие, образованное от приставочного глагола совершенного вида (украсить), пишется с «нн». Лошадиной — прилагательное, образовано от существительного «лошадь» при помощи суффикса «-ин-». Пишется с одной «н»
Украшенные — полное страдательное причастие, образованное от приставочного глагола совершенного вида (украсить), пишется с «нн». Лошадиной — прилагательное, образовано от существительного «лошадь» при помощи суффикса «-ин-». Пишется с одной «н» ..ый солдатик, сено высуше…о, нежда…ые гости
..ый солдатик, сено высуше…о, нежда…ые гости
Leave A Comment