928. Теплоход прошёл по течению реки 30 км и вернулся обратно… Математика Мордкович 6 класс – Рамблер/класс
928. Теплоход прошёл по течению реки 30 км и вернулся обратно… Математика Мордкович 6 класс – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
928.
Составьте уравнение по условию задачи.
тив на обратный путь на 20 мин больше, чем на путь по течению
реки. Найдите собственную скорость теплохода, если скорость тече-
ния реки 0,7 км/ч.
ответы
лови ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
3 класс
5 класс
Репетитор
похожие вопросы 5
Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра
10. При каких значениях р уравнение -х 2 + 6х — 2 = р:
а) не имеет корней;
б) имеет один корень; (Подробнее…)
ГДЗМордкович А.Г.Алгебра8 класс
Приветик! Кто решил? № 411 Математика 6 класс Виленкин.
Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)
ГДЗМатематика6 классВиленкин Н.Я.
Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.
Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.
Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Теплоход прошел 4 часа по течению реки и 3 часа против течения. путь, пройденный теплоходом по течению, на 48 км больше пути, пройденного против течения. Найдите скорость теплохода в стоячей воде, если скорость течения равна 2,5 км/ч.,По действмям!!!!
Ответы 2
спс бро!
Автор:
yeller
Оценить ответ:
0
x км/час-скорость теплохода в стоячей воде; (x+2,5)-скорость теплохода по течению реки; (x-2,5)- скорость теплохода против течения реки. составляем уравнение:4(x+2,5)=3*(x-2,5)+48; 4x+10=3x-7,5+48; 4x-3x=48-10-7,5; x=30,5 км/час.
Ответ: скорость теплохода в стоячей воде равна 30,5 км/час.
Знаешь ответ? Добавь его сюда!
Последние вопросы
Химия
1 час назад
2. Визначте масу калій гідроксиду ,що реагує з 5,6 л сульфур(IV) оксиду (н.у.).
3. Яка кількіст речовини солі утворюється при взаємодії ферум(ІІІ) оксиду з сульфатною кислотою масою 2,94 г.
Другие предметы
14 часов назад
Пользуясь определителем дикорастущих растений и опираясь на знания по курсу ботаники, определите, к какому виду, роду, семейству и классу относятся полезные растения, произрастающие в ближайшем лесу, поле или парке.
( Помогите срочно! )
Математика
1 день назад
24.
Ділянку прямокутної форми що має розміри 250м на 80м, засіяли кукурудзою. Скільки зерна було використано для цього, якщо на 10000м потрібно 18 кг?
Математика
1 день назад
32) найдите область определение функции z = (1/x) + (1/y)Математика
1 день назад
33) найдите область определение функции z = (y — 1) / (x² + y²)Математика
1 день назад
31) найдите область определение функции z = 1 / (x-y)Геометрия
1 день назад
100 баллов таму кто поможетАнглийский язык
1 день назад
Subjunctive Mood
Test
I.
1. Jack doesn’t speak English. If he (spoke/ had spoken) English, he would (get/ have got) a good job at a travel agency. 2. I was in Rome on business. If I (had/ had had) more free time, I would (go/ have gone) sightseeing. 3. It is unlikely that he will repair his car soon. He would (give/ have given) us a ride to the train station if he (repaired/ had repaired) his car soon enough. 4. Bob failed at his exams. If he (worked/ had worked) harder he wouldn’t (fail/ have failed
II. Describe these situations in a different way. Use the Subjunctive Mood.
- The problems of the company were very serious. As a result Tom worked hard all the weekends.
- The alarm clock was broken. And John was late for his first lesson.
- My mother was in Italy. I had to cook everything on my own.
- She lost her mobile phone. That’s why I gave her mine.
- She was late for their wedding. Her fiancé got angry.
III. Translation.
- Если бы Майк сдал отчет вовремя, его бы не уволили.
- Жаль, что арбуз оказался гнилой.
- Если бы она не вмешивалась в его дела, он бы не дерзил ей.
- Если бы не твоя помощь, я бы не смог закрепить эти шторы.
- Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
- Мне бы хотелось, чтобы ты заботился о своем здоровье!
- Если бы тебе было все равно, ты бы не ревновал ее к другим мужчинам.
Английский язык
1 день назад
Subjunctive Mood
Test
I. Choose the right form:
1. Jack doesn’t speak English. If he (spoke/ had spoken) English, he would (get/ have got) a good job at a travel agency. 2. I was in Rome on business
II. Describe these situations in a different way. Use the Subjunctive Mood.
- The problems of the company were very serious. As a result Tom worked hard all the weekends.
- The alarm clock was broken. And John was late for his first lesson.
- My mother was in Italy. I had to cook everything on my own.
- She lost her mobile phone. That’s why I gave her mine.
- She was late for their wedding. Her fiancé got angry.
III. Translation.
- Если бы Майк сдал отчет вовремя, его бы не уволили.
- Жаль, что арбуз оказался гнилой.
- Если бы она не вмешивалась в его дела, он бы не дерзил ей.
- Если бы не твоя помощь, я бы не смог закрепить эти шторы.
- Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
- Мне бы хотелось, чтобы ты заботился о своем здоровье!
- Если бы тебе было все равно, ты бы не ревновал ее к другим мужчинам.
Литература
2 дня назад
А где почему это напряжоный момент
Биология
2 дня назад
У голонасінних рослин уперше з’являєтся:
Математика
2 дня назад
Математика третий класс запиши все возможные значения длины и ширины по известному периметру прямоугольника периметр 98 м 120 м 140
Алгебра
2 дня назад
Решите графически системы уравнений (выражая у через х) 1 система {х+2у=6 х-4у=0} 2 система{3у-х=3 х-4у=1}
Физика
2 дня назад
Електричний нагрівник за 7 хв доводить до кипіння 10 кг води, початкова температура якої дорівнює 20 °С.
Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %.Физика
3 дня назад
Тело движется вдоль оси Ох. График зависимости проекции его скорости Vх от времени t изображён на рисунке. Найди путь S, пройденный телом за рассмотренный промежуток времени. Результат вырази в метрах, округлив до целого числа.
6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.
Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %.How much to ban the user?
1 hour 1 day 100 years
Задачи относительной скорости и речных судов
Иногда объекты перемещаются в среде, которая движется относительно наблюдателя. Например, самолет обычно сталкивается с ветром — воздухом, движущимся по отношению к наблюдателю, находящемуся внизу на земле. В качестве другого примера, моторная лодка движется по реке среди речного течения — воды, которая движется относительно наблюдателя на суше.
В таких случаях величина скорости движущегося объекта (будь то самолет или моторная лодка) относительно наблюдателя на суше не будет такой же, как показания спидометра транспортного средства. Другими словами, спидометр на моторной лодке может показывать 20 миль в час; однако моторная лодка может двигаться относительно наблюдателя на берегу со скоростью 25 миль в час. Движение относительно наблюдателя. Наблюдатель на суше, которого часто называют (или неправильно называют) «стационарным наблюдателем», будет измерять скорость так, чтобы она отличалась от скорости человека в лодке. Наблюдаемая скорость лодки всегда должна описываться относительно того, кто является наблюдателем.
Попутный, встречный и боковой ветер
Чтобы проиллюстрировать этот принцип, рассмотрим самолет, летящий при попутном ветре . Попутный ветер — это просто ветер, который приближается к самолету сзади, тем самым увеличивая его результирующую скорость.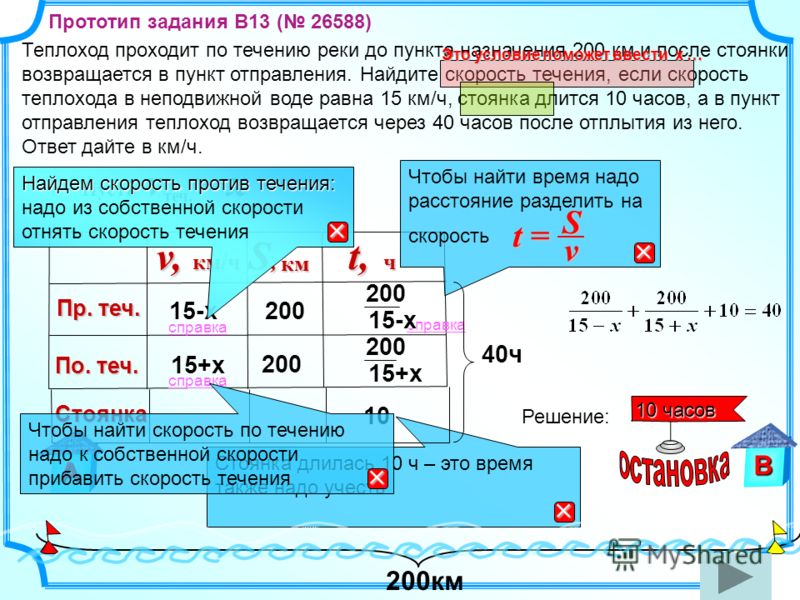
Если самолет движется со скоростью 100 км/ч относительно воздуха и скорость ветра 25 км/ч, то какова скорость самолета относительно наблюдателя на земле внизу? Результирующая скорость самолета (то есть результат того, что скорость ветра влияет на скорость двигателя самолета) представляет собой векторную сумму скорости самолета и скорости ветра. Эту результирующую скорость довольно легко определить, если ветер приближается к самолету прямо сзади. Как показано на диаграмме ниже, самолет движется с результирующей скоростью 125 км/ч относительно земли.
Если самолет встречает встречный ветер, результирующая скорость будет меньше 100 км/ч. Поскольку встречный ветер — это ветер, который приближается к самолету спереди, такой ветер уменьшит результирующую скорость самолета. Предположим, что самолет, летящий со скоростью 100 км/ч относительно воздуха, встречает встречный ветер со скоростью 25 км/ч. В этом случае результирующая скорость будет 75 км/ч; это скорость самолета относительно наблюдателя на земле.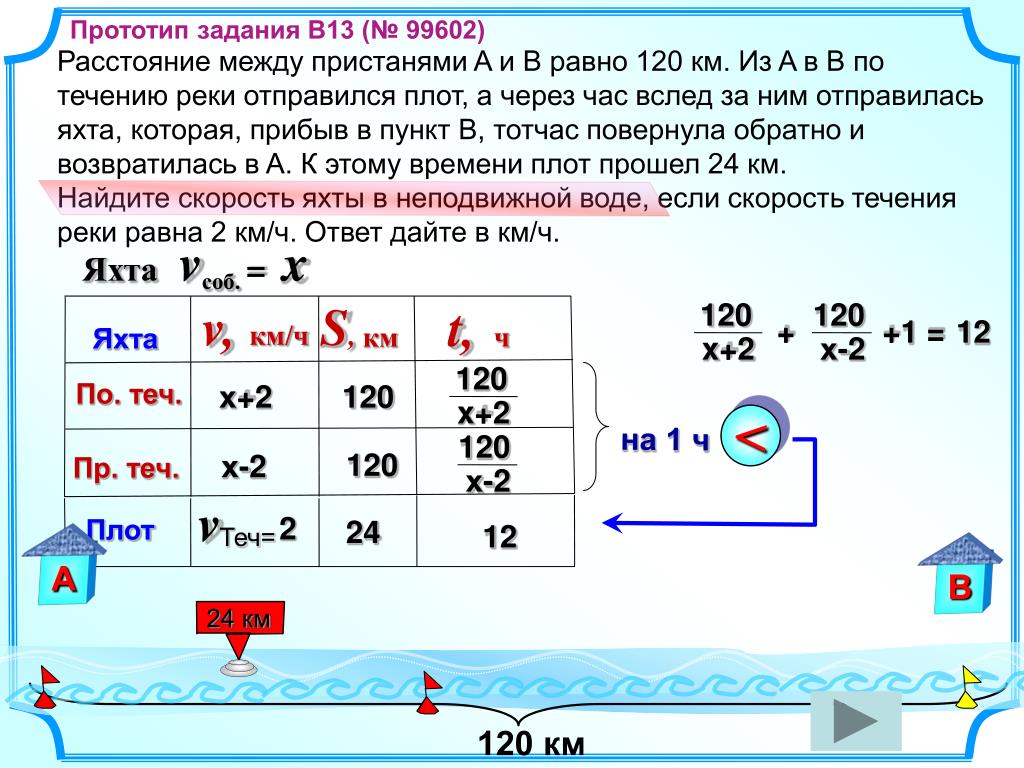
Это изображено на диаграмме ниже.
Теперь рассмотрим самолет, летящий со скоростью 100 км/ч на юг, который встречает боковой ветер со скоростью 25 км/ч на запад. Какова будет результирующая скорость самолета? На этот вопрос можно ответить так же, как и на предыдущие вопросы. Результирующая скорость самолета представляет собой векторную сумму двух отдельных скоростей. Чтобы определить результирующую скорость, скорость самолета (относительно воздуха) необходимо добавить к скорости ветра. Это та же самая процедура, которая использовалась выше для ситуаций встречного и попутного ветра; только теперь результат не так легко вычислить. Поскольку два добавляемых вектора — скорость южной плоскости и скорость западного ветра — находятся под прямым углом друг к другу, можно использовать теорему Пифагора. Это показано на диаграмме ниже.
В этой ситуации бокового ветра южный вектор может быть добавлен к западному вектору с использованием обычных методов сложения векторов.
Величина результирующей скорости определяется по теореме Пифагора. Алгебраические шаги следующие:
10 000 км 2 /час 2 + 625 км 2 /час 2 = R 2
10 625 км 2 /час 2 = R 2
SQRT(10 625 км 2 /час 2 ) =
рэндов103,1 км/ч =
р.
Направление результирующей скорости можно определить с помощью тригонометрической функции. Поскольку скорость самолета и скорость ветра образуют прямоугольный треугольник при сложении головой к хвосту, угол между результирующим вектором и вектором, направленным на юг, можно определить с помощью функций синуса, косинуса или тангенса. Можно использовать функцию касательной; это показано ниже:
тангенс (тета) = (25/100)
тета = инвтан (25/100)
тета = 14,0 градусов
Если равнодействующая скорость самолета образует угол 14,0 градусов с направлением на юг (тета на приведенной выше диаграмме), то направление равнодействующей составляет 256 градусов.
Как и любой вектор, направление равнодействующей измеряется как угол поворота против часовой стрелки с востока.
Воздействие ветра на самолет аналогично действию речного течения на моторную лодку. Если бы моторная лодка направилась прямо через реку (то есть, если бы лодка направила нос прямо на другой берег), она не достигла бы берега прямо напротив своей начальной точки. Речное течение влияет на движение лодки и несет ее вниз по течению. Моторная лодка может двигаться со скоростью 4 м/с прямо поперек реки, однако результирующая скорость лодки будет больше 4 м/с и под углом вниз по течению. Хотя спидометр лодки может показывать 4 м/с, ее скорость относительно наблюдателя на берегу будет больше 4 м/с.
Результирующую скорость моторной лодки можно определить так же, как это было сделано для самолета. Результирующая скорость лодки представляет собой векторную сумму скорости лодки и скорости реки.
Поскольку лодка движется прямо через реку, а течение всегда направлено прямо вниз по течению, два вектора находятся под прямым углом друг к другу. Таким образом, теорему Пифагора можно использовать для определения результирующей скорости. Предположим, что река двигалась со скоростью 3 м/с на север, а моторная лодка двигалась со скоростью 4 м/с на восток. Какова будет результирующая скорость моторной лодки (т. е. скорость относительно наблюдателя на берегу)? Величину равнодействующей можно найти следующим образом:
16 м 2 /с 2 + 9 м 2 /с 2 = R 2
25 м 2 /с 2 = R 2
SQRT (25 м 2 /с 2 ) = R
5,0 м/с = R
Направление равнодействующей — это угол поворота против часовой стрелки, на который равнодействующий вектор направлен строго на восток.
Этот угол можно определить с помощью тригонометрической функции, как показано ниже.
тангенс (тета) = (3/4)
тета = инвтан (3/4)
тета = 36,9 градусов
При скорости лодки 4 м/с на восток и скорости реки 3 м/с на север результирующая скорость лодки будет 5 м/с при 36,9 градусах.
Подобные проблемы с моторными лодками обычно сопровождаются тремя отдельными вопросами:
- Какова результирующая скорость (как величина, так и направление) лодки?
- Если ширина реки составляет х метров, то сколько времени потребуется лодке, чтобы добраться от берега до берега?
- На каком расстоянии по течению лодка достигает противоположного берега?
Ответ на первый из этих трех вопросов был дан выше; результирующая скорость лодки может быть определена с помощью теоремы Пифагора (величина) и тригонометрической функции (направление).
На второй и третий из этих вопросов можно ответить, используя уравнение средней скорости (и много логики).
Рассмотрим следующий пример.
Моторная лодка, движущаяся со скоростью 4 м/с на восток, встречает течение со скоростью 3,0 м/с на север.
|
Решение первого вопроса уже было показано в приведенном выше обсуждении. Результирующая скорость лодки 5 м/с при 36,9 градусах. Начнем со второго вопроса.
Ширина реки 80 метров. То есть расстояние от берега до берега, измеренное поперек реки, равно 80 метрам.
Время пересечения этой реки шириной 80 метров можно определить, переставив и подставив в уравнение средней скорости.
Расстояние 80 м можно подставить в числитель. Но как насчет знаменателя? Какое значение следует использовать для средней скорости? Следует ли использовать 3 м/с (текущая скорость), 4 м/с (скорость лодки) или 5 м/с (результирующая скорость) в качестве средней скорости прохождения 80 метров? С какой средней скоростью лодка плывет по реке шириной 80 м? Большинство студентов хотят использовать результирующую скорость в уравнении, так как это фактическая скорость лодки относительно берега. Тем не менее, значение 5 м/с — это скорость, с которой лодка преодолевает диагональное измерение реки. А расстояние по диагонали через реку в этом случае неизвестно. Если бы кто-то знал расстояние C на диаграмме ниже, то можно использовать среднюю скорость C для расчета времени, необходимого для достижения противоположного берега.
Точно так же, если бы кто-то знал расстояние B на диаграмме ниже, то среднюю скорость B можно было бы использовать для расчета времени, необходимого для достижения противоположного берега. И, наконец, если бы кто-то знал расстояние A на диаграмме ниже, то среднюю скорость A можно было бы использовать для расчета времени, необходимого для достижения противоположного берега.
В нашей задаче 80 м соответствуют расстоянию А, поэтому для определения времени в уравнение следует подставить среднюю скорость 4 м/с (средняя скорость в направлении прямо через реку).
Лодке требуется 20 с, чтобы пересечь реку. В течение этих 20 с перехода через реку лодка также дрейфует вниз по течению. Часть c задачи спрашивает: «На каком расстоянии по течению лодка достигает противоположного берега?» Это же уравнение должно быть использовано для расчета этого расстояние вниз по течению .
И снова возникает вопрос, какое из трех значений средней скорости нужно использовать в уравнении для расчета расстояния вниз по течению? Расстояние вниз по течению соответствует расстоянию B на приведенной выше диаграмме. Скорость, с которой лодка преодолевает это расстояние, соответствует средней скорости B на диаграмме выше (т. е. скорость, с которой движется течение — 3 м/с). И поэтому среднюю скорость 3 м/с (среднюю скорость в направлении вниз по течению) следует подставить в уравнение для определения расстояния.
расстояние = 60 м
Лодку уносит вниз по течению на 60 метров за 20 секунд, необходимых для пересечения реки.
Математика приведенной выше задачи не сложнее, чем деление или умножение двух числовых величин друг на друга. Математика проста! Сложность проблемы носит концептуальный характер; трудность заключается в том, чтобы решить, какие числа использовать в уравнениях.
Это решение вытекает из концептуального понимания (или, к сожалению, из-за непонимания) происходящего сложного движения. Движение речного судна можно разделить на две одновременные части — движение в направлении прямо поперек реки и движение в направлении вниз по течению. Эти две части (или компоненты) движения происходят одновременно в течение одинакового времени (которое в приведенной выше задаче составляло 20 секунд). Решение о том, какое значение скорости или значения расстояния использовать в уравнении, должно соответствовать приведенной выше диаграмме. Лодочный мотор — это то, что переносит лодку по реке Расстояние А ; поэтому любой расчет, включающий Distance A , должен включать значение скорости, обозначенное как Speed A (скорость лодки относительно воды). Точно так же это течение реки несет лодку вниз по течению на Расстояний B ; поэтому любой расчет, включающий Distance B , должен включать значение скорости, обозначенное как Speed B (скорость реки).
Вместе эти две части (или компоненты) составляют результирующее движение лодки. То есть составляющая смещения через реку добавляется к смещению вниз по течению, чтобы равняться результирующему смещению. Точно так же скорость лодки (по реке) добавляется к скорости реки (по течению), чтобы сравняться с результирующей скоростью. Таким образом, любое вычисление расстояния C или средней скорости C («Результирующая скорость») может быть выполнено с использованием теоремы Пифагора.
Теперь, чтобы проиллюстрировать важный момент, давайте попробуем решить вторую примерную задачу, похожую на первую. Попробуйте ответить на три вопроса, а затем нажмите кнопку, чтобы проверить свой ответ.
Пример 2 Моторная лодка, движущаяся со скоростью 4 м/с на восток, встречает течение со скоростью 7,0 м/с на север.
|
Из анализа двух приведенных выше примеров задач вытекает важная концепция.
В примере 1 время пересечения реки шириной 80 м (при движении со скоростью 4 м/с) составило 20 секунд. Это было при скорости течения 3 м/с. В примере 2 скорость течения была намного больше — 7 м/с, но время пересечения реки осталось неизменным. На самом деле скорость течения сама по себе не влияет на время, необходимое лодке для пересечения реки. Река движется вниз по течению параллельно берегам реки. Таким образом, течение никак не может помочь лодке пересечь реку. Хотя усиление течения может повлиять на результирующую скорость, заставив лодку двигаться с большей скоростью по отношению к наблюдателю на земле, оно не увеличивает скорость в направлении поперек реки. Составляющая результирующей скорости, которая увеличивается, — это составляющая, направленная вниз по реке. Часто говорят, что «перпендикулярные компоненты движения не зависят друг от друга». Применительно к задачам о речных судах это будет означать, что переменная поперек реки не зависит (т. е. не подвергается влиянию) переменной ниже по течению.
Время пересечения реки зависит от скорости, с которой лодка пересекает реку. Только составляющая движения, направленная поперек реки (т. е. скорость лодки), влияет на время прохождения пути непосредственно через реку (в данном случае 80 м). Составляющая движения, перпендикулярная этому направлению, — скорость течения — влияет только на расстояние, которое лодка проходит по реке. Эта концепция перпендикулярных составляющих движения будет исследована более подробно в следующей части Урока 1.
1. Самолет может двигаться со скоростью 80 миль/час относительно воздуха. Определите результирующую скорость самолета (только по величине), если он встретится с
а. Встречный ветер 10 миль/ч.б. Попутный ветер 10 миль в час.
в. Боковой ветер 10 миль в час.
д. Боковой ветер 60 миль в час.
2. Моторная лодка, движущаяся со скоростью 5 м/с на восток, встречает течение со скоростью 2,5 м/с на север.
а. Чему равна результирующая скорость моторной лодки?б. Если ширина реки 80 м, то сколько времени потребуется лодке, чтобы пройти от берега до берега?
в. На каком расстоянии по течению лодка достигает противоположного берега?
3. Моторная лодка, движущаяся со скоростью 5 м/с на восток, встречает течение со скоростью 2,5 м/с на юг.
а. Чему равна результирующая скорость моторной лодки?б. Если ширина реки 80 м, то сколько времени потребуется лодке, чтобы пройти от берега до берега?
в. На каком расстоянии по течению лодка достигает противоположного берега?
4. Моторная лодка, движущаяся со скоростью 6 м/с на восток, встречает течение со скоростью 3,8 м/с на юг.
а. Чему равна результирующая скорость моторной лодки?б. Если ширина реки 120 м, то сколько времени потребуется лодке, чтобы пройти от берега до берега?
в. На каком расстоянии по течению лодка достигает противоположного берега?
5. Если скорость течения в вопросе №4 увеличить до 5 м/с, то
a. сколько времени потребуется, чтобы пересечь ту же реку шириной 120 м?б. Какое расстояние по течению пройдёт лодка за это время?
Следующий раздел:
Перейти к следующему уроку:
Речное судно проходит 87 км вниз по течению за 3 часа. Он проходит 76 км вверх по течению за 4 часа. Найдите скорость лодки и скорость воды.
РЕШЕНИЕ: Речное судно проплыло 87 км вниз по течению за 3 часа. Он проходит 76 км вверх по течению за 4 часа.
Найдите скорость лодки и скорость воды.Алгебра -> Настраиваемые средства решения задач Word -> Путешествия -> РЕШЕНИЕ: Речное судно проходит 87 км вниз по течению за 3 часа. Он проходит 76 км вверх по течению за 4 часа. Найдите скорость лодки и скорость воды. Войти
|
Leave A Comment