Теорема п 5 стереометрия – Стереометрия (Геометрия в пространстве) — Все свойства, теоремы, аксиомы и формулы — Математика

Стереометрия (Геометрия в пространстве) — Все свойства, теоремы, аксиомы и формулы — Математика

Оглавление:

 

Базовые теоремы, аксиомы и определения стереометрии

Вводные определения и аксиомы стереометрии

К оглавлению…

Некоторые определения:

1. Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости. При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.
2. Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней – площадью (полной) поверхности.
3. Куб – это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины – вершинами куба.
4. Параллелепипед – это многогранник, у которого шесть граней и каждая из них – параллелограмм. Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра, а имеющие общее ребро называются смежными. Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его боковыми ребрами.
5. Прямой параллелепипед – это такой параллелепипед, у которого боковые грани – прямоугольники. Прямоугольный параллелепипед – это параллелепипед, у которого все грани – прямоугольники. Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный.
6. Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.
7. Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы. Равные n-угольники называются основаниями, а параллелограммы – боковыми гранями призмы . Прямая призма – это такая призма, у которой боковые грани – прямоугольники. Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники.
8. Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначается S_бок). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается S_полн).
9. Пирамида (n-угольная) – это многогранник, у которого одна грань – какой-нибудь n -угольник, а остальные n граней – треугольники с общей вершиной; n-угольник называется основанием; треугольники, имеющие общую вершину, называются боковыми гранями, а их общая вершина называется вершиной пирамиды. Стороны граней пирамиды называются ее ребрами, а ребра, сходящиеся в вершине, называются боковыми.
10. Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды (обозначается S_бок). Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается S_полн).
11. Правильная n-угольная пирамида – это такая пирамида, основание которой – правильный n-угольник, а все боковые ребра равны между собой. У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.
12. Треугольная пирамида называется тетраэдром, если все ее грани – равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида будет тетраэдром).

Аксиомы стереометрии:

1. Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.
2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Следствия из аксиом стереометрии:

• Теорема 1. Через прямую и не лежащую на ней точку проходит единственная плоскость.
• Теорема 2. Через две пересекающиеся прямые проходит единственная плоскость.
• Теорема 3. Через две параллельные прямые проходит единственная плоскость.

 

Построение сечений в стереометрии

К оглавлению…

Для решения задач по стереометрии остро необходимо умение строить на рисунке сечения многогранников (например, пирамиды, параллелепипеда, куба, призмы) некоторой плоскостью. Дадим несколько определений, поясняющих, что такое сечение:

• Секущей плоскостью пирамиды (призмы, параллелепипеда, куба) называется такая плоскость, по обе стороны от которой есть точки данной пирамиды (призмы, параллелепипеда, куба).
• Сечением пирамиды (призмы, параллелепипеда, куба) называется фигура, состоящая из всех точек, которые являются общими для пирамиды (призмы, параллелепипеда, куба) и секущей плоскости.
• Секущая плоскость пересекает грани пирамиды (параллелепипеда, призмы, куба) по отрезкам, поэтому сечение есть многоугольник, лежащий в секущей плоскости, сторонами которого являются указанные отрезки.

Для построения сечения пирамиды (призмы, параллелепипеда, куба) можно и нужно построить точки пересечения секущей плоскости с ребрами пирамиды (призмы, параллелепипеда, куба) и соединить каждые две из них, лежащие в одной грани. Заметим, что последовательность построения вершин и сторон сечения не существенна. В основе построения сечений многогранников лежит две задачи на построение:

1. Линии пересечения двух плоскостей.

Для построения прямой, по которой пересекаются некоторые две плоскости α и β

(например, секущая плоскость и плоскость грани многогранника), нужно построить две их общие точки, тогда прямая, проходящая через эти точки, есть линия пересечения плоскостей α и β.

2. Точки пересечения прямой и плоскости.

Для построения точки пересечения прямой l и плоскости α нужно построить точку пересечения прямой l и прямой l₁, по которой пересекаются плоскость α и любая плоскость, содержащая прямую l.

 

Взаимное расположение прямых и плоскостей в стереометрии

К оглавлению…

Определение: В ходе решения задач по стереометрии две прямые в пространстве называются

параллельными, если они лежат в одной плоскости и не пересекаются. Если прямые а и b, либо AB и CD параллельны, то пишут:

Несколько теорем:

• Теорема 1. Через любую точку пространства, не лежащую на данной прямой, проходит единственная прямая, параллельная данной прямой.
• Теорема 2. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
• Теорема 3 (признак параллельности прямых). Если две прямые параллельны третьей прямой, то они параллельны между собой.
• Теорема 4 (о точке пересечения диагоналей параллелепипеда). Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Возможны три случая взаимного расположения прямой и плоскости в стереометрии:

• Прямая лежит в плоскости (каждая точка прямой лежит в плоскости).
• Прямая и плоскость пересекаются (имеют единственную общую точку).
• Прямая и плоскость не имеют ни одной общей точки.

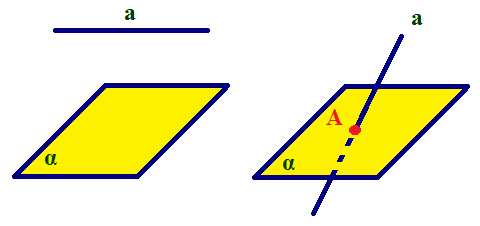
Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая а параллельна плоскости β, то пишут:

Теоремы:

• Теорема 1
  (признак параллельности прямой и плоскости). Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
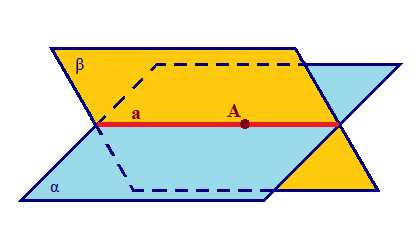
• Теорема 2. Если плоскость (на рисунке – α) проходит через прямую (на рисунке – с), параллельную другой плоскости (на рисунке – β), и пересекает эту плоскость, то линия пересечения плоскостей (на рисунке – d) параллельна данной прямой:

 

Если две различные прямые лежат в одной плоскости, то они либо пересекаются, либо параллельны. Однако, в пространстве (т.е. в стереометрии) возможен и третий случай, когда не существует плоскости, в которой лежат две прямые (при этом они и не пересекаются, и не параллельны).

Определение: Две прямые называются скрещивающимися, если не существует плоскости, в которой они обе лежат.

Теоремы:

• Теорема 1 (признак скрещивающихся прямых). Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещивающиеся.
• Теорема 2. Через каждую из двух скрещивающихся прямых проходит единственная плоскость, параллельная другой прямой.

Теперь введем понятие угла между скрещивающимися прямыми. Пусть a и b – две скрещивающиеся прямые. Возьмем произвольную точку O в пространстве и проведем через нее прямые a₁ и b₁, параллельные прямым a и b соответственно. Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми a₁ и b₁.

Однако на практике точку O чаще выбирают так, чтобы она принадлежала одной из прямых. Это обычно не только элементарно удобнее, но и рациональнее и правильнее с точки зрения построения чертежа и решения задачи. Поэтому для угла между скрещивающимися прямыми дадим такое определение:

Определение: Пусть a и b – две скрещивающиеся прямые. Возьмем произвольную точку O на одной из них (в нашем случае, на прямой b) и проведем через неё прямую параллельную другой из них (в нашем случае a₁ параллельна a). Углом между скрещивающимися прямыми a и b называется угол между построенной прямой и прямой, содержащей точку O (в нашем случае это угол β между прямыми a₁ и b).

Определение: Две прямые называются взаимно перпендикулярными (перпендикулярными), если угол между ними равен 90°. Перпендикулярными могут быть как скрещивающиеся прямые, так и прямые лежащие и пересекающиеся в одной плоскости. Если прямая a перпендикулярна прямой b, то пишут:

Определение: Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют общих точек. Если две плоскости α и β параллельны, то, как обычно, пишут:

Теоремы:

• Теорема 1 (признак параллельности плоскостей). Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
• Теорема 2 (о свойстве противолежащих граней параллелепипеда). Противолежащие грани параллелепипеда лежат в параллельных плоскостях.
• Теорема 3 (о прямых пересечения двух параллельных плоскостей третьей плоскостью). Если две параллельные плоскости пересечены третьей, то прямые их пересечения параллельны между собой.
• Теорема 4. Отрезки параллельных прямых, расположенные между параллельными плоскостями, равны.
• Теорема 5 (о существовании единственной плоскости, параллельной данной плоскости и проходящей через точку вне ее). Через точку, не лежащую в данной плоскости, проходит единственная плоскость, параллельная данной.

Определение: Прямая, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости. Если прямая a перпендикулярна плоскости β, то пишут, как обычно:

Теоремы:

• Теорема 1. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой.
• Теорема 2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
• Теорема 3 (о параллельности прямых, перпендикулярных плоскости). Если две прямые перпендикулярны одной плоскости, то они параллельны.
• Теорема 4 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
• Теорема 5 (о плоскости, проходящей через данную точку и перпендикулярной данной прямой). Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой.
• Теорема 6 (о прямой, проходящей через данную точку и перпендикулярной данной плоскости). Через любую точку пространства проходит единственная прямая, перпендикулярная данной плоскости.
• Теорема 7 (о свойстве диагонали прямоугольного параллелепипеда). Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, имеющих общую вершину:

Следствие: Все четыре диагонали прямоугольного параллелепипеда равны между собой.

 

Теорема о трех перпендикулярах

К оглавлению…

Пусть точка А не лежит на плоскости α. Проведем через точку А прямую, перпендикулярную плоскости α, и обозначим буквой О точку пересечения этой прямой с плоскостью α. Перпендикуляром, проведенным из точки А к плоскости α, называется отрезок АО, точка О называется основанием перпендикуляра. Если АО – перпендикуляр к плоскости α, а М – произвольная точка этой плоскости, отличная от точки О, то отрезок АМ называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок ОМ – ортогональная проекция (или, короче, проекция) наклонной АМ на плоскость α. Теперь приведем теорему, которая играет важную роль при решении многих задач.

Теорема 1 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и самой наклонной. Верно и обратное утверждение:

Теорема 2 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная наклонной, перпендикулярна и ее проекции на эту плоскость. Данные теоремы, для обозначений с чертежа выше можно кратко сформулировать так:

Теорема: Если из одной точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и две наклонные, то:

• две наклонные, имеющие равные проекции, равны;
• из двух наклонных больше та, проекция которой больше.

Определения расстояний объектами в пространстве:

• Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к данной плоскости.
• Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.
• Расстоянием между прямой и параллельной ей плоскостью называется расстояние от произвольной точки прямой до плоскости.
• Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до плоскости, проходящей через другую прямую и параллельной первой прямой.

Определение: В стереометрии ортогональной проекцией прямой a на плоскость α называется проекция этой прямой на плоскость α в случае, если прямая, определяющая направление проектирования, перпендикулярна плоскости α.

Замечание: Как видно из предыдущего определения, проекций бывает много. Другие (кроме ортогональной) проекции прямой на плоскость можно построить если прямая определяющая направление проецирования будет не перпендикулярна плоскости. Однако, именно ортогональную проекцию прямой на плоскость в будущем мы будем встречать в задачах. А называть ортогональную проекцию будем просто проекцией (как на чертеже).

Определение: Углом между прямой, не перпендикулярной плоскости, и этой плоскостью называется угол между прямой и ее ортогональной проекцией на данную плоскость (угол АОА’ на чертеже выше).

Теорема: Угол между прямой и плоскостью является наименьшим из всех углов, которые данная прямая образует с прямыми, лежащими в данной плоскости и проходящими через точку пересечения прямой и плоскости.

 

Двугранный угол

К оглавлению…

Определения:

• Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой и частью пространства, для которой эти полуплоскости служат границей.
• Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.

Таким образом, линейный угол двугранного угла – это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его ребру. Все линейные углы двугранного угла равны между собой. Градусной мерой двугранного угла называется градусная мера его линейного угла.

Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°). В дальнейшем, при решении задач по стереометрии, под двугранным углом будем понимать всегда тот линейный угол, градусная мера которого удовлетворяет условию:

Определения:

• Двугранным углом при ребре многогранника называется двугранный угол, ребро которого содержит ребро многогранника, а грани двугранного угла содержат грани многогранника, которые пересекаются по данному ребру многогранника.
• Углом между пересекающимися плоскостями называется угол между прямыми, проведенными соответственно в данных плоскостях перпендикулярно их линии пересечения через некоторую ее точку.
• Две плоскости называются перпендикулярными, если угол между ними равен 90°.

Теоремы:

• Теорема 1 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
• Теорема 2. Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная прямой, по которой они пересекаются, перпендикулярна другой плоскости.

 

Симметрия фигур

К оглавлению…

Определения:

1. Точки M и M₁ называются симметричными относительно точки O, если O является серединой отрезка MM₁.
2. Точки M и M₁ называются симметричными относительно прямой l, если прямая l проходит через середину отрезка MM₁ и перпендикулярна ему.
3. Точки M и M₁ называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка MM₁ и перпендикулярна этому отрезку.
4. Точка O (прямая l, плоскость α) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно точки O (прямой l, плоскости α) некоторой точке этой же фигуры.
5. Выпуклый многогранник называется правильным, если все его грани – равные между собой правильные многоугольники и в каждой вершине сходится одно и то же число ребер.

 

Призма

К оглавлению…

Определения:

1. Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
2. Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
3. Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
4. Боковая поверхность – объединение боковых граней.
5. Полная поверхность – объединение оснований и боковой поверхности.
6. Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
7. Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
8. Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
9. Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
10. Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
11. Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства и формулы для призмы:

• Основания призмы являются равными многоугольниками.
• Боковые грани призмы являются параллелограммами.
• Боковые ребра призмы параллельны и равны.
• Объём призмы равен произведению её высоты на площадь основания:

где: S_осн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).

• Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:

• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A₂B₂C₂D₂E₂).
• Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
• Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
• Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:

где: S_сеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA₁ или BB₁ и так далее).

• Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:

где: P_сеч – периметр перпендикулярного сечения, l – длина бокового ребра.

Виды призм в стереометрии:

• Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
• Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):

где: P_осн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = S_осн∙h = S_осн∙l.

• Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:

Свойства правильной призмы:

1. Основания правильной призмы являются правильными многоугольниками.
2. Боковые грани правильной призмы являются равными прямоугольниками.
3. Боковые ребра правильной призмы равны между собой.
4. Правильная призма является прямой.

 

Параллелепипед

К оглавлению…

Определение: Параллелепипед – это призма, основания которой параллелограммы. В этом определении ключевым словом является «призма». Таким образом, параллелепипед – это частный случай призмы, которая отличается от общего случая только тем, что в основании у нее не произвольный многоугольник, а именно параллелограмм. Поэтому все приведенные выше свойства, формулы и определения касающиеся призмы остаются актуальными и для паралле

educon.by

Основные понятия и аксиомы стереометрии

«Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей»

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.

Простейшие фигуры в пространстве: точка, прямая, плоскость.

Плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
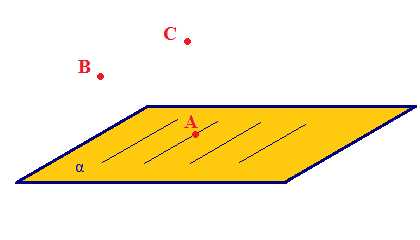
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,

Аксиомы стереометрии и их следствия

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты.

Некоторые следствия из аксиом

Теорема 1. Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.
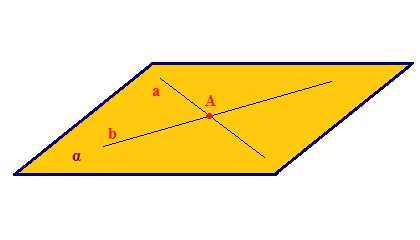
Теорема 2. Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.

Параллельные прямые в пространстве

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Лемма о пересечении плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Теорема о трех прямых в пространстве. Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b).

Параллельность прямой и плоскости

Прямая и плоскость называются параллельными, если они не имеют общих точек.

Признак параллельности прямой и плоскости Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Теорема. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. Теорема. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Взаимное расположение прямых в пространстве

Пересекающиеся прямые: лежат в одной плоскости, имеют одну общую точку.	Параллельные прямые: лежат в одной плоскости, не имеют общих точек (не пересекаются)	Скрещивающиеся прямые: не лежат в одной плоскости, не имеют общих точек (не пересекаются)

studfiles.net

Справочник стереометрия

Теоретический материал по теме «Стереометрия на ЕГЭ по математике, часть 2».

1. Плоскость в пространстве. Взаимное расположение плоскостей
Плоскость, прямая, точка — основные понятия геометрии.

Две плоскости в пространстве либо параллельны, либо пересекаются. Примеры в окружающем пространстве найти легко.

Мы не рассматриваем отдельно случай «плоскости совпадают». Раз совпадают — значит, это одна плоскость, а не две.

2. Прямые в пространстве. Пересекающиеся, параллельные, скрещивающиеся прямые

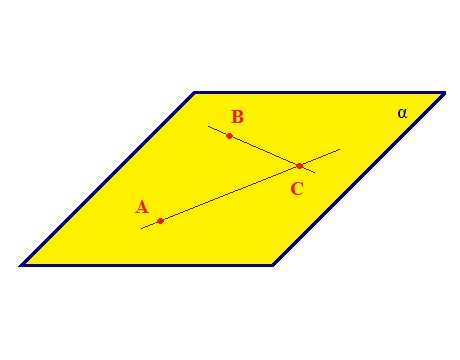
На плоскости две прямые или пересекаются, или параллельны друг другу. А в пространстве возможны три случая взаимного расположения прямых.

Две прямые в пространстве параллельны друг другу, пересекаются или скрещиваются.

Если две прямые параллельны третьей, то они параллельны друг другу.

Скрещивающиеся прямые не пересекаются и не параллельны друг другу. Через них невозможно провести плоскость. Скрещивающиеся прямые лежат в параллельных плоскостях.

3. Параллельность прямой и плоскости

Прямая и плоскость могут пересекаться или быть параллельными друг другу. Еще один случай — прямая лежит в плоскости.

Определение: Прямая параллельна плоскости, если она не имеет с плоскостью общих точек.

Но как на практике проверить, что бесконечная прямая нигде не пересечет бесконечную плоскость? Для практического применения используется признак параллельности прямой и плоскости:

Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости.

 

Этот признак часто используется в решении задач по стереометрии. Например, в правильной четырехугольной пирамиде SABCD прямая АВ параллельна прямой СD — значит, АВ параллельна всей плоскости SCD.

 

4. Угол между прямой и плоскостью. Перпендикулярность прямой и плоскости

Если две прямые лежат в одной плоскости, угол между ними легко измерить — например, с помощью транспортира. А как измерить угол между прямой и плоскостью?

Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной.

Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получили проекцию наклонной на плоскость.

 

Определение. Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

Обратите внимание — в качестве угла между прямой и плоскостью мы выбираем острый угол.

Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю.

Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°.

Определение. Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

На практике применяется признак перпендикулярности прямой и плоскости:

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

 

 

5. Параллельность плоскостей

Определение. Две плоскости параллельны, если они не имеют общих точек.

В практических целях чаще используется признак параллельности плоскостей:

Плоскости параллельны друг другу, если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.

 

Свойства параллельных плоскостей:

1) Если две плоскости параллельны третьей, то они параллельны друг другу.

 

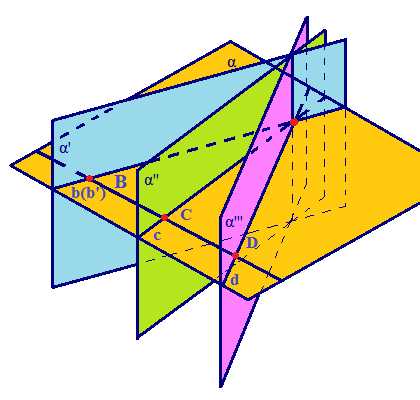
2) Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.

3) Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

 

 

6. Угол между плоскостями. Перпендикулярность плоскостей

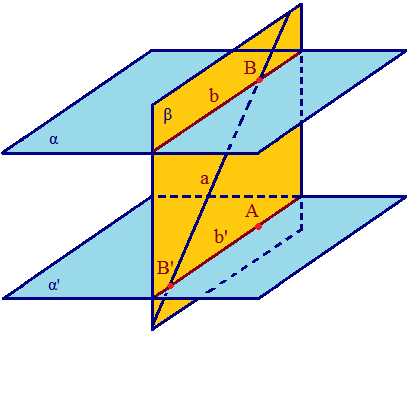
Пусть плоскости α и β пересекаются по прямой с.

Определение. Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.

Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.

Заметим, что при пересечении двух плоскостей вообще-то образуются четыре угла. В качестве угла между плоскостями мы берем острый угол.

Определение. Если угол между плоскостями равен 90 градусов, то плоскости перпендикулярны.

Решая задачи по стереометрии, мы используем также признак перпендикулярности плоскостей:
Если плоскость α проходит через перпендикуляр к плоскости β, то плоскости α и β перпендикулярны.

 

7. Угол между скрещивающимися прямыми и расстояние между ними.

Скрещивающиеся прямые не параллельны и не пересекаются. Они лежат в параллельных плоскостях, и поместить их в одну плоскость невозможно.

Часто в задачах требуется найти угол между скрещивающимися прямыми. Как это сделать?

Угол между прямыми, лежащими в одной плоскости, найти нетрудно. Можно измерить его транспортиром. Можно найти из какого-нибудь треугольника по теореме синусов или косинусов.

Пусть скрещивающиеся прямые a и b лежат в параллельных плоскостях α и β. Проведем в плоскости β прямую с, параллельную прямой а. Угол между прямыми а и b равен углу между прямыми b и с.

 

 

Можно сказать, что угол между скрещивающимися прямыми — это угол между параллельными им прямыми, лежащими в одной плоскости.

8. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.

 

 

Другими словами, расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых они лежат.

Расстояние между скрещивающимися прямыми можно найти также как расстояние от одной из них до параллельной ей плоскости, в которой лежит вторая прямая.

Все три способа используются при решении задач.

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из точки на плоскость.

Расстояние от прямой до параллельной ей плоскости — длина перпендикуляра, опущенного на плоскость из любой точки этой прямой.

Заметим, что расстояние от точки до плоскости или угол между скрещивающимися прямыми иногда проще найти с помощью координатно-векторного метода.

9. Теорема о трех перпендикулярах

Рассмотрим чертеж. На нем изображены плоскость α и лежащая в ней прямая m. Наклонная a пересекает плоскость α в точке М. Прямая а₁ — проекция наклонной а на плоскость α.

Сформулируем теорему о трех перпендикулярах:

Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость.

 

 

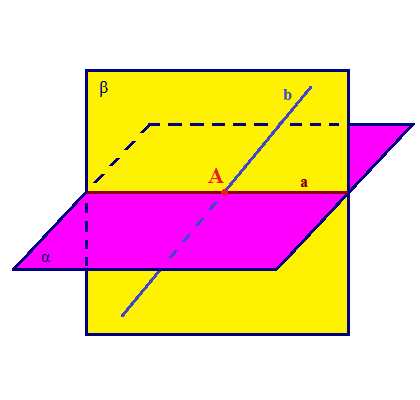
На рисунке показаны все три перпендикуляра.
Если прямая m, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.

Слова «тогда и только тогда» в формулировке теоремы означают, что прямая m перпендикулярна одновременно и наклонной, и ее проекции. Если m перпендикулярна наклонной, значит, перпендикулярна и ее проекции, и наоборот.

На нашем чертеже прямая m проведена через основание наклонной. Этого требует формулировка теоремы о трех перпендикулярах в большинстве учебников. Но прямая m, лежащая в плоскости, вовсе не обязана проходить через основание наклонной. Главное — чтобы она была перпендикулярна проекции наклонной. Тогда она будет перпендикулярна и самой наклонной:

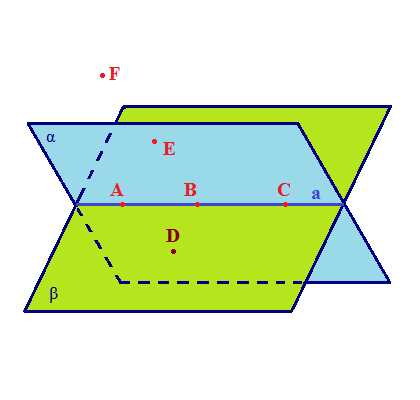
Теорема о трех перпендикулярах — полезный инструмент для решения задач.

Например, с ее помощью можно доказать, что диагональ куба АС₁ перпендикулярна прямой BD:

 

 

Или — что скрещивающиеся ребра тетраэдра взаимно перпендикулярны:

 

Или — что в правильной треугольной призме прямая А₁М (где М — середина ВС) перпендикулярна ребру ВС.

 

10. Параллельное проецирование. Площадь проекции фигуры

В задачах по геометрии успех зависит не только от знания теории, но от качественного чертежа.
С плоскими чертежами все более-менее понятно. А в стереометрии дело обстоит сложнее. Ведь изобразить надо трехмерное тело на плоском чертеже, причем так, чтобы и вы сами, и тот, кто смотрит на ваш чертеж, увидели бы то же самое объемное тело.

Как это сделать?
Конечно, любое изображение объемного тела на плоскости будет условным. Однако существует определенный набор правил. Существует общепринятый способ построения чертежей — параллельное проецирование.

Возьмем объемное тело.
Выберем плоскость проекции.
Через каждую точку объемного тела проведем прямые, параллельные друг другу и пересекающие плоскость проекции под каким-либо углом. Каждая из этих прямых пересекает плоскость проекции в какой-либо точке. А все вместе эти точки образуют проекцию объемного тела на плоскость, то есть его плоское изображение.

 

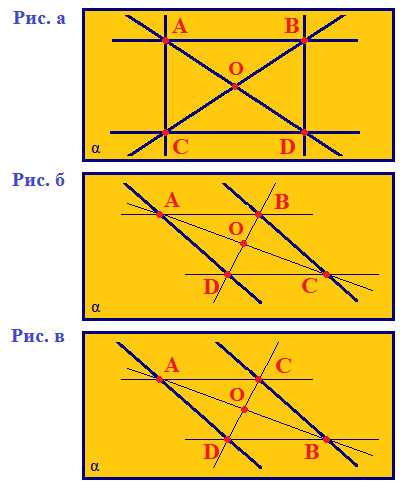
Как строить проекции объемных тел?
Представьте, что у вас есть каркас объемного тела — призмы, пирамиды или цилиндра. Освещая его параллельным пучком света, получаем изображение — тень на стене или на экране. Заметим, что в разных ракурсах получаются разные изображения, но некоторые закономерности все же присутствуют:

Проекцией отрезка будет отрезок.

 

Конечно, если отрезок перпендикулярен плоскости проекции — он отобразится в одну точку.
Проекцией круга в общем случае окажется эллипс.

 

 

Проекцией прямоугольника — параллелограмм.

 

Вот как выглядит проекция куба на плоскость:

Здесь передняя и задняя грани параллельны плоскости проекции

Можно сделать по-другому:

Какой бы ракурс мы ни выбрали, проекциями параллельных отрезков на чертеже тоже будут параллельные отрезки. Это один из принципов параллельного проецирования.

Рисуем проекции пирамиды,

цилиндра:

и шара:

Еще раз повторим основной принцип параллельного проецирования. Выбираем плоскость проекции и через каждую точку объемного тела проводим параллельные друг другу прямые. Эти прямые пересекают плоскость проекции под каким-либо углом. Если этот угол равен 90° — речь идет о прямоугольном проецировании. С помощью прямоугольного проецирования строятся чертежи объемных деталей в технике. В этом случае мы говорим о виде сверху, виде спереди и виде сбоку.

 

Иногда в задачах требуется найти площадь прямоугольной проекции фигуры.

Пусть S — площадь фигуры. Тогда площадь ее прямоугольной проекции равна S cosφ, где φ — угол между плоскостью фигуры и плоскостью проекции.

 

11. Как строить чертежи в задачах по стереометрии

Часто бывает так, что вы построили чертеж — и непонятно, что делать дальше. На чертеже ничего хорошего не видно. Почему?

Не спешите обвинять себя в отсутствии пространственного мышления. Может быть, просто ракурс выбран неудачно.

Очень важно, чтобы объемное тело на вашем чертеже выглядело действительно объемным, а не складывалось, как зонтик. Следите, чтобы одна грань не накладывалась на другую, а непараллельные отрезки (например, ребро куба и его диагональ) не совпадали.

Приведем примеры удачных и неудачных чертежей.

Мы рисуем чертеж крупным, чтобы на нем всё было хорошо видно.

Видимые линии изображаем сплошными, невидимые — штриховыми. Если решаете задачу векторно-координатным методом, ставьте рядом с точками их координаты. Это удобно.

Общий принцип: не понравился чертеж – не возитесь с ним, сделайте другой. Посмотрите на задачу с другого ракурса.

Иногда одного чертежа недостаточно. Чаще всего для решения задач по стереометрии, кроме «объемного» чертежа, нужен один или несколько плоских.

Чем же все-таки признак отличается от определения? Есть, например, определение перпендикулярности прямой и плоскости — и признак перпендикулярности прямой и плоскости. В чем разница между ними?

Предположим, в конкретной задаче нам надо доказать, что прямая l перпендикулярна плоскости α.

Если применять определение – придется перебрать все прямые, лежащие в плоскости α. Сделать это невозможно, да и не нужно. Достаточно, чтобы прямая l была перпендикулярна двум пересекающимся прямым в плоскости α

12. Еще две полезные теоремы для решения задач по стереометрии:

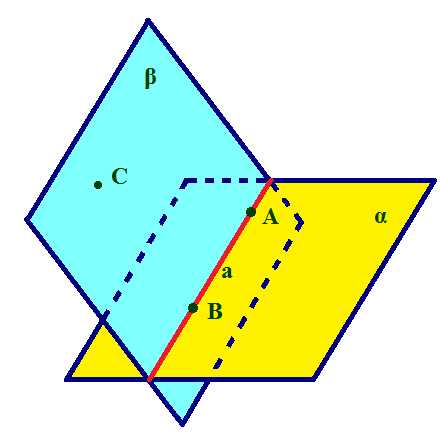
1) Теорема о прямой и параллельной ей плоскости.

Пусть прямая а параллельна плоскости α,
плоскость β проходит через прямую а.
Тогда линия пересечения плоскостей α и β параллельна прямой а.

 

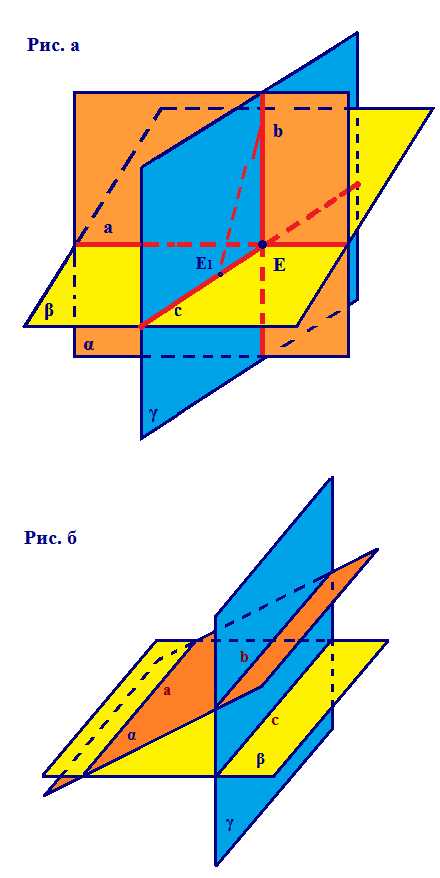
2) Теорема о трех плоскостях, пересекающихся по параллельным прямым.
Пусть пересекающиеся плоскости α и β проходят через параллельные прямые а и b. Тогда линия пересечения плоскостей α и β параллельна прямым а и b.

Легко запомнить – на рисунке эта конструкция похожа на домик : -)

13. Правила решения задач по стереометрии:

1. Начинаем с построения чертежа.

Строим чертеж ручкой,( не карандашом!), с помощью линейки. Невидимые элементы объемного тела изображаем штриховыми линиями.

2. Записываем каждый шаг решения. Помним, что в задаче по стереометрии необходимы подробные объяснения. Не просто «Прямая АВ перпендикулярна плоскости  », а «Прямая АВ перпендикулярна плоскости , потому что она перпендикулярна пересекающимся прямым  и , лежащим в плоскости ». Конечно, все это лучше записать не словами, а символами.

3. От объемной задачи переходим к плоской, планиметрической. Все необходимые плоские чертежи рисуем отдельно.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Следствия аксиом стереометрии. Теоремы 1,2.

Аксиомы стереометрии.

Стереометрия-раздел геометрии, в котором изучаются фигуры в пространстве.

Основные фигуры стереометрии:

1. Точка А

2. Прямая

3. Плоскость

Свойство 1. Какова бы не была плоскость, существуют точки, принадлежащие этой плоскости и принадлежащие ей. ∃α: А∈ α; В∈α; D∉α. ∃-существует.

Свойство 2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. Если А∈ α; А∈β, то ∃α: а ∈ α; α ∈ β, А∈а

Свойство 3. Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну. Если А∈а; А∈в, то ∃!α: а∈α; в∈α; А∈α

Свойство 4. Если две различны точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости. Если А∈α; В∈α, то АВ∈α

 

Следствия аксиом стереометрии. Теоремы 1,2.

Теорема 1. Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну. Дано: а; С∉а. Доказать: ∃!α: а∈α; С∈α. Доказательство: 1. В∈а (по аксиоме о том, что существует точки принадлежащие прямой и не принадлежащие ей). 2. ВС (по аксиоме о том, что через две точки можно провести одну прямую). 3. Т.к. В∈ВС, В∈а, то по Свойству 3 ∃α:ВС∈α, а∈α. 4. Пусть ∃α₁: а∈α₁; С∈α₁, тогда С∈α; С∈α₁, по свойству 2 имеем, что С ∈а, но по условию С∉а, значит наше предположение не верно и α₁ совпадают с Сα, т.е. α-единственная. чтд.

Теорема 2. Через 3 любые точки, не лежащие на 1 прямой можно провести плоскость и притом только 1. Дано: точка А, точка В, точка С. Доказать: ∃!α: А∈α; В∈α; С∈α. Доказательство:1. АВ, АС (по аксиоме о том, что через 2 точки можно провести 1 прямую). 2. Т.к. А∈АВ, А∈АС, то по Свойству 3 ∃α:АВ∈α, ВС∈α. 4. Пусть ∃α₂: а∈α₁; А∈α₁, тогда В∈α₁; С∈α₁, тогда по свойству 2 А, В, С лежат на одной прямой, но это противоречит условию, значит α-единственная. чтд.

 

Взаимное расположение прямых в пространстве.

2 прямые не лежащие в одной плоскости могут: пересекаться, быть параллельными, совпадать. Две прямые лежащие в одной плоскости называются параллельными, если они не пересекаются. Если прямые не лежат в одной плоскости и не пересекаются, то они будут параллельными.

Теорема 3. Через точку вне данной прямой можно провести прямую, параллельную этой прямой и притом только одну. Дано: а; А; А∉а. Доказать: ∃!а1: А∈а₁, а₁| |а. Доказательство: 1. По Т1 ∃!α: А∈α; а∈α. 2. А∈а₁, а₁| |а (по аксиоме планиметрии о том, что через точку к заданной прямой можно провести параллельную прямую и притом только одну). 3. Пусть ∃а₂: А∈а₂, а₂| |а, тогда через прямые а и а₂ проведем плоскость α, но по Т1 эта плоскость проходит через а и А, значит а₁ и а₂ совпадут, а₁-единственная. чтд.

Теорема 4. Признак параллельности прямых (теорема о транзитивности). Если две прямые параллельны третьей, то они параллельны друг другу. Дано: а,в,с. а| |в, а| |с. Доказать: в| |с. Доказательство:1. β: а∈β; в∈β. 2. α: а∈α; С∈α. 3. В∈в (по акстоме С1). 4. По Т1 ∃!α: С∈α₁; В∈α_1. 5. Т.к. В∈β, В∈α₁, то по аксиоме С2 ∃в: в∈β; в∈α₁; В∈в.

 

Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости.

Прямая и плоскость будут параллельны, если они не пересекаются.

Теорема 5. Если прямая не лежащая в плоскости параллельна, какой нибудь прямой в этой плоскости, то она параллельна и самой плоскости. Дано: α; а; а∈α; в∈α; а| |в. Доказать: а| |α. Доказательство:1. ∃β: а∈β; в∈β (Т1). 2. Пусть а непараллельная α, тогда ∃М: М∈а, М∈β; М∈α; значит по С2 М∈в. 3. Получим что М∈а, М∈в, но по условию а| |в, значит наше предположение не верно, ; а| |α. чтд.

Теорема 6. Справедлива обратная теорема: Если плоскость β, проходящая через прямую а, параллельную плоскости α, пересекает эту плоскость по прямой в, то прямые а и в параллельны. Дано: а; в; α; β; а∈β; а| |α; в∈α; в∈β. Доказать: а| |в. Доказательство:Пусть а непараллельная в, тогда ∃М: М∈а; М∈в; М∈β; М∈α. 2. Получит что М∈а, М∈α, значит а пересекает α, но по условию а| |в, значит наше предположение не верно. чтд.

Параллельность двух плоскостей. Две плоскости называются параллельными, если они не пересекаются.

Признаки параллельности плоскостей. Теорема 7. Если плоскость параллельна двум пересекающимся прямым лежащим в другой плоскости, то эти плоскости параллельны.Дано: α; β; а∈β; в∈β; а| |α; в| |α; А∈а; А∈в. Доказать: α| |β. Доказательство:1. Пусть α не параллельна β, тогда ∃С: С∈α; С∈β. 2. Тк а| |α и в| |α, имеем а| |с и в| |с (Т5). 3. Тк а| |с и в| |с то Т4 (о транзитивности) имеем а| |в, но по условию а не параллельна в, значит наше предположение не верно α| |β. чтд.

Теорема 8. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Если А∈а; А∈в; а∈β; в∈β; А₁∈а₁; А₁∈в₁; а₁∈α; в₁∈α; а| |а₁; в| |в₁, то α| |β.

 

Параллельное проектирование и его свойства. Изображение фигур в стереометрии.

Для изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием. Этот способ состоит в следующем. Берем произвольную прямую h, пересекающую плоскость чертежа а, проводим через произвольную точку А фигуры прямую, параллельную h. Точка А1 пересечение этой прямой с плоскостью чертежа будет изображением точки А.

Свойства:1. Прямолинейные отрезки фигуры изображаются на плоскости чертежа отрезками.

2. Параллельные отрезки изображаются на плоскости чертежа параллельными отрезками.

3. Отношение отрезков одной прямой или параллельных прямых сохраняется при параллельном проектировании.

Изображение фигур в стереометрии.1. Прямоугольные, равнобедренные и равносторонние треугольники изображаются в стереометрии произвольными треугольниками.

2. Квадрат, прямоугольник, ромб изображаются в стереометрии в виде параллелограмма.

3. Окружность или круг изображаются в стереометрии в виде эллипса.

 

Перпендикуляр и наклонная. Свойства перпендикуляра и наклонной проведенных из одной точки.

1. Перпендикуляром (АВ) опущенным из данной точки на плоскость, называют отрезок соединяющий данную точку с точкой плоскости и лежащей на прямой перпендикулярной этой плоскости. Точка В называется основанием перпендикуляра.

2. Расстоянием от точки до плоскости называют длину перпендикуляра опущенного из этой т очки на плоскость.

3. Наклонной проведенной из данной точки к плоскости называют любой отрезок не перпендикулярный плоскости, соединяющий данную точку с плоскостью (АС; АС1). Точки С и С1 называют основаниями наклонных.

4. Отрезок на плоскости соединяющий основание перпендикуляра (В) с основанием наклонной (АС, АС1) проведенных из одной точки называется проекцией наклонной на плоскость (ВС, ВС1).

Свойства наклонных и проекций.

1. Длина перпендикуляра к плоскости меньше длины любой наклонной к плоскости. (АВ<АС; АВ<АС1)

2. Большей наклонной соответствует большая проекция. Если АС1<АС, то ВС1>ВС.

3. Длины наклонных равны тогда и только тогда, когда равны длины их проекций.

 

Теорема о трех перпендикулярах.

Теорема 16. Прямая проведенная на плоскости через основание наклонной перпендикулярна ее проекции перпендикулярна и самой наклонной.

Обратная теорема. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции этой наклонной.

Дано: АВ┴α; АС-наклонная. С∈с. Доказать: 1. с┴АС; 2.с┴ВС. Доказательство:1.А^,С┴α; А^,С| |АВ (по Т15). 2. β:АВ∈β; А^,С∈β (по определению параллельных прямых). 3. Пусть СВ ┴с, А^,С┴с (по определению перпендикуляра к плоскости), значит по Т13 имеем, что прямая С┴β, значит по определению с┴АС. 4. Пусть АС┴с, А^,С┴с (по определ. перпендикуляра к плоскости), значит по Т13 имеем, что прямая с┴β, значит по определению с┴СВ. чтд.

 

Признак перпендикулярности двух плоскостей.

Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство: Пусть — плоскость , b — перпендикулярная ей прямая, — плоскость проходящая через прямую b, и с — прямая по которой пересекаются плоскости и . Докажем, что плоскости и перпендикулярны.

Проведем в плоскости через точку пересечения прямой b с плоскостью прямую а, перпендикулярную прямой с. Проведем через прямые а и b плоскость . Она перпендикулярна прямой с, так как прямые а и b перпендикулярны, то плоскости и перпендикулярны. Теорема доказана.

 

Трехгранный угол. Теорема о свойстве плоских углов многогранного угла.

Трехгранный угол – это фигура состоящая из 3 плоских углов. Точка S-вершина угла, a, b, c-ребра. Углы между прямыми ab; bc; ac-это плоские углы трехгранного угла.

Теорема 20. Величина каждого плоского угла, трехгранного угла меньше суммы величин двух других его плоских углов.

Теорема 20. Сумма величин всех трех плоских углов трехгранного угла меньше 360⁰.

Теорема о сумме плоских углов многогранника.

Теорема 20. Сумма величин всех трех плоских углов трехгранного угла меньше 360⁰.

 

Призма. Ее элементы.

Призма – это многогранник, образованный двумя параллельными плоскостями соединенными параллельными отрезками.

Элементы призмы.

Высота призмы – расстояние между плоскостями оснований. Диагональ призмы (CF₁; BE₁; BF₁) – отрезок соединяющий две вершины, не принадлежащие одной грани. Диагональное сечение (FCC₁F₁) – сечение призмы плоскостью, проходящей через два боковых ребра не принадлежащие одной грани.

1. Основания (ABCDEF, А₁В₁С₁В₁Е₁А₁)

2. Ребра оснований (АВ, ВС, СD, DE, EF, A₁D₁, D₁C₁, C₁D₁, D₁E₁, E₁F₁)

3. Боковые ребра (AA₁, FF₁, EE₁, DD₁, CC₁, BB₁)

4. Боковые грани (параллелограммы) (ABB₁A₁, BCC₁B₁, CDD₁C₁, DEE₁D₁, EFF₁E₁, AFF₁A₁)

Виды призм.

1. n-угольная призма (треугольная, четырехугольная).

2. Пряма призма-это призма у которой боковые ребра перпендикулярны основаниям, иначе призма наклонная.

3. Прямая призма называется правильной, если в ее основании лежит правильный многоугольник.

Sполн=Sбок + Sосн.

Боковой поверхностью призмы называют сумму площадей боковых граней. Полная поверхность призмы равна сумме боковой поверхности и двух площадей оснований.

Теорема 23. Боковая поверхность правильной (прямой) призмы равна произведению периметра основания на высоту, т.е. длину бокового ребра.

 

Виды пирамиды.

1. n-угольная пирамида (треугольная, четырехугольная)

2. Правильная пирамида-это пирамида в основании которой лежит правильный многоугольник и ее вершина проектируется в центр данного многоугольника.

Апофема-высота боковой грани правильной пирамиды. (SK)

Теорема27. Плоскость параллельная основанию пирамиды и пересекающая ее отсекает подобную пирамиду.

Sполн=Sбок+Sосн.

Теорема 28. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.

 

Правильные многогранники.

Многогранником называется тело ограниченное конечным числом плоскостей. Многогранник называется выпуклым, если он лежит по одну сторону каждой из ограниченных его плоскостей.

Элементы многогранника.

1. Вершины (точки)

2. Ребра (отрезки)

3. Грани (плоскости)

Многогранник называется правильным если его грани являются правильными многоугольниками и в каждой вершине сходится одинаковое число ребер.

Существует 5 видов многогранников:

1. Тетраэдр — грани правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.

2. Куб – все грани квадраты; в каждой вершине сходятся по три ребра. Куб представляет собой треугольный параллелепипед с равными ребрами.

3. У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра.

4. У додекаэдра грани — правильные пятиугольники.

5. У икосаэдра грани – правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер.

Теорема 22. Теорема Эйлера. Для любого выпуклого многогранника с числом вершин β, числом граней Г и числом ребер Р выполняется следующие равенство: В+Г-Р=2.

Для тетраэдра В=4, Г=4, Р=6. Имеем: 4+4-6=2. Для куба В=8, Г=6, Р=12. Имеем 8+6-12=2. Для октаэдра В=6, Г=8, Р=12. Имеем:6+8-12=2. Для додекаэдра В=20, Г=12, Р=30. Имеем: 20+12-30=2. Для икосаэдра В=12, Г=20, Р=30. Имеем: 12+20-30=2.

 

Объем шара и его частей.

V= ПR³

Аксиомы стереометрии.

Стереометрия-раздел геометрии, в котором изучаются фигуры в пространстве.

Основные фигуры стереометрии:

1. Точка А

2. Прямая

3. Плоскость

Свойство 1. Какова бы не была плоскость, существуют точки, принадлежащие этой плоскости и принадлежащие ей. ∃α: А∈ α; В∈α; D∉α. ∃-существует.

Свойство 2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. Если А∈ α; А∈β, то ∃α: а ∈ α; α ∈ β, А∈а

Свойство 3. Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну. Если А∈а; А∈в, то ∃!α: а∈α; в∈α; А∈α

Свойство 4. Если две различны точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости. Если А∈α; В∈α, то АВ∈α

 

Следствия аксиом стереометрии. Теоремы 1,2.

Теорема 1. Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну. Дано: а; С∉а. Доказать: ∃!α: а∈α; С∈α. Доказательство: 1. В∈а (по аксиоме о том, что существует точки принадлежащие прямой и не принадлежащие ей). 2. ВС (по аксиоме о том, что через две точки можно провести одну прямую). 3. Т.к. В∈ВС, В∈а, то по Свойству 3 ∃α:ВС∈α, а∈α. 4. Пусть ∃α₁: а∈α₁; С∈α₁, тогда С∈α; С∈α₁, по свойству 2 имеем, что С ∈а, но по условию С∉а, значит наше предположение не верно и α₁ совпадают с Сα, т.е. α-единственная. чтд.

Теорема 2. Через 3 любые точки, не лежащие на 1 прямой можно провести плоскость и притом только 1. Дано: точка А, точка В, точка С. Доказать: ∃!α: А∈α; В∈α; С∈α. Доказательство:1. АВ, АС (по аксиоме о том, что через 2 точки можно провести 1 прямую). 2. Т.к. А∈АВ, А∈АС, то по Свойству 3 ∃α:АВ∈α, ВС∈α. 4. Пусть ∃α₂: а∈α₁; А∈α₁, тогда В∈α₁; С∈α₁, тогда по свойству 2 А, В, С лежат на одной прямой, но это противоречит условию, значит α-единственная. чтд.

 

lektsia.info

Основные понятия и аксиомы стереометрии

ПЕРВУШКИН БОРИС НИКОЛАЕВИЧ

ЧОУ «Санкт-Петербургская Школа «Тет-а-Тет»

Учитель Математики Высшей категории

 

Основные понятия и аксиомы стереометрии

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
 Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.

Простейшие фигуры в пространстве: точка, прямая, плоскость.
 Плоскость. 

 Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.

На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит

 через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко

 это записывают так: А ∈ β, B ∈ β,

Аксиомы стереометрии и их следствия

Аксиома 1. 

 Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома 2. 

 Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).

Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.

 

Аксиома 3. 

 Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. 

В таком случае говорят, плоскости пересекаются по прямой.

Пример: пересечение двух смежных стен, стены и потолка комнаты

.

НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ АКСИОМ

Теорема 1. 

 Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.

Теорема 2. 

 Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.

xn--j1ahfl.xn--p1ai

Стереометрия основные понятия и определения

/ Основные понятия и аксиомы стереометрии

«Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей»

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.

Простейшие фигуры в пространстве: точка, прямая, плоскость.

Аксиомы стереометрии и их следствия

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты.

Некоторые следствия из аксиом

Теорема 1. Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.
Теорема 2. Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.

Параллельные прямые в пространстве

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Лемма о пересечении плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

zna4enie.ru

Решения задач по Теоремам стереометрии стр 1

Задания реальных ЕГЭ прошлых лет Skip Navigation Links. Главная Ошибки пособий Ященко Математика ГДЗ по математике 7 — 8 классы 7 класс Статград 4 марта 2019 Тренировочная работа в формате ВПР по математике 7 класс ВПР по математике 2019 7 класс КДР по АЛГЕБРЕ Краснодарский край Январь 2019 8 класс КДР по АЛГЕБРЕ Краснодарский край Январь 2019 10 класс 10 класс КДР по математике апрель 2019 Демонстрационный вариант Статград 06-02-2019 Тренировочная работа №1 по математике 10 класс Статград 18-12-2018 Диагностическая работа по Математике по теме Тригонометрия Статград 04-12-2018 Диагностическая работа по Алгебре и началам анализа (базовый уровень) Колмогоров Статград 04-12-2018 по учебнику Никольского Диагностическая работа по Алгебре и началам анализа (базовый уровень) Статград 04-12-2018 по учебникам Алимова и Колягина Диагностическая работа по Алгебре и началам анализа (базовый уровень) Подготовка к ОГЭ 9 класс ГИА

egeprof.ru