Тангенс трапеции угла: Как найти тангенс острого угла в трапеции

Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла

1. Формулы длины диагоналей прямоугольной трапеции по теореме Пифагора

a — нижнее основание

b — верхнее основание

c=h — боковая сторона, равная высоте трапеции

d₁ , d₂— диагонали трапеции

Формулы диагоналей трапеции:

Остальные формулы диагоналей как для произвольной трапеции

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

1. Формулы длины диагонали равнобедренной трапеции через ее стороны

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

d — диагональ трапеции

Формула диагонали трапеции (d ):

2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α, β — углы трапеции

d — диагональ трапеции

Формулы диагонали трапеции (d ):

Формула длины диагонали равнобедренной трапеции

a — нижнее основание

b — верхнее основание

α, β — углы между диагоналями

h — высота трапеции

m — средняя линия трапеции

S — площадь трапеции

d — диагональ трапеции

Формулы диагонали трапеции (d ):

Справедливо для данного случая :

Формулы длины диагонали трапеции через высоту и стороны

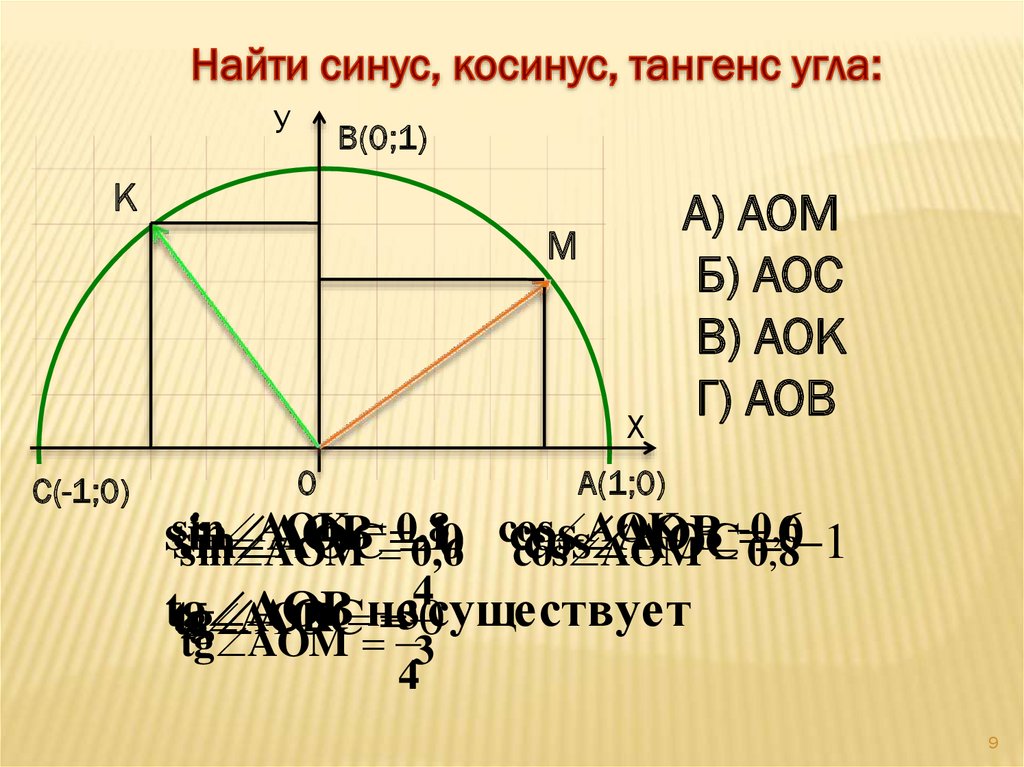
a — нижнее основание

b — верхнее основание

c — равные боковые стороны

h — высота трапеции

α — угол при нижнем основании

d — диагональ трапеции

Формулы диагонали трапеции (d ):

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

Найти длину диагонали трапеции

зная все четыре стороны

или две стороны и угол

или высоту, сторону и угол

или площадь, другую диагональ и угол

и еще много других формул.

1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

d₁ , d₂— диагонали трапеции

Формулы диагоналей трапеции по теореме косинусов:

Формулы диагоналей трапеции через четыре стороны:

2. Формула длины диагоналей трапеции через высоту

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

h — высота трапеции

d₁ , d₂

— диагонали трапеции

Формулы диагоналей трапеции через высоту:

3. Формула длины диагонали трапеции через другую диагональ

a — нижнее основание

b — верхнее основание

α, β — углы между диагоналями

h — высота трапеции

m — средняя линия трапеции

S — площадь трапеции

d₁ , d₂— диагонали трапеции

Формулы диагоналей трапеции :

Справедливо для данного случая :

4. Формулы длины диагонали трапеции через сумму квадратов диагоналей

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

d₁ , d₂— диагонали трапеции

Формула суммы квадратов диагоналей :

Формулы диагоналей трапеции :

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

1. Формула средней линии трапеции через основания (для всех видов трапеции)

a — нижнее основание

b — верхнее основание

m — средняя линия

Формула средней линии, (m ):

Формулы средней линии через основания, высоту и угол при нижнем основании

a, b — основания трапеции

c — боковая сторона под прямым углом к основаниям

d — боковая сторона

α — угол при основании

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции, (m ):

3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

d₁ , d₂— диагонали трапеции

α , β — углы между диагоналями

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции, (m ):

4. Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)

S — площадь трапеции

— высота трапеции

m — средняя линия

Формула средней линии трапеции, (m ):

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании

a — нижнее основание

b — верхнее основание

d — боковая сторона

α — угол при нижнем основании

h — высота трапеции

c — боковая сторона под прямым углом к основаниям

Формулы длины боковой стороны (с) :

2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними

a — нижнее основание

b — верхнее основание

d₁ , d₂— диагонали трапеции

α , β — углы между диагоналями

c — боковая сторона под прямым углом к основаниям

Формулы длины боковой стороны (с):

3. Формулы боковой стороны (с) прямоугольной трапеции через площадь

a — нижнее основание

b — верхнее основание

m — средняя линия трапеции

c — боковая сторона под прямым углом к основаниям

Формула длины боковой стороны (с) :

4. Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании

a — нижнее основание

b — верхнее основание

c — боковая сторона под прямым углом к основаниям

α — угол при нижнем основании

h — высота трапеции

d — боковая сторона

Формулы длины боковой стороны (d) :

5. Формула боковой стороны (d) прямоугольной трапеции через площадь

a — нижнее основание

b — верхнее основание

m — средняя линия трапеции

α — угол при нижнем основании

d — боковая сторона

Формула длины боковой стороны (d) :

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

1.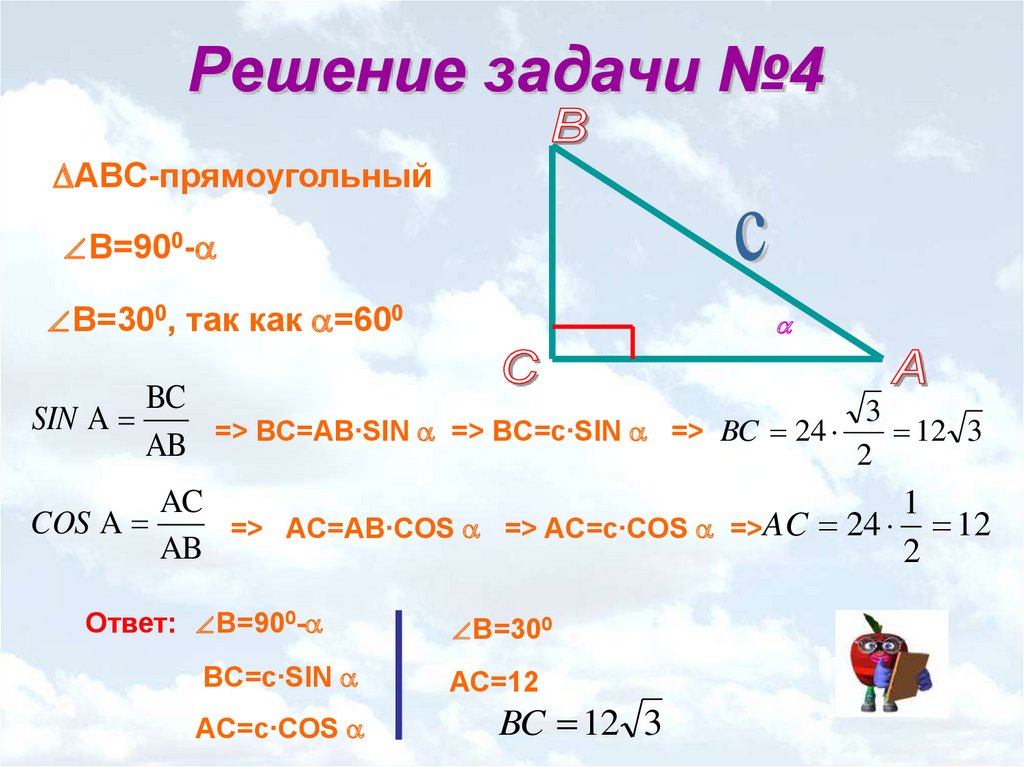 Формула длины оснований прямоугольной трапеции через среднюю линию

a — нижнее основание

b — верхнее основание

m — средняя линия

Формулы длины оснований :

2. Формулы длины оснований через боковые стороны и угол при нижнем основании

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α — угол при нижнем основании

Формулы длины оснований :

3. Формулы длины оснований трапеции через диагонали и угол между ними

a — нижнее основание

b — верхнее основание

c — боковая сторона под прямым углом к основаниям

d₁ , d₂— диагонали трапеции

α , β — углы между диагоналями

Формулы длины оснований :

4. Формулы длины оснований трапеции через площадь

a — нижнее основание

b — верхнее основание

c — боковая сторона под прямым углом к основаниям

h — высота трапеции

Формулы длины оснований :

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

1. Формула средней линии равнобедренной трапеции через основания

a — нижнее основание

b — верхнее основание

m — средняя линия

Формула средней линии, (m ):

2. Формулы средней линии через основание, высоту и углы при нижнем основании

a — нижнее основание

b — верхнее основание

c — боковая сторона

α — угол при нижнем осровании

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции, (m ):

3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

d — диагонали трапеции

α , β — углы между диагоналями

h — высота трапеции

m — средняя линия

Формула средней линии трапеции, (m ):

4. Формула средней линии трапеции через площадь и высоту

S — площадь трапеции

h — высота трапеции

α — угол при нижнем осровании

m — средняя линия

Формула средней линии трапеции, (m ):

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

1. Формула высоты равнобедренной трапеции через стороны и углы при основании

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α — угол при нижнем основании

h — высота трапеции

Формулы длины высоты, (h ):

2. Формула высоты равнобедренной трапеции через диагонали и углы между ними

_d— диагонали трапеции

α , β — углы между диагоналями

a , b — основания

h — высота трапеции

m — средняя линия

Формулы длины высоты, (h ):

3.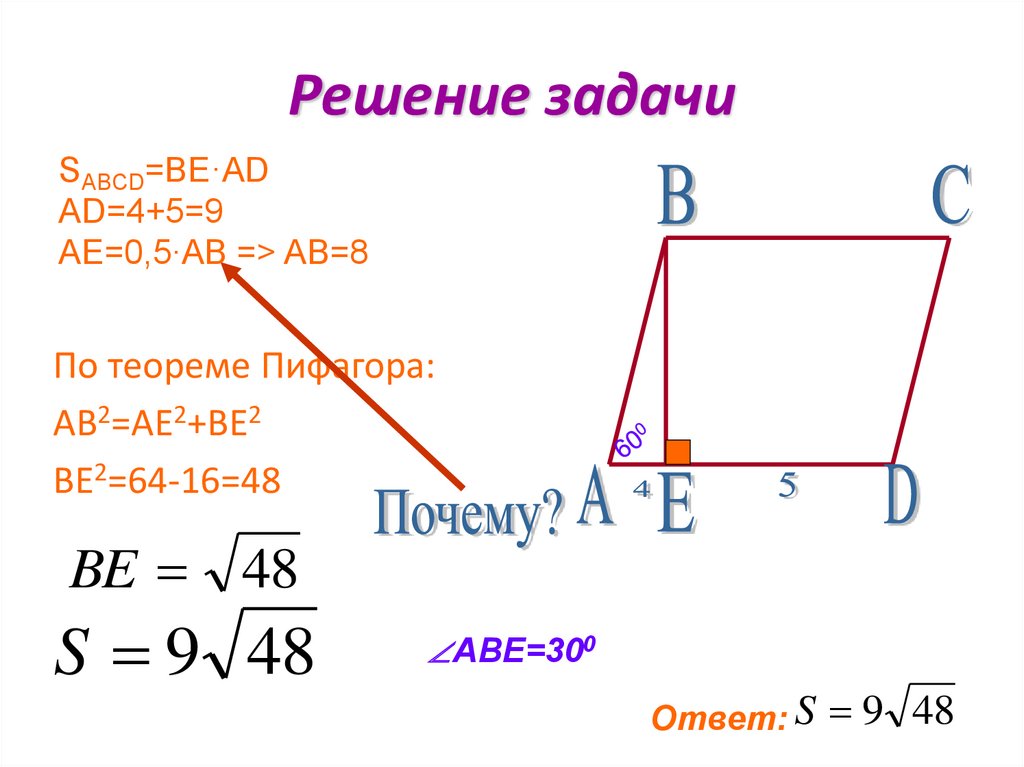 Формула высоты равнобедренной трапеции через площадь

S — площадь трапеции

a , b — основания

h — высота трапеции

m — средняя линия

Формулы длины высоты, (h ):

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

1. Формула длины основания равнобедренной трапеции через среднюю линию

a — нижнее основание

b — верхнее основание

m — средняя линия

Формулы длины основания:

2. Формулы длины сторон через высоту и угол при нижнем основании

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α — угол при основании трапеции

h — высота трапеции

Формулы всех четырех сторон трапеции:

3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

d — диагонали

α , β — углы между диагоналями

h — высота трапеции

Формулы длины сторон трапеции:

справедливо для данной ситуации:

4. Формулы длины сторон равнобедренной трапеции через площадь

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α , β — углы при основаниях

m — средняя линия

h — средняя линия

Формулы длины сторон равнобедренной трапеции через площадь:

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.

1. Формула высоты трапеции через стороны и углы при основании

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

h — высота трапеции

Формулы длины высоты, (h ):

2. Формула высоты трапеции через диагонали и углы между ними

d₁ , d₂— диагонали трапеции

α , β — углы между диагоналями

a , b — основания

h — высота трапеции

m — средняя линия

Формулы длины высоты, (h ):

3. Формула высоты трапеции через площадь

S — площадь трапеции

a , b — основания

h — высота трапеции

m — средняя линия

Формулы длины высоты, (h ):

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

Рейтинг: 5 / 5

Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции — отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.

1.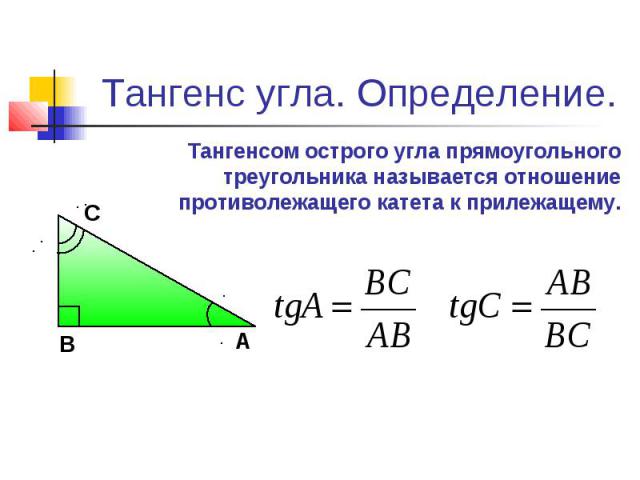 Формула средней линии трапеции через основания

b — верхнее основание

a — нижнее основание

m— средняя линия

Формула средней линии, (m ):

2. Формулы средней линии через основание, высоту и углы при нижнем основании

b — верхнее основание

a — нижнее основание

α, β — углы трапеции

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции, (m):

3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

α, β — углы между диагоналями

d₁ , d₂— диагонали трапеции

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции, (m ):

4. Формула средней линии трапеции через площадь и высоту

S — площадь трапеции

h — высота трапеции

m — средняя линия

Формула средней линии трапеции, (m):

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

1. Формула длины основания трапеции через среднюю линию

a — нижнее основание

b — верхнее основание

m — средняя линия

Формулы длины оснований :

2. Формулы длины сторон через высоту и углы при нижнем основании

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

h — высота трапеции

Формулы всех четырех сторон трапеции:

3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями

a — нижнее основание

b — верхнее основание

d₁ , d₂— диагонали трапеции

α , β — углы между диагоналями

h — высота трапеции

Формулы длины сторон трапеции:

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Запомнить

Восстановить пароль

Регистрация

Конспект

Гипотенуза прямоугольного треугольника – это сторона, лежащая напротив прямого угла.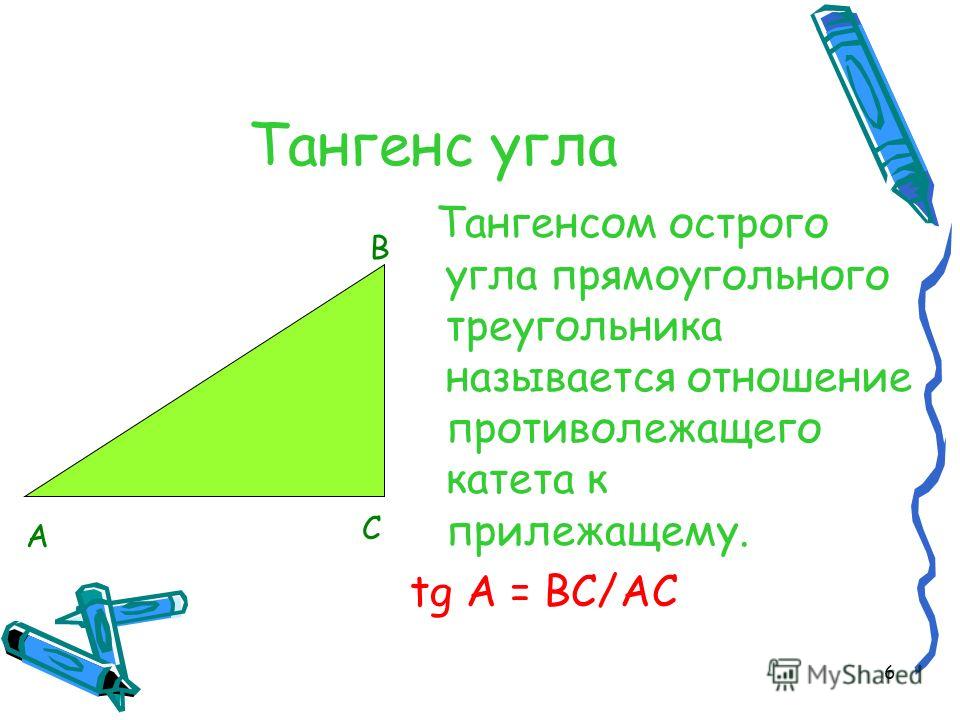

Катеты – стороны, лежащие напротив острых углов. Катет \(a\), лежащий напротив угла \(\alpha\), называется противолежащим (по отношению к углу \(\alpha\)). Другой катет \(b\), который лежит на одной из сторон угла \(\alpha\), называется прилежащим.

Синус острого угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе: \(sin∠A=\frac{a}{c} \).

Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе: \(cos∠A=\frac{b}{c} \).

В прямоугольном треугольнике синус одного острого угла равен косинусу другого, и наоборот:

\(sin∠A=cos∠B;\ \sin \angle A=\cos \angle B; \ sin∠A=cos∠B\; \\ sin∠B=cos∠A; \ \sin \angle B=\cos \angle A; \ sin∠B=cos∠A.\)

Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: \(tg ∠A=\frac{a}{b} \).

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу: \(tg\angle A=\frac{sin\angle A}{cos\angle A}\). {\circ}\) \(\sin \varphi\) \(0\) \(\begin{aligned} \frac{1}{2} \end{aligned}\) \(\begin{aligned} \frac{\sqrt 2}{2} \end{aligned}\) \(\begin{aligned} \frac{\sqrt 3}{2} \end{aligned}\)

\(1\)

\(\cos \varphi\)
\(1\) \(\begin{aligned} \frac{\sqrt 3}{2} \end{aligned}\) \(\begin{aligned} \frac{\sqrt 2}{2} \end{aligned}\) \(\begin{aligned} \frac{1}{2} \end{aligned}\)
\(0\)
\(\rm tg\ \varphi\) \(0\) \(\begin{aligned} \frac{1}{\sqrt 3} \end{aligned}\) \(1\) \(\begin{aligned} \sqrt 3 \end{aligned}\)
\(\color{red}-\)
\(\rm ctg\ \varphi\) \(\color{red}-\) \(\begin{aligned} \sqrt 3 \end{aligned}\) \(1\) \(\begin{aligned} \frac{1}{\sqrt 3} \end{aligned}\)
\(0\)

Вопросы
В прямоугольном треугольнике один из катетов равен 3, а котангенс прилежащего угла равен 0,75. \circ\). Найдите боковые стороны.

Сообщить об ошибке
Обязательные
Математическая грамотность
Грамотность чтения
История Казахстана
Предметы по профилю
Биология
Химия
Английский язык
Французский язык
География
Немецкий язык
Информатика
Основы права
Русская литература
Математика
Физика
Русский язык
Всемирная история
Укажите предмет *
Скопируйте и вставьте вопрос задания *
Опишите подробнее найденную ошибку в задании *
Прикрепите скриншот
Объем файла не должен превышать 1МБ
Казахский
Русский
Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market
2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами
Видео с вопросами: Использование тригонометрии для решения задач, связанных с равнобедренными трапециями
Стенограмма видео
Найдите 17 тангенса 𝐵 cos 𝐶 на квадрат греха 𝐶 плюс квадрат cos 𝐵, учитывая, что 𝐴𝐵𝐶𝐷 — равнобедренная трапеция, отрезок которой 𝐴𝐷 параллелен прямой отрезок 𝐵𝐶, 𝐴𝐷 равен восьми сантиметрам, 𝐴𝐵 равен 17 сантиметрам и 𝐵𝐶 равняется 24 сантиметрам.
А потом нам дали схему равнобедренной трапеции. Итак, давайте сначала напомним себе, что мы имеем в виду, когда говорим о равнобедренном суставе.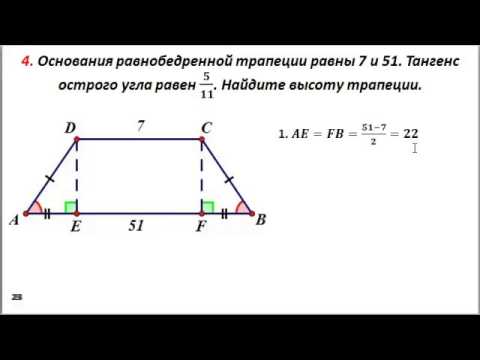 трапеция. Итак, в равнобедренной трапеции две непараллельные стороны равны по длине. Это также означает, что углы, которые эти непараллельные стороны образуют с двумя параллельные стороны равны.
Теперь в этом вопросе мы пытаемся найти выражение для различных тригонометрических функции углов 𝐵 и 𝐶. Итак, давайте определим углы 𝐵 и 𝐶 так, чтобы оба были равны 𝜃. Мы знаем тригонометрические соотношения для прямоугольного треугольника с включенным углом 𝜃 скажите нам что грех 𝜃 равен противоположному по гипотенузе. cos 𝜃 равен соседнему деленному на гипотенузу. А тангенс 𝜃 равен противоположному деленному на соседнее. Итак, где мы собираемся найти прямоугольный треугольник на нашей диаграмме? Что ж, мы можем добавить перпендикуляр прямо вверх из точки 𝐴. Мы знаем, что угол этого треугольника равен 𝜃, а гипотенуза равна 17. сантиметры. Итак, найдем длину стороны, примыкающей к углу 𝜃, и назовем что 𝑥 сантиметров.
Так как трапеция равнобедренная, мы знаем, если мы добавим второй перпендикуляр непосредственно вверх от точки 𝐷 мы получаем еще один треугольник со смежной стороной 𝑥 сантиметры. Затем у нас также есть прямоугольник, поэтому оставшаяся часть отрезка 𝐵𝐶 должна быть восемь сантиметров в длину. Следовательно, мы можем сказать, что, поскольку отрезок 𝐵𝐶 состоит из трех частей, 𝑥, восемь и 𝑥, что в сумме дает 24 сантиметра, два 𝑥 плюс восемь должны быть равны 24. Теперь у нас есть уравнение, которое мы можем решить для 𝑥. Начнем с вычитания восьми с обеих сторон, так что два 𝑥 равно 16. Затем, разделив на два, мы найдем 𝑥 равно восьми.
Итак, теперь у нас есть прямоугольный треугольник, для которого мы знаем два измерения. Мы собираемся разработать третье измерение, так как в какой-то момент мы собираемся вычислить грех 𝜃, cos 𝜃 и тангенс 𝜃. Вот интересующий нас треугольник. Мы можем использовать теорему Пифагора, чтобы вычислить недостающую длину в этом треугольнике, сторону, противоположную прилежащему углу. В качестве альтернативы мы могли бы заметить, что у нас есть тройка Пифагора, но давайте воспользуемся Теорема Пифагора проверить.
Назовем длину стороны, которую мы пытаемся найти, 𝑦 сантиметров. Тогда по теореме Пифагора сумма квадратов двух меньших сторон должен быть равен квадрату гипотенузы. Итак, восемь в квадрате плюс 𝑦 в квадрате равно 17 в квадрате. 64, то плюс 𝑦 в квадрате равно 289. Вычитая 64 из обеих частей, мы находим, что 𝑦 в квадрате равно 225. Затем, извлекая положительный квадратный корень из 225, мы находим, что 𝑦 равно 15. Итак, теперь мы имеем третья сторона треугольника. И есть пифагорейская тройка, которую мы могли бы распознать. Восемь в квадрате плюс 15 в квадрате равно 17 в квадрате.
Теперь у нас есть все необходимое для вычисления значения тангенса 𝐵, cos 𝐶, sin of 𝐶 и потому что 𝐵. Тангенс 𝐵, конечно же, тангенс 𝜃, и мы знаем, что тангенс 𝜃 противоположен соседнему. В нашем треугольнике противолежащая сторона равна 15 сантиметрам, а прилежащая — восьми. Таким образом, загар 𝜃 равен 15 на восемь. Далее нам нужно найти значение cos 𝐶 и cos 𝐵. Но поскольку и 𝐶, и 𝐵 являются 𝜃, нам просто нужно найти значение cos для 𝜃. Теперь, конечно, это смежное деление на гипотенузу. Итак, восемь больше 17, потому что 𝜃 равно восьми семнадцатым. Наконец, нам нужно знать значение греха 𝐶. Итак, это грех 𝜃, где грех 𝜃 противоположен гипотенузе. Таким образом, грех 𝜃 равен 15 на 17.
Теперь найдем значение 17 тангенса 𝐵 cos 𝐶 на квадрат квадрата 𝐶 плюс cos квадрат 𝐵. Числитель в 17 раз больше тангенса 𝐵, на 15 больше восьми, умножается на 𝐶, на восемь больше 17. Тогда знаменатель, квадрат греха 𝐶 плюс квадрат косинуса 𝐵, равен восьми. семнадцатые в квадрате плюс 15 на 17 в квадрате.
Теперь, прежде чем мы попытаемся оценить это в уме, мы могли бы заметить, что мы можем несколько упростить. Во-первых, наш числитель можно упростить, разделив на 17. Точно так же мы можем разделить на восемь, и тогда в числителе останется просто 15. нашего выражения. Далее, помните, что восемь в квадрате плюс 15 в квадрате равно 17 в квадрате. Это наша пифагорейская тройка. Таким образом, знаменатель этого выражения на самом деле будет равен единице. Это означает, что мы получаем 15 на единицу, что, конечно же, просто равно 15.
Таким образом, значение 17 тангенса 𝐵 косинуса 𝐶 больше квадрата греха 𝐶 плюс квадрата косинуса 𝐵 15.
Vintage Ironstone ‘sunbury’ Brown and Tan Trapezoid
Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.
Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.
Нажмите, чтобы увеличить
Редкая находка
Цена: €16,95
Загрузка
Доступен только 1
НДС включен (где применимо), плюс стоимость доставки
Звездный продавец
Star Sellers имеют выдающийся послужной список в обеспечении отличного обслуживания клиентов — они постоянно получали 5-звездочные отзывы, вовремя отправляли заказы и быстро отвечали на любые полученные сообщения.
| 8,291 продажа |
5 из 5 звезд
Вы можете сделать предложение только при покупке одного товара
Продавец звезд. Этот продавец неизменно получал 5-звездочные отзывы, вовремя отправлял товары и быстро отвечал на все полученные сообщения.
Исследуйте другие похожие поисковые запросы
Внесен в список 3 марта 2023 г.
13 избранных
Сообщить об этом элементе в Etsy
Выберите причину… С моим заказом возникла проблемаОн использует мою интеллектуальную собственность без разрешенияЯ не думаю, что это соответствует политике EtsyВыберите причину…
Первое, что вы должны сделать, это связаться с продавцом напрямую.
Если вы уже это сделали, ваш товар не прибыл или не соответствует описанию, вы можете сообщить об этом Etsy, открыв кейс.
Сообщить о проблеме с заказом
Мы очень серьезно относимся к вопросам интеллектуальной собственности, но многие из этих проблем могут быть решены непосредственно заинтересованными сторонами. Мы рекомендуем связаться с продавцом напрямую, чтобы уважительно поделиться своими проблемами.
Если вы хотите подать заявление о нарушении прав, вам необходимо выполнить процедуру, описанную в нашей Политике в отношении авторских прав и интеллектуальной собственности.
Посмотрите, как мы определяем ручную работу, винтаж и расходные материалы
Посмотреть список запрещенных предметов и материалов
Ознакомьтесь с нашей политикой в отношении контента для взрослых
Товар на продажу…
не ручной работы
не винтаж (20+ лет)
не ремесленные принадлежности
запрещены или используют запрещенные материалы
неправильно помечен как содержимое для взрослых
Пожалуйста, выберите причину
Расскажите нам больше о том, как этот элемент нарушает наши правила. Расскажите нам больше о том, как этот элемент нарушает наши правила.
1 товар добавлен в корзину
Посмотреть корзину и проверить
Сопутствующие товары, которые могут вам понравиться
Плакат карты Рамаллы Карта Рамаллы, плакат Рамаллы, плакат карты Рамаллы, искусство Рамаллы, карта Рамаллы, печать Рамаллы, плакат Рамаллы
реклама от NolDesignStudio
Реклама магазина NolDesignStudio
НолДизайнСтудио Из магазина НолДизайнСтудио
€56,24
Начните с «Бисмиллах», закончите деревянным знаком «Альхамдулиллах».