Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13
Найти точное значение		cos(30 град. )
14Найти точное значениеtan(60)
15Найти точное значениеcsc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град.
)
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значение
csc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значение
sin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град.
)
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град.
)
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Тригонометрические и геометрические преобразования, sin(A + B), sin(A

Коэффициенты для суммы углов

Как демонстрируют различные примеры, иногда нам нужны значения углов, отличных от 0, 30, 45, 60 и 90 градусов. В этой главе вы должны научиться двум вещам:
1. sin(A + B) не является равным sinA + sinB. В этом случае не срабатывает простое раскрытие скобок, как в алгебре.
2. Формулу, по которой вычисляется sin(A + B).

Во-первых, покажем, что раскрытие скобок не «срабатывает». Пусть A = 30 градусов и B = 45 градусов. Sin30 равен 0.5. Sin45 равен 0.7071. Складывая, получим 1.2071.

Вы знаете, что ни синус, ни косинус не может быть больше 1. Почему? Потому что в дробях, по которым они вычисляются, гипотенуза выступает в качестве знаменателя. Самое большее значение мы получим, если числитель равен знаменателю. Синус или косинус не может быть больше 1, и поэтому значение 1,2071 не верно.

Нахождение синуса, косинуса или тангенса полного угла (A + B)

Нахождение sin(A + B)

Самый простой способ найти sin (A + B) — используя геометрическое построение, показанное на рисунке. Большой угол (A + B), состоит из двух маленьких, А и В. Рисунок (1) показывает, что противоположная сторона состоит из двух частей.

Нижняя часть, разделенная линией между углами (2), есть синус А. Линия между двумя углами, разделенная гипотенузой (3), есть косинус B. Умножаем их. Средняя линия и в числителе, и в знаменателе, поэтому они сокращаются, оставляя нижнюю часть противоположной стороны над гипотенузой (4).

Обратите внимание на маленький прямоугольный треугольник (5). Затененный угол есть A, потому что линия на его верхней части параллельна линии в основании. Подобные прямоугольные треугольники с углом А показывают, что верхний угол, отмеченный А также равен оригинальному углу А. Верхняя часть противоположной (6) над длинной, заштрихованный треугольник является соs А. Противоположный над основной гипотенузой (7) есть синус. Поскольку стороны с пометкой «противоположные» (7) и в числителе и знаменателе, когда cos и sin перемножаются, cosAsinB есть верхняя часть оригинального противоположного — для (A + B) — разделенные основной гипотенузой (8).

Теперь, сложим это все вместе (9). Sin(A + B) есть две части противоположного — все разделенные гипотенузой (9). Записывая это в тригонометрическую форму: sin(A + B) = sin A cos B + cos A sin B.

Нахождение cos(A + B)

Очень похожая конструкция находит формулу для косинуса угла созданного двумя углами, сложенными вместе.

Используя ту же самую конструкцию (1), обратите внимание, что смежная сторона является полной линией основания (для соs A), c частью, которая вычитается справа. Каждая часть должна использовать тот же знаменатель, гипотенузу (A + B) треугольника.

Полная линия основания, разделенная линией между углами A и E есть cosA (2). Эта разделяющая линия, деленная гипотенузой (A + B) треугольника, есть cos B (3). Поэтому, полная линия основания, деленная гипотенузой есть произведение cosAcosB (4).

Теперь, небольшая часть, которая должна быть вычтена. Заштрихованная часть (5) представляет sinA, который умножается заштрихованной частью (6) есть sin E, который есть другой частью и , которая нам нужна (7). Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
            cos(A + B) = cos A cos B — sin A sin B

Нахождение tan(A + B)

Полный геометрический вывод формулы для tg (A + B) является сложным. Проще всего вывести его из двух формул, которые мы уже сделали. В любом угле, тангенс равен синус, деленному на косинус. Используя тот факт, tan (A + B) = sin(A + B)/соs(A + B). Это выражение можно расширить к виду:
      tan(A + B) = [sin A cos B + cos A sin B]/[cos A cos B — sin A sin B]
Разделив верхнюю и нижнюю часть на cos A cos B, что превращает все члены в тангенсы, получаем:
            tan(A + B) = [tan A + tan B]/[1 — tan A tan B]

Коэффициенты для 75 градусов

Покажем коэффициенты синуса, косинуса и тангенса, подставляя в формулу суммы, и потом упрощая результат к своей простейшей форме, прежде чем находить суммы. После внесения основных замен в каждом конкретном случае, примерная работа в заштрихованной части, чтобы показать, как результат сводится к простейшей форме для оценки.


Если вы используете ваш карманный калькулятор для оценки, скорей всего, не имеет значения или вы упрщаете выражения сначала или просто пропускаете его! Все зависит от калькулятора: некоторые вычисля. т разницу, некоторые нет!

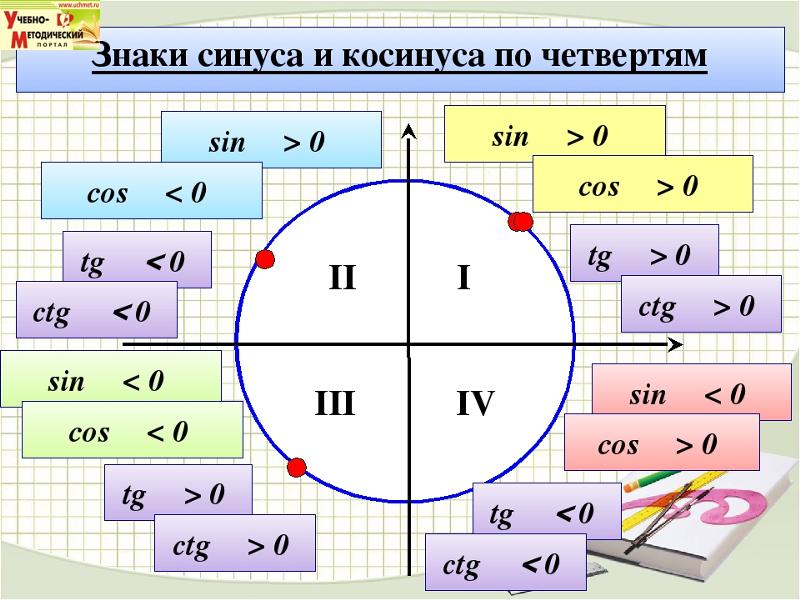
Коэффициенты углов, больших, чем 90 градусов

До сих пор рассматривалось соотношение острых углов (между 0 и 90 градусами). Другие треугольники с тупым углом (более 90 градусов) и до 180 градусов могут появиться в последующих задачах. Для упрощения классификации углов по размеру, они делятся на сектора (квадранты).

Квадрант есть четвертой частью круга. Так как круг делится на 360 градусов, квадранты имеют по 90 градусов. 0-90 градусов это первый квадрант, 90-180 — второй, 180-270 — третий и 270-360 — четвертый.

Используя линии, обозначающие границы квадранта, 0 или 360 это горизонталь направо, 90 — вертикально вверх, 180 — горизонталь слева и 270 сверху вниз. Теперь, используем этот метод для построения графиков.

Большие углы определяется вектором вращения, начиная с нуля и вращением против часовой стрелки. Горизонтальные элементы х: положительные справа, отрицательные слева. Вертикальные элементы у: положительные вверх, отрицательные вниз. Вращающийся вектор является р. Таким образом, синус угла есть y/r, косинус х/r, и тангенс у/х. Вектор r — всегда положителен. Таким образом, знак отношения может быть вычислен для различных секторов.

Здесь приведены знаки для трех отношений в четырех квадрантах. Кроме того, как эквивалентный угол в первой четверти «переключается» когда вектор переходит из одного квадранта в другой. В первой четверти, стороны определены в соотношениях для синуса, косинуса и тангенса. При перемещении к большим углам в остальных секторах, противоположная сторона всегда есть вертикальная (у). То, что называется смежное, всегда есть горизонталью (х). Гипотенуза это всегда вращающийся вектор (r). Вы можете видеть картину как изменяются тригонометрические соотношения для углов.

Отношения в четырех квадрантах

Отношения для различных углов

Теперь у вас есть два пути получить формулы для различных углов. Во-первых, используя геометрическую конструкцию, такую, которая, например, была использована для суммы углов, реверсивную так, что (A — B) есть угол B вычитающийся из угла A.

В рассуждениях, аналогичных тем, которые были использованы для суммы углов, здесь представлены несколько сокращенные формулы для синуса и косинуса:
        sin(A — B) = sin A cos B — cos A sin B
and
        cos(A — B) = cos A cos B + sin A sin B
      Геометрическая конструкция

Формулы суммы и разницы

Второй способ нахождения формулы для разницы углов использует уже полученную формулу суммы, но делает B отрицательным. Из нашего исследования знаков для различных секторов, отрицательные углы с 1-го квадранта будут в 4 квадранте. Проводя эту подстановку, получим тот же результат, который был получен геометрически в предыдущем разделе.

Поиск формулы тангенса проходит тем же методом, или заменой синуса и косинуса в формулах или более непосредственно, превращая tg(-B) = — tg B. В любом случае вы получите:
          tan(A — B) = [tan A — tan B]/[1 + tan A tan B]

Отношения с помощью четырех секторов

Вы можете вывести несколько отношений с формулами суммы и разности. Вы уже сделали соотношение для 75 градусов. Теперь можно выполнить то же для 15 градусов. Эти формулы дают соотношения для углов в 15 градусов интервалы через четыре квадранта. Построив их на 360 градусов, вы можете увидеть, как эти три соотношения изменяются, когда вектор проходит через четыре квадранта.

«Волна» синуса и косинуса колеблется вверх и вниз между +1 и -1. Обратите внимание, что «волны» смещены на 90 градусов друг относительно друга. Этот факт станет важным позже.

Кривая тангенса начинается, как синусоида, но вскоре она стремится достичь бесконечности на 90 градусах. Двигаясь » вне видимости» в положительном направлении, она «приходит» с отрицательного направления с другой стороны на 90 градусах. Проходя через точку в 180 градусов, функция тангенса повторяет то, что она «делала» проходя 0 или 360 градусов. На 270 градусах она повторяет то же, было на 90 градусах.

Пифагор в тригонометрии

Формула часто может быть упрощена, так как были найдены выводы формулы тангенса от формул синуса и косинуса, а также изменение ее членов одного отношения к другому отношению, использeущеuj другие члены. При этом, теорема Пифагора, выраженная в тригонометрическом соотношении, очень удобна.

Предположим, что прямоугольный треугольник имеет гипотенузу длиной 1. Тогда одна из сторон будет иметь длину sinA, а другая — cosA. Отсюда, согласно теореме Пифагора: cos2 A + sin2 A = 1. Это выражение всегда истинно для любого значения A.

Немного о том, как это было записано. Cos2 A означает (cos A)2. Если вы написали это как cos A2, уравнение будет означать что-то другое. A есть число в нескольких угловых значениях, которое представляет угол. A2 было бы то же самое число, возведенное в квадрат. Его значение зависело бы от использованного числового значения, поэтому это не очень хороший член для использования. Это означает квадрат синуса ли косинуса, не сам угол.

Формула Пифагора может быть выражена иначе. Например, две другие формы:
cos2 A = 1 — sin2 A, и sin2 = 1 — cos2 A.

Умножение углов

Формулы сумм, вместе с теоремой Пифагора, используются для углов, которые в 2, 3 или больше раз кратны любым оригинальным углам. Здесь приводятся формулы для 2А и 3А.

Формула суммы работает, когда оба угла одинаковые или различны: sin(A + B) или sin(A + A). Однако, sin(A + A) в действительности sin 2A. Поэтому, sin 2A есть sin A cos A + cos A sin A. Оба члена выражения есть одним и тем же произведением, записанным в разном порядке, так что это выражение может быть упрощено до sin 2A = 2 sin A cos A.

Подобным образом, cos 2A = cos A cos A — sin A sin A, что также может быть записано как: cos 2A = cos2 A — sin2 A. Используя теорему Пифагора, изменяем это к виду: cos 2A = 2cos2 A — 1. Наконец, tg 2A = 2 tg A/[1 — tg2 A].

Теперь тройной угол (3А) используется, чтобы показать, как получены следующие кратные углы. В основном, это так же просто, как запись 3A = 2 + A и повторного применения формулы суммы. Но тогда, чтобы получить в результате формулу в работающем виде, необходимо заменить часть 2А, на выражения с простым углом А.

На рисунках внизу вы можете видеть, что с каждым разом вычисления становятся сложнее.

УМНОЖЕНИЕ УГЛОВ       Производные от формул суммы

УМНОЖЕНИЕ УГЛОВ       Соотношения для 3A

Свойства равнобедренного треугольника

Вы уже видели, что прямоугольный треугольник является полезным строительным блоком для других фигур. Равнобедренный треугольник имеет несколько различных видов использования. Дело в том, что его использование основывается на том, что равнобедренный треугольник имеет две равные стороны и два равные углы между основанием и боковыми равными сторонами. Перпендикуляр из третьего угла на третью сторону делит ее пополам. Таким образом весь треугольник делится на два равных прямоугольных треугольника.

Любой треугольник, за исключением прямоугольного треугольника, можно разделить на три прилегающих равнобедренных треугольника, разделив каждую сторону на две равные части и построить перпендикуляры из точек разделения. Там, где любые два из этих перпендикуляров встречаются, если линии тянутся к углам исходного треугольника, три линии должны быть равны, потому что две из них образуют стороны равностороннего треугольника. Таким образом, перпендикуляр с третьей стороны исходного треугольника должен также встретиться в одной точке.

Это утверждение справедливо, как мы покажем здесь, независимо от того, является ли исходный треугольник острым или тупым. Разница с тупым прямоугольным треугольником в том, что место встречи перпендикуляров лежит снаружи исходного треугольника, а не внутри.

Что происходит в прямоугольном треугольнике? Перпендикуляры от средней точки гипотенузы другой стороны будут делить пополам эти две стороны — вы получаете два из трех! Место встречи находится гипотенузе.

Углы в окружности

Основное свойство окружности это то, что ее центр находится на одинаковом расстоянии от любой точки окружности. Это расстояние есть радиусом окружности.

Если вы нарисуете любой треугольник внутри круга, перпендикуляры из средней точки его сторон встретятся в центре окружности а радиусы из углов треугольника делят его на три равнобедренных треугольника

Теперь, если вы назовете равные пары углов в каждом равнобедренном треугольнике A, A, B, B, C, C, вы обнаружите, что исходный треугольник имеет один угол A+B, один угол B+C, и один угол A+ C. Три угла в сумме дают 2A + 2B + 2С, а это как известно равно 180 градусов.

В любом равнобедренном треугольнике угол при вершине равен 180 градусов минус удвоенный угол при основании. Поэтому, согласно предыдущего пункта, 180 — 2A должен быть такой же, как и 2B + 2С, например.

Рассмотрим угол правый нижний угол, опирающийся на окружность. Угол в центре равен 2B + 2С. Углом, опирающийся на окружность равен B + C. Вы видите, что для любого сегмента круга, угол в центре всегда в два раза больше угла, опирающегося на окружность.

Утверждение выше приводит к интересным фактам об углах в окружностях. Вместо определения углов со стороной треугольника, используют дугу (часть окружности) круга. Часть окружности, которая определяется углом в центре называется хордой окружности.

Угол в центре в два раза больше чем угол на окружности

Любой угол, касающийся окружности, используя хорду как ограничение угла, равен половине угла в центре. Таким образом, все углы в круге, с основанием на той же хорде, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Угол на окружности будет равен 60 градусам.

Особый случай представляет собой полукруг (точный полукруг). Угол в центре представляет собой прямую линию (180 градусов). Каждый угол в полукруге равен 90 градусам (прямой угол). Любой треугольник в полукруге является прямоугольным треугольником.

Определения

Выше мы часто использовали углы, которые дополняют углы до прямого угла (90 градусов) или до двух прямых углов (180 градусов). Когда два угла образовывают угол 180 градусов (два прямых угла), они называются дополнительными. Если два угла добавить до 90 градусов (один прямой угол), их называют комплементарными

Вопросы и задачи

1. Синус угла А равен 0,8 и синус угла B равен 0.6. Из различных зависимостей, полученных до сих пор, найдите следующее: тангенс А, тангенс B, синус (A + B), косинус (A + B), синус (A — B), косинус (A — B), тангенс (А + B) и тангенс (A — B) без использования таблиц или тригонометрических клавиш калькулятора.

2.На экваторе Земля имеет радиус 4000 км. Углы вокруг экватора измеряется в меридианах долготы, с линией с севера на юг проходящей через Гринвич (Англия), в качестве нулевого отсчета. Два места используются для наблюдения за луной: первое это Кения, на экваторе 37,5 к востоку от Гринвича, а другой является Суматра, на экваторе к востоку 100,5. Как далеко друг от друга эти два места, если расстояние измерять мнимой прямой, проходящей через Землю?

3.Если бы наблюдения были сделаны горизонтально от точки наблюдения в вопросе 2 (к востоку от первой, к западу от второй), под каким углом была бы линия пересечения наблюдений?

4.В определенное время, точно синхронизированное в обоих местах, наблюдается спутник. В Кении, высота линии визирования с центром на спутнике составляет 58 градусов выше горизонтали на восток. На Суматре, высота составляет 58 градусов выше горизонтали на запад. Как далеко находится спутник? Используйте расстояние между точками рассчитанное в вопросе 2.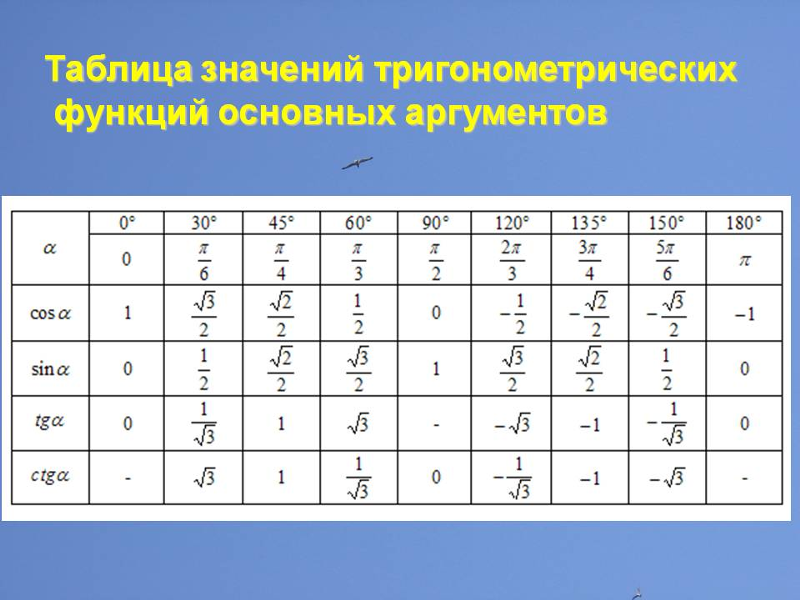

5. Косинус определенного угла в два раза больше синуса того же угла. Чему равен тангенс этого угла? Не используйте таблицы или калькулятор для ответа на этот вопрос.

6. Синус определенного угла равен именно 0.28. Найдите косинус и тангенс этого угла. Не используйте таблицы или калькулятор для ответа на этот вопрос.

7. Синус определенного угла равен 0.6. Найдите синус углов, больших чем заданный в два и три раза.

8. Найдите синус и косинус угла, большего ровно в два раза чем угол из вопроса 7.

9. Используя 15 градусов, как единичный угол, и формулы для отношения 2А и 3А найдите значения синусов 30 и 45 градусов.

10. Используя 30 градусов, как единичный угол, найти значения синусов 60 и 90 градусов.

11. Используя 45 градусов, как единичный угол, найдите значения тангенсов 60 и 90 градусов.

12. Используя 60 градусов, как единичный угол, найдите значения косинусов 120 и 180 градусов.

13. Используя 90 градусов, как единичный угол, найдите значения косинусов 180 и 270 градусов.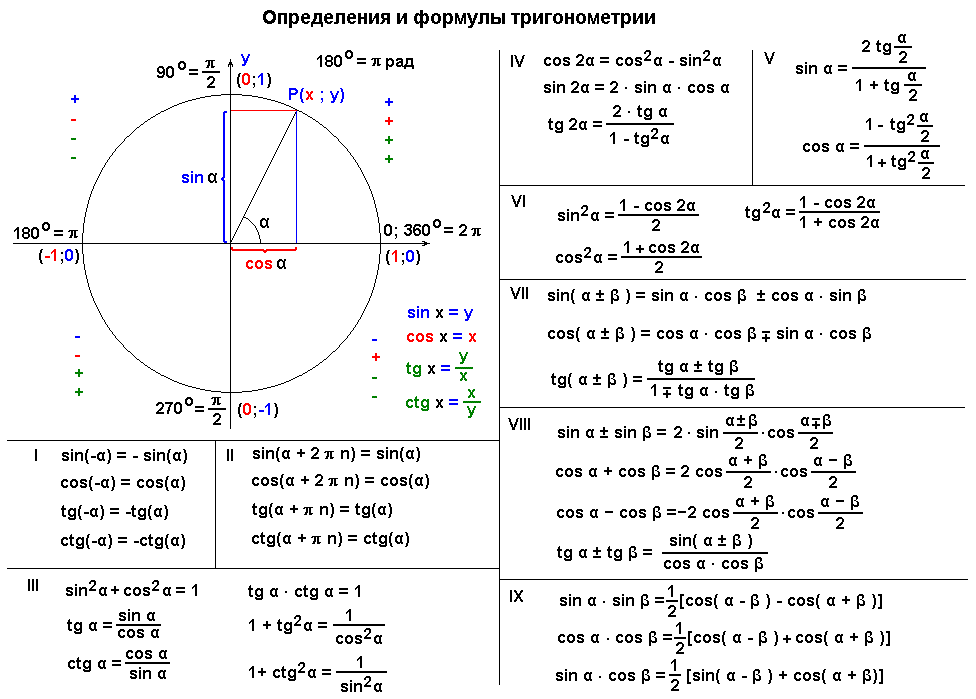

14. Используя формулы тангенса для умножения углов и таблицы, найдите тангенсы утроенных углов в 29, 31, 59 и 61 градусов. Посчитайте изменения знака между утроенным углом 29 и 31 градусов и между 59 и 61 градусов.

15. Синус угла составляет 0,96. Найдите синус и косинус удвоенного угла.

16. Задача сводится к алгебраической выражению вида 8cos2 A + cos A = 3. Решите для косинуса А, и укажите, в каком квадранте будет угол, представляющий каждое решение придет. Приведите приближенные значения из таблицы или используя калькулятор.

Основные тригонометрические отношения: Решение треугольников

Определения

Purplemath

Когда вы только начинаете работать с тригонометрическими отношениями, вы начнете с нахождения тригонометрических значений для данного треугольника. Чтобы найти ответы, вы просто подставите длины, которые они вам дали, к соответствующему соотношению триггеров.

  • Перечислите значения sin(α), cos(α), sin(β) и tan(β) для приведенного ниже треугольника с точностью до трех знаков после запятой:

Содержание продолжается ниже

MathHelp.

com

Основные тригонометрические соотношения

Гипотенуза любого из двух непрямых углов этого треугольника имеет длину 9,7. Прямоугольные треугольники имеют только одну гипотенузу, поэтому это значение не меняется по отношению к непрямым углам.

Для угла α «противоположная» сторона имеет длину 6,5, а «прилегающая» сторона имеет длину 7,2.

Отношение синуса «противоположно гипотенузе»; для этого треугольника это означает 6,5 на 9.7. Я подставлю данные значения в определение синуса:

sin(α) = 6,5/9,7 &приблизительно; 0,6701030928

Косинус α будет «смежным по гипотенузе»; для этого треугольника это означает 7,2 на 9,7. Я подставлю данные значения в определения косинуса:

cos(α) = 7,2/9,7 &приблизительно; 0,74225680412

Имею в виду, что «противоположные» и «прилежащие» находятся относительно названного угла. Так, для угла β противолежащая сторона имеет длину 7,2, а прилежащая сторона имеет длину 6,5.

Следовательно, для угла β синус определяется как:

sin(β) = 7,2/9,7 &приблизительно; 0,742268412

Отношение тангенса «противоположное к соседнему». По отношению к углу β значение тангенса определяется формулой:

tan(β) = 7,2/6,5 &приблизительно; 1,107692308

Округляя до трех знаков после запятой, я получаю:

sin(α) = 0,670, cos(α) = 0,742, sin(β) = 0,742, tan(β) = 1,108

Как только вы запомнили коэффициенты срабатывания, вы можете начать использовать их для поиска других значений. Для этого вам, скорее всего, понадобится калькулятор. Если в вашем калькуляторе нет клавиш или пунктов меню с «SIN», «COS» и «TAN», то сейчас самое время обновить его! Убедитесь, что вы также умеете пользоваться калькулятором; в руководстве по эксплуатации должны быть четкие инструкции.

(Да, я знаю, что у вас есть полнофункциональный калькулятор на вашем телефоне. У вас также есть приложения для текстовых сообщений и обмена сообщениями, которые можно использовать, скажем так, для «несанкционированной помощи» на тестах. Так что вы, вероятно, также нужен автономный калькулятор. Не думайте, что ваш инструктор будет холоден из-за того, что вы пользуетесь мобильным телефоном во время экзамена. ) прямоугольные треугольники.

Что значит «решить» прямоугольный треугольник?

«Решение прямоугольного треугольника» относится к процессу получения частичной информации (например, о длине одной из сторон треугольника и величине одного из непрямых углов) и вставки этой информации в тот или иной из шесть тригонометрических соотношений для создания уравнений, а затем решение этих уравнений (часто с помощью калькулятора), чтобы найти значения недостающих длин сторон или мер углов.

  • В показанном ниже треугольнике найдите значение x с точностью до трех знаков после запятой.

Мне дали меру угла и длину стороны, «противолежащей» этому углу, и спросили длину гипотенузы. Отношение синуса «противоположно гипотенузе», поэтому я могу преобразовать то, что они мне дали, в уравнение:

sin(20°) = 65/ x
x = 65/sin(20°)

Мне нужно вставить это в свой калькулятор, чтобы получить значение x : x = 190,047286. … Округлив до трех знаков после запятой, мой ответ:

x = 190,047

Примечание. Если ваш калькулятор показал значение 71,19813587… вместо 190,047286…, тогда проверьте «режим»; ваш калькулятор настроен на «радианы», а не на «градусы». (О радианах вы узнаете позже.)

  • Для показанного треугольника найдите значение y с точностью до четырех знаков после запятой.

Мне дали угол, значение для «примыкающего» и переменную для «противоположного», так что я могу составить уравнение:

тангенс (55,3°) = y /10
10tan(55,3°) = y

Подключив это к моему калькулятору, я получаю y = 14,44183406….. Округлив до четырех знаков после запятой, мой ответ:

y = 14,4413 900 Найти углы, обозначенные буквами на схеме. Дайте каждому ответу правильный ответ до ближайшего целого числа.

Поначалу это выглядит довольно устрашающе. Но потом я замечаю, что, чтобы найти длину высоты r , я могу использовать угол при основании 30° от большего треугольника и полную длину основания этого треугольника, равную 60, потому что r /60 является «противоположным» относительно «смежного», что является отношением касательной. Я использую эту информацию для создания уравнения, которое затем решу.

r /60 = tan(30°)
r = 60tan(30°) = 34,64101615…

Я должен с точностью до ближайшего целого числа, поэтому r = 35, что у меня стоит р , я могу использовать r и другой угол основания, 55°, чтобы найти длину другого основания, s , используя r / s = tan(55°):

35/ с = тангенс (55°)
35/tan(55°) = с = 24,50726384…

В инструкциях мне сказано округлить до ближайшего целого числа, поэтому мой ответ:

r = 35, с = 25

3

3

Если вы используете предварительно округленное значение 60tan(30°), то ваше значение 25/tan(55°) будет немного другим; это будет больше похоже на 24. 2559006…. Вот почему я не одобряю такое строгое округление, как «до ближайшего целого числа»; это может сильно отбросить ваши ценности. Имейте это в виду, когда делаете свою работу, особенно при решении текстовых задач. Чтобы получить полезный точный ответ, сохраняя как можно больше знаков после запятой, к концу упражнения можно получить большую разницу.

Примечание. Поскольку отношения синуса и косинуса включают деление катета (одной из двух более коротких сторон) на гипотенузу (которая всегда является самой длинной стороной), значения отношения никогда не будут больше 1, потому что (некоторое число) / (большее число) всегда будет меньше 1. Но у вас могут быть очень широкие и короткие или очень высокие и узкие прямоугольные треугольники, поэтому «противоположные» и «смежные» могут иметь очень разные значения. Это говорит вам о том, что отношение тангенса, будучи (противоположным) / (смежным), может иметь очень большие и очень маленькие значения, в зависимости от треугольника.

Итак, если вы получили значение синуса или косинуса больше 1, вам следует проверить свою работу. Если вы получите огромное значение тангенса для какого-то шаткого треугольника, не удивляйтесь.

URL: https://www.purplemath.com/modules/basirati2.htm

Страница 1

Касательная функция

Горячая математика

Касательная функция представляет собой периодический функция, которая очень важна в тригонометрии.

Самый простой способ понять функцию касательной — использовать единичную окружность. Для заданной угловой меры θ нарисуйте единичный круг на координатной плоскости и нарисуйте угол с центром в начале координат, с одной стороной как положительной Икс -ось. Икс -координата точки пересечения другой стороны угла с окружностью потому что ( θ ) и у -координата грех ( θ ) .

Есть несколько значений синуса и косинуса, которые следует запомнить, основываясь на 30 ° − 60 ° − 90 ° треугольники и 45 ° − 45 ° − 90 ° треугольники. Основываясь на них, вы можете определить соответствующие значения тангенса.

грех ( θ )

потому что ( θ )

загар ( θ )

грех ( 0 ° ) «=» 0 потому что ( 0 ° ) «=» 1 загар ( 0 ° ) «=» 0 1 «=» 0
грех ( 30 ° ) «=» 1 2 потому что ( 30 ° ) «=» 3 2 загар ( 30 ° ) «=» 1 2 ⋅ 2 3 «=» 3 3
грех ( 45 ° ) «=» 2 2 потому что ( 45 ° ) «=» 2 2 загар ( 45 ° ) «=» 2 2 ⋅ 2 2 «=» 1
грех ( 60 ° ) «=» 3 2 потому что ( 60 ° ) «=» 1 2 загар ( 60 ° ) «=» 3 2 ⋅ 2 1 «=» 3
грех ( 90 ° ) «=» 1 потому что ( 90 ° ) «=» 0 загар ( 90 ° ) «=» 1 0 «=» недеф .

Related Posts

Leave A Comment