Глава 7. Вращательное движение. Кинематика и динамика
Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7. 1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
(7.2) |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
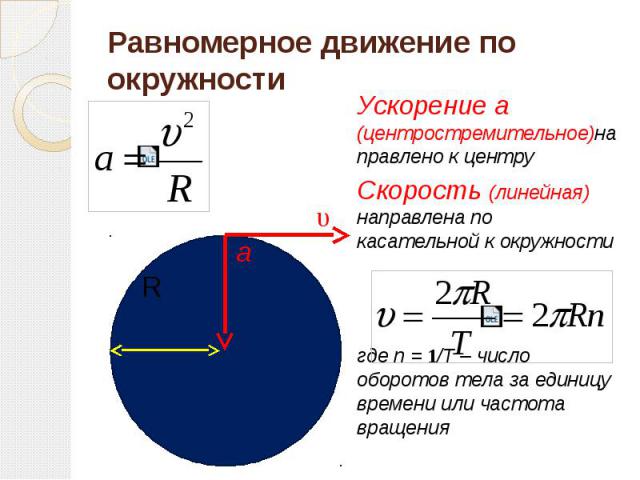
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7.3) |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.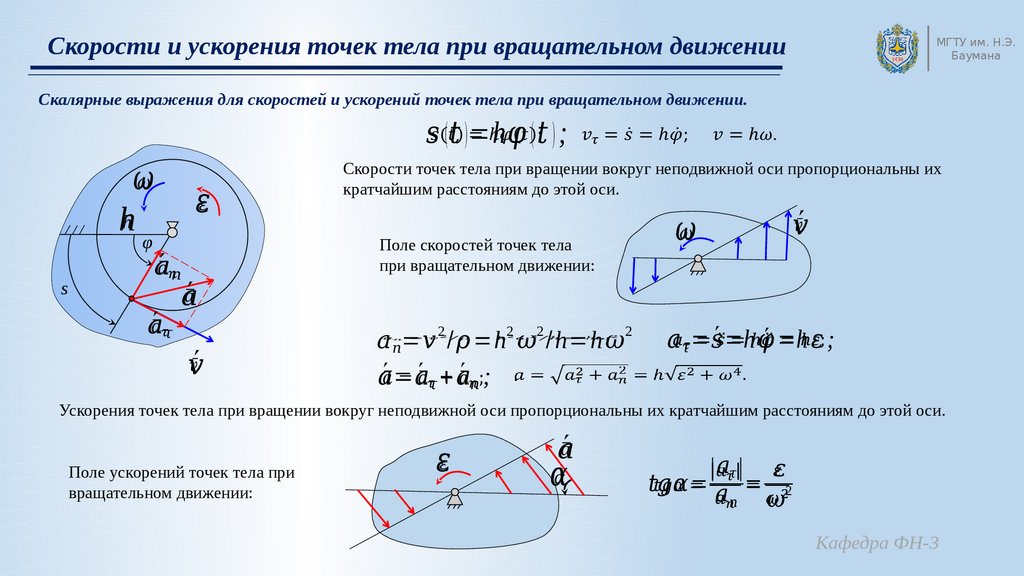
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7.5) |
Согласно второму закону Ньютона ускорения сообщаются телам силами.
(7.6) |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»).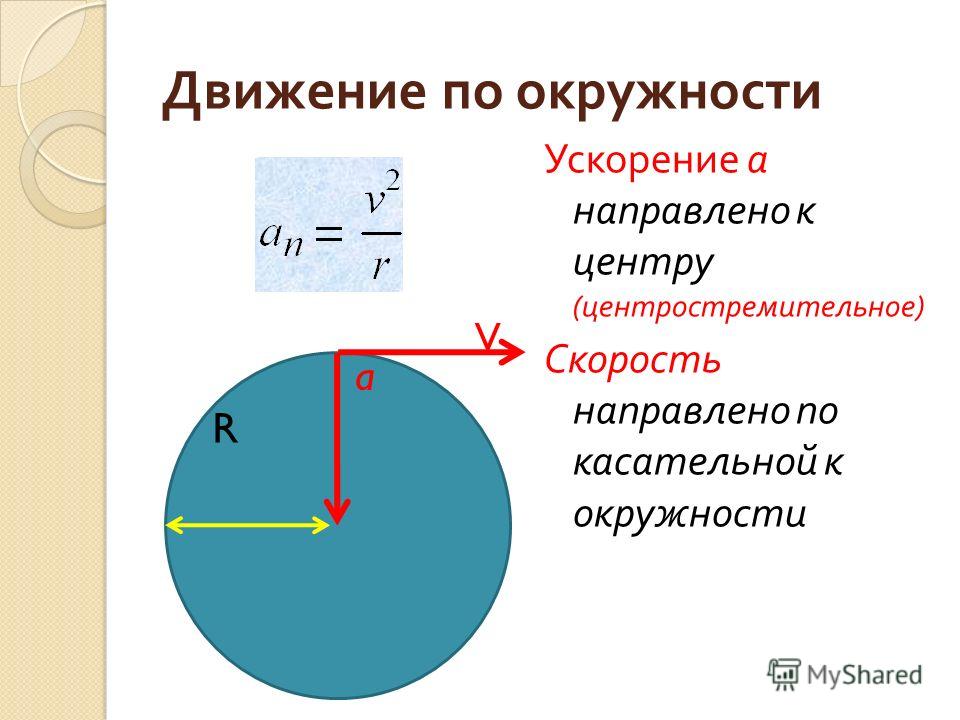 Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (задача 7.1.3), получаем
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7. 5) для второй точки получаем
5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.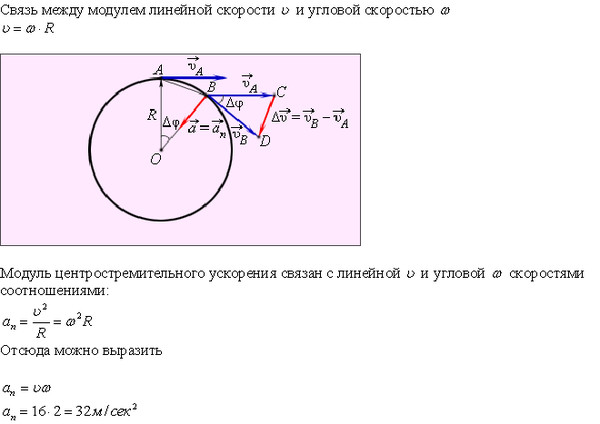 1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи –
1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи –
Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7.2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).
Для сравнения центростремительных ускорений тел в
 2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7.2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).
1.1.8 Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Видеоурок: Движение по окружности
Лекция: Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Движение по окружности
Траектория движения — окружность.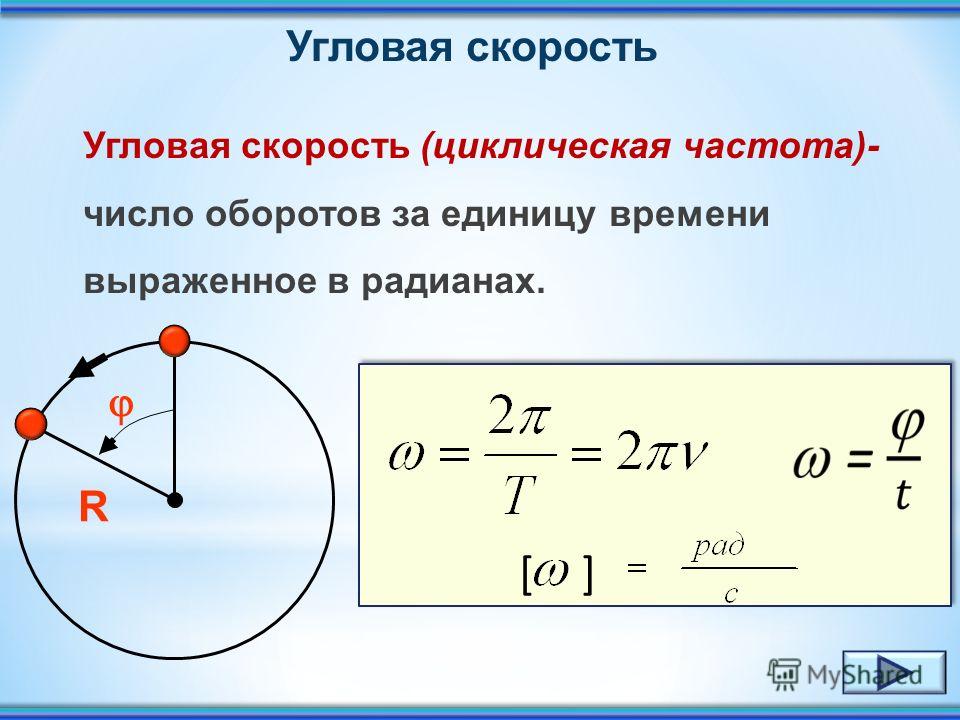
Так как скорость — векторная величина, то она зависит не только от модуля значения, но и от направления. Поэтому движение тела по окружности можно назвать равноускоренным. Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться.
Любое криволинейное движение можно свести к нескольким движениям по окружности. Примером данного движения является бег по стадиону, ход стрелки часов, прогулка на корде лошади и другое.
Основные характеристики движения
1. Линейная скорость
Мгновенная скорость (линейная) — на протяжении всего движения меняет свое направление вдоль касательной к траектории.
Так как траектория движения точки — окружность, то в качестве пути в числителе находится формула длины перемещения.
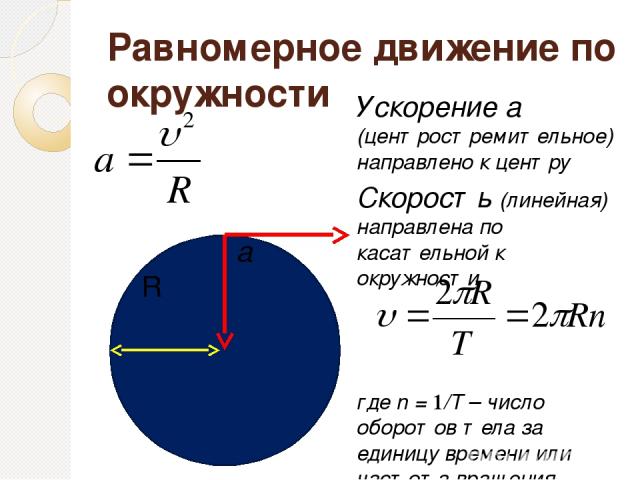
Поэтому формула мгновенной скорости приобретает следующий вид, где Т — период:
2. Центростремительное ускорение
Направлено перпендикулярно к линейной скорости на протяжении всего движения.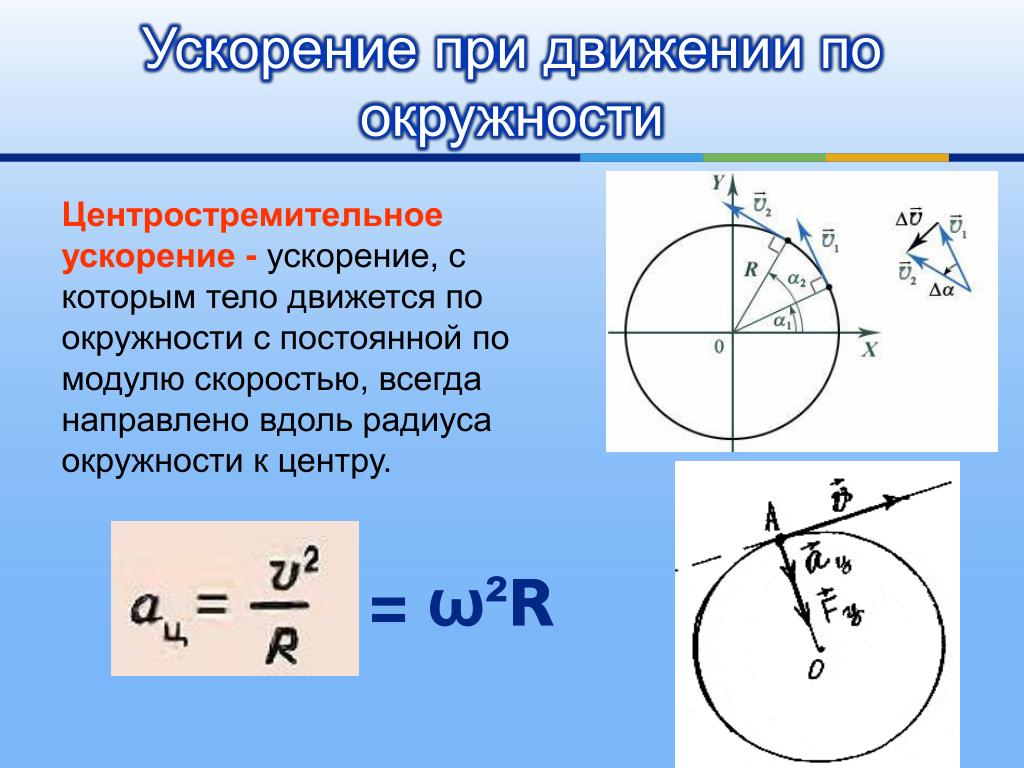
Центростремительное ускорение определяется по формуле:
3. Период вращения
Период вращения — это величина, определяющая время, за которое тело делает одно полное вращение.
Период — это скалярная величина. Основной единицей периода является [Т]=1с.
Период определяется по формуле:
где N — количество оборотов, t — время, за которое они были совершены.
4. Частота вращения
Определяет, насколько часто совершаются обороты в единицу времени.
Частота — скалярная величина. Измеряется в [n] = 1с-1.
Частота определяется по формуле:
5. Угловое перемещение
Угловое перемещение — величина, которая определяется углом поворота радиуса, соединяющего центр описываемой окружности, с точкой, где находится тело, относительно начального его положения.
Данная величина может измеряться в градусной или радианной мере углов.
6. Угловая скорость
Это значение, которое определяет, насколько изменяется угловое перемещение со временем.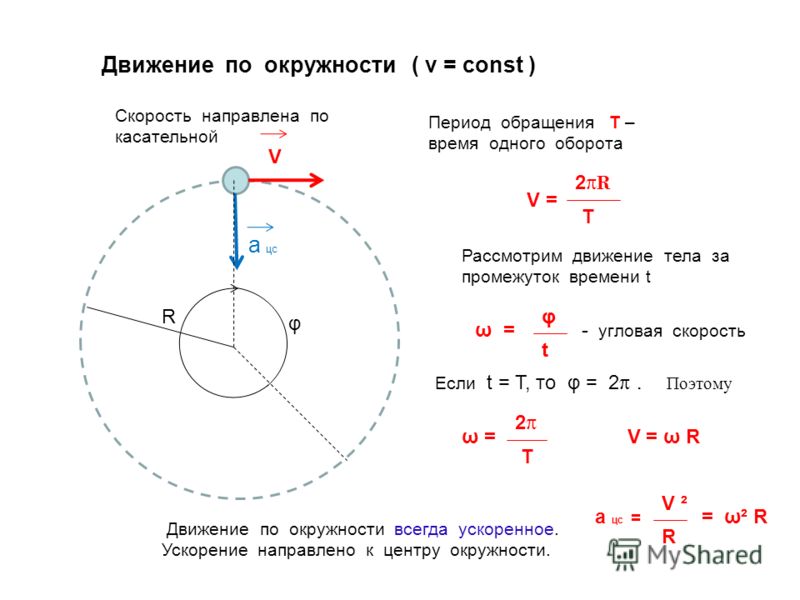
Измеряется в 1 рад/с.
Определяется по формуле:где
— угловая скорость материальной точки, 1/с
— угол поворота радиус — вектора, рад
— промежуток времени, сУгловое перемещение связано с линейной скоростью и центростремительным ускорением следующей формулой:
- Вконтакте
- Сайт
5.
 3: Скорость, ускорение и сила
3: Скорость, ускорение и сила- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14461
- Boundless (теперь LumenLearning)
- Boundless
Угол вращения и угловая скорость
Угол поворота является мерой того, насколько сильно вращается объект, а угловая скорость измеряет, насколько быстро он вращается.
цели обучения
- Выражают взаимосвязь между углом поворота и расстоянием
Угол вращения и угловая скорость
Когда объект вращается вокруг оси, например, автомобильная шина или пластинка на проигрывателе, движение можно описать двумя способами. Точка на краю вращающегося объекта будет иметь некоторую скорость и будет перемещаться по дуге, перемещаясь на вращающемся объекте. Точка пройдет расстояние \(\mathrm{ΔS}\), но часто удобнее говорить о степени вращения объекта. Величина вращения объекта называется углом поворота и может измеряться в градусах или радианах. Поскольку угол поворота связан с расстоянием \(\mathrm{ΔS}\) и с радиусом \(\mathrm{r}\) уравнением \(\mathrm{Δθ=\frac{ΔS}{R}} \), обычно удобнее использовать радианы.
Точка пройдет расстояние \(\mathrm{ΔS}\), но часто удобнее говорить о степени вращения объекта. Величина вращения объекта называется углом поворота и может измеряться в градусах или радианах. Поскольку угол поворота связан с расстоянием \(\mathrm{ΔS}\) и с радиусом \(\mathrm{r}\) уравнением \(\mathrm{Δθ=\frac{ΔS}{R}} \), обычно удобнее использовать радианы.
Угол θ и длина дуги s : Радиус окружности поворачивается на угол \(\mathrm{Δθ}\). Длина дуги \(\mathrm{Δs}\) описана на окружности.
Скорость, с которой вращается объект, определяется угловой скоростью, которая представляет собой скорость изменения угла поворота во времени. Хотя угол сам по себе не является векторной величиной, угловая скорость является вектором. Направление вектора угловой скорости перпендикулярно плоскости вращения в направлении, которое обычно задается правилом правой руки. Угловое ускорение дает скорость изменения угловой скорости. Угол, угловая скорость и угловое ускорение очень полезны при описании вращательного движения объекта.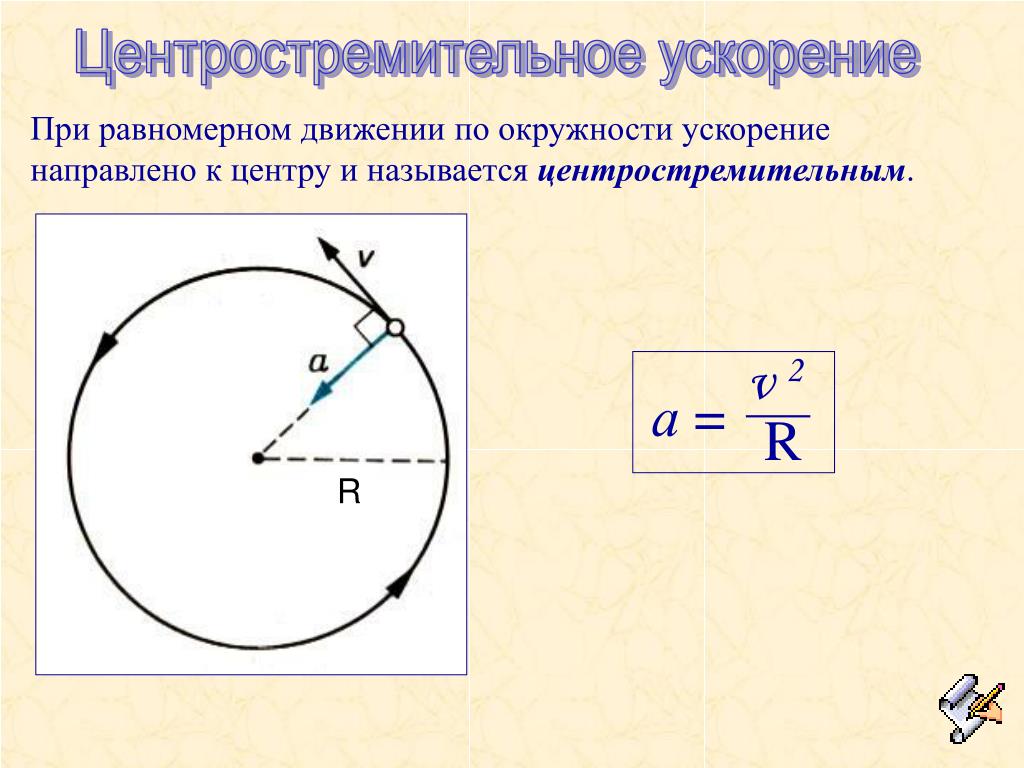
Направление угловой скорости : Угловая скорость описывает скорость вращения и ориентацию мгновенной оси, вокруг которой происходит вращение. Направление угловой скорости будет вдоль оси вращения. В этом случае (вращение против часовой стрелки) вектор направлен вверх.
Когда ось вращения перпендикулярна вектору положения, угловую скорость можно рассчитать, взяв линейную скорость \(\mathrm{v}\) точки на краю вращающегося объекта и разделив ее на радиус. Это даст угловую скорость, обычно обозначаемую \(\mathrm{ω}\), в радианах в секунду.
Угловая скорость : Муха на краю вращающегося объекта регистрирует постоянную скорость \(\mathrm{v}\). Объект вращается с угловой скоростью, равной \(\mathrm{\frac{v}{r}}\).
Центростремительное ускорение
Центростремительное ускорение — это постоянное изменение скорости, необходимое объекту для сохранения кругового пути.
цели обучения
- Выразите центростремительное ускорение через скорость вращения
Обзор
Как упоминалось в предыдущих разделах о кинематике, любое изменение скорости определяется ускорением. Часто изменения скорости являются изменениями величины. Когда объект ускоряется или замедляется, это изменение скорости объекта. Изменения величины скорости соответствуют нашему интуитивному и повседневному использованию термина ускорение. Однако, поскольку скорость является вектором, она также имеет направление. Следовательно, любое изменение направления движения объекта также должно сопровождаться ускорением.
Часто изменения скорости являются изменениями величины. Когда объект ускоряется или замедляется, это изменение скорости объекта. Изменения величины скорости соответствуют нашему интуитивному и повседневному использованию термина ускорение. Однако, поскольку скорость является вектором, она также имеет направление. Следовательно, любое изменение направления движения объекта также должно сопровождаться ускорением.
Равномерное круговое движение предполагает перемещение объекта по круговой траектории с постоянной скоростью. Поскольку скорость постоянна, обычно не думают, что объект ускоряется. Однако направление постоянно меняется по мере того, как объект пересекает круг. Таким образом, говорят, что он ускоряется. Это ускорение можно почувствовать, когда едешь на американских горках. Даже если скорость постоянна, быстрый поворот вызовет у гонщика ощущение силы. Это чувство — ускорение.
92r}\], где омега — скорость вращения, определяемая выражением \(\mathrm{\frac{v}{r}}\).
Центростремительное ускорение : Когда объект движется по окружности, направление вектора скорости постоянно меняется.
Центростремительная сила
Сила, вызывающая движение по криволинейной траектории, называется центростремительной силой (примером центростремительной силы является равномерное круговое движение).
цели обучения
- Выразите уравнения для центростремительной силы и ускорения
Сила, вызывающая движение по криволинейной траектории, называется центростремительной силой. Равномерное круговое движение является примером действия центростремительной силы. Это можно увидеть в движении спутников вокруг Земли, в натяжении веревки при игре в мяч, в петле на американских горках или в ведре, раскачиваемом вокруг тела.
Обзор центростремительной силы : Краткий обзор центростремительной силы.
Ранее мы узнали, что любое изменение скорости является ускорением. Когда объект движется по круговому пути, он постоянно меняет направление и, следовательно, ускоряется, в результате чего на объект действует постоянная сила. Эта центростремительная сила действует по направлению к центру кривизны, по направлению к оси вращения. Поскольку объект движется перпендикулярно силе, путь, по которому следует объект, является круговым. Именно эта сила удерживает мяч от выпадения из ведра, если вы непрерывно вращаете его по кругу. 92}\]
Ключевые точки
- Когда объект вращается вокруг оси, точки на краях объекта перемещаются по дуге.
- Угол, огибаемый этими дугами, называется углом вращения и обычно обозначается символом тета .
- Мера того, насколько быстро объект вращается относительно времени, называется угловой скоростью. Обычно он представлен греческим символом омега . Как и его аналог линейной скорости, это вектор.

- Чтобы объект мог двигаться по кругу, он должен постоянно менять направление.
- Поскольку скорость является вектором, изменения направления вызывают изменения скорости.
- Изменение скорости называется ускорением. Изменение скорости из-за кругового движения известно как центростремительное ускорение.
- Центростремительное ускорение можно рассчитать, разделив квадрат линейной скорости на радиус окружности, по которой движется объект.
- Когда объект находится в равномерном круговом движении, он постоянно меняет направление и, следовательно, ускоряется. Это угловое ускорение.
- Сила, действующая на объект при равномерном круговом движении (называемая центростремительной силой), действует на объект из центра окружности.
Ключевые термины
- радианы : Угол, образуемый в центре окружности дугой окружности той же длины, что и радиус окружности.
- ускорение : Величина, на которую увеличивается скорость или скорость (и, следовательно, скалярная величина или векторная величина).

- круговое движение : Движение таким образом, что выбранный путь является круговым.
- скорость : Векторная величина, обозначающая скорость изменения положения во времени или скорость с компонентом направления.
- центростремительный : Направленный или движущийся к центру.
- угловая скорость : Векторная величина, описывающая объект в круговом движении; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
ЛИЦЕНЗИИ И АВТОРСТВО
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ПРЕДОСТАВЛЕННОЕ РАНЕЕ
- Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, КОНКРЕТНОЕ АВТОРСТВО
- OpenStax College, Угол вращения и угловая скорость.
 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/ . Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/ . Лицензия : CC BY: Attribution - радиана. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/radians . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, угол поворота и угловая скорость. 25 января 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution - Угловая скорость. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Angular_velocity . Лицензия : CC BY: Attribution
- Колледж OpenStax, Центростремительное ускорение. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Адрес: : http://cnx.org/content/m42084/latest/ . Лицензия : CC BY: Attribution
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/circular-motion .
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - скорость. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/velocity . Лицензия : CC BY-SA: Attribution-ShareAlike
- ускорение. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/acceleration . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, угол поворота и угловая скорость.
 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution - Угловая скорость. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Angular_velocity . Лицензия : CC BY: Attribution
- Центростремительное ускорение. Расположен по адресу : http://www.youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, Центростремительное ускорение. 25 января 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg . Лицензия : CC BY: Attribution - Колледж OpenStax, Центростремительная сила. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42086/latest/ . Лицензия : CC BY: Attribution
- центростремительный. Предоставлено : Викисловарь. Расположен по адресу : http://en.wiktionary.org/wiki/centripetal . Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/angular-velocity .
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, угол поворота и угловая скорость. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
- Угловая скорость. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Angular_velocity . Лицензия : CC BY: Attribution
- Центростремительное ускорение.
 Расположен по адресу : http://www.youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Расположен по адресу : http://www.youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube - Колледж OpenStax, Центростремительное ускорение. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg . Лицензия : CC BY: Attribution
- Колледж OpenStax, Центростремительная сила. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42086/latest/Figure_07_03_01a.jpg . Лицензия : CC BY: Attribution
- Обзор центростремительной силы.
 Расположен по адресу : http://www.youtube.com/watch?v=ldQWTNDBSSE . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Расположен по адресу : http://www.youtube.com/watch?v=ldQWTNDBSSE . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Эта страница под названием 5.3: Velocity, Acceleration, and Force распространяется по незаявленной лицензии и была создана, изменена и/или курирована Boundless.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Безграничный
- Показать оглавление
- нет
- Теги
- ускорение
- угловая скорость
- центростремительный
- Круговое движение
- Радиан
- скорость
Центростремительная сила — Резюме – Гиперучебник по физике
[закрыть]
| Сила, которая… | превратит | или… |
|---|---|---|
| параллельно скорости | изменить скорость (ускорить) | ускорить (в обычном смысле этого слова) |
| антипараллельно скорости | изменить скорость (замедлить) | замедлить (это еще один способ ускориться) |
| перпендикулярно скорости | изменить направление (повернуть) | ускорение центростремительно (что также является еще одним способом ускорения) |
- A центростремительное ускорение ( a c )
- возникает всякий раз, когда движущийся объект меняет направление
- не меняет скорость объекта
- действует под прямым углом к скорости в любой момент
- направлен к центру круга (поиск центра)
- также известен как радиальное ускорение .

- A центростремительная сила ( F c )
- это сила, которая заставляет движущийся объект менять направление
- — это не конкретная сила, а название, данное любой силе или комбинации сил, ответственных за центростремительное ускорение
- действует под прямым углом к скорости в любой момент
- направлен к центру круга (поиск центра)
- также известен как радиальная сила .
- Направления в круговом движении
- Скорость ( v ) является касательной (лежит по касательной к траектории).
- Центростремительное ускорение и центростремительная сила бывают центростремительными (направлены к центру окружности) или радиальными (находятся на радиусе окружности).
- Центростремительное ускорение перпендикулярно скорости.
- Центростремительная сила параллельна центростремительному ускорению.
- Уравнения [в единицах СИ]
- скорость и скорость
линейные количества v = 2π р Т где v = скорость [м/с] π = математическая константа r = радиус кругового пути [м] Т = период обращения [с] угловые величины v = ω × r где v = вектор поступательной скорости [м/с] r = радиус-вектор [м] ω = вектор угловой скорости [рад/с] - частота и период
линейные количества ƒ = 1 Т где f = частота вращения [Гц = 1/с = с −1 ] Т = период обращения [с] угловые величины ω = 2π = 2πƒ Т где ω = величина угловой скорости или угловой частоты [рад/с] π = математическая константа Т = период обращения [с] f = частота вращения [Гц = 1/с = с −1 ] - центростремительное ускорение
линейные количества а в = v 2 = 4π 2 р р Т 2 где а в = центростремительное ускорение [м/с 2 ] v = скорость [м/с] r = радиус кругового пути [м] π = математическая константа Т = период обращения [с] угловые величины a c = −ω 2 r = ω × v где а в = вектор центростремительного ускорения [м/с 2 ] ω = величина угловой скорости или угловой частоты [рад/с] r = радиус-вектор [м] ω = вектор угловой скорости [рад/с] v = вектор поступательной скорости [м/с]
- скорость и скорость
- А центробежная сила …
- это фиктивная сила (он же кажущаяся сила или псевдосила )
- не является результатом взаимодействия между объектами
- перестает существовать, когда объект перестает двигаться по кругу
- — иллюзия во вращающейся системе отсчета .



 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/ . Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/ . Лицензия : CC BY: Attribution  Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution 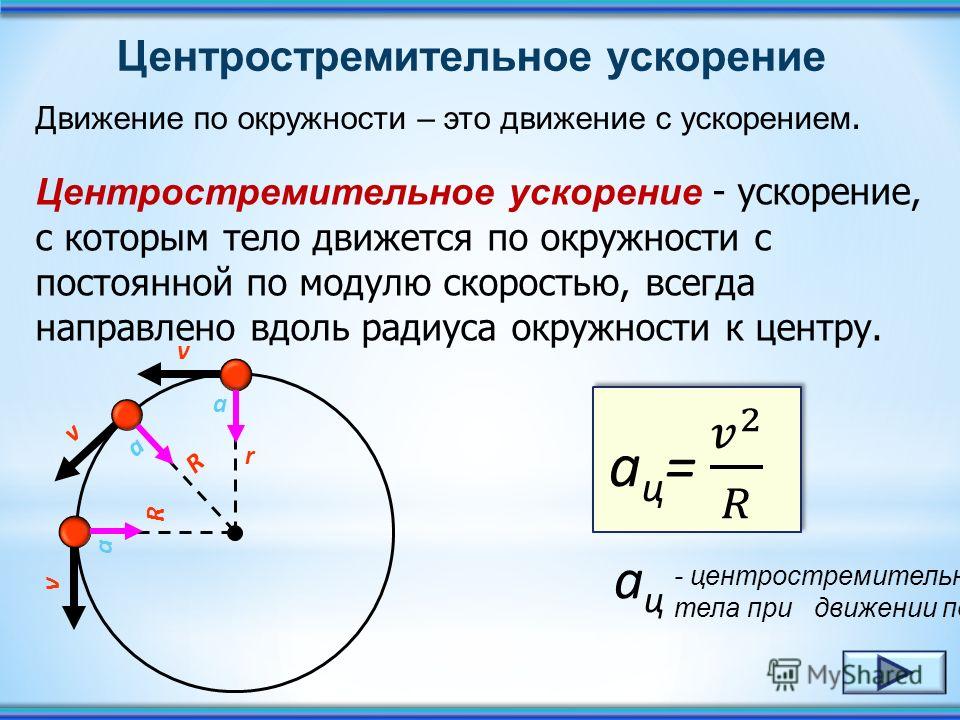 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution 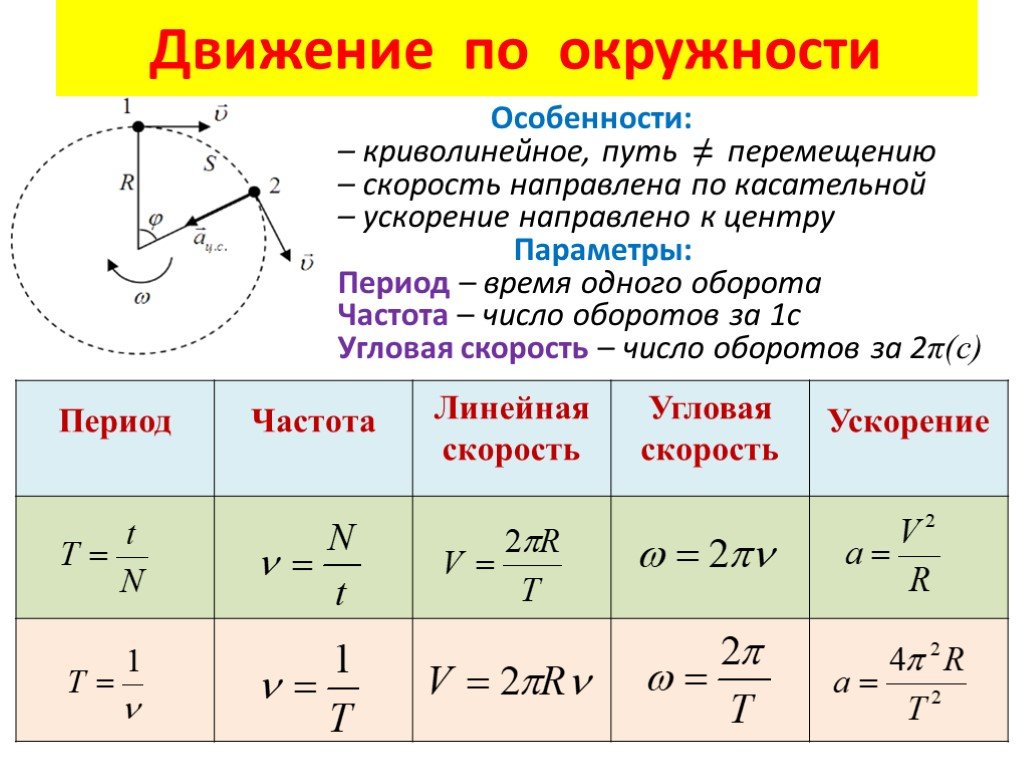 Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg . Лицензия : CC BY: Attribution
Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg . Лицензия : CC BY: Attribution  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Расположен по адресу : http://www.youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Расположен по адресу : http://www.youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube Расположен по адресу : http://www.youtube.com/watch?v=ldQWTNDBSSE . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Расположен по адресу : http://www.youtube.com/watch?v=ldQWTNDBSSE . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube

Leave A Comment