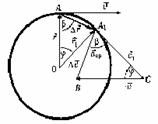
Вычислим величину ускорения при равномерном движении точки по окружности и найдем его направление. Пусть за некоторый промежуток времени t тело переместилось из точки А в точку А1 с постоянной по модулю скоростью. Изобразим вектора скорости в этих точках и найдем вектор изменения скорости Рассмотрим треугольники АА1О и А1СВ. Эти треугольники равнобедренные и углы при их вершинах равны, т.к. АО┴СВ и А1О┴А1С (углы со взаимно перпендикулярными сторонами). Следовательно, эти треугольники подобны. Из подобия треугольников следует пропорция: Разделим правую и левую части равенства на промежуток времени, за которое совершено перемещение, и учтем, что |
Примеры: — Земля при вращении вокруг оси ацс=0,03 м/с2, — Земля при вращении вокруг Солнца ацс=0,006 м/с2, — Солнечная система при вращении вокруг центра Галактики
| Теперь определим направление ускорения. Т.к. мы должны для определения ускорения брать предел при Δt→0, то из рисунка видно, что угол φ будет уменьшаться (→0), а b→900. Это значит, что прямая А1В (вектор Следовательно, вектор ускорения при равномерном движении по окружности направлен к центру окружности (центру вращения). | 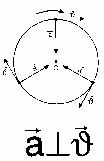 | Центростремительное ускорение меняет скорость только по направлению, но не меняет по величине. Вектор центростремительного ускорения перпендикулярен вектору скорости. Используя связь между угловой и линейной скоростями, получим: | 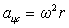 |
Центростремительное ускорение — вывод формулы и практическое применение :: SYL.ru
Центростремительное ускорение сопровождает нас повсюду. Именно оно заставляет нашу Землю вращаться вокруг Солнца. Возникающая при этом сила тяжести позволяет нам существовать на этой планете. Как можно понять, что представляет собой центростремительное ускорение? Определение этой физической величины представлено ниже.
Наблюдения
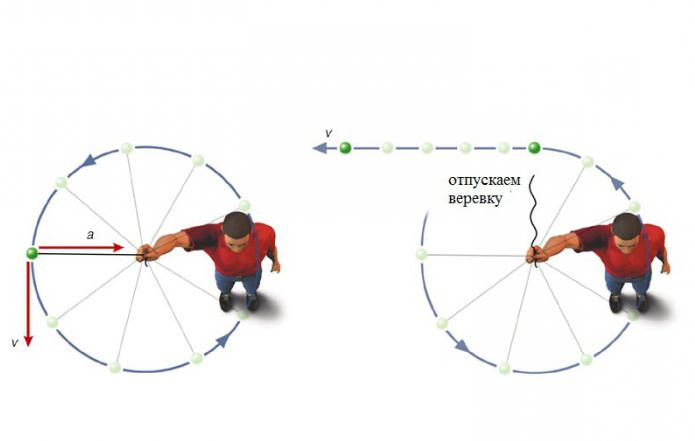
Самый простой пример ускорения тела, движущегося по окружности, можно наблюдать, вращая камень на веревке. Вы тянете веревку, а веревка тянет камень к центру. В каждый момент времени веревка сообщает камню некоторое количество движения, и каждый раз – в новом направлении. Можно представить движение веревки в виде серии слабых рывков. Рывок – и веревка изменяет свое направление, еще рывок – еще раз изменение, и так по кругу. Если вы внезапно отпустите веревку, рывки прекратятся, а вместе с ними и прекратится изменение направления скорости. Камень будет двигаться в направлении касательной к кругу. Возникает вопрос: «С каким ускорением будет двигаться тело в это мгновение?»
Формула центростремительного ускорения
Прежде всего стоит заметить, что движение тела по окружности является сложным. Камень участвует в двух видах движения одновременно: под действием силы он движется к центру вращения, и одновременно по касательной к окружности, от этого центра удаляется. Согласно Второму закону Ньютона, сила, удерживающая камень на веревке, направлена к центру вращения вдоль этой веревки. Туда же будет направлен вектор ускорения.
Пусть за некоторое время t наш камень, равномерно двигаясь со скоростью V, попадает из точки A в точку B. Предположим, что в момент времени, когда тело пересекало точку B, на него перестала действовать центростремительная сила. Тогда за промежуток времени оно попало бы в точку K. Она лежит на касательной. Если бы в тот же момент времени на тело действовали бы только центростремительные силы, то за время t, двигаясь с одинаковым ускорением, оно оказалось бы в точке O, которая расположена на прямой, представляющей собой диаметр окружности. Оба отрезка являются векторами и подчиняются правилу векторного сложения. В результате суммирования этих двух движений за отрезок времени t получаем результирующую движения по дуге AB.
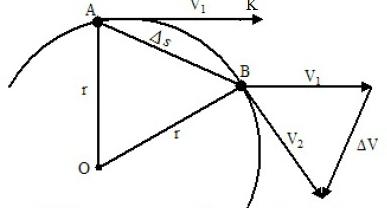
Если промежуток времени t взять пренебрежимо малым, то дуга AB будет мало отличаться от хорды AB. Таким образом, можно заменить движение по дуге движением по хорде. В этом случае перемещение камня по хорде будет подчиняться законам прямолинейного движения, то есть пройденное расстояние AB будет равно произведению скорости камня на время его движения. AB = V х t.
Обозначим искомое центростремительное ускорение буквой a. Тогда пройденный только под действием центростремительного ускорения путь можно рассчитать по формуле равноускоренного движения:
AO = at2 / 2.
Расстояние AB равно произведению скорости и времени, то есть AB = V х t,
AO – вычислено ранее по формуле равноускоренного движения для перемещения по прямой: AO = at2 / 2.
Подставляя эти данные в формулу и преобразуя их, получаем простую и изящную формулу центростремительного ускорения:
a = v2 / R
Словами это можно выразить так: центростремительное ускорение тела, двигающегося по окружности, равно частному от деления линейной скорости в квадрате на радиус окружности, по которой вращается тело. Центростремительная сила в таком случае будет выглядеть так, как на картинке ниже.
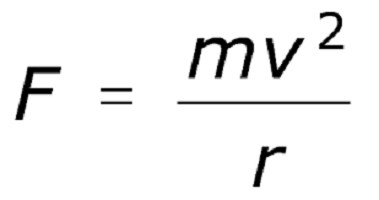
Угловая скорость
Угловая скорость равна частному от деления линейной скорости на радиус окружности. Верно и обратное утверждение: V = ωR, где ω – угловая скорость
Если подставить это значение в формулу, можно получить выражение центробежного ускорения для угловой скорости. Оно будет выглядеть так:
a = ω2R.
Ускорение без изменения скорости
И все же, отчего тело с ускорением, направленным к центру, не движется быстрее и не перемещается ближе к центру вращения? Ответ кроется в самой формулировке ускорения. Факты говорят о том, что движение по окружности реально, но для его поддержания требуется ускорение, направленное к центру. Под действием силы, вызванной данным ускорением, происходит изменение количества движения, в результате чего траектория движения постоянно искривляется, все время меняя направление вектора скорости, но не изменяя ее абсолютной величины. Двигаясь по кругу, наш многострадальный камень устремляется внутрь, в противном случае он продолжал бы двигаться по касательной. Каждое мгновение времени, уходя по касательной, камень притягивается к центру, но не попадает в него. Еще одним примером центростремительного ускорения может стать водный лыжник, описывающий небольшие круги на воде. Фигура спортсмена наклонена; он как бы падает, продолжая движение и наклонившись вперед.

Таким образом, можно сделать вывод о том, что ускорение не увеличивает скорость тела, так как векторы скорости и ускорения перпендикулярны друг к другу. Добавляясь к вектору скорости, ускорение лишь меняет направление движения и удерживает тело на орбите.
Превышение запаса прочности
В предыдущем опыте мы имели дело с идеальной веревкой, которая не рвалась. Но, допустим, наша веревка самая обычная, и даже можно вычислить усилие, после которого она просто порвется. Для того чтобы рассчитать эту силу, достаточно сопоставить запас прочности веревки с нагрузкой, которую она испытывает в процессе вращения камня. Вращая камень с большей скоростью, вы сообщаете ему большее количество движения, а значит, и большее ускорение.

При диаметре джутовой веревки около 20 мм ее прочность на разрыв равна около 26 кН. Примечательно, что длина веревки нигде не фигурирует. Вращая груз размером в 1 кг на веревке радиусом в 1 м, можно вычислить, что линейная скорость, необходимая для ее разрыва равна 26 х 103 = 1кг х V2 / 1 м. Таким образом, скорость, которую опасно превышать, будет равна √26 х 103 = 161 м/с.
Сила тяжести
При рассмотрении опыта мы пренебрегали действием силы тяжести, так как при таких больших скоростях ее влияние пренебрежимо мало. Но можно заметить, что при раскручивании длинной веревки тело описывает более сложную траекторию и постепенно приближается к земле.
Небесные тела
Если перенести законы движения по окружности в космос и применить их к движению небесных тел, можно заново открыть несколько давно знакомых формул. Например, сила, с которой тело притягивается к Земле, известна по формуле:
F= m*g.
В нашем случае множитель g и является тем самым центростремительным ускорением, которое было выведено из предыдущей формулы. Только в этом случае роль камня будет выполнять небесное тело, притягивающееся к Земле, а роль веревки – сила земного притяжения. Множитель g будет выражен через радиус нашей планеты и скорость ее вращения.
Итоги
Сущность центростремительного ускорения состоит в тяжелой и неблагодарной работе удержания движущегося тела на орбите. Наблюдается парадоксальный случай, когда при постоянном ускорении тело не изменяет величины своей скорости. Для неподготовленного ума такое заявление довольно парадоксально. Тем не менее и при расчете движения электрона вокруг ядра, и при вычислении скорости вращения звезды вокруг черной дыры, центростремительной ускорение играет не самую последнюю роль.
Глава 7. Вращательное движение. Кинематика и динамика
Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
(7.2) |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7.3) |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7.5) |
Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
(7.6) |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (
Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7.5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7.2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).
Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7.2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).
Конспект на тему «Центростремительное ускорение»
Казахско-Американский Университет Школа при КАУ Класс 9B Семестр осенний 2017-2018 учебный год Урок 5. Центростремительное ускорение Преподаватель: Шокпарбаева Э.Е |
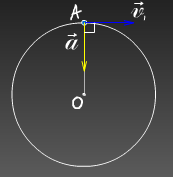
Центростремительное ускорение — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой.
Наиболее простым примером центростремительного ускорения является вектор ускорения при равномерном движении по окружности (направленный к центру окружности).
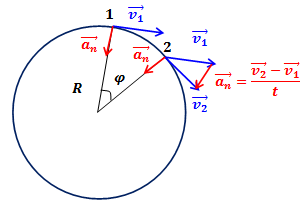
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
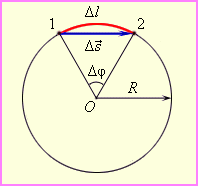
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
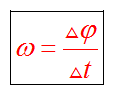
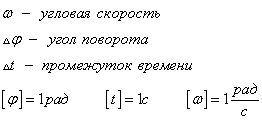
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
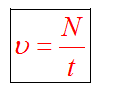
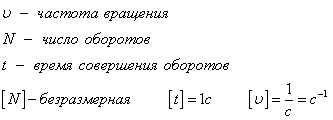
Частота и период взаимосвязаны соотношением
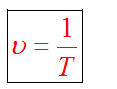
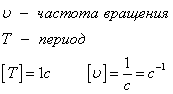
Связь с угловой скоростью
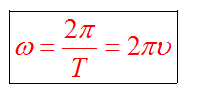
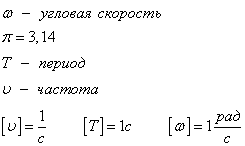
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
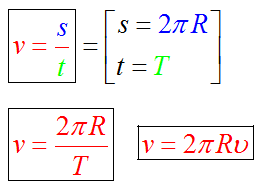
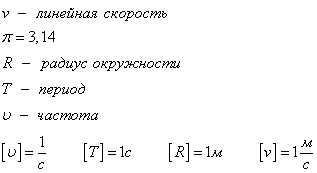
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
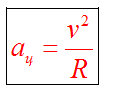
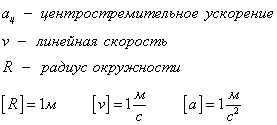
Используя предыдущие формулы, можно вывести следующие соотношения
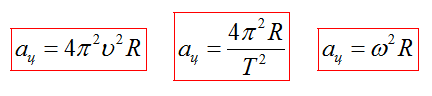
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Глоссарий
Вопросы:
1.Велосипедист едет по дороге со скоростью 10 м/с. Сколько оборотов за секунду делают колеса велосипеда, если они не скользят? Какое центростремительное ускорение точки обода колеса, если его радиус 35 см?
Ответ: ac ≈ 285 м/с2.
2.Материальная точка подвешена на нити длиной м и равномерно движется в горизонтальной плоскости. При этом ее центростремительное ускорение 10 м/с . Определить период движения точки, если нить образует с вертикалью угол ϕ=60
Ответ: T=1.8 c.
3.Рабочее колесо турбины Красноярской ГЭС им. 50-летия СССР имеет диаметр 7,5 м и вращается с частотой 93,8 об/мин. Каково центростремительное ускорение концов лопаток турбины?
Ответ: ac ≈ 360 м/с2.
4.Период вращения первого пилотируемого корабля-спутника «Восток» вокруг Земли был равен 90 мин. С каким ускорением двигался корабль, если его средняя высота над Землей 320 км? Радиус Земли принять равным 6400 км.
Ответ: ac ≈ 9,1 м/с2.
5.Угловая скорость вращения лопастей колеса ветродвигателя 6 рад/с. Найдите центростремительное ускорение концов лопастей, если линейная скорость концов лопастей 20 м/с.
Ответ: ac ≈ 120 м/с2.
СРС: упражнение в конце параграфа
Литература: Физика 9 класс
Движение по окружности с постоянной по модулю скоростью 🐲 СПАДИЛО.РУ
Понятия и определения

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
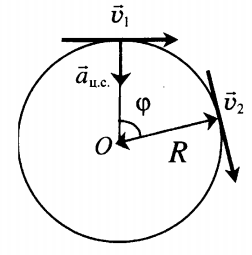

Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
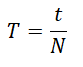
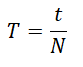
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
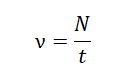
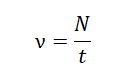
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:


Количество оборотов выражается следующей формулой:


Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.


Линейная и угловая скорости
Линейная скорость
Определение и формулыЛинейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
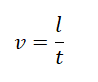
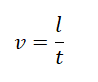
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:


R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:


Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
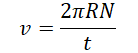
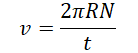
Угловая скорость
Определение и формулыУгловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).


ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные фактыРадиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
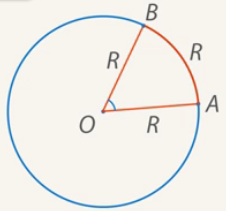

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
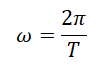
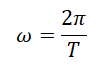
Выражая угловую скорость через частоту, получим:
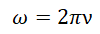
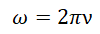
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
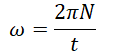
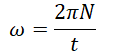
Сравним две формулы:
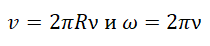
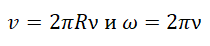
Преобразуем формулу линейной скорости и получим:
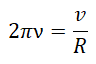
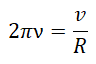
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
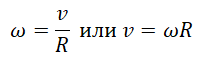
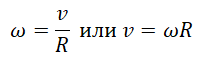
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.


За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формулаЦентростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
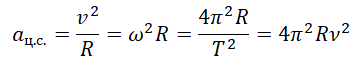
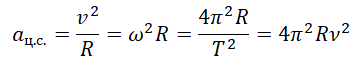
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:


Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:


Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:


Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
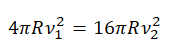
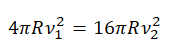
Произведем сокращения и получим:


Или:
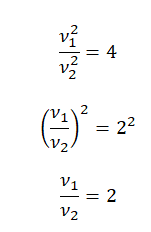
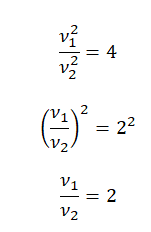
Отсюда:
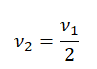
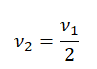
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: бpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18273 Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
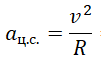
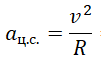
Подставляем известные данные в формулу и вычисляем:
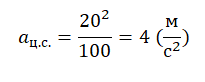
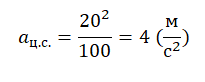
pазбирался: Алиса Никитина | обсудить разбор | оценить
Предложения со словосочетанием ЦЕНТРОСТРЕМИТЕЛЬНОЕ УСКОРЕНИЕ
Из (14. 5) легко получить формулу для центростремительного ускорения ацс. Если не помните из физики про центростремительное ускорение, то приведу простенькую схемку (см. В этом случае центростремительное ускорение строго симметрично, его гравитационное поле остаётся однородным, так что волны гравитации возникнуть не могут. Юбки вновь полетели из шкафа с центростремительным ускорением. Во время такого спинового вращения атомные ядра химических элементов, во-первых, образуют внутренние вектора центростремительного ускорения, которые проявляются как планетная масса, а во-вторых, синхронно перемещаются на бесконечно малые величины к центру тяжести планеты и образуют внешний суммарный вектор силы земного тяготения.
 Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: схлёстываться — это что-то нейтральное, положительное или отрицательное?
Положительное
Отрицательное
При образовании центростремительного ускорения, атомные ядра поглощают осколки фотонных квантов межатомных и межмолекулярных пространств и создают разряжение между атомным ядром и защитными оболочками электронных орбиталей атомов и молекул. Однако, например, в так называемой двойной звёздной системе, где массы обоих тел очень велики, радиусы их орбит достаточно малы, а центростремительные ускорения огромны, излучением гравитационных волн пренебречь нельзя. Сверхсветовое вращение (зарядка) с центростремительным ускорением магнитного заряда по волноводу в замкнутом фазовом пространстве электрона индуктирует в нём определённые инертные свойства, присущее всем механическим гироскопам — это и есть инертность и гравитационная масса покоя. Одна из основных компонент — центральна и индуктирована движением с определённой стороной вращения от центра микрочастиц по волноводам с центростремительным ускорением по окружностям увеличивающегося радиуса к поверхности. Внутренние свойства электрона, ответственные за это внешнее проявление, обусловлены движением резонансного полярного вихрона, в котором магнитный монополь периодически и всегда движется-вкручивается в одном направлении в сторону к центру поверхности полусферы, а также вращается с центростремительным ускорением вокруг электрического, причем последний оставляет в его фазовом замкнутом объёме электропотенциалы таким образом, размещённые на полусферическом замкнутом волноводе, что в окружающем пространстве создаётся его размер определённой структуры, электрический заряд, спин и собственный гравитационный заряд, жёстко связанный с этим его размером. К слову, если бросить камень в озеро, то сможем наблюдать работу этих сил наглядно: объект будет лететь до определённой точки; затем, поворот траектории и центростремительное ускорение камня к воде, оказывающее толчок на поверхность воды; толчок, в свою очередь, провоцирует центробежную силу, разносящую колебания воды по всему озеру, и выводящее его за пределы берегов. Специфика центростремительного ускорения в классической модели вращательного движения состоит в том, что оно не сообщает поступательного приращения движения в направлении своего действия. Однако изменение направления линейной скорости происходит исключительно только с центростремительным ускорением, о чём, не задумываясь ни на секунду, вам скажет каждый школьник! Классическое центростремительное ускорение ассоциируется в классической физике с единым линейным ускорением, направленным к центру вращения. Из классической физики, а именно из понятия годографа известно, что центростремительное ускорение — это линейная скорость линейной скорости. Никакого центростремительного ускорения по вращению радиальной скорости в его составе нет. По-разному будут вращаться только колёсики тележки, но и в их вращении будет проявляться только центростремительное ускорение. Если быть точными до конца, то нет и самого центростремительного ускорения вместе с центробежным ускорением, т. к. Их фраза: «… а также прибавляется ускорение в результате изменения центростремительного ускорения точки» (см. Получается, что центростремительное ускорение всегда перпендикулярно скорости. Это самое центростремительное ускорение и показывает, насколько сильно меняется направление твоего движения (по-умному — направление вектора скорости). Центростремительное ускорение показывает, как меняется направление вектора скорости, оно всегда направлено к центру. Центростремительное ускорение для первого составляет см/с2, так как радиус кругового пути на 60-й параллели равен 3200 км. Разница в величине центростремительного ускорения обоих поездов равна см/с2. Разницу между центростремительным ускорением и линейным замедлением ты, я надеюсь, помнишь? Следовательно, непрерывное изменение вектора скорости, например, центростремительным ускорением, приведёт к изменению характера воспоминаний. Движение с центростремительным ускорением (непрерывное изменение вектора скорости) это обычное вращательное движение. Назовите хоть одного человека, которому в обыденной жизни пригодилась функция F (x) или формула центростремительного ускорения. Но это есть не что иное, как равномерное вращательное движение, динамику которого с классической же точки зрения определяет исключительно только центростремительное ускорение. Фактически это означает, что приращение линейной скорости в направлении переносного вращения по абсолютной величине никак не сказывается на приращении радиальной скорости относительного движения по направлению, и наоборот — центростремительное ускорение, характеризующее изменение радиальной скорости относительного движения по направлению не имеет никакой корреляции с приращением линейной скорости переносного вращения по абсолютной величине. Однако в составе годографа абсолютной скорости даже зрительно всегда несложно увидеть приращение, обусловленное именно центростремительным ускорением переносного вращения. Однако при этом никто не утверждает, что центростремительное ускорение состоит из двух независимых ускорений — ускорения по изменению направления линейной скорости вращательного движения и поступательного радиального ускорения. Так, например, радиальное центростремительное ускорение в классической физике не имеет под собой реального приращения радиального движения тела и определяется только через годограф линейной скорости. Но, как мы показали выше, классическая динамика вращательного движения не учитывает затраты на преобразование движения по направлению, которые и показывает классическое же центростремительное ускорение. Но если угловая скорость абсолютного вращения с постоянным радиусом так же постоянная, то все составные вращения, которые появляются в формуле разложения центростремительного ускорения по формуле квадрата суммы двух чисел, это так же есть равномерные вращательные движения. В нашей модели равномерного вращательного движения центростремительное ускорение представляет собой академическую величину, в которой обобщены все ускорения, проявляющиеся на микроуровне в пределах одного полного цикла формирования сложного по своей реальной физической структуре вращательного движения. Именно поэтому обобщённое центростремительное ускорение в классической физике всегда считалось ускорением простого движения с простым линейным вращающимся ускорением, направленным к центру вращения. Он просто не видит этих промежуточных звеньев, а ощущает он только единое и неделимое абсолютное центростремительное ускорение в виде своего увеличившегося веса. Даже с точки зрения классической физики из конечного результата формулы для центростремительного ускорения равномерного вращательного движения однозначно следует, что в нём вращается только одна абсолютная линейная скорость только с одной абсолютной угловой скоростью под действием только одной центростремительной силы и с одним центростремительным ускорением. Как отмечалось выше разложение центростремительного ускорения равномерного вращательного движения по формуле квадрата суммы двух чисел это ещё не абсурд, а всего лишь математическая абстракция. Гравитационная втягивающая сила ртутного шара величиной 5, 6157 х10 — 9н — создаёт центростремительное ускорение для свинцового шара, а, следовательно, его центростремительную силу, которая и уравновешивает инерционную силу взаимодействия (силу упругости) свинцового шара. Следует отметить, что центростремительное ускорение меняет только направление вектора скорости, не влияя на его величину; ускорение ac направлено по радиусу окружности к её центру. Линейное ускорение спуска по горке переходит в центростремительное ускорение вращательного движения вокруг центра круга, где сидит на лыже рыжий ирландский сеттер, держащий в зубах алюминиевую палку, который внезапно на несколько порядков увеличил силу трения в данной точке. Последняя сформирована движением внутри него от центра квантов по волноводам с центростремительным ускорением по окружностям увеличивающегося радиуса к поверхности. Каждому увеличению линейной скорости прямолинейного движения, которое преобразуется во вращательное движение, неизменно сопутствует увеличение центростремительного ускорения. Причём сначала должна увеличиться именно скорость прямолинейного движения тела и, только потом в процессе дополнительного удлинения связующего тела и роста силы упругости возникает и новое центростремительное ускорение нового вращательного движения. Без дополнительного удлинения связующего тела, в результате которого в свою очередь и обеспечивается рост силы упругости невозможно физически обосновать рост центростремительного ускорения.Нормальное или центростремительное ускорение
В физике мы говорим, что тело имеет ускорение, когда происходит изменение вектора скорости, будь то по величине или направлению. В предыдущих разделах мы видели, что ускорение можно классифицировать в соответствии с эффектом, который оно производит на скорость, на тангенциальное ускорение (если оно изменяет величину вектора скорости) и на нормальное или центростремительное ускорение (если оно меняет свое направление. ). Это внутренние компоненты ускорения.В этом разделе мы более подробно изучим нормальное или центростремительное ускорение.
Нормальное или центростремительное ускорение
Нормальное или центростремительное ускорение измеряет изменений направления скорости во времени. Дается выражением:
Где:
- a → n: нормальное или центростремительное ускорение тела
- v: Скорость тела в исследуемой точке
- ρ: Радиус кривизны.В случае кругового движения он равен радиусу окружности
Нормальное ускорение может быть:
- = 0: при прямолинейном движении, при котором направление остается постоянным
- > 0: В криволинейном движении, при котором направление скорости изменяется
Обратите внимание, что любую траекторию, описываемую телом, можно рассматривать как комбинацию прямых и изогнутых траекторий. Криволинейные участки траектории также можно рассматривать как дуги окружности.Следующее изображение иллюстрирует эту концепцию

Внутренние компоненты ускорения
Тангенциальное ускорение (при →) | Нормальное ускорение (an →)
Как мы видим, центр кривизны в точке искривленной траектории совпадает с центром круга, который проходит через нее. Радиус этого круга — это радиус кривизны в этой точке.
Демонстрация нормального ускорения
Ранее мы видели, что мгновенное ускорение является производной скорости по времени.С другой стороны, мы видели, что мы можем выразить вектор скорости как произведение его величины и единичного вектора, касательного к траектории: v → = v⋅u → t Если мы развиваем эти две идеи, мы получаем:
a → = dv → dt = d (v · u → t) dt = ⏞D (a⋅b) dvdtu → t + vdu → tdt
Где мы применили производную от правила произведения D (ab) = a’b + ab ‘.
Мы видим, что второй член является произведением величины скорости и производной u → t по времени. Мы можем продемонстрировать, что этот вектор на самом деле нормален к пути:

Выразим u → t как функцию общего угла θ
u → t = cosθi → + sinθj →
Применяем цепное правило
du → tdt = du → tdθdθdt = -sinθi → + cosθj → dθdt = u → ndθdt = ⏞θ = s / ρu → n1ρdsdt = ⏞s = vtvρu → n
Из ранее упомянутого мы делаем вывод, что:
a → = dvdtu → t + vdu → tdt = dvdtu → t + vvρu → n = dvdtu → t + v2ρu → n
Термин в рамке соответствует нормальному центростремительному ускорению или и отвечает за изменение направления скорости с течением времени.
,10.4: Соотношение угловых и поступательных величин
Цели обучения
- Учитывая линейное кинематическое уравнение, напишите соответствующее вращательное кинематическое уравнение
- Вычисление линейных расстояний, скоростей и ускорений точек вращающейся системы с учетом угловых скоростей и ускорений
В этом разделе мы связываем каждую из вращательных переменных с трансляционными переменными, определенными в «Движение по прямой линии» и «Движение в двух и трех измерениях».Это завершит нашу способность описывать вращения твердого тела.
Угловые и линейные переменные
В вращательных переменных мы ввели угловые переменные. Если мы сравним определения вращения с определениями линейных кинематических переменных из «Движение по прямой линии» и «Движение в двух и трех измерениях», мы обнаружим, что существует отображение линейных переменных во вращательные. Линейное положение, скорость и ускорение имеют свои вращательные аналоги, как мы можем видеть, когда пишем их рядом:
| линейная | ротационный | |
|---|---|---|
| Позиция | $$ x $$ | $$ \ theta $$ |
| Скорость | $$ v = \ frac {dx} {dt} $$ | $$ \ omega = \ frac {d \ theta} {dt} $$ |
| Разгон | $$ a = \ frac {dv} {dt} $$ | $$ a = \ frac {d \ omega} {dt} $$ |
Давайте сравним линейные и вращательные переменные по отдельности.Линейная переменная положения имеет физические единицы измерения в метрах, тогда как переменная углового положения имеет безразмерные единицы радиан, как видно из определения \ (\ theta = \ frac {s} {r} \), которое является отношением двух длин. Линейная скорость измеряется в м / с, а угловая скорость — в рад / с. В разделе «Вращательные переменные» мы видели в случае кругового движения, что линейная тангенциальная скорость частицы на радиусе r от оси вращения связана с угловой скоростью соотношением v t = r \ (\ omega \) ,Это также может относиться к точкам на твердом теле, вращающемся вокруг фиксированной оси. Здесь мы рассматриваем только круговое движение. В круговом движении, как равномерном, так и неоднородном, существует центростремительное ускорение (движение в двух и трех измерениях). Вектор центростремительного ускорения направлен внутрь от частицы, совершающей круговое движение, к оси вращения. Вывод величины центростремительного ускорения дан в «Движении в двух и трех измерениях». Исходя из этого вывода, величина центростремительного ускорения оказалась равной
.\ [a_ {c} = \ frac {v_ {t} ^ {2}} {r}, \ label {10.14} \]
где r радиус окружности.
Таким образом, при равномерном круговом движении, когда угловая скорость постоянна, а угловое ускорение равно нулю, мы имеем линейное ускорение, то есть центростремительное ускорение, поскольку тангенциальная скорость в уравнении \ ref {10.14} является постоянной. Если присутствует неравномерное круговое движение, вращающаяся система имеет угловое ускорение, и у нас есть как линейное центростремительное ускорение, которое изменяется (потому что v t изменяется), так и линейное тангенциальное ускорение.
.Чем центростремительное ускорение отличается от линейного ускорения?
Наука
- Анатомия и физиология
- астрономия
- астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- физика
математический
- Алгебра
- Исчисление
- Геометрия
- Prealgebra
- тригонометрия и алгебра

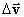 .
.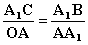 или, переходя к физическим обозначениям
или, переходя к физическим обозначениям 
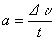 и
и  . Тогда:
. Тогда: 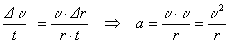 .
.
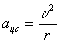
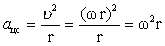 .
.
Leave A Comment