Тест «Проверь себя». ГИА (Четырёхугольники)
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Методическая разработка к уроку
математики в 9 классе
Мамаева Татьяна Евгеньевна
Учитель математики
МБОУ «СОШ № 11»
г.Бологое Тверской области
2. Тест «Проверь себя» ГИА (Четырёхугольники)
1.Укажите в ответе номера верныхутверждений.
1)В любом выпуклом четырёхугольнике все углыострые.
2)Существует выпуклый четырёхугольник, все углы
которого-острые.

3)В любом выпуклом четырёхугольнике все углыпрямые.
4)Существует выпуклый четырёхугольник, все углы
которого –прямые.
5)В любом выпуклом четырёхугольнике все углытупые.
6)Существует выпуклый четырёхугольник, все углы
которого-тупые.
2.Укажите в ответе номера верных
утверждений.
1)Есть один из углов параллелограмма — острый, то и
остальные его углы — острые.
2)Если один из углов трапеции — острый, то и
остальные её углы — острые.
3)Если один из углов параллелограмма-прямой, то и
остальные его углы-прямые.
4)Если один из углов трапеции прямой, то и
остальные её углы-прямые.
5)Если один из углов параллелограмма-тупой,то и
остальные его углы-тупые.
её углы-тупые.
3.Укажите в ответе номера верных
утверждений.
1)В любом ромбе диагонали равны.
2)В любом ромбе диагонали перпендикуляры.
3)В любом прямоугольнике диагонали равны.
4)В любом прямоугольнике диагонали
перпендикулярны.

5)В любой трапеции диагонали равны.
6)В любой трапеции диагонали
перпендикулярны.
4.Укажите в ответе номера
неверных утверждений.
1)В любом прямоугольнике диагонали
равны.
2)Существует прямоугольник, диагонали
которого различны.
3)В любом ромбе диагонали равны.
различны.
5)В любой трапеции диагонали равны.
6)Существует трапеция, диагонали которой
различны.
5.Укажите в ответе номера неверных
утверждений.
1)В любом ромбе все стороны равны.
2)Существует ромб, все стороны которогоразличны.
3)В любом прямоугольнике все стороны равны.
4)Существует прямоугольник, все стороны
которого-различны.
5)В любой трапеции все стороны равны.
6)Существует трапеция, все стороны которойразличны.
6.Укажите в ответе номера верных
утверждений.
1)В любом параллелограмме есть хотя бы один
острый угол.
2)В любом параллелограмме есть хотя бы один
прямой угол.
3) В любом параллелограмме есть хотя бы один
тупой угол.
4)В любой трапеции есть хотя бы один острый
угол.
5)В любой трапеции есть хотя бы один прямой
угол.
6)В любой трапеции есть хотя бы один тупой угол.
Правильные ответы
1)4
2)3
3)2,3
4)2,3,5
5)2,3,4,5
6)4,6
English Русский Правила
Укажите номера верных утверждений. — КиберПедия
1) В любой ромб можно вписать окружность.
2) В прямоугольном треугольнике косинус одного из углов равен 0.
3) Отношение площадей подобных треугольников равно коэффициенту подобия.
Укажите в порядке возрастания номера неверных утверждений.
1) Ромб, диагонали которого равны, является квадратом.
2) Противоположные углы параллелограмма равны между собой.
3) тангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету.
4) если в треугольнике все углы равны между собой, то это – равносторонний треугольник.
5) сумма углов треугольника равна 180 градусам.
Укажите в ответе номера неверных утверждений.
1) Около любого прямоугольника можно описать окружность.
2) В любой ромб можно вписать окружность.
3) Если в параллелограмм можно вписать окружность, то этот параллелограмм – ромб.
4) Если около параллелограмма можно описать окружность, то этот параллелограмм – прямоугольник.
5) Если в трапецию можно вписать окружность, то эта трапеция – равнобедренная.
Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
2) Середина гипотенузы прямоугольного треугольника равноудалена от всех его сторон.
3) Сумма углов выпуклого четырехугольника не превышает 3600 .
4) Если две стороны и три угла одного треугольника равны соответственно двум сторонам и трем углам другого треугольника, то такие треугольники равны.
5) Существует треугольник, в котором точка пересечения серединных перпендикуляров, проведенных ко всем его сторонам, лежит на одной из этих сторон.
Укажите в ответе номера неверных утверждений.
1) В любом ромбе все стороны равны.
2) Существует ромб, все стороны которого – различны.
3) В любом прямоугольнике все стороны равны.
4) Существует прямоугольник, все стороны которого – различны.
5) В любой трапеции все стороны равны.
Итоговый тест по теме: Основные теоремы и факты. Вариант 2.
1. Какие из данных утверждений верны? Запишите их номера.
1) Любой параллелограмм можно вписать в окружность.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти прямые параллельны.
3) Точка пересечения двух окружностей равно удалена от центров этих окружностей.
2. Какие из данных утверждений верны?
1) Сумма углов любого выпуклого шестиугольника равна 940°
2) В любой параллелограмм можно вписать окружность.
3) Существует только одна точка, равноудаленная от всех вершин данного треугольника.
4) Одна из высот прямоугольного треугольника всегда делит его на два подобных треугольника.
3. Укажите в порядке возрастания номера неверных утверждений:
1) Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
2) Соседние углы параллелограмма равны между собой.
3) Сумма углов треугольника равна 90°.
4) Параллелограмм, диагонали которого равны, является прямоугольником
5) Если в треугольнике два угла равны между собой, то это – равнобедренный треугольник.
4. Укажите в ответе номера неверных утверждений.
1) В любом прямоугольнике диагонали равны.
2) Существует прямоугольник, диагонали которого различны.
3) В любом ромбе диагонали равны.
4) Существует ромб, диагонали которого различны.
5) В любой трапеции диагонали равны.
5. Какие из следующих суждений верны?
1) если в ромбе диагонали равны, то этот ромб – квадрат.
2) Середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин.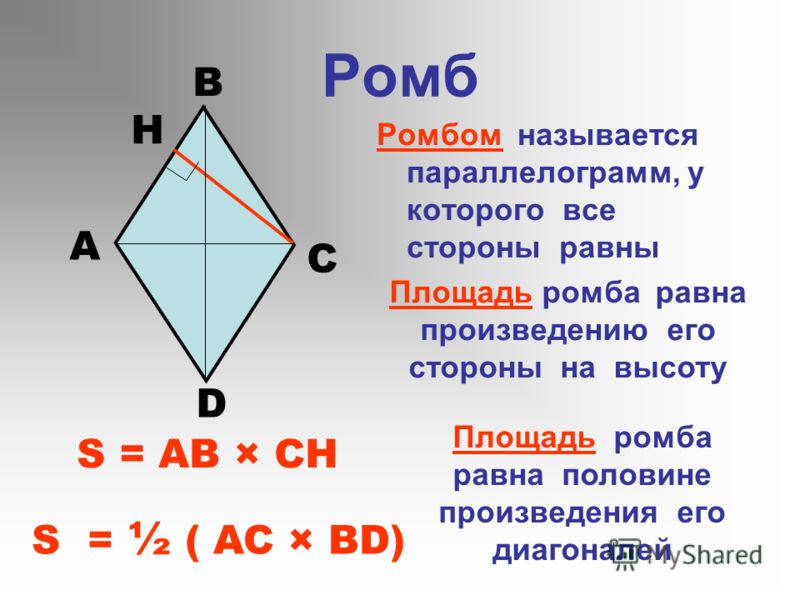
3) Сумма углов треугольника не превышает 180°.
4) Если сторона и три угла одного треугольника равны стороне и трем углам другого треугольника, то такие треугольники равны.
5) Существует треугольник, все высоты которого пересекаются в одной из его вершин.
6. Укажите в ответе номера верных утверждений.
1) В любом параллелограмме есть хотя бы один острый угол.
2) В любом параллелограмме есть хотя бы один прямой угол.
3) В любом параллелограмме есть хотя бы один тупой угол.
4) В любой трапеции есть хотя бы один острый угол.
5) В любой трапеции есть хотя бы один тупой угол.
Углы
1. В равнобедренном треугольнике угол при вершине, противолежащей основанию, равен 580.Найдите угол при основании. Ответ дайте в градусах.
2. В треугольнике АВС внешний угол при вершине А равен 125 0, а внешний угол при вершине В равен 59
3. В треугольнике АВС проведена высота СН, которая делит угол С на два угла, величины которых 470 и 710. Найдите наименьший из двух оставшихся углов. Ответ дайте в градусах.
4. В параллелограмме АВСМ прямая АС делит угол при вершине А пополам. Найдите угол, под которым пересекаются диагонали параллелограмма. Ответ дайте в градусах.
5. Угол А равнобедренной трапеции АВСD с основаниями ВС и AD равен 530. Найдите сумму углов В и С.
6. Два угла ромба относятся как 4:6. Найдите меньший угол Ответ дайте в градусах.
7. Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.
8. Найдите центральный угол АОВ, если он на 670 больше вписанного угла АСВ, опирающегося на ту же дугу.
Задачи повышенного уровня
9. Сумма углов А и В вписанного четырёхугольника АВСD равна 2040, а сумма углов В и С равна 1920. Найдите угол D.
10. Докажите, что биссектрисы смежных углов перпендикулярны.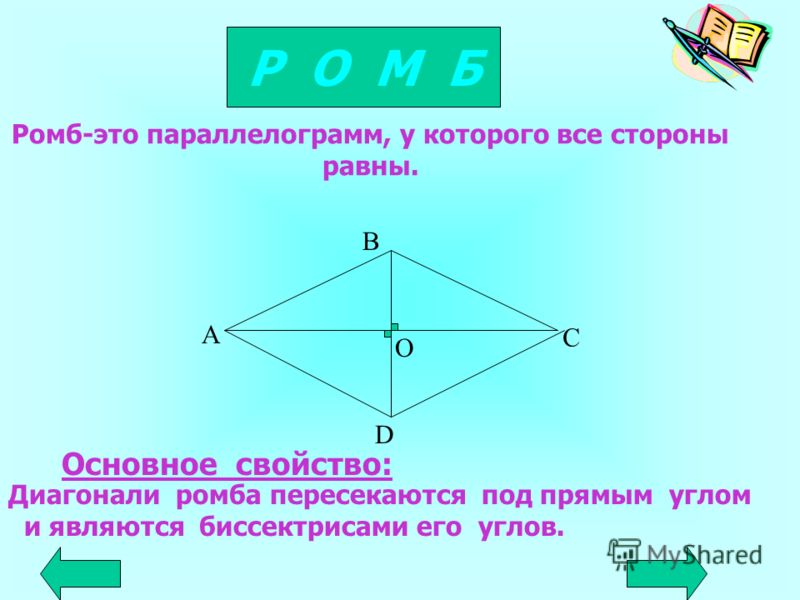
11. Докажите, что градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу.
12. Докажите, что если биссектриса пересекает основание трапеции, то от трапеции отсекается равнобедренный треугольник.
13. Биссектрисы всех внутренних углов параллелограмма попарно пересекаются. Докажите, что полученный четырёхугольник является прямоугольником.
14. Биссектриса угла В треугольника АВС делит медиану, проведённую из вершины С, в отношении 7:2, считая от вершины С. В каком отношении, считая от вершины А, эта биссектриса делит медиану, проведённую из вершины А?
Тема: Углы. Вариант 1
А
1.Какой угол (в градусах) образуют
минутная и часовая стрелки часов в 5 часов?
2. .На рисунке∠1=108°, ∠2=72°,∠5=83°. а в f
Найдите угол 4. 4
1 d
c
2 5
3. .Точка О – центр окружности ∠АОВ=84°
(см. рисунок). Найдите величину
угла AСB (в градусах) С О
А В
4. Найдите ∠ С, если ∠А=62°. В
Найдите ∠ С, если ∠А=62°. В
А О С
5. Найдите величину угла АВС. Ответ дайте в градусах
В
А С
Тема: Углы. Вариант 2
1.Точка О – центр окружности∠ВОС=50° (см. рисунок). Найдите величину угла ВАС (в градусах) А В
О С
2.На плоскости даны четыре прямые (см. рисунок) 3
.Известно, что ∠1=130°, ∠2=50°,∠3=45°. 2
Найдите ∠5. Ответ дайте в градусах. 1 6 4
3. Точка О – центр окружности,
∠АСВ=25° (см. рисунок). Найдите С О
величину угла АОВ (в градусах). А В
4 Точка О – центр окружности∠ВАС=70°
(см. рисунок). Найдите величину В
угла ВОС (в градусах). А О
С
5. Найдите величину угла АВС. Ответ дайте в градусах
В В
А С
Тема: Углы Вариант 5
1. Величина центрального угла AOD равна 1100.
Найдите величину вписанного угла ACB. Ответ дайте в градусах.
Ответ дайте в градусах.
2. В треугольнике ABC AD— биссектриса, угол С равен 300,
∠ BAD =220. Найдите угол ADB.
3. Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если ∠ВОС = 1140.
4. Отрезок АВ является диаметром окружности с центром О. Через точку В проведены касательная ВК и секущая ВМ. Докажите, что углы МВК и ВАМ равны.
Тема: Углы Вариант 6
1. Точки А, В, С и D лежат на одной окружности так, что хорды АВ и СD взаимно перпендикулярны, а ∠АСD = 550. Найдите величину угла ВDС.
2 . Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если ∠ВОС =1270. Ответ дайте в градусах.
3. Диагональ прямоугольника образует с одной из его сторон угол, равный 340. Найдите угол между прямыми, содержащими диагонали прямоугольника.
4. Отрезок АВ является диаметром окружности с центром О. Через точку В проведены касательная ВК и секущая ВМ. Докажите, что углы МВК и ВАМ равны.
Итоговый тест по теме: Углы
| 1.Хорда АВ стягивает дугу, равную 1600, а хорда АС – дугу в 600. Найдите угол ВАС. 1)700 , 2)1000, 3)1200, 4)1400 |
| 2.Найдите угол А, если угол С равен 320. |
3.Один из углов параллелограмма на 200 больше другого. Найдите наибольший угол параллелограмма (в градусах).
4. В окружности вписан равносторонний восьмиугольник. Найдите величину угла АВС . Найдите величину угла АВС .
|
5.В угол величиной 500 вписана окружность, которая касается его
| сторон в точках А и В. На одной из дуг этой окружности выбрали точку С так, как показано на рисунке. Найдите величину угла АCВ. |
Вариант-1
| 6.В треугольнике АВС АВ=ВС, а внешний угол при вершине С равен 1230. Найдите величину угла В. Ответ дайте в градусах. |
7.Сумма двух углов равнобедренной трапеции равна 960. Найдите
больший угол трапеции. Ответ дайте в градусах.
| 8.Найдите величину угла DOB, если ОЕ – биссектриса угла АОС, OD – биссектриса угла СОВ. |
9.Укажите номера неверных утверждений:
1) Если один из углов, прилежащих к стороне параллелограмма, равен 500, то другой угол, прилежащий к той же стороне, равен 400.
2) Если вписанный угол равен 240, то дуга окружности, на которую опирается этот угол, равна 480.
3) Внешний угол треугольника равен сумме двух его внутренних углов.
10. В треугольник АВС АС=18, АВ=12. Точки L и K отмечены на сторонах АС и АВ так, что АL= 6 и АК= 9. Докажите, что углы АВС и АLK равны.
Итоговый тест теме: Углы
- Хорда АВ стягивает дугу, равную 140°, а хорда ВС – дугу 60°. Найдите угол АВС. А
В С
- Найдите угол С, если АВ = ВС.
- Один из углов параллелограмма на 40° больше другого.
Найдите наименьший угол параллелограмма (в градусах).
| 4.В окружность вписан равносторонний восьмиугольник. Найдите величину угла АВС (см. рисунок). |
5.В угол величиной 70° вписана окружность, которая касается его сторон в точках А и В. На одной из дуг этой окружности выбрали точку С так, как показано на рисунке. Найдите величину угла АСВ.
Найдите величину угла АСВ.
Вариант 2
| 6.В треугольнике АВС АВ=ВС, а внешний угол при вершине С равен 132°. Найдите величину угла В. Ответ дайте в градусах. |
7.Сумма трёх углов равнобедренной трапеции равна 234°. Найдите меньший угол трапеции. Ответ дайте в градусах.
8.Найдите величину угла АОЕ, если ОЕ – биссектриса угла АОС, ОD – биссектриса угла СОВ, угол DOВ равен 250 .
9.Укажите номера верных утверждений:
1) Если один из углов вписанного в окружность четырехугольника равен 63°, то противоположный ему угол четырехугольника равен 117°.
2) Если дуга окружности составляет 73°, то вписанный угол, опирающийся на эту дугу, равен 730 …
3) Противоположные углы параллелограмма равны…
10.В треугольнике АВС АС = 24, ВС = 12. Точки L и K отмечены на сторонах АС и ВС так, что LC = 4 и КС = 8. Докажите, что углы ВАС и LKC равны.
Почему диагонали ромба не равны?
Ромб — разновидность четырехугольника. Ромб — частный случай параллелограмма, его диагонали пересекаются под углом 90°. Его также называют ромбом, потому что форма ромба имеет форму ромба.
Четырехугольник определяется как многоугольник, имеющий четыре стороны и четыре вершины, которые охватывают четыре угла. Сумма внутренних углов любого четырехугольника равна 360°. Они бывают шести типов:
- Параллелограмм
- Трапеция
- Квадрат
- Прямоугольник
- Воздушный змей
- Ромб
Ромб
Ромб можно определить как специальный параллелограмм или четырехугольник, так как он удовлетворяет всем условиям параллелограмма, и с двумя парами параллельных сторон, но можно сказать, что это тип параллелограмма с четырьмя конгруэнтными сторонами. Следовательно, ромб соответствует всем свойствам параллелограмма. Мы можем заметить на рисунке ниже, что все стороны остаются одинаковой длины, а противоположные стороны остаются параллельными.
Ромб
Является ли квадрат разновидностью ромба?
- У ромба все стороны равны, и Квадрат также имеет сходство с этим свойством.
- Диагонали квадрата делят противоположные углы пополам и перпендикулярны друг другу.
Вот почему квадрат является разновидностью ромба.
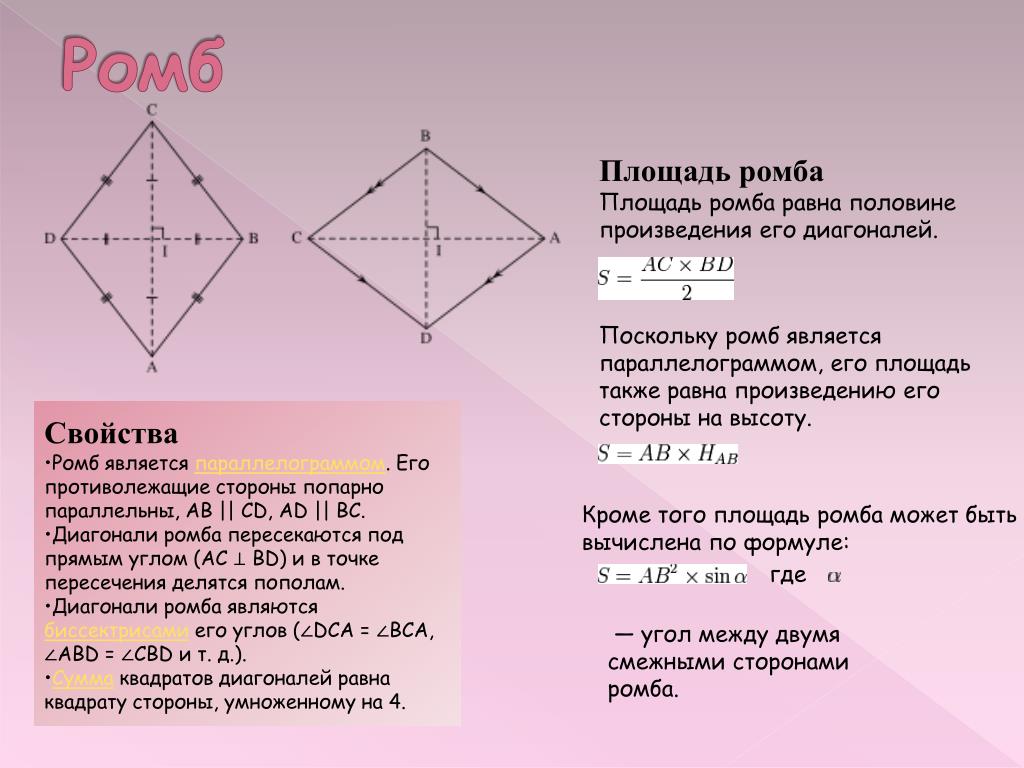
Формулы для ромба
Площадь ромба
Площадь ромба – это область, покрытая внутри плоскости или внутри стороны. Площадь ромба равна:
Area of Rhombus = (d1 x d2)/2 square units
Show that the area of Rhombus is (d1 × d2)/2 square units
Proof:
Рассмотрим треугольник ACD
Площадь треугольника ACD = 1/2 × AD × d1/2 = 1/4 × CD × d1 — (Площадь треугольника = 1/2 × основание × высота)
Площадь треугольника ABD = 1 /2 × AD × d2/2 = 1/4 × AB × d1
Площадь ромба = площадь треугольника ACD + площадь треугольника ABD
= 1/4 × AD × D1 + 1/4 × AD × D1
= 1/4 × AD (D1 + D1)
= 1/4 × AD × 2D1
= 1/2 (D1 × d2) (AD = d1)
Следовательно, площадь ромба равна (d1 × d2)/2 квадратных единиц.
Периметр ромба
Периметром ромба называется общая длина границ, покрывающих его длину, или сумма всех его четырех сторон, называемая его периметром.
Периметр ромба = 4a единиц
Свойства ромба
Ниже приведены важные свойства ромба, такие как:
Свойства ромба, основанные на этой фигуре
- выше рис. AB = BC = CD = DA).
- Противоположные стороны ромба параллельны (на приведенном выше рис. AB //el CD и AC //el BD).
- Противолежащие углы ромба равны (∠C = ∠B и ∠A = ∠D).
- Диагонали делят друг друга пополам под прямым углом (∠COD = ∠DOB = ∠BOA = ∠AOC = 90°).
- Диагонали ромба делят углы ромба пополам (при делении пополам все углы равны).
- Сумма двух смежных углов равна 180 градусам (∠ACD + ∠CDB = 180°).
- Четыре прямоугольных треугольника образованы двумя диагоналями ромба, конгруэнтными друг другу
- Если соединить середины диагоналей, получится еще один ромб.

- Нет возможности описать окружность вокруг ромба.
- Также в ромб нет вписанной окружности
- Там, где середины всех сторон соединены между собой, будет прямоугольник, а размеры, т.е. длина и ширина этого прямоугольника основного значения диагонали, следовательно, площадь прямоугольника составляет половину ромба.
Пример вопросаВ ромбе диагонали перпендикулярны друг другу, но не равны по длине. Это означает, что диагонали делят друг друга пополам.
В частном случае ромба, если все 4 угла равны по 90° каждый, то это случай квадрата, где диагонали равны по размеру и перпендикулярны друг другу.
Вопрос 1: Найдите площадь ромба, если его диагонали равны 9см и 8см.
Решение:
Площадь ромба = (d1 × d2)/2
= (9 × 8)/2 = 72/2
= 36 см 2
Вопрос 2: Если площадь ромбы составляет 121 см 2 , а мера длины — 22 см. Найдите диагонал ромба.
Найдите диагонал ромба.
Решение:
Дано,
Площадь ромба = 121 см 2
скажем, d1 = 22 см.
Площадь ромба, A = (d1 × d2)/2
121 = (22 × d2)/2121 = 11 × d2
или d2 = 11 см
Следовательно, длина другой диагонали равна 11 см.
Вопрос 3: Если периметр ромба равен 120 см, вычислите его длину.
Решение:
Периметр ромба = 4 × с
120 = 4 × с
или
S = 120/4 = 30
Все стороны ромба равны = 30 см
Вопрос 4: Найдите периметр ромба, если его диагонали равны 20 и 48 см.
Решение:
D1 = 20 см и D2 = 48 см
OA = AD/2 = 48/2 = 24 см
OC = BC/2 = 20/2 = 10CM
в Triangle AOC
9/2 = 10cm
.
используя теорему Пифагора
AC 2 = OA 2 + OC 2
AC = √(24) 2 + (10) 2
AC = √576 + 100 = √676 = 26 см
Периметр ромба = 4×сторона = 4×26 = 104 см 2 и 40см.
Решение:
Площадь ромба = B × H
200 = B × 40
B = 200/40 = 5 см
Вопрос 6: Найти периметр из ромба, область которой является область, область которой является. 315см 2 и высота 15см.
Решение:
Площадь ромба = B × H
315 = B × 15
B = 315/15 = 21 CM
Периметр Rhombus = 4 × 4 × 21 = 84C
Вопрос 7: Найдите высоту ромба, площадь и периметр которого равны 315см 2 и 180см 2 соответственно.
Решение:
Периметр ромба = 180см
4×s = 180
s = 45cm
Area of rhombus = b × h
315 = 45 × h
h = 315/45
h = 7cm
Definition, Angles, Properties, Формулы, примеры
Ромб – четырехугольник, у которого все стороны равны.
Так как противоположные стороны параллелограмма равны, то ромб является особым типом параллелограмма, у которого все стороны равны.
Разница между квадратом и ромбом в том, что все углы квадрата прямые, но углы ромба не обязательно должны быть прямыми.
Ромб можно найти в различных вещах вокруг нас, таких как кольца на пальцах, ромбовидная серьга, структура оконного стекла и т. д.
Площадь ромба вычисляется путем нахождения произведения его основания и соответствующей высота (высота).
Если известны длины диагоналей ромба, то его площадь равна половине их произведения.
Итак, площадь ромба = $\frac{(d1\times d2)}{2}$ квадратных единиц; где d1 и d2 — диагонали ромба.
Периметр ромба равен сумме длин его границ. Поскольку все четыре стороны ромба равны, его периметр рассчитывается путем умножения длины его стороны на 4.
То есть периметр ромба = 4 × единиц; где ‘ a ’ — длина стороны ромба.
Пример 1: Длины двух диагоналей ромба 18 см и 12 см.
Найдите площадь ромба.
Площадь ромба = $\frac{(d1\times d2)}{2}$ = $\frac{(18\times 12)}{2}$ кв.см = 108 кв.см
Пример 3: Площадь ромба 56 кв.см. Найдите длину другой диагонали, если длина одной из его диагоналей равна 14 см.
1
Какой из следующих четырехугольников определенно является ромбом?
Трапеция
Прямоугольник
Квадрат
Параллелограмм
Правильный ответ: Квадрат
Все стороны квадрата равны, значит все квадраты ромбы.2
Если длина одной из сторон ромба равна 10 см. Какова будет длина противоположной стороны данного ромба?
5 см
10 см
20 см
40 см
Правильный ответ: 10 см
Все стороны ромба равны по длине.3
Какой будет высота ромба, площадь которого 320 кв.см, а сторона 40см?
4 см
6 см
8 см
10 см
Правильный ответ: 8 см
Площадь = основание × высота
⇒ 320 = 40 × высота
⇒ Высота = 320 ÷ 40 = 8 см9 49 49 49
Площадь пола зала 500 000 кв.
см. Если пол должен быть покрыт плиткой с каждой диагональю 40 см и 25 см, найдите необходимое количество плиток.
50
500
1000
5000
Правильный ответ: 1000
Площадь пола = 500 000 кв. см
Площадь каждой плитки = $\frac{(d1\times d2)}{2}$ = $\frac{40\times 25}{2}$ = 500 кв. см
Количество плиток = Площадь пола ÷ Площадь 1 плитки
= 500 000 ÷ 500
= 1000 плиток
Итак, для покрытия требуется 1000 плиток пол.Каковы основные свойства ромба?
- Все стороны имеют одинаковую длину.
- В ромбе противоположные углы равны.
- Диагонали делят друг друга пополам в 90 градусов.
- Смежные углы в сумме дают 180 градусов.
Является ли ромб правильным многоугольником?
Нет, ромб не является правильным многоугольником. У правильного многоугольника все углы должны быть одинаковыми (равными).
Диагонали ромба делят фигуру на какие фигуры?
Две диагонали ромба образуют четыре прямоугольных треугольника.


 используя теорему Пифагора
используя теорему Пифагора Так как противоположные стороны параллелограмма равны, то ромб является особым типом параллелограмма, у которого все стороны равны.
Так как противоположные стороны параллелограмма равны, то ромб является особым типом параллелограмма, у которого все стороны равны. Найдите площадь ромба.
Найдите площадь ромба.  см. Если пол должен быть покрыт плиткой с каждой диагональю 40 см и 25 см, найдите необходимое количество плиток.
см. Если пол должен быть покрыт плиткой с каждой диагональю 40 см и 25 см, найдите необходимое количество плиток.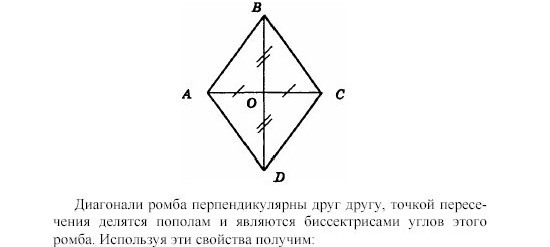
Leave A Comment