Сумма углов треугольника — урок. Геометрия, 7 класс.
Сумма углов треугольника равна \(180°\).

Доказательство
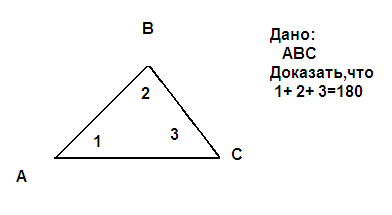
Рассмотрим произвольный треугольник \(KLM\) и докажем, что ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(M =\) 180°.
Проведём через вершину \(L\) прямую \(a\), параллельную стороне \(KM\).
Углы, обозначенные \(1\), являются накрест лежащими углами при пересечении параллельных прямых \(a\) и \(KM\) секущей \(KL\), а углы, обозначенные \(2\) — накрест лежащими углами при пересечении тех же параллельных прямых секущей \(ML\).
Очевидно, сумма углов \(1\), \(2\) и \(3\) равна развёрнутому углу с вершиной \(L\), т. е.
∡ \(1\) \(+\) ∡ \(2\) \(+\) ∡ \(3 =\) 180°, или ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(M =\) 180°.
Теорема доказана.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна 90°.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
Следствие 3. В равностороннем треугольнике каждый угол равен 60°.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Доказательство
Из равенств ∡ \(KML\) \(+\) ∡ \(BML=\) 180° и ∡ \(K\) \(+\) ∡ \(L\) \(+\) ∡ \(KML =\) 180° получаем, что ∡ \(BML =\) ∡ \(K\) \(+\) ∡ \(L\).
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.

У треугольника \(KLM\) все углы острые.

У треугольника \(KMN\) угол \(K = 90\)°.
У прямоугольного треугольника сторона, лежащая против прямого угла, называется гипотенузой, а две остальные стороны — катетами.
На рисунке \(MN\) — гипотенуза, \(MK\) и \(KN\) — катеты.

У треугольника \(KLM\) один угол тупой.
Сумма углов треугольника: чему равна и как найти?
Сумма треугольника равна 180 градусов.
Это легко доказать. Нарисуйте треугольник. Через одну из его вершин проведите прямую, параллельную противоположной стороне, и найдите на рисунке равные углы. Сравните с решением в конце статьи.

А мы разберем задачи ЕГЭ, в которых фигурирует сумма углов треугольника.
1. Один из внешних углов треугольника равен 85 градусов. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85 градусов, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х. Получим уравнение
Тогда .
Ответ: 51.
2. Один из углов равнобедренного треугольника равен 98 градусов. Найдите один из других его углов. Ответ дайте в градусах.
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98 градусов?
Нет, конечно! Ведь сумма углов треугольника равна 180 градусов. Значит, один из углов треугольника равен , а два других равны .
Ответ: 41.
3. На рисунке угол равен , угол равен , угол равен . Найдите угол . Ответ дайте в градусах.

Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.

Сначала найдем угол .
Он равен
Тогда
,
Угол , смежный с углом равен .
Ответ: .
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
Ты нашел то, что искал? Поделись с друзьями!
4. Углы треугольника относятся как . Найдите меньший из них. Ответ дайте в градусах.
Пусть углы треугольника равны , и . Запишем, чему равна сумма углов этого треугольника.
Тогда .
Ответ: .
Как же все-таки доказать, что сумма углов треугольника равна 180 градусов? Очень просто. На нашем рисунке угол равен углу (они накрест лежащие). Угол равен углу (тоже накрест лежащие). Развернутый угол равен . Значит, и сумма углов треугольника тоже равна 180 градусов.
Теорема о сумме углов треугольника / Блог :: Бингоскул
Теорема о сумме внутренних углов треугольника
Сумма углов треугольника равна 180°.
Доказательство:

- Дан треугольник АВС.
- Через вершину B проведем прямую DK параллельно основанию AC.
- \angle CBK= \angle C как внутренние накрест лежащие при параллельных DK и AC, и секущей BC.
- \angle DBA = \angle A внутренние накрест лежащие при DK \parallel AC и секущей AB. Угол DBK развернутый и равен
- \angle DBK = \angle DBA + \angle B + \angle CBK
- Так как развернутый угол равен 180 ^\circ, а \angle CBK = \angle C и \angle DBA = \angle A, то получим 180 ^\circ = \angle A + \angle B + \angle C.
Теорема доказана
Следствия из теоремы о сумме углов треугольника:
- Сумма острых углов прямоугольного треугольника равна 90°.
- В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
- В равностороннем треугольнике каждый угол равен 60°.
- В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
- Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Теорема о внешнем угле треугольника
Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом
Доказательство:

- Дан треугольник АВС, где ВСD — внешний угол.
- \angle BAC + \angle ABC +\angle BCA = 180^0
- Из равенств угол \angle BCD + \angle BCA = 180^0
- Получаем \angle BCD = \angle BAC+\angle ABC.
Дополнительный материал: Теорема Пифагора
Смотри также: Основные формулы по математике
Геометрия играючи или Почему сумма углов треугольника 180° ?: fotovivo — LiveJournal
Вдогонку ко вчерашнему:
Играем с мозаикой под сказку по геометрии:
Жили-были треугольники. Такие похожие, что просто копия друг друга.
Стали они как-то рядышком на прямую линию. А так как были они все одного роста —
то и верхушки их были на одном уровне, под линеечку:

Треугольники любили кувыркаться и стоять на голове. Взобрались в верхний ряд и стали на уголок, как акробаты.
А мы уже знаем — когда они стоят верхушками ровно в линию,
то и подошвы у них тоже по линеечке — потому что если кто одного роста, то он и верх ногами одного роста!

Во всем они были одинаковые — и высота одинаковая, и подошвы один в один,
и горки по сторонам — одна круче, другая более пологая — по длине одинаковые
и наклон у них одинаковый. Ну просто близнецы! (только в разных одежках, у каждого свой кусочек пазла).

— Где у треугольников одинаковые стороны? А где уголки одинаковые?
Постояли треугольники на голове, постояли, да и решили соскользнуть и улечься в нижнем ряду.
Заскользили и съехали как с горки; а горки-то у них одинаковые!
Вот и поместились аккурат между нижними треугольниками, без зазоров и никто никого не потеснил.

Огляделись треугольники и заметили интересную особенность.
Везде, где их углы вместе сошлись — непременно встретились все три угла:
самый большой — «угол-голова», самый острый угол и третий, средний по величине угол.
Они даже ленточки цветные повязали, что б сразу было заметно, где какой.
И получилось, что три угла треугольника, если их совместить —
составляют один большой угол, «угол нараспашку» — как обложка раскрытой книги,
______________________о___________________
он так и называется: развернутый угол.
У любого треугольника — будто паспорт: три угла вместе равны развернутому углу.
Постучится к вам кто-нибудь: — тук-тук, я треугольник, пустите меня переночевать!
А вы ему — Предъяви-ка сумму углов в развернутом виде!
И сразу понятно — настоящий ли это треугольник или самозванец.
Не прошел проверку — Разворачивайся на сто восемьдесят градусов и ступай восвояси!

Когда говорят «повернуть на 180° — это значит развернуться задом наперед и
идти в обратном направлении.
То же самое в более привычных выражениях, без «жили были»:

Совершим параллельный перенос треугольника АВС вдоль оси ОХ
на вектор АВ равный длине основания АВ.
Прямая, DF проходящая через вершины С и С1 треугольников
параллельна оси ОХ, в силу того, что перпендикулярные оси ОХ
отрезки h и h1 (высоты равных треугольников) равны.
Таким образом основание треугольника А2В2С2 параллельно основанию АВ
и равно ему по длине (т.к. вершина С1 смещена относительно С на величину АВ).
Треугольники А2В2С2 и АВС равны по трем сторонам.
А стало быть углы ∠А1 ∠В ∠С2, образующие развернутый угол, равны углам треугольника АВС.
=> Сумма углов треугольника равна 180°
С движениями — «трансляциями» так называемыми доказательство короче и наглядней,
на кусочках мозаики даже малышу может быть понятно.
Зато традиционное школьное:

опирающееся на равенство внутренних накрест-лежащих углов, отсекаемых на параллельных прямых

ценно тем, что дает представление о том — почему это так,
почему сумма углов треугольника равна развернутому углу?
— Потому что иначе параллельные прямые не обладали бы привычными нашему миру свойствами.
Теоремы работают в обе стороны. Из аксиомы о параллельных прямых следует
равенство накрест лежащих и вертикальных углов, а из них — сумма углов треугольника.
Но верно и обратное: пока углы треугольника составляют 180° — существуют параллельные прямые
(такие, что через точку не лежащую на прямой можно провести единственную прямую || данной).
Если однажды в мире появится треугольник, у которого сумма углов не равна развернутому углу —
то параллельные перестанут быть параллельны, весь мир искривится и перекособочится.
________________________________________
/\__||_/\__||_/\__||_/\__||_/\__| )0( |_/\__||_/\__||_/\__||_/\__||_/\=/\__||_/
Если полосы с орнаментом из треугольников расположить друг над другом —
можно покрыть все поле повторяющимся узором, будто пол плиткой:


можно обводить на такой сетке разные фигуры — шестиугольники, ромбы,
звездные многоугольники и получать самые разные паркеты


Замощение плоскости паркетами — не только занятная игра, но и актуальная математическая задача:

________________________________________
/\__||_/\__||_/\__||_/\__||_/\__| )0( |_/\__||_/\__||_/\__||_/\__||_/\=/\__||_/
Поскольку каждый четырехугольник — прямоугольник, квадрат, ромб и проч.,
может быть составлен из двух треугольников,
соответственно сумма углов четырехугольника: 180° + 180°= 360°
Одинаковые равнобедренные треугольники складываются в квадраты разными способами.
Маленький квадратик из 2-х частей. Средний из 4-х. И самый большой из 8-ми.
Сколько на чертеже фигур, состоящих из 6-ти треугольников?

Конспект урока: Сумма углов треугольника
Тема урока: Сумма углов треугольника.
Учебник: Геометрия 7-9 класс: учебник для 7-9 класс, Погорелов А.В.Издание М.: Просвещение, 2000г.
Тип урока: изучение нового материала
Цели урока:
— образовательные: создать условия для самостоятельного формулирования и доказательства теоремы о сумме углов треугольника; организовать деятельность обучающихся по восприятию, осмыслению и первичному закреплению новых знаний и способов деятельности;
— развивающие: формировать умения участвовать в диалоге; слушать и понимать других, высказывать свою точку зрения и аргументировано ее отстаивать с помощью фактов и дополнительных сведений, принимать участие в работе парами, договариваться и приходить к общему решению;
— воспитательные: воспитывать умение уважительного отношения к сверстникам и ответственного отношения к учебному труду
Место урока в системе уроков данного раздела: 1-й урок в главе раздела «Сумма углов треугольника».
Изучаемые понятия (термины): сумма углов треугольника.
Оборудование: · Учебник Геометрия 7-9 кл, учебник для общеобразоват. учреждений /, Погорелов А.В.
М.: Просвещение, 2000г.
· Компьютер, проектор, экран.
· Презентация Microsoft Power Point.
· Шаблоны треугольников для практической работы.
— Ножницы.
Структура урока
п/п
Этап урока
Время, мин.
Задачи этапа
Планируемые результаты
УУД
Личностные
1
Организационный этап
2
Сосредоточение учащихся на учебном процессе
___
П: Формулирование собственных ожиданий.
Р: Проявление эмоционального отношения к учебно-познавательной деятельности
Проявление дисциплинированности, трудолюбия и упорства в достижении поставленных целей
2
Актуализация знаний
5
Повторение раннее изученного материала.
Владение определением :сумма углов треугольника
П: формулировать проблему
К: слушать, вести диалог в соответствии с целями и задачами общения.
Активное включение в общение и взаимодействие со сверстниками на принципах уважения и доброжелательности, взаимопомощи и сопереживания
3
Закрепление изученного материала
8
Формирование у учащихся умения применять полученные знания при решении задач.
Умение применять полученные теоретические знания при выполнении задач.
К: умение с достаточной полнотой и точностью выражать свои мысли
Л: личностное самоопределение, оценивание усваиваемого содержания
Уметь применять теоретический материал на практике.
4
Подведение итогов
3
Формирование выводов учениками по изученному материалу.
Умение анализировать общие итоги работы, сравнивать эти результаты с намеченными в начале её, выявлять причины отклонений и намечать пути их устранения в дальнейшей работе.
П: анализ и синтез информации
К: умение полно и точно выражать свои мысли
Р: прогнозирование, саморегуляция, умение оценивать правильность выполнения действий на уровне адекватной оценки
Л: способность к самооценке на уровне критерия успешности учебной деятельности
Уметь обобщить изученный материал и сделать соответствующие выводы
5
Домашнее задание
2
Выполнение комментариев по домашнему заданию
Этап урока
Деятельность учителя
Деятельность учеников
ФОУД
1
Организационный этап
Приветствую учащихся, проверяю их готовность к уроку.
Приветствуют учителя, проверяют готовность к уроку.
Ф
2
Актуализация знаний
Эпиграфом нашего урока, я хочу предложить слова Пифагора:
— Мы закончили изучение большого раздела геометрии «Параллельные прямые». Рассмотрели определение параллельных прямых, их признаки и свойства. Давайте вспомним основные понятия, связанные с параллельными прямыми. Работаем устно.
-Назовите пары односторонних углов.
Назовите пары накрест лежащих углов.
Назовите пары соответственных углов.
(Слайд 3)
-Найдите все углы, если прямая а ‖‖ в и угол 1 равен 700. (Слайд 4)
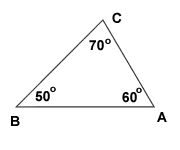
-Найдите углы 3,4,5, если АС ‖‖ m и угол 1 равен 600, Угол 2 равен 500. (Слайд 5).
— Молодцы, вы хорошо усвоили тему «Параллельные прямые». А, посмотрев следующий ролик, попытайтесь определить о чем сегодня на уроке пойдет речь.
Карнавал геометрических фигур. (Мультимедийная инсценировка).
Говорят три маски.
1 маска: — Мы дочери одной матери. Живем в одном семействе, но силы и свойства у нас разные.
2 маска: — Я очень правильная фигура. У меня все углы и стороны равны. К тому же у меня три оси симметрии.
3 маска: — А я тоже имею две равные стороны. У меня так же есть ось симметрии, а потому у меня два равных угла при основании.
1 маска: — Зато я имею прямой угол. Вот какие мы сильные и важные!
— Подумаешь, расхвастались,- сказали две маски, стоящие неподалеку,- мы тоже из вашего семейства. У меня, например, все уголки острые, а у моего друга есть один тупой угол. Но все мы обладаем замечательным свойством, которое сегодня откроют ребята.
Учитель: Ребята, как вы думаете, что скрывается за масками? Каким свойством обладают все треугольники?
— Итак, тема сегодняшнего урока «Сумма углов треугольника». (Слайд 7)
— Сегодня на уроке мы должны будем высказать гипотезу о сумме углов треугольника, потом доказать теорему о сумме углов треугольника и рассмотреть ее применение при решении задач. (Слайд 8)
Учащиеся отвечают:
(Слайд 3)
1)2 и 3, 1 и 4,6 и 7, 5 и 8
2)2 и 4,1 и 3,6 и 8, 5 и 7
3)2 и 6,3 и 7,1 и 5, 4 и 8
(Слайд 4)
∠1=∠3=∠5=∠7=700
∠2=∠4=∠6=∠8=1100
(Слайд 5)
Ð 3 =180°- (60°+50°)=70°,
Ð 4 = Ð 1 = 60°,
Ð 5 = Ð 2 = 50° .
Ответы учащихся:
-За масками скрываются треугольники.
-В любом треугольнике три угла и три стороны.
-Сумма углов любого треугольника равна 180.
-Против большего угла треугольника лежит большая сторона.
-Треугольники бывают остроугольными (если все его углы острые), тупоугольными (если один из его углов тупой), прямоугольными (если один из его углов прямой).
Записывают тему урока.
3
Изучение нового материала
Практическая работа (в парах)
Ребята, мы с вами измеряли углы и с помощью транспортира и находили их сумму еще в 5 классе. Сумма углов у всех получалась разная, но близкая к 1800 (так может получаться потому, что неточно приложили транспортир, небрежно выполнили подсчет и т.д.).
Я предлагаю найти сумму углов треугольника двумя другими способами. У каждого из вас есть на парте по одному треугольнику разных цветов. Возьмите их. Они желтого или розового цвета. Обозначьте углы треугольника цифрами 1, 2, 3. (Слайд 9)
Учащиеся с желтыми треугольниками: отрежьте два угла треугольника и приложите их к сторонам третьего угла так, чтобы все вершины были в одной точке. (Слайд 10)
Учащиеся с розовыми треугольниками: сложите углы во внутрь треугольника. Заметим, что перегибать треугольник надо по прямой параллельной к стороне, того угла который мы будем сгибать первым, а данный угол должен касаться данной стороны. (Слайд 10)
— Посмотрите, на получившуюся фигуру и скажите, какой угол образуют в сумме все углы треугольника?
— Замечаем, что все углы треугольника в сумме образуют развернутый угол.
— Чему равна градусная мера развернутого угла?
— К какому выводу мы пришли?
Можно ли быть уверенным в том, что в каждом треугольнике сумма углов равна 1800.
Можно ли измерить углы любого треугольника?
— Посмотрите карту звёздного неба. Найдите созвездие Большой Медведицы и Малой Медведицы. Найдите Полярную звезду – ориентир для путешественников и мореплавателей, — которая указывает направление на север.
Найдём ещё две яркие звезды: α-звезда Капелла в созвездии Возничего и α- звезда Вега в созвездии Лира. Мысленно соединим их отрезками, получим треугольник. Можно ли измерить углы этого треугольника? (Слайд 11)
В математике практическая работа дает возможность лишь сделать какое-то утверждение – гипотезу. Чтобы она стала истиной, её нужно доказать, убедиться, что она справедлива для любого треугольника.
Как называется утверждение, справедливость которого устанавливается с помощью доказательства
— Какую теорему нам нужно доказать?
.Доказательство теоремы. (Слайд 12)
Итак дан треугольник АВС, нужно доказать, что сумма его углов А, В, С равна 1800. Давайте оформим конспект.
Теорема: Сумма углов треугольников равна 1800.
Как доказать данную теорему?
Перед вами опорная схема, заполните пропуски в ней.
Теперь проверим (Слайд 13)
Но такой способ доказательства не единственный. Первое доказательство было дано еще Пифагором (5 в. до н.э.) В первой книге «Начала» Евклид излагает другое доказательство теоремы о сумме углов треугольника. (Слайд 14)
По готовой презентации ученик предлагает доказательство Евклида.
(Слайд 15)
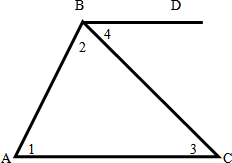
Доказательство:
1) Через вершину B проведем луч BD|| AC.
2)  4и
4и  3- накрест лежащие при BD||AC и секущей BC.
3- накрест лежащие при BD||AC и секущей BC.
3) BD|| AC и AB- секущая, то  1+
1+ ABD=180° – односторонние углы.
ABD=180° – односторонние углы.
4) тогда  1+
1+ 2+
2+ 4=180° , т.к
4=180° , т.к  4=
4= 3 ,то
3 ,то  1+
1+ 2+
2+ 3=180° или
3=180° или  A+
A+ B+
B+ C=180°
C=180°
Из данной теоремы вытекает несколько следствий справедливость которых мы с Вами сейчас обоснуем. Следствия из теоремы. (Слайд 17-19)
— Чему равен угол равностороннего треугольника?
— Чему равна сумма острых углов прямоугольного треугольника?
-Чему равен острый угол прямоугольного, равнобедренного треугольника?
А сейчас решим задачу
Дано: АВС- треугольник А: В: С = 2:3:4
Найти: А, В, С.
Решение: Пусть одна часть составляет х0. Тогда А=(2х)0,В=(3х)0,С=(4х)0. Зная, что по теореме о сумме углов треугольника А + В+ С=1800, составлю и решу уравнение.
2х+3х+4х=180,
9х=180,
х=20,
А=400, В=600, С=800.
Ответ:400,600,800.
-А теперь вы должны выполнить тест. Разделимся на 2 варианта.
Выполняют задание.
Отвечают на вопросы:
-Градусная мера развернутого угла равна 180 градусов.
-Выполнив практическую работу, мы установили, что сумма углов треугольника равна 180 градусов.
-Утверждение, справедливость которого устанавливается путем доказательства, называется теоремой.
— Сумма углов треугольника равна 180 градусов.
Теорема: Сумма углов треугольников равна 1800.

Дано: ∆ АВС
Доказать: Ð А +Ð В+Ð С =180°
Доказательство:
1) Проведём через вершину В MN II AC
2) Ð 1=Ð 4 (накрест лежащие углы при MN II AC и секущей АВ)
3) Ð 3=Ð 5 (накрест лежащие углы при MN II AC и секущей ВС)
4) Ð 4 +Ð 2+Ð 5=180° (образуют — развёрнутыйÐ МВN =180°)
5) из (2), (3), (4) получаем: Ð 1 +Ð 2+Ð 3=180°
или ÐА +Ð В+Ð С =180°
Теорема доказана

Доказательство:
1) Через вершину B проведем луч BD|| AC.
2)  4и
4и  3- накрест лежащие при BD||AC и секущей BC.
3- накрест лежащие при BD||AC и секущей BC.
3) BD|| AC и AB- секущая, то  1+
1+ ABD=180° – односторонние углы.
ABD=180° – односторонние углы.
4) тогда  1+
1+ 2+
2+ 4=180° , т.к
4=180° , т.к  4=
4= 3 ,то
3 ,то  1+
1+ 2+
2+ 3=180° или
3=180° или  A+
A+ B+
B+ C=180°
C=180°
Учащиеся отвечают:
-(60º)
-(90º)
-(45º)
Дано: АВС- треугольник А: В: С = 2:3:4
Найти: А, В, С.
Решение: Пусть одна часть составляет х0. Тогда А=(2х)0,В=(3х)0,С=(4х)0. Зная, что по теореме о сумме углов треугольника А + В+ С=1800, составлю и решу уравнение.
2х+3х+4х=180,
9х=180,
х=20,
А=400, В=600, С=800.
Ответ:400,600,800.
1 вариант
1.180 градусов
2.да
3.30 градусов
4.120 градусов
5.70 градусов.
2 вариант
1.180 градусов
2.нет
3.80 градусов
4.60 градусов
5.40 градусов
Г
4
Подведение итогов
— Какова была цель нашего урока?
-Какие определения, свойства, теоремы используются при доказательстве теоремы?
Выставление оценок.
Ответы учащихся:
-Выдвинуть гипотезу о сумме углов треугольника.
-Сформулировать и доказать теорему о сумме углов треугольника.
-Научиться решать задачи используя данную теорему
-В любом треугольнике три угла и три стороны.
-Сумма углов любого треугольника равна 180.
-Против большего угла треугольника лежит большая сторона.
-Треугольники бывают остроугольными (если все его углы острые), тупоугольными (если один из его углов тупой), прямоугольными (если один из его углов прямой).
Ф
6
Домашнее задание
Запишите домашнее задание:
Стр.46-47
Стр.52-53.Пункт 33(18,23,25,30)
Ученики записывают домашнее задание в дневники.
Стр.46-47
Стр.52-53.Пункт 33(18,23,25,30)
7
Рефлексия
(Слайд 23)
Притча: Шёл мудрец, а навстречу ему 3 человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил «Что ты делал целый день? И тот с ухмылкой ответил, что целый день возил тяжелые камни. У второго мудрец спросил «А что ты делал целый день?» и тот ответил «А я выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием «А я принимал участие в строительстве храма»
Ребята, давайте мы попробуем с вами оценить каждый свою работу за урок.
Кто возил камни? (поднимите синие треугольники)
Кто выполнял свою работу? (поднимите желтые треугольники)
Кто строил храм? (поднимите красные треугольники)
Решение домашнего задания
18.
сумма углов треугольника 180 градусов
1)180-50-30=100
2)180-40-75=65
3)180-65-80=35
4)180-120-25=35
23. Пусть х — угол при основании, тогда, т.к. треугольник равнобедренный, то составим уравнение:
1) 2х + 80° = 180°,
х = (180° — 80°) : 2, х = 50°;
2) (180° — 120°) : 2 = 30°;
3) (180° — 30°) : 2 = 75°.
Ответ: 1) 50°;2) 30°;3) 75°.
25. Пусть угол, равный 70°, является углом при вершине треугольника, тогда угол при основании будет:
½(180° — 70°) = ½ 110° = 55°.
∠1 = 55°, ∠2 = 55°, ∠3 = 70°.
Пусть угол, равный 70°, является углом при основании, тогда: 180° — 2 ⋅ 70° = 180° — 140° = 40°.
∠1 = 70°, ∠2 = 40°, ∠3 = 70°.
Ответ: 2 решения:
1) 40° и 70° или
2) 55° и 55°.
30. Все углы равны между собой и составляют 60°.
Сумма углов треугольника равна 180 °
Этот урок позволяет учащимся определить (путем измерения), что сумма углов в треугольнике равна 180 °. Урок также содержит простое доказательство этого факта и разнообразные упражнения.
1. Нарисуйте ЛЮБОЙ треугольник, который вам нравится.
(Используйте линейку!) Измерьте все его
углы. Рассчитайте сумму углов.
Это ______ °.
2.Нарисуйте здесь еще один треугольник.
Измерьте все его углы.
Рассчитайте сумму углов.
Это ______ °.
| Вы, наверное, догадались, что сумма
углы в треугольнике — 180 °. Это правда. Вот доказательство для него. Доказательство означает, что мы используем уже установленные принципы для доказательства что какое-то новое заявление всегда правда.Посмотрим, сможете ли вы понять рассуждения этого доказательства! | |||
Углы A и A ‘ соответствующие углы, поэтому ∠A = ∠A ‘. Итак, сумма углов ∠A + ∠B + ∠C равно сумме углов ∠A ‘+ ∠B’ + ∠C ‘. Три угла A ‘, B’ и C ‘вместе образуют
Прямо
угол (они по линии л ). |
3. Вычислите угол, отмеченный вопросительным знаком. Не Мера .
4.У определенного треугольника три равных угла.
Какова мера каждого угла? _______ °
Нарисуйте один с помощью транспортира.
Сделайте каждую его сторону длиной 5 см.
У этого треугольника есть особое название.
Что это?
5. Можете ли вы нарисовать треугольник,
два тупых угла?
Почему или почему нет?
6. а. Нарисуйте треугольник
с углами 65 ° и 50 °, с
а 7.Сторона 5 см между этими двумя
углы.
Начните с рисования 7,5-см
сторона.
б. Вычислите третий угол. Это _______ °.
Затем измерьте расстояние от треугольника до
чек.
г. Классифицируйте свой треугольник по его
стороны и углы:
Это _________________________
и _________________________.
|
Этот урок взят из книги Марии Миллер Math Mammoth Geometry 1 и размещен на сайте www.HomeschoolMath.net с разрешения автора.Copyright © Мария Миллер.
,
углов треугольника — Бесплатная математическая справка
Углы могут быть добавлены
Так же, как и обычные числа, углы можно складывать для получения суммы, возможно, с целью определения меры неизвестного угла. Иногда мы можем определить недостающий угол, потому что знаем, что сумма должна быть определенным значением. Помните — сумма углов в любом треугольнике равна 180 градусам.Ниже изображен треугольник ABC, где угол A = 60 градусов, угол B = 50 градусов и угол C = 70 градусов.
Если сложить все три угла в любом треугольнике, мы получим 180 градусов. Итак, мера угла A + угол B + угол C = 180 градусов. Это верно для любого треугольника в мире геометрии. Мы можем использовать эту идею, чтобы найти величину угла (углов), для которой градус отсутствует или не указан.
Нахождение недостающего угла
В треугольнике ABC ниже угол A = 40 градусов и угол B = 60 градусов.Какова мера угла C?
Мы знаем, что сумма мер любого треугольника равна 180 градусам. Используя тот факт, что угол A + угол B + угол C = 180 градусов, мы можем найти меру угла C.
угол A = 40
угол B = 60
угол C = мы не знаем.
Чтобы найти угол C, мы просто подставляем формулу выше и решаем относительно C.
A + B + C = 180
C = 180 — A — B
C = 180-40-60
C = 80
Чтобы проверить правильность 80 градусов, добавим все три угловые меры.Если мы получим 180 градусов, то наш ответ для угла C правильный.
Поехали:
40 + 60 + 80 = 180
180 = 180 … Проверяет!
Не всегда нужно подставлять эти значения в уравнение и решать. Как только вы освоитесь с такого рода проблемами, вы сможете сказать: «Хорошо, 40 + 60 = 100, поэтому другой угол должен быть 80!» и это намного быстрее.
Равносторонние треугольники
Если треугольник равносторонний, каков градус каждого из его углов?
Помните, что все стороны равностороннего треугольника имеют равную меру .У них также, как вы узнаете, равные углы! Пусть x = градус каждого угла. У треугольников три угла, поэтому мы прибавим x ТРИ раза.
У нас это:
x + x + x = 180
3x = 180
x = 60
Имеет смысл, правда? Если все углы равны и в сумме они равны 180, то это должно быть 60 градусов!
Соотношение углов
Градусы углов треугольника находятся в соотношении 4: 5: 9.
Какова величина НАИБОЛЬШЕГО угла треугольника в градусах?
Обратите внимание, что наименьший угол представлен наименьшим числом в данном соотношении.Наименьшее из приведенных чисел — 4, верно? Поскольку это соотношение, мы должны умножить все эти значения (4,5,9) на некоторый общий коэффициент, чтобы получить фактические углы. (Например, 60 и 80 находятся в соотношении 3: 4 с коэффициентом 20)
Пусть 4x = мера наименьшего угла треугольника. Теперь мы можем сказать, что 5x и 9x = градусы оставшихся углов треугольника. Мы просто складываем 4x + 5x + 9x, приравниваем сумму к 180 градусам и решаем относительно x. Найдя x, мы подставляем значение x в 4x и упрощаем, чтобы найти меру наименьшего угла треугольника.
4x + 5x + 9x = 180
9x + 9x = 180
18x = 180
x = 180/18
x = 10
Мы нашли значение x, но это НЕ означает, что мы закончили.
Чтобы найти величину наименьшего угла треугольника, умножим 4 на 10. Итак, 4 x 10 = 40.
Ответ — 40 градусов.
Помните, сумма углов треугольника равна 180 градусам. Просто возьмите то, что вам дано в задаче, и попытайтесь определить, в результате чего итоговый угол в сумме составит 180 градусов.
Урок, проводимый г-ном Фелизом
Воспользуйтесь «Калькулятором треугольников» ниже:
,Почему у треугольника 180 градусов?
Вы знаете, что сумма углов треугольника всегда равна 180 0 ? Это почему? В конце концов, 180 0 — это угол, который простирается от одной стороны прямой до другой, поэтому странно, что это количество градусов в углах треугольника.
Какое отношение треугольник имеет к единственной прямой? Оказывается, довольно много. Треугольники также имеют прямое отношение к прямоугольникам, пятиугольникам, шестиугольникам и всему семейству многогранных форм, известных как многоугольники.
В ближайшие несколько недель мы увидим, что я имею в виду. Но сегодня мы начнем с выяснения, почему именно углы треугольника всегда в сумме составляют 180 0 . Или вы так думали… потому что мы также увидим, что иногда они этого не делают;
Внутренние и внешние углы
Прежде чем мы зайдем слишком далеко в наш рассказ о треугольниках и общем количестве градусов в их трех углах, есть один небольшой геометрический словарь, о котором мы должны поговорить.И в этом разница между внутренним и внешним углом.
Самый простой способ описать разницу между этими двумя вещами — это на примере. Поскольку сегодняшняя тема — треугольник, давайте поговорим о внутреннем и внешнем углах треугольника. Короче говоря, внутренние углы — это все углы в пределах границ треугольника. Другими словами, это те углы, о которых мы говорили все время.
Внешние углы треугольника — это все углы между одной стороной треугольника и линией, которую вы получаете, расширяя соседнюю сторону за пределы границ треугольника.Если вы подумаете об этом, то увидите, что когда вы добавляете любой из внутренних углов треугольника к его соседнему внешнему углу, вы всегда получаете 180 0 — прямую линию.
Почему у треугольников 180 градусов?
Это подводит нас к главному вопросу на сегодня: почему внутренние углы треугольника всегда в сумме составляют 180 0 ? Как оказалось, вы можете понять это, подумав о внутреннем и внешнем углах треугольника. Чтобы понять, что я имею в виду, возьмите свое воображение или лист бумаги, потому что пришло время для небольшого математического проекта по рисованию декоративно-прикладного искусства.
Начните с рисования прямоугольного треугольника с одним горизонтальным участком, одним вертикальным участком и гипотенузой, проходящей от верхнего левого угла к нижнему правому. Теперь сделайте копию этого треугольника, поверните ее вокруг 180 0 и поместите гипотенузу в гипотенузу с оригиналом (точно так же, как мы это делали, когда выясняли, как найти площадь треугольника). Наконец, сделайте еще одну копию исходного треугольника и сдвиньте ее вправо, чтобы она располагалась прямо рядом с только что сформированным прямоугольником.Со мной так далеко? В таком случае ваше изображение должно выглядеть так:
В чем смысл этой фотографии? Взгляните на внутренний угол в правом нижнем углу исходного треугольника (помеченного буквой «A»). Теперь взгляните на два угла, которые составляют внешний угол для этого угла треугольника (обозначенные буквами «B» и «C»). Как мы знаем, если мы сложим внутренние и внешние углы одного угла треугольника, мы всегда получим 180 0 . И наш маленький рисунок показывает, что рассматриваемый внешний угол равен сумме двух других углов в треугольнике.Другими словами, два других угла в треугольнике (те, которые в сумме образуют внешний угол) должны объединиться с углом в правом нижнем углу, чтобы образовать угол 180 0 .
Для простоты мы использовали прямоугольный треугольник. Но оказывается, что вы можете сделать точно такой же рисунок, используя любой треугольник, который вам нравится, и всегда будете приходить к одному и тому же выводу. Попробуйте сделать несколько рисунков, начиная с разных треугольников по вашему выбору, чтобы убедиться в этом сами.В качестве примера вот еще один, который я сделал:
Неизбежный вывод этой игры состоит в том, что внутренние углы треугольника всегда должны составлять 180 0 . Наш милый и изящный маленький рисунок доказывает, что так и должно быть.
Могут ли треугольники иметь угол больше 180 градусов?
Или нет? Может быть, у нашего рисунка есть какие-то ограничения, которые не позволяют нам увидеть другую, более экзотическую возможность? Вот что вам стоит подумать или попробовать.Возьмите ненадутый воздушный шар, положите его на плоскую поверхность и нарисуйте на нем как можно более точный треугольник. Если у вас есть транспортир, было бы здорово измерить и сложить внутренние углы треугольника и убедиться, что они довольно близки к 180 0 .
Теперь надуйте воздушный шар и посмотрите на свой треугольник. Что с ним случилось? Если у вас есть транспортир, попробуйте еще раз просуммировать его внутренние углы. Что случилось с этой суммой? Вы все еще получаете 180 0 ? Что все это означает, когда дело доходит до вопроса о том, всегда ли внутренние углы треугольника в сумме составляют 180 0 , как мы, кажется, обнаружили?
К сожалению, на сегодня у нас совсем нет времени.Но обязательно загляните в следующий раз, когда мы начнем исследовать странный и чудесный мир, известный как неевклидова геометрия.
Заключение
Обязательно ознакомьтесь с моей книгой The Math Dude’s Quick and Dirty Guide to Algebra . И не забудьте стать поклонником The Math Dude на Facebook, где вы найдете множество замечательных математических публикаций в течение недели. Если вы в Твиттере, подпишитесь и на меня.
До следующего раза, это Джейсон Маршалл с «Быстрые и грязные советы математика, которые помогут упростить математику» . Спасибо за чтение, любители математики!
Инструменты для рисования, изображение любезно предоставлено Shutterstock.
.Калькулятор треугольников
Укажите 3 значения, включая хотя бы одну сторону в следующих 6 полях, и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбраны радианы, он может принимать такие значения, как пи / 2, пи / 4 и т. Д.
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, где встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами.Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют равную длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют равную длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
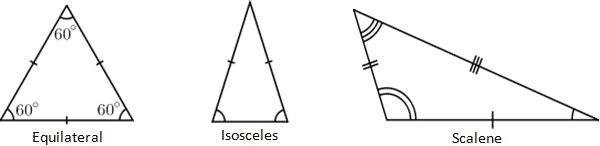
Отметки на краю треугольника — это обычное обозначение, которое отражает длину стороны, где одинаковое количество отметок означает одинаковую длину.Аналогичные обозначения существуют для внутренних углов треугольника, которые обозначаются разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из треугольников выше, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны равной длины. Обратите внимание, что треугольник, представленный в калькуляторе, не показан в масштабе; хотя он выглядит равносторонним (и имеет отметки угла, которые обычно воспринимаются как равные), он не обязательно является равносторонним и представляет собой просто представление треугольника.Когда введены фактические значения, выходные данные калькулятора будут отражать то, как должна выглядеть форма входного треугольника.
Треугольники, классифицируемые на основе их внутренних углов, делятся на две категории: прямые и наклонные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90 °, и обозначается двумя отрезками прямой, образующими квадрат в вершине, составляющей прямой угол. Самый длинный край прямоугольного треугольника, противоположный прямому углу, называется гипотенузой.Любой треугольник, который не является прямоугольным, классифицируется как наклонный треугольник и может быть тупым или острым. В тупоугольном треугольнике один из углов треугольника больше 90 °, а в остром треугольнике все углы меньше 90 °, как показано ниже.
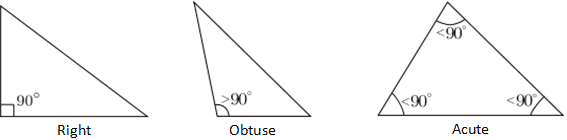
Факты, теоремы и законы о треугольнике
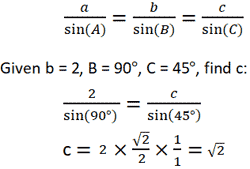
- Учитывая длины всех трех сторон любого треугольника, каждый угол можно рассчитать с помощью следующего уравнения.Обратитесь к треугольнику выше, предполагая, что a, b и c — известные значения.
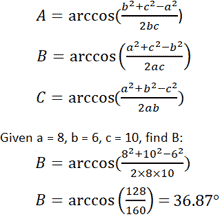
Площадь треугольника
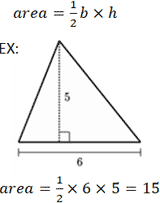
Существует несколько различных уравнений для вычисления площади треугольника в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b , и высоту, h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка линии, проведенного от вершины, противоположной основанию, до точки на основании, образующей перпендикуляр.
Учитывая длину двух сторон и угол между ними, следующую формулу можно использовать для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному на калькуляторе выше. Для a = 9, b = 7 и C = 30 °:
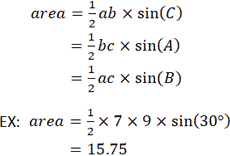
Другой метод вычисления площади треугольника основан на формуле Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат.Однако для этого требуется, чтобы длина трех сторон была известна. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:
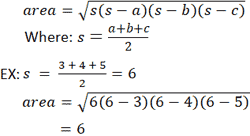
Медиана, внутренний радиус и радиус окружности
Медиана
Медиана треугольника определяется как длина отрезка прямой, который проходит от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек в треугольнике) треугольника.См. Рисунок ниже для пояснения.
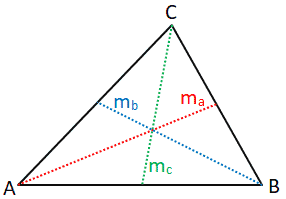
Медианы треугольника представлены отрезками m a , m b и m c . Длину каждой медианы можно рассчитать следующим образом:
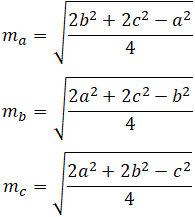
Где a, b и c обозначают длину стороны треугольника, как показано на рисунке выше.
В качестве примера, учитывая, что a = 2, b = 3 и c = 4, медиана m a может быть рассчитана следующим образом:
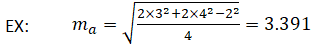
Inradius
Inradius — это радиус наибольшего круга, который может поместиться внутри данного многоугольника, в данном случае треугольника.Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это перпендикулярное расстояние между центром вращения и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром, поскольку центр, по определению, находится на равном расстоянии от каждой стороны треугольника.
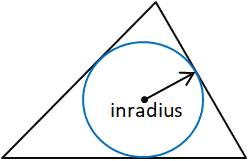
В данном калькуляторе внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (ов) треугольника по следующим формулам:
, где a, b и c — стороны треугольника
Круговой радиус
Радиус описанной окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника.Центр этой окружности, где пересекаются все срединные перпендикулярные стороны каждой стороны треугольника, является центром описанной окружности и точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.
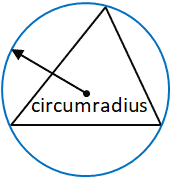
В данном калькуляторе радиус описанной окружности рассчитывается по следующей формуле:
Где a — сторона треугольника, а A — угол, противоположный стороне a
Хотя используются сторона a и угол A, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.
,
Leave A Comment