Сумма квадратов диагоналей параллелограмма — подготовка к ЕГЭ по Математике
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

Пусть AC и BD – диагонали параллелограмма ABCD.
Докажем, что .
Противоположные стороны параллелограмма равны , поэтому равенство, которое нужно доказать, можно записать в виде:
.
Самый простой способ – воспользоваться теоремой косинусов.
Из треугольника ABC:
Из треугольника BDC:
Сложим полученные равенства:
AB=CD, BC=AD (по свойству параллелограмма), тогда
(как односторонние углы при параллельных сторонах AB и CD), поэтому .
, что и требовалось доказать.
Теорема косинусов помогает найти решение многих задач по планиметрии из вариантов ЕГЭ по математике.
Прямоугольник. Свойства и признаки прямоугольника
Категория: Справочные материалы
Елена Репина 2013-07-26 2013-09-22Прямоугольник — параллелограмм, у которого все углы прямые.

Частным случаем прямоугольника является квадрат.
Свойства прямоугольника
1. Так как прямоугольник – это параллелограмм, то все свойства параллелограмма верны и для прямоугольника.
Помимо этого:
2. Стороны прямоугольника являются его высотами.
3. Диагонали прямоугольника равны.
4. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.

5. Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.

Признаки параллелограмма
Параллелограмм является прямоугольником, если выполняется любое из условий:
1. Диагонали параллелограмма равны.
2. Квадрат диагонали параллелограмма равен сумме квадратов соседних сторон.
3. Все углы параллелограмма равны.
Площадь прямоугольника





Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Автор: egeMax | Нет комментариев
Сумма квадратов диагоналей | Треугольники
Теорема. (Свойства диагоналей параллелограмма).
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Так как противолежащие стороны параллелограмма равны: AB=CD, AD=BC, то сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон:
Дано:
ABCD — параллелограмм,
AC и BD — диагонали.
Доказать:
Доказательство:
I споссоб.
1) Опустим перпендикуляры BK и CF на прямую, содержащую сторону AD.
2) Рассмотрим прямоугольный треугольник BDK.
По теореме Пифагора
3) Аналогично, из прямоугольного треугольника ACF
4) Сложим почленно полученные равенства:
BK=CF (как высоты параллелограмма, проведенные к одной стороне), поэтому
5) Из прямоугольного треугольника ABK по теореме Пифагора
6) KD=AD-AK, AF=AD+FD, поэтому
7) BK=CF, AB=CD. Значит, прямоугольные треугольники ABK и DCF равны (по катету и гипотенузе).
Следовательно, их соответствующие стороны равны: AK=DF. Отсюда,
Раскрываем скобки:
Упрощаем
Что и требовалось доказать.
II способ.
Свойство диагоналей параллелограмма можно рассматривать как следствие из теоремы косинусов.
Этот способ доказательства будет рассмотрен в следующий раз.
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника равна произведению его смежных сторон. Диагонали прямоугольника равны. Вторая формула нахождения площади прямоугольника исходит из формулы площади четырехугольника через диагонали.
Прямоугольник — это четырехугольник, у которого каждый угол является прямым.
Квадрат — это частный случай прямоугольника.
Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.

Свойства прямоугольника
1. Прямоугольник — это параллелограмм

Свойство объясняется действием признака 3 параллелограмма (то есть \( \angle A = \angle C \), \( \angle B = \angle D \))
2. Противоположные стороны равны
\( AB = CD,\enspace BC = AD \)

3. Противоположные стороны параллельны

4. Прилегающие стороны перпендикулярны друг другу
\( AB \perp BC,\enspace BC \perp CD,\enspace CD \perp AD,\enspace AD \perp AB \)

5. Диагонали прямоугольника равны
\( AC = BD \)

Согласно свойству 1 прямоугольник является параллелограммом, а значит \( AB = CD \).
Следовательно, \( \triangle ABD = \triangle DCA \) по двум катетам (\( AB = CD \) и \( AD \) — совместный).
Если обе фигуры — \( ABC \) и \( DCA \) тождественны, то и их гипотенузы \( BD \) и \( AC \) тоже тождественны.
Значит, \( AC = BD \).
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
Докажем и это.
\( \Rightarrow AB = CD \), \( AC = BD \) по условию. \( \Rightarrow \triangle ABD = \triangle DCA \) уже по трем сторонам.
Получается, что \( \angle A = \angle D \) (как углы параллелограмма). И \( \angle A = \angle C \), \( \angle B = \angle D \).
Выводим, что \( \angle A = \angle B = \angle C = \angle D \). Все они по \( 90^{\circ} \). В сумме — \( 360^{\circ} \).
6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон
Это свойство справедливо в силу теоремы Пифагора.
\( AC^2=AD^2+CD^2 \)
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника
\( \triangle ABC = \triangle ACD, \enspace \triangle ABD = \triangle BCD \)

8. Точка пересечения диагоналей делит их пополам
\( AO = BO = CO = DO \)

9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности
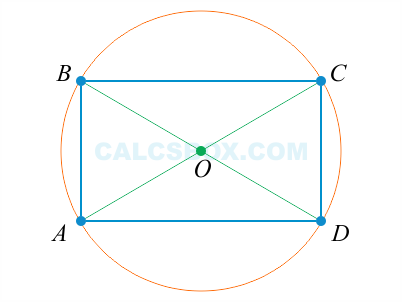
10. Сумма всех углов равна 360 градусов
\( \angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^{\circ} \)
11. Все углы прямоугольника прямые
\( \angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ} \)

12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника

13. Вокруг прямоугольника всегда можно описать окружность
Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна \( 180^{\circ} \)
\( \angle ABC = \angle CDA = 180^{\circ},\enspace \angle BCD = \angle DAB = 180^{\circ} \)
14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом)

Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Прямоугольник — Формулы | Свойства
Для расчёта всех основных параметров прямоугольника воспользуйтесь калькулятором.
Свойства прямоугольника
- Противоположные стороны прямоугольника равны
- Противоположные стороны прямоугольника параллельны
- Прилегающие стороны прямоугольника всегда перпендикулярны
- Все четыре угла прямоугольника прямые
- Сумма углов прямоугольника равна 360°
- Диагонали прямоугольника одинаковой длины
- Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон $$ 2 * BD^2 = 2 * AB^2 + 2 * BD^2 $$
- Каждая диагональ прямоугольника делит прямоугольник на два равных прямоугольных треугольника
- Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам
- Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
- Диагональ прямоугольника является диаметром описанной окружности
- Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180°
Формулы длин сторон прямоугольника
Длина стороны через диагональ и другую сторону
$$ AD = \sqrt{BD^2 — AB^2} $$ $$ AB = \sqrt{BD^2 — AD^2} $$Длина стороны через площадь (S) и другую сторону
$$ AD = {S \over AB} $$ $$ AB = {S \over AD} $$Длина стороны через периметр (P) и другую сторону
$$ AD = {P — 2 * AB \over 2} $$ $$ AB = {P — 2 * AD \over 2} $$Длина стороны через диагональ и угол ∠ACD
$$ AD = BD * sin(∠ACD) $$ $$ AB = BD * cos(∠ACD) $$Длина стороны через диагональ и угол ∠BOC
$$ AD = BD * sin({∠BOC \over 2}) $$ $$ AB = BD * cos({∠BOC \over 2}) $$Формулы длины диагонали прямоугольника
Длина диагонали прямоугольника через две стороны прямоугольника
$$ BD = \sqrt{AD^2 + AB^2} $$Длина диагонали прямоугольника через площадь (S) и любую сторону
$$ BD = {\sqrt{S^2 + AB^4} \over AB} = {\sqrt{S^2 + AD^4} \over AD} $$Длина диагонали прямоугольника через периметр и любую сторону
$$ BD = {\sqrt{P^2 — 4 * P * AB + 8 * AB^2} \over 2} = {\sqrt{P^2 — 4 * P * AD + 8 * AD^2} \over 2} $$Формулы периметра прямоугольника
Периметр прямоугольника через две стороны
$$ P = 2 * (AB + AD) $$Периметр прямоугольника через площадь (S) и любую сторону
$$ P = {2 * S + 2 * AB^2 \over AB} = {2 * S + 2 * AD^2 \over AD} $$Формулы площади прямоугольника
Площадь прямоугольника через две стороны
$$ S = AB * AD $$Площадь прямоугольника через периметр и любую сторону
$$ S = {P * AB — 2 * AB^2 \over 2} = {P * AD — 2 * AD^2 \over 2} $$Формулы радиуса описанной окружности прямоугольника
Радиус описанной окружности через диагональ
$$ R_O = {BD \over 2} $$Радиус описанной окружности через две стороны
$$ R_O = {\sqrt{AB^2 + AD^2} \over 2} $$Прямоугольник. Определение и свойства
Прямоугольник — это четырехугольник, у которого каждый угол является прямым.
Квадрат — это частный случай прямоугольника.
Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.
Свойства прямоугольника
1. Прямоугольник — это параллелограмм.
Доказательство
Свойство объясняется действием признака 3 параллелограмма (то есть \angle A = \angle C, \angle B = \angle D)
2. Противоположные стороны равны.
AB = CD,\enspace BC = AD
3. Противоположные стороны параллельны.
AB \parallel CD,\enspace BC \parallel AD
4. Прилегающие стороны перпендикулярны друг другу.
AB \perp BC,\enspace BC \perp CD,\enspace CD \perp AD,\enspace AD \perp AB
5. Диагонали прямоугольника равны.
AC = BD
Доказательство
Согласно свойству 1 прямоугольник является параллелограммом, а значит AB = CD.
Следовательно, \triangle ABD = \triangle DCA по двум катетам (AB = CD и AD — совместный).
Если обе фигуры — ABC и DCA тождественны, то и их гипотенузы BD и AC тоже тождественны.
Значит, AC = BD.
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
Докажем и это.
ABCD — параллелограмм \Rightarrow AB = CD, AC = BD по условию. \Rightarrow \triangle ABD = \triangle DCA уже по трем сторонам.
Получается, что \angle A = \angle D (как углы параллелограмма). И \angle A = \angle C, \angle B = \angle D.
Выводим, что \angle A = \angle B = \angle C = \angle D. Все они по 90^{\circ}. В сумме — 360^{\circ}.
Доказано!
6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон.
Это свойство справедливо в силу теоремы Пифагора.
AC^2=AD^2+CD^2
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника.
\triangle ABC = \triangle ACD, \enspace \triangle ABD = \triangle BCD
8. Точка пересечения диагоналей делит их пополам.
AO = BO = CO = DO
9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности.
10. Сумма всех углов равна 360 градусов.
\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^{\circ}
11. Все углы прямоугольника прямые.
\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ}
12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника.
13. Вокруг прямоугольника всегда можно описать окружность.
Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна 180^{\circ}
\angle ABC = \angle CDA = 180^{\circ},\enspace \angle BCD = \angle DAB = 180^{\circ}
14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом).
Сумма квадратов: SST, SSR, SSE
Вам может быть интересно, что означают все эти суммы квадратов . Может быть, именно это и привело вас сюда в первую очередь. Что ж, они являются определяющими факторами хорошей линейной регрессии . Это руководство основано на структуре ANOVA, о которой вы, возможно, слышали раньше.
Перед тем, как его читать, убедитесь, что вы не приняли регрессию за корреляцию . Если вы это проверили, мы можем сразу приступить к делу.
Небольшое примечание: хотите узнать больше о линейной регрессии? Посмотрите наши поясняющие видеоролики Модель линейной регрессии. Геометрическое представление и модель простой линейной регрессии.
SST, SSR, SSE: определение и формулы
Мы должны определить три термина. Сумма квадратов составляет , регрессия суммы квадратов и ошибка суммы квадратов .


Что такое SST?
Сумма квадратов всего , обозначенная SST , представляет собой квадраты разностей между наблюдаемой зависимой переменной и ее средним .Вы можете думать об этом как о дисперсии наблюдаемых переменных вокруг среднего значения — во многом как дисперсия в описательной статистике.
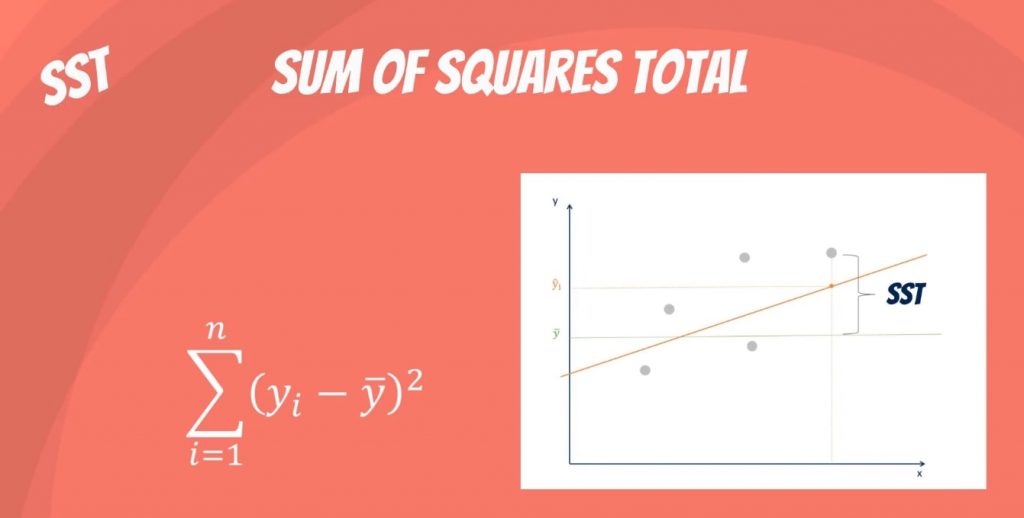

Это мера общей изменчивости набора данных.
Примечание : Есть другое обозначение для SST . Это TSS или общая сумма квадратов .
Что такое SSR?
Второй член — это сумма квадратов из-за регрессии , или SSR .Это сумма разностей между прогнозируемым значением и средним значением зависимой переменной . Думайте об этом как о мере, которая описывает, насколько хорошо наша линия соответствует данным.


Если это значение SSR равно сумме квадратов , это означает, что наша регрессия модель улавливает всю наблюдаемую изменчивость и является идеальной. Еще раз, мы должны упомянуть, что другое общее обозначение — ESS или объясненная сумма квадратов .
Что такое SSE?
Последний член — это ошибка суммы квадратов , или SSE . Ошибка — это разница между наблюдаемым значением и предсказанным значением .


Обычно мы хотим минимизировать ошибку. Чем меньше ошибка, тем лучше мощность оценки регрессии . Наконец, я должен добавить, что он также известен как RSS или остаточная сумма квадратов .Остаточный как в: остающийся или необъяснимый.
Путаница между различными сокращениями
Это действительно сбивает с толку, потому что некоторые люди обозначают его как SSR . Это делает неясным, говорим ли мы о сумме квадратов из-за регрессии или сумме квадратов остатков .


В любом случае ни один из них не принят повсеместно, так что путаница остается, и нам придется с ней жить.
Просто помните, что это два обозначения: SST , SSR , SSE или TSS , ESS , RSS .


Существует конфликт в отношении сокращений, но не в отношении концепции и ее применения. Итак, давайте сосредоточимся на этом.
Как они связаны?
Математически SST = SSR + SSE .
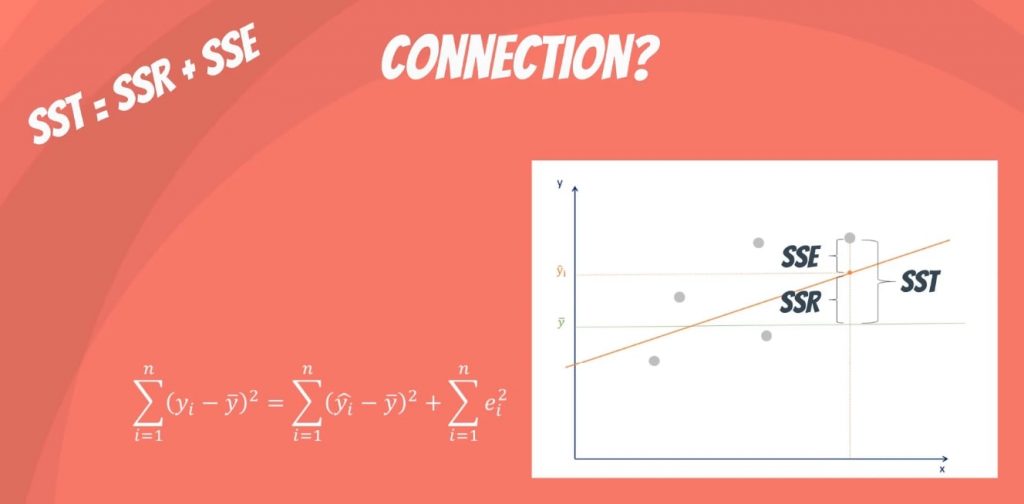

Обоснование следующее: общая изменчивость набора данных равна изменчивости, объясняемой линией регрессии , плюс необъяснимая изменчивость, известная как ошибка.
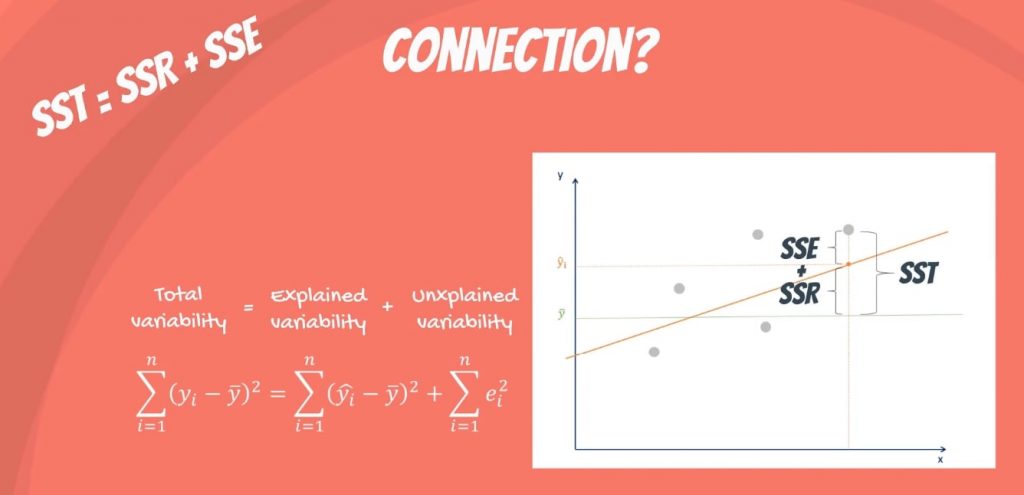

При постоянной общей изменчивости меньшая ошибка приведет к лучшей регрессии . И наоборот, более высокая ошибка вызовет менее мощную регрессию . И это то, что вы должны помнить, независимо от обозначений.
Следующий шаг: R-квадрат
Что ж, если вы не уверены, зачем нам нужны все эти сумм квадратов , у нас есть подходящий инструмент для вас. R-квадрат. Хотите узнать больше? Просто погрузитесь в связанный учебник, где вы поймете, как измеряется объяснительная сила линейной регрессии!
***
Хотите узнать больше? Вы можете улучшить свои навыки с помощью нашего курса статистики.
Попробовать курс статистики бесплатно
Следующее руководство: Измерение изменчивости с помощью R-квадрата
.диагоналей правильного восьмиугольника в геометрии GRE
Ученики любят пропустить основы, задавая такие вопросы, как: Сколько вершин у восьмиугольника? Сколько диагоналей у восьмиугольника? В чем разница между правильным восьмиугольником и ну восьмиугольником? И геометрия GRE действительно углубляется в сложную математику полигонов.
Но прежде чем мы перейдем к этому, я начну с двух сложных математических задач GRE.
Геометрия GRE: задачи многоугольников
1) В правильном пятиугольнике P нарисованы все пять диагоналей.Каков угол между двумя этими диагоналями в точке пересечения их в вершине пятиугольника?
(A) 12 °
(B) 36 °
(C) 54 °
(D) 60 °
(E) 72 °
2) Сколько диагоналей дает правильная 20-гранная многоугольник есть?
(A) 60
(B) 120
(C) 170
(D) 240
(E) 400
Объяснения этих практических проблем появятся в конце этой статьи блога.Забегайте вперед, нажав здесь.
Полигоны
Во-первых, некоторые основные термины, чтобы начать это обсуждение. Многоугольник — это любая геометрическая фигура, все стороны которой являются прямыми отрезками. Любой треугольник — многоугольник. Любой четырехугольник (включая трапеции, параллелограммы, ромбы, прямоугольники и квадраты) является многоугольником. Пятиугольник — это 5-сторонний многоугольник. Шестигранник
Точка пересечения двух сторон многоугольника называется вершиной . Количество вершин многоугольника всегда равно количеству его сторон.
Еще один важный факт о многоугольнике касается суммы углов. Возможно, вы знаете, что сумма трех углов в любом треугольнике равна 180 °. Возможно, вы даже знаете, что сумма четырех углов в любом четырехугольнике равна 360 °. Этот образец является обобщающим.Сумма всех n углов в любом n-стороннем многоугольнике составляет:
Таким образом, любой пятиугольник (n = 5) будет иметь углы, которые в сумме составляют 3 * 180 = 540 °. У любого шестиугольника (n = 6) углы в сумме составляют 4 * 180 = 720 °. Любой восьмиугольник (n = 8) будет иметь углы в сумме 6 * 180 = 1080 °. (См. Блог о геометрических формулах GRE)
Наконец, есть это парадоксальное слово « обычный ». На обыденном языке «обычный» означает «обычный, ничем не примечательный, банальный».«В геометрии это означает прямо противоположное! Форма является правильной тогда и только тогда, когда она одновременно и равносторонняя, и равноугольная, то есть тогда и только тогда, когда все стороны имеют одинаковую длину и все углы равны. «Обычная» версия любого многоугольника — это самая элитная, наиболее симметричная версия этого многоугольника. «Правильный треугольник» — это то, что мы называем равносторонним треугольником. «Правильный четырехугольник» — это квадрат. Для более высоких полигонов вы, скорее всего, увидите обычную версию на GRE, потому что тест (как и все математики) любит симметрию.
Диагонали многоугольника
Теперь мы можем поговорить о диагоналях. Диагональ — это любая линия, проходящая внутри многоугольника, которая соединяет две несмежные вершины. Что это значит? Во-первых, начиная с любой вершины, смежная вершина — это либо вершина, соединенная с начальной вершиной одной стороной многоугольника.
Рассмотрим неправильный четырехугольник:
Начнем с вершины A. Начиная с вершины A, мы соединяемся сторонами этого четырехугольника как с B, так и с D; вершины B и D — это те, которые смежны с вершиной A.Единственная вершина, не соединенная с A стороной четырехугольника, — это C. C — единственная несмежная вершина A, а A — это C. Таким образом, одна диагональ идет от A к C. Нетрудно заметить, что другая идет от B к D. Любой четырехугольник имеет только две диагонали.
Обратите внимание, что треугольника НИКОГДА не имеют диагоналей : если мы начнем с любой вершины треугольника, две другие вершины будут смежными. В треугольнике просто нет несмежных вершин, поэтому диагонали невозможны.Среди четырехугольников существуют особые правила для диагоналей параллелограмма и категорий внутри параллелограммов:
Диагонали параллелограмма делят друг друга пополам: то есть точка пересечения двух диагоналей является средней точкой каждой из них. .
Ромб — это параллелограмм с четырьмя равными сторонами. Диагонали ромба пересекают друг друга и перпендикулярны.
Прямоугольник — это параллелограмм с четырьмя углами 90 °. Прямоугольники ромба делят друг друга пополам и имеют одинаковую длину.Это связано со старинной уловкой плотников. Когда плотник отрезает две пары одинаковой длины, чтобы сделать стороны дверной или оконной рамы, он знает, что у него есть параллелограмм из-за одинаковой длины, но как он узнает, есть ли у него прямоугольник? Без точного оборудования очень трудно измерить разницу, скажем, между углом 89 ° или 90 °. Что ж, все, что нужно сделать плотнику, — это измерить две диагонали: если эти две легко измеряемые длины равны, то гарантировано, что у него четыре прямых угла!
Квадрат — это параллелограмм, прямоугольник и ромб.Это правильный четырехугольник с четырьмя равными сторонами и четырьмя углами 90 °. Диагонали квадрата делят друг друга пополам, имеют одинаковую длину и перпендикулярны.
Диагонали правильного пятиугольника
Пятиугольник — это любой пятисторонний многоугольник, сумма углов которого составляет 540 °, как мы видели выше. Единственный пятиугольник, который вы можете встретить на GRE, — это самый симметричный, правильный пятиугольник. Поскольку углы равны, мы можем разделить сумму углов на пять.
540 ° / 5 = 108 °
Это угол каждого из пяти углов пятиугольника.
Вот правильный пятиугольник с пятью диагоналями.
Сколько диагоналей у пятиугольника? У любого пятиугольника ровно пять диагоналей. Эти диагонали повторяют форму классической пятиконечной звезды, например, звезды на флаге Соединенных Штатов Америки. Длина и деления этой звезды тесно связаны с этим магическим и мистическим числом, золотым сечением; Сакральная геометрия призвана дать представление о смысле жизни, но вам не нужно знать ничего из этого для GRE!
Как мы можем найти углы в этой форме? Ну, мы знаем, что каждый большой угол пятиугольника составляет 108 °.Взгляните, например, на треугольник ABC. Этот треугольник является равнобедренным, потому что AB = BC, и мы знаем, что угол ABC = 108 °. Два других угла должны быть равны: назовите их x.
108 ° + x + x = 180 *
2x = 180 ° — 108 ° = 72 °
x = 36 °
Это означает, что угол BAC = угол BCA = 36 °, как и многие другие симметрично связанные углы вокруг формы. Мы могли бы вычесть (угол BAC) из (угла BAE), чтобы получить (угол CAE)
угол CAE = (угол BAE) — (угол BAC) = 108 ° — 36 ° = 72 °
Из этого мы могли бы найти много другие углы внутри формы.Мы могли бы использовать аналогичные средства, чтобы найти углы, включающие диагонали любого более высокого многоугольника.
Диагонали правильного шестиугольника
Шестигранник — это любой шестигранный многоугольник, сумма углов которого равна 720 °, как мы видели выше. В правильном шестиугольнике
каждый угол = 720 ° / 6 = 120 °
Сколько диагоналей у шестиугольника? Начиная с одной вершины, две другие вершины являются смежными, поэтому 3 вершины не являются смежными, что делает возможными три диагонали из одной вершины.Из A мы можем провести диагонали к C, D и E.
От каждой вершины есть три диагонали. Поскольку существует шесть вершин, вы можете подумать, что всего будет 3 * 6 = 18 диагоналей, но этот метод подсчета учитывает все дважды. Видите ли, диагональ от A до C будет считаться один раз как диагональ от A, а затем как диагональ от C до A. Таким образом, количество диагоналей в шестиугольнике равно 18/2 = 9. Это могут быть группы по две. виды. Шесть более коротких диагоналей вместе образуют шестигранную звезду, Маген Давид.Три более длинные диагонали образуют всего три симметрично пересекающихся сегмента, то, что в математике называется «вырожденной шестиконечной звездой».
На этих двух диаграммах показаны девять диагоналей правильного шестиугольника. Конечно, шестиконечная звезда просто состоит из двух перекрывающихся равносторонних треугольников, направленных в противоположных направлениях. (Этот геометрический факт привел к обширным мистическим рассуждениям о Звезде Давида в Каббале, но опять же, вам не нужно понимать никакой мистики для GRE!)
Диагонали правильного семиугольника
семиугольник — это любой семигранный многоугольник (n = 7).Иногда его называют «септагон», но математическое название предпочтительнее «семиугольник». Сумма его углов будет
(n — 2) * 180 ° = 5 * 180 ° = 900 °
Это означает, что каждый из семи углов в правильном семиугольнике будет иметь размер
каждый угол = 900 ° / 7 = 128,5714286… °
Угловые размеры не целые! Вот почему GRE вряд ли спросит вас о правильном семиугольнике, и именно поэтому вы, вероятно, никогда особо не говорили о правильных семиугольниках в школьной геометрии.Вот почему большинство людей даже не знают, как назвать этого зверя! Их нецелочисленная угловая мера делает их первой «белой вороной» в семействе обычных многоугольников! Я не буду больше ничего говорить о них, потому что они почти никогда не появляются на GRE, но я покажу вам две возможные семиконечные звезды по их диагоналям: эти звезды навязчиво красивы из-за их особой симметрии.
Диагонали правильного восьмиугольника
Восьмиугольник — это любой восьмиугольный многоугольник, сумма углов которого равна 1080 °, как мы видели выше.В правильном восьмиугольнике
каждый угол = 1080 ° / 8 = 135 °
Этот угол является дополнением к углу 45 °. Правильный восьмиугольник — типичная форма знака остановки во многих частях мира.
Сколько диагоналей у восьмиугольника? Сколько вершин у восьмиугольника?
Начиная с одной вершины, две другие вершины являются смежными, поэтому пять вершин не являются смежными, что делает возможными пять диагоналей из одной вершины. От A, B и H — симметричные вершины, поэтому мы можем провести диагонали к C, D, E, F и G.
Логика аналогична шестиугольнику: пять в каждой вершине, восемь вершин, но при этом каждая диагональ считается дважды, поэтому общее число равно 5 * 8/2 = 20. AC и AG — это то, что мы могли бы назвать «3 вершины». диагонали »: их восемь, которые образуют звезду. AF и AD, каждая из которых параллельна двум сторонам, — это то, что мы могли бы назвать «четырьмя диагоналями вершин»: восемь из них образуют другую звезду. Наконец, AE подобен диаметру всего восьмиугольника, пересекающему его центр: таких линий четыре, и они образуют вырожденную восьмиконечную звезду.
Так же, как шестиконечная звезда состояла из двух перекрывающихся равносторонних треугольников, первая восьмиконечная звезда слева состоит из двух отдельных перекрывающихся квадратов: квадратного ACEG и квадратного BDFG. (Названия этих квадратов напоминают линии на W. 4th Street!) Между этими тремя звездами (считая вырожденный объект справа как «звезду») у нас есть все 20 диагоналей правильного восьмиугольника.
Сводка
Вперед и вперед! Методы, обсуждаемые в этом блоге, могут быть расширены для применения к шестиугольнику (n = 9), десятиугольнику (n = 10) или любому более высокому многоугольнику.Вооружившись этой информацией, вы сможете ответить на все, что вас спросит GRE о диагонали многоугольника! Если при чтении этого блога у вас были моменты «ага», возможно, вы захотите еще раз взглянуть на практические задачи в верхней части, прежде чем читать пояснения ниже.
Объяснение практических задач
1) Давайте посмотрим на пятиугольник с его пятью диагоналями.
Примером угла между двумя диагоналями в вершине может быть угол EBD, где диагонали BD и BE пересекаются в вершине B.
Мы будем следовать логике, изложенной выше.
Треугольник BCD равнобедренный, BC = CD, угол BCD = 108 °. Два других угла равны: назовите их каждый x.
108 ° + x + x = 180 *
2x = 180 ° — 108 ° = 72 °
x = 36 °
Итак, угол CBD = 36 °. Итак, треугольник ABE во всех отношениях равен треугольнику BCD, поэтому угол ABE также должен быть равен 36 °. Таким образом, мы можем вычесть из большого угла в вершине B.
(угол EBD) = (угол ABC) — (угол CBD) — (угол ABE)
(угол EBD) = 108 ° — 36 ° — 36 ° = 36 °
Ответ = (B)
2) Если мы начнем с одной вершины 20-стороннего многоугольника, то с каждой стороны будет смежная вершина.Не считая этих трех вершин, было бы 17 несмежных вершин, поэтому из любой вершины можно было бы провести 17 возможных диагоналей. Двадцать вершин, 17 диагоналей из каждой вершины, но этот метод учитывает диагонали дважды, как указано выше.
Количество диагоналей = (17 * 20) / 2 = 17 * 10 = 170
Ответ = (C)
Примечание редактора: этот пост был первоначально опубликован в январе 2014 года и был обновлен за свежесть, точность и полноту.
П.С. Готовы улучшить свой GRE? Начни сегодня.

Leave A Comment