Задачи с шаблонами и числами
%PDF-1.6 % 827 0 объект > эндообъект 1904 0 объект >поток 2010-01-07T14:36:12+01:002010-04-27T15:39:11+01:002010-04-27T15:39:11+01:00ABBYY FineReader 9.0 Professional EditionKey Stage 4 Mathematics; Образцы чисел; Алгебра; Учебные ресурсыapplication/pdf
Пояснение к уроку: отношения и функции
описания, стрелочные диаграммы и декартовы диаграммы.
В математике и естественных науках мы часто заинтересованы в том, чтобы взять один объект и присвоить его новому объекту, используя для этого процесс. Например, мы можем взять количество прошедшего времени и использовать это значение, чтобы определить положение автомобиля в это время, или мы можем использовать количество испытаний для вычисления вероятность выпадения определенного числа на спиннере. В этих случаях мы берем входное число, а затем используем его для вычисления выходного значения; это примеры функций.
В общем, функция присваивает объект (называемый входом) другому объекту (называемому выходом). Прежде чем мы сможем точно описать, как функция присваивает эти объекты, нам нужно вспомнить, что понимается под бинарным отношением.
Определение: бинарное отношение на двух множествах
Бинарное отношение 𝑅 на двух множествах 𝑋 и 𝑌 (часто сокращается до просто «отношение»)
является подмножеством декартова произведения множеств 𝑋×𝑌.
Другими словами, это набор упорядоченных пар (𝑥,𝑦),
где 𝑥∈𝑋 и 𝑦∈𝑌.
Если (𝑥,𝑦)∈𝑅, то говорят, что 𝑥 связано с 𝑦.
Бинарное отношение присваивает объекты нескольким различным объектам; мы можем представить это с помощью стрелочной диаграммы. Рассмотрим следующий пример отношения «сын или дочь».
Стрелки указывают нам направление отношения. Например, мы видим, что Амира соединена с Фаресом стрелкой. Это говорит нам, что (Амира, Фарес) — элемент отношений, и что Амира — дочь Фареса. Мы также можем вывести другие соотношения из этой схемы. Мы видим, что у Далии и Амиры одни родители, значит, они должны быть сестрами. Мы также можем видеть, что Набиль и Адам у них одна мать, но разные отцы, так что они сводные братья.
Теперь мы готовы определить функцию как тип отношения.
Определение: Функция
Функция — это отношение, которое ставит в соответствие каждому входу ровно один выход.
В частности, если отношение существует между двумя множествами 𝑋 и 𝑌, то мы говорим, что 𝑋 является областью
функция, а 𝑌 — кодовый домен функции.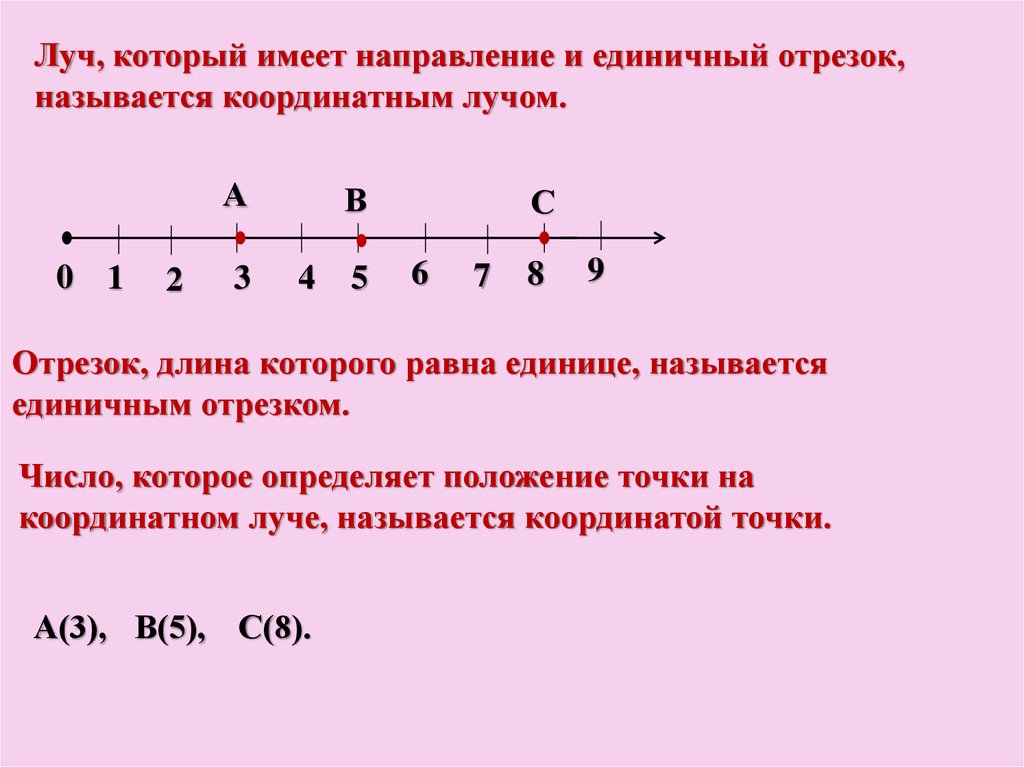
Мы также называем набор всех выходов функции диапазоном.
Это означает, что домен функции — это набор всех входных данных, а кодовый домен — это набор, содержащий все возможные выходные данные. Стоит отметить, что кодовый домен отличается от диапазона, а диапазон всегда является подмножеством кодового домена. Мы продемонстрируем разницу между доменом, кодовым доменом, и диапазон в деталях в одно мгновение.
Мы видим, что вышеприведенное отношение «сын или дочь» не является функцией, поскольку у каждого человека есть два родителя. Другими словами, каждый вход имеет два выхода вместо ровно одного. Это видно из стрелочной диаграммы.
Видим, что стрелок от Амиры две, значит у нее назначено два родителя.
Чтобы стрелочная диаграмма представляла функцию, каждому элементу первого набора должен соответствовать ровно один элемент второго набора; мы можем написать это как два отдельных свойства:
- Каждому элементу первого набора должен соответствовать элемент второго набора.
- Каждому элементу первого набора не может быть назначено более одного элемента второго набора.
Поскольку стрелки сообщают нам назначения, мы можем переписать эти свойства в терминах стрелок на диаграмме:
- Каждый элемент в первом наборе должен иметь стрелку, выходящую из него.
- От каждого элемента в первом наборе может исходить только одна стрелка.
Примером функции может быть «родился в», поскольку каждый человек родился только в одном месте и все где-то родились. Стрелочная диаграмма для этого может быть следующей.
Поскольку от каждого человека исходит ровно одна стрелка, мы можем заключить, что отношение представляет собой функцию. Мы также можем определить домен, кодовый домен и диапазон этой функции.
Во-первых, домен является первым набором в отношении. В данном случае это набор людей: {Амира, Далия, Набиль, Адам, Энги}.
Во-вторых, кодовый домен — это весь второй набор в отношении.
В данном случае это набор всех местоположений: {Нью-Йорк, Детройт, Сиэтл, Бостон, Чикаго}.
В-третьих, диапазон — это множество всех выходов функции, которые будут являться всеми местами рождения этих людей. В данном случае диапазоном является множество {Нью-Йорк, Детройт, Сиэтл, Бостон}. Мы можем видеть это на диаграмме как набор мест, на которые указывает стрелка.
Заметим, что кодомен и диапазон в этой функции разные, так как никто из перечисленных людей не родился в Чикаго. Как правило, диапазон всегда является подмножеством домена кода.
Теперь давайте рассмотрим пример, в котором мы определим, представляет ли отношение функцию из диаграммы отношений.
Пример 1. Определение того, является ли отношение функцией, по диаграмме отношений
Верно или неверно: данная цифра представляет функцию.
Ответ
Начнем с того, что вспомним, что функция — это отношение, которое сопоставляет каждому входу ровно один выход. На стрелочной диаграмме стрелка говорит нам, как отношение
присваивает элементы каждого набора.
Если два элемента соединены стрелкой, то они связаны.
Чтобы это отношение представляло функцию, каждый вход должен быть назначен только одному выходу. Это означает, что каждый элемент множества 𝑋 должен быть назначен ровно одному элементу в множестве 𝑌. Однако из диаграммы видно, что элемент 5 в множестве 𝑋 присваивается двум элементам множества 𝑌.
Поскольку функция не может сопоставить вход с двумя разными выходами, это не может быть функцией, поэтому утверждение ложно.
В нашем следующем примере мы определим, какое отношение представляет функцию, учитывая несколько различных стрелочных диаграмм отношения.
Пример 2. Определение отношений, являющихся функциями, по диаграмме отношений
Какое из следующих отношений представляет функцию?
Ответ
Начнем с того, что вспомним, что функция — это отношение, которое сопоставляет каждому входу ровно один выход. На стрелочной диаграмме стрелки показывают нам, как отношение
присваивает элементы каждого набора; если два элемента соединены стрелкой, то они связаны.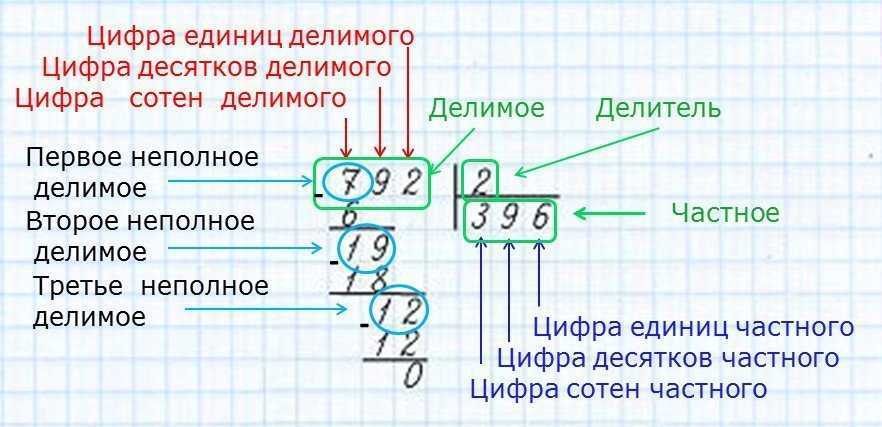
Таким образом, чтобы отношение, заданное стрелочной диаграммой, представляло функцию, должны быть верны два условия:
- Поскольку каждому входу должен быть назначен выход, каждый элемент в первом наборе должен иметь отходящую от него стрелку.
- Поскольку каждый вход должен быть назначен ровно одному выходу, от каждого входа может исходить только одна стрелка.
Мы могли бы объединить оба этих утверждения в одно; однако зачастую проще проверить каждое условие отдельно. Теперь проверим оба условия для каждого из отношений на данной диаграмме.
На рисунке A мы отмечаем, что входное значение 𝑏 не присваивается никакому выходному значению; следовательно, это не представляет собой функцию.
На рисунке B мы видим, что каждому входу соответствует выход; однако входное значение 𝑐 присваивается двум выходным значениям. Следовательно, это не представляет собой функцию.
На рисунке C мы видим, что каждый вход назначен выходу и что они назначены только одному выходу.
Следовательно, это представляет собой функцию.
Следовательно, только отношение на рисунке C представляет собой функцию.
Хотя это и не обязательно, мы также можем определить домен, кодовый домен и диапазон функции из варианта C в вопросе выше. Домен — это набор входных значений, которое представляет собой набор {𝑎,𝑏,𝑐}. Кодовый домен — это второй набор в отношении; это набор {1,2,3,4}. Диапазон — это набор всех выходных данных из домена, который представляет собой каждый элемент, отображаемый функцией. Так как только 1 и 3 являются выходами этой функции, ее диапазон равен {1,3}.
До сих пор мы видели только функции, представленные в виде диаграмм отношений. Однако напомним, что
мы можем представить отношения в виде таблиц, наборов упорядоченных пар и декартовых диаграмм. Это означает, что мы также можем
представлять функции всеми этими способами. Во всех случаях первый элемент упорядоченного
пара является входом, а вторая — выходом.
Напомним, что горизонтальная координата в
декартова диаграмма обычно является входом, а вертикальная координата — выходом.
Теперь давайте рассмотрим несколько примеров, в которых мы определяем, какие отношения представляют функцию из разных представлений, начиная с таблицы.
Пример 3. Определение того, является ли отношение функцией из таблицы
Что из следующего представляет функцию с входом 𝑋 и выходом 𝑌?
| Отношение А | |||||
|---|---|---|---|---|---|
| 𝑋 | −3 | 0 | 3 | 8 901 44 | −10 |
| 𝑌 | 6 | 8 | 20 | 4 | 8 |
| Отношение B | |||||
|---|---|---|---|---|---|
| 𝑋 | −2 | 0 | −2 | 7 | −8 |
| 𝑌 | 6 | 8 | 20 | 4 | 8 |
Ответ
90 002 Начнем с того, что вспомним, что функция — это отношение, которое сопоставляет каждому входу ровно один выход.
В таблице первый элемент обычно сообщает нам
вход, а соответствующий второй элемент является назначенным ему выходом.Следовательно, чтобы таблица представляла функцию, каждому входу должен быть назначен выход, и у него должен быть ровно один назначенный выход. Другими словами, у нас не может быть входного значения с двумя (или более) разными выходами. Мы можем проверить каждое отношение отдельно, чтобы увидеть, соответствуют ли они этим критериям.
В отношении A заметим, что пустых 𝑌-значений нет, поэтому каждому входу присваивается выход. Далее отметим, что каждое 𝑋-значение появляется только один раз, поэтому никакому входному значению не назначается несколько выходов. Следовательно, отношение A представляет собой функцию.
В отношении B заметим, что пустых 𝑌-значений нет, поэтому каждому входу назначается выход. Далее отметим, что ввод −2 повторяется в таблице.
Это означает, что в отношении B −2 присваивается нескольким элементам множества 𝑌, как 6, так и 20.
В функции
отношение может назначать каждому входу только один выход, поэтому это не может быть функцией.
Следовательно, только отношение A представляет собой функцию.
В нашем следующем примере мы определим, какое отношение представляет функцию из ее упорядоченных пар.
Пример 4. Определение того, является ли отношение функцией из набора упорядоченных пар
Какое из следующих отношений представляет функцию?
| Связь А | (4,12) | (4,15) | (5,18) | (5,21) | (6,24) ) |
|---|---|---|---|---|---|
| Связь Б | (4,12) | (5,15) | (6,18) | (7,21) | (8,24) |
Ответ
Мы начнем с того, что вспомним, что функция есть отношение, которое назначает каждому входу ровно один выход. В упорядоченной паре (𝑥,𝑦) первый элемент связан со вторым элементом.
Следовательно, чтобы набор упорядоченных пар (называемых отношением) представлял функцию, у нас не может быть одной и той же первой записи, связанной с двумя разными вторыми записями.
Мы можем проверить это, увидев, какое отношение имеет разные первые записи.
В отношении A мы видим, что 4 связано с элементами второго набора, как с 12, так и с 15. Точно так же 5 связано и с 18, и с 21. Следовательно, это не функция.
В отношении B мы видим, что каждая из упорядоченных пар имеет уникальную первую запись, поэтому мы можем сказать, что это отношение представляет собой функцию. Мы можем видеть это более наглядно, построив стрелочную диаграмму, представляющую каждое отношение.
В отношении A два элемента входного набора назначаются двум элементам выходного набора, поэтому это не функция. В отношении B каждый элемент в входной набор назначается ровно одному элементу выходного набора, так что это функция.
Следовательно, ответ состоит в том, что отношение B представляет собой функцию.
В нашем следующем примере мы определим, какая из данного списка декартовых диаграмм представляет функцию.
Пример 5. Определение того, является ли отношение, представленное декартовой диаграммой, функцией
Какая из следующих декартовых диаграмм представляет функцию от 𝑥 до 𝑥, где 𝑥={5,7,9,11}?
Ответ
Начнем с того, что вспомним, что функция — это отношение, которое сопоставляет каждому входу ровно один выход.
Любая точка (𝑎,𝑏)
на декартовой диаграмме отношения является упорядоченной парой и говорит нам, что 𝑎 связано с 𝑏.
Кроме того, горизонтальная координата обычно представляет вход, а вертикальная координата обычно представляет выход.
Следовательно, поскольку функция должна иметь каждый элемент входного набора, сопоставленный ровно с одним элемент выходного набора, следующие два условия должны быть верно для декартовой диаграммы для представления функции от 𝑥 до 𝑥:
- Поскольку каждому входу должен быть назначен выход, на диаграмме должна быть точка с 𝑥-координатой, равной каждому элемент 𝑥={5,7,9,11}.
- Поскольку мы не можем назначить два выхода одному и тому же входу, не может быть двух разных точек на диаграмме с той же 𝑥-координатой по горизонтальной оси.
Затем мы можем проверить каждую из диаграмм отдельно для каждого из этих условий.
Во-первых, на диаграмме а мы видим, что координаты точек на диаграмме равны
(5,5),(7,9),(9,7) и (11,11).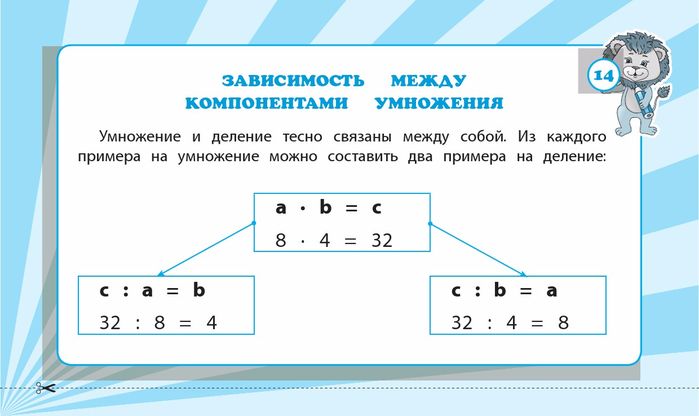
Мы видим, что каждый элемент 𝑥={5,7,9,11} является 𝑥-координатой точки, поэтому каждый элемент 𝑋
назначается выход. Мы также можем видеть, что каждый элемент появляется только один раз, поэтому каждому назначается только один выход; следовательно, это представляет собой функцию.
Во-вторых, на диаграмме b мы можем заметить, что на диаграмме нет точки с 𝑥-координатой 5.
Поскольку функция должна отображать каждый элемент входного множества в один элемент выходного множества, мы можем заключить это соотношение не представляет функцию, определенную на 𝑥, поскольку 5 не назначен выход.
В-третьих, у нас есть аналогичная история на диаграмме c.
11 не назначен выход, поэтому он не может представлять функцию, определенную на 𝑥.
Наконец, на диаграмме d мы видим, что каждому входному значению присваивается выходное значение. Однако мы также можем заметить, что 7 присвоено 2 выходных значения.
Поскольку (7,7) и (7,9) оба находятся на диаграмме этого отношения, отношение присваивает 7 двум различным значениям, как 7, так и 9.
Функция может присвоить каждому входу только один выход, поэтому это отношение не представляет собой функцию.
Следовательно, только отношение на диаграмме a представляет собой функцию от 𝑥 до 𝑥.
В нашем последнем примере мы будем использовать тот факт, что отношение является функцией для определения значений неизвестных в отношении.
Пример 6. Поиск неизвестных значений заданной функции между двумя наборами
Учитывая, что 𝑋={−7,−1,9} и 𝑅={(𝑎,−1),(𝑏,−7),(−7,9)}, где 𝑅 — функция на 𝑋, найдите числовое значение 𝑎+𝑏.
Ответ
Начнем с того, что вспомним, что функция на множестве 𝑋 — это отношение, которое сопоставляет каждому «входному» элементу 𝑋
ровно одному «выходному» элементу 𝑋. Следовательно, поскольку 𝑅 — функция на 𝑋,
это отношение на 𝑋, что означает, что оно является подмножеством 𝑋×𝑋. Другими словами, каждый элемент 𝑅
— упорядоченная пара, где первая запись в упорядоченной паре является входом, а вторая запись — выходом.
Поскольку 𝑅 — это функция, каждый вход должен быть назначен одному выходу; это означает, что каждый элемент 𝑋 должен быть первым вход в одну из упорядоченных пар 𝑅, и он не может появиться более чем в одной упорядоченной паре, иначе ему будут назначены два выхода.
Поскольку 𝑎 и 𝑏 являются первым элементом в упорядоченных парах 𝑅, они являются входными значениями функции. Это означает, что 𝑎,𝑏∈𝑋; мы также можем видеть, что 𝑎 выводит −1, а 𝑏 выдает −7.
Заметим, что (−7,9)∈𝑅, поэтому −7 присваивается выходное значение 9. Поскольку 𝑅 — функция, −7 также не может быть присвоено выходное значение -1 или -7, что означает, что 𝑎 и 𝑏 не могут быть -7.
На данный момент есть две возможности для 𝑎 и 𝑏. Заметим, что 𝑎 и 𝑏 не могут быть равны,
в противном случае одному и тому же входу назначаются два выхода. Мы также видим, что 𝑋 состоит только из трех элементов, и мы знаем, что 𝑎 и
𝑏 не может быть −7, поэтому у нас есть два варианта: 𝑎=9, 𝑏=−1 или 𝑎=−1, 𝑏=9.
Leave A Comment