🎓 Пар-мм. Ромб без отв
Параллелограмм
1. B 5 № 27585. Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 30°.
2. B 5 № 27809. Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма.
3. B 5 № 27824. Две стороны параллелограмма относятся как , а периметр его равен 70. Найдите большую сторону параллелограмма.
4. B 5 № 27825. Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.
5 № 245005. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
6. B 5 № 317338. Площадь параллелограмма равна 189. Точка — середина стороны . Найдите площадь трапеции
7. B 5 № 319056. Площадь параллелограмма равна 153. Найдите площадь параллелограмма , вершинами которого являются середины сторон данного параллелограмма.
Найдите площадь параллелограмма , вершинами которого являются середины сторон данного параллелограмма.
8. B 5 № 319057. Площадь параллелограмма равна 176. Точка – середина стороны . Найдите площадь треугольника .
9. B 8 № 27434. В параллелограмме высота, опущенная на сторону , равна 4, . Найдите .
10. B 8 № 27435. В параллелограмме . . Найдите высоту, опущенную на сторону .
11. B 8 № 27436. В параллелограмме , , . Найдите большую высоту параллелограмма.
12. B 8 № 27437. В параллелограмме . Найдите .
13. B 8 № 27438. В параллелограмме . Найдите .
14. B 8 № 27610.Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
15. B 8 № 27611. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
16. B 8 № 27612. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Найдите большую высоту этого параллелограмма.
17. B 8 № 27805. Найдите тупой угол параллелограмма, если его острый угол равен . Ответ дайте в градусах.
18. B 8 № 27806. Сумма двух углов параллелограмма равна . Найдите один из оставшихся углов. Ответ дайте в градусах.
19. B 8 № 27807. Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах.
20. B 8 № 27808. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.
21. B 8 № 27822. Найдите больший угол параллелограмма, если два его угла относятся как . Ответ дайте в градусах.
22. B 8 № 27826. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
23. B 8 № 27827. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне.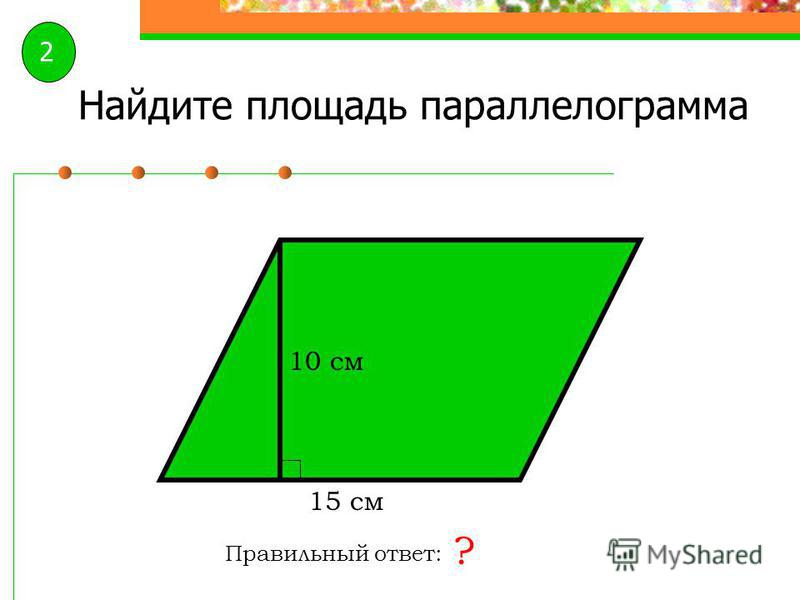 Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
Ромб
- B 5 № 27586. Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150°.
2. B 8 № 27613. Найдите площадь ромба, если его высота равна 2, а острый угол 30°.
3. B 8 № 27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
4. B 8 № 27616. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
5. B 8 № 27816. Найдите меньшую диагональ ромба, стороны которого равны 2, а острый угол равен .
6. B 8 № 27817. Найдите высоту ромба, сторона которого равна , а острый угол равен .
7. B 8 № 27828. Найдите большую диагональ ромба, сторона которого равна , а острый угол равен .
8. B 8 № 27829. Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
9. B 8 № 282851. В ромбе ABCD угол ABC равен 122°. Найдите угол ACD. Ответ дайте в градусах.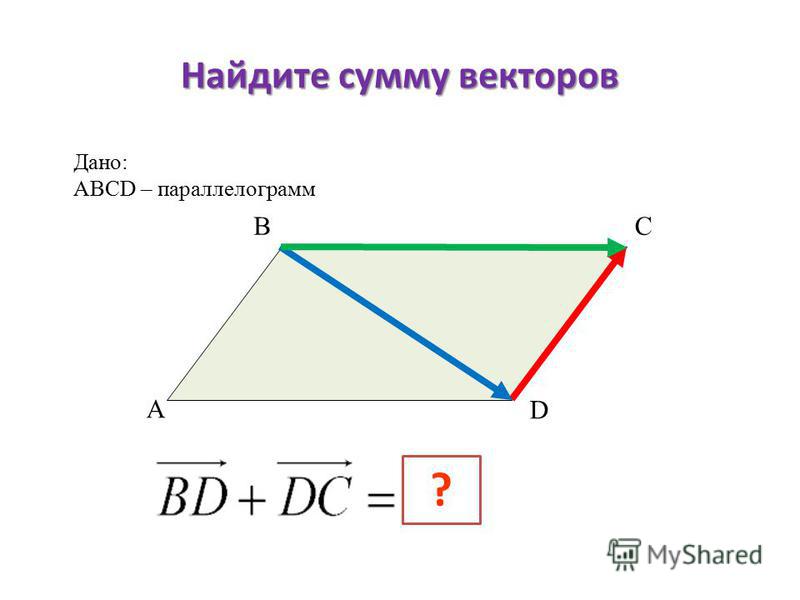
10. B 8 № 282852. В ромбе ABCD угол ACD равен 43°. Найдите угол ABC. Ответ дайте в градусах.
Дидактический материал к уроку математики «Площадь параллелограмма в задачах ОГЭ»; 9 класс — К уроку — Математика, алгебра, геометрия
Егорова Елена 5.0
Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям
Хочу выразить большую благодарность от лица педагогов начальных классов гимназии
«Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы
делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому
ученику и отчёт по классу. Великолепно, восторг! Преимущества мы оценили сразу. С
начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у
нас пока нет, одни благодарности. Очень простая и понятная инструкция, что
немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда
коллеги понимают, как можно «упростить» работу учителя.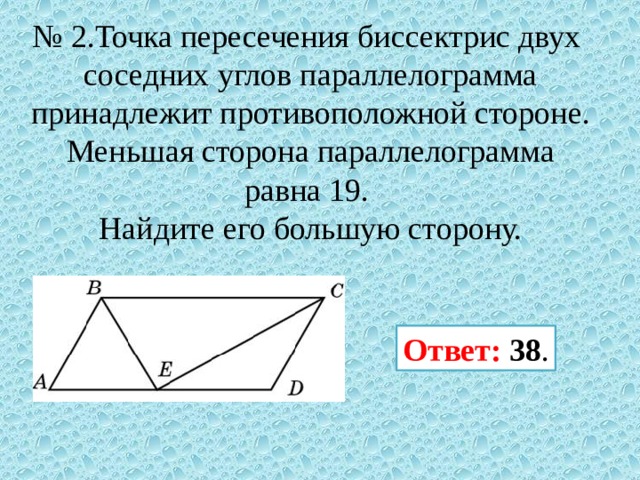
Наговицина Ольга Витальевна
учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ
по ХИМИИ
Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология. Очень облегчило аналитическую работу, выявляются узкие места в подготовке к экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.
Чазова Александра 5.0
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ
Очень хороший шаблон, удобен в использовании, анализ пробного тестирования 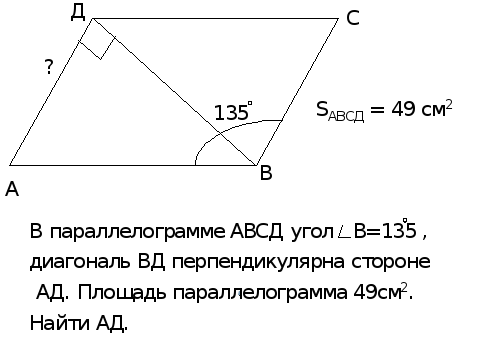
Лосеева Татьяна Борисовна 5.0
учитель начальных классов, МБОУ СОШ №1, г. Красновишерск, Пермский край
Отзыв о товаре Изготовление сертификата или свидетельства конкурса
Большое спасибо за оперативное изготовление сертификатов! Все очень красиво. Мой ученик доволен, свой сертификат он вложил в портфолио. Обязательно продолжим с Вами сотрудничество!
Язенина Ольга Анатольевна 4.0
учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы
Я посмотрела вебинар! Осталась очень довольна полученной
информацией. Всё очень чётко, без «воды». Всё, что сказано, показано, очень
пригодится в практике любого педагога. И я тоже обязательно воспользуюсь полезными материалами вебинара.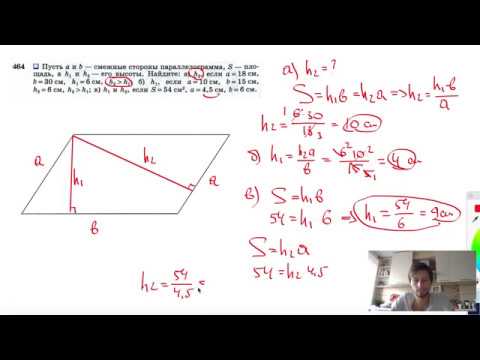 Спасибо большое лектору за то, что она
поделилась своим опытом!
Спасибо большое лектору за то, что она
поделилась своим опытом!
Арапханова Ашат 5.0
ША Табель посещаемости + Сводная для ДОУ ОКУД
Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень аккуратно и оперативно. Нет ни одного недостатка. Я не пожалела, что доверилась и приобрела у вас этот табель. Благодаря Вам сэкономила время, сейчас же составляю табель для работников. Удачи и успехов Вам в дальнейшем!
Дамбаа Айсуу 5.0
Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ
Спасибо огромное,
Подобные треугольники: периметры и площади
Когда два треугольника подобны, уменьшенное отношение любых двух соответствующих сторон называется масштабным коэффициентом подобных треугольников. На рисунке 1 Δ ABC ~ Δ DEF .
На рисунке 1 Δ ABC ~ Δ DEF .
Рисунок 1 Подобные треугольники с масштабным коэффициентом 2 : 1.
Соотношение соответствующих сторон 6/3, 8/4, 10/5. Все они уменьшаются до 2/1. Тогда говорят, что масштабный коэффициент этих двух подобных треугольников равен 2:1.
Периметр Δ ABC составляет 24 дюйма, а периметр Δ DEF — 12 дюймов. Когда вы сравниваете отношения периметров этих подобных треугольников, вы также получаете 2 : 1. Это приводит к следующей теореме.
Теорема 60: Если два подобных треугольника имеют масштабный коэффициент a : b, , то отношение их периметров равно a : b.
Пример 1: На рис. 2, Δ ABC ∼ Δ DEF . Найдите периметр Δ DEF
Рисунок 2 Периметр подобных треугольников.
 Поскольку GH ⊥ GI и JK ⊥ JL , их можно считать основанием и высотой для каждого треугольника. Теперь вы можете найти площадь каждого треугольника.
Поскольку GH ⊥ GI и JK ⊥ JL , их можно считать основанием и высотой для каждого треугольника. Теперь вы можете найти площадь каждого треугольника.Рисунок 3 Нахождение площадей подобных прямоугольных треугольников с масштабным коэффициентом 2 : 3.
Теперь вы можете сравнить отношение площадей этих подобных треугольников.
Это приводит к следующей теореме:
Теорема 61:
Пример 2: На рисунке 4 Δ PQR ∼ Δ STU . Найдите площадь Δ СТУ .
Рисунок 4 Использование коэффициента масштабирования для определения отношения между площадями подобных треугольников.
Масштаб этих подобных треугольников составляет 5 : 8.
Если назвать треугольники Δ 1 и Δ 2 , то
Согласно Теореме 60, это также означает, что масштабный коэффициент этих двух подобных треугольников равен 3 : 4.
Поскольку сумма площадей равна 75 см 2 , получается
Пример 4: Площади двух подобных треугольников равны 45 см 2 и 80 см 2 . Сумма их периметров равна 35 см. Найдите периметр каждого треугольника.
Назовите два треугольника Δ
a : b – сокращенная форма коэффициента масштабирования. 3 : 4 является сокращенной формой сравнения периметров.
Уменьшить дробь.
Извлечение квадратных корней из обеих сторон.
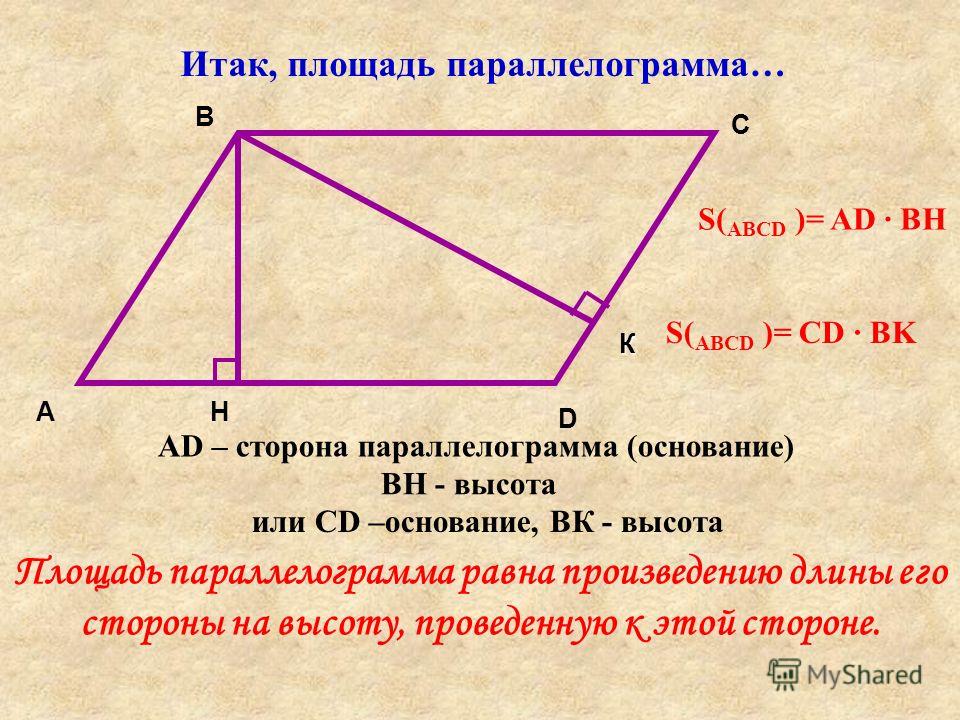
2.2: Основания и высоты параллелограммов
- Последнее обновление
- Идентификатор страницы
- 39636
- Иллюстративная математика
- Ресурсы OpenUp
Lesson
Давайте еще немного исследуем площадь параллелограмма.
Упражнение \(\PageIndex{1}\): параллелограмм и его прямоугольники
Елена и Тайлер находили площадь этого параллелограмма:
Рисунок \(\PageIndex{1}\)Переместите ползунок, чтобы увидеть, как это сделал Тайлер:
Переместите ползунок, чтобы увидеть, как это сделала Елена:
В чем сходятся две стратегии нахождения площади параллелограмма? Чем они отличаются?
Изучите примеры и не примеры основания и высоты параллелограмма.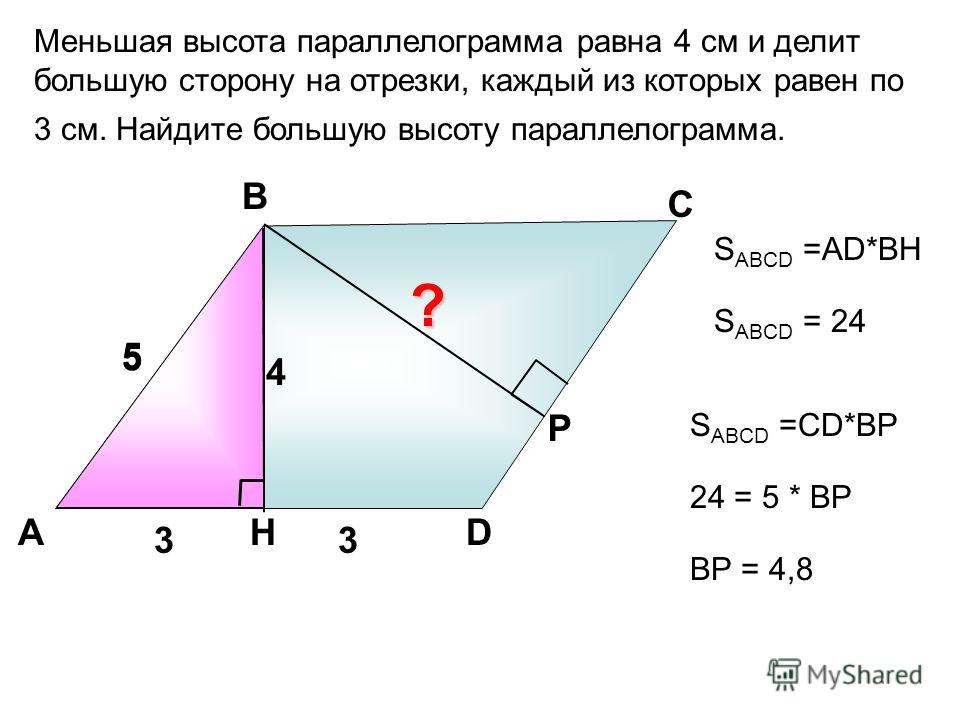
- Примеры: Пунктирные сегменты на этих рисунках представляют соответствующую высоту для данного основания.
- Непримеры: пунктирные сегменты на этих рисунках , а не представляют соответствующую высоту для данного основания.
- Выберите все утверждения, которые верны относительно оснований и высот в параллелограмме.
- Основанием может быть только горизонтальная сторона параллелограмма.
- Любая сторона параллелограмма может быть основанием.
- Высоту можно провести под любым углом к стороне, выбранной в качестве основания.
- Основание и соответствующая ему высота должны быть перпендикулярны друг другу.
- Высоту можно изобразить только внутри параллелограмма.
- Высоту можно провести за пределами параллелограмма, если он проведен под углом 90 градусов к основанию.

- Основание не может быть увеличено до высоты.
- Пять студентов обозначили основание \(b\) и соответствующую высоту \(h\) для каждого из этих параллелограммов. Все ли рисунки подписаны правильно? Объясните, откуда вы знаете.
Готовы ли вы к большему?
В апплете параллелограмм состоит из отрезков сплошных линий, а высота и опорные линии — из отрезков пунктирных линий. База b и соответствующая высота h помечены.
Упражнение \(\PageIndex{3}\): нахождение формулы площади параллелограмма
За каждый параллелограмм:
- Определите основание и соответствующую высоту и запишите их длины в таблицу.
- Найдите площадь параллелограмма и запишите ее в последний столбец таблицы.
| параллелограмм | база (шт.) | высота (ед. ) ) | площадь (кв.ед.) |
|---|---|---|---|
| А | |||
| Б | |||
| С | |||
| Д | |||
| любой параллелограмм | \(б\) | \(ч\) |
В последней строке напишите выражение для площади любого параллелограмма, используя \(b\) и \(h\).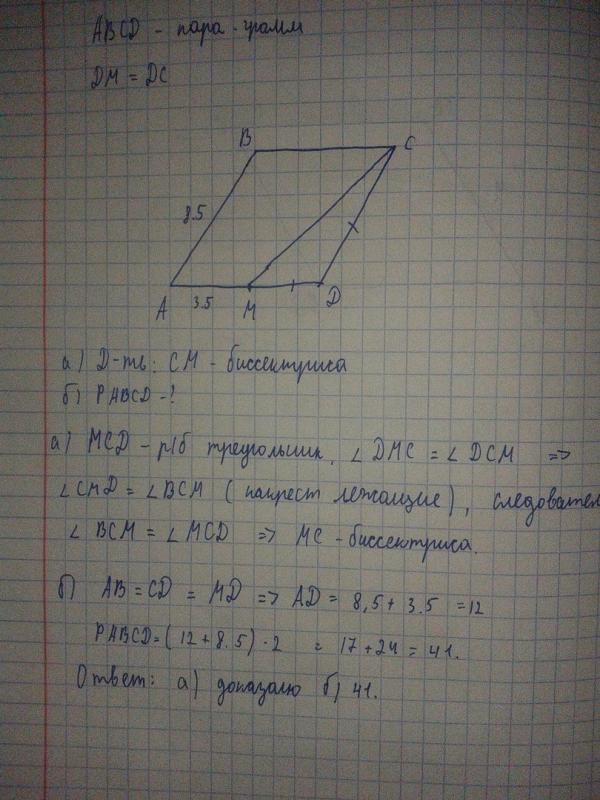
Готовы ли вы к большему?
- Что произойдет с площадью параллелограмма, если его высота удвоится, а основание не изменится? Если высота утроится? Если высота в 100 раз больше исходной?
- Что произойдет с площадью, если и основание, и высота удвоятся? Оба тройные? Обе в 100 раз длиннее своей первоначальной длины?
Резюме
- Мы можем выбрать любую из четырех сторон параллелограмма в качестве основания . И сторона (отрезок), и его длина (размер) называются основанием.
- Если мы проведем любой перпендикулярный отрезок из точки на основании к противоположной стороне параллелограмма, этот отрезок всегда будет иметь одинаковую длину. Мы называем это значение высотой . Существует бесконечно много сегментов, которые могут представлять высоту!
 Справа база = 5 единиц. Соответствующая высота = 4,8 единицы. Для обоих показаны 3 разных сегмента, представляющих высоту.
Справа база = 5 единиц. Соответствующая высота = 4,8 единицы. Для обоих показаны 3 разных сегмента, представляющих высоту.Вот две копии одного и того же параллелограмма. Слева сторона, являющаяся основанием, имеет длину 6 единиц. Соответствующая ему высота равна 4 единицам. Справа сторона, являющаяся основанием, имеет длину 5 единиц. Его соответствующая высота составляет 4,8 единицы. Для обоих показаны три разных сегмента, представляющих высоту. Мы могли бы привлечь гораздо больше!
Независимо от того, какая сторона выбрана в качестве основания, площадь параллелограмма равна произведению этого основания и соответствующей ему высоты. Мы можем проверить это:
\(4\times 6=24\qquad\text{ и }\qquad 4.8\times 5=24\)
Мы можем понять, почему это так, разложив и перестроив параллелограммы в прямоугольники.
Рисунок \(\PageIndex{7}\) Обратите внимание, что длины сторон каждого прямоугольника являются основанием и высотой параллелограмма. Несмотря на то, что у двух прямоугольников разные длины сторон, произведения длин сторон равны, поэтому они имеют одинаковую площадь! И оба прямоугольника имеют ту же площадь, что и параллелограмм.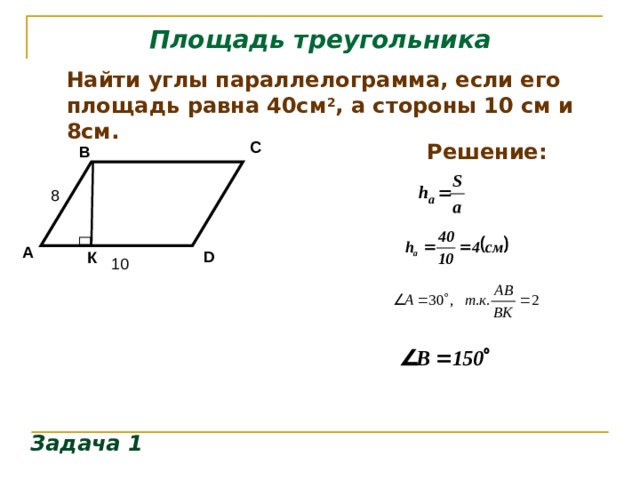
Мы часто используем буквы вместо цифр. Если \(b\) — основание параллелограмма (в единицах), а \(h\) — соответствующая высота (в единицах), то площадь параллелограмма (в квадратных единицах) равна произведению этих двух чисел. \(b\cdot h\)
Обратите внимание, что мы пишем символ умножения с маленькой точкой вместо символа \(\times\). Это сделано для того, чтобы мы не запутались в том, означает ли \(\times\) умножение или буква \(x\) заменяет число.
В старших классах вы сможете доказать, что отрезок перпендикуляра из точки на одной стороне параллелограмма к противоположной стороне всегда будет иметь одинаковую длину.
Рисунок \(\PageIndex{8}\)Легче всего это увидеть, нарисовав параллелограмм на миллиметровой бумаге. А пока мы просто будем использовать это как факт.
Словарь терминов
Определение: основание (параллелограмма или треугольника)
Мы можем выбрать любую сторону параллелограмма или треугольника в качестве основания фигуры. Иногда мы используем слово основание для обозначения длины этой стороны.
Иногда мы используем слово основание для обозначения длины этой стороны.
Определение: высота (параллелограмма или треугольника)
Высота – это кратчайшее расстояние от основания фигуры до противоположной стороны (для параллелограмма) или противоположной вершины (для треугольник).
Мы можем показать высоту более чем в одном месте, но она всегда будет перпендикулярна выбранному основанию.
Рисунок \(\PageIndex{10}\)Определение: параллелограмм
Параллелограмм — это тип четырехугольника, у которого две пары параллельных сторон.
Вот два примера параллелограмма.
Рисунок \(\PageIndex{11}\): два параллелограмма с указанными углами и длинами сторон. Слева верхняя и нижняя стороны = 5 единиц. Левая и правая стороны = 4,24 единицы. Верхний левый и нижний правый углы = 135 градусов. Верхний правый и нижний левый углы = 45 градусов. Справа верхняя и нижняя стороны = 9,34 единицы. Левая и правая стороны = 4 единицы.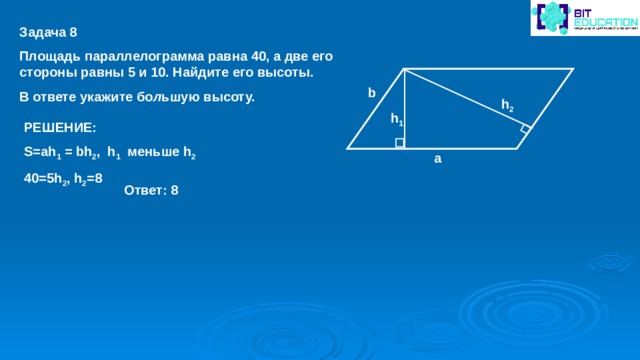 Верхний левый и нижний правый углы = 27,2 градуса. Верхний правый и нижний левый углы = 152,8 градуса.
Верхний левый и нижний правый углы = 27,2 градуса. Верхний правый и нижний левый углы = 152,8 градуса.Определение: Четырехугольник
Четырехугольник — это тип многоугольника, который имеет 4 стороны. Прямоугольник является примером четырехугольника. Пятиугольник не является четырехугольником, потому что у него 5 сторон.
Практика
Упражнение \(\PageIndex{4}\)
Выберите все параллелограмма, высота которых указана правильно для данного основания.
Рисунок \(\PageIndex{12}\): 4 параллелограмма на сетке, помеченные A, B, C, D. Параллелограмм A, основание = 3 единицы, высота = 2 единицы. Параллелограмм B, основание = 3 единицы, высота = 2 единицы. Параллелограмм С, основание = 3 звена, высота = 2 звена. Параллелограмм D, основание = диагональ двух единичных квадратов, высота = 3 единицы.- А
- Б
- С
- Д
Упражнение \(\PageIndex{5}\)
Сторона, обозначенная \(b\), выбрана в качестве основания этого параллелограмма.
Нарисуйте сегмент, показывающий высоту, соответствующую этому основанию.
Упражнение \(\PageIndex{6}\)
Найдите площадь каждого параллелограмма.
Рисунок \(\PageIndex{14}\): 3 параллелограмма на сетке, помеченные A, B, C. Параллелограмм A, основание = 4 единицы, высота = 2 единицы. Параллелограмм B, основание = 5 единиц, высота = 2 единицы. Параллелограмм С, основание = 2 единицы, высота = 4 единицы.Упражнение \(\PageIndex{7}\)
Если сторона, длина которой равна 6 единицам, является основанием этого параллелограмма, какова его соответствующая высота?
Рисунок \(\PageIndex{15}\): параллелограмм, нижняя и верхняя стороны которого обозначены цифрой 6, а правая сторона — цифрой 5. Пунктирная линия, перпендикулярная правой стороне, обозначена цифрой 4,8, а пунктирная линия, перпендикулярная нижней стороне, — с маркировкой 4.- 6 шт.
- 4,8 шт.
- 4 шт.
- 5 шт.

Упражнение \(\PageIndex{8}\)
Найдите площадь каждого параллелограмма.
Рисунок \(\PageIndex{16}\): 3 параллелограмма с обозначениями A, B, C. Параллелограмм A, основание = 9 сантиметров, высота = 4 сантиметра. Параллелограмм В, основание = 5 см, высота = 4 см. Параллелограмм C, основание = b, высота = h.Упражнение \(\PageIndex{9}\)
Согласны ли вы с каждым из этих утверждений? Объясните свои рассуждения.
- Параллелограмм имеет шесть сторон.
- Противоположные стороны параллелограмма параллельны.
- Параллелограмм может иметь одну или две пары параллельных сторон.
- Все стороны параллелограмма имеют одинаковую длину.
- Все углы параллелограмма имеют одинаковую величину.
(из блока 1.2.1)
Упражнение \(\PageIndex{10}\)
Квадрат площадью 1 квадратный метр разбит на 9 одинаковых маленьких квадратиков. Каждый маленький квадрат разбивается на два одинаковых треугольника.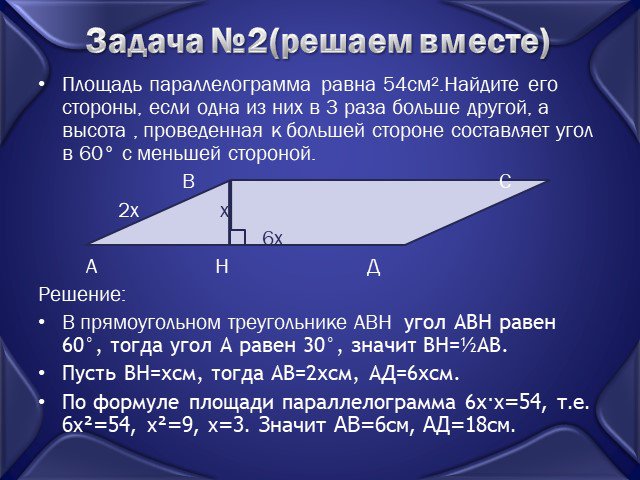


Leave A Comment