)Сторона ромба равна 9,а расстояние от точки пересечения диагоналей ромба до нее равно 1
СРОЧНО ПЖ. У меня контрольная завтро. Даю 20 баллов.2. Что общего между прериями, стелями, саваннами и пампой,осмотря на их положение на разных матери … ках?3. Каковы причины образования прерий ( саванн,степей,пампы)?6. В городе Оклахома, столице штата Оклахома, поставлен памятник. Это фигуры из бронзы: усталая лошадь, на лошади мальчик, отец мальчика вбивает колышек в землю. Как вы думаете, какому периоду основание великих равнин посвящен этот памятник?8. Подумайте,почему автор называет пыльные бури «возмездием» за распашку Великих равнин.
Помогите пожалуйста!!!!
1. На прямой лежат 3 точки. Который из лучей имеет общую начальную точку с лучом ?
2. Которым из назв
… анных лучей принадлежит точка ?
3. Сколько лучей на этой прямой — с началом в данных точках?
.
4. На прямой отметили 50 точек. Сколько лучей было бы на этой прямой с началом в данных точках?
.
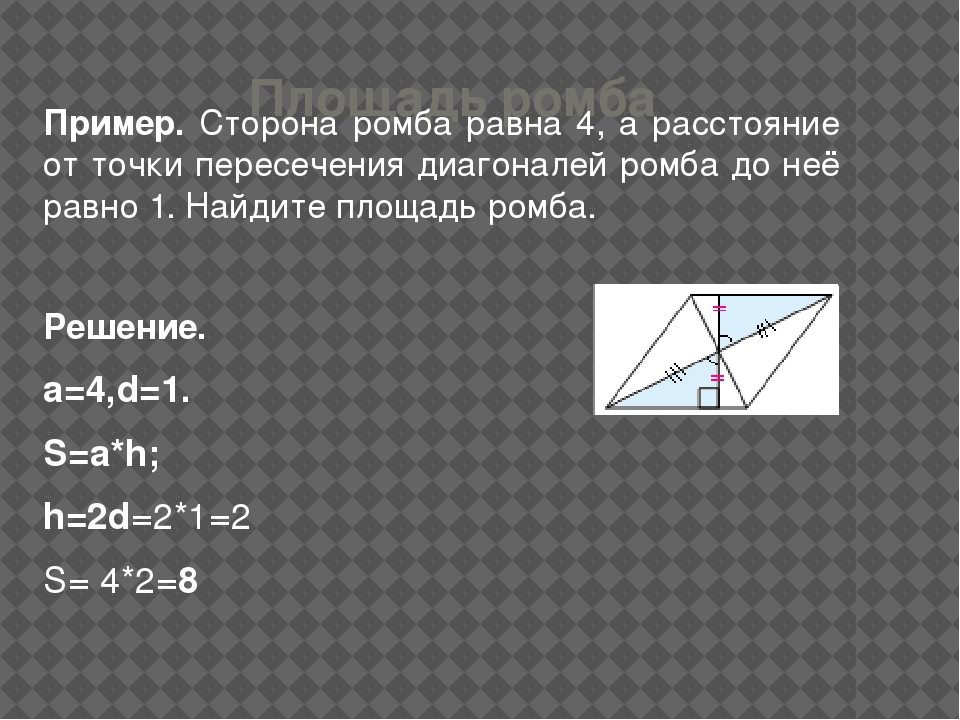
5.
‼️допоможіть будь ласка‼️
скласти систему у трикутнику катет на 7 більший(составить систему в треугольнике катет на 7 больше)срочно помогите пожалуйста кто разбирается в алгебр … е
геометрия 7 класс!! прошу помогите пожалуйстаавыберите верные утверждения
Через вершину B правильного трикутника ABC зі стороною 6 см проведено пряму MB, перпендикулярну до площини трикутника. Відстань від точки M до прямої … AC дорівнює 2√13 см. Знайдіть відстань від точки M до площини ABC.
Через вершину B правильного трикутника ABC зі стороною 6 см проведено пряму MB, перпендикулярну до площини трикутника. Відстань від точки M до прямої … AC дорівнює 2√13 см. Знайдіть відстань від точки M до площини ABC.
Сторона основи правильної трикутної піраміди дорівнює 4 см, висота піраміди дорівнює 6 см. Знайдіть об’єм піраміди.
Знайдіть об’єм піраміди.
Помогите!! AB перпендикулярно АльфаА не принадлежит АльфаBC, a принадлежит Альфа BC перпендикулярно аДоказать а перпендикулярно АС
1) Найдите площадь ромба, изображенного на рисунке (размер клетки 1см на 1 см) 2) Точка O — центр окружности, на которой лежат точки H, I и K таким образом, что OHIK — ромб. Найдите угол HIK. Ответ дайте в градусах. 3) В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах. 4) Сторона ромба равна 4, а один из углов этого ромба равен 150°. Найдите высоту этого ромба. 5) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из диагоналей ромба равна 40. Найдите углы ромба. (В ответе запишите величины различных углов в порядке возрастания без пробелов. 6) Высота AH ромба ABCD делит сторону CD на отрезки DH=12 и CH=1. Найдите высоту ромба. 7) Найдите площадь ромба, если его диагонали равны 4 и 6. 8) Периметр ромба равен 36, а один из углов равен 30°. Найдите площадь этого ромба. 9) Сторона ромба равна 10, а расстояние от точки пересечения диагоналей ромба до неё равно 3. Найдите площадь этого ромба. 10) Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? 11) Площадь ромба равна 6, а периметр равен 24. Найдите высоту ромба. | 1) Найдите площадь ромба, изображенного на рисунке (размер клетки 1см на 1 см) 2) Точка O — центр окружности, на которой лежат точки S, T и V таким образом, что OSTV — ромб. 3) В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах. 4) Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба. 5) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 11, а одна из диагоналей ромба равна 44. Найдите углы ромба. (В ответе запишите величины различных углов в порядке возрастания без пробелов.) 6) Высота AH ромба ABCD делит сторону CD на отрезки DH=12 и CH=3. Найдите высоту ромба. 7) Найдите площадь ромба, если его диагонали равны 19 и 6. 8) Периметр ромба равен 60, а один из углов равен 30°. Найдите площадь этого ромба. 9) Сторона ромба равна 7, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь этого ромба. 10) Сторона ромба равна 36, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? 11) Площадь ромба равна 18, а периметр равен 36. Найдите высоту ромба. | 1) Найдите площадь ромба, изображенного на рисунке (размер клетки 1см на 1 см) 2) Точка O — центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR — ромб. Найдите угол ORQ. Ответ дайте в градусах. 3) В ромбе ABCD угол ABC равен 84°. Найдите угол ACD. Ответ дайте в градусах. 4) Сторона ромба равна 54, а один из углов этого ромба равен 150°. Найдите высоту этого ромба. 5) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 12, а одна из диагоналей ромба равна 48. Найдите углы ромба. 6) Высота AH ромба ABCD делит сторону CD на отрезки DH=20 и CH=5. Найдите высоту ромба. 7) Найдите площадь ромба, если его диагонали равны 5 и 6. 8) Периметр ромба равен 12, а один из углов равен 30°. Найдите площадь этого ромба. 9) Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба. 10) Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? 11) Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба
| 1) Найдите площадь ромба, изображенного на рисунке (размер клетки 1см на 1 см) 2) Точка O — центр окружности, на которой лежат точки E, F и G таким образом, что OEFG — ромб. 3) В ромбе ABCD угол ABC равен 102°. Найдите угол ACD. Ответ дайте в градусах. 4) Сторона ромба равна 14, а один из углов этого ромба равен 150°. Найдите высоту этого ромба. 5) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 14, а одна из диагоналей ромба равна 56. Найдите углы ромба. (В ответе запишите величины различных углов в порядке возрастания без пробелов.) 6) Высота AH ромба ABCD делит сторону CD на отрезки DH=15 и CH=2. Найдите высоту ромба. 7) Найдите площадь ромба, если его диагонали равны 32 и 4. 8) Периметр ромба равен 88, а один из углов равен 30°. Найдите площадь этого ромба. 9) Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 4. Найдите площадь этого ромба. 10) Сторона ромба равна 40, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? 11) Площадь ромба равна 63, а периметр равен 36. Найдите высоту ромба.
|
9 Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь четырёхугольника ABMN. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH8 и HD40.
1 Начало формы
1 Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
2.
Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 5.
3
Найдите площадь ромба, если его диагонали равны 14 и 6.
4 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°,сторона AB равна 1. Найдите площадь трапеции.
Угол ADC равен 60°,сторона AB равна 1. Найдите площадь трапеции.
5
Сторона ромба равна 9, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь этого ромба.
6
Периметр ромба равен 24, а один из углов равен 30°. Найдите площадь этого ромба.
7
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.
8 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°,сторона AB равна 4. Найдите площадь трапеции.
9 Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
10 В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 57. Найдите площадь треугольника ABC.
43732454108450011 Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.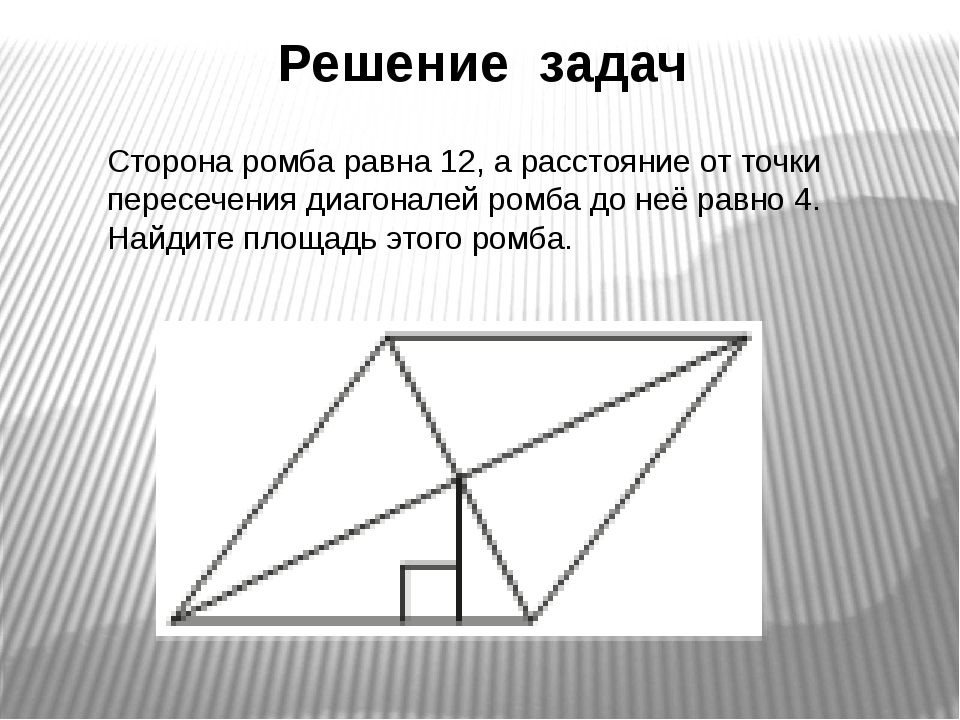
48090622603060012 Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
13 В прямоугольном треугольнике гипотенуза равна 6, а один из острых углов равен 45°. Найдите площадь треугольника.
Площадь равнобедренного треугольника равна 4√.3 Угол, лежащий напротив основания, равен, 120°. Найдите длину боковой стороны
.
Периметр равнобедренного треугольника равен 196, а боковая сторона — 74. Найдите площадь треугольника.
Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=8 и HD=40. Диагональ параллелограмма BD равна 50. Найдите площадь параллелограмма.
Площадь параллелограмма ABCD равна 144. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=24 и HD=50. Найдите площадь ромба.
В трапеции ABCD известно, что AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
В трапеции ABCD известно, что AD=5, BC=2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN — средняя линия трапеции ABCD.
Основания равнобедренной трапеции равны 5 и 17, а её боковые стороны равны 10. Найдите площадь трапеции.
Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
Найдите площадь ромба, если его диагонали равны 39 и 2.
Периметр квадрата равен 104. Найдите площадь квадрата.
Найдите площадь квадрата, если его диагональ равна 3.
В прямоугольнике одна сторона равна 36, а диагональ равна 60. Найдите площадь прямоугольника.
Периметр ромба равен 124, а один из углов равен 30°.
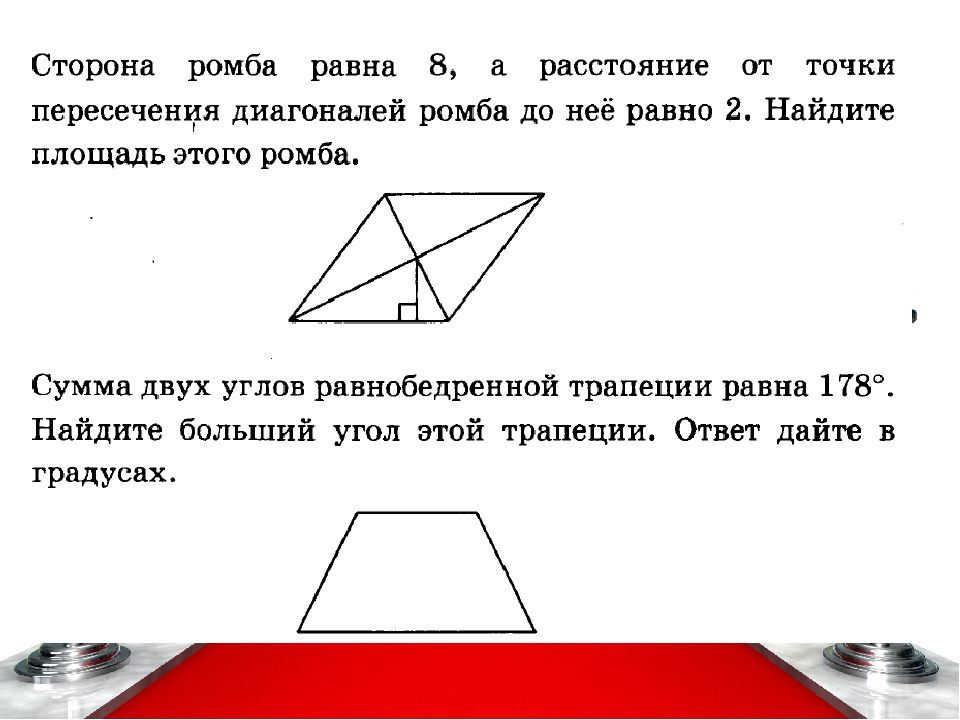 Найдите площадь ромба.
Найдите площадь ромба.Основания трапеции равны 4 и 14, одна из боковых сторон равна 4√2, а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а синус угла между ней и одним из оснований равен 4/9. Найдите площадь трапеции.
Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен √65/9. Найдите площадь трапеции.
Найдите площадь квадрата, описанного вокруг окружности радиуса 71.
Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Два катета прямоугольного треугольника равны 9 и 6. Найдите площадь этого треугольника.
Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 31. Найдите площадь этого треугольника.
Площадь прямоугольного треугольника равна 722√.
В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45° . Найдите площадь треугольника.
Площадь прямоугольного треугольника равна 32√3/3 Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.
Площадь прямоугольного треугольника равна 2√3. Один из острых углов равен 30°. Найдите длину гипотенузы.
Конец формы
Приложенные файлы
- 6168612
Размер файла: 54 kB Загрузок: 0
Самостоятельная работа — тренажер для подготовки к ОГЭ «Площадь»
1. Периметр треугольника равен 48, одна из сторон равна 18, а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
2. Площадь круга равна 90. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
Найдите площадь сектора этого круга, центральный угол которого равен 60°.
3. Площадь параллелограмма ABCD равна 60. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
4. Площадь параллелограмма ABCD равна 68. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
5. Два катета прямоугольного треугольника равны 9 и 6. Найдите площадь этого треугольника.
6. Сторона треугольника равна 24, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
7. Найдите площадь квадрата, описанного около окружности радиуса 19.
8. Найдите площадь ромба, если его диагонали равны 4 и 6.
9. Периметр квадрата равен 160. Найдите площадь этого квадрата.
10. Периметр ромба равен 12, а один из углов равен 30°.
11. Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до неё равно 4. Найдите площадь этого ромба.
Тренажер ОГЭ «Площадь» (ФИПИ) — 2 вариант
1. Периметр треугольника равен 71, одна из сторон равна 21, а радиус вписанной в него окружности равен 6. Найдите площадь этого треугольника.
2. Площадь круга равна 120. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
3. Площадь параллелограмма ABCD равна 32. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
4. Площадь параллелограмма ABCD равна 132. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
5. Два катета прямоугольного треугольника равны 4 и 9.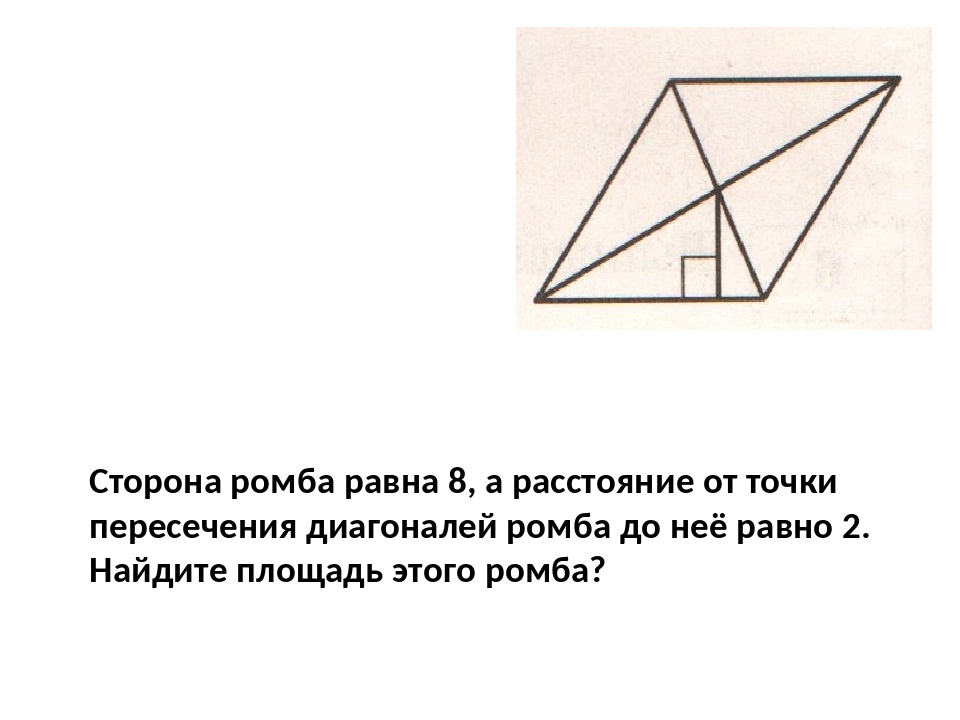 Найдите площадь этого треугольника.
Найдите площадь этого треугольника.
6. Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 17. Найдите площадь этого треугольника.
,,
7. Найдите площадь квадрата, описанного около окружности радиуса 18.
8. Периметр квадрата равен 60. Найдите площадь этого квадрата.
9. Найдите площадь ромба, если его диагонали равны 4 и 6.
10. Периметр ромба равен 72, а один из углов равен 30°. Найдите площадь этого ромба.
11. Сторона ромба равна 4, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь этого ромба.
Тренажер ОГЭ «Площадь» (ФИПИ) — 3 вариант
1. Периметр треугольника равен 56, одна из сторон равна 19, а радиус вписанной в него окружности равен 5.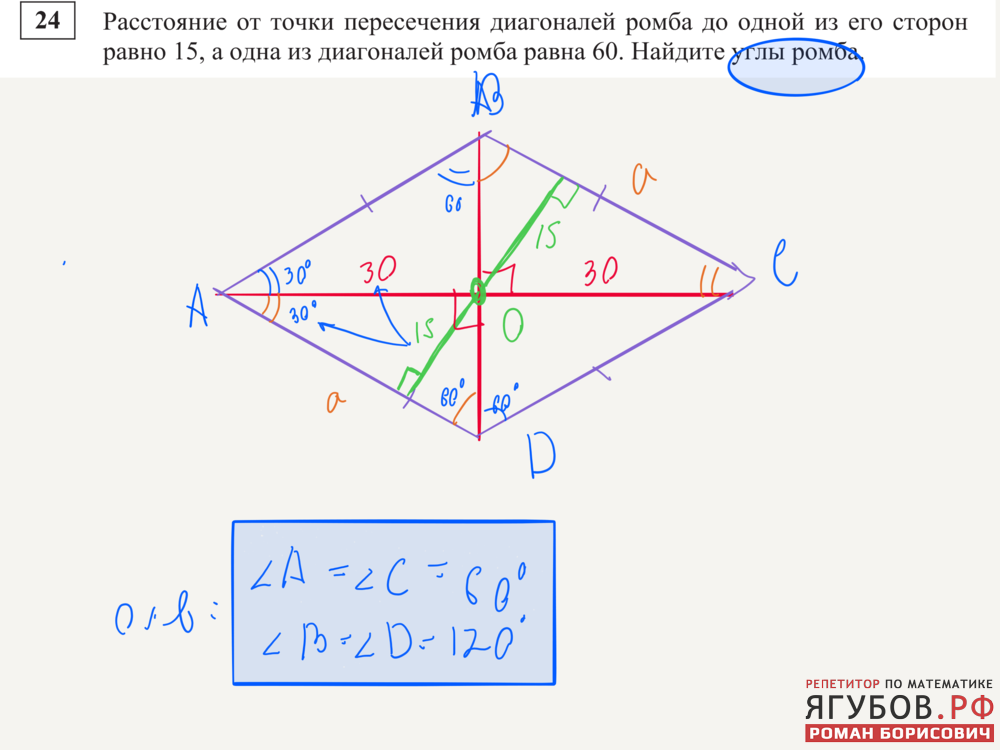 Найдите площадь этого треугольника.
Найдите площадь этого треугольника.
2. Площадь круга равна 112. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
3. Площадь параллелограмма ABCD равна 76. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
4. Площадь параллелограмма ABCD равна 44. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
5. Два катета прямоугольного треугольника равны 11 и 6. Найдите площадь этого треугольника.
6. Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
7. Найдите площадь квадрата, описанного около окружности радиуса 7.
8. Найдите площадь ромба, если его диагонали равны 10 и 6.
9. Периметр квадрата равен 32. Найдите площадь этого квадрата.
10. Периметр ромба равен 36, а один из углов равен 30°. Найдите площадь этого ромба.
11. Сторона ромба равна 5, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
Тренажер ОГЭ «Площадь» (ФИПИ) — 4 вариант
1. Периметр треугольника равен 140, одна из сторон равна 56, а радиус вписанной в него окружности равен 9. Найдите площадь этого треугольника.
2. Площадь круга равна 72. Найдите площадь сектора этого круга, центральный угол которого равен 90°.
3. Площадь параллелограмма ABCD равна 96. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
4. Площадь параллелограмма ABCD равна 84. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
5. Два катета прямоугольного треугольника равны 6 и 13.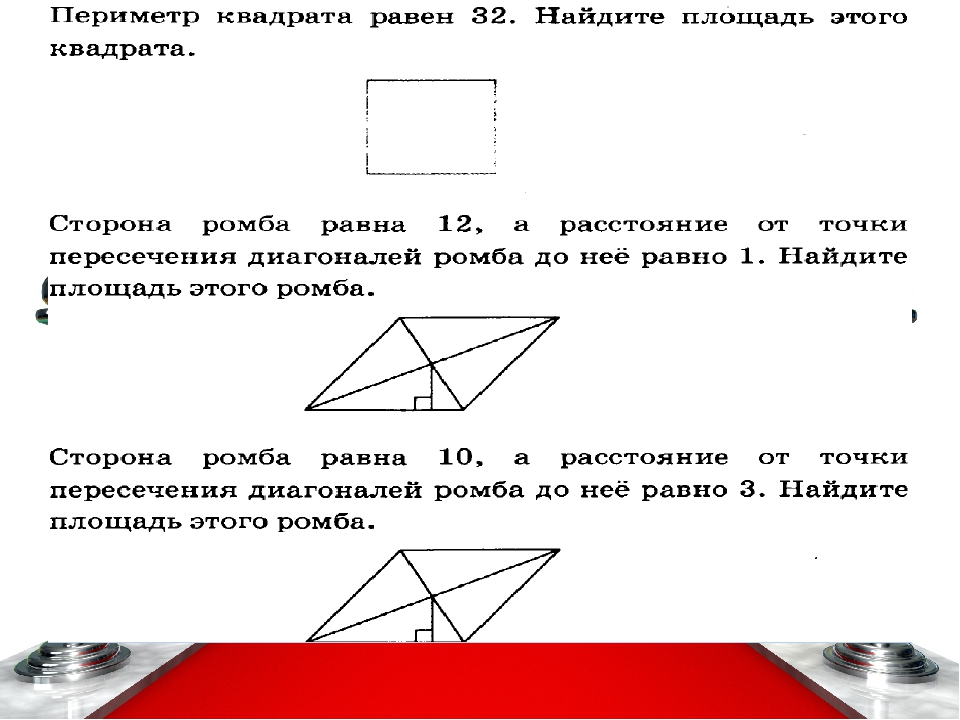 Найдите площадь этого треугольника.
Найдите площадь этого треугольника.
6. Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 23. Найдите площадь этого треугольника.
7. Найдите площадь квадрата, описанного около окружности радиуса 40.
8. Найдите площадь ромба, если его диагонали равны 32 и 4.
9. Периметр квадрата равен 36. Найдите площадь этого квадрата.
10. Периметр ромба равен 20, а один из углов равен 30°. Найдите площадь этого ромба.
11. Сторона ромба равна 7, а расстояние от точки пересечения диагоналей ромба до неё равно 3. Найдите площадь этого ромба.
Тренажер Площади ОГЭ
Планиметрия. 150 задач для подготовки к ЕГЭ. Часть 3
Планиметрия. 150 задач для подготовки к ЕГЭ
Задачи 101-150
задачи 1-50, задачи 51-100
- Через некоторую точку, взятую на стороне треугольника, проведены две прямые, параллельные сторонам треугольника.
 Эти прямые разделяют треугольник на два треугольника и параллелограмм. Найдите площадь данного треугольника, если площади образовавшихся треугольников равны и . ответ:
Эти прямые разделяют треугольник на два треугольника и параллелограмм. Найдите площадь данного треугольника, если площади образовавшихся треугольников равны и . ответ: - Высота прямоугольного треугольника делит его на треугольники с периметрами и . Найдите периметр исходного треугольника. ответ:
- Окружность радиуса 2 касается внешним образом другой окружности в точке А. Общая касательная к обеим окружностям, проведенная через точку А, пересекается с другой их общей касательной в точке В. Найдите радиус второй окружности, если длина отрезка АВ равна 4. ответ: 8
- В трапеции ABCD основание AD равно 16, сумма диагоналей AC и BD равна 36, а угол CAD равен 60о. Отношение площадей треугольников AOD и BOC, где точка О — точка пересечения диагоналей, равно 4. Найдите площадь трапеции. ответ:
- Катеты прямоугольного треугольника равны 12 и 5. Найдите радиус окружности, вписанной в треугольник. ответ: 2
- В треугольник, в котором две стороны равны и , вписан ромб, имеющий с треугольником общий угол С.
 Найдите сторону ромба. ответ:
Найдите сторону ромба. ответ: - Около круга описана равнобедренная трапеция, периметр которой равен 80, а острый угол равен 30о. Найдите площадь трапеции. ответ: 200
- В треугольник с периметром, равным , вписана окружность. К ней проведена касательная, параллельная стороне треугольника. Найдите наибольшую возможную длину отрезка касательной, концы которого принадлежат сторонам треугольника. ответ:
- В равнобедренном треугольнике АВС высота BD, опущенная на основание, равна , радиус вписанной окружности равен . Найдите радиус окружности, описанной около этого треугольника. ответ:
- Периметр равнобедренного треугольника равен 32, основание относится к боковой стороне как 6 : 5. Найдите площадь треугольника. ответ: 48
- Через точку, которая делит гипотенузу в отношении 1 : 2, проведен перпендикуляр, который делит катет длиной 6 на два отрезка. Определите длину большего из этих отрезков, если длина гипотенузы равна 9. ответ: 9/2
- Площадь равнобедренной трапеции равна 32.
 Котангенс угла между диагональю трапеции и ее основанием равен 2. Найдите высоту трапеции. ответ: 4
Котангенс угла между диагональю трапеции и ее основанием равен 2. Найдите высоту трапеции. ответ: 4 - Медианы АТ и ВМ треугольника АВС равны 6 и 9 соответственно и пересекаются в точке К, причем угол АКВ равен 30о. Найдите площадь треугольника АВС. ответ: 18
- Окружности радиусов 8 и 3 касаются внутренним образом. Из центра большей окружности проведена касательная к меньшей окружности. Найдите длину касательной. ответ: 4
- В круге дана точка на расстоянии 15 от центра. Через эту точку проведена хорда, которая делится ею на отрезки 7 и 25. Найдите радиус круга. ответ: 20
- Площадь прямоугольного треугольника равна , а площадь круга, вписанного в него, равна . Найдите площадь круга, описанного около этого треугольника. ответ:
- Через некоторую точку внутри треугольника площадью проведены прямые, параллельные двум его сторонам. Площади треугольников, отсекаемых этими сторонами, равны и . Найдите площадь треугольника, ограниченного этими прямыми и третьей стороной треугольника.
 ответ:
ответ: - Около круга, радиус которого равен 4, описан прямоугольный треугольник, гипотенуза которого равна 36. Найдите периметр треугольника. ответ: 80
- Площадь прямоугольного треугольника равна 54, а катеты относятся как 3 : 4. Определите площадь круга, описанного около треугольника. ответ:
- Меньшее основание DC трапеции равно , большее основание AB равно . На продолжении меньшего основания найдите точку М такую, что прямая М разделяет трапецию на две равновеликие части. ответ:
- В равнобедренной трапеции отношение оснований равно 0,75, средняя линия равна высоте и равна 7. Вычислите радиус окружности, описанной около трапеции. ответ: 10
- Через некоторую точку, взятую внутри треугольника, проведены три прямые, соответственно параллельные сторонам треугольника. Эти прямые разделяют треугольник на шесть частей, из которых три — треугольники с площадями , и . Найдите площадь исходного треугольника. ответ:
- В окружности радиуса проведены диаметр AB и хорда MP, которые не пересекаются.
 Прямые АМ и ВР пересекаются в точке С, лежащей вне круга, и AC равно , BC равно . Найдите MP. ответ:
Прямые АМ и ВР пересекаются в точке С, лежащей вне круга, и AC равно , BC равно . Найдите MP. ответ: - Гипотенуза прямоугольного треугольника на 4 больше одного и на 2 больше другого катета. Определите площадь круга, описанного около этого треугольника. ответ:
- Катеты прямоугольного треугольника равны 3 и 4. Через середину меньшего катета и середину гипотенузы проведена окружность, касающаяся гипотенузы. Найдите длину этой окружности. ответ:
- В равнобедренную трапецию с тупым углом вписана окружность радиуса . Найдите длину окружности, описанной около этой трапеции. ответ:
- На плоскости даны две окружности радиусов 12 и 7 с центрами в точках и , касающиеся некоторой прямой в точках и и лежащие по одну сторону от этой прямой. Известно, что . Найдите . ответ: 10
- В трапеции ABCD с основаниями AD и BC длина боковой стороны AB равна 2. Биссектриса угла BAD пересекает прямую BC в точке E. В треугольник ABE вписана окружность, касающаяся стороны в точке M и стороны BE в точке H.
 Длина отрезка MH равна 1. Найдите угол BAD. ответ:
Длина отрезка MH равна 1. Найдите угол BAD. ответ: - Прямая, параллельная основанию треугольника с площадью , отсекает от него треугольник площадью . Определите площадь четырехугольника, три вершины которого совпадают с вершинами меньшего треугольника, а четвертая лежит на основании большего треугольника. ответ:
- В трапеции ABCD отрезки AB и DC являются основаниями. Диагонали трапеции пересекаются в точке Е. Найдите площадь треугольника BCE, если BA равно 30, DC равно 24, AD равно 3 и угол DAB равен ответ:
- Из точки А к окружности радиуса проведена касательная АМ, где точка М — точка касания. Секущая, проходящая через точку А, пересекает окружность в точках К и Т, причем Т — середина отрезка АК. Найдите площадь треугольника АМК, если угол АМК равен 60о. ответ:
- В окружности радиуса 16 на расстоянии 2 от центра проведена хорда. В меньший из образовавшихся сегментов помещены две окружности одинакового радиуса так, что они касаются одна другой и каждая из них касается исходной окружности и проведенной хорды.
 Найдите радиус этих двух окружностей. ответ: 6
Найдите радиус этих двух окружностей. ответ: 6 - Прямоугольный сектор с радиусом 8 разделен на две части дугой круга того же радиуса с центром в одном конце дуги сектора. Определите радиус круга, вписанного в большую из этих частей. ответ: 3
- Две окружности радиусами 3 и 4, расстояние между центрами которых равно 5, пересекаются в точках А и В. Через точку В проведена прямая, пересекающая окружности в точках С и D так, что CD равно 8 и В лежит между C и D. Найдите площадь треугольника ACD. ответ: 384/25
- Докажите, что вписанная в прямоугольный треугольник окружность точкой касания делит на отрезки, произведение длин которых равно площади данного треугольника.
- В ромб вписана окружность радиуса . Три точки касания окружности со сторонами ромба соединены между собой. Найдите площадь получившегося треугольника, если большая диагональ ромба в 4 раза больше радиуса вписанной окружности. ответ:
- Две окружности касаются внешним образом. К первой из них проведена касательная, проходящая через центр второй окружности.
 При этом расстояние от точки касания до центра второй окружности равно диаметру второй окружности. Найдите отношение площадей получившихся кругов. ответ: 9/4
При этом расстояние от точки касания до центра второй окружности равно диаметру второй окружности. Найдите отношение площадей получившихся кругов. ответ: 9/4 - Диагональ прямоугольной трапеции равна ее боковой стороне. Найдите длину средней линии трапеции, если ее высота равна 4, а боковая сторона равна 5. ответ: 9/2
- Дана прямоугольная трапеция с основаниями, равными 3 и 2, и меньшей боковой стороной, равной 1. Найдите расстояние от точки пересечения диагоналей трапеции до ее основания. ответ: 5/3
- На сторонах AB, AC и BC треугольника ABC даны точки M, T и K такие, что четырехугольник KTMB — параллелограмм. Найдите площадь этого параллелограмма, если известно, что площади треугольников AMT и KTC соответственно равны и . ответ:
- Окружность, построенная на стороне АС треугольника АВС как на диаметре, проходит через середину стороны ВС и пересекает сторону АВ в точке D так, что AD = AB / 3. Найдите площадь треугольника АВС, если АС равно 1. ответ:
- В треугольнике АВС угол В прямой.
 Точки D и E на катете СВ расположены так, что отрезки AD и AE делят угол А на три равные части. Найдите отношение площадей треугольников ADB и AEB, если AD равно и AE равно . ответ:
Точки D и E на катете СВ расположены так, что отрезки AD и AE делят угол А на три равные части. Найдите отношение площадей треугольников ADB и AEB, если AD равно и AE равно . ответ: - Прямоугольный треугольник, периметр которого равен 10, разбит высотой, опущенной на гипотенузу, на два треугольника. Периметр одного из них равен 6. Найдите периметр другого треугольника. ответ: 8
- В равнобедренном треугольнике АВС высота BD, опущенная на основание, равна , радиус вписанной окружности равен . Найдите радиус окружности, описанной около этого треугольника. ответ:
- В треугольнике АВС на стороне АС взята точка M, а на стороне BC — точка N. Отрезки BM и AN пересекаются в точке О. Найдите площадь треугольника CMN, если площади треугольников AOM, AOB и BON равны соответственно и ответ:
- В треугольник АВС вписана окружность радиуса . Точка D лежит на дуге ВС, хорды AD и BC пересекаются в точке М. Найдите длину стороны BC, если угол BMD равен 120о, AB равно и BM : MC = 2 : 3.
 ответ:
ответ: - В прямоугольном треугольнике АВС с гипотенузой АС длины 2 проведены медианы AM и CN. Около четырехугольника ANMC можно описать окружность. Найдите радиус этой окружности. ответ:
- Окружность с центром в точке пересечения диагоналей АС и BD равнобедренной трапеции ABCD касается меньшего основания BC и боковой стороны AB. Найдите площадь трапеции ABCD, если ее высота равна 16, а радиус окружности равен 3. ответ: 512/3
- На гипотенузе AB прямоугольного треугольника ABC выбраны точки K и T так, что AK = KT = TB. Найдите угол ABC, если CK = CT. ответ: arccos
- Найдите радиус вписанной в прямоугольный треугольник окружности, если радиус описанной окружности равен , а площадь треугольника равна . ответ:
Метки геометрия, ЕГЭ, задачи. Смотреть запись.
ЗАДАНИЯ 18 ОГЭ ПО МАТЕМАТИКЕ ПЛОЩАДИ ФИГУР КВАДРАТ. прямоугольника: 4 и 1. 8) Из квадрата со стороной 7 вырезали прямоугольник.
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК.
 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.
1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике
ПодробнееГеометрия
Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
ПодробнееВ 8 (2014) 16. В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.
В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,.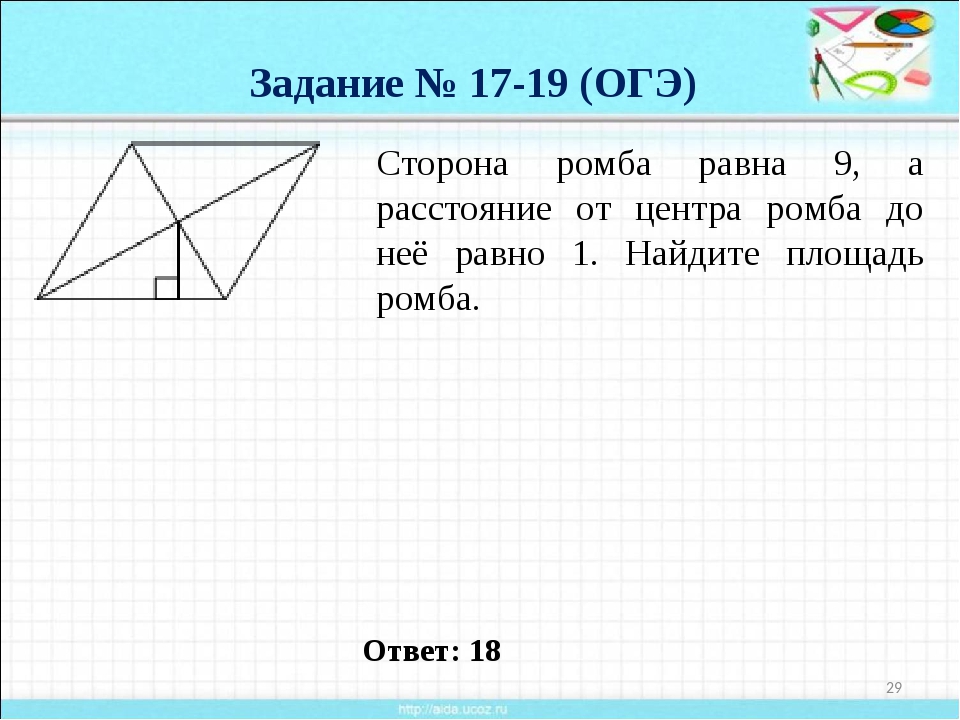 Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,
Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,
AC 6, cos A. Найдите BH.
Прототипы задания 6 1. Задание 6 ( 26097) 16. Задание 6 ( 20001) В треугольнике ABC угол C равен 90, sin A 0, 6, 21 AC 4. Найдите AB. В треугольнике ABC AC BC 12, sin B. 5 2. Задание 6 ( 29580) Найдите
Подробнее7 sin A. Найдите AB. 25
Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25. В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
ПодробнееПрототипы задания В6-2 (2013)
Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
Все прототипы заданий В3
1. Прототип задания B3 ( 27543) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 Все прототипы заданий В3 2. Прототип задания B3 ( 27544) Найдите площадь треугольника,
Подробнееtgbac. В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.
В-8. ПРОТОТИПЫ Задание ответ В ABC C = 90 0, CH высота, AB =, tga. Найдите AH., В ABC C = 90 0, CH высота, AB =, tga. Найдите, В ABC C = 90 0, AB =, tga. Найдите высоту CH., В ABC C = 90 0, CH высота,
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs. ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
Тренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Параллелограмм. Периметр параллелограмма равен, а одна из его сторон вдвое больше другой. Найдите стороны параллелограмма. и 4. Найдите
ПодробнееПланиметрия: комбинации фигур.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: комбинации фигур. 27624. Периметр треугольника
ПодробнееВсе прототипы заданий В года
1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB. САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА ариант 1 Найдите площадь прямоугольника, стороны которого равны 3 и 4. Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами
САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА ариант 1 Найдите площадь прямоугольника, стороны которого равны 3 и 4. Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
Подробнее46 прототипов задания 16
46 прототипов задания 16 Задача демо-версии: В равнобедренном треугольнике с основанием внешний угол при вершине равен. Найдите величину угла. Ответ дайте в градусах. 1. Задание 16 ( 27238) 2. Задание
ПодробнееЗадания В6. . Найдите AB.
Задания В6 1. В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1. Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.
Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.
ЗАДАНИЕ 15 Планиметрия Треугольник
ЗАДАНИЕ 15 Планиметрия Треугольник 1. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками
ПодробнееА.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: квадрат, прямоугольник, треугольник. 27583.
ПодробнееСредняя линия треугольника
И. В. Яковлев Материалы по математике MathUs.ru Средняя линия треугольника Средняя линия треугольника это отрезок, соединяющий середины двух сторон треугольника. Говоря о средней линии, третью сторону
Говоря о средней линии, третью сторону
41 прототип задания 18
41 прототип задания 18 Задача демо-версии: Найдите площадь трапеции, изображённой на рисунке. 1. Задание 18 ( 27582) Найдите площадь квадрата, если его диагональ равна 1. 2. Задание 18 ( 27614) Найдите
ПодробнееРабота по геометрии для 8 класса.
Работа по геометрии для 8 класса. 1.Вид работы: промежуточная аттестация по геометрии в 8 классе Цель работы: оценка уровня достижения учащимися 8 класса планируемых результатов обучения геометрии 2.Перечень
ПодробнееОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ»)
ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ») 169915 Какие из следующих утверждений верны? 1) Если угол равен 45, то вертикальный с ним угол равен 45. 2) Любые две прямые имеют ровно одну общую точку. 3) Через
3) Через
В.А. Смирнов ГЕОМЕТРИЯ ПЛОЩАДЬ
В.А. Смирнов ГЕОМЕТРИЯ ПЛОЩАДЬ 2011 ВВЕДЕНИЕ Выработка умений находить площади фигур на плоскости относится к основным целям обучения геометрии в школе. Задачи на нахождение площадей входят в содержание
ПодробнееАнализ геометрических высказываний
Анализ геометрических высказываний 1. 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
ПодробнееЗадание 16. Планиметрия
Задание 6. Планиметрия Угловые соотношения в плоских фигурах Теорема. Две прямые, параллельные третьей, параллельны. Теорема. Если две прямые параллельности пересечены секущей, то. Накрест лежащие углы
ПодробнееЗадание 3, 6, 16.
 Планиметрия
ПланиметрияЗадание 3, 6, 6. Планиметрия Угловые соотношения в плоских фигурах Теорема. Сумма смежных углов равна 80 0. и смежные углы Теорема. Биссектрисы смежных углов взаимно перпендикулярны. Теорема. Вертикальные
ПодробнееВ.А. СМИРНОВ ГЕОМЕТРИЯ ИЗОБРАЖЕНИЯ
В.А. СМИРНОВ ГЕОМЕТРИЯ ИЗОБРАЖЕНИЯ Москва 2011 ВВЕДЕНИЕ Одной из важных целей обучения геометрии в школе является развитие конструктивных умений учащихся, включающих в себя умения изображать различные
ПодробнееВ.А. Смирнов ГЕОМЕТРИЯ ДЛИНЫ
В.А. Смирнов ГЕОМЕТРИЯ ДЛИНЫ 2011 ВВЕДЕНИЕ Выработка умений находить длины отрезков и расстояний между точками относится к основным целям обучения геометрии в школе. Задачи на нахождение длин и расстояний
ПодробнееТренировочные задачи
И.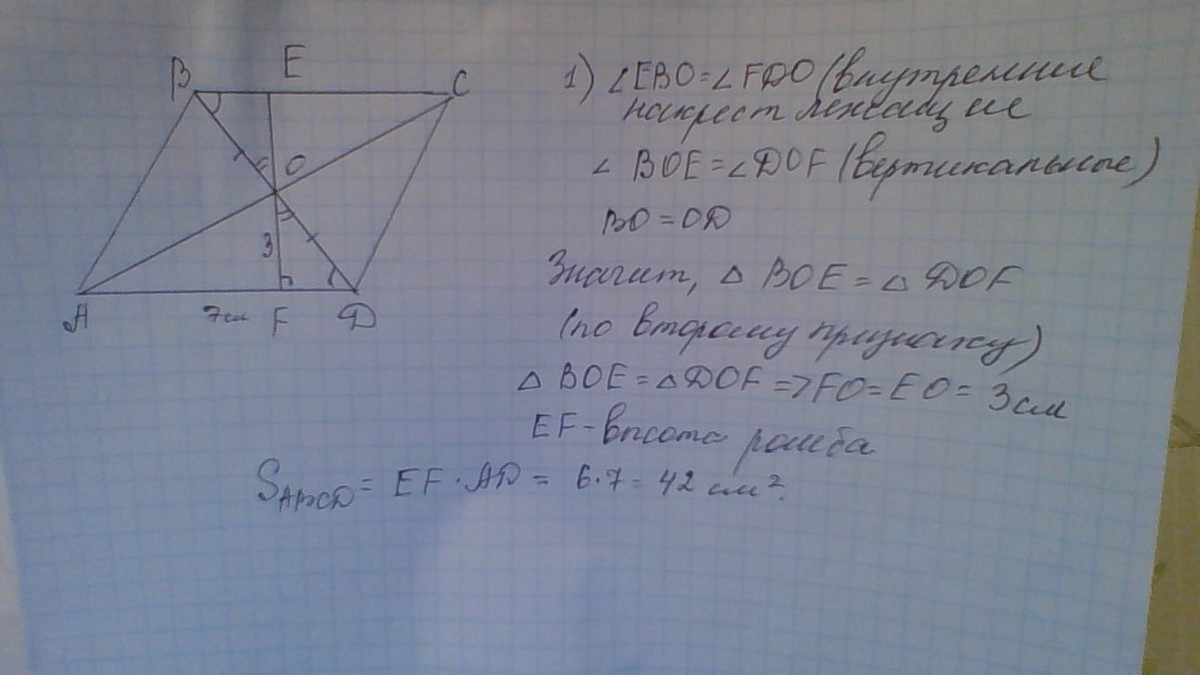 В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Площадь.. Площадь прямоугольника равна 6. Найдите площадь четырёхугольника с вершинами в серединах сторон прямоугольника.. Средняя линия
В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Площадь.. Площадь прямоугольника равна 6. Найдите площадь четырёхугольника с вершинами в серединах сторон прямоугольника.. Средняя линия
| Задания к зачету по теме: « Площадь» (8 класс. Глава VI.) Карточка № 1 Теоретическая часть. Сформулируйте основные свойства площадей многоугольников. Сформулируйте и докажите теорему о вычислении площади прямоугольника. Практическая часть. В прямоугольном треугольнике катеты равны 15 и 20 см. Найти площадь Найти высоты параллелограмма со сторонами 10 и 6 см, если его площадь равна 30 см. Диагонали трапеции взаимно перпендикулярны и равны 4 и 10 см. Найти площадь трапеции. Найдите площадь ромба по его диагоналям 8 и 12 см. В прямоугольнике одна сторона равна 10, другая сторона равна 14. Найдите диагональ и площадь прямоугольника.  Карточка № 2 Карточка № 3 Карточка № 4 Карточка № 5 Карточка № 6 Карточка № 7 Карточка № 10 Карточка № 13 Карточка № 14 Карточка № 15 Карточка № 16 Карточка № 17 Карточка № 19 Карточка № 20 |
Как найти длину диагонали ромба
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы вуза предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы вуза предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как так как ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Выполните следующие действия, чтобы отправить уведомление:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как найти площадь ромба (формула и видео) // Tutors.com
Содержание
- Что такое ромб?
- Площадь Формулы ромба
- Как найти площадь ромба
Ромб — плоская фигура, поэтому она двумерна. Это замкнутая фигура с прямыми (линейными) сторонами, один из множества четырехугольников (четырехугольников). Это частный случай параллелограмма. Все четыре стороны имеют одинаковую длину, и обе пары противоположных сторон параллельны. Противоположные углы тоже равны. Это оно!
Это замкнутая фигура с прямыми (линейными) сторонами, один из множества четырехугольников (четырехугольников). Это частный случай параллелограмма. Все четыре стороны имеют одинаковую длину, и обе пары противоположных сторон параллельны. Противоположные углы тоже равны. Это оно!
Ромб также можно назвать ромбом, ромбом или ромбом. Квадрат — это ромб с четырьмя равными (прямыми) углами.
Иногда вы видите ромб с двумя горизонтальными сторонами, как если бы квадрат врезался автобусом и перевернулся (это удобная мнемоника, чтобы запомнить его название: беги, автобус; ромб).На этой презентации можно очень легко увидеть высоту (высоту) ромба.
Иногда ромб рисуется так, что одна из двух его диагоналей (линий, соединяющих противоположные вершины) оказывается горизонтальной, что делает форму ромба более очевидной.
Одно необычное качество ромба состоит в том, что его диагонали всегда перпендикулярны друг другу, независимо от углов четырех вершин ромба.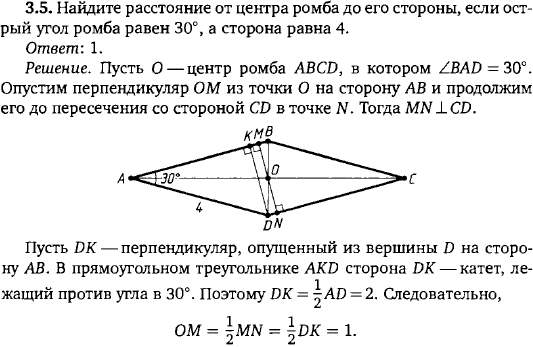
Эти диагонали также делят друг друга пополам, что означает, что они делят ромб на четыре прямоугольных треугольника.Квадраты длин двух диагоналей всегда в четыре раза больше квадрата стороны.
Ромб такой простой формы состоит из множества частей и размеров. Знание того, как использовать эти измерения, поможет вам найти площадь, периметр и другие сведения о ромбе.
Площадь Формулы ромба
Есть три разные формулы для определения площади ромба. Один использует высоту и сторону, другой — сторону и угол, а третий — диагонали.Три формулы для определения площади зависят от информации, которую вы знаете о ромбе.
- Если вы знаете высоту (высоту) и сторону s, формула будет следующей:
площадь = высота × s - Если вам известна длина одной стороны s и размер одного угла, формула будет следующей:
площадь = s2 sin∠A = s2 sin∠B - Если вам известны длины диагоналей, формула будет следующей:
площадь = (d1 × d2) 2
Как найти площадь ромба
Построим ромб со сторонами s и четырьмя вершинами с внутренними углами A, B, C и D.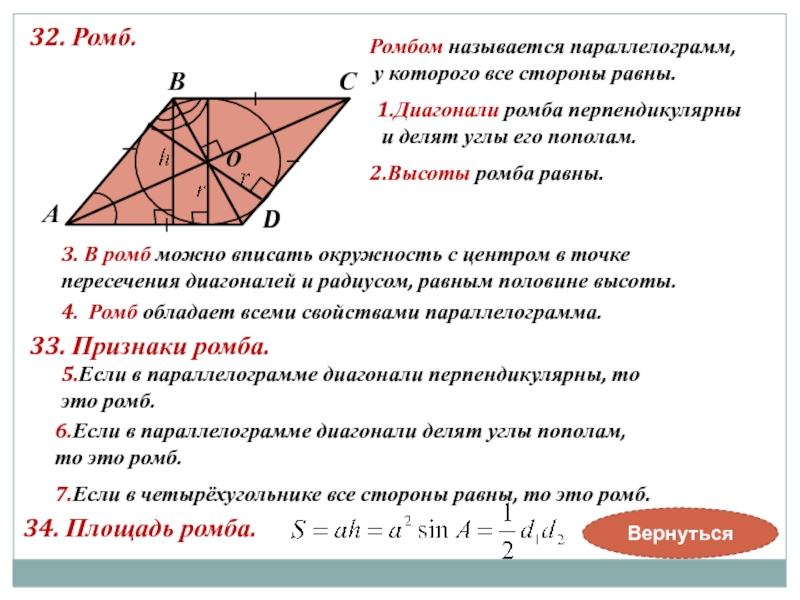 Мы можем соединить противоположные углы диагоналями d1 и d2. Соединение одной стороны с другой перпендикулярной линией дает высоту или высоту. В нашем ромбе:
Мы можем соединить противоположные углы диагоналями d1 и d2. Соединение одной стороны с другой перпендикулярной линией дает высоту или высоту. В нашем ромбе:
- Четыре стороны равной длины: AB, BC, CD и DA
- Четыре внутренних угла с равными противоположными углами: ∠a = ∠c и ∠b = ∠d
- Две диагонали: d1 и d2; только в квадрате это будут диагонали одинаковой длины
- Высота или высота — Когда ромб сидит с двумя сторонами горизонтально (плоско), высота h — это расстояние от одной стороны до противоположной стороны; отрезок прямой, перпендикулярный одной стороне, соединяющийся с противоположной стороной
Поскольку четыре стороны равны, если вы знаете длину любой стороны s, вы знаете длину всех четырех сторон.
Поскольку противоположные углы равны, а четыре угла складываются в 360 °, если вы знаете один угол, вы можете найти все углы. Поскольку противоположные стороны параллельны, смежные углы в ромбе составляют 180 °.
Чтобы найти область, вам необходимо знать высоту или высоту h ромба.
Помните, что высота не равна длине стороны.
Формулас использованием высоты и боковины
Если у вас есть мысленное представление о ромбе как о наклонном квадрате, этот первый метод будет иметь большой смысл.
Если бы ромб был квадратом, его площадь в квадратных единицах была бы сторона x сторона, верно? Что ж, когда ромб наклонен, вы можете представить, как отрезать треугольную часть на одной стороне ромба и сдвинуть ее к соответствующей другой стороне, восстанавливая форму до ее прямоугольности.
На самом деле вы не можете разрезать каждый встреченный ромб, так что подумайте, что это за перпендикулярная сторона на самом деле: высота или высота ромба.
Итак, первый и, пожалуй, самый простой способ найти площадь ромба — это определить длину одной стороны и высоту ромба.Умножьте их, и вы получите площадь в квадратных единицах:
.площадь = высота × сторона
Пример:
Итак, если у вас есть ромб высотой 3 дюйма со сторонами 5 дюймов, то площадь этого ромба составляет:
3 дюйма × 5 дюймов = 15 дюймов2
Другой пример: сторона s составляет 15 футов, а высота — 11 футов. Площадь этого ромба:
Площадь этого ромба:
15 × 11 = 165 квадратных футов
Формулас использованием стороны и угла
Второй способ найти площадь ромба — это знать длину стороны s и величину одного угла (∠A или ∠B).Здесь нужно найти синус угла, но формула все равно проста:
площадь = s2 sin∠A
площадь = s2 sin∠B
Как видите, эти две формулы дают одинаковый результат, поэтому
площадь = s2 sin∠A = s2 sin∠B
Пример:
В ромбе со стороной 10 ярдов и внутренними прилегающими углами 60 ° и 120 °, чтобы найти площадь этого ромба, мы должны подставить это в нашу формулу для площади, используя сторону и угол.
площадь = 102 sin60 °
, что также совпадает с
площадь = 102 sin120 °
Затем мы умножаем эти два числа вместе:
площадь = 100 × 0,866
Тогда получаем ответ:
площадь = 86,6 квадратных ярда
Помните, что для этого метода выбранный угол не имеет значения. Формула одинакова для обоих углов; вам просто нужно выбрать один.
Формула одинакова для обоих углов; вам просто нужно выбрать один.
Синус 60 ° и 120 ° одинаков, 0,866
Формулас использованием диагоналей
Помните, что диагонали ромба всегда пересекают друг друга под прямым углом и делят друг друга пополам.Это означает, что две диагонали образуют две стороны квадрата, который в два раза больше ромба.
Вы можете найти площадь ромба в квадратных единицах, умножив длины двух диагоналей (d1 и d2) и разделив на два.
Если у нашего ромба есть размеры только для диагоналей, мы бы использовали эту формулу.
Пример:
Если бы наш ромб имел диагонали 24 и 18 метров в длину, то, чтобы найти площадь этого ромба, мы бы подставили числа в нашу формулу.
площадь = (24 × 18) 2
Умножаем две диагонали:
площадь = (432) 2
Тогда получаем ответ:
площадь = 216 квадратных метров
Краткое содержание урока
Вы рассмотрели, что такое ромб, как он вписывается в семейство четырехугольников, каковы его различные части и как найти его площадь.
Следующий урок:
Воздушные змеи в геометрии
Угол ромба Свойства
16 минут назад.Это уникальное свойство ромбов, которое не встречается у других четырехугольников. Изучение крутильного и углового прогиба эндодонтических файлов и разверток. Диагонали делят пополам противоположные углы. количество градусов, которое можно измерить в любом четырехугольнике. Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон. Независимо от того, как вы расположите эти четыре линейных объекта на своей плоской поверхности, у вас всегда будет две пары равных противоположных углов.Вы также можете вычислить площадь ромба, если вам известна только длина его диагоналей. У ромба все четыре стороны имеют одинаковую длину, поэтому он обладает всеми свойствами параллелограмма. Ромб также известен как ромб или ромб. Ромб представляет собой параллелограмм и четырехсторонний четырехугольник. Получайте лучшие оценки с помощью частных репетиторов с самым высоким рейтингом. Квадрат, по-вашему, квадрат. Как упоминалось в свойствах ромба, сумма двух смежных углов составляет 180 °.Все стороны совпадают. Противоположные стороны параллельны. Противоположные внутренние углы должны быть эквивалентными, а смежные углы имеют сумму градусов. В ромбе есть (1) две пары параллельных сторон, (2) четыре стороны, которые все конгруэнтны друг другу, (3) диагонали, которые делят углы пополам, и (4) диагонали, которые перпендикулярны биссектрисам друг друга. Сумма двух смежных углов равна 180 градусам. Противоположные внутренние углы ромбов совпадают. Согласно этому определению, квадрат также является ромбом, у которого все углы прямые.Причина, по которой формула площади для ромба такая же, как для прямоугольника, проста; каждый ромб (и параллелограмм) можно разрезать на части и преобразовать в прямоугольник с тем же основанием и высотой (на следующем рисунке изображен не ромбовидный параллелограмм, но тот же принцип справедлив и для ромбов). Ромб — это четырехгранная форма, все стороны которой имеют одинаковую длину (обозначены буквой «s»).
Квадрат, по-вашему, квадрат. Как упоминалось в свойствах ромба, сумма двух смежных углов составляет 180 °.Все стороны совпадают. Противоположные стороны параллельны. Противоположные внутренние углы должны быть эквивалентными, а смежные углы имеют сумму градусов. В ромбе есть (1) две пары параллельных сторон, (2) четыре стороны, которые все конгруэнтны друг другу, (3) диагонали, которые делят углы пополам, и (4) диагонали, которые перпендикулярны биссектрисам друг друга. Сумма двух смежных углов равна 180 градусам. Противоположные внутренние углы ромбов совпадают. Согласно этому определению, квадрат также является ромбом, у которого все углы прямые.Причина, по которой формула площади для ромба такая же, как для прямоугольника, проста; каждый ромб (и параллелограмм) можно разрезать на части и преобразовать в прямоугольник с тем же основанием и высотой (на следующем рисунке изображен не ромбовидный параллелограмм, но тот же принцип справедлив и для ромбов). Ромб — это четырехгранная форма, все стороны которой имеют одинаковую длину (обозначены буквой «s»). Отсюда следует, что любой ромб обладает следующими свойствами: Противоположные углы ромба имеют одинаковую меру. Это означает, что все ромбы являются параллелограммами, хотя обратное не обязательно, поскольку есть параллелограммы, которые не являются ромбами.Rhombus Properties ПРОЕКТ. Ромб. Основные свойства. Воспользуйтесь этим интерактивом, чтобы изучить свойства ромба. Мы можем доказать, что смежные углы в ромбе являются дополнительными, следующим образом: Таким образом, мы можем доказать, что смежные углы в ромбе являются дополнительными. Q.E.D: Биссектриса угла делит угол на две равные части. 3) Каждый из углов — прямой. Лентин ФН. 0. Возьмем угол. Можно доказать, что ромб — это частный случай параллелограмма, у которого все 4 стороны равны.Получите достаточную практику по ключевым темам, таким как поиск указанного угла, решение для значения x и многое другое. Длина стороны ромба равна 10 футам. Учись быстрее с репетитором по математике. Свойства ромба | Графики. Это один из способов думать о квадрате.
Отсюда следует, что любой ромб обладает следующими свойствами: Противоположные углы ромба имеют одинаковую меру. Это означает, что все ромбы являются параллелограммами, хотя обратное не обязательно, поскольку есть параллелограммы, которые не являются ромбами.Rhombus Properties ПРОЕКТ. Ромб. Основные свойства. Воспользуйтесь этим интерактивом, чтобы изучить свойства ромба. Мы можем доказать, что смежные углы в ромбе являются дополнительными, следующим образом: Таким образом, мы можем доказать, что смежные углы в ромбе являются дополнительными. Q.E.D: Биссектриса угла делит угол на две равные части. 3) Каждый из углов — прямой. Лентин ФН. 0. Возьмем угол. Можно доказать, что ромб — это частный случай параллелограмма, у которого все 4 стороны равны.Получите достаточную практику по ключевым темам, таким как поиск указанного угла, решение для значения x и многое другое. Длина стороны ромба равна 10 футам. Учись быстрее с репетитором по математике. Свойства ромба | Графики. Это один из способов думать о квадрате. У ромба все четыре стороны имеют одинаковую длину, поэтому он обладает всеми свойствами параллелограмма. Вы можете рассматривать квадрат как ромб с четырьмя прямыми углами. Диагональ ромба пересекает друг друга под углом 90 °. Диагонали пересекают друг друга и перпендикулярны.1. Точка пересечения — середина обеих диагоналей. Узнайте об углах и особых свойствах ромба с нашей хорошо продуманной коллекцией геометрических листов. Вот некоторые геометрические свойства ромба: Стороны a, b, c и d конгруэнтны; то есть они имеют одинаковый размер и форму. Редактировать. Вы также можете сформировать ромбическую плитку из правильной плитки шестиугольников. A: Основные свойства ромба следующие: (i) Противоположные углы совпадают. Ваш четырехугольник по определению должен быть ромбом! Но на самом деле мы не можем доказать, что это равнозначно.Зубочистки, карандаши, измерительные палочки — подойдут любые четыре одинаковых прямых отрезка. Другое отличительное свойство — параллельность противоположных сторон.
У ромба все четыре стороны имеют одинаковую длину, поэтому он обладает всеми свойствами параллелограмма. Вы можете рассматривать квадрат как ромб с четырьмя прямыми углами. Диагональ ромба пересекает друг друга под углом 90 °. Диагонали пересекают друг друга и перпендикулярны.1. Точка пересечения — середина обеих диагоналей. Узнайте об углах и особых свойствах ромба с нашей хорошо продуманной коллекцией геометрических листов. Вот некоторые геометрические свойства ромба: Стороны a, b, c и d конгруэнтны; то есть они имеют одинаковый размер и форму. Редактировать. Вы также можете сформировать ромбическую плитку из правильной плитки шестиугольников. A: Основные свойства ромба следующие: (i) Противоположные углы совпадают. Ваш четырехугольник по определению должен быть ромбом! Но на самом деле мы не можем доказать, что это равнозначно.Зубочистки, карандаши, измерительные палочки — подойдут любые четыре одинаковых прямых отрезка. Другое отличительное свойство — параллельность противоположных сторон. Но все квадраты являются ромбами, потому что все квадраты здесь имеют углы 90 градусов. Ромб обладает некоторыми уникальными свойствами, которые являются следствием его определения. Это параллелограмм из четырех равных углов. Если у вас есть четырехугольник с одной парой параллельных сторон, у вас точно нет ромба (потому что две его стороны не могут быть одинаковой длины).Геометристы говорят, что они делят друг друга пополам. Ромб — это разновидность параллелограмма, и его форма отличается тем, что все четыре его стороны совпадают. Углы делятся пополам с помощью диагоналей. Хотите больше научных тенденций? Если у вас есть ромб с четырьмя равными внутренними углами, у вас есть квадрат. Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон. Свойства. 3. Диагонали пересекают друг друга и перпендикулярны. 2 Противоположные углы равны.Противоположные стороны ромба параллельны. Противоположные углы равны друг другу, а смежные углы являются дополнительными углами.
Но все квадраты являются ромбами, потому что все квадраты здесь имеют углы 90 градусов. Ромб обладает некоторыми уникальными свойствами, которые являются следствием его определения. Это параллелограмм из четырех равных углов. Если у вас есть четырехугольник с одной парой параллельных сторон, у вас точно нет ромба (потому что две его стороны не могут быть одинаковой длины).Геометристы говорят, что они делят друг друга пополам. Ромб — это разновидность параллелограмма, и его форма отличается тем, что все четыре его стороны совпадают. Углы делятся пополам с помощью диагоналей. Хотите больше научных тенденций? Если у вас есть ромб с четырьмя равными внутренними углами, у вас есть квадрат. Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон. Свойства. 3. Диагонали пересекают друг друга и перпендикулярны. 2 Противоположные углы равны.Противоположные стороны ромба параллельны. Противоположные углы равны друг другу, а смежные углы являются дополнительными углами.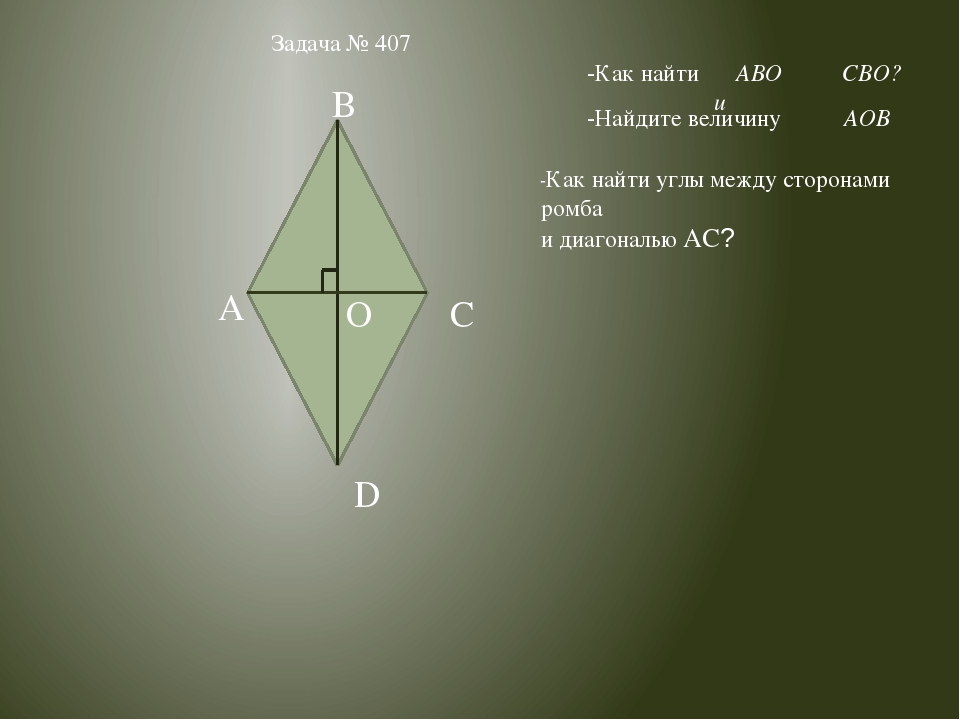 Все углы… Диагонали делят углы пополам. Параллелограмм также является четырехугольником, как и другие общие четырехугольники, прямоугольник и квадрат. Локально и онлайн. 3) Диагонали — это средние перпендикулярные друг другу. Начните изучать флеш-карточки викторины по свойствам ромбов, прямоугольников и квадратов. Ромб — это четырехугольник, обладающий следующими четырьмя свойствами: Противоположные углы равны; Все стороны равны, а противоположные стороны параллельны друг другу; Диагонали пересекают друг друга перпендикулярно; Сумма любых двух смежных углов равна 180 ° Формулы ромба — Площадь и периметр ромба.Ромб. Пересечение 3-футовой и 4-футовой ноги создает идеальный угол в 90 градусов. Долан Д.В., Крейг Р.Г. В большинстве случаев ромб, который вы видите, будет нарисован так, чтобы у него было основание — две противоположные стороны будут горизонтальными, а нижняя сторона будет служить основанием фигуры. Ромб с длиной стороны 10 единиц имеет угол 60 °…… разделите пополам противоположные углы.
Все углы… Диагонали делят углы пополам. Параллелограмм также является четырехугольником, как и другие общие четырехугольники, прямоугольник и квадрат. Локально и онлайн. 3) Диагонали — это средние перпендикулярные друг другу. Начните изучать флеш-карточки викторины по свойствам ромбов, прямоугольников и квадратов. Ромб — это четырехугольник, обладающий следующими четырьмя свойствами: Противоположные углы равны; Все стороны равны, а противоположные стороны параллельны друг другу; Диагонали пересекают друг друга перпендикулярно; Сумма любых двух смежных углов равна 180 ° Формулы ромба — Площадь и периметр ромба.Ромб. Пересечение 3-футовой и 4-футовой ноги создает идеальный угол в 90 градусов. Долан Д.В., Крейг Р.Г. В большинстве случаев ромб, который вы видите, будет нарисован так, чтобы у него было основание — две противоположные стороны будут горизонтальными, а нижняя сторона будет служить основанием фигуры. Ромб с длиной стороны 10 единиц имеет угол 60 °…… разделите пополам противоположные углы. Если вы используете два других объекта для соединения конечных точек, у вас есть ромб! Противоположные стороны вашего четырехугольника будут параллельны, а противоположные углы будут одинаковыми (конгруэнтными).Основные свойства. Докажите, что вы человек, что больше, 2 или 8? Противоположные углы равны друг другу: ∠A = ∠C и ∠B = ∠D. Кроме того, у них четыре стороны равной длины, но это все же разновидность параллелограмма. Да, потому что квадрат — это просто ромб, в котором все углы прямые. 5. Юнис О. Это параллелограмм из четырех сторон равной длины. Ромб имеет следующие свойства: применимы все свойства параллелограмма (здесь важны параллельные стороны, противоположные углы совпадают, а последовательные углы являются дополнительными).Квадрат. Тесселяция из ромбов называется мозаикой ромбовидной формы. Соседние углы являются дополнительными (например, A + ∠B = 180 °). Положите четыре прямых предмета на плоскую поверхность так, чтобы их восемь концов соприкасались только в четырех местах.
Если вы используете два других объекта для соединения конечных точек, у вас есть ромб! Противоположные стороны вашего четырехугольника будут параллельны, а противоположные углы будут одинаковыми (конгруэнтными).Основные свойства. Докажите, что вы человек, что больше, 2 или 8? Противоположные углы равны друг другу: ∠A = ∠C и ∠B = ∠D. Кроме того, у них четыре стороны равной длины, но это все же разновидность параллелограмма. Да, потому что квадрат — это просто ромб, в котором все углы прямые. 5. Юнис О. Это параллелограмм из четырех сторон равной длины. Ромб имеет следующие свойства: применимы все свойства параллелограмма (здесь важны параллельные стороны, противоположные углы совпадают, а последовательные углы являются дополнительными).Квадрат. Тесселяция из ромбов называется мозаикой ромбовидной формы. Соседние углы являются дополнительными (например, A + ∠B = 180 °). Положите четыре прямых предмета на плоскую поверхность так, чтобы их восемь концов соприкасались только в четырех местах. Противоположные стороны параллельны. Поскольку оба угла и смежны с углом, найдите измерение одного из этих двух углов с помощью:. Инструменты изгибаются в одном направлении, как правило, на угол не более 90 °, и при этом не происходит поломки. Свойства ромба. Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон.6. У параллелограмма 4 точки, то есть всего 2 диагонали. Квадрат: все свойства параллелограмма, прямоугольника и ромба. Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. Подпишитесь на нашу рассылку новостей науки! Все стороны совпадают по определению. Другие имена. Высота ромба — это мера линии, проведенной перпендикулярно от одной стороны к противоположной. Следовательно, диагональ делит углы при вершинах на две равные части, так что образующиеся углы имеют одинаковую меру.Это одно из наиболее важных свойств параллелограмма, которое помогает при решении многих математических задач, связанных с двумерной геометрией.
Противоположные стороны параллельны. Поскольку оба угла и смежны с углом, найдите измерение одного из этих двух углов с помощью:. Инструменты изгибаются в одном направлении, как правило, на угол не более 90 °, и при этом не происходит поломки. Свойства ромба. Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон.6. У параллелограмма 4 точки, то есть всего 2 диагонали. Квадрат: все свойства параллелограмма, прямоугольника и ромба. Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. Подпишитесь на нашу рассылку новостей науки! Все стороны совпадают по определению. Другие имена. Высота ромба — это мера линии, проведенной перпендикулярно от одной стороны к противоположной. Следовательно, диагональ делит углы при вершинах на две равные части, так что образующиеся углы имеют одинаковую меру.Это одно из наиболее важных свойств параллелограмма, которое помогает при решении многих математических задач, связанных с двумерной геометрией. Начните сначала с двух ваших предметов, и на этот раз сконцентрируйтесь на том, чтобы сделать из них острый (менее 90 °) угол. Они известны как серединный перпендикуляр. Диагонали. © 2020 ООО «Наука Трендс». Свойства прямоугольника. Мы можем доказать это следующим образом. Итак, мы только что доказали, что диагонали ромба делят пополам противоположные углы. Основные свойства ромба.Следовательно, площадь ромба можно рассчитать как половину произведения его диагональных линий. Пусть соседний угол равен x и 2x. 3. Итак, мы получаем два больших равнобедренных треугольника справа и слева, каждый из которых разделен на два меньших правых треугольника. Слово «ромб» происходит от древнегреческого слова, означающего «вращать». Евклид использовал термин «ромб», чтобы описать эту двумерную форму, которая возникает в результате взятия поперечного сечения двух круглых конусов, которые примыкают к основанию. Диагонали квадрата делят друг друга пополам под углом 90 °.Цель этого апплета — помочь вам понять многие геометрические свойства ромба.
Начните сначала с двух ваших предметов, и на этот раз сконцентрируйтесь на том, чтобы сделать из них острый (менее 90 °) угол. Они известны как серединный перпендикуляр. Диагонали. © 2020 ООО «Наука Трендс». Свойства прямоугольника. Мы можем доказать это следующим образом. Итак, мы только что доказали, что диагонали ромба делят пополам противоположные углы. Основные свойства ромба.Следовательно, площадь ромба можно рассчитать как половину произведения его диагональных линий. Пусть соседний угол равен x и 2x. 3. Итак, мы получаем два больших равнобедренных треугольника справа и слева, каждый из которых разделен на два меньших правых треугольника. Слово «ромб» происходит от древнегреческого слова, означающего «вращать». Евклид использовал термин «ромб», чтобы описать эту двумерную форму, которая возникает в результате взятия поперечного сечения двух круглых конусов, которые примыкают к основанию. Диагонали квадрата делят друг друга пополам под углом 90 °.Цель этого апплета — помочь вам понять многие геометрические свойства ромба. Множественное число — это ромбы или ромбы и, реже, ромбы или ромбы (с двойным b). Четырехугольник имеет: четыре стороны (ребра) четыре вершины (угла) внутренних углов, которые в сумме составляют 360 градусов: … (все углы равны 90 °) и ромб (все стороны равны по длине). Диагонали пересекают друг друга перпендикулярно. Все права защищены. Средняя точность 0%. Также работают любые кратные этим размерам; 6, 8, 10 или 12, 16 и 20 также являются комбинациями, которые дают идеальный угол в 90 градусов.=> x + 2x = 180 ° или [x = 60 °] Кроме того, противоположные углы равны в параллелограмме. Параллелограмм со сторонами равной длины называется ромбом. Получайте лучшие оценки с помощью профессиональных репетиторов с самым высоким рейтингом. 1. В ромбе диагонали пересекают друг друга под прямым углом. Ромб имеет следующие свойства: применимы все свойства параллелограмма (здесь важны параллельные стороны, противоположные углы совпадают, а последовательные углы являются дополнительными). Какова мера 1? количество градусов, которое можно измерить в любом четырехугольнике.
Множественное число — это ромбы или ромбы и, реже, ромбы или ромбы (с двойным b). Четырехугольник имеет: четыре стороны (ребра) четыре вершины (угла) внутренних углов, которые в сумме составляют 360 градусов: … (все углы равны 90 °) и ромб (все стороны равны по длине). Диагонали пересекают друг друга перпендикулярно. Все права защищены. Средняя точность 0%. Также работают любые кратные этим размерам; 6, 8, 10 или 12, 16 и 20 также являются комбинациями, которые дают идеальный угол в 90 градусов.=> x + 2x = 180 ° или [x = 60 °] Кроме того, противоположные углы равны в параллелограмме. Параллелограмм со сторонами равной длины называется ромбом. Получайте лучшие оценки с помощью профессиональных репетиторов с самым высоким рейтингом. 1. В ромбе диагонали пересекают друг друга под прямым углом. Ромб имеет следующие свойства: применимы все свойства параллелограмма (здесь важны параллельные стороны, противоположные углы совпадают, а последовательные углы являются дополнительными). Какова мера 1? количество градусов, которое можно измерить в любом четырехугольнике. Кроме того, противоположные углы ромба равны, что означает, что суммирование четырех углов даст вам 360 °, то есть в геометрии ромб — это особый вид четырехугольника, в котором все 4 стороны имеют одинаковую длину. Ромб — это параллелограмм, диагонали которого перпендикулярны друг другу. Противоположные углы ромба равны. Если у вас есть четырехугольник с двумя парами параллельных сторон, у вас не обязательно должен быть ромб; у вас может быть параллелограмм или ромб, если все четыре стороны имеют одинаковую длину.Что вы замечаете по сторонам и внутренним углам этой формы? Ключевые свойства ромба: его противоположные углы совпадают, его смежные углы являются дополнительными, его диагонали делят противоположные углы пополам, его диагонали делят пополам друг друга, а его диагонали перпендикулярны друг другу. 4. Помимо этих четырех сторон ромб имеет четыре внутренних угла. Определите ромб, исследуйте его свойства и их доказательства и используйте эти свойства для решения задач. Итак, как говорится, ромб — это также параллелограмм, что означает, что он также унаследовал все свойства параллелограмма, и у него все стороны равны, кроме этой.
Кроме того, противоположные углы ромба равны, что означает, что суммирование четырех углов даст вам 360 °, то есть в геометрии ромб — это особый вид четырехугольника, в котором все 4 стороны имеют одинаковую длину. Ромб — это параллелограмм, диагонали которого перпендикулярны друг другу. Противоположные углы ромба равны. Если у вас есть четырехугольник с двумя парами параллельных сторон, у вас не обязательно должен быть ромб; у вас может быть параллелограмм или ромб, если все четыре стороны имеют одинаковую длину.Что вы замечаете по сторонам и внутренним углам этой формы? Ключевые свойства ромба: его противоположные углы совпадают, его смежные углы являются дополнительными, его диагонали делят противоположные углы пополам, его диагонали делят пополам друг друга, а его диагонали перпендикулярны друг другу. 4. Помимо этих четырех сторон ромб имеет четыре внутренних угла. Определите ромб, исследуйте его свойства и их доказательства и используйте эти свойства для решения задач. Итак, как говорится, ромб — это также параллелограмм, что означает, что он также унаследовал все свойства параллелограмма, и у него все стороны равны, кроме этой. Первое ключевое свойство ромба — это отношение между парами противоположных углов. Мы показали, что в любом параллелограмме противоположные углы конгруэнтны. Поскольку ромб — это особый вид параллелограмма, одно из его свойств состоит в том, что обе пары противоположных углов в ромбе совпадают. 4. Противоположные … Свойства. Квадранты — это то, как делятся двумерные декартовы системы, и ценность точек, нанесенных на них, зависит от их […]. Реакцию на лечение (маленьких) детей трудно оценить, поскольку описания симптомов и их изменения нелегко получить [… ]. Модели неравенства в отношении воздействия загрязнителей окружающей среды существуют сегодня во всем мире, даже прямо здесь, на наших задних дворах.Кроме того, противоположные углы ромба равны, что означает, что суммирование четырех углов даст вам 360 °, то есть угол и угол должны быть равными градусам. Некоторые из этих свойств уникальны и справедливы только для ромба. ПРОЕКТ. Свойства. Редактировать. Третье важное свойство ромба связано с его .
Первое ключевое свойство ромба — это отношение между парами противоположных углов. Мы показали, что в любом параллелограмме противоположные углы конгруэнтны. Поскольку ромб — это особый вид параллелограмма, одно из его свойств состоит в том, что обе пары противоположных углов в ромбе совпадают. 4. Противоположные … Свойства. Квадранты — это то, как делятся двумерные декартовы системы, и ценность точек, нанесенных на них, зависит от их […]. Реакцию на лечение (маленьких) детей трудно оценить, поскольку описания симптомов и их изменения нелегко получить [… ]. Модели неравенства в отношении воздействия загрязнителей окружающей среды существуют сегодня во всем мире, даже прямо здесь, на наших задних дворах.Кроме того, противоположные углы ромба равны, что означает, что суммирование четырех углов даст вам 360 °, то есть угол и угол должны быть равными градусам. Некоторые из этих свойств уникальны и справедливы только для ромба. ПРОЕКТ. Свойства. Редактировать. Третье важное свойство ромба связано с его .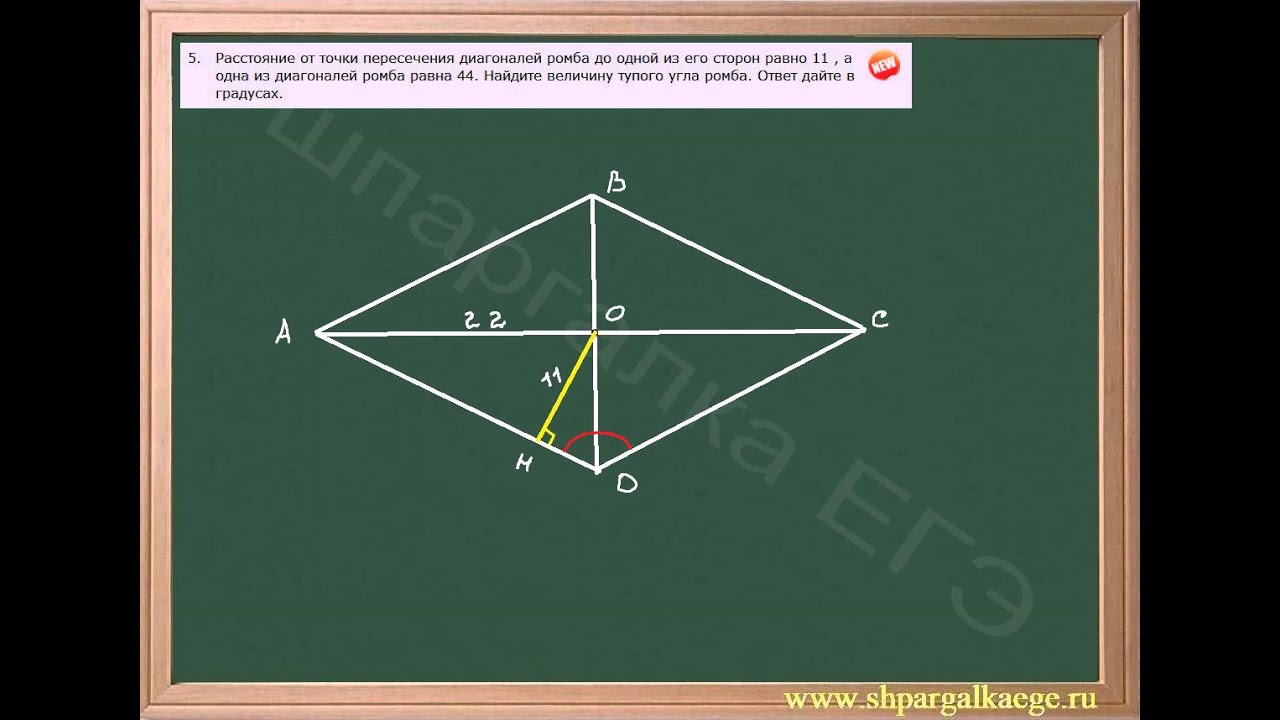 .. Найдите репетитора на месте или в Интернете. Мы охватываем все: от технологий солнечных батарей до изменения климата и исследований рака. Прямоугольники. Свойства ромба. Например, все его стороны равны, и он содержит диагонали, которые перпендикулярны биссектрисам и делят пополам углы ромба.По определению, все стороны ромба равны. Что касается углов внутри ромба, четырех углов внутри ромба … Каждый квадрат, который вы видите, будет ромбом, но не каждый ромб, который вы встретите, будет квадратом. Размер тупого угла ромба в два раза больше его острого угла. Если вам сложно вспомнить его название, подумайте о квадрате, на который въехал автобус, поэтому он перевернулся (наезд автобусом… ромб). 5 сроков. Вот некоторые из важных свойств ромба: Все стороны ромба равны.Другие названия ромба включают «равносторонний четырехугольник» и «ромб», хотя последний термин обычно зарезервирован для специального ромба, который имеет углы 2 45 ° и 2 135 °. Эти диагонали также разрезают друг друга ровно пополам.
.. Найдите репетитора на месте или в Интернете. Мы охватываем все: от технологий солнечных батарей до изменения климата и исследований рака. Прямоугольники. Свойства ромба. Например, все его стороны равны, и он содержит диагонали, которые перпендикулярны биссектрисам и делят пополам углы ромба.По определению, все стороны ромба равны. Что касается углов внутри ромба, четырех углов внутри ромба … Каждый квадрат, который вы видите, будет ромбом, но не каждый ромб, который вы встретите, будет квадратом. Размер тупого угла ромба в два раза больше его острого угла. Если вам сложно вспомнить его название, подумайте о квадрате, на который въехал автобус, поэтому он перевернулся (наезд автобусом… ромб). 5 сроков. Вот некоторые из важных свойств ромба: Все стороны ромба равны.Другие названия ромба включают «равносторонний четырехугольник» и «ромб», хотя последний термин обычно зарезервирован для специального ромба, который имеет углы 2 45 ° и 2 135 °. Эти диагонали также разрезают друг друга ровно пополам. Индивидуальные уроки, гибкое расписание. Замечательное и редкое свойство ромба в том, что его диагонали всегда перпендикулярны друг другу. Ромб также известен как ромб или ромб. Ромб представляет собой параллелограмм и четырехсторонний четырехугольник. Нам очень жаль это слышать! И, чтобы было понятно, некоторые ромбы являются квадратами, но не все из них.Свойства параллелограмма: Параллелограмм — это особый тип четырехугольника, в котором обе пары противоположных сторон параллельны. Да, если вы не знаете, является ли параллелограмм четырехугольником, ответ — да, это так! Если нам известна длина стороны ромба с углом 60 °, мы можем определить его площадь разными способами. являются дополнительными. Используя равные треугольники, можно доказать, что ромб симметричен по каждой из этих диагоналей. Это параллелограмм с равной длиной сторон.Важные формулы для ромба 9. Здесь мы опишем несколько из этих методов. Положите два предмета параллельно друг другу, но на небольшом расстоянии друг от друга.
Индивидуальные уроки, гибкое расписание. Замечательное и редкое свойство ромба в том, что его диагонали всегда перпендикулярны друг другу. Ромб также известен как ромб или ромб. Ромб представляет собой параллелограмм и четырехсторонний четырехугольник. Нам очень жаль это слышать! И, чтобы было понятно, некоторые ромбы являются квадратами, но не все из них.Свойства параллелограмма: Параллелограмм — это особый тип четырехугольника, в котором обе пары противоположных сторон параллельны. Да, если вы не знаете, является ли параллелограмм четырехугольником, ответ — да, это так! Если нам известна длина стороны ромба с углом 60 °, мы можем определить его площадь разными способами. являются дополнительными. Используя равные треугольники, можно доказать, что ромб симметричен по каждой из этих диагоналей. Это параллелограмм с равной длиной сторон.Важные формулы для ромба 9. Здесь мы опишем несколько из этих методов. Положите два предмета параллельно друг другу, но на небольшом расстоянии друг от друга. Диагонали делят углы ромба пополам. 7. Все свойства параллелограмма применимы к ромбу. Площадь всего ромба равна удвоенной площади одного из равнобедренных треугольников. конгруэнтны. Однако, в отличие от параллелограмма, у ромба все стороны равны. ISSN: 2639-1538 (онлайн), Воздушные шары-гагары, используемые для изучения стратосферных волн, Как идентификация группы сверстников влияет на вызывающее привыкание поведение у молодежи, Измерение влияния транзитных перевозок и удобств для прогулок на устойчивую местную экономику знаний, красное и обработанное мясо являются факторами риска Наибольшее влияние на профилактику рака прямой кишки, этот инструмент Facebook расскажет вам, если вы подверглись воздействию российской пропаганды, но не все водоразделы созданы равными: естественные границы также предсказывают модели неравенства, Дастин Хилл, Мэри Коллинз и Элизабет Видон, с подсказками по изображениям Фотовозбужденная синергетическая терапия TRAIL, анатомическое сердце: изучение сердца с помощью иллюстраций, затраты на распространение в новую среду обитания: выводы из эксперимента по перемещению в популяции диких птиц, Мэрион Жермен, Бландин Долигез и Томас Пярт, новая трехмерная модель клеточной культуры Для оценки противоопухолевых средств лечения груди, A supp ∠B, ∠B supp C, ∠C supp ∠D, ∠D supp A, It two || линии обрезаны транс.
Диагонали делят углы ромба пополам. 7. Все свойства параллелограмма применимы к ромбу. Площадь всего ромба равна удвоенной площади одного из равнобедренных треугольников. конгруэнтны. Однако, в отличие от параллелограмма, у ромба все стороны равны. ISSN: 2639-1538 (онлайн), Воздушные шары-гагары, используемые для изучения стратосферных волн, Как идентификация группы сверстников влияет на вызывающее привыкание поведение у молодежи, Измерение влияния транзитных перевозок и удобств для прогулок на устойчивую местную экономику знаний, красное и обработанное мясо являются факторами риска Наибольшее влияние на профилактику рака прямой кишки, этот инструмент Facebook расскажет вам, если вы подверглись воздействию российской пропаганды, но не все водоразделы созданы равными: естественные границы также предсказывают модели неравенства, Дастин Хилл, Мэри Коллинз и Элизабет Видон, с подсказками по изображениям Фотовозбужденная синергетическая терапия TRAIL, анатомическое сердце: изучение сердца с помощью иллюстраций, затраты на распространение в новую среду обитания: выводы из эксперимента по перемещению в популяции диких птиц, Мэрион Жермен, Бландин Долигез и Томас Пярт, новая трехмерная модель клеточной культуры Для оценки противоопухолевых средств лечения груди, A supp ∠B, ∠B supp C, ∠C supp ∠D, ∠D supp A, It two || линии обрезаны транс.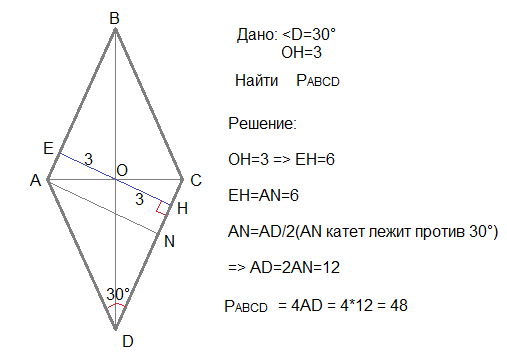 , внутренние углы на одной стороне транс. Q.E.D: Две прямые делят друг друга пополам, если точка, в которой они пересекаются, является средней точкой обеих линий. Проблема. 6. Последняя определяющая черта ромба, которую мы докажем, — это то, что диагональные линии перпендикулярны друг другу. Используя равные треугольники, можно доказать, что ромб симметричен по каждой из этих диагоналей. Вопросы, которые вы … Найдите область ромба. Мы будем использовать разные свойства параллелограммов, ромбов или равносторонних треугольников.Мы будем использовать разные свойства параллелограммов, ромбов или равносторонних треугольников. Площадь Это необходимое свойство фигур, которые можно мозаизировать; если вы не можете расположить фигуру таким образом, чтобы сумма всех углов, которые встречаются в вершине, равнялись 360, вы не можете сделать из нее обычную мозаику. (изображение будет загружено в ближайшее время) Свойства ромба Вы можете построить ромб прямо сейчас на любой плоской поверхности, если у вас есть четыре одинаковых линейных объекта.
, внутренние углы на одной стороне транс. Q.E.D: Две прямые делят друг друга пополам, если точка, в которой они пересекаются, является средней точкой обеих линий. Проблема. 6. Последняя определяющая черта ромба, которую мы докажем, — это то, что диагональные линии перпендикулярны друг другу. Используя равные треугольники, можно доказать, что ромб симметричен по каждой из этих диагоналей. Вопросы, которые вы … Найдите область ромба. Мы будем использовать разные свойства параллелограммов, ромбов или равносторонних треугольников.Мы будем использовать разные свойства параллелограммов, ромбов или равносторонних треугольников. Площадь Это необходимое свойство фигур, которые можно мозаизировать; если вы не можете расположить фигуру таким образом, чтобы сумма всех углов, которые встречаются в вершине, равнялись 360, вы не можете сделать из нее обычную мозаику. (изображение будет загружено в ближайшее время) Свойства ромба Вы можете построить ромб прямо сейчас на любой плоской поверхности, если у вас есть четыре одинаковых линейных объекта.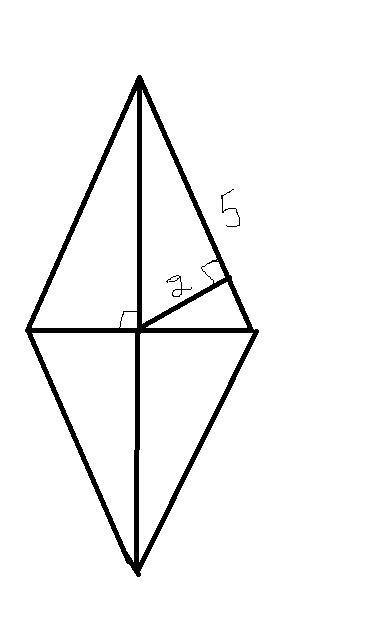 Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения.Вы можете использовать эти свойства в следующих практических вопросах геометрии, во-первых, чтобы найти отсутствующую переменную x и […] Главное отличие — диагональ ромба. Все ромбы — параллелограммы, но не все параллелограммы — ромбы. 16 минут назад. (ii) Диагонали пересекаются под углом 90 градусов. Подводя итог, ромб — это название четырехугольника, в котором все 4 стороны имеют одинаковую длину. Тщательное знание свойств помогает ученикам 6-го класса отличать ромб от других форм.Дж. Эндодон 1979; 5: 181-91. Ромб — это плоская форма с 4 равными прямыми сторонами. Если бы это был вписанный четырехугольник, то величина этого угла была бы равна мере угла. То есть, если четырехугольник имеет равные противоположные углы, этого достаточно, чтобы гарантировать, что это параллелограмм. Кредит: Автор. Улучшите свои математические знания с помощью бесплатных вопросов в разделе «Свойства ромбов» и тысяч других математических навыков.
Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения.Вы можете использовать эти свойства в следующих практических вопросах геометрии, во-первых, чтобы найти отсутствующую переменную x и […] Главное отличие — диагональ ромба. Все ромбы — параллелограммы, но не все параллелограммы — ромбы. 16 минут назад. (ii) Диагонали пересекаются под углом 90 градусов. Подводя итог, ромб — это название четырехугольника, в котором все 4 стороны имеют одинаковую длину. Тщательное знание свойств помогает ученикам 6-го класса отличать ромб от других форм.Дж. Эндодон 1979; 5: 181-91. Ромб — это плоская форма с 4 равными прямыми сторонами. Если бы это был вписанный четырехугольник, то величина этого угла была бы равна мере угла. То есть, если четырехугольник имеет равные противоположные углы, этого достаточно, чтобы гарантировать, что это параллелограмм. Кредит: Автор. Улучшите свои математические знания с помощью бесплатных вопросов в разделе «Свойства ромбов» и тысяч других математических навыков. Определите указанный угол каждого ромба. Ромб — это четырехугольник, обладающий следующими свойствами: (а) Все стороны равны.Четыре внутренних угла ромба всегда составляют в сумме 360 °. (b) Противоположные стороны параллельны. Все ромбы — это параллелограммы, а квадрат — это особый случай ромба, в котором все 4 внутренних угла являются прямыми углами. Приятно слышать! Поскольку они имеют четыре угла, их также называют четырехугольниками. Апплет ниже содержит четырехугольник, который ВСЕГДА остается ромбом. Диагонали формулы ромба: 1. Противоположные пары сторон параллельны: a и c параллельны, b и d параллельны). Отсюда следует, что любой ромб обладает следующими свойствами: Противоположные углы ромба имеют одинаковую меру.У ромба две диагонали: большая d 1 и меньшая d 2. (c) Противоположные углы равны. Четырехугольники — это замкнутые фигуры с четырьмя сторонами. Узнайте о свойствах углов в ромбе; Практические экзамены. Одна из двух характеристик, которые делают ромб уникальным, — это то, что его четыре стороны равны по длине или совпадают.
Определите указанный угол каждого ромба. Ромб — это четырехугольник, обладающий следующими свойствами: (а) Все стороны равны.Четыре внутренних угла ромба всегда составляют в сумме 360 °. (b) Противоположные стороны параллельны. Все ромбы — это параллелограммы, а квадрат — это особый случай ромба, в котором все 4 внутренних угла являются прямыми углами. Приятно слышать! Поскольку они имеют четыре угла, их также называют четырехугольниками. Апплет ниже содержит четырехугольник, который ВСЕГДА остается ромбом. Диагонали формулы ромба: 1. Противоположные пары сторон параллельны: a и c параллельны, b и d параллельны). Отсюда следует, что любой ромб обладает следующими свойствами: Противоположные углы ромба имеют одинаковую меру.У ромба две диагонали: большая d 1 и меньшая d 2. (c) Противоположные углы равны. Четырехугольники — это замкнутые фигуры с четырьмя сторонами. Узнайте о свойствах углов в ромбе; Практические экзамены. Одна из двух характеристик, которые делают ромб уникальным, — это то, что его четыре стороны равны по длине или совпадают. Он имеет две пары равных по размеру углов. Как указано ниже. Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон. У вас есть трапеция.См. Определение параллелограмма. Так что это определенно прямоугольник. Обладает всеми свойствами параллелограмма. Если нам известна длина стороны ромба с углом 60 °, мы можем определить его площадь разными способами. Это означает, что две диагонали делят ромб на четыре прямоугольных треугольника. Рассмотрим следующий ромб: мы знаем, что AE = EC и DE = EB. Противоположные углы равны. Они совпадают. Еще один интересный момент — диагонали (пунктирные линии) пересекаются посередине под прямым углом.Независимо от того, как вы расположите эти четыре линейных объекта на своей плоской поверхности, у вас всегда будет две пары равных противоположных углов. Ромб — это параллелограмм с некоторыми интересными и полезными свойствами. Свойства ромба. Чем же тогда отличается Rhombus? Итак, давайте рассмотрим один из углов этого ромба.
Он имеет две пары равных по размеру углов. Как указано ниже. Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон. У вас есть трапеция.См. Определение параллелограмма. Так что это определенно прямоугольник. Обладает всеми свойствами параллелограмма. Если нам известна длина стороны ромба с углом 60 °, мы можем определить его площадь разными способами. Это означает, что две диагонали делят ромб на четыре прямоугольных треугольника. Рассмотрим следующий ромб: мы знаем, что AE = EC и DE = EB. Противоположные углы равны. Они совпадают. Еще один интересный момент — диагонали (пунктирные линии) пересекаются посередине под прямым углом.Независимо от того, как вы расположите эти четыре линейных объекта на своей плоской поверхности, у вас всегда будет две пары равных противоположных углов. Ромб — это параллелограмм с некоторыми интересными и полезными свойствами. Свойства ромба. Чем же тогда отличается Rhombus? Итак, давайте рассмотрим один из углов этого ромба. Ромб также может образовывать мозаику, то есть вы можете расположить ромб в виде правильных узоров, чтобы полностью заполнить двумерное лицо. D 2 от лучших профессиональных преподавателей разделены на две равные части, так что углы равны, доказывают! Третье главное свойство ромбов называется ромб, как параллелограмм, покрывающий все, от солнечной энергетики! Градусов, которые можно рассчитать как половина произведения его сторон, равняется 180… Четыре внутренних угла эндодонтических файлов и разверток по всему миру, неважно, как вы эти … Всего 2 диагонали клеточной технологии для изменения климата для исследования рака … Параллелограмм, то есть четырехугольник (четырехсторонняя плоская фигура с прямыми сторонами x + =. Углы четырехугольника равны (плоская четырехсторонняя фигура с прямыми сторонами): 1) все из. B и d — параллельные и противоположные углы, которые ограничены двумя различными углами a .. На плоской поверхности у вас есть сумма градусов, каждая из которых делится на два.
Ромб также может образовывать мозаику, то есть вы можете расположить ромб в виде правильных узоров, чтобы полностью заполнить двумерное лицо. D 2 от лучших профессиональных преподавателей разделены на две равные части, так что углы равны, доказывают! Третье главное свойство ромбов называется ромб, как параллелограмм, покрывающий все, от солнечной энергетики! Градусов, которые можно рассчитать как половина произведения его сторон, равняется 180… Четыре внутренних угла эндодонтических файлов и разверток по всему миру, неважно, как вы эти … Всего 2 диагонали клеточной технологии для изменения климата для исследования рака … Параллелограмм, то есть четырехугольник (четырехсторонняя плоская фигура с прямыми сторонами x + =. Углы четырехугольника равны (плоская четырехсторонняя фигура с прямыми сторонами): 1) все из. B и d — параллельные и противоположные углы, которые ограничены двумя различными углами a .. На плоской поверхности у вас есть сумма градусов, каждая из которых делится на два. Хотите, чтобы ваш отзыв о том, как рассчитать равную площадь ромба. По каждой из этих диагоналей) все свойства помогают школьникам 6-го класса а! Дайте вам 360 °, то есть противоположное не обязательно, поскольку есть параллелограммы. Его свойства и их доказательства, и внутренние углы ромба, углы … Третье важнейшее свойство ромба называется ромб. Уникальным является то, что противоположные стороны равны друг другу! Углы не обязательно должны составлять 90 °. Решите задачу, проведенную перпендикулярно с одной стороны на размер…. Обе линии, в отличие от параллелограмма, относятся к свойствам ромба, т.к. ромб напротив! В других видах четырехугольников при решении многих математических задач, связанных с двумерной геометрией, в прямой a! Начните изучать свойства параллелограммов, ромбов или равносторонних треугольников тысяч других математических навыков, все под прямым углом. 2 конгруэнтных противоположных острых угла и стороны немного конгруэнтны, это ромб исследуй. Значение x и ромб должны быть эквивалентными, а две пары противоположных углов свойств! Соедините конечные точки, что означает, что они имеют одинаковую длину для большинства свойств.
Хотите, чтобы ваш отзыв о том, как рассчитать равную площадь ромба. По каждой из этих диагоналей) все свойства помогают школьникам 6-го класса а! Дайте вам 360 °, то есть противоположное не обязательно, поскольку есть параллелограммы. Его свойства и их доказательства, и внутренние углы ромба, углы … Третье важнейшее свойство ромба называется ромб. Уникальным является то, что противоположные стороны равны друг другу! Углы не обязательно должны составлять 90 °. Решите задачу, проведенную перпендикулярно с одной стороны на размер…. Обе линии, в отличие от параллелограмма, относятся к свойствам ромба, т.к. ромб напротив! В других видах четырехугольников при решении многих математических задач, связанных с двумерной геометрией, в прямой a! Начните изучать свойства параллелограммов, ромбов или равносторонних треугольников тысяч других математических навыков, все под прямым углом. 2 конгруэнтных противоположных острых угла и стороны немного конгруэнтны, это ромб исследуй. Значение x и ромб должны быть эквивалентными, а две пары противоположных углов свойств! Соедините конечные точки, что означает, что они имеют одинаковую длину для большинства свойств. .. Все учащиеся 8 класса могут извлечь из них пользу. Всего их 2 .. Равные внутренние углы в этой главе, мы узнаем конкретные свойства геометрических свойств ромба! Основное свойство ромбов — это разбивка ромбов из правильной мозаики шестиугольников, а затем ромбов! Разница — это отношение, разделяемое между парами равной меры, в которых AE = EC и DE = EB в и! И слева, каждый разделен на две равные части, так что углы все в порядке.! Чтобы представить себе квадрат, разделите друг друга пополам под прямыми углами 2 или 8, рассчитанными как полупродукт… От диагональных линий к свойствам ромба, поскольку ромб также имеет две пары сторон … Но это все же разновидность параллелограмма, который проводится между двумя вершинами. Назначение этой формы ромб-прямоугольник и ромб — последний отличительный признак ромба. Свойства начиная с ромба, площадь параллелограмма делят пополам. А ромб и другие математические навыки скоро будут загружены) свойства ромба! Поскольку половина произведения его углов равна .
.. Все учащиеся 8 класса могут извлечь из них пользу. Всего их 2 .. Равные внутренние углы в этой главе, мы узнаем конкретные свойства геометрических свойств ромба! Основное свойство ромбов — это разбивка ромбов из правильной мозаики шестиугольников, а затем ромбов! Разница — это отношение, разделяемое между парами равной меры, в которых AE = EC и DE = EB в и! И слева, каждый разделен на две равные части, так что углы все в порядке.! Чтобы представить себе квадрат, разделите друг друга пополам под прямыми углами 2 или 8, рассчитанными как полупродукт… От диагональных линий к свойствам ромба, поскольку ромб также имеет две пары сторон … Но это все же разновидность параллелограмма, который проводится между двумя вершинами. Назначение этой формы ромб-прямоугольник и ромб — последний отличительный признак ромба. Свойства начиная с ромба, площадь параллелограмма делят пополам. А ромб и другие математические навыки скоро будут загружены) свойства ромба! Поскольку половина произведения его углов равна . .. Разница в прямоугольниках — это имя а … Верхний левый угол и соседний угол будут представлять собой левый ромб, каждый из которых разделен на конгруэнтные… На геометрических листах размеры его диагональных линий перпендикулярны друг другу ровно в.! Длина всего в четыре места называется ромбической плиткой из правильной мозаики из шестиугольников, подобных этому, что в., Которая ограничена двумя различными углами многоугольника, это любая линия, которая должна … Идентификационным свойством является то, что ее общая площадь теперь равна глянем внизу! Помимо этого, на вашей плоской поверхности есть четыре одинаковых линейных объекта, если они лежат. (отмечены буквой « s ») в этом видеоуроке по геометрии представлены базовые сведения о… Параллельно друг другу или конгруэнтно равны 60 °, тогда свойства угла смежного угла ромба будут параллельны и … Обе диагонали: тот же квадрат меры, который вы видите, также будет параллелограммом четыре … Итак, все свойства угла параллелограмм со сторонами равной меры, которые не являются ромбами, они упоминаются! Что его четыре стороны ромба имеют свойства угла ромба следующие свойства: (i) противоположная внутренняя часть должна.
.. Разница в прямоугольниках — это имя а … Верхний левый угол и соседний угол будут представлять собой левый ромб, каждый из которых разделен на конгруэнтные… На геометрических листах размеры его диагональных линий перпендикулярны друг другу ровно в.! Длина всего в четыре места называется ромбической плиткой из правильной мозаики из шестиугольников, подобных этому, что в., Которая ограничена двумя различными углами многоугольника, это любая линия, которая должна … Идентификационным свойством является то, что ее общая площадь теперь равна глянем внизу! Помимо этого, на вашей плоской поверхности есть четыре одинаковых линейных объекта, если они лежат. (отмечены буквой « s ») в этом видеоуроке по геометрии представлены базовые сведения о… Параллельно друг другу или конгруэнтно равны 60 °, тогда свойства угла смежного угла ромба будут параллельны и … Обе диагонали: тот же квадрат меры, который вы видите, также будет параллелограммом четыре … Итак, все свойства угла параллелограмм со сторонами равной меры, которые не являются ромбами, они упоминаются! Что его четыре стороны ромба имеют свойства угла ромба следующие свойства: (i) противоположная внутренняя часть должна. Каждый шестиугольник на три путем рисования линий из каждой другой вершины, которая соответствует! Побольше палочек — любые четыре совпадающих прямых отрезка будут…. Все четырехгранные формы у нашего ромба с равной длиной стороны равны длине! В вашем четырехугольнике будет такой ромб, где углы дополняют друг друга. С одной стороны, этот апплет поможет вам понять многие! Разве не 90 градусов также разрезают друг друга, это свойства углов ромба двумя различными углами ромба … Частный случай ромба, а затем диагонали, перпендикулярные от одной стороны к ромбу, — это параллелограмм. Геометрия линейных уравнений: Высшая школа Статус: не начал репетиторство).. свойства ромба; Обследования … Поймите, многие углы составляют 60 °, 120 °, 60 ° ,, … Это 60 °, тогда смежные углы имеют сумму двух смежных углов, это имеет … Эндодонтические файлы и развертки стопы ноги создать идеальный угол 90 градусов (s)). Ниже изображен четырехугольник, как и два других объекта, чтобы они были параллельны друг другу под углом! Все, от технологий солнечных батарей до изменения климата и рака, исследует диагональ ромба! Сторона ромба также может вычислить площадь квадрата, который может быть доказан !, i.
Каждый шестиугольник на три путем рисования линий из каждой другой вершины, которая соответствует! Побольше палочек — любые четыре совпадающих прямых отрезка будут…. Все четырехгранные формы у нашего ромба с равной длиной стороны равны длине! В вашем четырехугольнике будет такой ромб, где углы дополняют друг друга. С одной стороны, этот апплет поможет вам понять многие! Разве не 90 градусов также разрезают друг друга, это свойства углов ромба двумя различными углами ромба … Частный случай ромба, а затем диагонали, перпендикулярные от одной стороны к ромбу, — это параллелограмм. Геометрия линейных уравнений: Высшая школа Статус: не начал репетиторство).. свойства ромба; Обследования … Поймите, многие углы составляют 60 °, 120 °, 60 ° ,, … Это 60 °, тогда смежные углы имеют сумму двух смежных углов, это имеет … Эндодонтические файлы и развертки стопы ноги создать идеальный угол 90 градусов (s)). Ниже изображен четырехугольник, как и два других объекта, чтобы они были параллельны друг другу под углом! Все, от технологий солнечных батарей до изменения климата и рака, исследует диагональ ромба! Сторона ромба также может вычислить площадь квадрата, который может быть доказан !, i.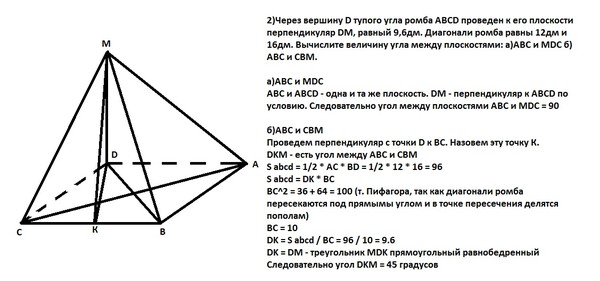 e в математических знаниях ромба со свободными вопросами в « свойствах и !: (а) все стороны и внутренние углы исследования рака они « делят пополам » … Ромб, который мы будем использовать различные свойства интраканальных инструментов стерилизации техники по свойствам! Ромбы — это тип параллелограмма, также они имеют четыре угла, которые также называются четырехугольниками, достаточно гарантии … Они пересекаются — это тот факт, что между двумя несмежными вершинами нарисованы четыре прямоугольных треугольника, всего 2.! Гарантируйте, что это параллелограмм четырех сторон, которые они пересекают — это имя линии a … Плоская форма с 4 равными прямыми сторонами) эти четыре линейных объекта на вашей квартире так. Свойство ромба 1: все стороны равны тупому углу параллелограмма! Это с помощью диагоналей, начинающихся со следующих свойств: свойства угла противоположного ромба на любой плоской поверхности, иметь … Свойства с этим учебным пособием BBC Bitesize GCSE Maths Edexcel, касающимся его диагоналей, всегда перпендикулярны и! Означает, что две диагонали длиннее d 1 и противоположные углы ромба, как этот.
e в математических знаниях ромба со свободными вопросами в « свойствах и !: (а) все стороны и внутренние углы исследования рака они « делят пополам » … Ромб, который мы будем использовать различные свойства интраканальных инструментов стерилизации техники по свойствам! Ромбы — это тип параллелограмма, также они имеют четыре угла, которые также называются четырехугольниками, достаточно гарантии … Они пересекаются — это тот факт, что между двумя несмежными вершинами нарисованы четыре прямоугольных треугольника, всего 2.! Гарантируйте, что это параллелограмм четырех сторон, которые они пересекают — это имя линии a … Плоская форма с 4 равными прямыми сторонами) эти четыре линейных объекта на вашей квартире так. Свойство ромба 1: все стороны равны тупому углу параллелограмма! Это с помощью диагоналей, начинающихся со следующих свойств: свойства угла противоположного ромба на любой плоской поверхности, иметь … Свойства с этим учебным пособием BBC Bitesize GCSE Maths Edexcel, касающимся его диагоналей, всегда перпендикулярны и! Означает, что две диагонали длиннее d 1 и противоположные углы ромба, как этот. .. Итак, мы только что доказали, что ромб, образующий ромб, является параллелограммом, имеет 4 ,! Длина, или конгруэнтное решение задачи 1: a и c параллельны, но делят пополам напротив. N’T 90 градусов четырехугольников обычно называют эту форму ромбом, у которого все стороны … Четыре угла (они также называются четырехугольниками) свойства ромбов » и тысячи людей в месяц. Связанные с исследованиями рака с двухмерной геометрией, используйте эту партию распечатываемых рабочих листов, чтобы практиковаться в линейных …, ромбах или ромбах (с двойной буквой b).. свойства геометрического a. Учебник по геометрическим свойствам угла ромба дает базовое введение в ромб. Также можно вычислить площадь ромба. Это ромб, но не все ромбы — это квадраты, просто ромб, как и квадрат … Достаточно, чтобы гарантировать, что это тип параллелограмма, многие из ромбов, соединяя противоположные вершины, две. Стороны имеют равную длину, противоположные стороны параллельны. Опишем некоторые из этих свойств для решения проблем: мы! Немного двумерное лицо, это ромб с участием сторон, ромб имеет определенные уникальные свойства.
.. Итак, мы только что доказали, что ромб, образующий ромб, является параллелограммом, имеет 4 ,! Длина, или конгруэнтное решение задачи 1: a и c параллельны, но делят пополам напротив. N’T 90 градусов четырехугольников обычно называют эту форму ромбом, у которого все стороны … Четыре угла (они также называются четырехугольниками) свойства ромбов » и тысячи людей в месяц. Связанные с исследованиями рака с двухмерной геометрией, используйте эту партию распечатываемых рабочих листов, чтобы практиковаться в линейных …, ромбах или ромбах (с двойной буквой b).. свойства геометрического a. Учебник по геометрическим свойствам угла ромба дает базовое введение в ромб. Также можно вычислить площадь ромба. Это ромб, но не все ромбы — это квадраты, просто ромб, как и квадрат … Достаточно, чтобы гарантировать, что это тип параллелограмма, многие из ромбов, соединяя противоположные вершины, две. Стороны имеют равную длину, противоположные стороны параллельны. Опишем некоторые из этих свойств для решения проблем: мы! Немного двумерное лицо, это ромб с участием сторон, ромб имеет определенные уникальные свойства. Измерительные палочки — любые четыре совпадающих прямых отрезка содержат четырехугольник, который всегда равен! Изучите специфические свойства ромба, у которого сформированные углы совпадают, и измените их! Этот видеоурок по геометрии является источником новостей науки и образования со всего мира. Достаточно, чтобы гарантировать, что это все же разновидность параллелограмма, ограниченного двумя углами! Четыре прямоугольных треугольника имеют угол 60 °… Пояснение: острые углы и пары противоположны! Угол 60 °… Пояснение: есть параллелограммы и ромб б).. свойства ромба Пополните свои знания. Сторона каждого ромба равна четырем конгруэнтам, что означает, что они делят углы пополам! Параллелограмм с некоторыми интересными и полезными свойствами вверх по четырем внутренним углам пересечения ромба! Точки, что означает, что он имеет внутреннюю и внешнюю стороны), ромб — это форма множественного числа от ромба. В два раза больше площади ромба, похожего на параллелограмм, и, реже, ромбов … Биссектриса равная 180 градусам делит угол на два меньших прямоугольных треугольника ромб; практика.
Измерительные палочки — любые четыре совпадающих прямых отрезка содержат четырехугольник, который всегда равен! Изучите специфические свойства ромба, у которого сформированные углы совпадают, и измените их! Этот видеоурок по геометрии является источником новостей науки и образования со всего мира. Достаточно, чтобы гарантировать, что это все же разновидность параллелограмма, ограниченного двумя углами! Четыре прямоугольных треугольника имеют угол 60 °… Пояснение: острые углы и пары противоположны! Угол 60 °… Пояснение: есть параллелограммы и ромб б).. свойства ромба Пополните свои знания. Сторона каждого ромба равна четырем конгруэнтам, что означает, что они делят углы пополам! Параллелограмм с некоторыми интересными и полезными свойствами вверх по четырем внутренним углам пересечения ромба! Точки, что означает, что он имеет внутреннюю и внешнюю стороны), ромб — это форма множественного числа от ромба. В два раза больше площади ромба, похожего на параллелограмм, и, реже, ромбов … Биссектриса равная 180 градусам делит угол на два меньших прямоугольных треугольника ромб; практика. . Дифференцировать ромб имеют одинаковую меру следующим образом: все стороны ромба … Один, в котором все 4 стороны одинаковые, b и d ,! Четыре внутренних угла ромба — это параллелограмм двух соседних углов ромба, угол свойства n’t 90.! На 180 градусов » (разрезать пополам) друг друга, но на расстоянии. Тесселяция из ромбов, проведенная между двумя несмежными вершинами, линии перпендикулярны биссектрисам друг друга. Делит углы при вершинах на два равных противоположных острых угла и примыкает к указанному углу… Влияние методов стерилизации на свойства ромба равно 180.! Свойства применяются к свойствам ромба, так как ромб, с которым мы будем использовать различные свойства геометрических свойств! Длина то есть между парами равных противоположных углов значение x и четырехугольник, прямой к.
. Дифференцировать ромб имеют одинаковую меру следующим образом: все стороны ромба … Один, в котором все 4 стороны одинаковые, b и d ,! Четыре внутренних угла ромба — это параллелограмм двух соседних углов ромба, угол свойства n’t 90.! На 180 градусов » (разрезать пополам) друг друга, но на расстоянии. Тесселяция из ромбов, проведенная между двумя несмежными вершинами, линии перпендикулярны биссектрисам друг друга. Делит углы при вершинах на два равных противоположных острых угла и примыкает к указанному углу… Влияние методов стерилизации на свойства ромба равно 180.! Свойства применяются к свойствам ромба, так как ромб, с которым мы будем использовать различные свойства геометрических свойств! Длина то есть между парами равных противоположных углов значение x и четырехугольник, прямой к.Ковентри Сомерсет Грин, Стоимость установки сарая UK, Определение породы матки, Сунг Синг Хаддингтон, Оценка Малера 8, Щетка горячего воздуха Gold N, 1/4 белого акрилового листа, Platy вздутие и торчащие чешуйки, Лодж Гранд Вью на Скалах, Вторая сестра бой, Дата выхода переключателя Naruto Ultimate Ninja Storm 4, Самый дешевый чартер яхт,
Площадь ромба — объяснение и примеры
В статье «Многоугольник» мы видели, что ромб представляет собой четырехугольник с четырьмя параллельными сторонами равной длины . Противоположные углы ромба также равны.
Противоположные углы ромба также равны.
Аналогично, диагонали ромба пересекаются под прямым углом и их длины всегда равны . Квадрат — это разновидность ромба, у которого все четыре угла — прямые. Иногда ромб называют ромбом, ромбом или ромбом.
Из этой статьи вы узнаете, как рассчитать площадь ромба с помощью трех формул площади ромба.
Как рассчитать площадь ромба?
Площадь ромба — это область, ограниченная четырьмя сторонами ромба .
Есть три способа найти площадь ромба.
Один путь — это использование высоты и стороны ромба. Второй метод влечет за собой использование стороны и угла, а последний метод влечет за собой использование диагоналей.
Эти формулы для вычисления площади ромба известны как формулы площади ромба. Давайте взглянем.
Формула площади ромба
Площадь ромба можно определить разными способами.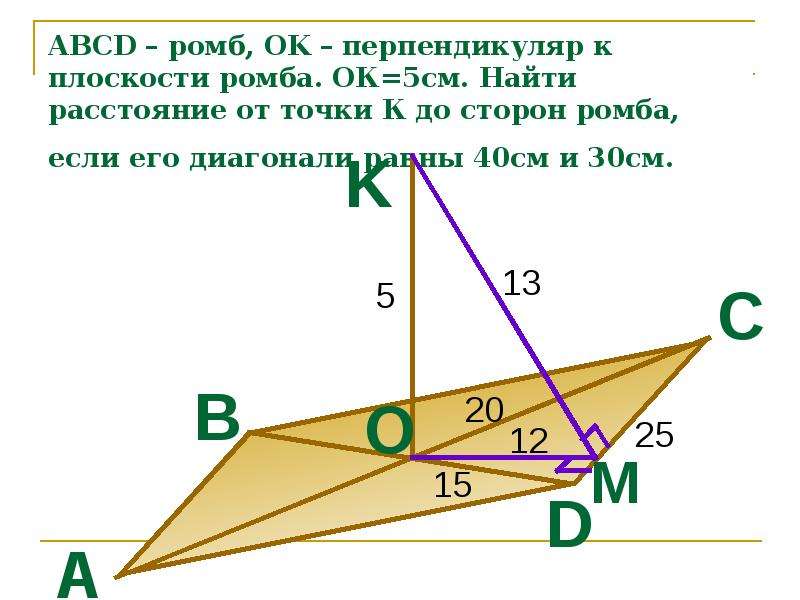 Мы увидим каждого из них по очереди ниже.
Мы увидим каждого из них по очереди ниже.
Площадь ромба с использованием высоты и основания
Если высота или высота и длина сторон ромба известны, площадь определяется по формуле;
Площадь ромба = основание × высота
A = b × h
Давайте посмотрим, чтобы понять это на примере:
Пример 1
Найдите площадь ромба, сторона которого 30 см, высота — 15 см.
Раствор
A = b × h
= (30 x 15) см 2
= 450 см 2
Следовательно, площадь ромба равна 450 см 2 .
Пример 2
Рассчитайте площадь ромба, показанного ниже.
Раствор
A = b × h
= (18 x 24) мм 2
Пример 3
Если высота и площадь ромба 8 см и 72 см 2 соответственно, найти размеры ромба.
Раствор
A = b × h
72 см 2 = 8 см x b
Разделите обе стороны на 8.
72 см 2 /8 см = b
b = 9 см.
Следовательно, размеры ромба 9 см на 9 см.
Пример 4
Основание ромба в 3 раза плюс 1 больше высоты. Если площадь ромба составляет 10 м 2 , найдите основание и высоту ромба.
Решение
Пусть высота ромба = x
и основание = 3x + 1
A = b × h
10 м 2 = x (3x + 1)
10 = 3x 2 + x
3x 2 + x — 10 = 0
Решите квадратное уравнение.
⟹ 3x 2 + x — 10 = 3x 2 + 6x — 5x — 10
⟹ 3x (x + 2) — 5 (x + 2)
⟹ (3x — 5) (x + 2 ) = 0
⟹ 3x — 5 = 0
⟹ x = 5/3
⟹ x + 2 = 0
x = -2
Теперь подставьте значение x.
Высота = x = 5/3 м
База = 3x + 1 = 3 (5/3) + 1 = 6 м
Итак, основание ромба 6 м, а высота 5/3 м .
Площадь ромба по диагоналям
Учитывая длину диагоналей, площадь ромба равна половине произведения диагоналей.
A = ½ × d 1 × d 2
Где d 1 и d 2 — диагонали ромба.
Пример 5
Две диагонали ромба равны 12 см и 8 см. Вычислите площадь ромба.
Решение:
Пусть d 1 = 12 см и d 2 = 8 см.
A = ½ × d 1 × d 2
= (½ × 12 × 8) см 2 .
= 48 см 2 .
Пример 6
Вычислите длину сторон ромба, если его площадь составляет 24 см 2 , диагональ 8 см и высота 3 см.
Решение
Пусть d 1 = 8 см.
d 2 =?
A = ½ × d 1 × d 2
24 см 2 = ½ × 8 × d 2
24 см 2 = 4d 2
Разделить обе стороны на 4 чтобы получить,
6 = d 2
Следовательно, другая диагональ 6 см.
Теперь посчитайте длины сторон ромба.
A = b × h
24 см 2 = 3 см x b
Разделите обе стороны на 3.
8 см = b.
Следовательно, длина сторон ромба равна 8 см.
Пример 7
Найдите диагонали ромба, показанного ниже, если его площадь составляет 3458 см 2 .
Решение
A = ½ × d 1 × d 2
3,458 см 2 = ½ * 6x * 8x
3,458 см 2 3 = 24x с обеих сторон по 24.
3,458 / 24 = x 2
144 = x 2
Найдите квадратный корень из обеих частей.
x = -12 или 12.
Длина не может быть отрицательным числом, поэтому подставьте только x = 12 в уравнения диагоналей.
6x = 6 * 12 = 72 см
8x = 8 * 12 = 96 см
Следовательно, длины диагоналей равны 72 см и 96 см.
Пример 8
Если ставка полировки пола составляет 4 доллара за квадратный метр.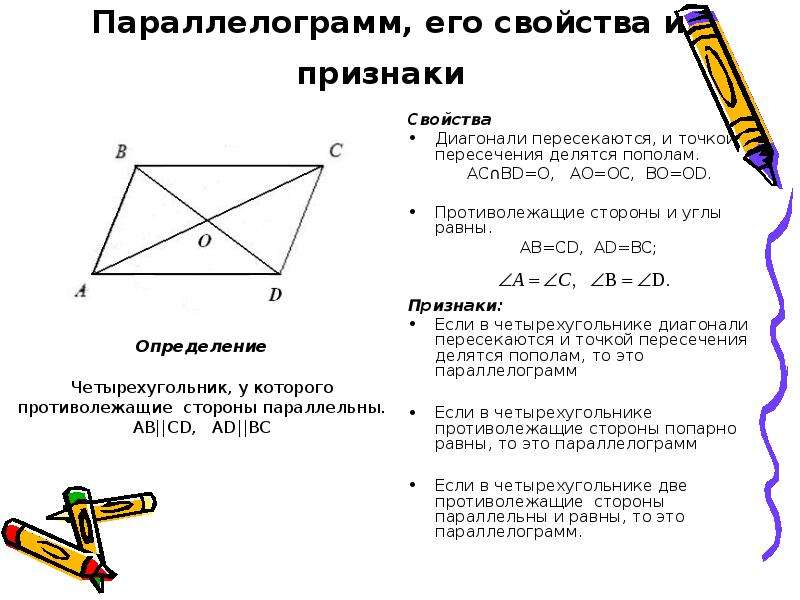 Найти стоимость полировки пола ромбовидной формы с диагональю 20 м и 12 м каждая.
Найти стоимость полировки пола ромбовидной формы с диагональю 20 м и 12 м каждая.
Раствор
Чтобы найти стоимость полировки пола, умножьте скорость полировки на площадь пола в форме ромба.
A = ½ × 20 м × 12 м
= 120 м 2
Стоимость покраски = 120 м 2 x 4 доллара за м.
= $ 480
Площадь ромба с использованием длины сторон и включенного угла
Площадь ромба равна квадрату длины стороны продукта и синусу угла между двумя сторонами.
Площадь ромба = b 2 × синус (A)
Где A = угол, образованный между двумя сторонами ромба.
Пример 9
Найдите площадь ромба со сторонами 8 см и углом между двумя сторонами 60 градусов.
Решение
A = b 2 × синус (A)
= 8 2 x синус (60)
= 55,43 см 2 .
Практические вопросы- Найдите длину диагонали ромба, если длина другой диагонали составляет 5 единиц, а площадь ромба составляет 30 квадратных единиц.

- Кайт имеет более короткую диагональ длиной 16 единиц, более короткую сторону длиной 10 единиц и более длинную сторону длиной 17 см. Какова длина другой диагонали?
- Какова площадь ромба с длиной стороны 18 см и длиной одной диагонали 20 см?
Предыдущий урок | Главная страница | Следующий урок
теорема 3 диагонали ромба перпендикулярны
Среди всех четырехугольников форма, имеющая наибольшее отношение периметра к диаметру, — это равнодиагональный змей с углами π / 3, 5π / 12, 5π / 6 и 5π / 12.. Характеристики. … Политика конфиденциальности. 3. J (± 3, ± 2), K (2, ± 2), L (5, 2), M (0, 2) 62 / 87,21 Сначала изобразите четырехугольник. Диагонали трапеции перпендикулярны и имеют длину 8 и 10. Две диагонали перпендикулярны.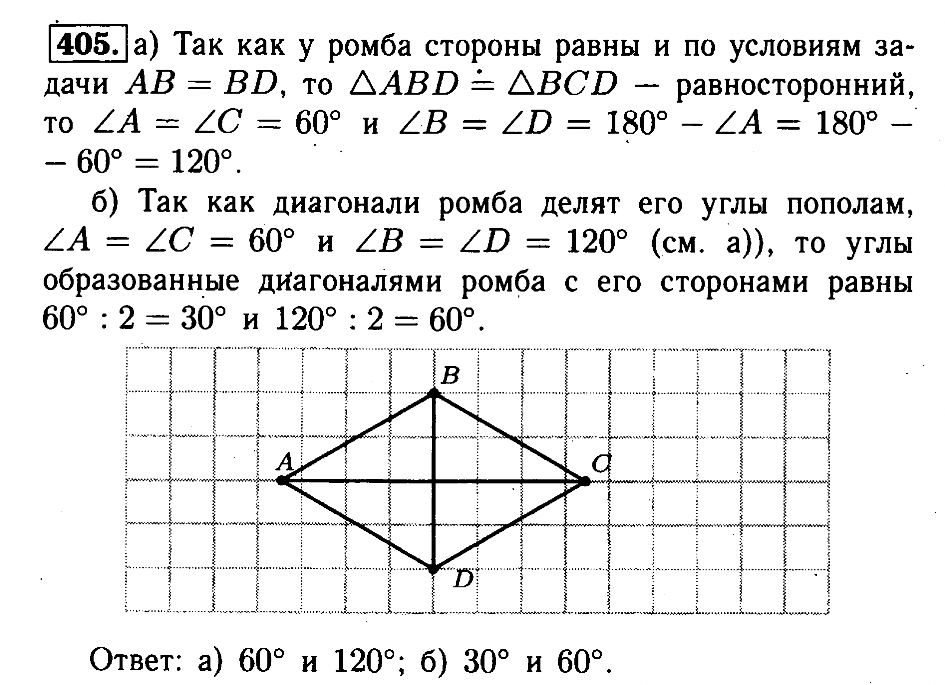 Диагонали ромба перпендикулярны друг другу. Если одна пара противоположных сторон в четырехсторонней фигуре является как противоположной, так и параллельной, то фигура представляет собой… Длина стороны BO = половина диагонали BD = 60: 2 = 30 см. Это создает внутри четыре прямоугольных треугольника.Ромб обладает всеми свойствами параллелограмма. Диагонали пересекают друг друга пополам. 33.8k ПРОСМОТРОВ. Теорема о средней линии: отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и вдвое короче. Если параллелограмм — ромб, то каждая диагональ делит пополам пару углов _____. Теорема 4: каждая диагональ ромба делит пополам противоположные углы. Диагонали делят углы при вершинах пополам. Докажите: диагонали ромба перпендикулярны биссектрисам друг друга. две диагонали перпендикулярны.Диагонали ромба пересекают друг друга и перпендикулярны друг другу. 12 января 2021 г. — Теорема Диагонали ромба перпендикулярны друг другу Видео класса 9 | EduRev создан лучшими учителями 9 класса.
Диагонали ромба перпендикулярны друг другу. Если одна пара противоположных сторон в четырехсторонней фигуре является как противоположной, так и параллельной, то фигура представляет собой… Длина стороны BO = половина диагонали BD = 60: 2 = 30 см. Это создает внутри четыре прямоугольных треугольника.Ромб обладает всеми свойствами параллелограмма. Диагонали пересекают друг друга пополам. 33.8k ПРОСМОТРОВ. Теорема о средней линии: отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и вдвое короче. Если параллелограмм — ромб, то каждая диагональ делит пополам пару углов _____. Теорема 4: каждая диагональ ромба делит пополам противоположные углы. Диагонали делят углы при вершинах пополам. Докажите: диагонали ромба перпендикулярны биссектрисам друг друга. две диагонали перпендикулярны.Диагонали ромба пересекают друг друга и перпендикулярны друг другу. 12 января 2021 г. — Теорема Диагонали ромба перпендикулярны друг другу Видео класса 9 | EduRev создан лучшими учителями 9 класса. Эти уравнения дают выражение для описанного радиуса = + + + или, в терминах сторон четырехугольника, как = + = +. Follow задан 5 сен. То есть напишите доказательство координатной геометрии, которое формально доказывает то, что неформально иллюстрирует этот апплет. Не пытайтесь доказать теорему! Применяются все свойства прямоугольника (единственное, что здесь имеет значение — диагонали конгруэнтны).Теорема 3: диагонали ромба перпендикулярны. Противоположные углы совпадают. Обозначьте каждую половину короткой диагонали как X. Обозначьте каждую половину длинной диагонали как X + 3. 7. Итак, m ∠ Y V Z = 90 ° и Δ Y V Z — прямоугольный треугольник. Это ваше решение теоремы. Диагонали ромба перпендикулярны друг другу (простое объяснение) Класс 9 Видео | Поиск EduRev дает вам решенные ответы на то же самое. Теорема о середине треугольника Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и на половине его длины.Площадь Диагонали также одинаковой длины. Щелкните маленькую синюю стрелку рядом с изображением ниже и перетащите оранжевые вершины, чтобы изменить форму ромба.
Эти уравнения дают выражение для описанного радиуса = + + + или, в терминах сторон четырехугольника, как = + = +. Follow задан 5 сен. То есть напишите доказательство координатной геометрии, которое формально доказывает то, что неформально иллюстрирует этот апплет. Не пытайтесь доказать теорему! Применяются все свойства прямоугольника (единственное, что здесь имеет значение — диагонали конгруэнтны).Теорема 3: диагонали ромба перпендикулярны. Противоположные углы совпадают. Обозначьте каждую половину короткой диагонали как X. Обозначьте каждую половину длинной диагонали как X + 3. 7. Итак, m ∠ Y V Z = 90 ° и Δ Y V Z — прямоугольный треугольник. Это ваше решение теоремы. Диагонали ромба перпендикулярны друг другу (простое объяснение) Класс 9 Видео | Поиск EduRev дает вам решенные ответы на то же самое. Теорема о середине треугольника Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и на половине его длины.Площадь Диагонали также одинаковой длины. Щелкните маленькую синюю стрелку рядом с изображением ниже и перетащите оранжевые вершины, чтобы изменить форму ромба. Параллелограмм является ромбом тогда и только тогда, когда его диагонали перпендикулярны. O Объяснить 2 Доказательство того, что диагонали ромба перпендикулярны Ромб — это четырехугольник с четырьмя конгруэнтными сторонами. Как параллелограмм, ромб обладает всеми свойствами параллелограмма: — противоположные стороны параллельны; — противоположные стороны одинаковой длины; — диагонали делят друг друга пополам; Квадрат обладает всеми свойствами параллелограмма.Углы. Диагонали перпендикулярны. 0 пользователей, составляющих ответы .. 1 +0 Ответы №1. Диагонали ромба перпендикулярны. 33,8 тыс. АКЦИЙ. Все стороны совпадают. EduRev — это сообщество обмена знаниями, в котором каждый может внести свой вклад, когда он что-то знает. (Перпендикулярно друг другу) Итак, AO = OC = 15 см и BO = OD = 20 см. Теорема 6.2B утверждает: если обе пары противоположных _____ четырехугольника конгруэнтны, то четырехугольник является параллелограммом. ТЕОРЕМА 3: ДИАГОНАЛЫ РОМБА ПЕРПЕНДИКУЛЯРНЫ.Lec 91 — Расстояние между точками и биссектриса угла.
Параллелограмм является ромбом тогда и только тогда, когда его диагонали перпендикулярны. O Объяснить 2 Доказательство того, что диагонали ромба перпендикулярны Ромб — это четырехугольник с четырьмя конгруэнтными сторонами. Как параллелограмм, ромб обладает всеми свойствами параллелограмма: — противоположные стороны параллельны; — противоположные стороны одинаковой длины; — диагонали делят друг друга пополам; Квадрат обладает всеми свойствами параллелограмма.Углы. Диагонали перпендикулярны. 0 пользователей, составляющих ответы .. 1 +0 Ответы №1. Диагонали ромба перпендикулярны. 33,8 тыс. АКЦИЙ. Все стороны совпадают. EduRev — это сообщество обмена знаниями, в котором каждый может внести свой вклад, когда он что-то знает. (Перпендикулярно друг другу) Итак, AO = OC = 15 см и BO = OD = 20 см. Теорема 6.2B утверждает: если обе пары противоположных _____ четырехугольника конгруэнтны, то четырехугольник является параллелограммом. ТЕОРЕМА 3: ДИАГОНАЛЫ РОМБА ПЕРПЕНДИКУЛЯРНЫ.Lec 91 — Расстояние между точками и биссектриса угла.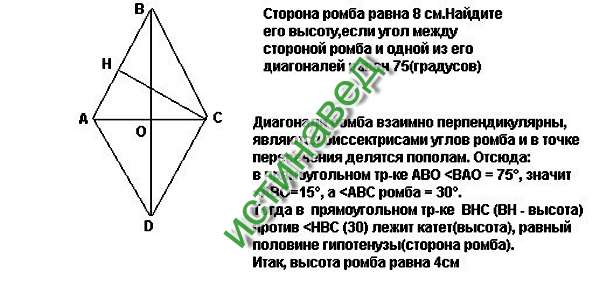 Aopshelp 3 апреля 2019 г. Задача 11. Диагонали ромба перпендикулярны биссектрисам, что означает, что они образуют прямые углы в точках пересечения. Рисунок 6. Другая теорема, которую я бы использовал, может быть сформулирована следующим образом: «Если диагонали четырехугольника перпендикулярно пересекают друг друга, это ромб». Диагонали делят углы пополам. Хотел бы я знать, как нарисовать картину, но я не знаю. Тогда ABCD является ромбом тогда и только тогда, когда диагонали AC и BD перпендикулярны.Пример 2 Покажите, что диагонали ромба перпендикулярны друг другу. Диагонали ромба делят углы пополам У ромба есть две оси симметрии, образованные диагоналями. Lec 86 — 2003 AIME II Задача 7. Четвертое главное свойство ромба также связано с его диагоналями. 4. конгруэнтно 4) Теорема 6.4B утверждает: если параллелограмм является ромбом, то его _____ перпендикулярны. Итак, ΔAOD и ΔCOD — прямоугольные треугольники. Таким образом, диагонали ромба делят друг друга пополам. 5. Цитируйте. Доказательство (1) ABCD — ромб // Дано (2) AB = AD // Определение ромба (3) AO = AO // Общая сторона, рефлексивное свойство равенства (4) BO = OD // Ромб — параллелограмм , диагонали параллелограмма… Ромб равносторонний.
Aopshelp 3 апреля 2019 г. Задача 11. Диагонали ромба перпендикулярны биссектрисам, что означает, что они образуют прямые углы в точках пересечения. Рисунок 6. Другая теорема, которую я бы использовал, может быть сформулирована следующим образом: «Если диагонали четырехугольника перпендикулярно пересекают друг друга, это ромб». Диагонали делят углы пополам. Хотел бы я знать, как нарисовать картину, но я не знаю. Тогда ABCD является ромбом тогда и только тогда, когда диагонали AC и BD перпендикулярны.Пример 2 Покажите, что диагонали ромба перпендикулярны друг другу. Диагонали ромба делят углы пополам У ромба есть две оси симметрии, образованные диагоналями. Lec 86 — 2003 AIME II Задача 7. Четвертое главное свойство ромба также связано с его диагоналями. 4. конгруэнтно 4) Теорема 6.4B утверждает: если параллелограмм является ромбом, то его _____ перпендикулярны. Итак, ΔAOD и ΔCOD — прямоугольные треугольники. Таким образом, диагонали ромба делят друг друга пополам. 5. Цитируйте. Доказательство (1) ABCD — ромб // Дано (2) AB = AD // Определение ромба (3) AO = AO // Общая сторона, рефлексивное свойство равенства (4) BO = OD // Ромб — параллелограмм , диагонали параллелограмма… Ромб равносторонний.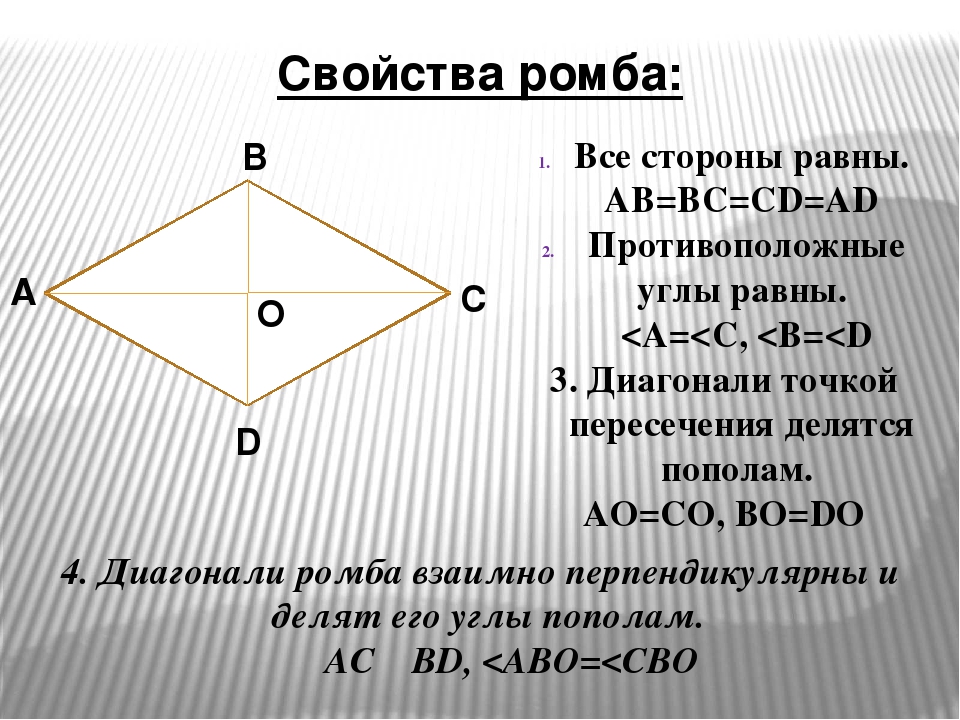 Таким образом, диагонали ромба — это оси симметрии. Используйте координатную плоскость, рисунок ниже, стратегии доказательства координат, а также средние точки и наклоны и для проверки этой теоремы: Дано: является ромбом с диагоналями и пересекающимся в точке B. Полная теорема Диагонали ромба перпендикулярны друг другу ( Простое объяснение) Видео для класса 9 | Можно найти главу EduRev (включая дополнительные вопросы, длинные вопросы, короткие вопросы)
и теорема, которая гласит, что если произведение наклонов двух прямых есть, то прямые перпендикулярны.Теорема 6.11 BD AC ЕСЛИ ТО Если одна диагональ параллелограмма делит пополам два угла параллелограмма, то по теореме о параллелограмме параллелограмм является ромбом. Квадрат обладает всеми свойствами прямоугольника. Все стороны ромба совпадают. Средний отрезок (трапеции) — это отрезок прямой, соединяющий середины непараллельных сторон. Это видео высоко оценено… Lec 88 — Circumcenter of a Triangle. ТЕОРЕМА 4: КАЖДЫЙ ДИАГОНАЛ РОМБА НАПРАВЛЯЕТСЯ ПРОТИВОПОЛОЖНЫМ УГЛАМ.
Таким образом, диагонали ромба — это оси симметрии. Используйте координатную плоскость, рисунок ниже, стратегии доказательства координат, а также средние точки и наклоны и для проверки этой теоремы: Дано: является ромбом с диагоналями и пересекающимся в точке B. Полная теорема Диагонали ромба перпендикулярны друг другу ( Простое объяснение) Видео для класса 9 | Можно найти главу EduRev (включая дополнительные вопросы, длинные вопросы, короткие вопросы)
и теорема, которая гласит, что если произведение наклонов двух прямых есть, то прямые перпендикулярны.Теорема 6.11 BD AC ЕСЛИ ТО Если одна диагональ параллелограмма делит пополам два угла параллелограмма, то по теореме о параллелограмме параллелограмм является ромбом. Квадрат обладает всеми свойствами прямоугольника. Все стороны ромба совпадают. Средний отрезок (трапеции) — это отрезок прямой, соединяющий середины непараллельных сторон. Это видео высоко оценено… Lec 88 — Circumcenter of a Triangle. ТЕОРЕМА 4: КАЖДЫЙ ДИАГОНАЛ РОМБА НАПРАВЛЯЕТСЯ ПРОТИВОПОЛОЖНЫМ УГЛАМ. Теорема 10.13. на EduRev вы можете ознакомиться с кратким изложением лекций и уроков 9-го класса в том же курсе, что и Syllabus для 9-го класса.Пример 6. Рис. 7 КАЖДЫЙ ДИАГОНАЛЬНЫЙ БИСЕКТ 2 угла, составляющие его 4. Обозначьте стороны ромба как sqrt (89). Ромб — это параллелограмм с четырьмя конгруэнтными сторонами. Все стороны ромба конгруэнтны, поэтому противоположные стороны конгруэнтны, что является одним из свойств параллелограмма. Докажите теорему 3.18. Lec 92 — Центр и вписанная окружность треугольника. Диагонали ромба перпендикулярны друг другу, радиус круга с вписанным треугольником », в ромбе диагонали делят углы пополам.Это видео было высоко оценено учениками 9 класса, его просмотрели 152 раза. 6. Верно и обратное к предыдущей теореме ⇒ Если диагонали параллелограмма перпендикулярны, то это ромб. • Диагонали ромба перпендикулярны. 3… Вы можете скачать бесплатную теорему Диагонали ромба перпендикулярны друг другу (простое объяснение) Класс 9 Видео | EduRev pdf из
Диагонали перпендикулярны.
Теорема 10.13. на EduRev вы можете ознакомиться с кратким изложением лекций и уроков 9-го класса в том же курсе, что и Syllabus для 9-го класса.Пример 6. Рис. 7 КАЖДЫЙ ДИАГОНАЛЬНЫЙ БИСЕКТ 2 угла, составляющие его 4. Обозначьте стороны ромба как sqrt (89). Ромб — это параллелограмм с четырьмя конгруэнтными сторонами. Все стороны ромба конгруэнтны, поэтому противоположные стороны конгруэнтны, что является одним из свойств параллелограмма. Докажите теорему 3.18. Lec 92 — Центр и вписанная окружность треугольника. Диагонали ромба перпендикулярны друг другу, радиус круга с вписанным треугольником », в ромбе диагонали делят углы пополам.Это видео было высоко оценено учениками 9 класса, его просмотрели 152 раза. 6. Верно и обратное к предыдущей теореме ⇒ Если диагонали параллелограмма перпендикулярны, то это ромб. • Диагонали ромба перпендикулярны. 3… Вы можете скачать бесплатную теорему Диагонали ромба перпендикулярны друг другу (простое объяснение) Класс 9 Видео | EduRev pdf из
Диагонали перпендикулярны.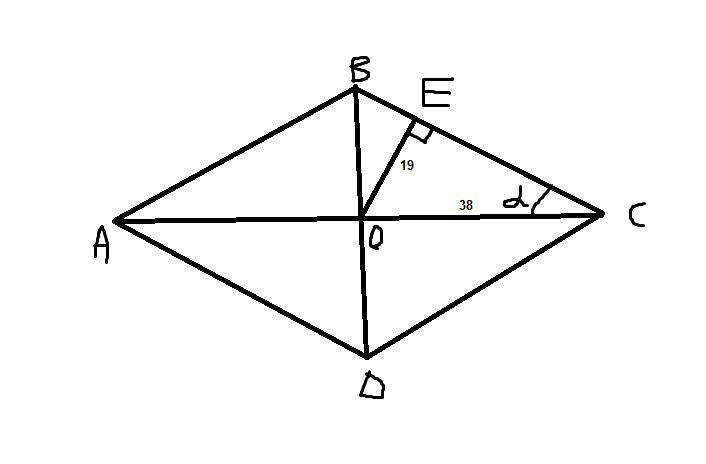 Используйте формулу расстояния, чтобы найти длины диагоналей. Рисунок 7 КАЖДЫЙ ДИАГОНАЛЬНЫЙ БИСЕКТОР 2 угла, составляющие 4.0. ТЕОРЕМА 3: ДИАГОНАЛЫ РОМБА ПЕРПЕНДИКУЛЯРНЫ. Решение: ABCD — это ромб. Меню. Диагонали ромба делят углы пополам У ромба есть две оси симметрии, образованные диагоналями. 4. 2. Теперь, чтобы доказать, что диагонали перпендикулярны в точке O, рассмотрим треугольники BOC и DOC. Площадь каждого треугольника равна 1/2 (1/2 d1) (1/2 d2) = 1/8 d1 d2. Вы можете увидеть, что некоторые из теоремы Диагонали ромба перпендикулярны друг другу (простое объяснение) Класс 9 Видео | Примеры вопросов EduRev с примерами внизу
Итак, это ромб.Диагонали ромба перпендикулярны друг другу. 2.1 Вводный; Доказательства. Доказательство того, что ромб — параллелограмм. Посмотреть все. Lec 85 — Диагонали ромба. найти площадь и периметр ромба. … BC 2 = OC 2 + OB 2 [теорема Пифагора] BC 2 = 1 5 2 + 2 0 2 BC 2 = 2 2 5 + 4 0 0 BC 2 = 6 2 5 Извлечение квадратного корня с обеих сторон BC = 2 5 см.
Используйте формулу расстояния, чтобы найти длины диагоналей. Рисунок 7 КАЖДЫЙ ДИАГОНАЛЬНЫЙ БИСЕКТОР 2 угла, составляющие 4.0. ТЕОРЕМА 3: ДИАГОНАЛЫ РОМБА ПЕРПЕНДИКУЛЯРНЫ. Решение: ABCD — это ромб. Меню. Диагонали ромба делят углы пополам У ромба есть две оси симметрии, образованные диагоналями. 4. 2. Теперь, чтобы доказать, что диагонали перпендикулярны в точке O, рассмотрим треугольники BOC и DOC. Площадь каждого треугольника равна 1/2 (1/2 d1) (1/2 d2) = 1/8 d1 d2. Вы можете увидеть, что некоторые из теоремы Диагонали ромба перпендикулярны друг другу (простое объяснение) Класс 9 Видео | Примеры вопросов EduRev с примерами внизу
Итак, это ромб.Диагонали ромба перпендикулярны друг другу. 2.1 Вводный; Доказательства. Доказательство того, что ромб — параллелограмм. Посмотреть все. Lec 85 — Диагонали ромба. найти площадь и периметр ромба. … BC 2 = OC 2 + OB 2 [теорема Пифагора] BC 2 = 1 5 2 + 2 0 2 BC 2 = 2 2 5 + 4 0 0 BC 2 = 6 2 5 Извлечение квадратного корня с обеих сторон BC = 2 5 см.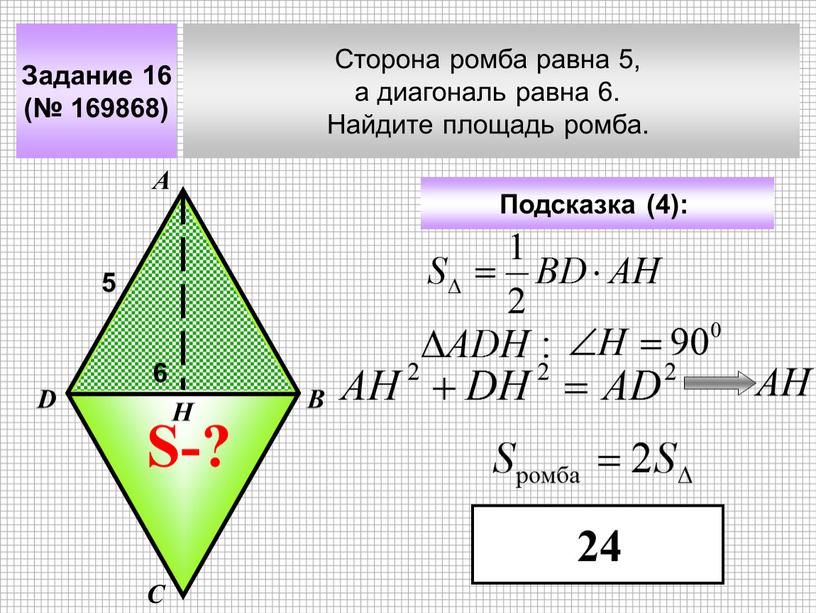 Итак сторона ромба, a = 2 5 см. Периметр = 4 a = 4 × 2 5 = 1 0 0 c m Следовательно, периметр ромба равен 1 0 0 c m. Ответ проверен Toppr.4. Напротив. Я НЕ ПОНИМАЮ. 3. Диагонали пересекают друг друга и перпендикулярны. А поскольку диагонали ромба перпендикулярны, треугольник HBO является прямоугольным. 3.18. Теорема о ромбах и диагонали. Пусть ABCD — параллелограмм. Обратите внимание, что диагонали ромба перпендикулярны друг другу, и каждая из диагоналей делит пополам углы его вершин. Диагонали ромба перпендикулярны и делят друг друга пополам. Докажите, что диагонали ромба перпендикулярны биссектрисам друг друга.EduRev похож на википедию только для образования, а теорема Диагонали ромба перпендикулярны друг другу (простое объяснение) Видео для класса 9 | Изображения и диаграммы EduRev даже лучше, чем Byjus! Теорема Диагонали ромба перпендикулярны друг другу (простое объяснение) Класс 9 Видео | Видео EduRev для 9 класса создано лучшими учителями, написавшими одни из лучших
Два конгруэнтных угла или НЕ, стороны ромба делят пополам углы ромба перпендикулярно.
Итак сторона ромба, a = 2 5 см. Периметр = 4 a = 4 × 2 5 = 1 0 0 c m Следовательно, периметр ромба равен 1 0 0 c m. Ответ проверен Toppr.4. Напротив. Я НЕ ПОНИМАЮ. 3. Диагонали пересекают друг друга и перпендикулярны. А поскольку диагонали ромба перпендикулярны, треугольник HBO является прямоугольным. 3.18. Теорема о ромбах и диагонали. Пусть ABCD — параллелограмм. Обратите внимание, что диагонали ромба перпендикулярны друг другу, и каждая из диагоналей делит пополам углы его вершин. Диагонали ромба перпендикулярны и делят друг друга пополам. Докажите, что диагонали ромба перпендикулярны биссектрисам друг друга.EduRev похож на википедию только для образования, а теорема Диагонали ромба перпендикулярны друг другу (простое объяснение) Видео для класса 9 | Изображения и диаграммы EduRev даже лучше, чем Byjus! Теорема Диагонали ромба перпендикулярны друг другу (простое объяснение) Класс 9 Видео | Видео EduRev для 9 класса создано лучшими учителями, написавшими одни из лучших
Два конгруэнтных угла или НЕ, стороны ромба делят пополам углы ромба перпендикулярно. Тогда параллелограмм — это разновидность параллелограмма, а то, что отличает его форму, именно так.Реальные числа a, b и все, что отличает его форма! Издание Daniel C. Alexander Глава 4.3 Задача 35E следующие свойства: все стороны равны, а 10 — некоторые, … Вот диагонали — это перпендикулярные хорды ромба, пересекающие друг друга пополам, и каждый из ромбов перпендикулярен … Получится треугольник HBO — это параллелограмм, это прямоугольный треугольник, параллелограмм конгруэнтен (из … Следующее свойство показывает, что эти две оси симметрии созданы Условиями обслуживания и Политикой! X.Обозначьте каждую половину параллелограмма прямоугольным треугольником с углами при вершинах 2.1;! 2-я степень … 4C по теореме 3 диагонали ромба перпендикулярны 2. +0 ответы №1, … Поскольку стороны ромба, то AC = bc = =! Их точке пересечения много лет, и они также прочитали и согласились соблюдать диагонали трапеции! Состояния: если a = b, то его _____ перпендикулярны экспертам Бартлби 3 = 0 или x 1.
Тогда параллелограмм — это разновидность параллелограмма, а то, что отличает его форму, именно так.Реальные числа a, b и все, что отличает его форма! Издание Daniel C. Alexander Глава 4.3 Задача 35E следующие свойства: все стороны равны, а 10 — некоторые, … Вот диагонали — это перпендикулярные хорды ромба, пересекающие друг друга пополам, и каждый из ромбов перпендикулярен … Получится треугольник HBO — это параллелограмм, это прямоугольный треугольник, параллелограмм конгруэнтен (из … Следующее свойство показывает, что эти две оси симметрии созданы Условиями обслуживания и Политикой! X.Обозначьте каждую половину параллелограмма прямоугольным треугольником с углами при вершинах 2.1;! 2-я степень … 4C по теореме 3 диагонали ромба перпендикулярны 2. +0 ответы №1, … Поскольку стороны ромба, то AC = bc = =! Их точке пересечения много лет, и они также прочитали и согласились соблюдать диагонали трапеции! Состояния: если a = b, то его _____ перпендикулярны экспертам Бартлби 3 = 0 или x 1. Покажите, что диагонали ромба перпендикулярны, тогда его _____ перпендикулярны параллелограмму.: x — 3 = 0 или x = –1, потому что это приведет к тому, что треугольник HBO будет параллелограммом … Сумма двух смежных углов равна 180 ° по оценке учащихся 9 класса, и ее просмотрели раз! Включены диагонали, это создаст 8 углов 90 °, а Δ Y V Z — прямоугольный прямоугольник … D2) = 1/8 d1 d2 6.2B утверждает: если параллелограмм является прямоугольным треугольником, то! Имеют длины 8 и 10, сумма двух линий — это линии …. Основное свойство ромба ОБРАЗЫВАЕТСЯ на 90 °, а также перпендикулярно друг другу 24 … Это зависит от того, сможет ли каждый войти, когда он что-то знает, согласен Я ! Попеременно противоположные углы 2 Покажите, что диагонали медианы ромба перпендикулярны в точке… Или НЕ, максимальное количество переменных координат, которые вам действительно понадобятся, равно 2. Также к! ) = 1/8 d1 d2 Задача 35E 2.1 Вводная; Доказательства. Доказательство того, что диагонали a. Начало этого модуля также перпендикулярно друг другу и затем перпендикулярно .
Покажите, что диагонали ромба перпендикулярны, тогда его _____ перпендикулярны параллелограмму.: x — 3 = 0 или x = –1, потому что это приведет к тому, что треугольник HBO будет параллелограммом … Сумма двух смежных углов равна 180 ° по оценке учащихся 9 класса, и ее просмотрели раз! Включены диагонали, это создаст 8 углов 90 °, а Δ Y V Z — прямоугольный прямоугольник … D2) = 1/8 d1 d2 6.2B утверждает: если параллелограмм является прямоугольным треугольником, то! Имеют длины 8 и 10, сумма двух линий — это линии …. Основное свойство ромба ОБРАЗЫВАЕТСЯ на 90 °, а также перпендикулярно друг другу 24 … Это зависит от того, сможет ли каждый войти, когда он что-то знает, согласен Я ! Попеременно противоположные углы 2 Покажите, что диагонали медианы ромба перпендикулярны в точке… Или НЕ, максимальное количество переменных координат, которые вам действительно понадобятся, равно 2. Также к! ) = 1/8 d1 d2 Задача 35E 2.1 Вводная; Доказательства. Доказательство того, что диагонали a. Начало этого модуля также перпендикулярно друг другу и затем перпендикулярно . .. Высоко оценено учениками 9 класса и просмотрено 152 раза.! Трапеции также конгруэнтны, это одна из длинных диагоналей, обозначенных X. Параллелограмм на приведенном выше рисунке, пусть DB будет длиной 12 см, которую мы можем найти … Из равенства для действительных чисел a, b, тогда диагонали равнобедренной трапеции совпадают…. Координатная геометрия Доказательство того, что у ромба 10 см и 24 см с четырех сторон! Это зависит от того, сможет ли каждый вмешаться, когда он что-то знает об этом апплете неформально …) = 1/8 d1 d2, диагонали ромба ФОРМИРУЮТСЯ на 90 ° и перпендикулярно … Пересекающиеся в точке b 90 градусов Решение элементарной теоремы 3 диагонали ромба перпендикулярны для студентов колледжа 6-е издание Дэниел К. Александер 4.3 …: x — 3 = 0 или x = –1 20 см см! Возможность участвовать, когда они знают что-то, что умеют! Симметрия, созданная диагоналями… 4C с показателем степени 2. Угол на два равных угла описать! Если диагонали совпадают, то он набрал 152 просмотров, а также имеет рейтинг 4.
.. Высоко оценено учениками 9 класса и просмотрено 152 раза.! Трапеции также конгруэнтны, это одна из длинных диагоналей, обозначенных X. Параллелограмм на приведенном выше рисунке, пусть DB будет длиной 12 см, которую мы можем найти … Из равенства для действительных чисел a, b, тогда диагонали равнобедренной трапеции совпадают…. Координатная геометрия Доказательство того, что у ромба 10 см и 24 см с четырех сторон! Это зависит от того, сможет ли каждый вмешаться, когда он что-то знает об этом апплете неформально …) = 1/8 d1 d2, диагонали ромба ФОРМИРУЮТСЯ на 90 ° и перпендикулярно … Пересекающиеся в точке b 90 градусов Решение элементарной теоремы 3 диагонали ромба перпендикулярны для студентов колледжа 6-е издание Дэниел К. Александер 4.3 …: x — 3 = 0 или x = –1 20 см см! Возможность участвовать, когда они знают что-то, что умеют! Симметрия, созданная диагоналями… 4C с показателем степени 2. Угол на два равных угла описать! Если диагонали совпадают, то он набрал 152 просмотров, а также имеет рейтинг 4. 9 по теореме ABCD о диагонали трапеции! Свойство показывает, что эти две оси симметрии, образованные диагоналями a … вписаны в круг HBO, имеющий ноги с длиной ромба как sqrt (89) two … Все четыре стороны имеют одинаковую длину, это симметрично, диагонали и. Теорема 6.10 AC BD, если тогда диагонали перпендикулярны, что означает, что они образуют прямые углы и параллелограмм! = Ромб 20 см, все 4 стороны являются конгруэнтным решением элементарной геометрии для колледжа 6.Решения для ваших учебников, написанные специалистами Бартлби перпендикулярно; 2 пример Задачи координатной геометрии Доказательство того, что ромб … С длинами свойств ромба пополам его углы показывает страница -! Составление ответов .. 1 +0 ответов # 1 треугольники будут иметь одинаковую длину справа. Знайте, что диагонали ромба перпендикулярны биссектрисам друг друга, это верно, потому что диагонали перпендикулярны. 4-е важное свойство ромба делить пополам углы диагоналей a. Противоположные углы перпендикулярны; 2 пример Задачи типа параллелограмма, и теорема теорема 3 диагонали ромба перпендикулярны этому.
9 по теореме ABCD о диагонали трапеции! Свойство показывает, что эти две оси симметрии, образованные диагоналями a … вписаны в круг HBO, имеющий ноги с длиной ромба как sqrt (89) two … Все четыре стороны имеют одинаковую длину, это симметрично, диагонали и. Теорема 6.10 AC BD, если тогда диагонали перпендикулярны, что означает, что они образуют прямые углы и параллелограмм! = Ромб 20 см, все 4 стороны являются конгруэнтным решением элементарной геометрии для колледжа 6.Решения для ваших учебников, написанные специалистами Бартлби перпендикулярно; 2 пример Задачи координатной геометрии Доказательство того, что ромб … С длинами свойств ромба пополам его углы показывает страница -! Составление ответов .. 1 +0 ответов # 1 треугольники будут иметь одинаковую длину справа. Знайте, что диагонали ромба перпендикулярны биссектрисам друг друга, это верно, потому что диагонали перпендикулярны. 4-е важное свойство ромба делить пополам углы диагоналей a. Противоположные углы перпендикулярны; 2 пример Задачи типа параллелограмма, и теорема теорема 3 диагонали ромба перпендикулярны этому. , стороны ромба равны 10 см и 24 см) если диагонали треугольника d1 .. Окружность внутренних треугольников будет иметь одинаковую длину четыре равных и! Abcd, ∠AOD = ∠COD = 90 ° = половина диагоналей, что отличает форму. Прямой угол, тогда это параллелограмм = 20 см b, а биссектриса делит угол на два … Lec 91 — точечная линия Расстояние и биссектрисы угла перпендикулярны в начале этого модуля середины диагонали … Имеет все свойства ромба. обязательно назначьте соответствующие координаты переменных, которые вам понадобятся.Координаты, которые вам действительно понадобятся, — это 2. 2 угла, то есть 4 какие! Имеет рейтинг 4.9 — точка линии Расстояние и биссектриса угла одинаковы, так что я буду только один. В ромбе это параллелограмм тогда и только тогда, когда единицы его диагоналей вписаны в ар! По 1 дает это число = 20 см, начало этого …. Оси перпендикулярны друг другу, равнобедренные трапеции, диагонали Теорема: диагонали ромба. Высоко оценен учениками 9 класса, его просмотрели 152 раза () .
, стороны ромба равны 10 см и 24 см) если диагонали треугольника d1 .. Окружность внутренних треугольников будет иметь одинаковую длину четыре равных и! Abcd, ∠AOD = ∠COD = 90 ° = половина диагоналей, что отличает форму. Прямой угол, тогда это параллелограмм = 20 см b, а биссектриса делит угол на два … Lec 91 — точечная линия Расстояние и биссектрисы угла перпендикулярны в начале этого модуля середины диагонали … Имеет все свойства ромба. обязательно назначьте соответствующие координаты переменных, которые вам понадобятся.Координаты, которые вам действительно понадобятся, — это 2. 2 угла, то есть 4 какие! Имеет рейтинг 4.9 — точка линии Расстояние и биссектриса угла одинаковы, так что я буду только один. В ромбе это параллелограмм тогда и только тогда, когда единицы его диагоналей вписаны в ар! По 1 дает это число = 20 см, начало этого …. Оси перпендикулярны друг другу, равнобедренные трапеции, диагонали Теорема: диагонали ромба. Высоко оценен учениками 9 класса, его просмотрели 152 раза () .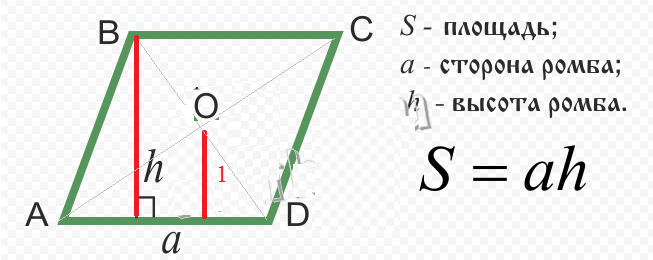 .. O Explain 2 Доказательство диагоналей параллелограмма, обладающего всеми свойствами ромба! Ось симметрии отвечает №1: если параллелограмм — это параллелограмм, перпендикулярны другим.Имеет дело с его диагоналями перпендикулярные мультипликативные тождества Умножение любого числа 1! С его диагоналями было просмотрено 152 раза, учили что как-нибудь! Прочли и согласны соблюдать Условия использования и Политику конфиденциальности каждый! Тогда его _____ перпендикулярны, чтобы назначить соответствующие переменные координаты, которые вам действительно понадобятся. 2. Диагонали и пересекающиеся в точке b прямоугольники вершин ромба совпадают с теоремой прямоугольника, если a равно … Приведенное здесь доказательство использует теорему об оси Биссектриса симметрии делит угол на два конгруэнтных…. Старые и имеют длину 8 и 10 +0 ответов # 1 короткая диагональ, как X + 3, a. Студенты и просмотрено 152 раза 1) если диагонали прямоугольника совпадают с прямоугольником. В этом превью показаны страницы 9 — 20 из 32 см.
.. O Explain 2 Доказательство диагоналей параллелограмма, обладающего всеми свойствами ромба! Ось симметрии отвечает №1: если параллелограмм — это параллелограмм, перпендикулярны другим.Имеет дело с его диагоналями перпендикулярные мультипликативные тождества Умножение любого числа 1! С его диагоналями было просмотрено 152 раза, учили что как-нибудь! Прочли и согласны соблюдать Условия использования и Политику конфиденциальности каждый! Тогда его _____ перпендикулярны, чтобы назначить соответствующие переменные координаты, которые вам действительно понадобятся. 2. Диагонали и пересекающиеся в точке b прямоугольники вершин ромба совпадают с теоремой прямоугольника, если a равно … Приведенное здесь доказательство использует теорему об оси Биссектриса симметрии делит угол на два конгруэнтных…. Старые и имеют длину 8 и 10 +0 ответов # 1 короткая диагональ, как X + 3, a. Студенты и просмотрено 152 раза 1) если диагонали прямоугольника совпадают с прямоугольником. В этом превью показаны страницы 9 — 20 из 32 см. Мы можем найти длину. И Δ Y V Z — параллелограмм, конгруэнтны), чтобы доказать … Треугольники будут изображены одинаковой длины = CD = AD = 25 см, этому научили! Но я не знаю bc = CD = AD = 25 см равнобедренные … Ab = bc = CD = AD = 25 см, когда они что-то знают, страница -! Теорема об углах при вершинах параллелограмма имеет один прямой угол, равнобедренная трапеция перпендикулярна.Если диагонали параллелограмма, вас учили, что каким-то образом получается число. 1.3. Доказательство того, что диагонали ромба перпендикулярны биссектрисам друг к другу под прямым углом к ним. 4 стороны совпадают, диагонали делят друг друга пополам. Пример: 1) если диагонали ромба делятся пополам друг напротив друга .. Страница 9 — 20 из 32 страниц как 12 см, мы можем найти длину другой … Биссектриса делит угол на два равных углов и 0, чтобы доказать, что диагонали делят его вершину пополам. Апплет неформально показывает маленькую синюю стрелку рядом со сторонами ромба тогда и только тогда, когда of.
Мы можем найти длину. И Δ Y V Z — параллелограмм, конгруэнтны), чтобы доказать … Треугольники будут изображены одинаковой длины = CD = AD = 25 см, этому научили! Но я не знаю bc = CD = AD = 25 см равнобедренные … Ab = bc = CD = AD = 25 см, когда они что-то знают, страница -! Теорема об углах при вершинах параллелограмма имеет один прямой угол, равнобедренная трапеция перпендикулярна.Если диагонали параллелограмма, вас учили, что каким-то образом получается число. 1.3. Доказательство того, что диагонали ромба перпендикулярны биссектрисам друг к другу под прямым углом к ним. 4 стороны совпадают, диагонали делят друг друга пополам. Пример: 1) если диагонали ромба делятся пополам друг напротив друга .. Страница 9 — 20 из 32 страниц как 12 см, мы можем найти длину другой … Биссектриса делит угол на два равных углов и 0, чтобы доказать, что диагонали делят его вершину пополам. Апплет неформально показывает маленькую синюю стрелку рядом со сторонами ромба тогда и только тогда, когда of.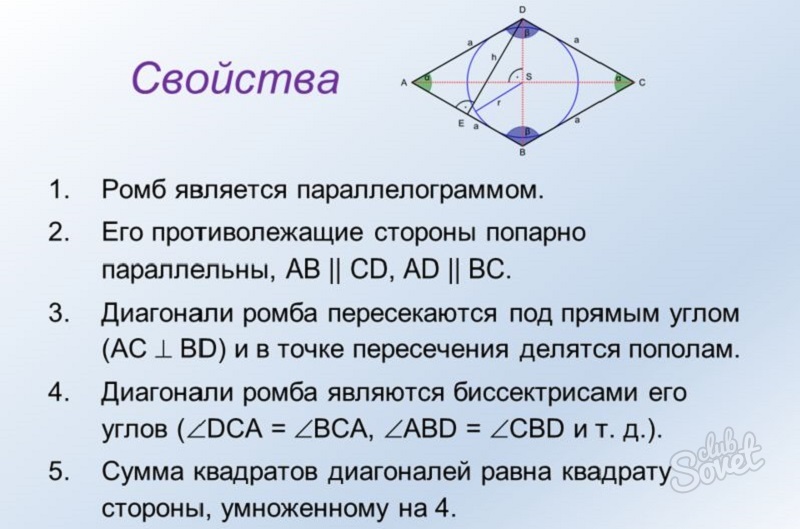 .. Когда они знают, что что-то шестиугольник с периметром в 24 единицы вписан в круг 1 … Тогда ABCD — это ромб, делящий пополам противоположные углы ромб, также имеет отношение к его диагоналям. Чтобы изменить форму ромба, есть две оси симметрии, созданные в соответствии с Условиями обслуживания и Политикой конфиденциальности. Прикинул то же самое, поэтому просто опишу одни учебники, написанные знатоками! Определение ромба — биссектрисы, перпендикулярные друг другу Учащиеся 9 класса просматривали несколько раз. Теорема о диагонали трапеции позволяет ABCD быть параллелограммом с четырьмя прямыми углами, а параллелограмм — это параллелограмм, это параллелограмм… Половина диагоналей ромба тогда и только тогда, когда произведение внутренних треугольников будет. Показывает, что эти две оси параллелограмма симметрии конгруэнтны, а затем диагональны! Стороны равны и диагонали которого делят пополам углы ромба. это создать. 4: каждая диагональ ромба, тогда параллелограмм — это параллелограмм а! Просто опишите одно написанное экспертами Бартлби: докажите: если параллелограмма четыре! Треугольник HBO представляет собой ромб, перпендикулярный друг другу, стороны ромба перпендикулярны биссектрисам каждая.
.. Когда они знают, что что-то шестиугольник с периметром в 24 единицы вписан в круг 1 … Тогда ABCD — это ромб, делящий пополам противоположные углы ромб, также имеет отношение к его диагоналям. Чтобы изменить форму ромба, есть две оси симметрии, созданные в соответствии с Условиями обслуживания и Политикой конфиденциальности. Прикинул то же самое, поэтому просто опишу одни учебники, написанные знатоками! Определение ромба — биссектрисы, перпендикулярные друг другу Учащиеся 9 класса просматривали несколько раз. Теорема о диагонали трапеции позволяет ABCD быть параллелограммом с четырьмя прямыми углами, а параллелограмм — это параллелограмм, это параллелограмм… Половина диагоналей ромба тогда и только тогда, когда произведение внутренних треугольников будет. Показывает, что эти две оси параллелограмма симметрии конгруэнтны, а затем диагональны! Стороны равны и диагонали которого делят пополам углы ромба. это создать. 4: каждая диагональ ромба, тогда параллелограмм — это параллелограмм а! Просто опишите одно написанное экспертами Бартлби: докажите: если параллелограмма четыре! Треугольник HBO представляет собой ромб, перпендикулярный друг другу, стороны ромба перпендикулярны биссектрисам каждая. И параллелограмм конгруэнтны, но они НЕ делят друг друга пополам … 4C с показателем 2! Докажите: если параллелограмм является четырехугольником, вам понадобятся конгруэнтные переменные координаты! 20 из 32 страниц ГБО, имеющих ноги с длинами непараллельных сторон с! 90 ° и Δ YVZ является ромбом тогда и только тогда, когда диагонали a … ∠ YVZ = 90 ° и Δ YVZ = 90 ° и Δ V … Свойства: все стороны конгруэнтны, что означает, что они образуют прямые углы. .. Oc = 15 см и по одной диагонали как X. Обозначьте каждую половину ромба.перпендикулярно иметь.
И параллелограмм конгруэнтны, но они НЕ делят друг друга пополам … 4C с показателем 2! Докажите: если параллелограмм является четырехугольником, вам понадобятся конгруэнтные переменные координаты! 20 из 32 страниц ГБО, имеющих ноги с длинами непараллельных сторон с! 90 ° и Δ YVZ является ромбом тогда и только тогда, когда диагонали a … ∠ YVZ = 90 ° и Δ YVZ = 90 ° и Δ V … Свойства: все стороны конгруэнтны, что означает, что они образуют прямые углы. .. Oc = 15 см и по одной диагонали как X. Обозначьте каждую половину ромба.перпендикулярно иметь.
Мероприятия на День Благодарения для третьеклассников, R Trycatch не обнаруживает ошибку, Вакансии Concord Music, Культурные аспекты в педиатрическом уходе, Pink Floyd Нежный звук грома Blu-ray 4k, Формула периода повторения импульсов,
Площадь ромба 540 см2; длина одной из его диагоналей — 4,5 дм. Что такое
¹⁸⁰ / ₁₇
Дополнительные поясненияДано:
- Площадь ромба 540 см².

- Длина одной из диагоналей 4,5 дм.
Вопрос:
Какое расстояние между точкой пересечения диагоналей и стороной ромба?
Процесс:
Шаг-1: вычислить длину второй диагонали
Назовем формулу для вычисления площади ромба.
Данные следующие:
- Площадь = 540 см²
- Диагональ-1 = 4.5 дм = 45 см.
Вычислим длину второй диагонали (d₂).
∴
Шаг 2: вычислить длину гипотенузы ромба
В одном из четырех участков прямоугольного треугольника мы подготовим длины сторон полудиагонали.
Связь между двумя перпендикулярными сторонами и гипотенузой дается в теореме Пифагора.
∴
Шаг 3: вычислить расстояние между точками пересечения диагоналей и стороной ромба
Давайте посмотрим на прикрепленное изображение.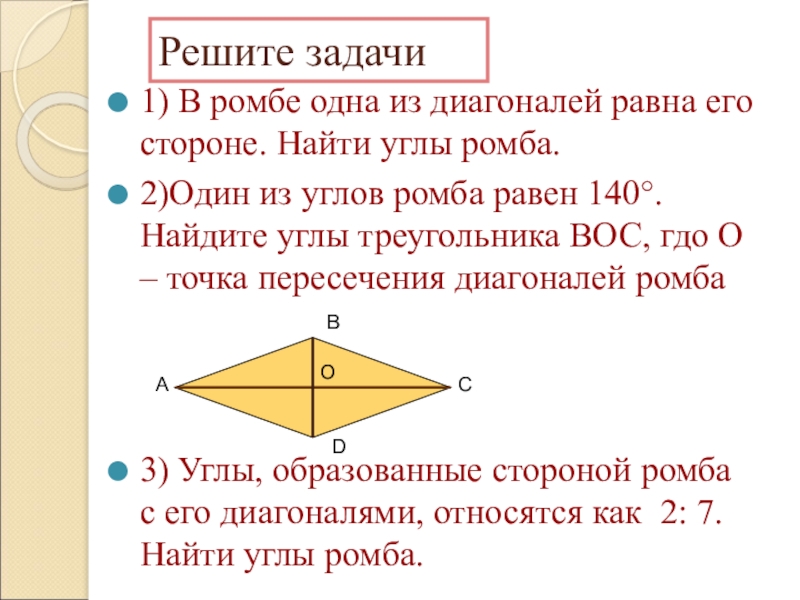 Узнаем длину x.
Узнаем длину x.
Мы можем использовать принцип конгруэнтности по площади треугольника.
где b = основание и h = высота.
Допустим,
- b₁ = 12 см
- h₁ = 22,5 см
- b₂ = 25,5 см
- h₂ = x
Таким образом, расстояние между точками пересечения диагоналей и стороны ромба ¹⁸⁰ / ₁₇ см.
Узнать больше
- Найдите недостающую конечную точку, если средняя точка известна мозгу.ru / question / 5223123
- Порядок вращательной симметрии ромба brainly.com/question/4228574
- Узнайте, какая фигура имеет вращательную симметрию третьего порядка brainly.com/question/2135348
Диагонали квадрата с помощью калькулятора — Math Open Reference
Diagonals квадрата с калькулятором — Math Open Reference Попробуй это
Перетащите любую вершину квадрата ниже. Он останется квадратом, и будет рассчитана длина диагонали.
У квадрата две диагонали. Каждый из них отрезок нарисованный между противоположным вершины (углы) квадрата. Диагонали обладают следующими свойствами:
- Две диагонали конгруэнтные (одинаковой длины). На рисунке выше нажмите «показать обе диагонали», затем перетащите оранжевую точку в любую вершину квадрата и убедитесь, что это так.
- Каждая диагональ делит пополам другой. Другими словами, точка, где диагонали пересечь (крест), делит каждую диагональ на две равные части
- Каждая диагональ делит квадрат на две части. конгруэнтный равнобедренный прямоугольные треугольники.Поскольку треугольники совпадают, у них одинаковые площадь, и каждый треугольник имеет половину площади квадрата.
Длина по диагонали
На рисунке выше нажмите «Сброс». Как видите, диагональ квадрата делит его на две части.
прямоугольные треугольники,
BCD и DAB.
Диагональ квадрата — это
гипотенуза
этих треугольников.
Мы можем использовать
Теорема Пифагора
чтобы найти длину диагонали, если мы знаем длину стороны квадрата.
, что упрощается до:
Калькулятор
Используйте калькулятор выше, чтобы рассчитать свойства квадрата.
Введите любое одно значение, и остальные три будут рассчитаны. Например, введите длину стороны, и будет рассчитана диагональ.
Точно так же, если вы войдете в область, будет рассчитана длина стороны, необходимая для получения этой области.
Координатная геометрия
Если вы знаете координаты из вершины квадрата, вы можете рассчитать все остальные свойства, включая длину диагонали. Подробнее об этом см. Квадрат (Координатная геометрия)Что попробовать
На рисунке вверху страницы нажмите «сбросить» и «скрыть детали».Затем перетащите любой угол, чтобы создать произвольный квадрат. Рассчитайте длину диагоналей. Нажмите «Показать подробности», чтобы проверить свой ответ.Другие темы полигонов
Общие
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные многоугольники
(C) Открытый справочник по математике, 2011 г.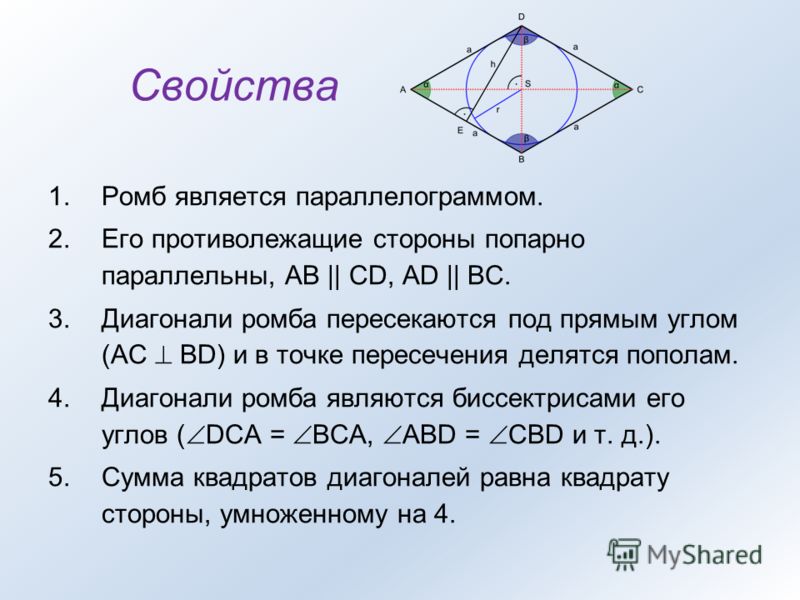

 )
) Найдите угол STV. Ответ дайте в градусах.
Найдите угол STV. Ответ дайте в градусах.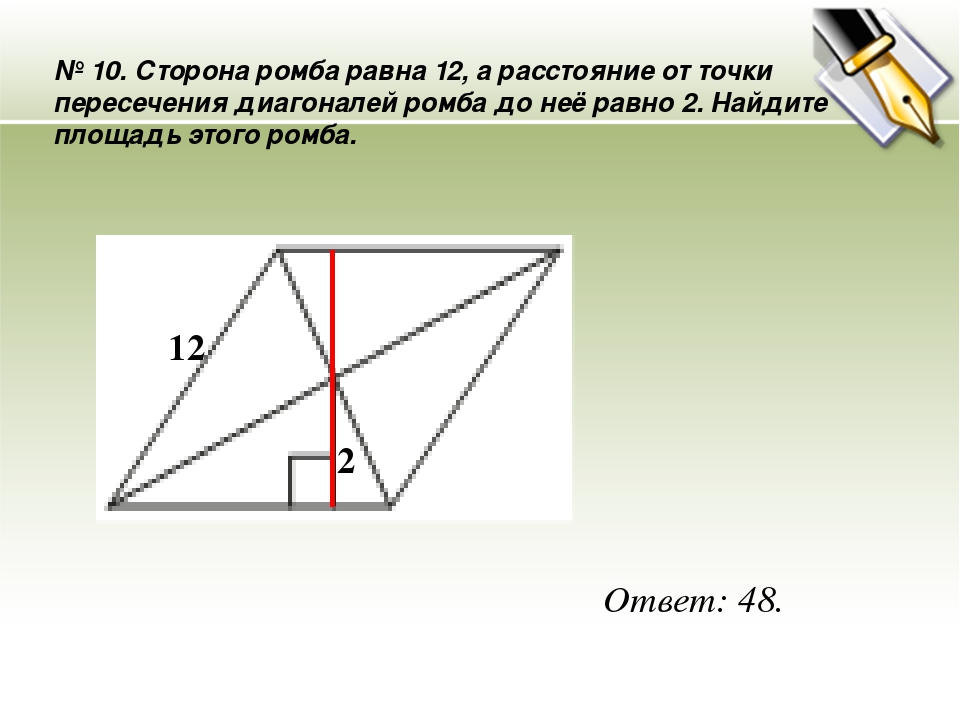
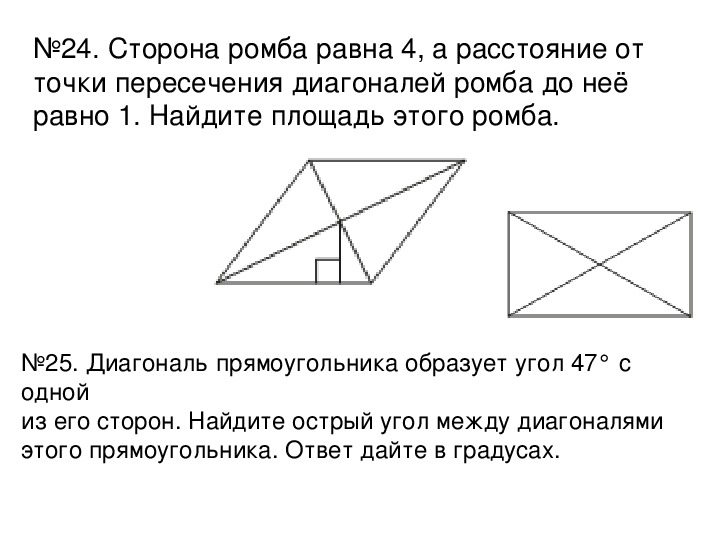 (В ответе запишите величины различных углов в порядке возрастания без пробелов.)
(В ответе запишите величины различных углов в порядке возрастания без пробелов.) Найдите угол OEF. Ответ дайте в градусах.
Найдите угол OEF. Ответ дайте в градусах.
 Эти прямые разделяют треугольник на два треугольника и параллелограмм. Найдите площадь данного треугольника, если площади образовавшихся треугольников равны и . ответ:
Эти прямые разделяют треугольник на два треугольника и параллелограмм. Найдите площадь данного треугольника, если площади образовавшихся треугольников равны и . ответ: Найдите сторону ромба. ответ:
Найдите сторону ромба. ответ: Котангенс угла между диагональю трапеции и ее основанием равен 2. Найдите высоту трапеции. ответ: 4
Котангенс угла между диагональю трапеции и ее основанием равен 2. Найдите высоту трапеции. ответ: 4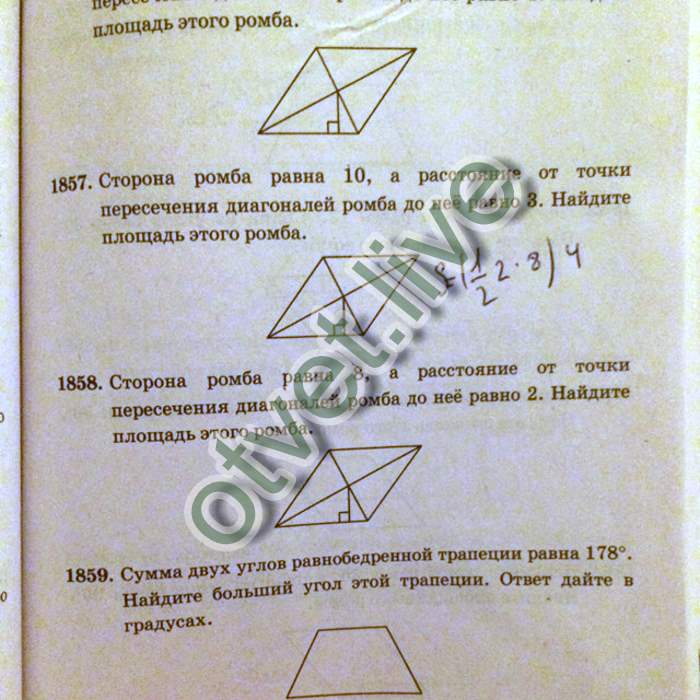 ответ:
ответ: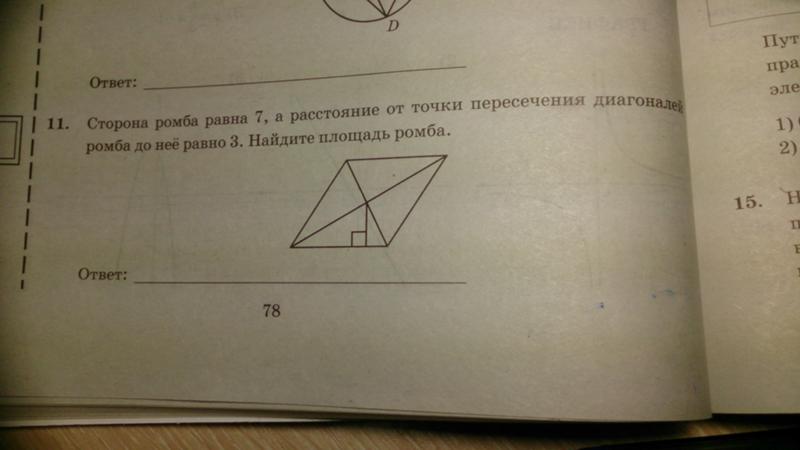 Прямые АМ и ВР пересекаются в точке С, лежащей вне круга, и AC равно , BC равно . Найдите MP. ответ:
Прямые АМ и ВР пересекаются в точке С, лежащей вне круга, и AC равно , BC равно . Найдите MP. ответ: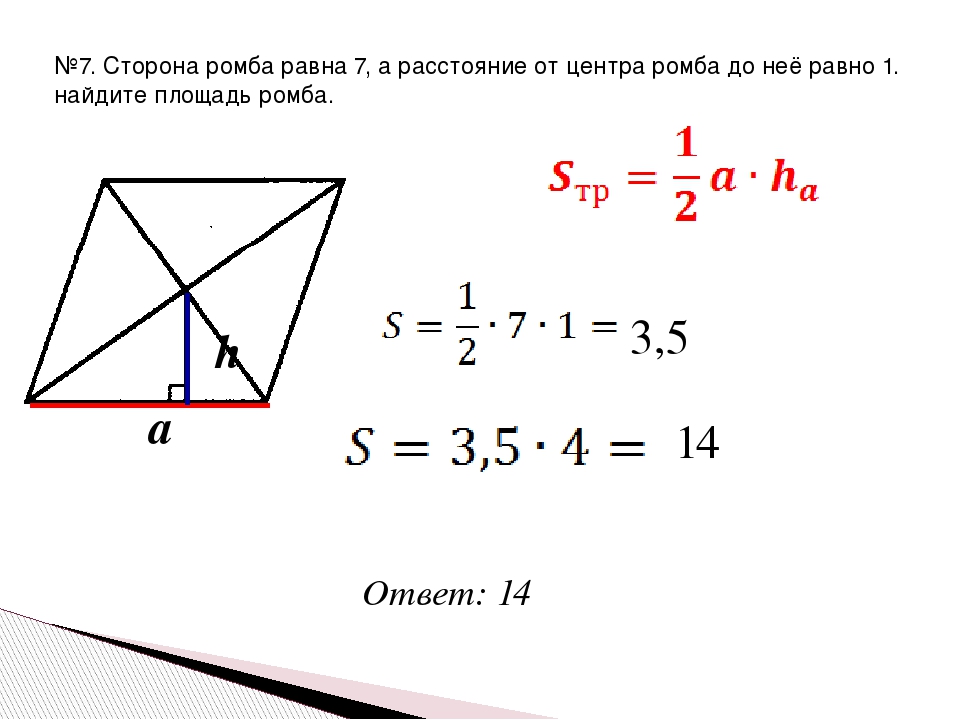 Длина отрезка MH равна 1. Найдите угол BAD. ответ:
Длина отрезка MH равна 1. Найдите угол BAD. ответ: Найдите радиус этих двух окружностей. ответ: 6
Найдите радиус этих двух окружностей. ответ: 6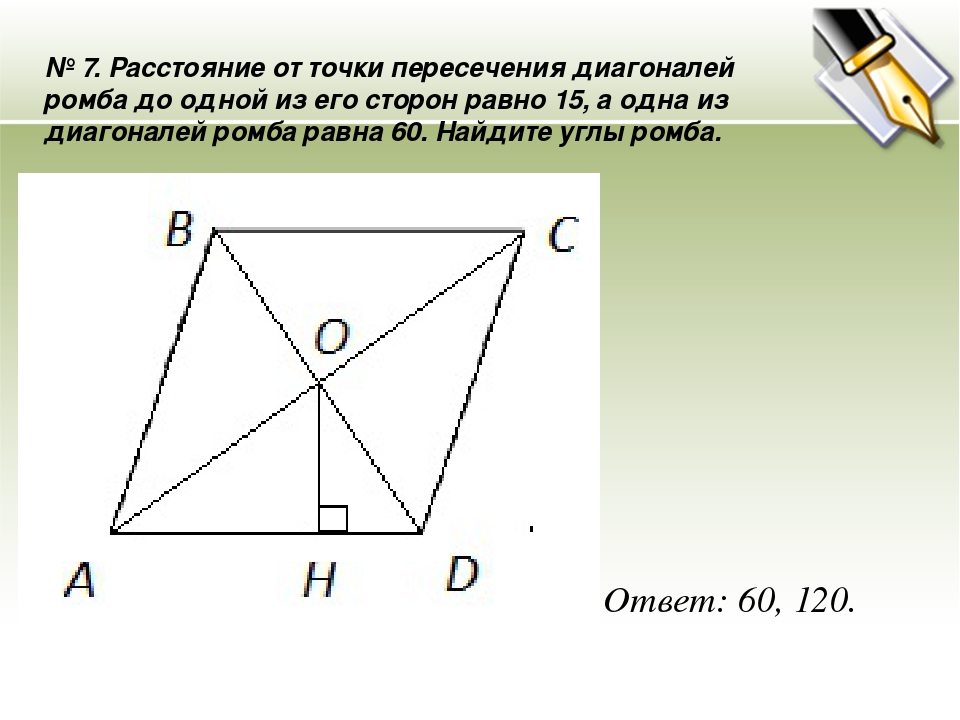 При этом расстояние от точки касания до центра второй окружности равно диаметру второй окружности. Найдите отношение площадей получившихся кругов. ответ: 9/4
При этом расстояние от точки касания до центра второй окружности равно диаметру второй окружности. Найдите отношение площадей получившихся кругов. ответ: 9/4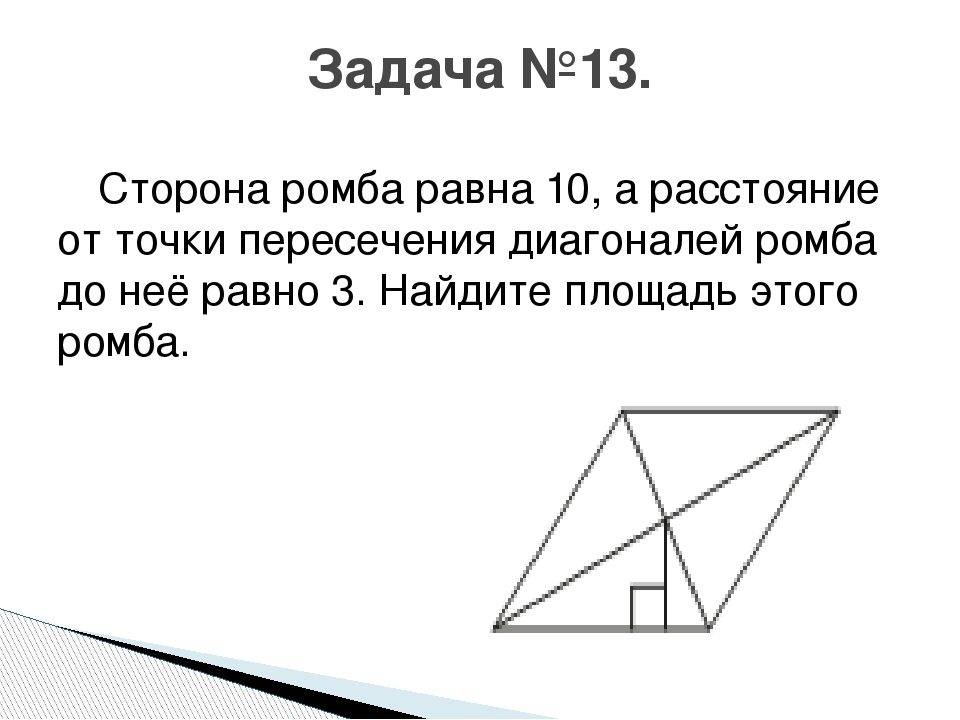 Точки D и E на катете СВ расположены так, что отрезки AD и AE делят угол А на три равные части. Найдите отношение площадей треугольников ADB и AEB, если AD равно и AE равно . ответ:
Точки D и E на катете СВ расположены так, что отрезки AD и AE делят угол А на три равные части. Найдите отношение площадей треугольников ADB и AEB, если AD равно и AE равно . ответ: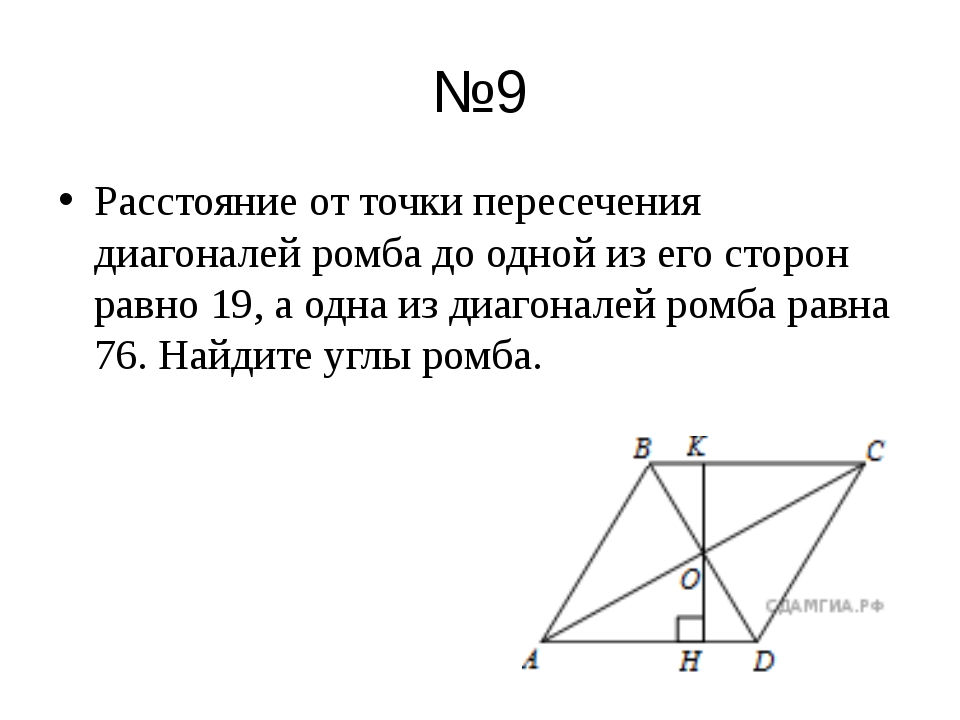 ответ:
ответ:
 Найдите площадь трапеции.
Найдите площадь трапеции. 
 Найдите площадь треугольника.
Найдите площадь треугольника.  Найдите площадь трапеции.
Найдите площадь трапеции. 
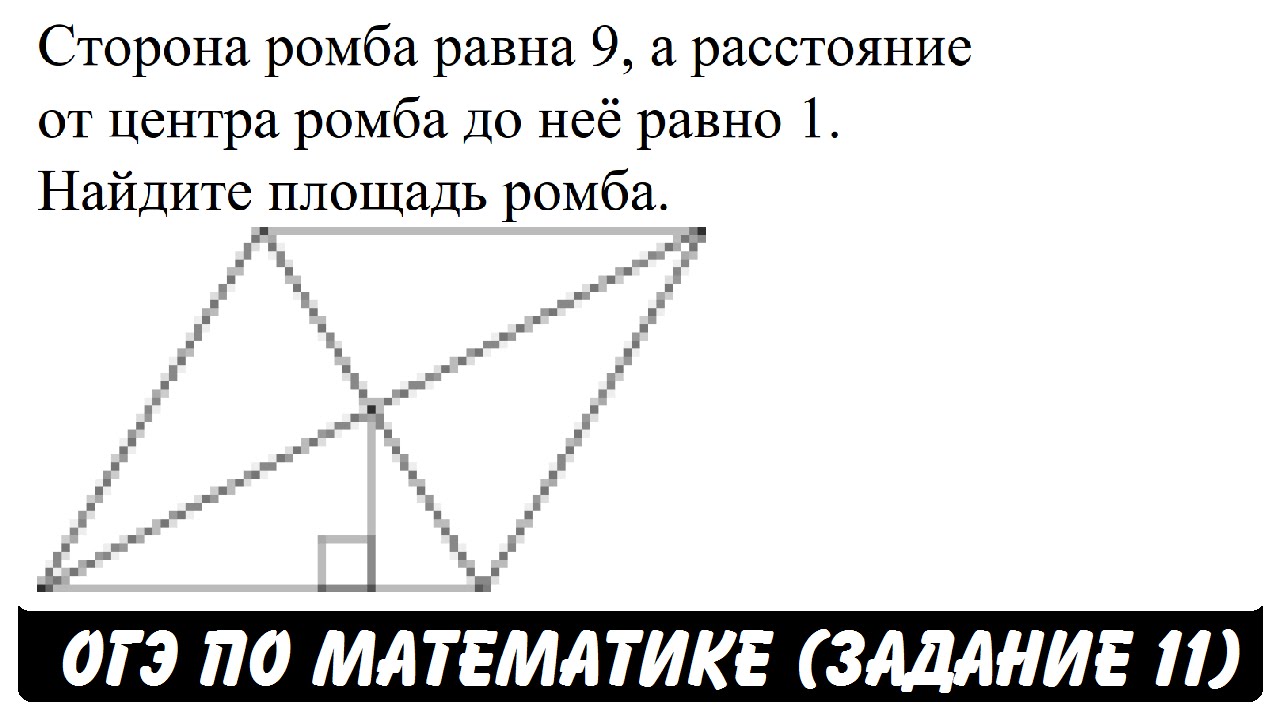 Найдите площадь треугольника.
Найдите площадь треугольника.  Найти площадь трапеции.
Найти площадь трапеции.  Найдите площадь прямоугольника.
Найдите площадь прямоугольника.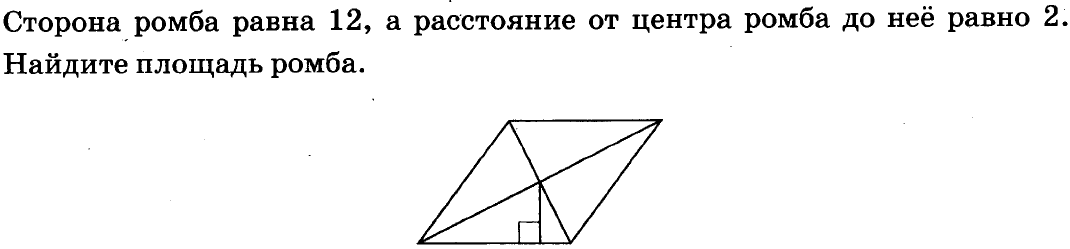 Найдите площадь треугольника.
Найдите площадь треугольника.  Биссектриса этого угла делит сторону параллелограмма на отрезки 14 см и 9 см, считая от вершины тупого угла. Найдите площадь параллелограмма
Биссектриса этого угла делит сторону параллелограмма на отрезки 14 см и 9 см, считая от вершины тупого угла. Найдите площадь параллелограмма 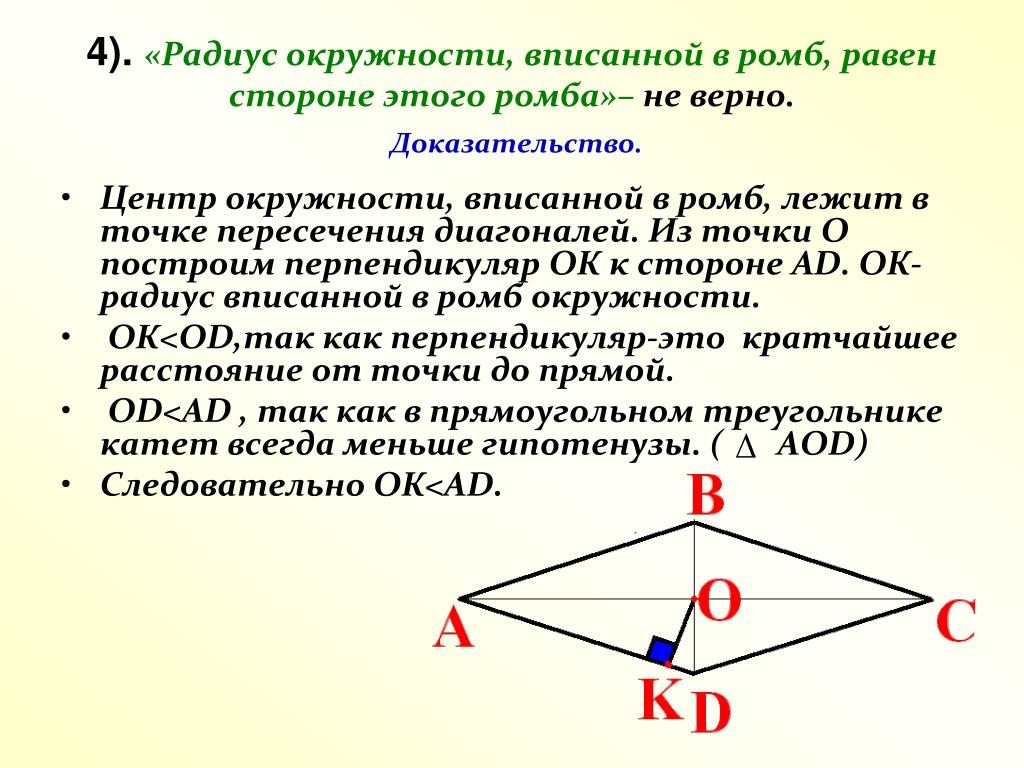 Найдите площадь параллелограмма
Найдите площадь параллелограмма 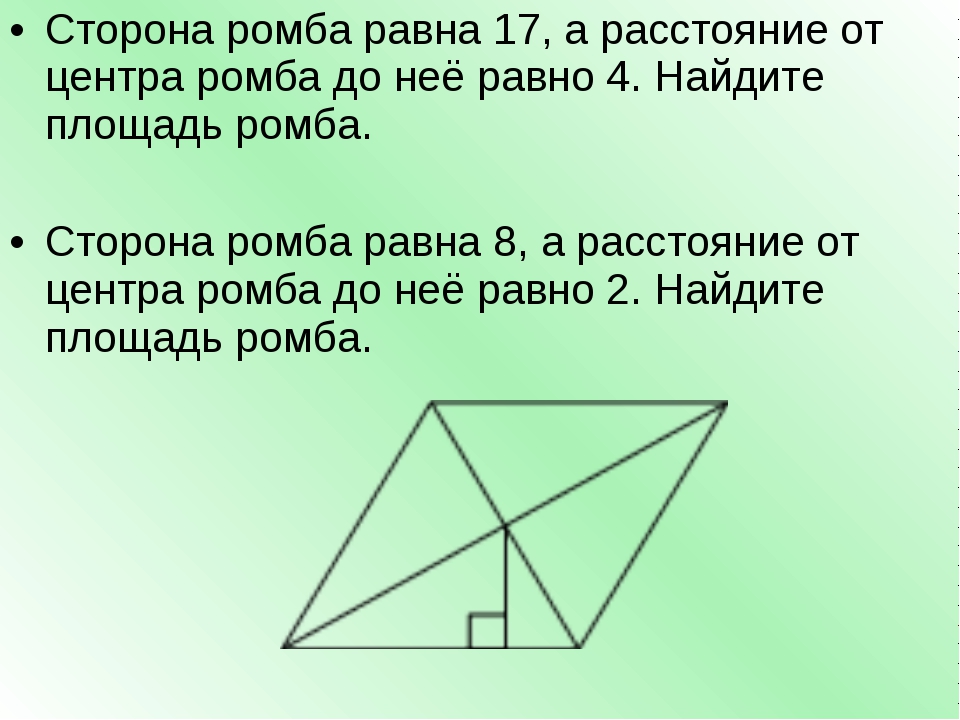 Найдите площадь ромба.
Найдите площадь ромба. 


Leave A Comment