Сторона ромба равна 5 а одна из его диагоналей равна 6 площадь ромба: Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба

Тест по геометрии. 8 класс. Обобщение темы «Площадь». Вариант 1

ТЕСТ ПО ГЕОМЕТРИИ

8 КЛАСС

ОБОБЩЕНИЕ ТЕМЫ «ПЛОЩАДЬ»

ВАРИАНТ 1

  А1. Сторона ромба равна 5 см, а одна из его диагоналей — 6 см. Чему равна площадь ромба?

  1) 30 см²

  2) 24 см²

  3) 15 см²

  4) 12 см²

  Ответ: 2.

  А2. Биссектриса угла А прямоугольника ABCD пересекает сторону ВС в точке Е так, что ВЕ = 4,5 см, СЕ = 5,5 см. Чему равна площадь прямоугольника?

  1) 55 см²

  2) 100 см²

  3) 110 см²

  4) 45 см²

  Ответ: 4.

  А3. Чему равна площадь ромба со стороной 8 см и углом, равным 60°?

  1) 32 см²

  2) 32√3 см²

  3) 38 см²

  4) 16√3 см²

  Ответ: 2.

  А4. Чему равна площадь прямоугольного треугольника с гипотенузой 26 см, один из катетов которого равен 24 см?

  1) 120 см²

  2) 60 см²

  3) 312 см²

  4) 240 см²

  Ответ: 1.

  А5. Одна из сторон треугольника равна 16 см, а высота, проведенная к ней, — 9 см. Чему равна высота, проведенная к стороне треугольника, равной 24 см?

  1) 5 см

  2) 12 см

  3) 13 см

  4) 6 см

  Ответ: 4.

  А6. Площадь квадрата равна 48 см². Чему равен периметр данного квадрата?

  1) 12√3 см

  2) 8√3 см

  3) 16√3 см

  4) 144 см

  Ответ: 3.

  А7. Площадь ромба равна 36 см², а одна из его диагоналей в два раза меньше другой. Чему равна сторона ромба?

  1) 3 см

  2) 3√5 см

  3) 3√3 см

  4) 3√2 см

  Ответ: 2.

  В1. В трапеции ABCD угол А = 60°, угол D = 45°, основание ВС равно 3 см, BF и СЕ — высоты трапеции, ED = 4 см. Найдите площадь трапеции.

  Ответ: S_ABCD = 4(5 + 2√3/3)см².

  В2. В треугольнике АВС биссектриса AD равна 7 см, АВ = 6 см, АС = 8 см. Найдите S_ABD : S_ACD.

  Ответ: S_ABD : S_ACD = 3 : 4.

  В3. В трапеции ABCD основания ВС и AD равны 8 см и 12 см, диагональ АС равна 40 см и пересекает диагональ BD в точке О. Найдите разность АО и СО.

  Ответ: 8 см.

  С1. В параллелограмме ABCD диагональ BD перпендикулярна стороне АВ, один из углов параллелограмма равен 120°, AD = 12 см, О — точка пересечения диагоналей. Найдите диагонали параллелограмма и площадь треугольника CDO.

  Ответ: АС = 6√7; BD = 6√3 см; S_CDO = 9√3 см².

  С2. В прямоугольной трапеции ABCD меньшее основание равно меньшей боковой стороне. Диагональ, проведенная из вершины тупого угла, перпендикулярна большей боковой стороне, равной 8√2 см. Найдите периметр и площадь трапеции.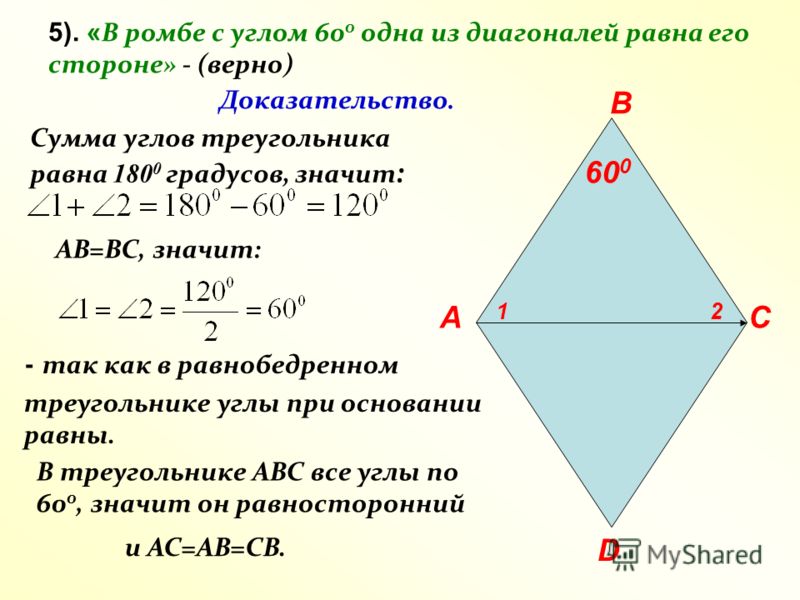

  Ответ: P_ABCD = 8(4 + √2) см; S = 96 см².

Геометрия для 8 класса — тест с ответами

«По геометрии проверить знания учеников по пройденной теме можно с помощью тестов. На этой странице представлен тест по теме геометрия для 8 класса. Правильные варианты ответов выделены символом [+]. Обращаем ваше внимание что на решение теста отводится всего 20-30 минут, поэтому вы должны поторопиться, чтобы успеть выполнить задание полностью.

Площадь прямоугольника АВСD равна 15. Необходимо найти сторону ВС прямоугольника, если известно, что АВ = 5:
[-] а) 5
[+] б) 3
[-] в) 10

Что из представленного называется квадратом:
[+] а) ромб, у которого все углы прямые
[-] б) прямоугольник, у которого диагонали равны
[-] в) параллелограмм, у которого все углы прямые

В ромбе АВСD проведена диагональ АС. Необходимо найти угол АВС, если известно, что угол АСD равен 35°:
[-] а) 150°
[-] б) 75°
[+] в) 110°

Выберите правильное утверждение:
[+] а) Если противоположные стороны четырехугольника попарно равны, то он параллелограмм
[-] б) Диагонали прямоугольника являются биссектрисами его углов
[-] в) Если диагонали четырехугольника перпендикулярны, то он ромб

Сторона ромба равна 5 , а одна из его диагоналей равна 6.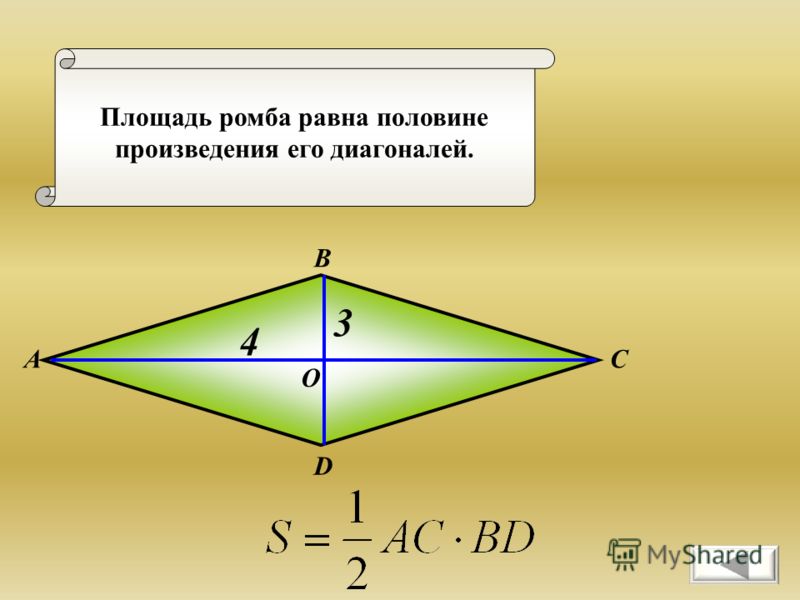 Чему равна площадь ромба:
[-] а) 18
[-] б) 26
[+] в) 24

Четырёхугольник будет являться ромбом, если его:
[-] а) диагонали точкой пересечения делятся пополам
[+] б) диагонали перпендикулярны и точкой пересечения делятся пополам
[-] в) диагонали перпендикулярны

Чему равна площадь квадрата со стороной 5:
[-] а) 50
[-] б) 30
[+] в) 25

Прямоугольником называется:
[+] а) параллелограмм, у которого все углы прямые
[-] б) четырехугольник, у которого противолежащие стороны равны
[-] в) параллелограмм, у которого все стороны равны

Квадрат вписан в окружность диаметра 8. Чему равен периметр квадрата:
[-] а) 32
[-] б) 18
[-] в) 16

Биссектриса острого угла А параллелограмма ABCD пересекает сторону ВС в точке М, которая делит ВС на два отрезка 8 см и 12 см. Прямая АМ пересекает продолжение стороны CD в точке F. Необходимо найти длину отрезка DF:
[-] а) 40
[-] б) 16
[+] в) 20

Угол между высотами ромба ABCD, опущенными из вершины В, равен 123°. Необходимо найти острый угол ромба:
[+] а) 57°
[-] б) 67°
[-] в) 23°

Трапеция называется равнобедренной в этом случае:
[-] а) если две стороны равны
[+] б) если боковые стороны равны
[-] в) если основания параллельны и равны

Периметр ромба ABCD равен 40, периметр треугольника ABD равен 32. Необходимо найти периметр треугольника АВС:
[+] а) 36
[-] б) 32
[-] в) 26

В треугольнике АВС, АВ = 12, АС = 16, ВС = 10 вписана окружность, касающаяся стороны АС в точке В1. Необходимо найти АВ1:
[-] а) 6
[-] б) 12
[+] в) 9

Выберите правильное утверждение:
[-] а) Любые две прямые имеют ровно одну общую точку
[+] б) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны
[-] в) Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны

Углы при основании трапеции равны 710 и 340.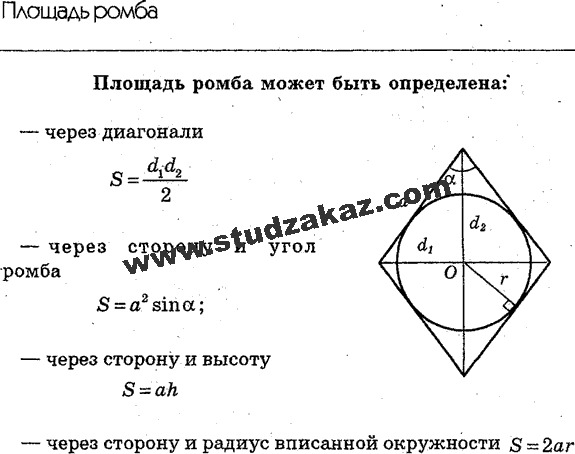 Чему равны остальные углы трапеции:
[-] а) 560 и 190
[-] б) 340 и 710
[+] в) 1090 и 1460

Выберите правильное утверждение:
[+] а) Отношение площадей подобных треугольников равно квадрату коэффициента подобия
[-] б) Диагонали параллелограмма перпендикулярны
[-] в) Если дуга окружности составляет 800, то центральный угол, опирающийся на эту дугу, равен 400

Чему равна сумма углов выпуклого четырехугольника:
[-] а) 360 n
[+] б) 180 (n — 2)
[-] в) 180 n

Четырёхугольник будет являться параллелограммом, если его:
[+] а) диагонали пересекаются и точкой пересечения делятся пополам
[-] б) все стороны параллельны
[-] в) две пары равных сторон

Периметр прямоугольника равен 18 см, а она из его сторон на 1 см больше другой. Площадь прямоугольника равна:
[-] а) 16 кв. см
[-] б) 72 кв. см
[+] в) 20 кв. см

Площадь квадрата равна 36 кв.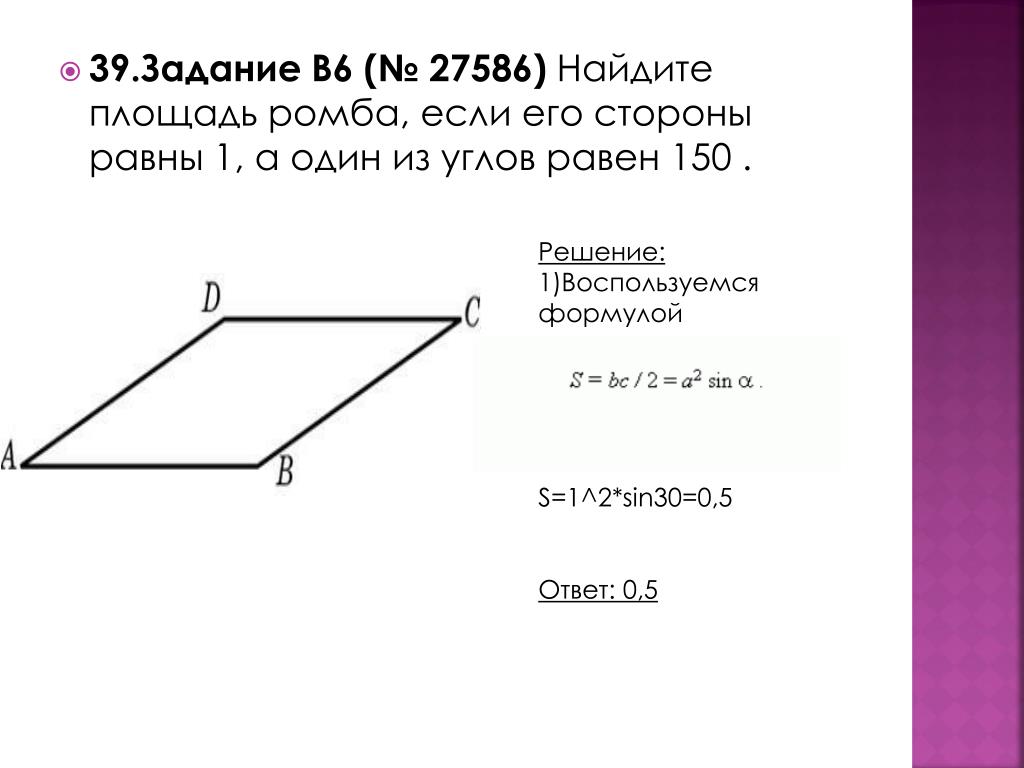 см. Его периметр равен:
[-] а) 36 см
[+] б) 24 см
[-] в) 12 см

В прямоугольнике ABCD сторона AB равна 12 см. Расстояние от точки пересечения диагоналей до этой стороны равно 8 см. Необходимо найти площадь треугольника ABC:
[+] а) 96 кв. см
[-] б) 24 кв. см
[-] в) 48 кв. см

Периметр прямоугольника равен 40 см., а одна из его сторон равна 4 см. Прямоугольник имеет такую же площадь, что и квадрат. Периметр квадрата равен:
[-] а) 40 см
[+] б) 32 см
[-] в) 16 см

В прямоугольном треугольнике АВС угол С = 90°, АС = 12, sin А = 0,8. Необходимо найти ВС, высоту СС1 и длину отрезка ВС1:
[+] а) ВС = 16; СС1 = 9,6; ВС1 = 12,8
[-] б) ВС = 24; СС1 = 9,6; ВС1 = 12,8
[-] в) ВС = 18; СС1 = 9,6; ВС1 = 12,8

В треугольнике АВС угол В = 60°, угол А = 50°. Окружность, проходящая через точки В и С вторично пересекает стороны АС и АВ в точках K и L соответственно. Необходимо определить угол ALK:
[-] а) 60°
[-] б) 80°
[+] в) 70°

Точки А, В, С и D в указанной последовательности лежат на окружности радиуса 10 и делят её в отношении 2 : 3 : 4 : 3. Необходимо найти длину отрезка, соединяющего середины сторон АВ и AD:
[-] а) 2,7(√2 + √6)
[+] б) 2,5(√2 + √6)
[-] в) 3,5(√2 + √6)

Основание Н высоты прямоугольного треугольника делит его гипотенузу АВ на отрезки, отношение которых 1:4. Необходимо найти площадь этого треугольника, если АВ=25:
[+] а) 125
[-] б) 100
[-] в) 75

В трапеции АВСD – АВ и СD параллельны. Отношение оснований равно 2:3 и диагонали пересекаются в точке О. Необходимо найти площадь треугольника СОD, если площадь треугольника АОD равна 6:
[-] а) 24
[-] б) 18
[+] в) 9

В равнобедренной трапеции большее основание равно 25, а боковая сторона 15 и диагональ перпендикулярна боковой стороне. Необходимо найти меньшее основание трапеции:
[-] а) 11
[+] б) 7
[-] в) 15

Прямая, параллельная стороне АВ треугольника АВС, пересекает его стороны ВС и АС в точках K и L соответственно. Известно, ВК=8, KL=8, АВ=12. Необходимо найти чему равно ВС:
[-] а) 16
[+] б) 8
[-] в) 24″

Одна из диагоналей ромба площадью 24 кв м равна 6 м, какова длина его другой диагонали?

Ромб представляет собой ромбовидный четырехугольник с равными сторонами, но неравными углами наклона между этими двумя сторонами. У него четыре стороны одинаковой длины, так как это четырехугольник. Можно сказать, что ромб — это особый тип параллелограмма, если все стороны параллелограмма равны, он станет фигурой, известной как ромб.

Используя площадь диагоналей ромба:  = (d ₁ × d ₂ )/2 кв.

Где d ₁ — длина диагонали 1 и d ₂ — длина диагонали 2.

Одна из диагоналей ромба площадью 24 м² равна 6 м, какова длина другой диагональ?

Решение:  

Чтобы найти длину диагонали d _2,

Площадь ромба = 24 м²

Длина диагонали d ₁ = 6 м

Следовательно, площадь ромба = (D ₁ × D ₂ ) / 2 кв. 2

d ₂ = 24/3

d ₂ = 8 м

Таким образом, длина диагонали d ₂ равна 8 м.

Примеры вопросов 

Вопрос 1. Вычислите площадь ромба (по диагонали), диагонали которого равны 5 см и 4 см.

Решение:

, дано,

Длина диагонали 1 (D ₁ ) = 5 см

Длина диагонали 2 (D ₂ ) = 4 см

Теперь

область из рисома Rhombus. (A) = 1/2 D ₁ × D ₂

= 1/2 × 5 × 4

= 1/2 × 20

= 10 см ²

Вопрос 2: Найти. диагональ ромба, если его площадь 100 см ² и длина наибольшей диагонали равна 10 см.

Решение:  

Дано: площадь ромба = 100 см ² и диагональ d ₁ = 10 см.

Отсюда, Площадь ромба по формуле, A = (d ₁ × d ₂ )/2 квадратных единиц, получаем

100 = (10 × d ₂ )/2

100 = 10 100 ₂ / 2

Или 5d ₂ = 100

d ₂ = 20

Следовательно, длина другой диагонали d ₂ равна 20 см.

Вопрос 3: Вычислите площадь ромба, диагонали которого равны 15 см и 4 см?

Решение:

Дано: Диагональный D ₁ = 15 см

Диагональный D ₂ = 4 см

Область ромба, A = (D ₁ × D ₂ )). / 2

= (15 × 4) / 2

= 60/2

= 30 см ²

Следовательно, площадь ромба равна 30 см ² .

Вопрос 4: Найдите площадь ромба, сторона которого равна 4 см, а один из внутренних углов равен 30°.

Решение:

. ² × sin(30°)

= 16 × (1/2)

= 8 см ²

Значит, площадь ромба равна 8 см ² .

Вопрос 5: Найдите периметр ромба, сторона которого равна 6 см.

Решение:

Указанная сторона S = 6 см

Следовательно, периметр ромба = 4 × S

SO, периметр (P) = 4 × 6 CM

= 24 см

11110003

= 24 см

9000 2 11111110003 = 24 см

9000 2 111111103 = 24 см

9000 2 111113

= 24 см

9000 2 11111. 6: Одна из диагоналей ромба площадью 30 кв м равна 6 м, какова длина его другой диагонали?

Решение:

Чтобы найти длину диагонали d ₂ ,

Площадь ромба = 30 кв.м )/2 кв. Значит, длина диагонали d ₂ равна 10 м.

Вопрос 7: Найдите высоту ромба, площадь которого 200 м², а периметр 100 м?

Решение:

Дан периметр ромба = 120 м

Значит, сторона ромба = 100/4

= 25 м

Следовательно, высота 200 = 25 × h

h = 200/25

h = 8

Следовательно, высота ромба равна 8 м.

Задача по математике: Диагонали — вопрос № 3816, контуры, корень квадратный

Диагональ ромба имеет длину 20 см. Найдите длину другой диагонали, если ее сторона равна 26 см.

Правильный ответ:

Вы нашли ошибку или неточность? Не стесняйтесь

написать нам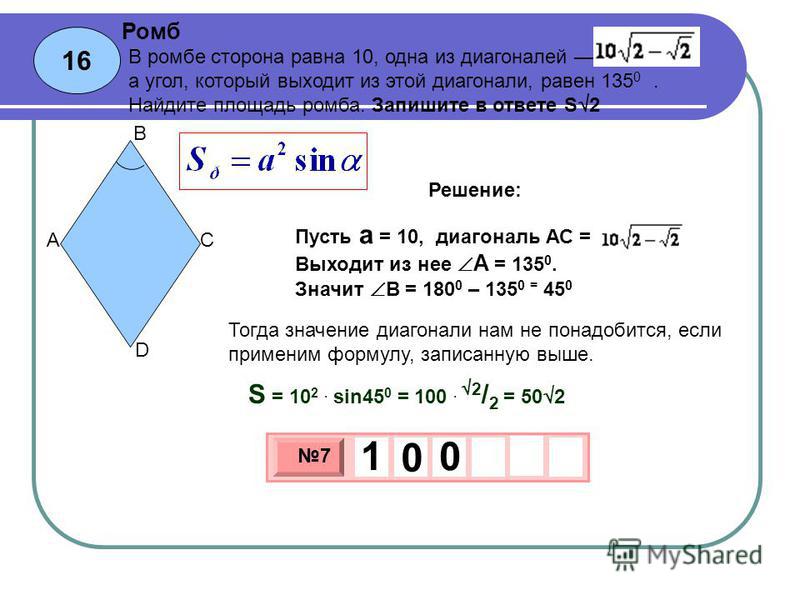

. Спасибо!

Советы по использованию связанных онлайн-калькуляторов

См. также наш калькулятор прямоугольного треугольника.

Вам необходимо знать следующие знания для решения этой задачи по математике:

• Арифметика
• квадратный корень
• Planimetrics
• .0326
• Rhombus
• Diagonal

Оценка слова Проблема:

• Практика для 13 -летнего возраста
• . задача: видео1   видео2   видео3
  • Алмаз
    Сторона ромба 17 см, а одна диагональ 22 см. Вычислите его площадь.
  • Ромб
    Вычислите длину диагонали AC ромба ABCD, если его периметр равен 84 дм, а другая диагональ BD имеет длину 20 дм.
  • Алмаз
    Алмаз имеет площадь S = 120 см ² , а отношение длин его диагоналей равно e:f = 5:12. Найдите длину стороны и высоту этого ромба.
  • Диагонали ромба
    Какой длины диагонали e, f в ромбе, если длина его стороны 5 см, а площадь 20 см²?
  • Диагонали ромба 2
    Одна диагональ ромба больше другой на 4 см. Если площадь ромба 96 см ² , найдите сторону ромба.
  • Диагонали
    Вычислите длину диагоналей ромба, если длина его стороны равна 5, а один из внутренних углов равен 80°.
  • Ромб
    Если мы увеличим сторону ромба на 2,4 см, его периметр составит 20 см. Какой длины была сторона ромба?
  • Ромб
    Найдите длину каждой стороны ромба, если его периметр равен 89 см.
  • Диагонали ромба
    Одна из диагоналей ромба вдвое больше другой. Найдите площадь ромба, если сумма длин диагоналей равна 24.
  • Алмаз
    Найдите сторону ромба, если его площадь S = 490 см² и одна диагональ u ₂ = 39 см.
  • Окружность 4712
    Если увеличить сторону ромба на 4 см, его окружность будет 20 см. Какой длины была сторона исходного алмаза?
  • Ромб
    Найдите длину другой диагонали и площадь ромба. Периметр ромба равен 40 см, а длина одной из диагоналей 10 см.
  • Ромб
    Один угол ромба равен 136°, а его меньшая диагональ равна 8 см.