Квадрат, его свойства и признаки.
Квадрат, его свойства и признаки.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Для квадрата можно ввести несколько определений. Самое ёмкое мы уже привели. Но можно определить квадрат следующим образом:
а) Квадратом называется четырёхугольник, у которого все стороны равны, а углы прямые.
б) Квадратом называется параллелограмм, у которого все стороны и углы равны.
в) Квадратом называется ромб, у которого все углы прямые.
Поскольку квадрат является и параллелограммом, и прямоугольником, и ромбом, то он обладает теми же свойствами, что и все перечисленные четырёхугольники.
1. У
квадрата диагонали пересекаются и точкой пересечения делятся пополам.
2. У квадрата диагонали взаимно перпендикулярны.
3. У квадрата диагонали являются биссектрисами его углов.
4. У квадрата диагонали равны.
5. У квадрата стороны являются высотами.
6. Каждая диагональ квадрата делит его на равные прямоугольные треугольники.
Теперь определим признаки квадрата.
ТЕОРЕМА (I признак). Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
Дано: – прямоугольник
Доказать: – квадрат.
Доказательство.
Так как – прямоугольник, то у него
противолежащие стороны равны.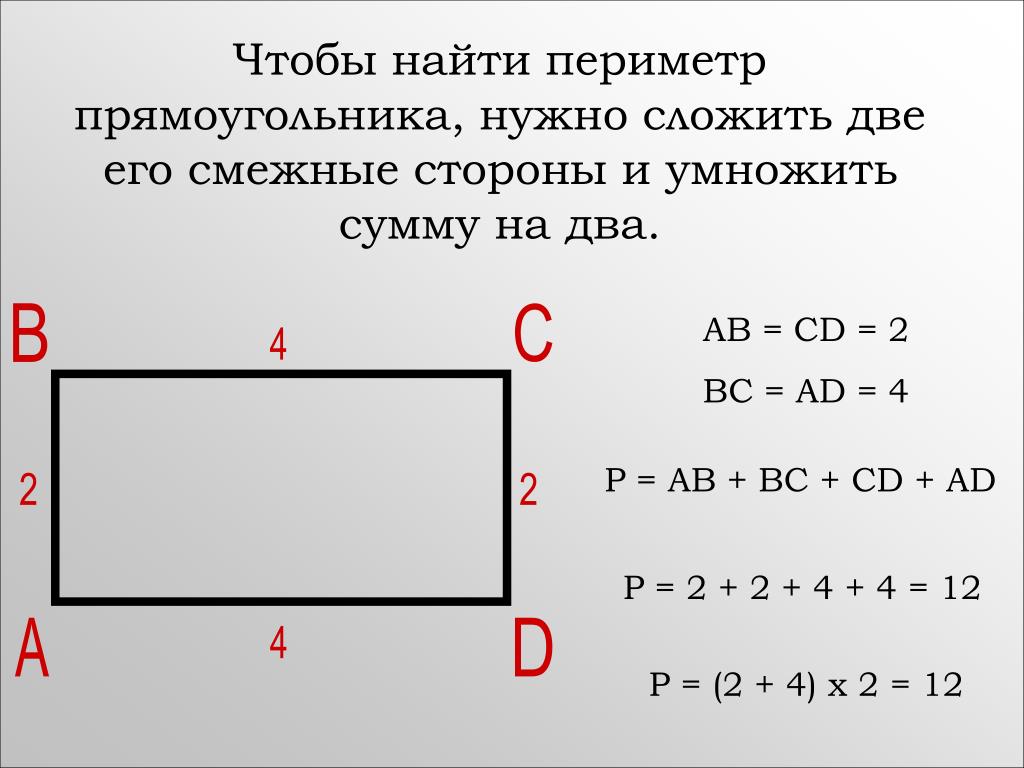
– квадрат (по определению), ч.т.д.
ТЕОРЕМА (II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
Доказать: – квадрат.
Доказательство.
Рассмотрим .
по свойству диагоналей прямоугольника, значит, – медиана (по опред-нию).
– высота , т.к. . Значит, в является и медианой и высотой, поэтому этот треугольник является равнобедренным (по признаку равнобедренного треугольника), т.е. . Согласно I признаку квадрата, прямоугольник является квадратом, ч.т.д.
ТЕОРЕМА (III признак). Если в прямоугольнике одна
из диагоналей является биссектрисой его угла, то такой прямоугольник является
квадратом.
Если в прямоугольнике одна
из диагоналей является биссектрисой его угла, то такой прямоугольник является
квадратом.
Дано: – прямоугольник
– диагональ
– биссектриса
Доказать: – квадрат.
Доказательство.
Так как – биссектриса
по свойству внутренних накрест лежащих углов при параллельных прямых. Значит, , следовательно – равнобедренный, и . По I признаку квадрата, прямоугольник является квадратом, ч.т.д.
ТЕОРЕМА (IV признак). Если в ромбе диагонали равны, то этот ромб является квадратом.
Дано: – ромб
— диагонали
Доказать: – квадрат.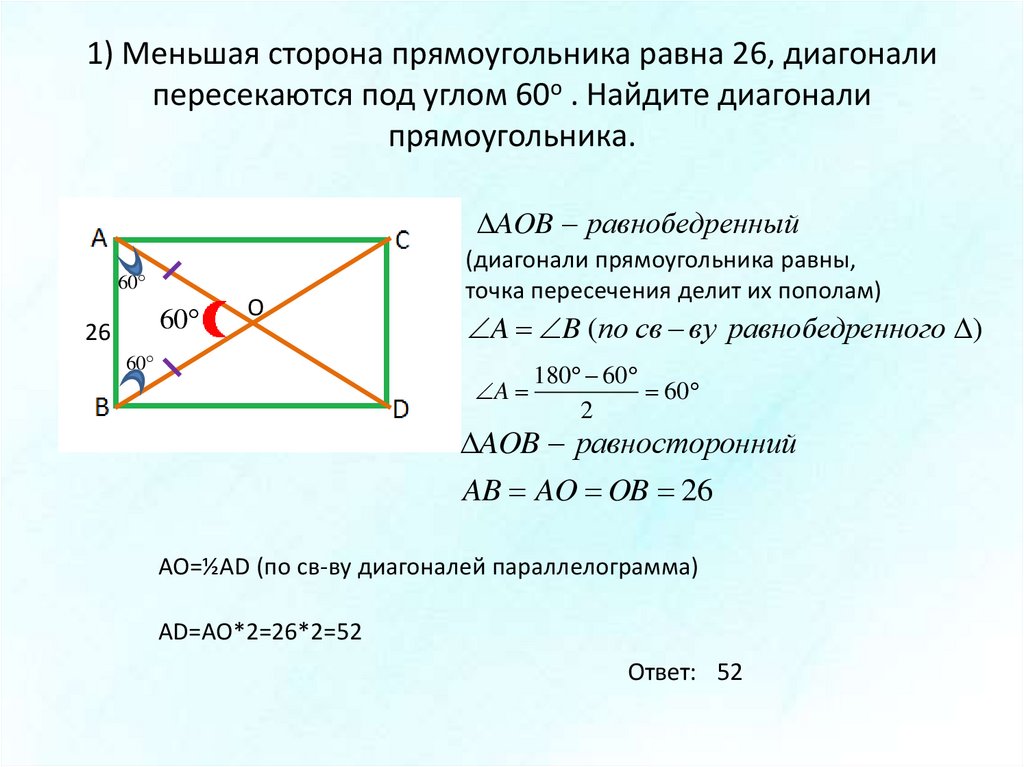
Доказательство.
Рассмотрим и .
по III признаку равенства треугольников. Значит, все соответствующие углы у этих треугольников равны, т.е. . Эти углы являются внутренними односторонними при параллельных прямых и , следовательно, их сумма равна , т.е. , а, значит, и . Так как в ромбе противолежащие углы равны, то и все остальные углы также равны по . Значит, такой ромб является квадратом, ч.т.д.
ТЕОРЕМА (V признак). Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
Дано: – параллелограмм
Доказать: – квадрат.
Доказательство.
Так как , то по II признаку ромба, параллелограмм является ромбом.
Так как , то по IV признаку квадрата, ромб является квадратом, ч.т.д.
ТЕОРЕМА (VI признак).
Дано: – четырёхугольник
Доказать: – квадрат.
Доказательство.
1. Так как , то четырёхугольник является параллелограммом (по признаку параллелограмма).
2. Так как , то параллелограмм является квадратом (по
 т.д.
т.д.
ТЕОРЕМА (VII признак). Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
Дано: – четырёхугольник
Доказать: – квадрат.
Доказательство.
2. Так как , то ромб, который по определению является параллелограммом, является прямоугольником (по III признаку прямоугольника), значит, все углы в этом четырёхугольнике прямые.
3. Итак, прямоугольник , у которого все стороны
равны, является квадратом (по определению), ч. т.д.
т.д.
Итак, признаки квадрата:
1. Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
2. Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
3. Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
4. Если в ромбе диагонали равны, то этот ромб является квадратом.
5. Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
6. Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
7. Если в четырёхугольнике все стороны равны и среди внутренних
углов есть один прямой угол, то такой четырёхугольник является квадратом.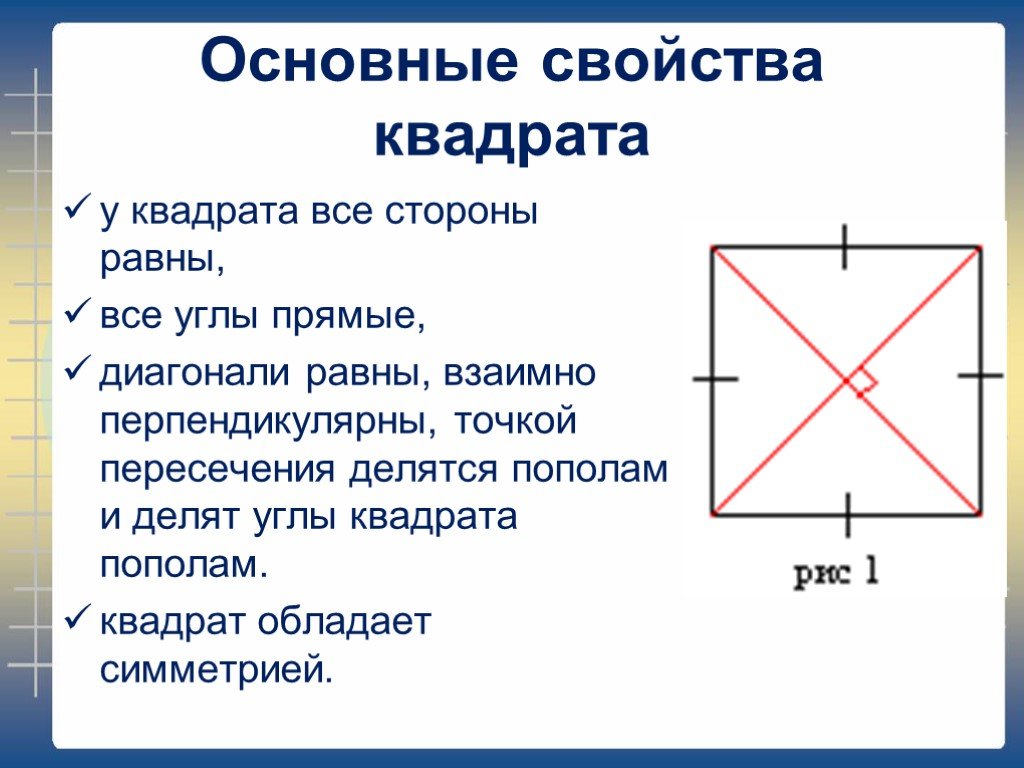
1. Периметр квадрата равен см. Найдите сторону квадрата .
2.
На рисунке четырёхугольник – квадрат, . Докажите, что выпуклый четырёхугольник также является квадратом.
3.
На рисунке четырёхугольник – прямоугольник, . Докажите, что выпуклый четырёхугольник является квадратом.
4. В треугольнике . На сторонах и взяты точки и , а на стороне – точки и так, что четырёхугольник является квадратом, . Найдите .
5. В треугольнике . На сторонах отмечены точки соответственно так, что четырёхугольник является квадратом, . Найдите .
6. На
сторонах и квадрата отмечены точки и соответственно, . Отрезки и пересекаются в точке . Найдите .
Отрезки и пересекаются в точке . Найдите .
7. На сторонах квадрата отмечены соответственно точки . Сравните отрезки и .
8. На катетах и прямоугольного треугольника построены квадраты и . Докажите, что сумма расстояний от точек и до прямой равна .
9. На катетах и прямоугольного треугольника построены квадраты и . Прямые и пересекаются в точке . Докажите, что .
10. Длина проекции одной из сторон квадрата на его диагональ равна . Найдите длину диагонали.
11.
В четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что отрезки, соединяющие середины противоположных сторон, равны.
12. Дан квадрат . Докажите, что – квадрат.
13. Дан квадрат . Докажите, что – ромб.
14. Дан
квадрат . На стороне взята точка такая, что . Докажите, что точки – вершины равнобедренного
треугольника.
Докажите, что точки – вершины равнобедренного
треугольника.
15. Дан квадрат . Точки – середины его сторон соответственно. Докажите, что .
16. Дан квадрат . Точки и делят его стороны и так, что . Докажите, что .
17.
Квадраты и имеют общую вершину . Докажите, что медиана треугольника перпендикулярна отрезку .
18. Внутри квадрата взята точка так, что . Докажите, что треугольник равносторонний.
19.
На рисунке – квадрат, точка принадлежит , точка принадлежит , точка принадлежит , прямые и пересекаются в точке . Докажите, что .
20. В
равнобедренный прямоугольный треугольник, каждый катет которого равен см, вписан квадрат, имеющий с
ним один общий угол.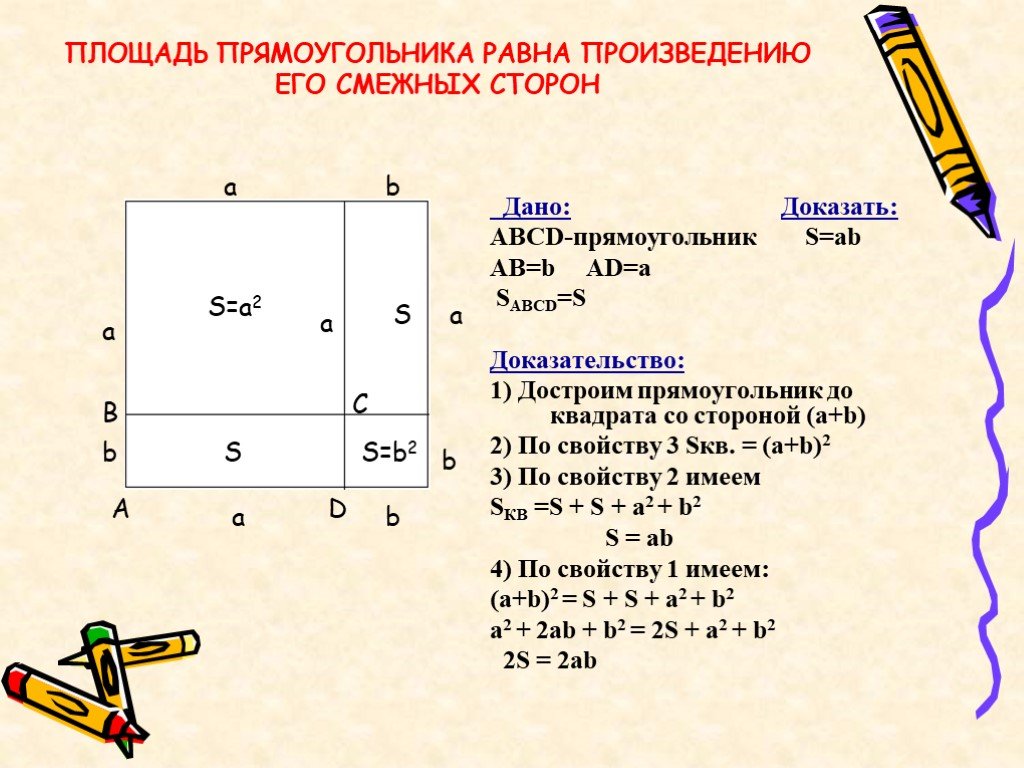 Найдите периметр квадрата.
Найдите периметр квадрата.
21. В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Определите сторону квадрата, если известно, что гипотенуза равна 30 дм.
22. В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них втрое больше другой и что диагональ квадрата равна дм.
23. В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна см.
24. Точка расположена во внутренней
области квадрата так, что расстояния от неё до
сторон и пропорциональны
соответственно числам и , а расстояние от до прямой равно см. Найдите периметр этого
квадрата.
Найдите периметр этого
квадрата.
25. Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно м. Найдите периметр этого квадрата.
26. Точка лежит на стороне квадрата . Высоты треугольников и , проведённые из точки , равны соответственно и . Найдите произведение длин диагоналей этого квадрата.
27. Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно м. Найдите периметр этого квадрата.
28.
Точка лежит на стороне квадрата . Высоты треугольников и , проведённые из точки , равны соответственно и .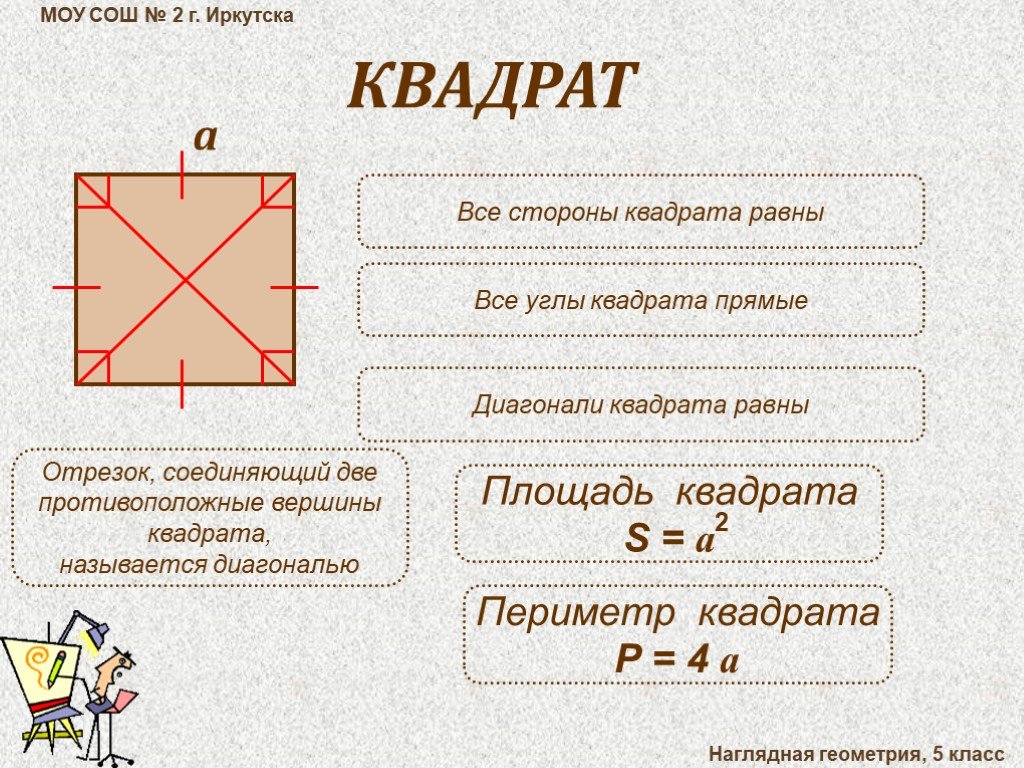 Найдите произведение длин
диагоналей этого квадрата.
Найдите произведение длин
диагоналей этого квадрата.
29. На сторонах и квадрата отмечены точки и соответственно так, что . Определите взаимное расположение прямых и .
30.
В равнобедренный прямоугольный треугольник вписан квадрат , имеющий с ним общий угол . Найдите периметр квадрата, если катет треугольника равен см.
31.
Внутри квадрата отмечена такая точка , что треугольник равносторонний. Найдите угол .
32. В равнобедренный прямоугольный треугольник вписан квадрат , имеющий с ним общий прямой угол. Найдите катет треугольника, если периметр квадрата равен см.
33.
Внутри квадрата отмечена такая точка , что треугольник равносторонний. Найдите угол .
Найдите угол .
34. Через вершины квадрата проведены прямые, параллельные его диагоналям. Определите вид образованного ими четырёхугольника и вычислите его периметр, если диагональ квадрата равна см.
35. Через точку – точку пересечения диагоналей квадрата проведена прямая, параллельная стороне и пересекающая стороны и в точках и соответственно. Найдите периметр квадрата, если известно, что .
36.
Найдите периметр квадрата по данным на рисунке.
Прямоугольник, ромб и квадрат – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
Прямоугольник – параллелограмм, у которого все углы прямые.
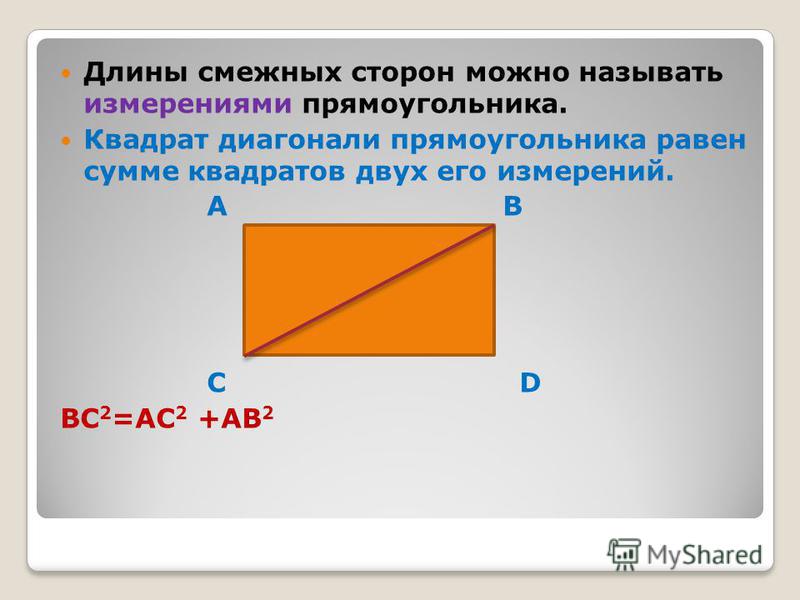
Диагональю прямоугольника называется любой отрезок, соединяющий две вершины противоположных углов прямоугольника. Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
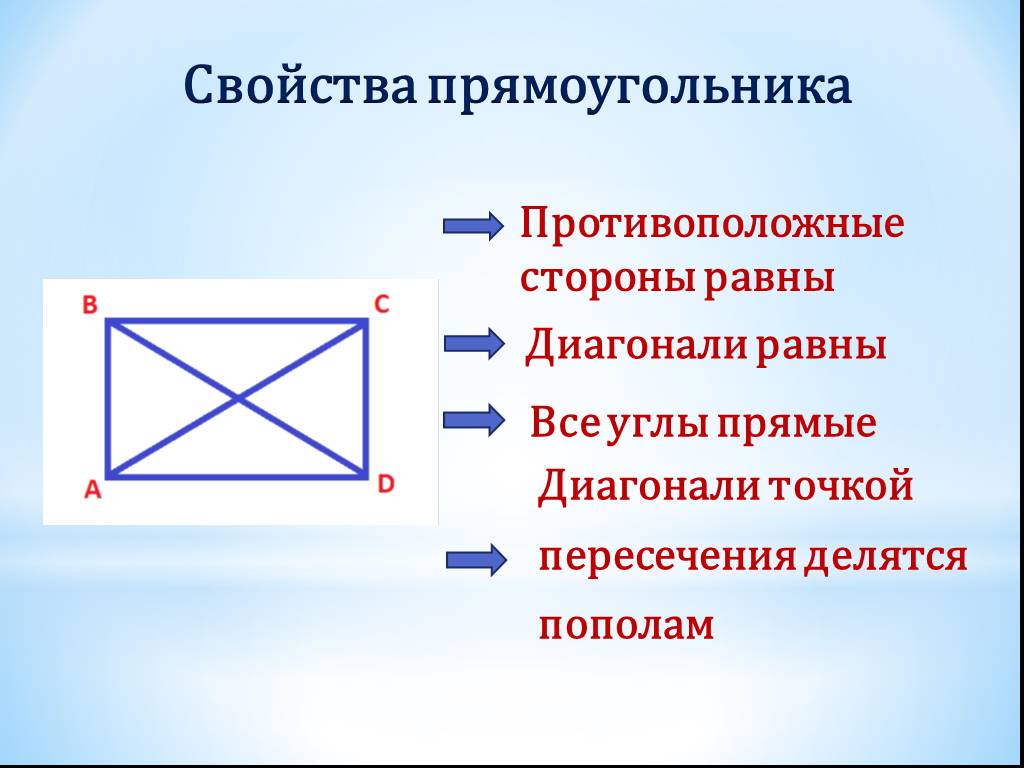
Свойства прямоугольника
- Противоположные стороны прямоугольника равны.
- Каждый угол прямоугольника равен 90°.
- Значит, противоположные углы равны и сумма углов, прилежащих к одной стороне, равна 180°.
- Диагонали прямоугольника точкой пересечения делятся пополам.
- Диагональ прямоугольника делит его на два равных прямоугольных треугольника.
- Накрест лежащие углы при диагонали равны.
- Диагонали прямоугольника равны.
- Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности.
- Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.

Признаки прямоугольника
- Если три угла четырехугольника прямые, то этот четырехугольник является прямоугольником.
- Если один угол параллелограмма прямой, то этот параллелограмм является прямоугольником.
- Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником.
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата
Все свойства параллелограмма, ромба, прямоугольника верны и для квадрата.
- Все четыре стороны квадрата имеют одинаковую длину, то есть они равны.
- Противоположные стороны квадрата параллельны.
- Сумма углов квадрата равна 360°.
- Диагонали квадрата имеют одинаковые длины.
- Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам.
- Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружностей.

- Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружностей.
- Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные, и прямоугольные.
Признаки квадрата
- Если две смежные стороны прямоугольника равны, то этот прямоугольник является квадратом.
- Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом.
Формулы определения длины диагонали квадрата:
\(d=a\sqrt{2}; \ d=\sqrt{2S}; \ d=2R; \ d=2r\sqrt{2}\).
Ромбом называется параллелограмм, у которого все стороны равны. Если у ромба все углы прямые, тогда он называется квадратом.
Свойства ромба
- Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
- Противолежащие стороны равны.
- Противоположные углы равны.
 2}\).
2}\).Вопросы
Диагональ ромба равна его стороне. Найдите меньший угол ромба.
В параллелограмме \(ABCD\) сторона \(AB=7, AD=3,sinA=\frac67\). Найдите большую высоту параллелограмма.
Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна 10.
Диагональ квадрата равна \(2\sqrt{8}\) см. Найдите сторону квадрата.
Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.

Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Числовое значение площади прямоугольника принадлежит промежутку
Сообщить об ошибке
Обязательные
Математическая грамотность
Грамотность чтения
История Казахстана
Предметы по профилю
Биология
Химия
Английский язык
Французский язык
География
Немецкий язык
Информатика
Основы права
Русская литература
Математика
Физика
Русский язык
Всемирная история
Укажите предмет *
Скопируйте и вставьте вопрос задания *
Опишите подробнее найденную ошибку в задании *
Прикрепите скриншот
Объем файла не должен превышать 1МБ
Казахский
Русский
Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены.
 В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market
2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами
Разница между квадратом и прямоугольником
LearnPracticeDownload
Разница между квадратом и прямоугольником в том, что у квадрата все стороны равны, а у прямоугольника противоположные стороны равны. В геометрии есть много форм, таких как круги, треугольники, квадраты, прямоугольники, кубы, конусы, цилиндры и так далее. Среди них фигуры, имеющие четыре стороны, называются четырехугольниками. Квадраты и прямоугольники — самые распространенные формы, которые мы видим вокруг. На первый взгляд они кажутся довольно похожими, однако математически они разные.
 Другими словами, квадрат — это прямоугольник, у которого смежные стороны равны, а внутренние углы равны 90°.
Другими словами, квадрат — это прямоугольник, у которого смежные стороны равны, а внутренние углы равны 90°.1. Что такое квадрат и прямоугольник? 2. Свойства квадрата и прямоугольника 3. Разница между квадратом и прямоугольником 4. Почему квадрат называют прямоугольником? 5. Часто задаваемые вопросы о разнице между квадратом и прямоугольником Что такое квадрат и прямоугольник?
Хотя квадраты и прямоугольники являются четырехугольниками, существуют определенные свойства, которые их отличают.
Квадрат
Квадрат — это плоская двумерная фигура (2D-форма), имеющая четыре равные стороны, четыре внутренних прямых угла и четыре вершины.
Прямоугольник
Прямоугольник — это двумерная фигура, у которой противоположные стороны равны.
 У него четыре равных угла и четыре вершины. Все четыре угла прямоугольника равны 90°.
У него четыре равных угла и четыре вершины. Все четыре угла прямоугольника равны 90°.Свойства квадрата и прямоугольника
Важные свойства квадрата и прямоугольника приведены ниже. Обратите внимание на приведенный ниже рисунок, чтобы определить и различить эти два рисунка.
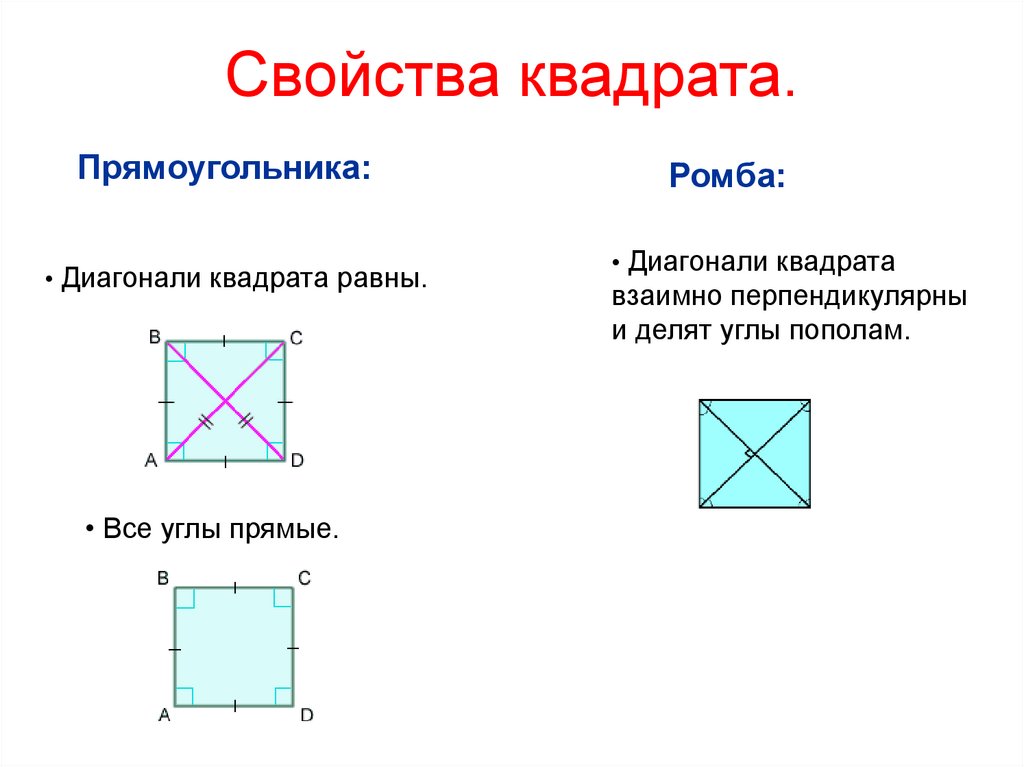
Свойства квадрата
- Все четыре стороны квадрата равны по длине.
- Все внутренние углы квадрата равны 90°.
- Противоположные стороны квадрата параллельны друг другу.
- Диагонали квадрата равны по длине и делят друг друга пополам.
Свойства прямоугольника
- Противоположные стороны прямоугольника равны и параллельны друг другу.
- Все внутренние углы прямоугольника равны 90°.
- Диагонали прямоугольника имеют одинаковую длину и делят друг друга пополам.
Разница между квадратом и прямоугольником
Важные различия между квадратом и прямоугольником перечислены в таблице ниже.

Квадрат против прямоугольника
Свойство Квадрат Прямоугольник Стороны У квадрата четыре равные стороны. В прямоугольнике противоположные стороны равны. Диагонали Диагонали квадрата делятся пополам под углом 90°. Диагонали прямоугольника пересекаются под разными углами. Один угол тупой, а другой острый угол. Зона Площадь квадрата измеряется по формуле: Площадь = Сторона × Сторона Площадь прямоугольника измеряется как произведение его длины на ширину. Площадь = длина × ширина Периметр Периметр квадрата вычисляется по формуле:
Периметр = 4 × Сторона
Периметр прямоугольника вычисляется по формуле:
Периметр = 2 (длина + ширина)
Длина диагонали Согласно теореме Пифагора (теорема Пифагора), длина диагонали квадрата равна произведению квадратного корня из 2 на сторону квадрата.

Длина диагонали = √(2 × сторона)
Согласно теореме Пифагора (теорема Пифагора), длина диагонали прямоугольника равна квадратному корню из суммы квадратов длины и ширины.
Длина диагонали = √(Длина 2 + Ширина 2 )
Почему квадрат называется прямоугольником?
Мы называем квадрат особым типом прямоугольника, потому что они оба имеют некоторые общие свойства, перечисленные ниже.
- У квадрата и прямоугольника внутренние углы равны 90°.
- Противоположные стороны обеих фигур равны и параллельны.
- Диагонали, делящие друг друга пополам, равны по длине.
Вот некоторые свойства, которые не относятся к прямоугольникам и встречаются только в квадратах.
- Все четыре стороны равны.
- Диагонали делят друг друга пополам под прямым углом.
☛Статьи по теме
- Твердые формы
- Геометрия
- Является ли квадрат прямоугольником?
- Свойства прямоугольника
Примеры отличия квадрата от прямоугольника
Пример 1: Запишите формулу, по которой находят:
а.
 ) Площадь квадрата
) Площадь квадратаб.) Площадь прямоугольника
Решение:
Формула, по которой находят :
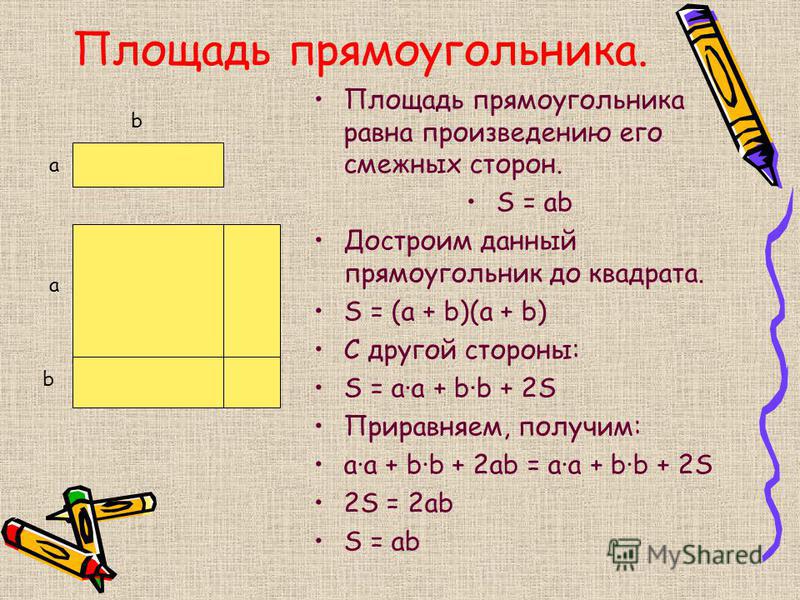
а.) Площадь квадрата: Площадь квадрата = сторона × сторона
б.) Площадь прямоугольника площадь прямоугольника = длина × ширина
Пример 2: Найдите периметр (i) квадрата со стороной 10 единиц и (ii) прямоугольника длиной 12 единиц и шириной 7 единиц.
Решение:
Периметр квадрата = (4 × сторона)
Сторона квадрата = 10 единиц
Следовательно, периметр = 4 × 10
= 40 единицПериметр прямоугольника = 2 (длина + ширина)
Длина = 12 единиц и ширина = 7 единиц
Следовательно, периметр = 2 (12 + 7)
= 38 единицПример 3: Укажите верно или неверно:
а.) Диагонали квадрата делятся пополам под углом 90°.
б.) Противоположные стороны прямоугольника равны и параллельны.

Решение:
а.) Верно, диагонали квадрата делятся пополам под углом 90°.
б.) Верно, что противоположные стороны прямоугольника равны и параллельны.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по квадратам и прямоугольникам? Решайте их мгновенно
Живые онлайн-уроки Куэмата оставляют много места для прояснения сомнений. Выберите дату и посетите бесплатное пробное занятие!
Запишитесь на бесплатный пробный урок
Практические вопросы о разнице между квадратом и прямоугольником
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о разнице между квадратом и прямоугольником
В чем разница между квадратом и прямоугольником?
Основные отличия квадрата от прямоугольника:
- У квадрата четыре равные стороны, а у прямоугольника противоположные стороны равны.
- Диагонали квадрата делятся пополам под углом 90°, а диагонали прямоугольника делятся пополам под разными углами.

В чем сходство между квадратом и прямоугольником?
Квадрат и прямоугольник имеют следующие сходства:
- Все четыре угла равны 90°.
- Диагонали равны по длине.
- Их противоположные стороны равны и параллельны.
Какое свойство квадрата отличается от свойства прямоугольника?
Свойство квадрата, отличающее его от прямоугольника, состоит в том, что у квадрата все четыре стороны равны и параллельны, тогда как у прямоугольника равны и параллельны только противоположные стороны.
Является ли квадрат ромбом?
Квадрат можно назвать ромбом, потому что он выполняет свойства ромба, который имеет четыре равные стороны, а его противоположные стороны параллельны друг другу.
Является ли квадрат прямоугольником?
Да, квадрат — это прямоугольник, потому что он обладает всеми свойствами прямоугольника. Его противоположные стороны параллельны и равны, а внутренние углы равны 90 90 167 ∘ 90 168 каждый.
 Следовательно, квадрат можно назвать особым типом прямоугольника.
Следовательно, квадрат можно назвать особым типом прямоугольника.Может ли прямоугольник быть квадратом?
Поскольку у прямоугольника все четыре стороны не равны, он не может быть квадратом.
Какие важные свойства подтверждают, что квадрат является прямоугольником?
Перечисленные ниже свойства подтверждают, что квадрат является прямоугольником:
- У квадрата все внутренние углы равны 90°.
- Противоположные стороны квадрата равны и параллельны.
- Диагонали делятся пополам и имеют одинаковую длину.
Загрузить БЕСПЛАТНЫЕ учебные материалы
Квадраты и прямоугольники. Рабочие листы
Математические рабочие листы и
наглядный учебный планБазовая геометрия. Четырехугольники | Шмуп
Четырехугольники
Четырехугольники представляют собой четырехсторонние фигуры. Наиболее распространены квадраты и прямоугольники, но есть и множество других. Как и треугольники, они классифицируются по углам и сторонам.

В этом разделе мы рассмотрим шесть обычных четырехугольников, которые вы постоянно видите.
Параллелограмм- Параллелограммы — это все четырехугольники, у которых противоположные стороны параллельны.
Все это параллелограммы:
У параллелограммов есть много особых свойств. Вот те, которые вам, вероятно, нужно знать.
Противоположные стороны параллельны. Противоположные углы равны. Противоположные стороны равны. Смежные углы являются дополнительными. - Все четырехсторонние фигуры с двумя наборами пробелов и четырьмя янгами по имени. Вот два разных прямоугольника:
Теперь давайте посмотрим на все свойства прямоугольников.
Ромб
- У ромба два набора параллельных сторон, и все стороны должны быть конгруэнтны. Это ромбы:
Вот свойства ромба:
Квадрат- Каждый параллелограмм с четырьмя конгруэнтными сторонами и четырьмя углами по 90° является квадратом.
Это свойства квадратов:
Трапеция- Трапеции имеют только один набор параллельных сторон. Если две стороны конгруэнтны, то трапеция называется равнобедренной.
Вот свойства всех трапеций:
Воздушный змейВоздушный змей (также известный как дельтовидный ) представляет собой четырехугольник с двумя наборами конгруэнтных сторон. В отличие от параллелограмма, эти стороны смежные. Это похоже на (вздох) воздушного змея!
Вот свойства воздушных змеев:
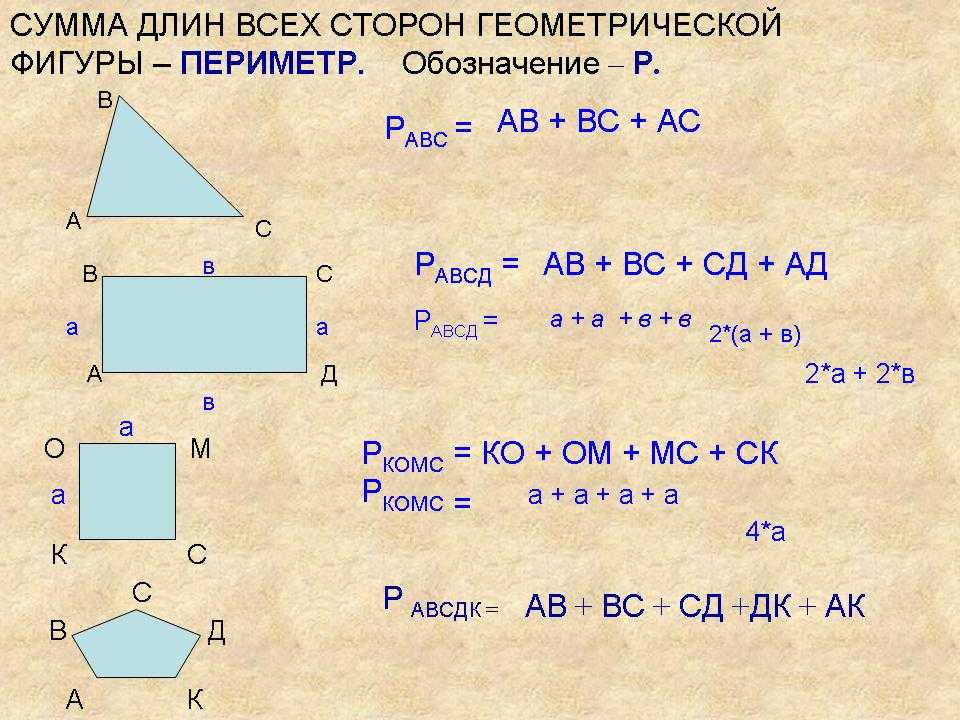
Может быть сложно уследить, что есть что, поэтому вот схема:
И, если вы действительно визуал, вот диаграмма Венна.



 2}\).
2}\).
 В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен. Другими словами, квадрат — это прямоугольник, у которого смежные стороны равны, а внутренние углы равны 90°.
Другими словами, квадрат — это прямоугольник, у которого смежные стороны равны, а внутренние углы равны 90°. У него четыре равных угла и четыре вершины. Все четыре угла прямоугольника равны 90°.
У него четыре равных угла и четыре вершины. Все четыре угла прямоугольника равны 90°.
 ) Площадь квадрата
) Площадь квадрата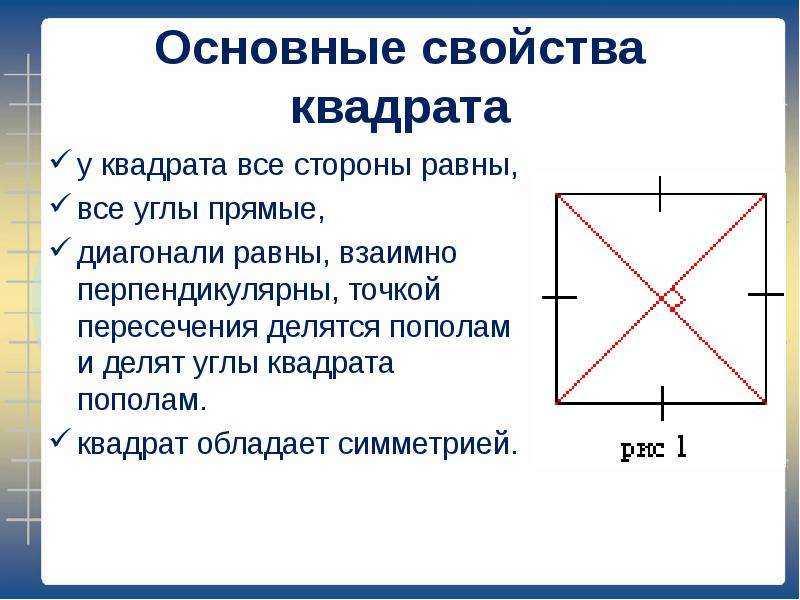

 Следовательно, квадрат можно назвать особым типом прямоугольника.
Следовательно, квадрат можно назвать особым типом прямоугольника.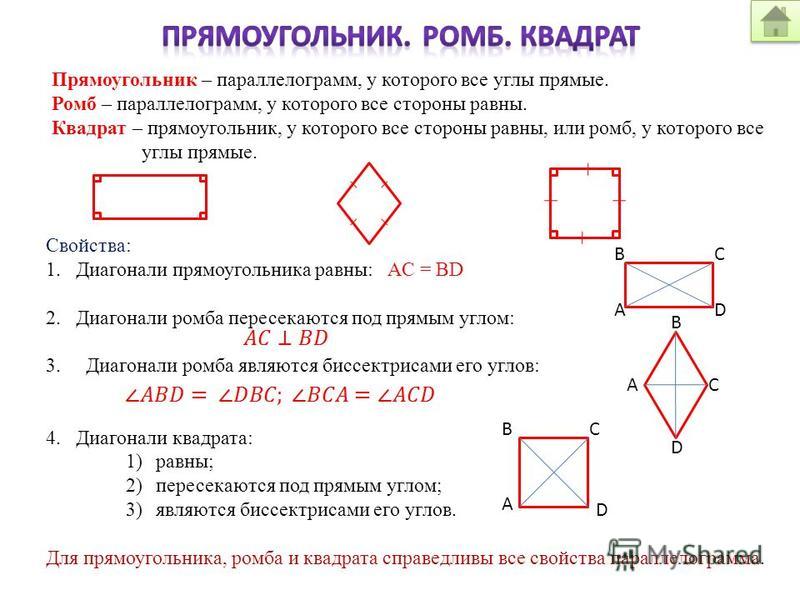

Leave A Comment