как решать, правила с подробным решением, простейшие примеры
Определение логарифмического неравенства
В процессе решения заданий в виде логарифмических неравенств пригодится знание теории: свойства монотонности и ключевых формул.
Определение 1Логарифмом положительного числа b по основанию a называют показатель степени, в которую необходимо возвести a, чтобы получить b:
logab=c⇔ac=b.
Здесь b > 0, a > 0, a отлично от единицы.
Главным логарифмическим тождеством является:
alogab=b,
logaac=c.
В процессе решения задач будут полезны такие формулы для логарифмов:
- Логарифм произведения равен сумме логарифмов: loga(bc)=logab+logac.
- Логарифм частного равен разности логарифмов: logabc=logab-logac.
- Формула для вычисления логарифма степени: logabm=mlogab.
Переход к другому основанию реализован по формуле:
logab=logcblogca
logab=1logba.
Простейшее логарифмическое неравенство — это соотношение, которое записано в виде:
loga fx > logagx,
при fxиgx некоторых выражениях, которые зависят от x. Например, fx=1+2x+x2, gx=3x-1.
Заметим, что знак «>» — больше — допускается заменять другими знаками: ≥,≤,<.
- loga fx >loga gx => fx>gx при a>1
- loga fx >loga gx => fx<gx при 0<a<1
Виды логарифмических неравенств
Логарифмические неравенства могут быть записаны в следующем виде:
- Простейшие, как log2x>-1.
- Неравенства, которые могут быть сведены к простейшим: как log12(x+1)≤log12(2x+3).
- Неравенства, в которых использованы логарифмические свойства: как log2(x+1)+log2(x-1)≤2.
- Неравенства, решаемые с помощью замены: такие, как log22x-log2x-2≤0.
- Выражения с основанием, где присутствует переменная: например, logx2≤1.
Нахождение области допустимых значений логарифмического неравенства
Корректность решения логарифмических неравенств зависит от правильности определения области допустимых значений.
Разберем наглядный пример:
log 22x+4 > log 23
Заметим, что в стандартной формуле логарифма роль b играет в данном случае выражение 2x+4. Тогда по определению:
2x+4>0
Если обратиться к определению логарифмического неравенства, то можно убедиться в том, что записанное выражение должно быть больше нуля. В результате х >-2.
После определения ОДЗ можно приступить к решению неравенства:
log22x+4>log23
В первую очередь следует избавиться от log2 в обеих частях выражения. Тогда:
2x+4>3
Таким образом:
2x>-1
x>-12
Далее требуется доказать, что решение, которое получилось, соответствует определенной ранее области допустимых значений:
Изобразим числовую прямую, на которой определим полученные точки:
-2 и -12).
В итоге окончательное решение неравенства является участком с двумя проходящими дугами:
x∈-0.5;+∞
Разберем несколько иной пример:
log0.22x+4>log0.
23
По сравнению с предыдущей задачей здесь изменено основание с 2 на 0,2. На принцип решения задачи это сильно не повлияет. Область допустимых значений остается прежней:
x>-2
Таким образом:
2x+4<3
x<-12
В результате начальное неравенство является равносильным системе:
x>-2x<-12
Решим эту систему:
x∈-2;-12.
Правило 1Когда основание логарифма в неравенстве больше по сравнению с единицей, знак неравенства остается без изменений и в случае fx, и в случае gx. Когда основание логарифма больше нуля и меньше единицы, знак между fx и gx следует изменить на противоположный:
logafx>logagx⇒fx>gx при a>1logafx>logagx⇒fx<gx при 0<a<1
Руководствуясь записанным правилом, можно рассмотреть еще одно логарифмическое неравенство:
log0.2×2+6x+8>log0.25x+10.
Определим ОДЗ:
x2+6x+8>0.
Такое неравенство решается с помощью метода интервалов. Вычислим корни уравнения:
x2+6x+8=0
Получим:
x1=-4, x2=-2.
Перенесем значения на числовую ось. Для определения знаков можно использовать подстановку нуля в начальное выражение. При этом получится число 8, которое является положительным. В результате первый интервал имеет знак плюс:
В данном случае нам интересен промежуток с положительным знаком. Для первого выражения областью допустимых значений является следующее множество:
.
Вторым ОДЗ является:
5x+10>0
Тогда:
x>-2.
На координатной прямой необходимо совместить оба ОДЗ:
Участок, на котором совпадают все ОДЗ, соответствует окончательной области допустимых значений:
-2;+∞.
Решим неравенство:
log0.2×2+6x+8>log0.25x+10
Заметим, что основание 0.2<1. В таком случае, следует изменить знак неравенства:
x2+6x+8<5x+10
Выражение можно упростить:
x2+x-2<0
С помощью уже знакомого метода интервалов, найдем решения:
x∈-2;1.
Итоговое решение соответствует участку, на котором ОДЗ пересекается с полученным множеством:
В соответствии с полученной областью можно записать ответ:
x∈-2;1.
Методы решения логарифмических неравенств
Простейшие логарифмические неравенства, которые записаны в виде:
logafx>logagx
решают по алгоритму:
- Поиск ОДЗ: . Запись в виде системы означает одновременное выполнение условий.
- Исследование основания. При a>1 следует решить неравенство fx>gx. При 0<a<1 необходимо решить неравенство fx<gx.
- Полученное решение требуется совместить с определенным ранее ОДЗ.
Другие виды логарифмических неравенств также можно решать с помощью описанной последовательности действий.
В том случае, когда основание не является однозначным, а переменным, следует рассмотреть два варианта:
- основание больше, чем единица;
- основание заключено в промежуток между нулем и единицей.
Когда логарифмическое неравенство не записано в виде простейшего, его решение сводится к приведению к простейшему виду.
Рассмотрим применение алгоритма на примере. Допустим, требуется решить неравенство:
log0.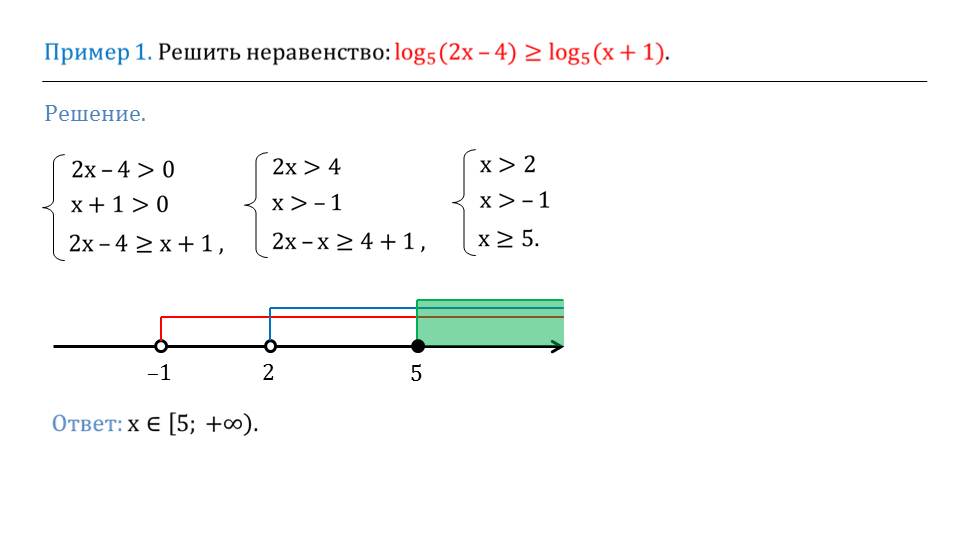
3x+4>log0.3×2+2x-2
В первую очередь следует определить область допустимых значений:
Заметим, что в первом неравенстве:
x>-4
Второе неравенство целесообразно решить с помощью метода интервалов. В результате получаются следующие корни:
x1=3-1
x2=-1-3
В таком случае, множество решений x2+2x-2>0 определено, как:
Заметим, что -4<-1-3. Результирующее ОДЗ:
Приступим к решению неравенства:
x+4<x2+2x-2
Данное неравенство является равносильным следующему:
0<x2+x-6
С помощью метода интервалов получим:
Исходя из того, что -3<-1-3, 2>3-1:
Правило 2Решение логарифмического неравенства, которое записано в виде logafx<logagx, сводится к решению таких систем:
Неравенство logafx>logagx в каждом из рассмотренных вариантов сводится к какой-то из этих систем:
Упростить решение логарифмических неравенств можно путем перехода к постоянному основанию.
Разберем данный метод на примере:
log|x|-2|x-3|≤0.
Определим ОДЗ:
Источник: ege-study.ru
Руководствуясь формулой logab=logcblogca, выполним переход к основанию 10:
lg|x-3|lg(|x|-2)≤0.
С помощью обобщенного метода интервалов можно представить в виде функции левую часть выражения:
g(x)=lg|x-3|lg(|x|-2).
Заметим, что данная функция изменяет знак при переходе точек с нулевыми значениями или при отсутствии значений. Выражение lg |x − 3| примет нулевое значение при |x − 3| = 1.
В таком случае: x = 4, либо x = 2. Выражение lg (|x| − 2) примет нулевое значение при |x| = 3. Такими точками являются 3 и −3. Учитывая область допустимых значений для начального неравенства, изобразим числовую прямую с определенными точками:
Источник: ege-study.ru
Определим знаки, которые принимает функция g(x) для каждого интервала и запишем ответ.
Ответ: x∈-3;-2∪(3;4].
Следующий пример заключается в решении логарифмического неравенства через систему:
log3x2+7x+10+log13x+59+1≥log33x2+16x+20
Записанное выражение является равносильным системе:
x2+7x+10>0x+5>03×2+16x+20>0log3x2+7x+10-log3x+59+log33≥log33x2+16x+20
⇔(x+5)(x+2)>0x+5>0(x+2)(x+103)>0log3(x+5)(x+2)·9·3(x+5)>log33(x+2)(x+103)
x>-29·(x+2)≥(x+2)(x+103)
x>-2x+103≤9<=>x>-2x≤173
x2+7x+10=0\hfill D=0; x1,2 =-7±32; x1=-5x; x2=-2; 3×2+16x+20=0 D=162-12·20= =16·(16-3·5)=16; x1,2=-16±46; x1=-2; x2=-103
Ответ: x∈-2;173.
Простейшие примеры
Задача 1Решить неравенство:
log0.3-x+2≤log0.32x-2
Решение
Определим ОДЗ:
Таким образом:
x∈1;2
Решим неравенство:
log0.3-x+2≤log0.32x-2
Так как 0.3<1, нужно изменить знак:
-x-2≥2x-2
-3x≥0
x≤0
Данное решение не соответствует ОДЗ. Неравенство не имеет решений.
Ответ: решения отсутствуют.
Задача 2Найти решения неравенства:
4logx4+3log4x4+4log16x4≤0
Решение
Заметим, что основание логарифма должно быть больше нуля и отлично от единицы:
x>0;4x≠1;x≠1;16x≠1.
Преобразуем систему, чтобы записать ее в упрощенном варианте:
Получилось определить ОДЗ неравенства. Заметим наличие переменной в основании логарифма. Тогда следует перейти к постоянному основанию 4:
4log4x+3log44x+4log4(16x)≤0;
4log4x+31-log4x+42+log4x≤0
Выполним замену log4x=t:
4t+31-t+42+t≤0
Упростим выражение и вычислим его решения способом интервалов:
(t-2)(t+45)t(1-t)(2+t)≥0.
В результате:
t∈-∞;-2∪-45;0∪(1;2].
Источник: ege-study.ru
Обратимся к переменной х:
Источник: ege-study.ru
С учетом условия x > 0, согласно определенной ОДЗ, запишем ответ.
Ответ: x∈0;116∪4-45;1∪(4;16]
Задача 3Решить неравенство, используя метод интервалов:
log132-3xx≥-1
Решение
Определим ОДЗ:
2-3xx>0
Перепишем выражение слева в виде логарифма с основанием 3:
log3x2-3x≥-1.
Выражение справа также можно переписать в виде логарифма с основанием 3. Тогда получим алгебраическое неравенство:
log3x2-3x≥log313
x2-3x≥13
Заметим, что условие по соответствию ОДЗ будет выполнено автоматически, что делает решение проще:
x2-3x-13≥0
3x-12-3x≥0
Воспользуемся методом интервалов и запишем ответ.
Источник: ege-study.ru
Ответ: x∈13;23.
Задача 4Найти решения неравенства:
log25-x2-35-x2+9-1+log25-x2-35-x2+9-1>log254-x2-22.
Решение
Обратим внимание на повтор выражения:
5-x2
Выполним замену:
5-x2=t
Исходя из того что показательная функция может иметь лишь положительные значения, запишем:
t > 0
В результате:
5-x2+9=59·t
54-x2=54·t=625t
Преобразуем неравенство:
log2t-359·t-1+log2t-359·t-1>log2625t-22
Определим ОДЗ:
t > 0
(t − 3) (59 · t − 1) > 0
При выполнении записанного условия значение частного t-359·t-1 также является положительным.
Выражение справа, расположенное под логарифмом, (625t-2)2 имеет знак плюс. Тогда:
(625t-2)2≠0
t≠2625
Определим ОДЗ:
С помощью метода интервалов найдем решения:
Источник: ege-study.ru
В результате:
t∈0;159∪3;+∞.
Решим неравенство путем представления суммы логарифмов в виде логарифма произведения:
Источник: ege-study.ru
Избавимся от логарифмов, а знак неравенства оставим без изменений:
(t-3)2>(625t-2)2
Перенесем имеющиеся выражения влево. Воспользуемся формулой разности квадратов:
(t-3)2-(625t-2)2>0
(t-3-625t+2)(t-3+625t-2)>0
(-624t-1)(626t-5)>0
Источник: ege-study.ru
Вспомним ОДЗ неравенства:
t∈0;159∪3;+∞
Определим, где пересекаются полученные промежутки:
Источник: ege-study.ru
В результате:
t<159
Зная, что:
t=5-x2
Получим:
5-x2<5-9;-x2<-9;x2>9;(x-3)(x+3)>0
Источник: ege-study.ru
Ответ: x∈(-∞;-3)∪(3;+∞).
Требуется решить неравенство:
logx+2(36+16x-x2)-116logx+22(x-18)2≥2.
Решение
Определим ОДЗ:
x+2>0x+2≠136+16x-x2>0x≠18 ⇔ x>-2x≠-1x∈(-2;18)
x∈(-2;-1)∪(1;18)
Заметим, что:
36+16x-x2=-(x+2)(x-18).
Начальное неравенство можно переписать в кратком виде, то есть упростить:
logx+2((18-x)(x+2))-116logx+22(x-18)2≥2
1+logx+2(18-x)-116logx+22(x-18)2≥2
При условии, что:
(x-18)2=(18-x)2
В таком случае:
1+logx+2(18-x)-116logx+22(18-x)2≥2
Обратим внимание на запись:
loga2b
Данное выражение означает, что в первую очередь следует определить логарифм, а далее можно приступать к возведению выражения, которое получилось, в квадрат.
logx+22(18-x)2=(logx+2(18-x)2)2=(2logx+2(18-x))2=4logx+22(18-x).
Выполним замену:
logx+2(18-x)=t
t-14t2≥1
t2-4t+4≤0
(t-2)2≤0
Выражение слева не может быть меньше нуля. По этой причине:
t = 2
В результате:
logx+2(18-x)=2; logx+2(18-x)=logx+2(x+2)2; 18-x=x2+4x+4; x2+5x-14=0;
x1=-7 является посторонним корнем, так как не соответствует ОДЗ
x2=2
Ответ: 2
Логарифмические неравенства 11 класс онлайн-подготовка на Ростелеком Лицей
Тема: Метод интервалов
Урок: Логарифмические неравенства
1.
Важные опорные факты
Ключом к решению логарифмических неравенств являются свойства логарифмической функции, т. е. функции вида (). Здесь t – независимая переменная, а – конкретное число, у – зависимая переменная, функция.
Вспомним основные свойства логарифмической функции.
Рис. 1. График логарифмической функции при различных основаниях
1. Область определения: ;
2. Область значений: ;
3. Функция монотонна на всей своей области определения. При монотонно возрастает (когда аргумент возрастает от нуля до плюс бесконечности, функция возрастает от минус до плюс бесконечности, ). При монотонно убывает (когда аргумент возрастает от нуля до плюс бесконечности, функция убывает от плюс до минус бесконечности, ).
Именно монотонность логарифмической функции позволяет решать простейшие логарифмические неравенства.
2. Методика решения простейших логарифмических неравенств с основанием большим единицы, пример
Рассмотрим решение логарифмического неравенства, когда основание логарифма .
Неравенство необходимо решать, применяя эквивалентные, равносильные преобразования. Рассмотрим схему. Поскольку мы рассматриваем логарифмическую функцию с основанием, большим единицы, помним, что функция монотонно возрастает. Отсюда:
При этом необходимо не забыть про ОДЗ, т. к. под логарифмом могут стоять строго положительные выражения. ОДЗ представлено системой:
Решением исходного неравенства является эквивалентное неравенство , поэтому для соблюдения ОДЗ достаточно защитить меньшее из чисел. Получаем систему неравенств, которая соответствует исходному неравенству:
Например:
Рис. 2. Иллюстрация решения примера
Ответ:
3. Методика решения простейших логарифмических неравенств с основанием, лежащим в пределах от нуля до единицы, пример
Рассмотрим решение логарифмического неравенства, когда основание логарифма .
Поскольку мы рассматриваем логарифмическую функцию с основанием, лежащим в пределах от нуля до единицы, помним, что функция монотонно убывает.
Отсюда:
При этом необходимо не забыть про ОДЗ, т. к. под логарифмом могут стоять строго положительные выражения. ОДЗ представлено системой:
Решением исходного неравенства является эквивалентное неравенство , поэтому для соблюдения ОДЗ достаточно защитить меньшее из чисел. Получаем систему неравенств, которая соответствует исходному неравенству:
Например:
Рис. 3. Иллюстрация решения примера
Ответ: нет решений
4. Обобщение методики
Выполним обобщение. Мы рассматриваем простейшие логарифмические неравенства, т. е. неравенства вида:
Все остальные более сложные логарифмические неравенства сводятся к простейшим.
Методика решения:
1. Уравнять основания логарифмов;
2. Сравнить подлогарифмические выражения:
— при сохранить знак неравенства;
— при изменить знак неравенства на противоположный;
3. Учесть ОДЗ;
5.
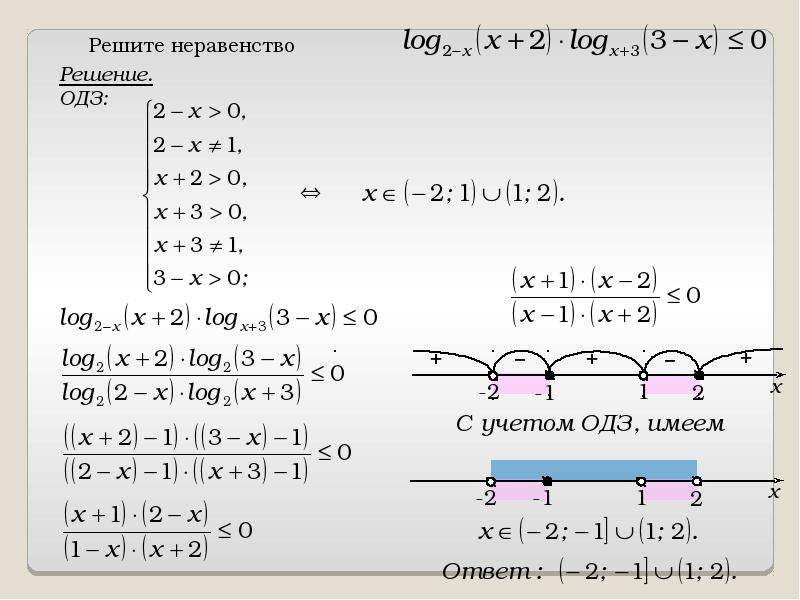Решение примеров
Пример 1 – решить неравенство:
Уравняем основания логарифмов. Для этого число в правой части представим в виде логарифма с нужным основанием:
Итак, имеем неравенство:
Основание логарифма меньше единицы, имеем эквивалентную систему:
Рис. 4. Иллюстрация решения примера 1
Ответ:
Пример 2 – решить неравенство:
Уравняем основания:
Имеем неравенство:
Основание логарифма меньше единицы, имеем эквивалентную систему:
Имеем систему двух простейших логарифмических неравенств. Уравняем основания в каждом из них:
В обоих случаях основание логарифма больше единицы, запишем эквивалентные системы:
Рис. 5. Иллюстрация к решению примера 2
Ответ:
Итак, мы изучили простейшие логарифмические неравенства. На следующем уроке мы рассмотрим, каким образом более сложные неравенства сводятся к простейшим
Список литературы
1.
Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Webmath.ru (Источник).
2. Tutoronline.ru (Источник).
Домашнее задание
1. Алгебра и начала анализа, 10–11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, № 516, 517, 525;
2. Решить неравенство:
а) ;
б) ;
в) ;
г) ;
3. Решить неравенство:
а) ;
б) ;
в) ;
г)
логарифмических неравенств | Brilliant Math & Science Wiki
Александр Кац, Маянк Чатурведи, Андрес Гонсалес, и
способствовал
Содержимое
- Введение
- Логарифмические неравенства — одно и то же основание
- Логарифмические неравенства — основание меньше 1
- Логарифмические неравенства — аналогичное основание
- Логарифмические неравенства — другое основание
- Логарифмические неравенства — несколько терминов
- Логарифмические неравенства — решение задач
- Смотрите также
Ключом к работе с логарифмическими неравенствами является следующий факт:
Если \(a>1\) и \(x>y\), то \(\log_ax>\log_ay\).
В противном случае, если \(0
В противном случае, если \(0Конечно, основание логарифма не может быть 1 или неположительным. Что еще более важно, верно и обратное:
Если \(a>1\) и \(\log_ax>\log_ay\), то \(x>y\). В противном случае, если \(0
Говоря более формально, логарифмическая функция \(f(x)=\log_a x\) есть монотонно возрастающая \(\big(\)возрастающая \(x\) всегда возрастает \(f(x)\big )\) при \(a>1\) и монотонно убывающих \(\big(\)возрастающих \(x\) всегда убывающих \(f(x)\big)\) при \(0 К счастью, оба этих факта интуитивно понятны: когда основание больше 1, сторона с большим аргументом будет больше, и наоборот, когда основание меньше 1. Например, без всякого Зная факты, формализованные выше, можно было бы интуитивно ожидать, что \(\log_2100\) будет больше, чем \(\log_295\). Также важно иметь в виду следующий факт: Аргумент логарифма должен быть положительным! Таким образом, также необходимо учитывать любые неравенства, возникающие в результате положительности аргументов; например, неравенство, включающее термин \(\log_2 (2x-3)\), немедленно требует \(x>\frac{3}{2}\). Когда обе части неравенства имеют одну и ту же основу, ключевые факты из введения могут быть применены напрямую. Например, Какие значения \(x\) удовлетворяют следующему неравенству: \[\log_2(2x+3)>\log_2(3x)?\] Поскольку основание равно 2, что больше 1, тот факт, что \(\log_2(2x+3)>\log_2(3x)\), подразумевает, что \(2x+3>3x\). Вычитание \(2x\) с обеих сторон дает \(3>x\). Кроме того, аргументы обоих логарифмов должны быть положительными, поэтому дополнительно \(3x>0\) и \(2x+3>0\). Первый более строгий, так как \(x>0\), поэтому окончательный набор решений равен \(0 Истинно, только если \( n \leq 10 \)
Ложь всегда
Верно, только если \( n \leq 100 \)
Всегда верно Верно или неверно? Для всех положительных целых чисел \(n \geq 2\), \[ \log_{10} (n-1) + \log_{10} (n+1) < 2 \log_{10} n. \[ \dfrac{1}{\log_{4}\left(\dfrac{x+1}{x+2}\right)}<\dfrac{1}{\log_{4}(x +3)}\] Если диапазон \(x\), удовлетворяющих приведенному выше равенству, равен \((a,\infty)\), найдите значение \(a\). Та же концепция может быть применена к большим «стекам» логарифмов: Какие значения \(x\) удовлетворяют следующему неравенству: \[\log_2\big(\log_3(4x+1)\big)>\log_2\big(\log_3(2x+3)\big)?\] Поскольку основание равно 2, что больше 1, данное неравенство подразумевает \(\log_3(4x+1) > \log_3(2x+3)\). Это также означает, что \(4x+1>2x+3\) или что \(2x>2 \подразумевает x>1\). Следовательно, \(х\) должно быть больше 1,9.{ 2 }+4x+а) }. \] Если диапазон значений \(a\) может быть выражен в виде \( (A,B],\), то найти значение \( A + B. \) В случае где основание меньше 1, предыдущая интуиция существенно меняется на противоположную: большая сторона теперь та, у которой меньший показатель Какие значения \(x\) удовлетворяют следующему неравенству: \[\log_{\frac{1}{2}}(3x)>\log_{\frac{1}{2}}(2x+3)?\] Поскольку основание равно \(\frac{1}{2}\), что меньше 1, из данного неравенства следует \(3x<2x+3\).
\]
Найдите \(x\).
\[ x\in \left(\frac { 4 }{ 3 } ,\frac { 17 }{ 22 } \ right ) \] \[ x\in \left(\frac { 4 }{ 3 } ,-\ frac { 17 }{ 22 } \right ) \] \[ x\in \left(-\frac { 4 }{ 3 } ,\frac { 17 }{ 22 } \right ) \] \[ x\in \left(-\frac { 4 }{ 3 } ,-\frac { 17 }{ 22 } \right ) \]
\[ \log _{ 3x+5 }{ \big(9{ 2 }+8x+8\big) } >2 \]
Решите приведенное выше неравенство для \( x \).
Попробуйте Fun с неравенствами-1 и Fun с неравенствами-3.
Та же концепция может применяться, когда имеется несколько терминов:
Какие значения \(x\) удовлетворяют следующему неравенству:
\[\log_2(x)>\log_2(3)+\log_4(25)+\log_8(343)?\]
Запись всех логарифмов по основанию 2 дает
\[\begin{выравнивание} \log_2(x)&>\log_2(3)+\log_2(5)+\log_2(7)\\ \стрелка вправо \log_2(x)&>\log_2(105), \конец{выравнивание}\]
, значит \(х>105\).
Все \(х\) больше 105 удовлетворяют исходному неравенству. \(_\квадрат\)Когда основания разные и не связаны общей основой (как в предыдущем разделе), становится необходимым использование формулы смены основания. Например,
Какие значения \(x\) удовлетворяют следующему неравенству:
\[ \log_7(x+5)>\log_5(x+5)?\]
При замене основания неравенство дает
\[\frac{\log(x+5)}{\log 7}>\frac{\log(x+5)}{\log 5}.\]
Это верно только тогда, когда \(\log(x+5)\) отрицательно, что означает, что
\[\log(x+5)<0 \подразумевается x+5<1 \подразумевается x<-4,\]
, и поскольку \(x+5\) должно быть положительным, \(x>-5\), а окончательный набор решений равен \(-5
\[2 Сколько натуральных решений могут удовлетворять приведенному выше неравенству? В случае цепочки неравенств обычно целесообразно рассматривать каждое неравенство отдельно, а затем объединять результаты. Какие значения \(x\) удовлетворяют следующему неравенству: \[\log_{\frac{1}{2}}(x+2)<-2<\log_{\frac{1}{4}}(2x)?\] Первое неравенство: \(\log_{\frac{1}{2}}(x+2)<-2\), или \(\log_{\frac{1}{2}}(x+2 )<\log_{\frac{1}{2}}(4)\). Поскольку основание \(\frac{1}{2}\) меньше 1, это означает, что \(x+2>
Например,
Второе неравенство имеет вид \(-2<\log_{\frac{1}{4}}(2x)\), или \(\log_{\frac{1}{4}}(16)<\log_{ \frac{1}{4}}(2x)\). Опять же, основание меньше 1, так что это означает \(16>2x\) или \(8>x\).
Таким образом, \(2 Имейте в виду, что основание логарифма может быть меньше 1, что связано с равенством \[\large \log_ab = -\log_{\frac{1}{a}}b,\] так что не забудьте этот случай! Решить неравенство \[\log_{\frac{x+4}{2}}\left(\log_{2}\frac{2x-1}{3+x}\right)<0. Во-первых, основание должно быть положительным и не равным 1, поэтому сразу \(x>-4\) и \(x \neq -2\). Точно так же аргумент \(\log_2\frac{2x-1}{3+x}\) должен быть положительным, поэтому \(\frac{2x-1}{x+3}>0 \подразумевает x>\frac12 \ текст{ или } x<-3\). Таким образом, единственными возможными значениями \(x\) являются \(x>\frac12 \, \text{ или }\, -4 Теперь рассмотрим два случая: Случай 1. В этом случае необходимо, чтобы \(\log_2\frac{2x-1}{3+x}>1\) или \(\frac{2x-1}{3+x}>2\), поэтому \(\frac{2x-1}{3+x}-2=\frac{-7}{3+x}>0\). Следовательно, \(3+x\) отрицательно, или \(x<-3\). Итак, все \(x\), такие что \(-4 Помните, что эта стратегия вычитания двух сторон, а не умножения, позволяет избежать работы с делами, связанной с умножением, поскольку больше нет необходимости учитывать последствия отрицательного значения умноженного количества. Случай 2. \(\frac{x+4}{2}>1 \iff x>-2\) В этом случае необходимо, чтобы \(\log_2\frac{2x-1}{3+x}<1\) или \(\frac{2x-1}{3+x}<2\), поэтому \(\frac{2x-1}{3+x}-2=\frac{-7}{3+x}<0\). Это всегда верно как \(x>-2\), так что любой \(x>-2\) будет работать. Однако помните, что только \(x>\frac12 \text{ или } -4 Следовательно, набор решений равен \[x>\frac12,\-4 Типичная стратегия решения проблем заключается в использовании формулы замены основания, чтобы все логарифмы имели одинаковое основание. Это значительно упрощает применение других неравенств, таких как AM-GM. Покажите, что \[\log_n(n+1)>\log_{n+1}(n+2)\] для всех целых чисел \(n \geq 2\). Использование смены основания, \[\begin{выравнивание}
\ log_n (n + 1)> \ log_ {n + 1} (n + 2) &\ тогда и только тогда, когда \ frac {\ log (n + 1)} {\ log n}> \ frac {\ log (n + 2) {\log (n+1)}\\
&\iff \big(\log (n+1)\big)^2>\log n\log(n+2). , доказывающее исходное неравенство. \(_\квадрат\) Процитировать как: Логарифмические неравенства. Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/логарифмические-неравенства/ В разделе 6.
\]
\конец{выравнивание}\] 92>\лог п\лог(п+2),\] 6.4: Логарифмические уравнения и неравенства
2-7x-4=0\). Решая, находим \(x = -\frac{1}{2}\) и \(x=4\). Построив график, находим \(y = f(x) = \frac{\ln(1-2x)}{\ln(7)}\) и \(y=g(x) = 1 — \frac{\ln (3-x)}{\ln(7)}\) пересекаются только в точке \(x=-\frac{1}{2}\). Проверка \(x=4\) в исходном уравнении дает \(\log_{7}(-7) = 1 — \log_{7}(-1)\), что является явным нарушением предметной области. 9{3} = \frac{x+3}{6-x}\nonumber\] Это сводится к линейному уравнению \(8(6-x) = x+3\), которое дает нам \(x = 5\ ). Когда мы рисуем \(f(x) = \frac{\ln(x+3)}{\ln(2)}\) и \(g(x) = \frac{\ln(6-x)}{ \ln(2)} + 3\), мы находим, что они пересекаются в точке \(x=5\).
Используя квадратичную формулу, мы получаем \(x = 1 \pm \sqrt{3}\). Графики \(f(x) = 1 + \frac{2\ln(x+1)}{\ln(4)}\) и \(g(x) = \frac{2 \ln(x)}{ \ln(2)}\), мы видим, что графики пересекаются только в точке \(x = 1 + \sqrt{3} \приблизительно 2,732\). Решение \(x = 1 — \sqrt{3} < 0\), что означает, что при подстановке в исходное уравнение член \(2 \log_{2}\left(1 - \sqrt{3}\right) \) не определено.
Как минимум, пример 6.4.1 демонстрирует важность проверки на наличие посторонних решений 2 при решении уравнений с логарифмами. Несмотря на то, что мы проверили наши ответы графически, посторонние решения легко обнаружить — любое предполагаемое решение, которое приводит к отрицательному числу внутри логарифма, должно быть отброшено. Как и в случае с уравнениями в примере 6.3.1, многое можно узнать, проверив все ответы в примере 6.4.1 аналитически. Мы оставляем это читателю и обращаем наше внимание на неравенства с логарифмическими функциями.
{1}\), что допускает \(x = 9\). Мы выбираем тестовые значения \(x\) так, чтобы \(x+1\) было степенью \(10\), и мы получаем \(-1 < -0,9 < 0 < \sqrt{10} -1 < 9 < 99\). Наша диаграмма знаков дает решение \((-1,0] \cup [9, \infty)\). Калькулятор указывает, что график \(y= f(x) = x \log(x+1)\) находится выше \(y=g(x) = x\) на интервалах решения, и графики пересекаются в \ (х=0\) и \(х=9\).
Наш следующий пример пересматривает понятие pH, впервые использованное в упражнении 77 в разделе 6.1. 9{-1}(x)\) и проверьте свой ответ графически с помощью калькулятора.
Решение
Сначала запишем \(y=f(x)\), затем поменяем местами \(x\) и \(y\) и найдем \(y\).
\[\begin{array}{rclr} y & = & f(x) & \\ y & = & \dfrac{\log(x)}{1-\log(x)} & \\[8pt ] x & = & \dfrac{\log(y)}{1-\log(y)} & \mbox{Поменять местами $x$ и $y$.}\\[8pt] x\left(1-\log (y)\right) & = & \log(y) & \\ x — x\log(y) & = & \log(y) & \\ x & = & x \log(y) + \log( y) & \\ x & = & (x+1) \log(y) & \\ \dfrac{x}{x+1} & = & \log(y) & \\ y & = & 10^{ \frac{x}{x+1}} & \mbox{Перепишите как показательное уравнение.
}\\ \end{массив}\nonumber\] 9{-12}}\справа) = 150\)
Leave A Comment