Относительность движения. Свободное падение. Уравнения и графики движения.
Задания по физике: Относительность движения. Свободное падение. Уравнения и графики движения. |
Пример задания по теме «Относительность движения. Свободное падение. Уравнения и графики движения.» |
|
Сколько времени длился разгон?Показать материал полностью и распечатать.
Задание такого типа у нас считается одним из самых полезных.
Первые пять задач представляют комплекс прямых и обратных задач (см. у Эрдниева). Несмотря на то, что эти задачи, как правило, в одно действие, на них мы отрабатываем весьма важные вопросы: есть начальная скорость или ее нет, какая из формул быстрее приведет к ответу, км/час или м/с, разгон или торможение и пр.
Задачи 7 и 8 — обычные задачи на свободное падение, то есть те же задачи 1 — 5, только в них всегда известно ускорение.
Задачи 9 и 10 позволяют нам уйти от оскопленного навыка — взял формулу, подставил, сосчитал. Все предыдущие задачи были лишь для того, чтобы подобраться к решению задач типа 9 и 10.
Избыточное количество задач позволяет ученику работать в зоне его ближайшего развития, а, значит, работать с максимальным КПД на уроке.
Ответы к задачам 9 — 4.
| задача\вариант | 9 — 4 — 1 | 9 — 4 — 2 | 9 — 4 — 3 | 9 — 4 — 4 | 9 — 4 — 5 | 9 — 4 — 7 | 9 — 4 — 8 | 9 — 4 — 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0,5 м/с2 |
10 м/с |
10 с |
1,25 м/с |
15 м/с |
20 с |
1 м/с2 |
15 м/с |
20 с |
| 2 | 8 с |
— 4 м/с2 |
9 км/с |
500 м |
20 с |
300 м/с |
-2,5 м/с2 |
5 м/с2 |
4 с |
| 3 | 3000 м |
25 м |
300 м |
16 м/с |
35 м |
95 м |
875 м |
60 м |
62,5 м |
| 4 | 37,5 м |
270 км |
1000 м |
250 м |
750 м |
37,5 м |
250 м |
30 м |
288 км |
| 5 | 2,5 м/с2 |
20 м/с |
400 м/с |
— 0,5 м/с2 |
1000 м/с2 |
не более 100 м/с |
400 с |
4,5 м/с2 |
4 с |
| 6 | 2,5 м/с2; 40 м |
-5 м/с2; 1000 м |
1,2 м/с2; 140 м |
— 2 м/с2; 48 м |
0,4 м/с2 |
-2 м/с2; 96 м |
1 м/с2; 72 м |
-4 м/с2; 200 м |
0 м/с2; 200 м |
| 7 | 5 с |
20 м/с |
45 м |
1,3 с |
11,25 м/с |
12,8 м |
1 с |
180 км/час |
11,25 м |
| 8 | 20 м |
2 с |
— 5 м/с |
500 м |
2 с |
500 м |
95 м |
4 с |
10 м |
| 9 | 450 м |
4 м/с |
30 с |
156 м |
5,25 м/с |
87,5 м |
85 м |
150 м |
400 м |
| 10 | 100 с |
— 2 м/с2 |
16 м/с |
7 м/с |
19 м/с |
-0,5 м/с2 |
2 м |
55 м |
3,5 с |
16.
Сколько времени длилось торможение автомобиля до полной остановки… Задачи и упражнения. Физика Громов, Родина 8 класс ГДЗ. – Рамблер/класс 16. Сколько времени длилось торможение автомобиля до полной остановки… Задачи и упражнения. Физика Громов, Родина 8 класс ГДЗ. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
16.
Сколько времени длилось торможение автомобиля до полной остановки, если его начальная скорость была равна 72 км/ч,
а ускорение при торможении — 5 м/с2?
ответы
ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Психология
Химия
похожие вопросы 5
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
В.Перышкин Задание №474 В каком случае жидкость имеет большую плотность?Привет, есть варианты, как ответить на вопрос???
На рисунке изображен деревянный брусок, плавающий в двух разных жидкостях. В (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?
Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
42. Тело массой 4 кг движется с ускорением 0,5 м/с2.
Чему равна сила… Задачи и упражнения. 8 класс физика Громов, Родина ГДЗ.
42. Тело массой 4 кг движется с ускорением 0,5 м/с2. Чему
равна сила, сообщающая телу это ускорение?
ГДЗГромов С.В.Физика8 класс
Видео с вопросами: Расчет тормозного пути с учетом времени реакции, скорости автомобиля и замедления
Стенограмма видео
Время реакции водителя автомобиля, движущегося со скоростью 20 метров в секунду, составляет 1,2 секунды. Тормоза автомобиля замедляют автомобиль со скоростью 4,5 метра в секунду в квадрате после их активации. Каков тормозной путь автомобиля с точностью до метра?
Итак, в этом вопросе мы рассматриваем автомобиль, который изначально движется. И тогда это прекратится. Предположим, что эта оранжевая коробка представляет нашу машину. Нам сказали, что эта машина изначально движется со скоростью 20 метров в секунду. Итак, давайте произвольно решим, что автомобиль изначально двигался вправо со скоростью 20 метров в секунду.
Это начальная скорость автомобиля, которую мы будем называть 𝑢. Теперь с этой машиной происходит то, что она изначально движется со скоростью 20 метров в секунду. И тут водитель замечает опасность.
Допустим, это та опасность, которую замечает водитель. Это огромный валун на пути машины. Теперь предположим также, что водитель замечает опасность, когда автомобиль находится в этом положении. И с этого момента драйвер начинает обрабатывать то, что им нужно сломать. Однако, поскольку время реакции водителя составляет 1,2 секунды, он не нажимает на тормоз мгновенно. Другими словами, автомобиль все еще движется со скоростью 20 метров в секунду на небольшом расстоянии еще до того, как водитель нажмет на тормоз.
Итак, все это расстояние отсюда и сюда водитель вместе с автомобилем продолжает двигаться со скоростью 20 метров в секунду, пока водитель думает о том, чтобы нажать на тормоз. Теперь это конкретное расстояние известно как расстояние мышления, которое мы будем называть индексом 𝑑 𝑡.
Но затем, как только машина достигает этой точки, водитель нажимает на тормоз. И в этот момент машина начинает тормозить. Другими словами, начиная с этого момента автомобиль ускоряется в направлении, противоположном направлению его первоначального движения, со скоростью 4,5 метра в секунду в квадрате.
В этот момент мы видим, что ускорение, которое машина испытывает из-за тормозов, направлено в сторону, противоположную ее начальной скорости. И это, конечно, потому, что машина тормозит. Но поскольку мы имеем дело со скоростью автомобиля, изначально направленной в направлении, противоположном ускорению, хорошей идеей будет выбрать условное обозначение. Давайте выберем, что все, что движется вправо, движется в положительном направлении. А все, что движется влево, движется в отрицательном направлении. Другими словами, тогда начальная скорость автомобиля, движущегося вправо, равна 20 метрам в секунду, а ускорение или, вернее, замедление автомобиля, движущегося влево, будет обозначено как отрицательное 4,5 метра в секунду.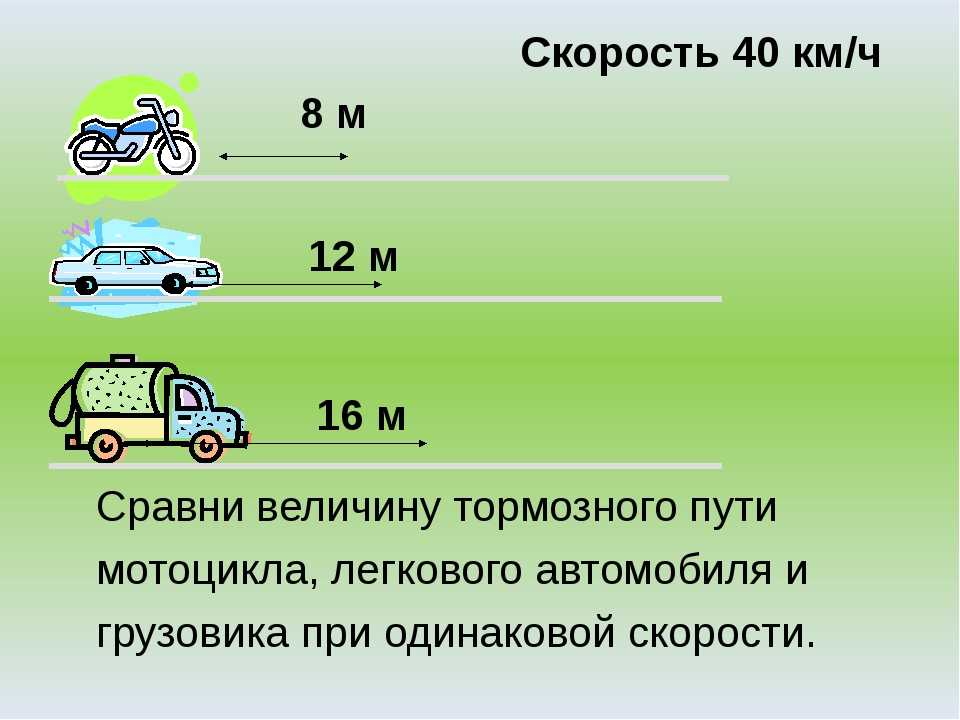
в наших расчетах.
Теперь назовем ускорение автомобиля 𝑎. И затем, как только автомобиль начинает замедляться в этой точке, мы знаем, что в конечном итоге автомобиль остановится, надеюсь, до того, как он достигнет опасности. Итак, в этот момент автомобиль остановился, а это означает, что конечная скорость автомобиля, которую мы назовем 𝑣, равна нулю метров в секунду, потому что автомобиль теперь неподвижен. Таким образом, расстояние, которое автомобиль проходит за период замедления, называется тормозным путем, который мы будем называть 𝑑 нижним индексом 𝑏.
Причина, по которой это называется тормозным путем, заключается в том, что это расстояние, на протяжении которого автомобиль затормозил. И, кстати, стоит отметить, что в начале тормозного пути скорость машины была еще 20 метров в секунду. Теперь нас просят найти тормозной путь автомобиля. Итак, давайте вспомним, что тормозной путь автомобиля определяется как путь мышления плюс тормозной путь. Итак, допустим, что тормозной путь автомобиля мы будем называть 𝑑 нижним индексом 𝑠.
И, как мы уже видели, дистанция мышления — это 𝑑 нижний индекс 𝑡. И тормозной путь 𝑑 подстрочный 𝑏.
Другими словами, тормозной путь здесь равен общему расстоянию. Это расстояние, пройденное автомобилем между моментом, когда водитель впервые осознает, что впереди опасность, и моментом, когда автомобиль, наконец, останавливается. Итак, давайте запишем здесь, что тормозной путь равен мысленному пути плюс тормозной путь. И давайте проработаем дистанцию мышления и дистанцию торможения по отдельности.
Начнем с дистанции мышления. Теперь, когда машина движется от точки, в которой водитель понимает, что нужно тормозить, до точки, когда водитель действительно нажимает на тормоза, как мы говорили ранее, машина продолжает двигаться со скоростью 20 метров в секунду, потому что тормоза не работают. еще не нажали. Другими словами, автомобиль движется с постоянной скоростью 𝑢 на всем протяжении этого пути. И тогда мы можем вспомнить, что если объект движется с постоянной скоростью, давайте назовем эту скорость 𝑣 индексом const, тогда эта скорость равна расстоянию, пройденному объектом, деленному на время, затраченное на то, чтобы этот объект прошел это расстояние.
Итак, в нашем конкретном случае автомобиль движется с постоянной скоростью 𝑢. И эта постоянная скорость равна пройденному расстоянию, то есть мысленному расстоянию, деленному на время, затраченное автомобилем на преодоление этого расстояния.
Теперь, как мы знаем, автомобиль фактически преодолевает это расстояние за время 1,2 секунды, потому что это время реакции водителя, другими словами, время, которое проходит между здесь, когда водитель понимает, что ему нужно затормозить, и здесь , когда они фактически нажимают на тормоз. Итак, мы знаем значение 𝑢, 20 метров в секунду. И мы знаем значение 𝑡, время реакции, 1,2 секунды. Таким образом, мы можем изменить это уравнение, чтобы найти 𝑑 𝑡. Мы делаем это, умножая обе части уравнения на время реакции 𝑡. Таким образом, он отменяется с правой стороны. И что у нас остается, так это то, что время реакции водителя, умноженное на постоянную скорость, с которой движется автомобиль, равно дистанции мышления.
Тогда мы можем сказать, что расстояние мышления равно времени реакции, 1,2 секунды, умноженному на скорость автомобиля, 20 метров в секунду.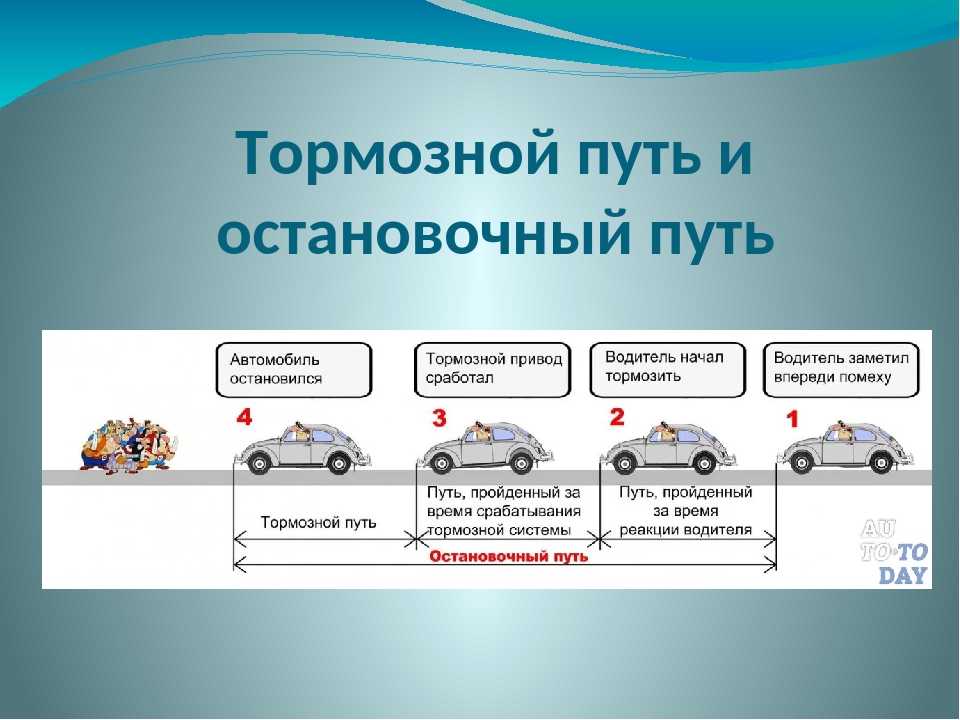
И очень быстро подумав о единицах, мы увидим, что здесь у нас есть секунды в числителе. И затем у нас есть посекунды, что означает, что единицы секунд будут отменены. И у нас останется единица метров. Теперь это имеет смысл, потому что мы вычисляем дистанцию мышления. Таким образом, оценивая правую часть этого уравнения, мы находим, что расстояние мышления автомобиля составляет 24 метра.
Итак, давайте запишем эту часть информации здесь. Мы только что выяснили, что такое 𝑑 𝑡. Итак, чтобы вычислить 𝑑 𝑠, все, что нам теперь нужно сделать, это вычислить значение 𝑑 𝑏, тормозной путь. Чтобы сделать это, нам нужно понять, что в этой фазе движения автомобиля он больше не движется с постоянной скоростью. На самом деле он замедляется с постоянной скоростью 4,5 метра в секунду в квадрате или, если хотите, ускоряется с отрицательными 4,5 метрами в секунду в квадрате.
Итак, что мы знаем об этой фазе движения автомобиля, так это то, что начальная скорость составляет 20 метров в секунду.
И эта скорость положительна, потому что она направлена вправо. Мы также знаем, что конечная скорость автомобиля здесь равна нулю метров в секунду. И мы также знаем ускорение автомобиля, минус 4,5 метра в секунду в квадрате, потому что помните, что ускорение направлено влево, другими словами, против движения самого автомобиля. Итак, если мы знаем эти три величины, 𝑢, 𝑣 и 𝑎, и пытаемся найти тормозной путь 𝑑 𝑏, то для этого нам нужно вспомнить одно из кинематических уравнений.
Конкретное уравнение, которое мы ищем, это уравнение, которое говорит нам, что квадрат конечной скорости равен квадрату начальной скорости плюс два, умноженные на ускорение объекта, умноженное на пройденное расстояние. прямая линия рядом с объектом. Но тогда в этой ситуации расстояние, пройденное по прямой объектом, которым в данном случае является автомобиль, на самом деле является тормозным путем. И, следовательно, мы можем заменить 𝑑 𝑠 в уравнении на 𝑑 𝑏, тормозной путь.
Все остальные величины можно оставить прежними, потому что мы назвали их 𝑢, 𝑣 и 𝑎.
И, конечно же, они означают одно и то же. Итак, на данный момент мы можем взять наше уравнение и изменить его так, чтобы найти 𝑑 𝑏. Если мы начнем с вычитания 𝑢 в квадрате из обеих частей уравнения, то у нас останется 𝑣 в квадрате минус 𝑢 в квадрате с одной стороны и только два 𝑎𝑑 𝑏 с правой. Затем мы делим обе части уравнения на два 𝑎, чтобы получить 𝑣 в квадрате минус 𝑢 в квадрате, деленное на два 𝑎 слева и просто 𝑑 𝑏 справа. Итак, теперь все, что нам нужно сделать, это подставить некоторые значения.
Когда мы это делаем, мы получаем 𝑣 в квадрате минус 𝑢 в квадрате, деленное на два 𝑎. И тогда мы можем упростить числитель, прежде всего, который становится отрицательным 400 метров в квадрате на секунду в квадрате, когда мы не забудем возвести в квадрат все, что было в скобках из предыдущего, и знаменатель станет двумя, умноженными на отрицательные 4,5 метра в секунду в квадрате, что станет отрицательным девятью метрами. за секунду в квадрате. И затем в этот момент мы видим, что отрицательный знак числителя и знаменателя сокращаются, поэтому для нас было так важно учитывать направление ускорения автомобиля.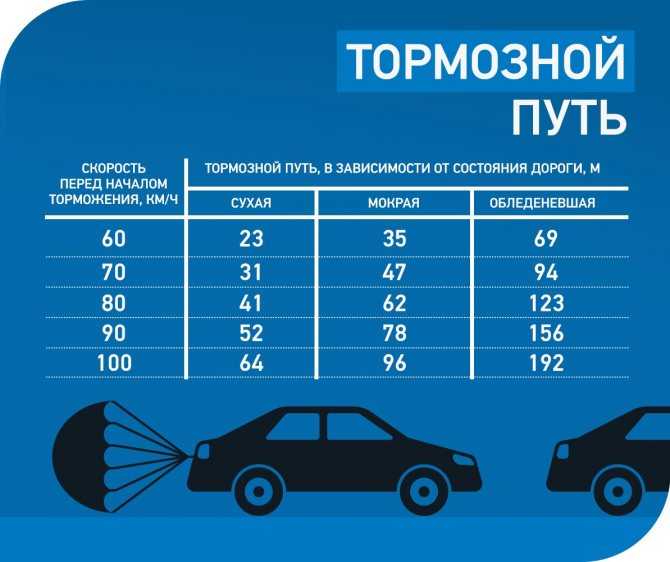
И если мы подумаем о единицах, мы увидим, что у нас есть метр в квадрате на секунду в квадрате в числителе и метр в секунду в квадрате в знаменателе.
У нас одинаковые степени секунды. И отменят. Но в числителе у нас метры в квадрате, тогда как в числителе у нас просто метры. Таким образом, только одна мощность метров в числителе будет сокращаться с одной мощностью метров в знаменателе. И окончательный результат будет в метрах, и это здорово, потому что мы снова находим расстояние. Таким образом, наше расстояние будет равно 400, разделенным на девять метров. Когда мы оценим это, мы обнаружим, что это становится 44,44 и так далее метра.
Итак, давайте запишем эту информацию здесь. 𝑑 𝑏 равно 44,4 повторяющихся метра. И в этот момент мы понимаем, что мы почти у цели. Мы видим, что 𝑑 𝑠, тормозной путь, который мы пытаемся рассчитать, равен сумме мысленного пути и тормозного пути. Итак, мы можем сказать, что тормозной путь равен 24 метрам плюс 44,4 повторяющихся метра. В итоге получается 68,4 повторяющихся метра.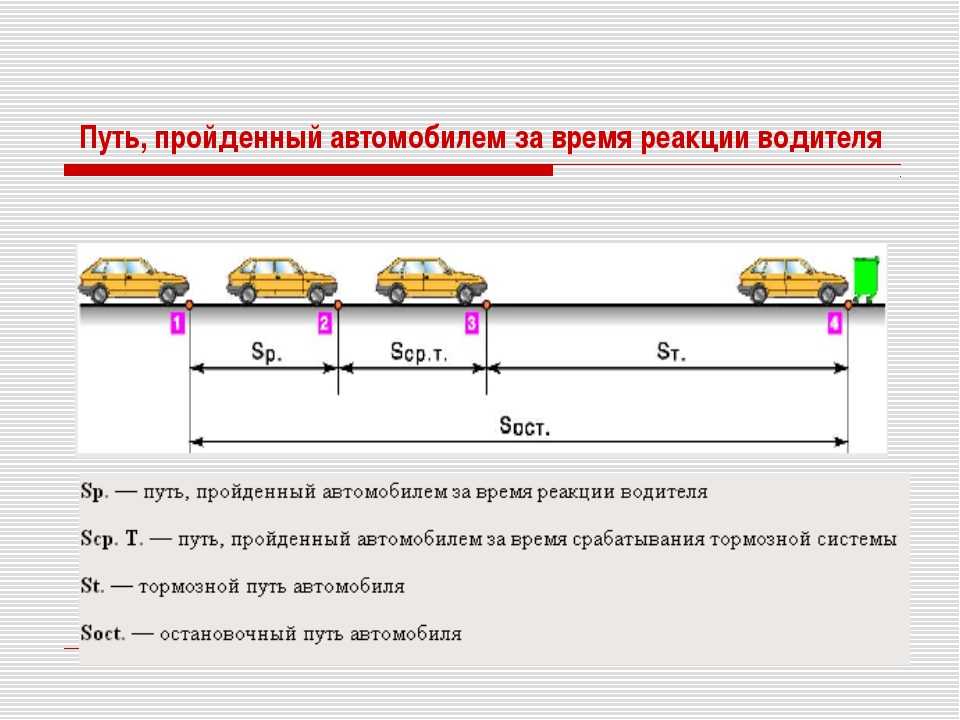
Однако окончательного ответа на наш вопрос мы еще не получили.
Помните, нас попросили определить тормозной путь автомобиля с точностью до метра. Итак, нам нужно округлить 68,4 метра до ближайшего метра. Для этого нам нужно посмотреть на это значение здесь после запятой. Это значение равно четырем, что меньше пяти. И, следовательно, это значение, восемь, останется прежним. Не собирается округляться. И вот, мы подошли к ответу на наш вопрос. Тормозной путь этого автомобиля составляет 68 метров с точностью до метра.
Как рассчитать замедление | наука
Обновлено 14 декабря 2020 г.
Автор: Don Patton
Замедление на самом деле означает ускорение в обратном направлении; в то время как ускорение означает скорость, с которой объект ускоряется, замедление означает скорость, с которой объект замедляется. Например, останавливающийся самолет должен иметь высокую скорость торможения, чтобы оставаться на взлетно-посадочной полосе, а автомобиль иногда должен замедляться с определенной скоростью, чтобы оставаться в потоке движения.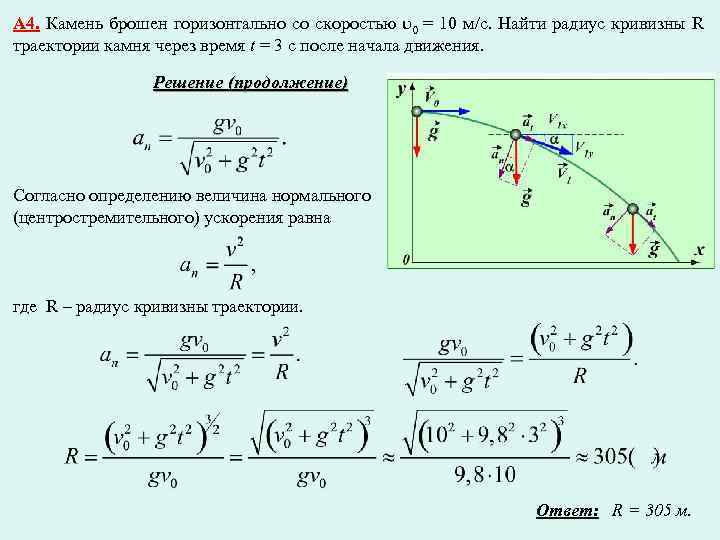
Два уравнения полезны для расчета замедления. Одна формула включает время, необходимое для замедления объекта, а другая формула использует расстояние. Расчетные скорости замедления могут быть выражены в единицах стандартной земной гравитации (G).
Замедление может быть рассчитано как изменение скорости за определенный период времени по формуле конечная скорость (s f ) минус начальная скорость (s i ), деленная на время изменения скорости (t):
\text{deceleration}=\frac{s_f-s_i}{t}
Замедление также может быть рассчитано как изменение скорости в зависимости от расстояния по формуле конечная скорость в квадрате (s f 2 ) минус начальная скорость квадрат (s i 2 ) разделить на удвоенное расстояние (d): 92}{2d}
При необходимости преобразуйте единицы измерения, чтобы убедиться, что единицы измерения, будь то футы в секунду или метры в секунду, остаются согласованными.
Использование разницы скоростей и времени
Вычтите конечную скорость из начальной скорости.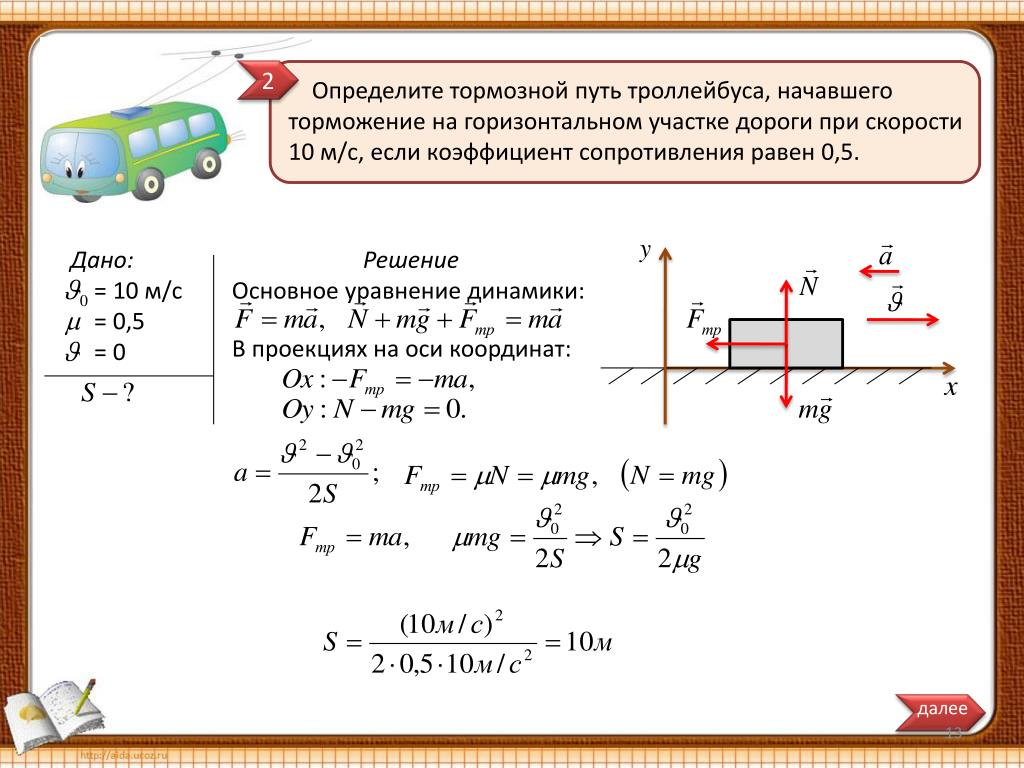
Преобразование разницы скоростей в единицы скорости, совместимые с вычисляемым ускорением. Ускорение обычно выражается в футах в секунду в секунду или метрах в секунду в секунду. Если скорость выражена в милях в час, преобразуйте эту скорость в футы в секунду, умножив результат на 1,47 (5 280 футов на милю разделить на 3 600 секунд в час). Точно так же умножьте километры в час на 0,278, чтобы преобразовать скорость в метры в секунду.
Разделите изменение скорости на время, в течение которого произошло изменение. Этот расчет дает среднюю скорость замедления.
Рассчитайте, например, замедление, необходимое для снижения скорости приземляющегося самолета с 300 миль в час до 60 миль в час за 30 секунд.
Преобразуйте скорости следующим образом:
300 х 1,47 = 440 футов в секунду и }60 х 1,47 = 88 футов в секунду второй. Скорость замедления рассчитывается как:
\frac{212}{30} = 7,07 \text{ футов в секунду в секунду}
Использование разницы скоростей и расстояния
Преобразуйте начальную и конечную скорости в единицы, которые будут полезны для расчета ускорения (футы в секунду или метры в секунду).
Также убедитесь, что расстояние, на котором происходит изменение скорости, указано в совместимых единицах измерения (футы или метры).
Возведение в квадрат начальной и конечной скорости.
Вычесть квадрат конечной скорости из квадрата начальной скорости.
Разделить расстояние на два. Это средний показатель замедления.
Рассчитайте, например, замедление, необходимое для остановки автомобиля на расстоянии 140 футов, если он движется со скоростью 60 миль в час.
Преобразование 60 миль в час в 88 футов в секунду. Поскольку конечная скорость равна нулю, разница равна этому результату в квадрате: 7744 фута в квадрате на секунду в квадрате. Скорость замедления:
\frac{7744}{2\times 140}=27,66\text{ футов в секунду в секунду}
Замедление в единицах силы тяжести (G)
Рассчитайте скорость замедления, используя один из двух методов, описанных выше.
Разделить замедление на стандартное ускорение свободного падения.
Leave A Comment