Треугольная призма. Правильная треугольная призма вершины. Основание правильной треугольной призмы. Боковые грани правильной треугольной призмы
- Альфашкола
- Статьи
- Призма
Призма представляет собой многогранник — трехмерную геометрическую фигура с плоскими гранями и прямыми ребрами, которые имеет одинаковую форму поперечного сечения по всей длине и ограниченной на каждом конце двумя равными и параллельными многоугольниками. Остальные грани призмы (боковые грани) являются параллелограммами. Треугольная призма показана ниже:
Если количество сторон одного из могоугольников в основании призмы равно \(n\), то призма будет иметь \(N + 2\) грани, \(3n\) ребер и \(2n\) вершин.
Треугольная призма
Также вы можете встретить правильную призма, то есть все базовые грани в основании призмы являются правильными многоугольниками. Из этого следует, что все боковые грани неправильной призмы не будут иметь одинаковые размеры.
Регулярная шестиугольная призма (слева) и неправильная призма (справа)
Возникает интересный вопрос о том, можно ли иметь цилиндрическую призму. Если боковые грани цилиндра оба равны и параллельны, то сечение, безусловно, соответствуют требованиям призмы. Точка прилипания находится над требованием, что базовые грани призмы должны быть многоугольниками. Поскольку базовая грань цилиндра должна быть либо кругом, либо эллипсом, часто утверждается, что цилиндр не может быть призмой, потому что ни круг, ни эллипс не являются многоугольником. С другой стороны, можно также утверждать, что, поскольку теоретически нет предела количеству сторон, которые может иметь многоугольник, круг (или эллипс) — это просто многоугольник с бесконечным числом сторон.
Как найти объем призмы. Для правильной призмы найти объем относительно просто. Все, что нам нужно сделать, это умножить площадь одной базовой грани призмы на длину призмы. Здесь полезно думать о призме как о стоящей на одной из ее базовых граней. Длина призмы это высота \(h\). Поэтому мы можем написать формулу для нахождения объема \(V\) призмы как:
\(V = S_{осн}h\)
Это также работает для косой, смещенной призмы, если мы рассматриваем высоту как перпендикулярное расстояние между двумя базовыми гранями.
Высота призмы — это перпендикулярное расстояние между ее гранями в основании.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Станислав Николаевич Перепада
Репетитор по математике
Стаж (лет)
Образование:
Челябинский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Виктория Игоревна Лаптик
Репетитор по математике
Стаж (лет)
Образование:
Мозырский государственный педагогический университет им. И.П. Шамякина
И.П. Шамякина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Елена Сергеевна Чаплина
Репетитор по математике
Стаж (лет)
Образование:
Омский государственный педагогический институт им. А.М.Горького
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Репетитор по олимпиадной математике
- Репетитор по алгебре
- Репетитор по химии для подготовки к ЕГЭ
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Репетитор по английскому языку для подготовки к ЕГЭ
- Репетитор по английскому языку для подготовки к ОГЭ
- Английский язык для начинающих
- Репетитор для подготовки к ОГЭ по истории
- Репетитор для подготовки к ВПР по обществознанию
- Репетитор по географии для подготовки к ЕГЭ
Похожие статьи
- Высшая Школа Бизнеса МГУ: стоимость обучения и проходной балл
- Факультет Менеджмента Финансового Университета: отзывы
- РУДН: факультет Экологии и Природопользования
- Как найти точку пересечения плоскости и прямой
- Решаем задание №13 из ОГЭ
- Лучшие идеи декора на Хэллоуин своими руками
- Что такое снег, как появляется и зачем он нужен?
- Как использовать материнский капитал на образование: полная инструкция для родителей
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Какая пространственная геометрическая форма имеет столько граней, сколько граней?
Шестигранник, также называемый кубом, образован 12 ребрами, 8 вершинами и 6 гранями. Согласно греческому философу Платону, шестигранник представляет собой элемент земли, фигуру, образованную 12 ребрами, 8 вершинами и 6 гранями в четырехугольном формате. Шестигранник также можно назвать кубом.
Согласно греческому философу Платону, шестигранник представляет собой элемент земли, фигуру, образованную 12 ребрами, 8 вершинами и 6 гранями в четырехугольном формате. Шестигранник также можно назвать кубом.
Также известный как шестигранник, куб представляет собой геометрическое тело, все грани которого образованы квадратами. У него 6 граней, 12 ребер и 8 вершин. Куб представляет собой шестигранный многогранник, все грани которого квадратные.
Две пространственные геометрические фигуры, имеющие одинаковое количество граней, — это параллелепипед и куб, обе с 6 гранями. Мы также можем связать пирамиды с правильными призмами.
Сколько граней у пространственной фигуры? Грани: у него 6 квадратных граней; Диагонали: внутри куба 4 диагонали; Вершины: имеет 8 вершин; Углы: 24 прямых угла.
У него 8 вершин, 12 ребер и 6 граней, две из которых являются основаниями, а остальные прямоугольными.
Параллелепипед – это геометрическое тело, грани которого образованы параллелограммами. Он состоит из 8 вершин, 12 ребер и 6 граней. Он классифицируется как прямой, если его края перпендикулярны, и как косой, если его края не перпендикулярны.
Он состоит из 8 вершин, 12 ребер и 6 граней. Он классифицируется как прямой, если его края перпендикулярны, и как косой, если его края не перпендикулярны.
Призмы: это многогранники с двумя параллельными и конгруэнтными основаниями, n боковыми гранями (параллелограммами) и (n+2) гранями. Пирамиды: многогранники, имеющие основание, n боковых граней (треугольников) и (n+1) граней.
Цилиндр представляет собой геометрическое тело с двумя плоскими круглыми гранями, являющимися его основаниями, и изогнутой боковой гранью.
Октаэдр имеет 8 конгруэнтных треугольных граней и 6 конгруэнтных тетраэдрических углов.
Правильный октаэдр образован 12 ребрами, 6 вершинами и 8 гранями. Его грани имеют форму равностороннего треугольника.
В геометрии лицо — это как бы одна сторона пространственной геометрической формы. Каждая грань состоит как минимум из трех ребер, чтобы иметь определенную форму (треугольник). В 3D-форме каждая сторона представляет собой лицо.
Пространственные фигуры необходимо определять в трехмерных пространствах, так как они имеют глубину в дополнение к длине и ширине. Кубы, призмы, цилиндры, конусы и сферы, например, являются фигурами, которые могут быть определены только в трехмерном пространстве.
Кубы, призмы, цилиндры, конусы и сферы, например, являются фигурами, которые могут быть определены только в трехмерном пространстве.
Параллелепипед — это геометрическое тело, имеющее 6 граней, 8 вершин и 12 ребер. Грани параллелепипеда образованы параллелограммами. Параллелепипед может быть прямым или косым.
Многогранники — это геометрические фигуры, образованные плоскостями и имеющие в качестве элементов вершины, ребра и грани. Каждая фигура или геометрическое тело имеет некоторые характерные элементы, которые часто используются в математических расчетах и определениях.
Это геометрическое тело очень круглое. У него нет плоских граней: на самом деле у него только одна изогнутая грань, и он катится, как футбольный мяч.
Треугольная пирамида: ее основание представляет собой треугольник, состоящий из четырех граней: трех боковых граней и базовой грани.
Шестиугольная призма — это призма, у которой шестиугольные основания параллельны друг другу. Шестиугольные основания соединены шестью прямоугольными боковыми гранями. Шестиугольные призмы имеют в общей сложности 8 граней, 12 вершин и 18 ребер.
Шестиугольные призмы имеют в общей сложности 8 граней, 12 вершин и 18 ребер.
Ответ проверен экспертами. У прямоугольника 8 вершин, 12 ребер и 6 граней. Прямоугольник классифицируется как многогранник, то есть это трехмерная геометрическая фигура, образованная правильными плоскими геометрическими фигурами, такими как грани (квадрат, треугольники, шестиугольники и др.).
При беглом наблюдении можно заметить, что у куба шесть граней: квадрат вверху, квадрат внизу и четыре квадрата по бокам. Разделения между этими квадратами образуют 12 ребер: четыре на верхней грани, четыре на нижней грани и четыре на вертикальных гранях.
Пятиугольная призма – это призма, имеющая два параллельных пятиугольных основания и пять прямоугольных боковых граней. Эти призмы также считаются семигранниками. Эти трехмерные фигуры имеют всего 7 граней, 10 вершин и 15 ребер. Каждая из пятиугольных граней имеет пять ребер и пять вершин.
Куб также является случаем призмы, так как все его квадратные грани конгруэнтны. У призмы все грани образованы многоугольниками, следовательно, это частный случай многогранника.
У призмы все грани образованы многоугольниками, следовательно, это частный случай многогранника.
Например, если пирамида имеет треугольное основание, она называется пирамидой с треугольным основанием, теперь, если пирамида имеет четырехугольное основание, она называется пирамидой с четырехугольным основанием и так далее.
Кубы — это многогранники, классифицируемые как призмы. Эти многогранники имеют два конгруэнтных основания. Таким образом, зная, что все основания куба — квадраты, мы можем сказать, что два его основания — конгруэнтные квадраты и, следовательно, имеют одинаковую площадь. «l» — это сторона квадрата или ребро куба.
Семиугольная базовая призма (основание с 7 сторонами) имеет 14 вершин и 9 граней.
Таким образом, Эннеагон имеет 9 равных сторон, 9 вершин (вершина соответствует точке пересечения двух сторон геометрической фигуры) и 9 внутренних углов, равных 140º.
Этот вопрос связан с полигонами. Многоугольник – это замкнутая геометрическая фигура, имеющая углы и вершины. Он состоит из отрезков линии. Номенклатура многоугольников варьируется в зависимости от количества существующих сторон.
Он состоит из отрезков линии. Номенклатура многоугольников варьируется в зависимости от количества существующих сторон.
Грани — это многоугольники («стороны» многогранника), ребра — стороны многоугольника, а вершины — вершины многоугольника.
Пирамида: пространственная геометрическая фигура, образованная многоугольной гранью и треугольными боковыми гранями.
Что такое вершины, грани и ребра? Объяснение для начальной школы
Вершины, грани и ребра часто встречаются в геометрии, когда дети изучают свойства трехмерных фигур. Здесь мы объясним, что означает каждый из них, и как рассчитать количество вершин, граней и ребер для любой формы. Мы также включаем количество ребер, граней и вершин наиболее распространенных форм.
- Что такое вершины фигур?
- Что такое ребра?
- Что такое лица?
- Вершины, грани и ребра обычных трехмерных фигур
- Сколько граней, ребер и вершин имеет прямоугольный параллелепипед?
- Сколько граней, ребер и вершин у цилиндра?
- Сколько граней, ребер и вершин у полушария?
- Сколько граней, ребер и вершин у конуса?
- Сколько граней, ребер и вершин у тетраэдра?
- Сколько граней, ребер и вершин у сферы?
- Сколько граней, ребер и вершин у призмы?
- Треугольная призма
- Пятиугольная призма
- Шестиугольная призма
- Куб
- Куб
- Когда дети узнают о гранях, ребрах и вершинах?
- Как вершины, грани и ребра связаны с другими областями математики?
- Как вершины, грани и ребра соотносятся с реальной жизнью?
- Примеры вопросов о вершинах, гранях и ребрах
БЕСПЛАТНЫЙ набор математических игр и заданий для 5-го класса
17 увлекательных математических игр и заданий для учащихся 5-х классов, которые можно выполнять самостоятельно или с партнером.
Вершины в фигурах — это точки, в которых встречаются два или более сегмента линии или ребра (например, угол). Единственное число вершин является вершиной. Например, у куба 8 вершин, а у конуса одна вершина.
Вершины иногда называют углами, но при работе с 2D- и 3D-формами предпочтительнее слово вершины.
Куб имеет 8 вершин. 7 видны здесь, а один скрыт.
Что такое ребра?Ребра — это сегменты линии, которые соединяют одну вершину с другой, а также являются местом соединения граней фигуры. Их можно использовать для описания 2d и 3d форм.
Хотя многие фигуры имеют прямые линии и прямые края, существуют формы с изогнутыми краями, например полусфера. Куб будет иметь 12 прямых ребер, как показано ниже; 9 видимых и 3 скрытых.
Что такое лица? Грани — это плоские поверхности твердотельной формы. Например, кубоид имеет 6 граней. Размышляя о 2D- и 3D-формах, важно знать, что 2D-форма просто представляет собой грань 3D-фигуры.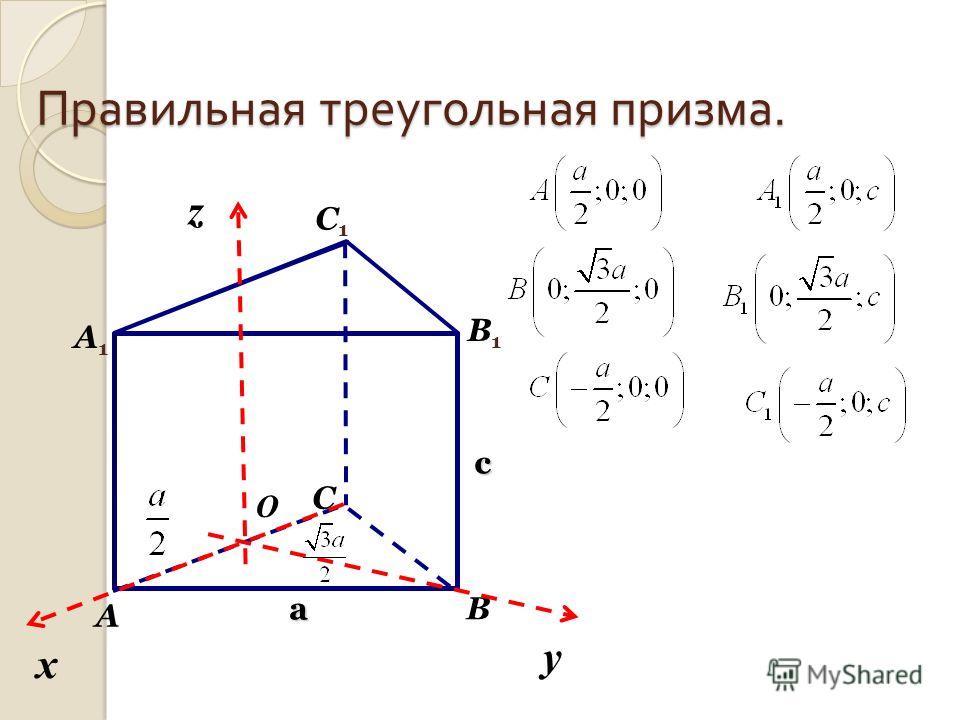
Также важно знать, что поскольку наша реальность построена в трех измерениях, физически невозможно обращаться с двухмерными формами, поскольку мы окружены трехмерными формами. Поэтому, если в вашем классе есть ящик с надписью «2d Shapes», его следует убрать, так как он учит детей неправильному пониманию. Несмотря на интерактивную концепцию для классной комнаты, 2D-формы могут существовать только в виде 2-мерных рисунков.
У вас могут быть как плоские грани, так и изогнутые грани, но я считаю полезным называть изогнутые грани изогнутыми поверхностями, поскольку это хорошо сочетается с визуальным видом формы.
На кубе внизу есть три видимые грани и три скрытые.
Вершины, грани и ребра обычных трехмерных фигур Сколько граней, ребер и вершин у прямоугольного параллелепипеда?Кубоид имеет 8 вершин.
Прямоугольный параллелепипед имеет 12 ребер.
Прямоугольный параллелепипед имеет 6 граней.
Цилиндр имеет 0 вершин.
Цилиндр имеет 2 грани.
Цилиндр имеет 2 грани и 1 изогнутую поверхность.
Сколько граней, ребер и вершин у полусферы?Полусфера имеет 0 вершин.
Полусфера имеет 1 изогнутую кромку.
Полусфера имеет 1 грань и 1 изогнутую поверхность.
Сколько граней, ребер и вершин у конуса?Конус имеет 1 вершину.
Конус имеет 1 ребро.
Конус имеет 1 грань и 1 изогнутую поверхность.
Сколько граней, ребер и вершин у тетраэдра?Тетраэдр имеет 4 вершины.
Тетраэдр имеет 6 ребер.
Тетраэдр имеет 4 грани.
Сколько граней, ребер и вершин у сферы?Сфера имеет 0 вершин.
Сфера имеет 0 ребер.
Сфера имеет 1 изогнутую поверхность.
Сколько граней, ребер и вершин у призмы? Призма представляет собой твердое тело, геометрическую фигуру или многогранник, у которого грани обоих концов имеют одинаковую форму.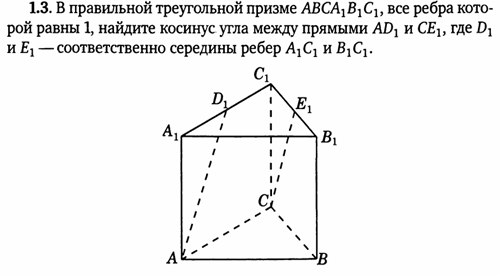 Таким образом, учащиеся будут сталкиваться со многими типами призм на протяжении всего обучения. Обычные включают кубы, параллелепипеды, треугольные призмы, пятиугольные призмы и шестиугольные призмы.
Таким образом, учащиеся будут сталкиваться со многими типами призм на протяжении всего обучения. Обычные включают кубы, параллелепипеды, треугольные призмы, пятиугольные призмы и шестиугольные призмы.
Треугольная призма
- Количество граней: 5
- Ребра: 9
- Вершин: 6
Пятиугольная призма
- Количество граней: 7
- Ребра: 15
- Вершин: 10
Шестиугольная призма
- Количество граней: 8
- Края: 18
- Вершин: 12
Куб
- Граней: 6
- Ребра: 12
- Вершин: 8
Прямоугольный
- Количество граней: 6
- Ребра: 12
- Вершин: 8
Дети должны быть формально ознакомлены со словарем вершин, граней и ребер, когда они только начинают изучать геометрию. Тем не менее, учителя могут решить ввести эту лексику раньше.
Учащиеся должны уметь:
- определять и описывать свойства трехмерных фигур, включая количество ребер, вершин и граней
- Учащиеся усваивают и называют множество распространенных 2D- и 3D-форм, включая четырехугольники и многоугольники, прямоугольные параллелепипеды, призмы и конусы, и определяют свойства каждой формы (например, количество сторон, количество граней).
- Ученики идентифицируют, сравнивают и сортируют фигуры на основе их свойств и точно используют словарный запас, например стороны, ребра, вершины и грани.
Учащиеся будут использовать знания о вершинах, гранях и ребрах при рассмотрении двухмерных и трехмерных фигур. Знание того, что такое ребра, и их идентификация на составных фигурах имеет решающее значение для нахождения периметра и площади составных двумерных фигур. Это важная основа для последующих лет работы с различными математическими теоремами, такими как теория графов и параболы.
Это важная основа для последующих лет работы с различными математическими теоремами, такими как теория графов и параболы.
Любой объект в реальной жизни имеет вершины, грани и ребра. Например, кристалл — это октаэдр — у него восемь граней, двенадцать ребер и шесть вершин. Знание этих свойств различных трехмерных форм закладывает основу для различных отраслей, таких как архитектура, дизайн интерьера, машиностроение и многое другое.
Вершины, грани и ребра примеры вопросов1. Объясните, что такое вершина.
(Ответ: вершина — это место, где встречаются две прямые)
2. Сколько ребер у треугольной призмы?
(ответ: 9)
3. Сколько вершин у конуса?
(Ответ: 1 вершина)
4. Сколько граней у прямоугольного параллелепипеда? Каковы 2d формы этих лиц?
(Ответ: 6 граней. Они могут иметь 2 квадратных грани и 4 прямоугольных грани или только 6 прямоугольных граней.)
Они могут иметь 2 квадратных грани и 4 прямоугольных грани или только 6 прямоугольных граней.)
5. Для всех обычных призм (кубов, кубоидов, треугольных призм, пятиугольных призм и шестиугольных призм) сложите грани и вершины вместе и вычтите ребра. Что вы заметили в ответах?
(Ответ: ответ всегда равен 2. Это известно как формула Эйлера (количество вершин – количество ребер + количество граней = 2) Ваши дети? Посмотрите наш математический словарь для детей или попробуйте эти:
- Что такое математические способности?
- Что такое двумерные фигуры?
- Что такое трехмерные фигуры?
Вы можете найти множество планов уроков геометрии и печатных рабочих листов на Third Space Learning Math Hub .
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте своим учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.
Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.
Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.
Содержание этой статьи было первоначально написано ведущим учителем начальной школы Нилом Алмондом, а затем было отредактировано и адаптировано для школ США учителем математики начальной школы Кристи Кулешей.
Видео с вопросами: определение фигур | Нагва
Стенограмма видео
Оливия купила большую бусину, чтобы повесить ее на ожерелье. Бусина имеет пять граней, девять ребер и шесть вершин. К какому из перечисленных типов относится фигура? И затем нам дается пять возможных ответов: сфера, цилиндр, куб, треугольная призма или прямоугольная призма.
Итак, эта задача требует от нас определить трехмерную фигуру, бусину, которую Оливия купила, чтобы повесить на ожерелье. И мы знаем, что шарик представляет собой трехмерную форму, потому что у него есть грани, ребра и вершины. И все это особенности трехмерных фигур. Таким образом, три признака, которые мы можем использовать для идентификации формы, заключаются в том, что у нее пять граней, девять ребер и шесть вершин. Что означают эти три слова? Давайте быстро напомним о себе.
Грань трехмерной фигуры — это многоугольник или двухмерная фигура, образующая плоскую поверхность части фигуры. Ребро 3D-фигуры — это отрезок линии, в котором сходятся две грани. А вершина трехмерной фигуры — это любая точка, в которой сходятся несколько ребер. Мы можем думать о них как об углах формы, более чем одной вершине. Мы называем это вершинами.
Итак, возникает вопрос, какая из этих пяти фигур имеет пять граней, девять ребер и шесть вершин? Один из способов найти ответ — пройтись по каждой фигуре отдельно и подумать о том, сколько граней, ребер и вершин имеет каждая фигура. Но есть более быстрый способ. У двух фигур в списке вообще нет вершин. Поэтому нам не нужно думать о других функциях. Сфера не имеет вершин. А у цилиндра нет вершин. И поэтому можно сказать, что бусина Оливии не сфера и не цилиндр.
Но есть более быстрый способ. У двух фигур в списке вообще нет вершин. Поэтому нам не нужно думать о других функциях. Сфера не имеет вершин. А у цилиндра нет вершин. И поэтому можно сказать, что бусина Оливии не сфера и не цилиндр.
Теперь у нас остались только три возможные формы: куб, треугольная призма и прямоугольная призма. Что мы знаем о кубиках? Мы знаем, что грани куба — квадраты. Но сколько их? Если мы посмотрим на наш куб здесь, мы увидим, что вокруг стороны есть четыре грани, одна сверху и одна снизу. Всего шесть лиц. Но у бусины Оливии пять граней. Нам не нужно проверять другие функции. Можно сказать, что ее бусинка не куб.
А как насчет треугольной призмы? Если мы посмотрим на эту треугольную призму, то увидим, что у нее пять граней, три прямоугольных грани по сторонам и по одной треугольной грани на каждом конце. Всего пять. Давайте проверим другие функции, чтобы увидеть, совпадают ли они. Сколько ребер у треугольной призмы? На нашей диаграмме мы видим, что есть два треугольника, по одному на каждом конце треугольной призмы.

Leave A Comment