Сколько лет по собственным часам двигался с постоянной скоростью: Замедление времени при скорости света

Замедление времени при скорости света

В современную эпоху люди разработали несколько действительно быстрых устройств. У нас есть невероятно быстрые самолеты, сверхбыстрые истребители, скоростные пассажирские железнодорожные экспрессы и так далее. Тем не менее, во вселенной есть нечто, что движется быстрее всего того, что мы можем создать – это свет.

Возможно, некоторые из вас задумывались – а каково это было бы путешествовать со скоростью света?

И что происходит, когда мы путешествуем со скоростью света? Краткий ответ таков: например, человек, путешествующий с такой скоростью, испытывает замедление времени. Для этого человека время будет двигаться медленнее, чем для того, кто не движется.

До 1900-х годов мир твердо верил в взгляд Исаака Ньютона с точки зрения объектов и гравитации. Однако в 20 веке Альберт Эйнштейн навсегда изменил этот мир.

Теория относительности, выдвинутая Эйнштейном, прояснила многие сомнения относительно массы и энергии. Уравнение эквивалентности массы и энергии доказало, что масса и энергия взаимопревращаемы, а это означает, что масса может быть преобразована в энергию и наоборот.

Он предположил, что нет стандартной системы отсчета. Все относительно – даже время. Исходя из этого, был сделан вывод, что скорость света постоянна и не зависит от наблюдателя. Следовательно, если человек движется со скоростью, равной половине скорости света, в том же направлении, что и сам свет, то луч света для него будет выглядеть так же, как и для неподвижного человека.

Что означает эквивалентность массы-энергии?

Это означает, что если объект движется со скоростью, которая составляет 10% от скорости света, то он будет испытывать увеличение своей массы на 0,5% от его первоначальной массы. С другой стороны, если объект путешествовал бы со скоростью 90% скорости света, тогда его масса была бы в 2 раза больше его первоначальной массы.

Скорость света “С” (имеется в виду скорость света в вакууме) — это фундаментальная постоянная, не зависящая от выбора системы отсчёта. Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства геометрии пространства-времени в целом. А теперь ответим на некоторые вопросы.

Можем ли мы путешествовать со скоростью света?

Нет, к сожалению мы не можем путешествовать со скоростью света.

Видите ли, если объект движется со скоростью света, его масса будет расти в геометрической прогрессии! Подумайте об этом – скорость света составляет около 299 792 километров в секунду (1.079.252.848,8 км. в час) и когда объект движется с такой скоростью, его масса становится бесконечной.

Поэтому для перемещения объекта потребуется бесконечная энергия, что невозможно. Вот почему ни один материальный объект не может двигаться со световой скоростью или со скоростью, превышающей скорость света.

Сколько понадобиться времени, чтобы преодолеть расстояние в один световой год? (световой год – это расстояние, которое свет проходит в вакууме за один год, около 10 триллионов километров).

На световой скорости: один год
На половине скорости света: два года
Корабли Breakthrough Starshot, что будут путешествовать со скоростью 0,2с: ~ 5 лет
На скорости самого быстрого за всю историю человека искусственного объекта (Гелиос 2,): ~ 4.269 лет
При скорости атома водорода в ядре Солнца: ~ 15.500 лет
На максимальной скорости ракеты Saturn V, которая доставила человека на Луну: ~ 108.867 лет
На скорости самого быстрого самолета в мире: ~ 305.975 лет
На скорости звука: ~ 882327 лет
На скорости автомобиля по шоссе: ~ 8.388.270 лет
При скорости ходьбы : ~ 215.993.799 лет
В темпе улитки: ~ 83.304.201.370.000 лет

Сколько времени займет путешествие на расстояние одного светового года со скоростью в одну десятую скорости света?

Логично предположить, что путешественнику понадобиться десять лет.

Однако, странные вещи могут случаться, когда вы путешествуете со скоростью, близкой к скорости света.

Допустим, космонавт находится на космическом корабле, движущемся со скоростью в одну десятую скорости света, и он покидает Землю и летит на какую-то гипотетическую планету на расстоянии одного светового года.

Наблюдатель остается на Земле и смотрит, как путешествует космонавт. И действительно, с точки зрения наблюдателя, космонавту понадобится десять лет, чтобы добраться до этой планеты. Но поскольку путешественник движется с субсветовой скоростью, время течет медленнее для него, чем для наблюдателя.

То есть каждый раз, когда часы на Земле отсчитывают минуту, на космическом корабле часы проходят чуть меньше одной минуты.

Смотрите также

Это означает, что с точки зрения путешественника (на космическом корабле) понадобится менее десяти лет, чтобы добраться до пункта назначения!

Разница в этом случае довольно мала: она составляет около 99,4% из десяти лет. Это означает, что космический полет окажется примерно на двадцать дней короче, чем для наблюдателя на Земле.

Существует уравнение для расчета замедления времени с учетом относительной скорости объекта:

Δ?′= Δ?₀ / √1− ?² / ?²

Где Δ?0 – временной интервал путешественника (называемый собственным временем), Δ? ′ – временной интервал Земли, ? – скорость путешественника (на который ссылается Земля), а ? – скорость света.

Для повседневных скоростей (например, скорости самолета) ? мала, поэтому эффекты замедления времени незначительны. Но если мы двигаемся со скоростью больше чем 1/10 скорости света, мы начинаем видеть заметные эффекты.

Что если мы будем двигаться почти со скоростью света?
Если мы говорим о скорости, почти равной скорости света, скажем, 90% скорости света, то будут весьма интересные наблюдения.

С одной стороны, человек, путешествующий с такой скоростью, испытает замедление времени. Для этого человека время будет идти медленнее, чем для того, кто не движется.

Например, если человек путешествует в космосе со 90% скорости света, то для этого человека будут проходить только 10 минут времени, в то время как для наблюдателя на Земле пройдет 20 минут. Время будет сокращено вдвое!

Кроме того, поле зрения космического путешественника резко изменится. Мир предстанет перед ним через окно в форме туннеля перед космическим кораблем, в котором он путешествует. Кроме того, звезды впереди будут казаться голубыми, а звезды позади – красными.

Это связано с тем, что световые волны от звезд перед кораблем будут собираться вместе, в результате чего объекты будут казаться синими, а световые волны от звезд за кораблем будут расходиться и выглядеть красными, вызывая экстремальный эффект Доплера.

После определенной скорости космический путешественник увидит только черноту, потому что длина волны света, попадающего на его глаза, будет вне видимого спектра.

Но эффект замедления времени усиливается, если двигаться все быстрее и быстрее. Скажем, космический корабль летит со скоростью 99,999999% от скорости света – тогда, с точки зрения наблюдателя на Земле, космонавт в основном движется со скоростью света, и ему понадобится один год, чтобы добраться до планеты, расположенной на расстоянии одного светового года.

Но с точки зрения космонавта, такое путешествие займет только чуть более часа! Этот эффект называется релятивистским замедлением времени, и он связан со многими другими странными вещами, которые происходят, когда объекты движутся с релятивистскими скоростями (то есть со скоростями, близкими к скорости света).

Эти понятия замедления времени и специальной теории относительности особенно интересны для размышления. Например, если в один прекрасный день у нас развивается скорость, близкая к скорости света, мы можем двигаться «вперед» во времени относительно Земли.

Космонавт может путешествовать в течение нескольких месяцев или лет на своем космическом корабле и вернуться на Землю, чтобы обнаружить, что все остальные постарели на десятилетия или столетия!

Другая возможность состоит в том, что те путешественники, которые исследуют глубокие просторы космоса, смогут перемещаться на большие расстояния, не состарившись, и все благодаря замедлению времени. Вы сами можете посчитать, как зависит течение времени от скорости:

Замедление времени

Калькулятор показывает замедление времени для космического путешественника по сравнению с наблюдателем с Земли, где временной интервал – это время, прошедшее на земле, скорость ракеты – это скорость космического корабля и космонавта, а относительное время – это время, которое прошло для космонавта на космическом корабле. Считать можно как в одну, так и в другую стороны.

На калькуляторе вы сможете видеть, что для того, чтобы разница в двух временных интервалах была заметной, скорость путешественника (скорость ракеты) должна быть чрезвычайно высокой – того же порядка, что и скорость света (299792.4 км/с).

Вот почему релятивистские эффекты настолько противоречивы: мы не можем испытать их в повседневной жизни и не замечаем их.

Конечно, эти эффекты реальны и измеримы. Часы на спутниках идут немного медленнее, чем на поверхности Земли. Как только мы сможем путешествовать со скоростью, достаточно близкой к скорости света – например, при 0,8 С – мы также увидим релятивистский эффект.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

0 0 голос

Рейтинг

Подписывайтесь на наш новый канал в и наши каналы в соц.сетях

Глава 4. Основы специальной теории относительности
	Лабораторная работа 4.1. Относительность промежутков времени

Относительность промежутков времени – одно из важных следствий специальной теории относительности Эйнштейна.

Интервал времени между двумя событиями может быть разным в разных системах отсчета.

Если два события происходят в одной и той же точке пространства в некоторой системе отсчета, и интервал времени, измеренный по часам неподвижного наблюдателя, оказался равным τ

0, то для наблюдателя в другой системе, которая движется относительно первой с постоянной скоростью υ, интервал времени между двумя этими событиями будет равен τ:

Здесь c – скорость света, β = υ / c.

Интервал τ всегда больше интервала τ₀, который называется собственным временем. Это означает, в частности, что ход часов, движущихся относительно наблюдателя, замедляется. Этот вывод теории относительности вытекает из постулата о постоянстве скорости света в различных системах отсчета.

Компьютерная модель позволяет познакомиться с одним из важных следствий специальной теории относительности Эйнштейна — относительностью промежутков времени. На экране дисплея представлен эксперимент по измерению интервала времени между двумя событиями наблюдателями в различных системах отсчета. Результаты измерения собственного времени и времени по часам движущегося наблюдателя выводятся на экран дисплея.

В левой части экрана воспроизводится эксперимент по измерению времени распространения светового импульса туда и обратно на неподвижной базе l = 1 км. Событие 1 – (световая вспышка) и событие 2 – (возвращение светового импульса) происходят в одной точке системы отсчета. Поэтому часы измеряют собственное время τ

0 = 2l / c. В правой части этот эксперимент рассматривается с точки зрения наблюдателя, который движется с некоторой скоростью υ перпендикулярно базе. События 1 и 2 в системе отсчета этого наблюдателя происходят в пространственно разобщенных точках. Время τ = 2L / c, измеренное по синхронизованным часам этой системы, окажется больше собственного времени τ₀.

В компьютерной модели можно изменять величину γ, которая связана со скоростью υ соотношением

При нажатии кнопки «Сброс» на часах в обеих системах отсчета высвечивается время наступления событий 1и 2.

Основы специальной теории относительности

В.А.ЕМЕЛЬЯНОВ,
Автодорожный лицей им. А.А.Николаева, г. Москва

Разноуровневые вопросы и задачи

В специальной теории относительности рассматриваются только инерциальные системы отсчета, т.е. такие, в которых выполняется закон инерции и скорость света в вакууме является универсальной постоянной.

Постулаты теории относительности

Первый постулат: законы физики имеют одинаковую форму во всех инерциальных системах отсчета. Это обобщение принципа относительности Ньютона на законы не только механики, но и всех других областей физики, носит название принципа относительности Эйнштейна.

Второй постулат: свет распространяется в вакууме с определенной скоростью c, не зависящей от скорости источника или наблюдателя. Согласно специальной теории относительности (СТО) скорость света в вакууме является абсолютной величиной, а такие абсолютные с точки зрения классической механики Ньютона понятия, как длина и время, стали относительными.

Из постулатов СТО следует, что скорость света в вакууме является предельно возможной. Никакой сигнал, никакое воздействие одного тела на другое не могут распространяться со скоростью, превышающей скорость света в вакууме.

Релятивистский закон сложения скоростей: если в неподвижной ситеме отсчета скорость тела и скорость движущейся системы отсчета направлены по одной прямой, то:

где u ‘ – скорость движения тела в движущейся системе отсчета; v – скорость движущейся системы K ‘ относительно неподвижной системы K;
u – скорость тела относительно неподвижной системы отсчета K (рис. 1).

Релятивистское замедление времени

Если t₀ – интервал времени между двумя событиями, происходящими в одной и той же пространственной точке, неподвижной относительно системы K ‘, а t – интервал времени между этими же событиями в системе K, то

где c – скорость света в вакууме. Время t₀, отсчитываемое по часам, покоящимся относительно данного тела, называется собственным временем. Оно всегда меньше времени, измеренного по движущимся часам: t₀ < t.

Релятивистское сокращение длины

Если l₀ – длина расположенного вдоль оси x ‘ стержня в системе K ‘, относительно которой он покоится, а

l – длина этого стержня в системе K, относительно которой он движется вдоль оси x со скоростью v, то:

Поперечные размеры движущегося стержня не изменяются. Линейный размер стержня l₀ в той системе отсчета, где он покоится, называется собственной длиной. Эта длина максимальна: l₀ > l.

Импульс движущегося тела (релятивистский импульс):

Полная энергия тела или системы тел:

Кинетическая энергия движущегося тела:

где E₀ = mc² – энергия покоящегося тела.

Соотношение Эйнштейна

Энергия, импульс и масса. Для свободной частицы E² = p²c² + m²c⁴.

При изменении массы тела на Dm выделяется эквивалентная энергия DE = Dmc².

Примеры решения задач

Задача 1. Две частицы движутся в вакууме вдоль прямой навстречу друг другу со скоростями 0,5 с и 0,75 с. Определите их относительную скорость.

Дано:

u = 0,5 с,
v = 0,75 с.
________

u ‘ – ?

Решение

Свяжем с первой частицей неподвижную систему отсчета

K, относительно которой она движется со скоростью u. Со второй частицей свяжем систему K ‘, движущуюся вдоль оси x со скоростью v относительно неподвижной системы K в направлении, противоположном оси x, то есть противоположном скорости u. Используя релятивистский закон сложения скоростей и учитывая, что проекция скорости v на ось x отрицательна, запишем выражение для скорости в неподвижной системе отсчета:

Отсюда находим относительную скорость частиц u ‘:

Подставляя численные значения, имеем:

Задача 2. Время жизни p-мезона в системе отсчета, связанной с ним, равно 2,6 • 10

–8 с. Определите время жизни p-мезона для наблюдателя, относительно которого он движется со скоростью 0,99с.
Дано:

t₀ = 2,6 • 10^–8 с,
v = 0,99 с.
_______

t – ?
Решение
Время жизни p-мезона, который движется со скоростью v, найдем по формуле:
где t₀ – собственное время жизни p-мезона. Подставляя численные данные, получаем:
Задача 3. Жесткий стержень AB длиной l₀ = 1 м покоится в системе K ‘ (рис. 2). Стержень расположен так, что составляет угол j₀ = 45° с осью x ‘. Определите длину l и угол

j в системе K, если скорость v системы K ‘ относительно K равна 0,8 с.

Дано:

l₀ = 1 м,
j₀ = 45°,
v = 0,8 с.
________

l – ? j – ?

Решение
Если отрезок, изображающий стержень, разложить на две компоненты, параллельные осям x ‘ и z ‘ соответственно, то длины его компонент, измеренные в системе K ‘, будут равны Dx ‘ = l₀ cos j₀, Dz‘ = l₀ sin j₀. При переходе от системы K‘ к K вертикальная компонента перпендикулярна
v и не испытывает никакого сокращения, а горизонтальная компонента, параллельная v, сокращается. Тогда:
Длина стержня, измеренная наблюдателем из K, будет равна:
Подставляя численные значения величин, получаем:
Для определения угла j воспользуемся соотношением:
Тогда:
Задача 4. Протон движется со скоростью 0,75 с. Определите его энергию покоя, полную энергию и кинетическую энергию.

Дано:

v = 0,75 с,
m = 1,67 • 10^–27 кг,
c = 3 • 108 м/с.
E₀ – ? E – ? E_к – ?
________
Решение
Энергия покоя протона определяется по формуле Эйнштейна: E₀ = mc².

Полная энергия протона:
В релятивистской механике кинетическая энергия E_к частицы определяется как разность между полной энергией E и энергией покоя E₀ этой частицы: E_к = E – E₀. Подставляя числовые значения величин, получаем:
E₀ = 1,67 • 10^–27 кг • (3 • 10⁸)² м²/с² = 15 • 10^–11 Дж.
E = 2,52 • 10^–27 кг • (3 • 10⁸)² м²/с² = 22,7 • 10^–11 Дж.
E_к = 22,7 • 10^–11 Дж – 15 • 10^–11 Дж = 7,7 • 10^–11 Дж.
Первый уровень
1. Какие системы отсчета называются инерциальными?
2. Сформулируйте и разъясните содержание первого постулата СТО – принципа относительности Эйнштейна.
3. В чем отличие первого постулата теории относительности в релятивистской физике от принципа относительности в классической физике?
4. Сформулируйте второй постулат СТО.
5. Сформулируйте закон сложения скоростей в классической механике.
6. Напишите релятивистский закон сложения скоростей.
7. Покажите, что классический закон сложения скоростей является частным случаем релятивистского закона сложения скоростей.
8. Может ли электрон двигаться со скоростью, превышающей скорость света в данной среде?
9. Какое время, отсчитанное между событиями, называется собственным?
10. В каких условиях наблюдается эффект замедления времени?
11. Что такое собственная длина стержня? Одинакова ли длина стержня в различных инерциальных системах отсчета? Имеет ли смысл понятие длина стержня вне связи с системой отсчета?
12. Какой стала бы длина тела в направлении вдоль скорости движения относительно неподвижного наблюдателя при v = c?
13. Какое выражение имеет закон релятивистской динамики?
14. По какой формуле определяется релятивистский импульс тела?
15. Что такое энергия покоя тела?
16. В чем состоит универсальный характер взаимосвязи импульса, энергии и массы тела?
17. Нагретая добела железная деталь охлаждена до комнатной температуры. Произошло ли изменение массы детали?
Второй уровень
18. Две космические ракеты движутся по одной прямой в одном направлении со скоростями 0,6 с и 0,8 с относительно неподвижного наблюдателя. Определите скорость удаления второй ракеты от первой по классической и релятивистской формулам сложения скоростей.
19. Две ракеты, снабженные ионными двигателями, приближаются одна к другой с противоположно направленными скоростями, равными 0,80 с и 0,70 с, относительно наблюдателя, покоящегося в некоторой точке на линии их сближения. Определите относительную скорость ракет по законам классической и релятивистской механики.
20. Определите количество лет, прошедших на Земле, если в космическом корабле при скорости его движения относительно Земли, равной 0,80 с, прошло 12 лет.
21. Определите промежуток времени, прошедший за 35 земных лет на звездолете, движущемся относительно Земли со скоростью 0,40 с.
22. Фотонная ракета движется относительно Земли со скоростью 0,60 с. Определите, во сколько раз замедляется ход времени в ракете с точки зрения земного наблюдателя.
23. Определите скорость движения космического корабля относительно Земли, при которой часы на нем идут в четыре раза медленнее, чем на Земле.
24. Собственная длина стержня равна 2,0 м. Определите его длину для наблюдателя, относительно которого стержень перемещается со скоростью 0,98 с, направленной вдоль стержня.
25. Жесткий стержень длиной 1 м измеряется двумя наблюдателями: первый покоится относительно стержня, второй движется вдоль него. Определите скорость движения второго наблюдателя, если измеренная им длина стержня равна 0,50 м.
26. Определите скорость движения космического корабля, если его продольные размеры для земного наблюдателя кажутся в пять раз меньше «истинных».
27. Определите размеры и форму квадратной пластинки с длиной стороны 1 м, которая удаляется от наблюдателя по прямой, параллельной одной из ее сторон, с относительной скоростью 0,80 c. Сравните площади покоящейся и движущейся пластинки.
28. Покажите, что объем куба, движущегося со скоростью v в направлении, параллельном одному из его ребер, равен
29. Определите импульс электрона, летящего со скоростью 0,98 с.
30. Определите кинетическую энергию электрона при движении его со скоростью 0,75 с по классическим и релятивистским формулам.
31. Определите скорость движения любой частицы вещества, при которой ее кинетическая энергия равна энергии покоя.
32. Определите энергию покоя электрона и нейтрона.
33. Одинакова ли масса сжатой и свободной пружины?
34. Определите изменение массы тела, если полная энергия этого тела возросла на 1 Дж.
35. Определите скорость движения частицы, если ее полная энергия равна E, а энергия покоя E₀.
36. Мощность излучения Солнца 3,9 • 10²³ кВт. Определите эквивалентное уменьшение массы Солнца за одну секунду при данном излучении.
Третий уровень
37. Мезон, движущийся со скоростью 0,99 с относительно Земли, пролетел от места своего рождения до точки распада расстояние 4,7 км. Определите собственное время жизни мезона и расстояние, которое пролетел бы мезон относительно Земли, если бы релятивистский эффект относительности интервала времени не имел места.
38. Жесткий стержень покоится в подвижной системе отсчета и ориентирован в ней под углом 37° к оси абсцисс. Определите скорость движения этого стержня параллельно оси абсцисс неподвижной системы отсчета, при которой он с точки зрения неподвижного наблюдателя наклонен к ней под углом 45°.
39. Покажите, что плотность материала куба, движущегося со скоростью v в направлении, параллельном одному из его ребер, равна
40. Определите скорость движения тела, если его плотность возросла на 10 %.
41. Определите скорость движения стержня, при которой релятивистское сокращение его длины составит 20 %.
42. Определите угол между диагоналями квадрата при его движении со скоростью 0,90 с в направлении, параллельном одной из сторон.
43. Определите скорость и кинетическую энергию, которая должна быть сообщена космическому кораблю массой 104 кг, чтобы его часы по возвращении на Землю показывали вдвое меньшее время, чем часы на Земле.
44. Определите работу, совершаемую однородным электрическим полем при разгоне электрона от скорости 0,980 c до 0,999 c.
45. Протон, имеющий начальную скорость 0,9 c, попадает в однородное электрическое поле и, двигаясь вдоль линии напряженности, полностью теряет свою скорость. Определите разность потенциалов двух точек, между которыми перемещался протон.
46. Определите скорость и импульс частицы массой m, если ее кинетическая энергия равна удвоенной энергии покоя.
47. Какую ускоряющую разность потенциалов должен пройти протон, чтобы его полная энергия стала в одиннадцать раз больше энергии покоя?
48. Находящаяся в озере вода объемом 2•10⁶ м³, нагрелась на 5 °С. Определите эквивалентное изменение массы.
49. На 1 м² поверхности, перпендикулярной направлению солнечных лучей около Земли, но вне ее атмосферы, приходит ежесекундно примерно 1,4 кДж энергии излучения Солнца. На какое время хватит массы водорода на Солнце, чтобы поддерживать это излучение? Расстояние от Солнца до Земли около 1,5 • 10⁸ км, масса Солнца 2 • 10³⁰ кг, количество водорода составляет 75 % по массе.
Четвертый уровень
50. Электрон испускается под углом 37° к оси x со скоростью 0,5 с. Определите абсолютное значение и направление скорости этого электрона относительно инерциальной системы, движущейся со скоростью с (рис. 3).
51. Стержень собственной длиной l₀ движется в лаборатории поступательно так, что вектор его скорости v образует угол j со стержнем. Определите длину стержня в лабораторной системе отсчета.
52. В лабораторной системе отсчета (K-система) движется стержень со скоростью 0,98 с. По измерениям, произведенным к K-системе, его длина оказалась равной 1,08 м, а угол, который он составляет с осью x, равным 78,7°. Определите собственную длину стержня в K ‘-системе, связанной со стержнем, и угол, который он составляет с осью x ‘.
53. Частица массой m0, двигаясь со скоростью 0,8 c, испытывает неупругое столкновение с покоящейся частицей той же массы. Определите скорость и энергию покоя составной частицы, которая образовалась в результате соударения.
Ответы
2. Все инерциальные системы отсчета эквивалентны в отношении любых физических процессов. Система отсчета, движущаяся с постоянной скоростью относительно данной ИСО, также есть ИСО, поэтому, кроме исходной, имеется множество других ИСО.
8. Может, но его скорость все равно меньше скорости света в вакууме.
10. Эффект замедления времени наблюдается только в тех системах отсчета, которые движутся друг относительно друга со скоростями, близкими к скорости света в вакууме.
11. Собственной длиной стержня l0 называется длина стержня в системе отсчета, относительно которой он покоится; длина стержня в различных системах отсчета неодинакова. Не имеет.
12. Из формулы следует, что при v ® c, l ® 0, следовательно, при v = с длина тела стала бы равной нулю, что невозможно.
15. Энергия покоя тела – это внутренняя энергия тела.
17. Да, произошло, на величину Dm = Q/c², где Q – количество теплоты, отданное деталью окружающей среде при ее охлаждении.
18. 0,2с; 0,385с.
19. 1,5с; 0,96с.
20. 20 лет.
21. 32 года.
22. 1,25.
23. 2,9 • 10⁸ м/с.
24. 0,4 м.
25. 0,866с.
26. 2,94 •10⁸ м/с.
27. Прямоугольник со сторонами 1 м и 0,6 м. Площадь уменьшилась на 0,4 м².
29. 1,34 • 10^–21 кг • м/с.
30. 2,3 • 10^–14 Дж; 4 • 10^–14 Дж.
31. 0,866с = 2,596•108 м/с.
32. 0,51 МэВ; 939,6 МэВ.
33. Масса сжатой пружины больше, чем свободной, на величину Dm =kx²/2c² , где k – коэффициент упругости, Dx – удлинение пружины.
34. 11,1 • 10^–18 кг.
35.
36. 4,4 • 10⁶ т.
37. 2,21 мкс; 665 м.
38. 0,66с.
40. 0,42с.
41. 0,6с.
42. 47°.
43. 260 000 км/с; 9 • 10²⁰ Дж.
44. 8,9 • 10⁶ эВ.
45. 1,216 • 10⁹ В.
46. 0,943с; 2,83mc.
47. 9,4 • 10⁹ В.
48. 4,67 • 10^–4 кг.
49. 14 400 млрд лет.
50. 0,325с; 67,3°.
51. b =v/c .
52. 1,5 м; 45°.
53. 0,5547с; 2,3m₀.
Задачи по физике и математике с решениями и ответами
Задача по физике — 6866
Покоящийся прямой конус имеет угол полураствора $\theta = 45^{ \circ}$ и площадь боковой поверхности $S_{0} = 4,0 м^{2}$. Найти в системе отсчета, движущейся со скоростью $v = 4/5$ с вдоль оси конуса:
а) его угол полураствора; б) площадь боковой поверхности. Подробнее
Задача по физике — 6867
С какой скоростью двигались в K-системе отсчета часы, если за время $t = 5,0 с$ (в K-системе) они отстали от часов этой системы на $\Delta t = 0,10 с$? Подробнее
Задача по физике — 6868
Стержень пролетает с постоянной скоростью мимо метки, неподвижной в K-системе отсчета. Время пролета $\Delta t =20 нс$ — в K-системе. В системе же отсчета, связанной со стержнем, метка движется вдоль него в течение $\Delta t^{ \prime} = 25 нс$. Найти собственную длину стержня. Подробнее
Задача по физике — 6869
Собственное время жизни некоторой нестабильной частицы $\Delta t_{0} = 10 нс$. Найти путь, который пролетит эта частица до распада в лабораторной системе отсчета, где ее время жизни $\Delta t = 20 нс$. Подробнее
Задача по физике — 6870
В K-системе отсчета мю-мезон, движущийся со скоростью $v = 0,990 с$, пролетел от места своего рождения до точки распада расстояние $l = 3,0 км$. Определить:
а) собственное время жизни этого мезона;
б) расстояние, которое пролетел мезон в K-системе с «его точки зрения». Подробнее
Задача по физике — 6871
Две частицы, двигавшиеся в лабораторной системе отсчета по одной прямой о одинаковой скоростью $v = 3/4 с$, попали в неподвижную мишень с интервалом времени $\Delta t = 50 нс$. Найти собственное расстояние между частицами до попадания в мишень. Подробнее
Задача по физике — 6872
Стержень движется вдоль линейки с некоторой постоянной скоростью. Если зафиксировать положение обоих концов данного стержня одновременно в системе отсчета, связанной с линейкой, то разность отсчетов по линейке $\Delta x_{1} = 4,0 м$. Если же положение обоих концов зафиксировать одновременно в системе Отсчета, связанной со стержнем, то разность отсчетов по этой же линейке $\Delta x_{2} = 9,0 м$. Найти собственную длину стержня и его скорость относительно линейки. Подробнее
Задача по физике — 6873
Два стержня одинаковой собственной длины $l_{0}$ движутся навстречу друг другу параллельно общей горизонтальной оси. В системе отсчета, связанной с одним из стержней, промежуток времени между моментами совпадения левых и правых концов стержней оказался равным $\Delta t$. Какова скорость одного стержня относительно другого? Подробнее
Задача по физике — 6874
Две нестабильные частицы движутся в К -системе отсчета по некоторой прямой в одном направлении со скоростью $v = 0,990 с$. Расстояние между ними в этой системе отсчета $l = 120 м$. В некоторый момент обе частицы распались одновременно в системе отсчета, связанной с ними. Какой промежуток времени между моментами распада обеих частиц наблюдали в K-системе? Какая частица распалась позже в K-системе? Подробнее
Задача по физике — 6875
Стержень АВ, ориентированный вдоль оси х K-системы отсчета, движется с постоянной скоростью и в положительном направлении оси х. Передним (по ходу движения) концом стержня является точка А, задним — точка В. Найти:
а) собственную длину стержня, если в момент $t_{A}$ координата точки А равна $x_{A}$, а в момент $t_{B}$ координата точки В равна $x_{B}$;
б) через какой промежуток времени надо зафиксировать координаты начала и конца стержня в K-системе, чтобы разность координат оказалась равной собственной длине стержня? Подробнее
Задача по физике — 6876
Стержень $A^{ \prime}B^{ \prime}$ движется с постоянной скоростью $v$ относительно стержня АВ (рис.). Оба стержня имеют одинаковую собственную длину $l_{0}$ и на концах каждого из них установлены синхронизированные между собой часы: A с В и $A^{ \prime}$ с $B^{ \prime}$. Пусть момент, когда часы $B^{ \prime}$ поравнялись с часами Л, взят за начало отсчета времени в системах отсчета, связанных с каждым из стержней. Определить:
а) показания часов В и $B^{ \prime}$ в момент, когда они окажутся напротив друг друга;
б) то же для часов A и $A^{ \prime}$.
Подробнее
Задача по физике — 6877
Имеются две группы синхронизированных часов К и $K^{ \prime}$, движущихся одна относительно другой со скоростью $v$, как показано на рис. Возьмем за начало отсчета времени момент, когда часы $A^{ \prime}$ окажутся напротив часов А. Изобразить примерное расположение стрелок всех часов в этот момент с «точки зрения» K-часов; $K^{ \prime}$ — часов.
Подробнее
Задача по физике — 6878
$K^{ \prime}$ — система отсчета движется в положительном направлении оси х K-системы со скоростью $V$ относительно последней. Пусть в момент совпадения начал координат О и $O^{ \prime}$ показания часов обеих систем в этих точках равны нулю. Найти в K-системе скорость $\dot{x}$ перемещения точки, в которой показания часов обеих систем отсчета будут все время одинаковы. Убедиться, что $\dot{x} Подробнее
Задача по физике — 6879
В двух точках K-системы отсчета произошли события, разделенные промежутком времени $\Delta t$. Показать, что если эти события причинно связаны в K-системе (например, выстрел и попадание пули в мишень), то они причинно связаны и в любой другой инерциальной $K^{ \prime}$ — системе отсчета. Подробнее
Задача по физике — 6880
На диаграмме пространства — времени (рис.) показаны три события А, В и С, которые произошли на оси х некоторой инерциальной системы отсчета. Найти:
а) промежуток времени между событиями A и В в той системе отсчета, где оба события произошли в одной точке;
б) расстояние между точками, где произошли события A и С, в той системе отсчета, где они одновременны.
Подробнее
удивительный феномен искривленного пространства-времени — Naked Science
Свою первую известную на весь мир теорию Эйнштейн назвал Специальной теорией относительности. Она была специальной, так как имела дело с постоянными скоростями. Чтобы примирить ее с реальным миром, в котором объекты постоянно ускоряются и замедляются, ему было необходимо исследовать последствия своей теории, когда речь заходила об ускорении. Эта попытка обобщить и учесть все общие феномены привела к открытию отношения между временем и гравитацией. Эйнштейн назвал свою новую теорию Общей теорией относительности.

Ньютон считал, что поток времени похож на стрелу. Оно непоколебимо движется только в одну сторону — вперед. Эйнштейн предположил, что время изменяется обратно пропорционально скорости. И благодаря своей текучести, подобно пространству, оно «заслуживало» собственного измерения. Более того, Эйнштейн утверждал, что пространство и время представляют собой единое целое — гибкую четырехмерную ткань, на которой происходят все события Вселенной. Он так и назвал это — ткань пространства-времени. Когда физик опубликовал свою работу со всеми ее выводами, ее встретили с недоверием.

Согласно Общей теории относительности, вещество растягивает и сжимает ткань пространства-времени. Получается, что объекты не притягиваются к центру Земли каким-то таинственным образом, а скорее, наоборот, подталкиваются искривленным пространством вокруг себя. Подобно склону, искривление пространства-времени ускоряет объекты, движущиеся вниз, хотя степень этого ускорения не всегда одинакова. Сила гравитации возрастает с приближением к поверхности Земли, где искривление интенсивнее.

История Вселенной на стреле времени / © NASA/GSFC

Если сила гравитации возрастает при движении вниз, объект свободно упадет в точку Б на поверхности быстрее, чем в точку А на большей высоте. Согласно Специальной теории относительности, время для свободно падающего объекта в точке Б должно идти медленнее относительно объекта в точке А из-за того, что скорость объекта в точке Б выше.

Что такое время

Какое время верное? Эйнштейн постулировал, что абсолютного времени нет. Время относительно в зависимости от системы сил, которым оно подвергается. Формально это называется системой отсчета. Время, протекающее в рамках вашей системы, называется собственным временем. Если законы движения должны быть одинаковыми для всех наблюдателей, независимо от их движения, то время должно замедляться. То есть чем быстрее вы движетесь, тем медленнее ваши часы тикают относительно других часов. Именно об этом героиня Энн Хэтэуэй говорила персонажу Мэтью МакКонахи в «Интерстелларе» после спуска на далекую планету: «Один час на этой планете равен семи земным годам».

Итак, является ли наблюдение замедленного времени ограничением нашего примитивного неврологического строения или же время действительно замедляется? И что вообще означает замедление времени? В итоге это приводит нас к вопросу: что есть время? Это не просто вопрос, который задают друг другу студенты философского факультета за бокалом пива. Понятие времени озадачивало натурфилософов и физиков с незапамятных времен.

Главная функция времени — отслеживание хронологии событий. Однако вплоть до последних 400 лет люди определяли время, основываясь на предположении, что звезды движутся вокруг Земли, а не наоборот. Несмотря на это, все работало до определенной степени приемлемо — из-за того, что дни и времена года предсказуемо повторялись, а когда у вас есть что-то предсказуемо повторяющееся, то есть и механизм для отслеживания времени.

Галилео использовал рекурсивную природу такого механизма для вычисления движения. Описание движения было бы невозможным без какого-либо обозначения времени. Но это время никогда не было абсолютным. Даже когда Ньютон формулировал свои законы движения, он использовал понятие времени, в котором две пары часов тикают синхронно не с абсолютным, независимым временем, а друг с другом. Синхронизация — причина, по которой человечество соорудило такие сложные и точные атомные часы.

Понятие времени построено на одновременности или решающем совпадении двух событий — вроде прибытия поезда и уникального совпадения стрелок часов в этот момент. Теория Эйнштейна утверждает, что на это должно влиять движение. Если два наблюдателя на платформе и поезд не могут прийти к единому мнению о том, что одновременно, они не могут прийти к согласию о том, как течет само время.

Движение искажает время

Чтобы понять влияние движения на предсказуемость, рассмотрим простейший механизм для отсчета времени. Представьте себе аппарат для отслеживания времени, состоящий из фотона, который отражается между двумя зеркалами, расположенными на конечном расстоянии друг от друга. Пусть за период отражения фотона проходит одна секунда. Теперь расположим два таких аппарата в точках А и Б над поверхностью Земли и прямо на ней (как в примере, описанном выше) и посмотрим, как они отсчитывают время, когда мимо них проносится свободно падающий объект. В свою очередь, этот объект измеряет собственное время при помощи таких же часов. Что они покажут?

Наблюдение отражения фотона между двумя движущимися зеркалами похоже на наблюдение теннисного мяча, прыгающего по движущемуся поезду. Даже если мяч отскакивает перпендикулярно для кого-то в поезде, для неподвижного наблюдателя снаружи он описывает треугольники.

Эксперимент с падающими часами / © Science ABC

При движении аппарата вперед кажется, что фотон, подобно мячу, преодолевает большее расстояние после отражения. Получается, один результат нашего эксперимента искажен! Более того, чем быстрее движется аппарат, тем больше фотону нужно времени для отражения, тем самым растягивается и длительность секунды. Именно поэтому ход времени в точке Б оказывается медленнее, чем в точке А (вспомним: из-за гравитации объект падает в точке Б быстрее, чем в точке А).

Конечно, эта разница ничтожна. Разница между временем, измеренным часами на вершинах гор и на поверхности Земли, — всего несколько наносекунд. Тем не менее открытие Эйнштейна стало настоящим прорывом. Гравитация действительно мешает ходу времени, а значит, чем массивнее объект, тем медленнее время течет вблизи него. Некоторые физики даже делают оговорку о том, что все объекты во Вселенной будто чувствуют это и стараются падать туда, где время идет медленнее, из мест, где время идет быстрее.

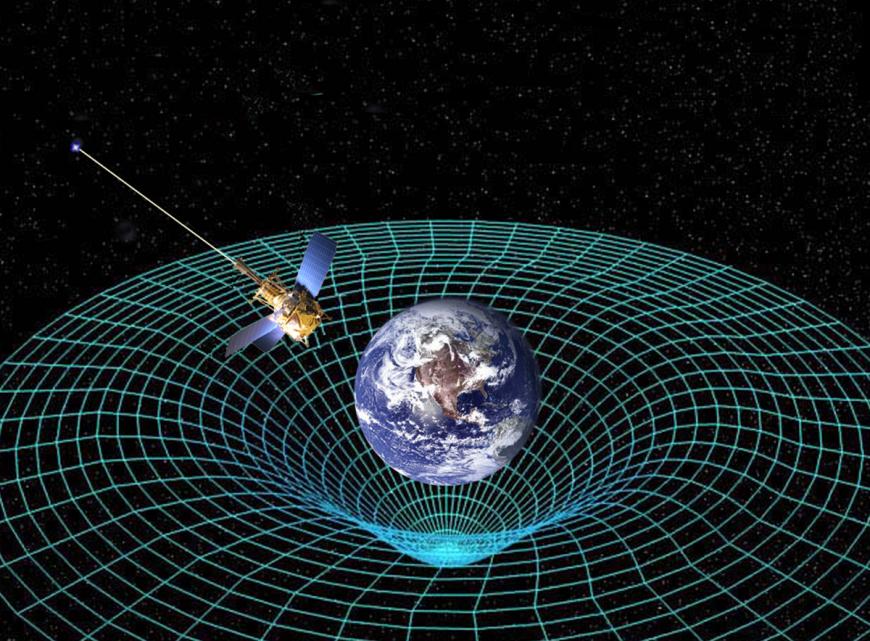
Гравитационное поле Земли и GPS-спутник / © NASA

Ноги моложе головы

Сегодня гравитационное замедление времени не только известный феномен из области теоретической физики, но и практический инструмент. Благодаря открытию Эйнштейна и его уравнениям, у нас есть такая замечательная вещь, как GPS-навигация, которая не смогла бы работать так точно, если бы не была учтена разница между ходом времени на поверхности Земли и ходом времени на околоземной орбите. Гравитационное замедление времени также помогает физикам-теоретикам и астрофизикам строить точные теории о том, что происходит в далеком космосе вблизи объектов, к которым мы пока не можем подобраться физически (например, черные дыры и нейтронные звезды). И да, учитывая этот феномен, получается, что ваши ноги — пусть и бесконечно незначительно — младше вашей головы.
Нашли опечатку? Выделите фрагмент и нажмите Ctrl + Enter.
Скопировать ссылку
Теория относительности в картинках / Хабр
В своей статье я хотел бы рассказать о теории относительности. Эта теория не требуется в представлении. С самого своего создания она была окутана ореолом тайны, поскольку полностью подрывает наши привычные представления о пространстве и времени. Все мы в школе учили формулы теории относительности, но мало кто действительно понимал их. И это не удивительно, ведь человеку, чтобы по-настоящему понять какую-то теорию во всей её красоте, полноте и непротиворечивости, не достаточно знать формулы. Нужно иметь какой-то визуальный ориентир, нужна динамика, чтобы было что-то, что можно повертеть в руках. Я решил восполнить этот пробел и написал небольшую программку, в которой можно «повертеть в руках» пространство-время. Мы, как настоящие исследователи, с помощью небольших экспериментов попытаемся выяснить основные свойства этой загадочной материи.
Под катом много картинок (и ни одной формулы).

Сразу следует прояснить, что существует две теории относительности:
— специальная теория относительности (СТО) рассматривает механику движения тел в пустом (не искривленном) пространстве-времени.
— общая теория относительности (ОТО) изучает явления гравитации и искривление пространства-времени объектами, обладающими массой.
Все описанное ниже относится к первой из них.
Прежде, чем рассматривать пространство-время, давайте вспомним, что такое обычное евклидово пространство.
И так, у нас имеется плоскость. В этой плоскости имеются некоторые геометрические фигуры: точки, отрезки. Так же у нас имеются две операции: параллельный перенос, и поворот. Давайте внимательно рассмотрим эти две операции.
Далее перейдем к рассмотрению так называемого пространства Минковского. В нем мы оставили параллельный перенос, но операцию поворота заменили на другую операцию. Как видите, при «повороте» каждая точка движется вдоль сереньких кривых. В результате все точки вытягиваются либо вдоль одной желтой прямой, либо вдоль другой.

При таком «повороте» отрезки сохраняют свою форму и переходят в отрезки.
Собственно, это и есть пространство-время. Давайте, будем считать, что горизонтальная ось — это пространство, а вертикальная — время. Будем считать, что время идет снизу вверх. Точка в пространстве-времени — это некоторое событие, которое произошло в некотором месте в некоторое время. А отрезок — это некоторый процесс. Например, если объект движется, то будем обозначать его движение отрезком.
Чтобы Вы немного сориентировались, поставим первый эксперимент.

Первым делом будем рассматривать объекты движущиеся с небольшими скоростями (много меньше скорости света).
Допустим, имеется некоторый неподвижный объект, например дерево. Нарисуем его с помощью вертикального отрезка.
Так же у нас имеется некоторый движущийся объект — автомобиль. Мы видим, что автомобиль едет навстречу дереву.

Нарисуем еще один движущийся объект. В результате получаем картину:

Обратите внимание, что чем сильнее наклон, тем скорость объекта больше.
Так выглядит наша картина из неподвижной системы отсчета. А что мы увидим, если будем сидеть в автомобиле? Для этого нам нужно немножко «перекосить» нашу плоскость.

Все правильно. Автомобиль теперь неподвижен, а дерево и человек движутся нам навстречу.
Точно так же мы можем перейти в систему отсчета, связанную с человеком. Для этого нам нужно «перекосить» пространство-время в другую сторону. В целом процесс перехода от одной системы отсчета в другую выглядит следующим образом:

Такое преобразование называется «преобразованием Галилея». При этом каждая точка движется вдоль горизонтальной прямой. Это значит, что время одинаково во всех системах отсчета (время абсолютно).
Давайте теперь перейдем к бОльшим масштабам, «сжав» нашу ось X.

На самом деле, переход от одной системы отсчета в другую есть ни что иное, как «поворот» в пространстве Минковского, а преобразования Галилея — это всего лишь предельный случай для маленьких скоростей.
Мы видим, что точки теперь движутся не горизонтально. Т.е. время не является абсолютной величиной, а зависит от выбранной системы отсчета.

Допустим имеются два наблюдателя, один неподвижный, другой летит на своем космическом корабле от него с некоторой скоростью.

Отметки на отрезке показывают, как идет время внутри объекта. Мы видим, что время неподвижного наблюдателя движется быстрее, чем у подвижного (один час у движущегося наблюдателя наступает позже, чем у неподвижного).
Но точно такую же картину видит и второй наблюдатель.

Вот так одна система отсчета переходит в другую

Получается странная ситуация — два наблюдателя смотрят друг на друга, и они друг другу кажутся «заторможенными».
Чтобы выяснить, кто же из них на самом деле «тормоз», второй наблюдатель разворачивает свой космический корабль и летит обратно.

Вместе они сверяют часы и выясняют, что у неподвижного наблюдателя прошло 5 единиц времени, а у подвижного — чуть больше 4. Т.е. наблюдатель, который «сделал крюк» в пространстве-времени потратил меньше своего внутреннего времени, чем неподвижный наблюдатель.
Но то же самое, только с точностью до наоборот, произошло бы, если бы первый наблюдатель полетел на встречу второму.

Вывод: у неподвижного наблюдателя время всегда идет быстрее, чем у движущегося.

Допустим, у нас имеется неподвижная космическая станция. От неё отстыковался некоторый корабль.
Перейдем в систему отсчета этого корабля. Далее от этого корабля отстыковался другой корабль.

Затем от второго корабля отстыковался третий.

и так далее.
Таким образом я пытался изобразить процесс ускорения. Очевидно, что каждый следующий корабль будет двигаться с большей скоростью, чем предыдущий. Давайте теперь вернемся к первому кораблю и посмотрим.

Напомню Вам, что наклон определяет скорость. Желтая линия, а точнее её наклон, показывает скорость света.
По картинке видно, что каждый следующий корабль приближается к скорости света, но не может превысить её. Так же видно, что внутреннее время с увеличением скорости все больше замедляется. Из этого мы делаем вывод, что ничто не может двигаться со скоростью, превышающей скорость света.
Пусть теперь каждый корабль выпускает луч света.

Мы видим, что свет в любой системе отсчета движется со скоростью света.

Две желтые линии очерчивают фигуру, называемую «световой конус». Световой конус разделяет пространство-время на две области, которые я отметил красным и зеленым цветами.

Если какое-то событие находится в красной области, то мы будем говорить, что событие находится в пределах светового конуса. Это означает, что свет из начала координат успевает долететь до нашей точки.
Если событие находится в зеленой области, то мы говорим, что событие находится за пределами светового конуса, и свет из начала координат не успевает долететь до этого события.
Рассмотрим следующий пример. Имеется три одновременных события

Давайте посмотрим, что произойдет, если мы будем менять систему отсчета.

Мы видим, что в другой системе отсчета события вовсе не являются одновременными. Теперь события не просто смещаются во времени, они еще меняют свой хронологический порядок. Событие, которое произошло раньше некоторого события, в другой системе отсчета может произойти позже. Но как такое может быть? Не является ли это нарушением причинно-следственных связей?
Напомню, что если событие находится за пределами светового конуса, это значит, что свет не может долететь до этого события за отведенное время. А поскольку ничто (никакой объект или сигнал) не может двигаться быстрее скорости света, получается, что событие, произошедшее в точке А, никак не может повлиять на событие в точке Б.

То же самое справедливо и в обратную сторону. Событие в точке Б никак не может повлиять на событие в точке А.

Про такие события говорят, что они не связаны причинно-следственными связями. Получается, что событие, находящееся за пределом светового конуса относительно данного, не связано с ним причинно-следственными связями.
Все космические объекты: солнечные системы, галактики — находятся на гигантских расстояниях друг от друга. И даже двигаясь со скоростью света, нам потребуется очень много времени, чтобы преодолеть эти расстояния. Например, ближайшая к нам звезда (альфа-Центавра) находится на расстоянии 4 световых года, а ближайшая галактика (Большое Магелланово Облако) — уже 160 тысяч световых лет. Если до альфа-Центавра мы еще можем слетать «туда и обратно», то слетать «туда и обратно» в соседнюю галактику уже не получится. Точнее, улететь-то мы сможем, а вот когда вернемся, на Земле пройдет уже 320 тысяч лет (напомню, что внутри объекта, движущегося со скоростью света, время практически стоит на месте). Что же делать?
Писатели-фантасты в своих произведениях очень ловко обходят это ограничение. Чего-только они не напридумывали: сверхскоростные двигатели, гипер-пространства, мультиплексы, искривление пространства-времени, прыжки через червоточины, черные дыры и т.д. На самом деле, проблема гораздо глубже, чем может показаться. Заключается она в том, что за пределами светового конуса НЕ МОГУТ существовать причинно-следственные связи. Иначе мы неизбежно придем к противоречиям.
Рассмотрим пример. Мы сидим на своей планете. В один прекрасный момент наши ученые изобретают «супер-телепортатор» способный телепортировать нас на любое расстояние за минимальное количество времени. Ну мы взяли и телепортировались в соседнюю галактику. Посидев в другой галактике, мы отправились на дальнейшее исследование космоса.

Если мы теперь перейдем в систему отсчета, связанную с нашим кораблем, то увидим следующее.

Мы видим, что наша исходная точка (планета Земля) сместилась в будущее. А поскольку законы природы во всех системах отсчета работают одинаково, то мы можем снова воспользоваться нашим «супер-телепортатором» и вернуться в собственное прошлое.

Получается, что движение со сверх-световой скоростью, эквивалентно перемещению во времени, а оно тянет за собой кучу парадоксов. Таким образом, проблема космических путешествий не в том, что мы не умеем искривлять пространство-время или строить сверх-световые двигатели, а в том, что даже теоретическая возможность таких перемещений подрывает все причинно-следственные связи.

На этом в общем-то и все. Самое основное, кажется, рассказал. Надеюсь, было понятно.
При написании статьи была использована программка (Ссылка на github)
Тренировочные варианты «Школково». Вариант — 1

1) $\color{red}{\small\text{Неверно }}$
Модуль ускорения тела в промежутке времени от 60 до 80 с: \[|a_{x1}| = \left|\dfrac{\Delta v_x}{\Delta t}\right| = \left|\dfrac{4\text{ м/с}-3\text{ м/с}}{20\text{ с}}\right| = 0,05 \text{ м/с}^2\] Модуль ускорения тела в промежутке времени от 80 до 100 с: \[|a_{x2}| = \left|\dfrac{\Delta v_x}{\Delta t}\right| = \left|\dfrac{3\text{ м/с}-0\text{ м/с}}{20\text{ с}}\right| = 0,15 \text{ м/с}^2\] Таким образом, модуль ускорения тела в промежутке времени от 60 до 80 с в 3 раза меньше модуля ускорения тела в промежутке времени от 80 до 100 с: \[\dfrac{|a_{x1}|}{|a_{x2}|} = \dfrac{0,05 \text{ м/с}^2}{ 0,15 \text{ м/с}^2} = \dfrac{1}{3}\] 2) $\color{green}{\small\text{Верно }}$
Путь, пройденный телом, можно найти как площадь фигуры под графиком.
Тогда путь, пройденный телом за время с 80 до 100 с, равен: \[S = \dfrac{1}{2}\cdot20\text{ с}\cdot3\text{ м/с} = 30\text{ м}\] 3) $\color{red}{\small\text{Неверно }}$
По второму закону Ньютона модуль равнодействующей сил равен: \[|F_x| = m|a_x|\] В момент времени 90 с ускорение тела равно: \[|a_x| = \left|\dfrac{\Delta v_x}{\Delta t}\right|= \left|\dfrac{3\text{ м/с}-0\text{ м/с}}{20\text{ с}}\right| = 0,15 \text{ м/с}^2\] Равнодействующая сил равна: \[F_x = 20\text{ кг} \cdot 0,15\text{ м/с}^2 = 3\text{ Н}\] 4) $\color{red}{\small\text{Неверно }}$
Импульс тела в момент времени 60 с: \[p_1 = mv_1 = 20\text{ кг}\cdot4\text{ м/с} = 80\text{ кг}\cdot\dfrac{\text{м}}{\text{с}}\] Импульс тела в момент времени 80 с: \[p_2 = mv_2 = 20\text{ кг}\cdot3\text{ м/с} = 60\text{ кг}\cdot\dfrac{\text{м}}{\text{с}}\] Так как $p_2 < p_1$, то можно сделать вывод, что в промежутке времени от 60 до 80 с импульс тела не увеличился, а уменьшился.
5) $\color{green}{\small\text{Верно }}$
Кинетическая энергия тела в момент времени 10 с: \[E_{\text{к}1} = \dfrac{mv_3^2}{2} = \dfrac{20\text{ кг}\cdot(2\text{ м/с})^2}{2} = 80\text{ Дж}\] Кинетическая энергия тела в момент времени 20 с: \[E_{\text{к}2} = \dfrac{mv_4^2}{2} = \dfrac{20\text{ кг}\cdot(4\text{ м/с})^2}{2} = 320\text{ Дж}\] Таким образом, кинетическая энергия тела в промежутке времени от 10 до 20 с увеличилась в 4 раза: \[\dfrac{E_{\text{к}2} }{E_{\text{к}1}} = \dfrac{ 320\text{ Дж}}{80\text{ Дж}} = 4\]
Ответ: 25
90000 Time Travel: Theories, Paradoxes & Possibilities 90001 90002 90003 Time travel may be theoretically possible, but it is beyond our current technological capabilities. (Image credit: argus Shutterstock) 90002 Time travel — moving between different points in time — has been a popular topic for science fiction for decades. Franchises ranging from «Doctor Who» to «Star Trek» to «Back to the Future» have seen humans get in a vehicle of some sort and arrive in the past or future, ready to take on new adventures.Each come with their own time travel theories. 90003 90002 The reality, however, is more muddled. Not all scientists believe that time travel is possible. Some even say that an attempt would be fatal to any human who chooses to undertake it. 90003 90008 Understanding time 90009 90002 What is time? While most people think of time as a constant, physicist Albert Einstein showed that time is an illusion; it is relative — it can vary for different observers depending on your speed through space. To Einstein, time is the «fourth dimension.»Space is described as a three-dimensional arena, which provides a traveler with coordinates — such as length, width and height -showing location. Time provides another coordinate — direction — although conventionally, it only moves forward. (Conversely, a new theory asserts that time is «real.») 90003 90002 90003 Most physicists think time is a subjective illusion, but what if time is real? (Image credit: Shutterstock / Kim D. French) 90002 Einstein’s theory of special relativity says that time slows down or speeds up depending on how fast you move relative to something else.Approaching the speed of light, a person inside a spaceship would age much slower than his twin at home. Also, under Einstein’s theory of general relativity, gravity can bend time. 90003 90002 Picture a four-dimensional fabric called space-time. When anything that has mass sits on that piece of fabric, it causes a dimple or a bending of space-time. The bending of space-time causes objects to move on a curved path and that curvature of space is what we know as gravity. 90003 90002 Both the general and special relativity theories have been proven with GPS satellite technology that has very accurate timepieces on board.The effects of gravity, as well as the satellites ‘increased speed above the Earth relative to observers on the ground, make the unadjusted clocks gain 38 microseconds a day. (Engineers make calibrations to account for the difference.) 90003 90002 In a sense, this effect, called time dilation, means astronauts are time travelers, as they return to Earth very, very slightly younger than their identical twins that remain on the planet. 90003 90008 Through the wormhole 90009 90002 General relativity also provides scenarios that could allow travelers to go back in time, according to NASA.The equations, however, might be difficult to physically achieve. 90003 90002 One possibility could be to go faster than light, which travels at 186,282 miles per second (299,792 kilometers per second) in a vacuum. Einstein’s equations, though, show that an object at the speed of light would have both infinite mass and a length of 0. This appears to be physically impossible, although some scientists have extended his equations and said it might be done. 90003 90002 A linked possibility, NASA stated, would be to create «wormholes» between points in space-time.While Einstein’s equations provide for them, they would collapse very quickly and would only be suitable for very small particles. Also, scientists have not actually observed these wormholes yet. Also, the technology needed to create a wormhole is far beyond anything we have today. 90003 90008 Alternate time travel theories 90009 90002 While Einstein’s theories appear to make time travel difficult, some groups have proposed alternate solutions to jump back and forth in time. 90003 90002 90035 Infinite cylinder 90036 90003 90002 Astronomer Frank Tipler proposed a mechanism (sometimes known as a Tipler Cylinder) where one would take matter that is 10 times the sun’s mass, then roll it into very long but very dense cylinder.90003 90002 After spinning this up a few billion revolutions per minute, a spaceship nearby — following a very precise spiral around this cylinder — could get itself on a «closed, time-like curve», according to the Anderson Institute. There are limitations with this method, however, including the fact that the cylinder needs to be infinitely long for this to work. 90003 90002 90003 An artist’s impression of a black hole like the one weighed in this work, sitting in the core of a disk galaxy. The black-hole in NGC4526 weighs 450,000,000 times more than our own Sun.(Image credit: NASA / JPL-Caltech) 90002 90035 Black holes 90036 90003 90002 Another possibility would be to move a ship rapidly around a black hole, or to artificially create that condition with a huge, rotating structure. 90003 90002 «Around and around they’d go, experiencing just half the time of everyone far away from the black hole. The ship and its crew would be traveling through time,» physicist Stephen Hawking wrote in the Daily Mail in 2010. 90003 90002 «Imagine they circled the black hole for five of their years.Ten years would pass elsewhere. When they got home, everyone on Earth would have aged five years more than they had. «90003 90002 However, he added, the crew would need to travel around the speed of light for this to work. Physicist Amos Iron at the Technion-Israel Institute of Technology in Haifa, Israel pointed out another limitation if one used a machine: it might fall apart before being able to rotate that quickly. 90003 90002 90035 Cosmic strings 90036 90003 90002 Another theory for potential time travelers involves something called cosmic strings — narrow tubes of energy stretched across the entire length of the ever-expanding universe.These thin regions, left over from the early cosmos, are predicted to contain huge amounts of mass and therefore could warp the space-time around them. 90003 90002 Cosmic strings are either infinite or they’re in loops, with no ends, scientists say. The approach of two such strings parallel to each other would bend space-time so vigorously and in such a particular configuration that might make time travel possible, in theory. 90003 90008 Time machines 90009 90002 It is generally understood that traveling forward or back in time would require a device — a time machine — to take you there.Time machine research often involves bending space-time so far that time lines turn back on themselves to form a loop, technically known as a «closed time-like curve.» 90003 90002 90003 The Doctor’s time machine is the TARDIS, which stands for Time and Relative Dimensions in Space. (Image credit: BBCAmerica) 90002 To accomplish this, time machines often are thought to need an exotic form of matter with so-called «negative energy density.» Such exotic matter has bizarre properties, including moving in the opposite direction of normal matter when pushed.Such matter could theoretically exist, but if it did, it might be present only in quantities too small for the construction of a time machine. 90003 90002 However, time-travel research suggests time machines are possible without exotic matter. The work begins with a doughnut-shaped hole enveloped within a sphere of normal matter. Inside this doughnut-shaped vacuum, space-time could get bent upon itself using focused gravitational fields to form a closed time-like curve. To go back in time, a traveler would race around inside the doughnut, going further back into the past with each lap.This theory has a number of obstacles, however. The gravitational fields required to make such a closed time-like curve would have to be very strong, and manipulating them would have to be very precise. [Related: Warp Speed, Scotty? Star Trek’s FTL Drive May Actually Work] 90003 90008 Grandfather paradox 90009 90002 Besides the physics problems, time travel may also come with some unique situations. A classic example is the grandfather paradox, in which a time traveler goes back and kills his parents or his grandfather — the major plot line in the «Terminator» movies — or otherwise interferes in their relationship — think «Back to the Future» — so that he is never born or his life is forever altered.90003 90002 If that were to happen, some physicists say, you would be not be born in one parallel universe but still born in another. Others say that the photons that make up light prefer self-consistency in timelines, which would interfere with your evil, suicidal plan. 90003 90002 Some scientists disagree with the options mentioned above and say time travel is impossible no matter what your method. The faster-than-light one in particular drew derision from American Museum of Natural History astrophysicist Charles Lu.90003 90002 That «simply, mathematically, does not work,» he said in a past interview with sister site LiveScience. 90003 90002 Also, humans may not be able to withstand time travel at all. Traveling nearly the speed of light would only take a centrifuge, but that would be lethal, said Jeff Tollaksen, a professor of physics at Chapman University, in 2012. 90003 90002 Using gravity would also be deadly. To experience time dilation, one could stand on a neutron star, but the forces a person would experience would rip you apart first.90003 90008 Time travel in fiction 90009 90002 Two 2015 articles by Space.com described different ways in which time travel works in fiction, and the best time-travel machines ever. Some methods used in fiction include: 90003 90002 90035 One-way travel to the future: 90036 The traveler leaves home, but the people he or she left behind might age or be dead by the time the traveler returns. Examples: «Interstellar» (2014 року), «Ikarie XB-1» (1963) 90003 90002 90035 Time travel by moving through higher dimensions: 90036 In «Interstellar» (2014 року), there are «tesseracts» available in which astronauts can travel because the vessel represents time as a dimension of space.A similar concept is expressed in Madeleine L’Engle’s «A Wrinkle In Time» (2018, based on the book series that started in 1963), where time is folded by means of a tesseract. The book, however, uses supernatural beings to make the travel possible. 90003 90002 90035 Travelling the space-time vortex: 90036 The famous «Doctor Who» (1963-present) TARDIS ( «Time And Relative Dimension In Space») uses an extra-dimensional vortex to go through time, while the travelers inside feel time passing normally.90003 90002 90035 Instantaneous time jumping: 90036 Examples include «The Girl Who Leapt Through Time» (2006), the DeLorean from «Back To The Future» (1985), and the Mr. Peabody’s WABAC machine from «The Rocky and Bullwinkle Show» (1959-64). 90003 90002 90035 Time travelling while standing still: 90036 Both the «Time Machine» (1895 book) and Hermione Granger’s Time-Turner from «Harry Potter» keep the traveler still while they move through time. 90003 90002 90035 Slow time travel: 90036 In «Primer» (2004), a traveler stays in a box while time traveling.For each minute they want to go back in time, they need to stay in the box for a minute. If they want to go back a day in time, they have to stay there for 24 hours. 90003 90002 90035 Traveling faster than light: 90036 In «Superman: The Movie» (1979), Superman flies faster than light to go back in time and rescue Lois Lane before she is killed. The concept was also used in the 1980 novel «Timescape» by Gregory Benford, in which the protagonist sends (hypothetical) faster-than-light tachyon particles back to Earth in тисячу дев’ятсот шістьдесят дві to warn of disaster.In several «Star Trek» episodes and movies, the Enterprise travels through time by going faster than light. In the comic book and TV series «The Flash,» the super-speedster uses a cosmic treadmill to travel through time. 90003 90002 90035 Difficult methods to categorize: 90036 There’s a rocket sled in «Timecop» (1994) that pops in and out of view when it’s being used, which has led to much speculation about what’s going on. There’s also the Time Displacement Equipment in «The Terminator» movie series, which shows off how to fight a war in four dimensions (including time).90003 90008 So is time travel possible? 90009 90002 While time travel does not appear possible — at least, possible in the sense that the humans would survive it — with the physics that we use today, the field is constantly changing. Advances in quantum theories could perhaps provide some understanding of how to overcome time travel paradoxes. 90003 90002 One possibility, although it would not necessarily lead to time travel, is solving the mystery of how certain particles can communicate instantaneously with each other faster than the speed of light.90003 90002 In the meantime, however, interested time travelers can at least experience it vicariously through movies, television and books. 90003 .90000 Einstein’s Theory of Special Relativity 90001 90002 The theory of special relativity explains how space and time are linked for objects that are moving at a consistent speed in a straight line. One of its most famous aspects concerns objects moving at the speed of light. 90003 90002 Simply put, as an object approaches the speed of light, its mass becomes infinite and it is unable to go any faster than light travels. This cosmic speed limit has been a subject of much discussion in physics, and even in science fiction, as people think about how to travel across vast distances.90003 90002 The theory of special relativity was developed by Albert Einstein in 1905 and it forms part of the basis of modern physics. After finishing his work in special relativity, Einstein spent a decade pondering what would happen if one introduced acceleration. This formed the basis of his general relativity, published in 1915. 90003 90008 History 90009 90002 Before Einstein, astronomers (for the most part) understood the universe in terms of three laws of motion presented by Isaac Newton in 1686.These three laws are: 90003 90002 (1) Objects in motion (or at rest) remain in motion (or at rest) unless an external force imposes change. 90003 90002 (2) Force is equal to the change in momentum per change of time. For a constant mass, force equals mass times acceleration. 90003 90002 (3) For every action, there is an equal and opposite reaction. 90003 90002 But there were cracks in the theory for decades before Einstein’s arrival on the scene, according to Encyclopedia Britannica. In тисяча вісімсот шістьдесят п’ять, Scottish physicist James Clerk Maxwell demonstrated that light is a wave with both electrical and magnetic components, and established the speed of light (186,000 miles per second).Scientists supposed that the light had to be transmitted through some medium, which they called the ether. (We now know that no transmission medium is required, and that light in space moves in a vacuum.) 90003 90002 Twenty years later, an unexpected result threw this into question. Physicist A.A. Michelson and chemist Edward Morley (both Americans at the time) calculated how Earth’s motion through this «ether» affected how the speed of light is measured, and found that the speed of light is the same no matter what Earth’s motion is.This led to further musings on light’s behavior — and its incongruence with classical mechanics — by Austrian physicist Ernst Mach and French mathematician Henri Poincare. 90003 90002 Einstein began thinking of light’s behavior when he was just 16 years old, in 1895. He did a thought experiment, the encyclopedia said, where he rode on one light wave and looked at another light wave moving parallel to him. 90003 90002 Classical physics should say that the light wave Einstein was looking at would have a relative speed of zero, but this contradicted Maxwell’s equations that showed light always has the same speed: 186,000 miles a second.Another problem with relative speeds is they would show that the laws of electromagnetism change depending on your vantage point, which contradicted classical physics as well (which said the laws of physics were the same for everyone.) 90003 90002 This led to Einstein’s eventual musings on the theory of special relativity, which he broke down into the everyday example of a person standing beside a moving train, comparing observations with a person inside the train. He imagined the train being at a point in the track equally between two trees.If a bolt of lightning hit both trees at the same time, due to the motion of the train, the person on the train would see the bolt hit one tree before the other tree. But the person beside the track would see simultaneous strikes. 90003 90002 «Einstein concluded that simultaneity is relative; events that are simultaneous for one observer may not be for another,» the encyclopedia stated. «This led him to the counterintuitive idea that time flows differently according to the state of motion, and to the conclusion that distance is also relative.»90003 90008 Famous equation 90009 90002 Einstein’s work led to some startling results, which today still seem counterintuitive at first glance even though his physics is usually introduced at the high school level. 90003 90002 90003 2015 marks 100 years since the publication of Albert Einstein’s General Theory of Relativity. Learn the basics of Einstein’s theory of relativity in our infographic here. (Image credit: By Karl Tate, Infographics Artist) 90002 One of the most famous equations in mathematics comes from special relativity.The equation — 90037 E = mc 90038 90037 90040 2 90041 90038 — means «energy equals mass times the speed of light squared.» It shows that energy (90037 E 90038) and mass (90037 m 90038) are interchangeable; they are different forms of the same thing. If mass is somehow totally converted into energy, it also shows how much energy would reside inside that mass: quite a lot. (This equation is one of the demonstrations for why an atomic bomb is so powerful, once its mass is converted to an explosion.) 90003 90002 This equation also shows that mass increases with speed, which effectively puts a speed limit on how fast things can move in the universe. Simply put, the speed of light (90037 c 90038) is the fastest velocity at which an object can travel in a vacuum. As an object moves, its mass also increases. Near the speed of light, the mass is so high that it reaches infinity, and would require infinite energy to move it, thus capping how fast an object can move. The only reason light moves at the speed it does is because photons, the quantum particles that make up light, have a mass of zero.90003 90002 A special situation in the universe of the small, called «quantum entanglement,» is confusing because it seems to involve quantum particles interacting with each other at speeds faster than the speed of light. Specifically, measuring the property of one particle can instantly tell you the property of another particle, no matter how far away they are. Much has been written about this phenomenon, which is still not fully explained in terms of Einstein’s conclusions. 90003 90002 Another strange conclusion of Einstein’s work comes from the realization that time moves relative to the observer.An object in motion experiences time dilation, meaning that time moves more slowly when one is moving, than when one is standing still. Therefore, a person moving ages more slowly than a person at rest. So yes, when astronaut Scott Kelly spent nearly a year aboard the International Space Station in 2015-16, his twin astronaut brother Mark Kelly aged a little faster than Scott. 90003 90002 This becomes extremely apparent at speeds approaching the speed of light. Imagine a 15-year-old traveling at 99.5 percent the speed of light for five years (from the astronaut’s perspective). When the 15-year-old gets back to Earth, according to NASA, he would be only 20 years old. His classmates, however, would be 65 years old. 90003 90002 While this time dilation sounds very theoretical, it does have practical applications as well. If you have a Global Positioning Satellite (GPS) receiver in your car, the receiver attempts to find signals from at least three satellites to coordinate your position. The GPS satellites send out timed radio signals that the receiver listens to, triangulating (or more properly speaking, trilaterating) its position based on the travel time of the signals.The challenge is, the atomic clocks on the GPS are moving and would therefore run faster than atomic clocks on Earth, creating timing issues. So, engineers need to make the clocks on a GPS tick slower, according to Richard Pogge, an astronomer at Ohio State University. 90003 90002 The clocks in space tick faster, according to Physics Central, because the GPS satellites are above Earth and experience weaker gravity. So even though the GPS satellites are moving and experience a seven-microsecond slowing every day because of their movement, the result of the weaker gravity causes the clocks to tick about 45 microseconds faster than a ground-based clock.Adding the two together results in the GPS satellite clock ticking faster than a ground-based clock, by about 38 microseconds daily. 90003 90008 Special relativity and quantum mechanics 90009 90002 As our knowledge of physics has advanced, scientists have run into more counterintuitive situations. One is trying to reconcile general relativity — which describes well what’s going on with large objects — with quantum mechanics, which is best used for very small things (such as uranium atom decay).The two fields, which excellently describe their individual fields, are incompatible with one another — which frustrated Einstein and generations of scientists after him. 90003 90002 «Relativity gives nonsensical answers when you try to scale it down to quantum size, eventually descending to infinite values in its description of gravity. Likewise, quantum mechanics runs into serious trouble when you blow it up to cosmic dimensions,» an article in The Guardian pointed out in 2015. 90003 90002 «Quantum fields carry a certain amount of energy, even in seemingly empty space, and the amount of energy gets bigger as the fields get bigger.According to Einstein, energy and mass are equivalent (that’s the message of E = mc 90040 2 90041), so piling up energy is exactly like piling up mass. Go big enough, and the amount of energy in the quantum fields becomes so great that it creates a black hole that causes the universe to fold in on itself. Oops. «90003 90002 There are several ideas to overcome this (which are beyond the scope of this article), but one approach is to imagine a quantum theory of gravity that would have a massless particle (called the graviton) to generate the force.But as physicist Dave Goldberg pointed out in io9 in 2013, there are problems with that. At the smallest scales, gravitons would have infinite energy density, creating an unimaginably powerful gravity field. More study will be required to see if this is possible. 90003 .90000 Activity: Clocks and Angles 90001 90002 90003 This activity is about Analog clocks and the angles made by the hands of the clock. You can find out more about angles and how they’re measured on the page Degrees (Angles). 90004 90005 90002 90005 90008 What is the angle between the hands of a clock at 1 o’clock? 90009 90002 90005 90002 At 1 o’clock the minute hand (Red) points to the 12 and the hour hand (blue) points to the 1. So we need to find the angle between the 12 and the 1.90005 90008 How many of this angle are there in a complete turn? 90009 90002 90005 90002 There are 12 of them in a complete turn (360 °), so each one must be 90019 360 ° ÷ 12 = 30 ° 90020 90005 90002 So the angle between the hands of a clock at 1 o’clock is 90019 30 ° 90020 . 90005 90002 90019 Note: 90020 90005 90030 90031 It does not matter whether we are talking about 1 am or 1 pm, the answer is exactly the same for both. 90032 90031 The angle between the hands at 1 o’clock could also be given as the reflex angle 330 °, but we will always give the smaller (acute or obtuse) angle.90032 90035 90036 90037 90038 90008 What is the angle between the hands of a clock at 2:30? 90009 90002 90005 90002 At 2:30 the minute hand (Red) points to the 6 and the hour hand (Blue) points halfway between the 2 and the 3. 90005 90008 90037 So how many lots of 30 ° do we have this time? 90009 90002 90005 90030 90031 The angle between the 5 and the 6 is 90019 30 ° 90020 90032 90031 The angle between the 4 and the 5 is 90019 30 ° 90020 90032 90031 The angle between the 3 and the 4 is 90019 30 ° 90020 90032 90031 The remaining angle is 90019 ½ × 30 ° = 15 ° 90020 90032 90035 90002 So the angle between the hands of a clock at 90019 2:30 = 30 ° + 30 ° + 30 ° + 15 ° = 105 ° 90020 90005 90002 90005 90074 Your Turn 90075 90008 Complete the following table (give the smaller angle in each case): 90037 90009 90079 90080 90081 90082 90019 Time 90020 90085 90082 1:00 90085 90082 2:30 90085 90082 7:00 90085 90082 10:30 90085 90082 11:20 90085 90082 3:40 90085 90082 5:15 90085 90082 8:45 90085 90102 90081 90082 90019 Angle 90020 90085 90082 30 ° 90085 90082 105 ° 90085 90082 90037 90085 90082 90037 90085 90082 90037 90085 90082 90037 90085 90082 90037 90085 90082 90037 90085 90102 90131 90132 90002 Check your answers at the bottom of the page.90005 90002 90005 90074 More Complicated Times 90075 90002 Finding the angle between the hands of a clock is easy as long as we do not use complicated times. 90005 90002 For example finding the angle between the hands at 9:37 is much more difficult. You can try that one if you wish, but it’s probably too hard. 90005 90008 90037 Example: At what times is the angle between the hands of a clock equal to 30 °? 90009 90002 Notice that the question asks for ‘times’. There are many possible answers.Some of them are easy to find, others much more difficult. 90005 90002 Here are two easy answers: 90005 90150 90080 90081 90082 90085 90082 90085 90102 90158 90082 1 o’clock 90085 90082 11 o’clock 90085 90102 90081 90082 90085 90082 90085 90102 90081 90171 90019 But what about this one? 90020 90085 90102 90081 90177 90085 90102 90081 90177 4:15 PM 90085 90102 90131 90132 90002 90005 90002 At first glance, it looks like this might be a 30 ° angle also, but at 4:15, the hour hand has already moved a quarter of the way between the 4 and the 5.90005 90002 So the angle is 90019 30 ° + ¼ × 30 ° = 30 ° + 7½ ° = 37½ ° 90020 . 90005 90002 This might be a more accurate answer: 90005 90002 90005 90002 Can you find more 30 ° angles like this one? 90005 90002 90005 90074 At what times of the day do the hands of a clock lie in a straight line? 90075 90002 90019 In other words the angle between them is 180 °? 90020 90005 90002 One obvious answer is 6 o’clock: 90005 90002 90005 90008 90009 90008 But what other answers could there be? 90009 90002 9:15 is not correct for a similar reason that 4:15 did not give us exactly a 30 ° angle… the hour hand has moved on beyond the 9. 90005 90002 This seems to be a very difficult question to answer, but there is an easy way. 90005 90008 How many times between 6:00 am and 6:00 pm do the hands make a straight line? 90037 90009 90002 There must be at least one point time for each hour: 90005 90030 90031 one between 7:00 am and 8:00 am, 90032 90031 one between 8:00 am and 9:00 am, 90032 90031 one between 9:00 am and 10:00 am, 90032 90031 etc, up to… 90032 90031 one between 4:00 pm and 5:00 pm 90032 90035 90002 That makes 11 equal parts, and so: 90005 90002 12 Hours / 11 90005 90002 = 1 + 90242 1 90243/90244 11 90245 hours 90005 90002 = 1 hour + 90242 60 90243/90244 11 90245 minutes 90005 90002 = 1 hour 5 90242 5 90243/90244 11 90245 minutes 90005 90002 = 1 hour 5 ½ minutes (approximately) 90005 90002 The next time after 6:00 am that the hands make a straight line is about 90019 7: 05½ am 90020 : 90005 90002 90005 90074 Your Turn! 90075 90079 90080 90081 90082 90019 Hours 90020 90085 90082 7am — 8am 90085 90082 8am — 9am 90085 90082 9am — 10am 90085 90082 10am — 11am 90085 90082 11am — 12pm 90085 90082 12pm — 1pm 90085 90082 1pm — 2pm 90085 90082 2pm — 3pm 90085 90082 3pm — 4pm 90085 90082 4pm — 5pm 90085 90102 90081 90082 90019 Time 90020 90085 90082 90019 7: 05½ am 90020 90085 90082 90085 90082 90037 90085 90082 90037 90085 90082 90037 90085 90082 90037 90085 90082 90037 90085 90082 90037 90085 90082 90037 90085 90082 90037 90085 90102 90131 90132 90002 You might like to check your answers on the page Analog and Digital Clocks Animation 90005 90074 90075 90074 Can you work out the times of the day when the hands of a clock make a right angle? 90075 90002 (Hint: there are 22 of them) 90005 90002 90005 90002 90005 90008 Answer to the earlier exercise: 90009 90079 90080 90081 90082 90019 Time 90020 90085 90082 1:00 90085 90082 2:30 90085 90082 7:00 90085 90082 10:30 90085 90082 11:20 90085 90082 3:40 90085 90082 5:15 90085 90082 8:45 90085 90102 90081 90082 90019 Angle 90020 90085 90082 30 ° 90085 90082 105 ° 90085 90082 150 ° 90085 90082 135 ° 90085 90082 140 ° 90085 90082 130 ° 90085 90082 67½ ° 90085 90082 7½ ° 90085 90102 90131 90132 90002 90005 .90000 What is computing power? | HowStuffWorks 90001 90002 What makes a supercomputer so super? Can it leap tall buildings in a single bound or protect the rights of the innocent? The truth is a bit more mundane. Supercomputers can process complex calculations very quickly. 90003 90002 As it turns out, that’s the secret behind computing power. It all comes down to how fast a machine can perform an operation. Everything a computer does breaks down into math.Your computer’s processor interprets any command you execute as a series of math problems. Faster processors can handle more calculations per second than slower ones, and they’re also better at handling really tough calculations. 90003 90002 Within your computer’s CPU is an electronic clock. The clock’s job is to create a series of electrical pulses at regular intervals. This allows the computer to synchronize all its components and it determines the speed at which the computer can pull data from its memory and perform calculations.90003 90002 When you talk about how many gigahertz your processor has, you’re really talking about 90009 clock speed 90010. The number refers to how many electrical pulses your CPU sends out each second. A 3.2 gigahertz processor sends out around 3.2 billion pulses each second. While it’s possible to push some processors to speeds faster than their advertised limits — a process called 90009 overclocking 90010 — eventually a clock will hit its limit and will go no faster. 90003 90002 As of March 2010 the record for processing power goes to a Cray XT5 computer called Jaguar.The Jaguar supercomputer can process up to 2.3 quadrillion calculations per second [source: National Center for Computational Sciences]. 90003 90002 Computer performance can also be measured in 90009 floating-point operations per second 90010, or 90009 flops 90010. Current desktop computers have processors that can handle billions of floating-point operations per second, or gigaflops. Computers with multiple processors have an advantage over single-processor machines, because each processor core can handle a certain number of calculations per second.Multiple-core processors increase computing power while using less electricity [source: Intel] 90003 90002 Even fast computers can take years to complete certain tasks. Finding two prime factors of a very large number is a difficult task for most computers. First, the computer must determine the factors of the large number. Then, the computer must determine if the factors are prime numbers. For incredibly large numbers, this is a laborious task. The calculations can take a computer many years to complete.90003 90002 Future computers may find such a task relatively simple. A working quantum computer of sufficient power could calculate factors in parallel and then provide the most likely answer in just a few moments. However, quantum computers have their own challenges and would not be suitable for all computing tasks, but they could reshape the way we think of computing power. 90003 90002 Learn more about computers and processors by following the links below.90003 90002 90003 90030 Related HowStuffWorks Articles 90031 90030 More Great Sites 90031 90030 Sources 90031 90036 90037 Clay Mathematics Institute. «Prime numbers and cryptography.» 2010. (March 22, 2010) http://www.claymath.org/posters/primes/ 90038 90037 Computer Power User. «Processing Power.» 2010. (March 22, 2010) http://www.computerpoweruser.com/Editorial/article.asp?article=articles/archive/u0413/08u13/08u13.asp 90038 90037 Computer User. «Clock Rate.» 2010. (March 22, 2010) http://www.computeruser.com/dictionary/clock-rate/ 90038 90037 Intel. Intel® Multi-core Technology. (June 20, 2010) http://www.intel.com/multi-core/ 90038 90037 National Center for Computational Sciences. «World’s Most Powerful Computer for Science!» (March 22, 2010) http://www.nccs.gov/jaguar/ 90038 90037 Red Hat. «Red Hat Enterprise Linux 3: Introduction to System Administration.» (March 22, 2010) https: // www.redhat.com/docs/manuals/enterprise/RHEL-3-Manual/admin-guide/s1-bandwidth-processing.html 90038 90037 Shinder, Deb. «What’s the best way to increase processing power?» Aug. 2, 2006. (March 22, 2010) http://www.zdnet.co.uk/news/servers/2006/08/02/whats-the-best-way-to-increase-processing-power-39280352/ 90038 90051 .
Share This Story, Choose Your Platform!
Facebook Twitter LinkedIn Reddit Whatsapp Google+Tumblr Pinterest Vk Email
Related Posts
Насморк при прорезывании зубов у детей: причины, симптомы и лечение
Насморк при прорезывании зубов у детей: причины, симптомы и лечение

Как развивать ребенка в 10 месяцев: игры и занятия для малыша
Как развивать ребенка в 10 месяцев: игры и занятия для малыша

Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования
Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов
УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

Когда и как вводить прикорм грудному ребенку: рекомендации педиатров
Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

Leave A Comment Отменить ответ
Comment

Save my name, email, and website in this browser for the next time I comment.