Huawei Watch GT2 Pro vs Samsung Galaxy Watch4
В нынешнем году рынок смарт-часов пополнился двумя новыми моделями для простых смертных. Почему для простых смертных? Да потому что фанаты айфонов в любом случае предпочтут Apple Watch. А вот приверженцев операционной системы Android наверняка заинтересуют новинки от Samsung и Huawei. Попробуем разобраться, насколько хороши эти часы?
Оговоримся сразу, рынок часов можно разделить на четыре сегмента: смарт-часы, фитнес-браслеты, спортивные часы и обычные наручные часы. На настенных часах мы останавливаться не будем, хотя среди них тоже иногда попадаются умные экземпляры.
Теперь коротко о моих отношениях с часами. Начались они 12 лет назад, и самыми первыми были обычные наручные часы. Спустя 6 лет, я перешел на спортивные Polar. Честно говоря, смарт-часы и прочие фитнес-браслеты меня никогда не волновали: я не хотел быть частым объектом внимания и рабом зарядки. И только сейчас, уж не знаю к счастью или к сожалению, ситуация начинает меняться…
Мне довелось тестировать Samsung Galaxy Watch4 (41 мм) бронзового цвета, которые в силу их размера больше подходят дамам, и темные Huawei Watch GT2 Pro (46 мм) – судя по диаметру, их, скорее всего, можно назвать мужской моделью. Последние мне сразу понравились, и я бы их наверняка выбрал, даже если бы мне предложили хронометр Samsung с 45-миллиметровым циферблатом.
Последние мне сразу понравились, и я бы их наверняка выбрал, даже если бы мне предложили хронометр Samsung с 45-миллиметровым циферблатом.
Часы Huawei в титановом корпусе заметно тоньше и выглядят более строго. На керамической задней панели разместились пульсометр и пульсоксиметр, который замеряет содержание кислорода в крови. На их фоне Samsung Galaxy Watch4 в стальном корпусе, с пластиковой крышкой и зубчатым безелем (поворотным кольцом на циферблате) воспринимаются как более массивные. Что касается безеля, то с его помощью действительно удобно перемещаться в меню, если бы не одно но: он то и дело норовил зацепиться и застрять в рукаве куртки. Несмотря на внушительные размеры, часы Samsung довольно легкие – порядка 50 г (женская модель – 48 г, мужская – 52 г). Часы Huawei весят 52 г.
На обеих моделях справа расположены по две кнопки, которые можно крутить. Однако реальная польза от них только после нажатия. На корпусе также можно различить отверстия микрофона и динамика. Ремешок кожаный, и его при желании вы можете заменить, например, отправляясь на тренировку. Экраны сенсорные – яркие и красивые.
Ремешок кожаный, и его при желании вы можете заменить, например, отправляясь на тренировку. Экраны сенсорные – яркие и красивые.
Победитель в этой категории: часы Huawei. Они годятся на все случаи жизни: как для тренировок, досуга, так и для более торжественных мероприятий.
Идем на тренировкуКак и в случае предыдущих тестирований (когда я испытывал на точность Apple Watch 4 и анализировал Huawei Watch GT2), первым делом я решил разобраться в пригодности часов для спортивных занятий. Логика здесь простая: мне нужны только одни часы – и для повседневной жизни, и для тренировок. До сих пор это не удавалось: если часы Polar были явно со спортивным уклоном, то смарт-часы не устраивали меня на тренировках.
Посмотрим, насколько новым моделям удастся справиться со своими задачами. В памяти Huawei Watch GT2 Pro заложено свыше 100 видов спорта, включая танец живота, прыжки с парашютом, дартс, перетягивание каната и прочую экзотику. Samsung Galaxy Watch4 готовы предложить порядка 40 видов тренировок, в основном для завсегдатаев тренажерного зала.
Samsung Galaxy Watch4 готовы предложить порядка 40 видов тренировок, в основном для завсегдатаев тренажерного зала.
Для полноты картины я добавил к тестируемым часам еще Polar Vantage M и выбрал для проверки три вида спорта: бег, велосипед и тренажерный зал. С GPS проблем не было: все трое часов замерили практически одинаковую дистанцию. А вот с пульсом не задалось. Особенно «отличились» Huawei, которые значительно занижали реальные результаты (я брал за основу данные комбинации Polar c нагрудным пульсометром). Вызывали сомнения и странные разночтения в результатах при беге с постоянной скоростью и одинаковым пульсом, когда на первой половине дистанции GT2 Pro показывали стабильно 120 ударов в минуту, а на второй – 160.
Samsung Galaxy Watch4 со своей задачей в целом справились лучше. Но больше всего огорчил слабый аккумулятор. Приведу в качестве примера велосипедный заезд на 32 км, который у меня занял 1 час 20 минут. Если аккумулятор часов Huawei потратил за это время всего 4% своей энергии, то у Samsung он сел аж на 23%.
На 6-километровой пробежке царило, можно сказать, единогласие. Пояс Polar зафиксировал на финише средний пульс – 153 удара в минуту, часы Samsung показали 152 удара в минуту, а Huawei – 157 ударов. С часами Samsung, благодаря их безелю, бегать удобнее: мне не пришлось снимать перчатки и свайпить потным пальцем на ходу. Результаты тренировки можно потом посмотреть в приложениях Samsung Health или Huawei Health. Для управления часами Samsung вам также понадобится приложение Galaxy Wearable.
Победитель в данной категории отсутствует. Для получения достоверных результатов мне придется по-прежнему использовать свой нагрудный пульсометр. А от смарт-часов, пока они не научатся взаимодействовать с пульсометром, на тренировке толку мало. Часы Huawei измеряют пульс неверно. Samsung из-за своего хилого аккумулятора не годятся для продолжительных занятий.
Часы Huawei измеряют пульс неверно. Samsung из-за своего хилого аккумулятора не годятся для продолжительных занятий.
О слабом аккумуляторе Samsung Galaxy Watch4 я уже говорил. Но это, как любят интриговать в рекламе, еще не всё (в данном случае, к сожалению). Выяснилось, что передо мной не только часы-однодневки, но и то, что их не так-то просто заряжать. Обе модели поддерживают беспроводную зарядку, зато часы Huawei признали также зарядные подставки, оказавшиеся у меня дома.
Оказалось, что часы Samsung не могут подпитываться энергией через зарядное устройство стандарта Qi – они соглашались только на родную зарядку, входившую в комплект. Попробовал зарядить от телефона – тоже ничего не вышло. И это огромный минус. Какая, спрашивается, польза от часов, которые теряют силы у вас на глазах и при этом еще выбирают, как им заряжаться? На зарядку им требуется в среднем 2 – 3 часа. И если к утру у них останется процентов 20, то до обеда они точно не дотянут.
Зато очень порадовал аккумулятор Huawei Watch GT2 Pro – он просто невероятный. У вас будут часы, которые смогут запросто продержаться одну-две недели в зависимости от того, как часто вы собираетесь тренироваться и выключать экран. Как такое возможно? Во-первых, у них более мощный аккумулятор – 455 мАч против самсунговских 244/340 мАч (в зависимости от размера часов), но мощность здесь – не определяющий фактор. Всё дело в чипе А1 и 32 Мбайт RAM, которыми оснащены Huawei. Именно эта комбинация дает такой поразительный эффект. Может быть, эти часы не так плавно функционируют, как Watch4, но их аккумулятор лучше в разы и это дорого стоит.
Победитель в данной категории: Huawei и еще раз Huawei.
Общее впечатлениеОдними из самых главных достоинств часов Samsung являются их плавный интерфейс и приятная анимация. Может быть, именно на это и уходит весь аккумуляторный ресурс? Если обе модели замечают, что вы уже долгое время находитесь без движения, то советуют вам немного размяться.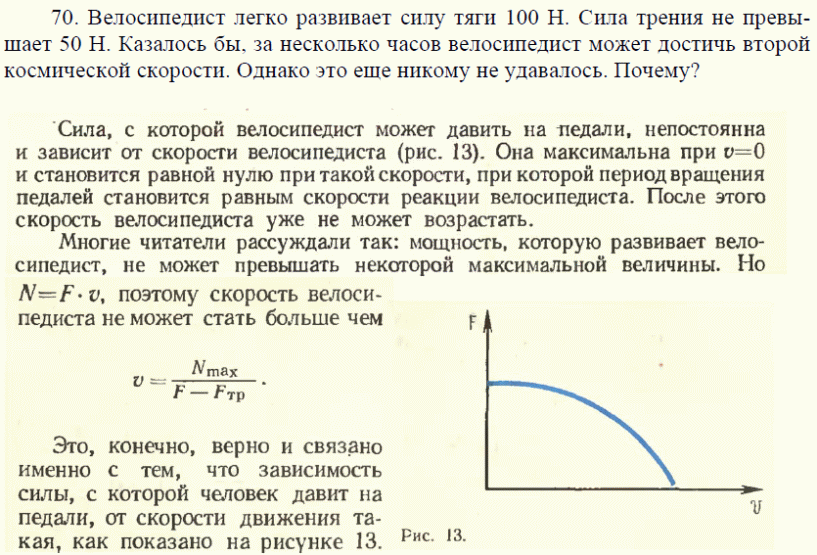 Причем рекомендации Samsung гораздо содержательнее: вам предложат упражнения на растяжку с подсчетом повторов.
Причем рекомендации Samsung гораздо содержательнее: вам предложат упражнения на растяжку с подсчетом повторов.
Продумано у Samsung и управление уведомлениями: вы можете читать их прямо с часов и сразу же отвечать. Huawei пока ограничивается только показом уведомлений. Обе модели позволяют также делать звонки и отвечать на них. В закрытом помещении всё это действительно удобно, а вот на улице, скорее, проблематично.
И те, и другие часы следят на протяжении всего дня за частотой пульса своего владельца. Huawei по умолчанию делает это непрерывно, Samsung – с интервалом в пять минут (бережет заряд аккумулятора). Разумеется, эти настройки можно менять. Как и положено, есть шагомер, мониторинг сна, дыхательные упражнения и общие кольца активности, которые следует замкнуть в течение дня. Из новых функций можно отметить измерение содержания кислорода в крови (обе модели) и отслеживание менструального цикла (Samsung).
Еще одна новая функция Samsung – распознавание падений. В этом случае контактным лицам высылаются SMS с координатами и делается SOS-звонок. Обе модели не боятся непогоды.
В этом случае контактным лицам высылаются SMS с координатами и делается SOS-звонок. Обе модели не боятся непогоды.
Большой плюс я ставлю часам Samsung за музыку: кроме всего прочего, они поддерживают приложение Spotify, через которое можно загружать плейлисты. Watch GT2 Pro, видно, застряли в прошлом – в мире MP3-файлов. С навигацией у обоих часов всё в порядке, как и с изобилием вариантов циферблатов, которых, наверное, сотни.
Победитель в данной категории
На момент написания этой статьи Huawei Watch GT2 Pro можно было купить за 299 €, а Samsung Watch4 BT (41 мм) – за 429 €.
Победитель в ценовой категории: Huawei.
РезюмеС рациональной точки зрения, мои симпатии принадлежат часам Huawei. У них невероятно выносливый аккумулятор, респектабельный вид, великолепная сборка и разумная цена. Главные недостатки: не поддерживают сторонние приложения (например, Spotify) и неточно замеряют пульс. Первый недочет вроде бы будет скоро исправлен, а вот со вторым придется подождать, пока часы ни научатся взаимодействовать с наружным пульсометром.
Главные недостатки: не поддерживают сторонние приложения (например, Spotify) и неточно замеряют пульс. Первый недочет вроде бы будет скоро исправлен, а вот со вторым придется подождать, пока часы ни научатся взаимодействовать с наружным пульсометром.
Что касается часов Samsung, то они, безусловно, очень продвинутые, с ярким экраном и одни из лучших в своем классе. Под стать этим качествам и немалая цена. Их главный недостаток – слабый аккумулятор. Если вы согласны заряжать часы каждый вечер и таскать повсюду с собой зарядную подставку – флаг вам в руки. Для меня это непреодолимое препятствие.
P.S. К вашему сведению: обе модели можно спаривать с айфонами. Но лучше, конечно, когда «браки» заключаются с устройствами своего круга: часы Samsung используются вместе с телефоном Samsung, часы Huawei с телефоном Huawei, ну и так далее по списку. Это правило распространяется также и на беспроводные наушники.
Силвер Тилк
25.11.2020
почти 650 км на одной зарядке — Авторевю
Фото: компания Tesla Motors
По общеавтомобильным меркам Модели S уже пора на пенсию: буквально на днях этому электромобилю исполнится восемь лет, причем за это время был проведен лишь один номинальный рестайлинг. Однако техническим доработкам не было счета, и компания до сих пор продолжает совершенствовать «эску». И сейчас подоспел очередной пакет обновлений, после которого паспортный пробег на одной зарядке превысил 400 миль по американскому стандарту EPA.
Однако техническим доработкам не было счета, и компания до сих пор продолжает совершенствовать «эску». И сейчас подоспел очередной пакет обновлений, после которого паспортный пробег на одной зарядке превысил 400 миль по американскому стандарту EPA.
Почему именно 400 миль, то есть 643 км? Да потому что столько обещано для электромобиля Lucid Air в топ-версии со 130-киловаттной батареей: компания Lucid Motors открыла прием заказов в конце прошлого года и обещает начать поставки осенью. Чтобы удержать пальму первенства, Tesla провела очередную модернизацию «эски» и увеличила паспортный пробег «дальнобойной» версии Long Range Plus (она появилась в гамме год назад) с 390 до 402 миль, то есть с 628 до 647 км. Что любопытно, тяговая батарея емкостью 100 кВт∙ч осталась прежней: новые аккумуляторы еще не готовы к серийному производству. А выжать дополнительные мили удалось с миру по нитке.
Во-первых, частичная унификация с более современными Теслами Model 3 и Model Y позволила снизить массу. В частности, «эска» обрела более легкие каркасы сидений, корпус аккумулятора и некоторые элементы ходовой части. Во-вторых, появились шины со сниженным сопротивлением качению и колеса Tempest с более эффективной аэродинамической проработкой. В-третьих, доработаны электромоторы и редукторы: у переднего модуля снижено трение, а у заднего появился электрический масляный насос вместо механического. Наконец, изменено управление рекуперацией: теперь она работает и на самой низкой скорости, вплоть до полной остановки.
В частности, «эска» обрела более легкие каркасы сидений, корпус аккумулятора и некоторые элементы ходовой части. Во-вторых, появились шины со сниженным сопротивлением качению и колеса Tempest с более эффективной аэродинамической проработкой. В-третьих, доработаны электромоторы и редукторы: у переднего модуля снижено трение, а у заднего появился электрический масляный насос вместо механического. Наконец, изменено управление рекуперацией: теперь она работает и на самой низкой скорости, вплоть до полной остановки.
Мощность электромоторов Tesla с некоторых пор официально не публикует, зато известны динамические характеристики (они после модернизации не изменились): лифтбек Tesla Model S Long Range Plus может разогнаться до 100 км/ч за 3,8 с, максимальная скорость — 249 км/ч. Цена в США без учета субсидий — 75 тысяч долларов. Также в гамме осталась самая экстремальная модификация Performance за 95 тысяч: она разменивает «сотню» всего за 2,5 с, набирает 261 км/ч, но дальность хода только 560 км по циклу EPA. Остальные версии Модели S (с менее емкими аккумуляторами и задним приводом) исключены из гаммы сразу после начала производства седанов Tesla Model 3.
Остальные версии Модели S (с менее емкими аккумуляторами и задним приводом) исключены из гаммы сразу после начала производства седанов Tesla Model 3.
Путенихин П.В. Обзор решений парадокса близнецов в СТО
Путенихин Пётр Васильевич
независимый исследователь
Библиографическая ссылка на статью:
Путенихин П.В. Обзор решений парадокса близнецов в СТО // Современные научные исследования и инновации. 2019. № 9 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2019/09/90186 (дата обращения: 12.01.2021).
Обзор решений парадокса близнецов в СТО
Парадокс близнецов берёт своё начало в основополагающей работе Эйнштейна “К электродинамике движущихся тел” от 1905 года. Это первый и наиболее известный парадокс СТО, сформулированный Эйнштейном как “своеобразное следствие” из факта замедления темпа хода движущихся часов. Статус “парадокса” и название “парадокс близнецов” появились позднее в результате расширения формулировки: согласно принципу относительности с точки зрения движущихся часов отставать должны неподвижные.
Более чем за сто лет после публикации работы Эйнштейна решению парадокса было посвящено множество статей, однако дискуссии по нему не прекращаются и в наши дни (2019 год). Видимо, главной причиной продолжающихся споров является то, что ни одно из предложенных решений, по сути, не является бесспорным. Аргументы, использованные разными авторами, нередко не дополняют, а противоречат друг другу, приводя к весьма спорным решениям парадокса. Практически всегда указывается, что парадокс близнецов в специальной теории относительности, её средствами не имеет решения, что для его решения необходимо использовать формализм общей теории относительности:
“При изучении СТО указывается, что “парадокс близнецов” не может быть объяснен в рамках этой теории. … Только в рамках ОТО мы можем понять и объяснить “парадокс близнецов” естественным образом, опираясь на положения OТО” [11, c.220].
“… парадокс близнецов … ограничен специальной теорией относительности, которую можно сразу отбросить из-за абсолютного характера ускоренного движения в этой теории” [3].
Согласно ещё одному замечанию [10, с.40], мнение о возможности использования формулы Лоренца для замедления времени в ускоренных системах ошибочно, поскольку эта формула “… справедлива только для инерциалышх систем и совершенно неприменима к системе R, скорость которой изменяется от v до – v.”Найти вместо этого уравнения “… уравнение, справедливое для системы R, в рамках специальной теории относительности невозможно, так как последняя справедлива лишь для систем отсчета, движущихся с постоянной скоростью” [10, с.40].
“Эйнштейн допускает существование парадокса, если он признает, что одной специальной теории относительности достаточно для анализа ситуаций, в которых нет истинного гравитационного поля” [5, с.2011].
“… парадокс часов есть результат ошибочного применения специальной теории относительности, именно ее применения к случаю, когда следует использовать общую теорию” [7 с.346].
Следует явно отметить, что у парадокса близнецов есть весьма широко используемая собственная проблема. Считается, что для сравнивания возрастов путешествующий близнец должен обязательно вернуться к своему брату. Однако это очевидная ошибка. Для того чтобы сравнить часы C с часами A, совсем не обязательно к ним приближаться. Вполне достаточно сравнить показания часов C с показаниями других часов B, которые синхронизированы с часами A, но могут находиться от них на любом расстоянии. То же самое относится и к парадоксу близнецов. Чтобы сравнить их возраст после того, как один из них удалился на большое расстояние, вполне достаточно сравнить возраст путешественника с возрастом ровесника своего брата в конечной точке путешествия. Или же просто посмотреть в этой точке на календарь, синхронный со всеми календарями в этой ИСО, относительно которой совершено путешествие. Более того, совершенно оставлено без внимания обстоятельство, что с определённой точки зрения, в противоположность традиционным решениям парадокса, путешественник окажется старше своего брата, остававшегося неподвижным.
Считается, что для сравнивания возрастов путешествующий близнец должен обязательно вернуться к своему брату. Однако это очевидная ошибка. Для того чтобы сравнить часы C с часами A, совсем не обязательно к ним приближаться. Вполне достаточно сравнить показания часов C с показаниями других часов B, которые синхронизированы с часами A, но могут находиться от них на любом расстоянии. То же самое относится и к парадоксу близнецов. Чтобы сравнить их возраст после того, как один из них удалился на большое расстояние, вполне достаточно сравнить возраст путешественника с возрастом ровесника своего брата в конечной точке путешествия. Или же просто посмотреть в этой точке на календарь, синхронный со всеми календарями в этой ИСО, относительно которой совершено путешествие. Более того, совершенно оставлено без внимания обстоятельство, что с определённой точки зрения, в противоположность традиционным решениям парадокса, путешественник окажется старше своего брата, остававшегося неподвижным.
Рассмотрим несколько вариантов решения парадокса (перевод статей наш). Выбор статей для рассмотрения произведён буквально наугад, но при условии наличия в них хоть какого-то решения, а не распространённого простого описания парадокса.
1. Еще одна заметка о парадоксе близнецов, Eisenlohr H.
В этой короткой заметке [2] автор использует вместо часов сердцебиения участников эксперимента, приняв их в состоянии покоя равными единице. Один из участников, астронавт удаляется от Земли со скоростью β на расстояние L, где мгновенно разворачивается и движется к Земле. На Земле, после возвращения астронавта мы просматриваем журналы двух участников и обнаруживаем в них следующие записи. В журнале астронавта указано, что за время полёта, равное T’, им отправлено на Землю R’emitted = 1×T’ = T’ импульсов его сердца. При этом им было получено с Земли, от второго участника количество импульсов его сердца, равное R’. В период удаления от Земли, равный T’/2, для астронавта частота сердцебиений землянина была пониженной:
а на обратном пути – повышенной:
Следовательно, за весь период путешествия астронавт получил с Земли количество импульсов:
(7. 1)
1)
Не откладывая на потом, заметим, что пояснений к уравнениям для p’ и q’ автор заметки не приводит. Однако по виду уравнений догадываемся, что используются уравнения для релятивистского эффекта Доплера:
где принято, что скорость света равна единице, v – относительная скорость приёмника и источника. Если источник и приемник сближаются, то скорость имеет знак “плюс”. Если удаляются друг от друга, то скорость имеет знак “минус”. Таким образом, на этом этапе выкладки вполне корректны.
Далее в журнале земного близнеца находим схожие записи: количество отправленных астронавту импульсов равно Remitted = 1×T = T. С точки зрения землянина, частота поступающих импульсов от астронавта также меняется согласно эффекту Доплера. При удалении астронавта частота импульсов понижена:
а на обратном пути – повышена:
Но вот что интересно. “Половина” пути для земного близнеца в заметке оказывается смещённой. Импульсы повышенной частоты начинают поступать на Землю не ровно через половину времени в пути, а на величину времени, необходимого на приход сигнала из самой дальней точки траектории:
Импульсы повышенной частоты начинают поступать на Землю не ровно через половину времени в пути, а на величину времени, необходимого на приход сигнала из самой дальней точки траектории:
“Импульс, испускаемый в точке поворота, требует времени τ=L/c=(T/2)β, чтобы пройти расстояние L и достичь Земли”.
То есть, импульсы пониженной частоты приходят на Землю более длительное время, чем импульсы повышенной частоты. Исходя из этого, суммарное количество импульсов, полученных землянином равно:
(7.2)
Теперь из простого сравнения полученных величин, находим, что землянин испустил T импульсов, а получил R импульсов, а астронавт, соответственно, испустил T’ импульсов, а получил R’ импульсов. Из чего делается вывод:
“Следовательно, оба близнеца приходят к одному и тому же выводу: во время путешествия сердце космонавта билось меньше в (1-β2)1/2 раза, чем сердце его брата. Кстати, формула для замедления времени получается, если положить R = T’ или R’ = T…”
Действительно, на первый взгляд всё строго сходится:
Однако обратим внимание на последнюю фразу в цитате “если положить…“. Воспользуемся указанным предположением, но в инверсном виде. Подставим в уравнение одно из этих соотношений:
Воспользуемся указанным предположением, но в инверсном виде. Подставим в уравнение одно из этих соотношений:
Сразу же возникает вопрос, в чём смысл этого нового, явно странного равенства? Обратимся к значениям этих же величин, полученных ранее, рассматривая их не как время, а как количества импульсов. Астронавт, как указано, испустил T’ импульсов, следовательно, землянин все их должен был получить. То есть, согласно сравнению величин, мы должны сделать несколько изменённую запись. Согласно исходным условиям задачи астронавт отправил на Землю R’ = 1×T’ = T’ импульсов своего сердца. Именно их и получил землянин, то есть, согласно уравнению (7.1):
Здесь к величинам, обозначающим количества импульсов, мы добавили нижние индексы, поясняющие направление передачи, получателя и отправителя. Буквально полученное уравнение означает, что астронавт отправил на Землю R’ импульсов, а землянин получил R импульсов:
(7.3)
Ситуация противоречивая, невозможная: отправлено импульсов меньше, чем получено.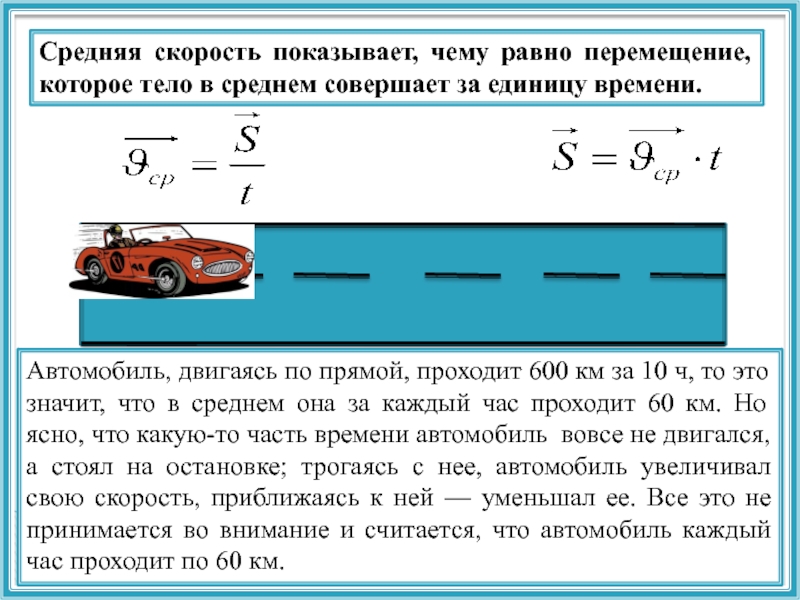 Действительно, рассматривать ситуацию, когда получено импульсов больше, чем отправлено, не имеет никакого смысла. Как легко заметить, совпадут эти два количества только в единственном случае, когда астронавт никуда не улетал:
Действительно, рассматривать ситуацию, когда получено импульсов больше, чем отправлено, не имеет никакого смысла. Как легко заметить, совпадут эти два количества только в единственном случае, когда астронавт никуда не улетал:
Обнаруженное противоречие не надуманное, а является следствием весьма завуалированной подмены понятий, которая произошла, очевидно, вследствие приравнивания частот сердцебиений единице. Проделаем повторно преобразования, отказавшись от этого приравнивания v0=v0‘ = 1. Тогда астронавт за время полёта, равное T’, отправил на Землю R’emitted = v0‘T’ импульсов своего сердца, где индекс emitted мы добавили выше как для уточнения отправителя, так и во избежание одинаковых обозначений, поскольку R’ обозначает количество импульсов, полученных землянином. Приняв v0‘ = 1, мы, разумеется, получим тот же результат, что и ранее. Но при отличии частот сердцебиений от единицы результат уже несколько иной. В период удаления от Земли, равный T’/2, для астронавта частота сердцебиений землянина была пониженной:
В период удаления от Земли, равный T’/2, для астронавта частота сердцебиений землянина была пониженной:
а на обратном пути – повышенной:
Следовательно, за весь период путешествия астронавт получил с Земли количество импульсов вместо (7.1):
(7.4)
Соответственно, и для землянина при удалении астронавта частота импульсов понижена:
а на обратном пути – повышена:
То есть, в общем случае частоты получаемых сигналов сердцебиений не равны для участников. С учётом времени получения последнего сигнала до разворота, суммарное количество импульсов, полученных землянином вместо (7.2) равно:
(7.5)
Вот теперь мы можем принять некоторые конкретные, условные значения величин и описать их физический смысл. Пусть v0 = v0‘ = v60 ≈ 60 ударов в минуту. Тогда уравнения (7.4) и (7.5) можно записать в расшифрованном виде. С Земли астронавт получил следующее количество импульсов:
С Земли астронавт получил следующее количество импульсов:
(7.6)
Соответственно, землянин получил от астронавта импульсы в количестве:
(7.7)
Обращаем внимание, что произведения v60T’ и v60T не просто количественно равны, соответственно, отправленным импульсам с Земли R’emitted = v60T’ и от астронавта Remitted = v60T, это и есть эти величины, которые ранее были обозначены как R’ и R. Отметим, что штрихи в уравнениях (7.6) и (7.7) и других вносят некоторую двусмысленность, которую мы снимаем окончательно нижними индексами, точно указывая получателя-отправителя:
Мы пришли к выражениям, подобным выражению (7.3), и выявили источник подмены понятий. Рассматривать ситуацию, когда получено импульсов меньше, чем отправлено, не имеет никакого смысла. Таким образом, хотя метод решения парадокса, описанный в заметке, оригинален, но решить парадокс близнецов как таковой он не позволил.
2. Парадокс близнецов и принцип относительности, Grøn Ø.
Отметим, что традиционное замечание о возможности решения парадокса в специальной теории относительности приводится в самом начале, во введении к рассматриваемой статье:
“Можно сразу избавиться от парадокса близнецов, заметив, что для того, чтобы встретиться, отойти и встретиться снова, по крайней мере, один из близнецов должен ускориться. А в рамках специальной теории относительности принцип относительности не действует для ускоренного движения. Ускорение абсолютно. Следовательно, по крайней мере, один из близнецов не может считать себя в состоянии покоя. Близнец с наибольшей средней скоростью между событиями P1 и P2 будет моложе, когда близнецы встречаются в P2″ [3, с.1].
Однако далее автор всё-таки использует парадокс близнецов, как он указал, в качестве “педагогического входа в общую теорию относительности”. При этом он ссылается на Эйнштейна, который указал на необходимость расширения постулата относительности на любые виды движения, а не только инерциальные. Исходя из этого, теперь уже “оба близнеца имеют право считать себя в состоянии покоя”. В качестве примера автор рассматривает обычную версию парадокса с полётом близнеца к ближайшей звезде Альфа-Проксима. Звезда находится в 4-х световых годах от Земли. Скорость полёта туда и обратно равна v = 0.8c. Автор вычисляет с точки зрения Земли возраст близнеца A, остававшегося на Земле, и возраст близнеца-путешественника B в момент его возвращения, которые равны:
Исходя из этого, теперь уже “оба близнеца имеют право считать себя в состоянии покоя”. В качестве примера автор рассматривает обычную версию парадокса с полётом близнеца к ближайшей звезде Альфа-Проксима. Звезда находится в 4-х световых годах от Земли. Скорость полёта туда и обратно равна v = 0.8c. Автор вычисляет с точки зрения Земли возраст близнеца A, остававшегося на Земле, и возраст близнеца-путешественника B в момент его возвращения, которые равны:
Затем, используя принцип относительности, он делает такие же расчёты, считая теперь находящимся в покое близнеца B, а движущимся – близнеца A. Поскольку теперь движущимися являются Земля и звезда, то этот интервал близнецу B виден сократившимся [3, с.3]:
Следовательно, с его точки зрения он провёл в пути [3, с.4]:
Таким образом, предсказания обоих близнецов относительно возраста близнеца B совпали:
Но вот в отношении возраста близнеца A их предсказания разнятся. По мнению близнеца B его брат состарится меньше [3, с.4]:
По мнению близнеца B его брат состарится меньше [3, с.4]:
Однако это вычисление вызывает некоторое недоумение. Автор выше отметил, что близнец B “видит” трассу Земля-звезда укороченной, поскольку эта трасса является движущимся стержнем в его системе отсчёта. Следовательно, близнецу B определённо известно, что в собственной системе покоя её длина больше, чем вычисленная по уравнению (3):
Поэтому близнец B должен определить время старения A как время, за которое он, близнец B с точки зрения A совершит своё путешествие:
В этом случае предсказания двух близнецов совпали бы и в отношении старения близнеца A, что означает строго корректное решение парадокса близнецов в рамках специальной теории относительности. На этом дальнейшие выкладки мы могли бы опустить, поскольку нас как раз и интересовал способ решения парадокса в рамках СТО. Однако это решение автор отклонил, обосновав это в выводах тем, что в рассмотренной ситуации:
“… ускоренный близнец не имеет права говорить, что он находится в покое, потому что гравитационное поле, которое он испытывает, не имеет источника. Это специальное гравитационное поле вводится в описание, когда мы говорим, что близнец A находится в покое, а B путешествует” [3, c.12].
Это специальное гравитационное поле вводится в описание, когда мы говорим, что близнец A находится в покое, а B путешествует” [3, c.12].
Это довольно странно, поскольку выше он указал, что трасса Земля-Звезда близнецу B видна сократившейся, а это является прямым следствием преобразований Лоренца, если считать близнеца B неподвижным. Тем не менее, вывод сделан и он совпадает с традиционным мнением, что СТО неприменима из ускоренных систем отсчёта, поэтому в ней парадокс не имеет решения и даже не может быть корректно сформулирован. Дальнейшие выкладки автор приводит уже без использования формализма специальной теории относительности.
3. Парадокс близнецов и принцип Маха, Lichtenegger H. and Iorio L.
Авторы статьи рассматривают различные варианты парадокса близнецов. Но мы обратимся только к разделу работы, рассматривающему парадокс в формулировке, близкой к традиционной. В этом варианте близнец-путешественник не возвращается в исходную точку, а сравнение его возраста в конечной точке пути производится с возрастом третьего участника в неподвижной системе отсчёта. Такой вариант правильнее назвать парадоксом трёх часов или парадоксом ровесников. Сами авторы назвали этот вариант “модифицированной версией стандартного парадокса близнецов“.
Такой вариант правильнее назвать парадоксом трёх часов или парадоксом ровесников. Сами авторы назвали этот вариант “модифицированной версией стандартного парадокса близнецов“.
Основным достоинством этого варианта является то, что в процессе движения не используются ускорения, и применение формализма общей теории относительности здесь не требуется. Вариант не имеет принципиальных отличий от традиционного, поскольку возрасты двух близнецов или показания часов рядом с ними, находящихся в неподвижной системе отсчёта всегда тождественны. Поэтому сравнивать возраст путешественника можно с любыми часами в этой неподвижной системе отсчёта.
В работе учитываются текущие показания часов, то есть, в начальный момент движения они не обнулены. Следствием этого стали довольно длинные уравнения и замысловатые обозначения переменных, изобилующие “крышками” – короткой горизонтальной чертой над переменной, эквивалентами обычных штрихов. Рассматривая выкладки, мы сделаем два изменения: вместо “крышек” будем ставить традиционный штрих – неподвижные участники A и B, а путешественник – A’. Показания всех часов в начальный момент движения примем равными нулю. Уравнения станут заметно короче, но, хотя это будут, по сути, другие уравнения, мы будем давать им прежние, авторские номера.
Показания всех часов в начальный момент движения примем равными нулю. Уравнения станут заметно короче, но, хотя это будут, по сути, другие уравнения, мы будем давать им прежние, авторские номера.
Итак, в работе рассмотрены два состояния участников: в начальный момент времени и после перемещения в неподвижной системе K. Скорость перемещения путешествующих часов A’ и их наблюдателя в конечную точку равна V. Расстояние перемещения из положения A в положение B равно Δx = AB. В конечной точке наблюдатель A’, находящийся в движущейся ИСО K’, встречается с третьим участником B. По часам неподвижных наблюдателей A и B от начала движения и до этой встречи прошёл интервал времени [4, с.3]:
Наблюдатель A’ движется инерциально относительно K, поэтому с точки зрения этой ИСО и наблюдателей A и B часы A’ покажут время:
Следовательно, разница в показаниях часов B и A’ при их встрече в ИСО K равна:
С другой стороны, с точки зрения часов A’ и наблюдателей в ИСО K’ движущейся является ИСО K и находящиеся в ней часы A и B. Однако наблюдатели в K’ видят, что интервал Δx испытал лоренцево сокращение, стал короче, поскольку движется со скоростью V относительно ИСО K’. Следовательно, с точки зрения A’ и K’ время в пути составило:
Однако наблюдатели в K’ видят, что интервал Δx испытал лоренцево сокращение, стал короче, поскольку движется со скоростью V относительно ИСО K’. Следовательно, с точки зрения A’ и K’ время в пути составило:
Здесь мы должны заметить, что в отличие от парадокса с ускоренным движением при развороте, в данном случае наблюдатель в движущейся ИСО K’ имеет полное право считать себя неподвижным. В этом случае для наблюдателя A’ часы, находящиеся в ИСО K теперь уже не синхронизированы, с его точки зрения, вследствие движения, они показывают разное время. В соответствии с преобразованиями Лоренца он считает, что часы B опережают часы A с коэффициентом ΔxV/c2, причём, как мы установили для начального момента, t’A = 0, т.е.:
Действительно, уравнение преобразований Лоренца для времени имеет вид:
Правое слагаемое в числителе и есть это опережение (5) двух движущихся часов, разделённых интервалом x.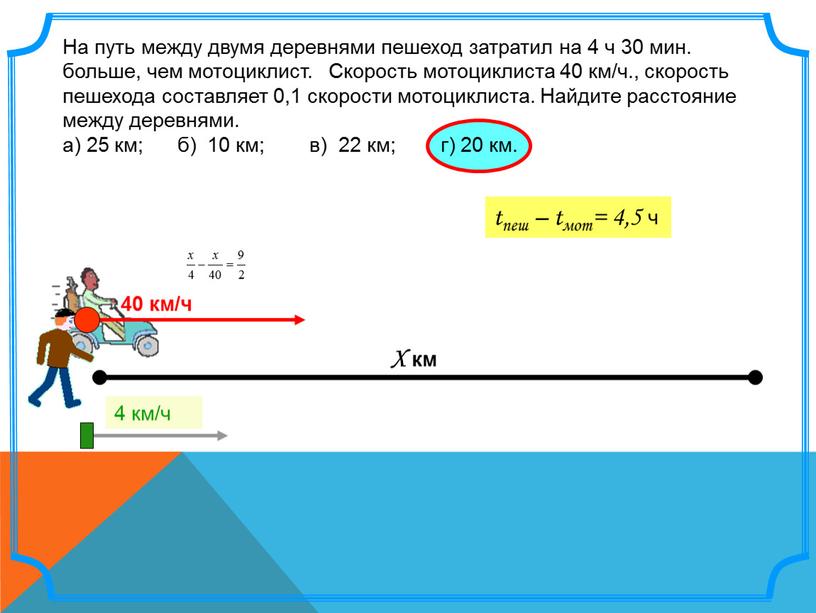 По той же причине движения часов A и B относительно ИСО K’, интервал времени движения, отображаемый часами B, с точки зрения K’ на этом интервале движения от A к B (4) сокращается, уменьшается относительно tA = tB с коэффициентом γ−1, то есть время t’B, увиденное в K’ на часах B при встрече с A’, равно сумме сократившегося интервала (4) и опережения (5) часов B над часами A:
По той же причине движения часов A и B относительно ИСО K’, интервал времени движения, отображаемый часами B, с точки зрения K’ на этом интервале движения от A к B (4) сокращается, уменьшается относительно tA = tB с коэффициентом γ−1, то есть время t’B, увиденное в K’ на часах B при встрече с A’, равно сумме сократившегося интервала (4) и опережения (5) часов B над часами A:
Таким образом, часы A’ с точки зрения ИСО K’ с показаниями (6) отстают от часов B с показаниями (4) на время:
Часы A’ находятся в состоянии покоя в ИСО K’ и показывают меньший интервал времени между показаниями, полученными при последовательном, поочерёдном сравнении с парой часов A и B, синхронизированных в ИСО K. Таким образом, сравнение пар уравнений (2) с (4) и (1) с (6) показывает, что оба наблюдателя – A и B в ИСО K и наблюдатель A’ в ИСО K’ приходят к согласию о показаниях часов при одновременной проверке их в одном и том же месте.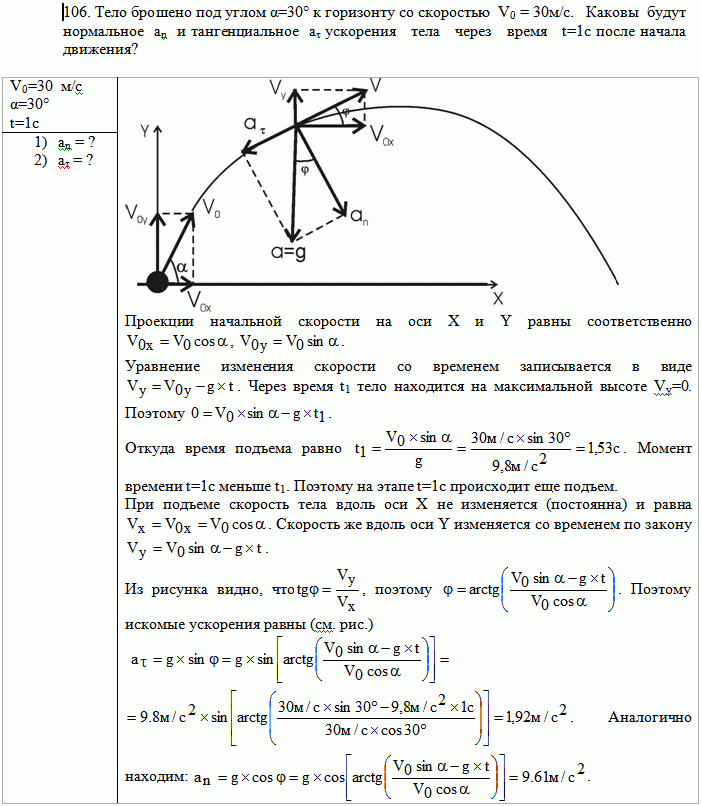 Иначе говоря, в рассмотренном варианте парадокса близнецов в формализме специальной теории относительности нет никакого парадокса и моложе при встрече оказался путешественник A’.
Иначе говоря, в рассмотренном варианте парадокса близнецов в формализме специальной теории относительности нет никакого парадокса и моложе при встрече оказался путешественник A’.
4. Парадокс близнецов, Witman D.M.
Рассматриваемый парадокс близнецов описан в одной из глав данного учебника, предлагаемого как курс теории относительности для неспециалистов. Парадокс рассматривается в традиционном виде, а в качестве близнецов выступают ставшие традиционными участниками в квантовой физике близнецы, ровесники Алиса и Боб. Алиса улетает на ракете в путешествие по галактике. В процессе путешествия близнецы ежегодно посылают друг другу радиосигналы с приглашениями на свои дни рождения.
В общем, представленная картина традиционна: по возвращению Алиса оказывается моложе Боба. При этом отмечено, что парадокс возникает, если применяются правила для инерциального движения к явно неинерциальному движению Алисы [6, с.117]. В этом отношении представляет особый интерес напоминание о том, что Алиса не может рассматривать движение Боба как ускоренное, поскольку у неё есть объективные тесты для определения собственного ускоренного движения. Из этого делается и традиционный вывод, что из-за релятивистского замедления времени в инерциальной системе отсчёта Боба действительно моложе именно Алиса.
Из этого делается и традиционный вывод, что из-за релятивистского замедления времени в инерциальной системе отсчёта Боба действительно моложе именно Алиса.
Словесное решение парадокса сопровождается диаграммами Минковского и не содержит уравнений. Большое внимание уделено тому, что наблюдает путешествующая Алиса, что сопровождается множеством рисунков, правда, довольно абстрактных: круги – планеты и космолёты, на фоне которых изображены годы их текущего времени.
Следует с сожалением отметить, что такая художественная иллюстрация довольно слабо улучшила понимание, аргументацию. Например, планеты с одинаковыми датами на их фоне ничего, по существу, не добавили к тексту в подписи к рисунку 10.3:
“На мгновение остановившись на развороте, Алиса обнаруживает, что все часы планет снова синхронизированы по значению часов локальной планеты. Она прочитали на них четыре года с начала ее путешествия, несмотря на то, что прошло всего два года по ее собственным часов” [6, с. 120].
120].
Поясняется, что в этот момент Алиса ненадолго перешла в систему покоя планет. Это устранило релятивистское искажение времени, и Алиса оказалась в том же 2529 году, что и на этих планетах, несмотря на то, что была в пути только 2 года, начав его в 2025 году:
“Алиса уже моложе Боба, и обратный путь лишь увеличит эффект вдвое, повторяя процесс. Ключевым действием была смена системы отсчёта, также известная как ускорение. Ускорение фактически не повлияло ни на какие часы планеты, но оно изменило набор отдаленных событий, которые Алиса считает одновременными событию здесь и сейчас” [6, с.120].
Задаётся, можно сказать, риторический вопрос:
“Кажется, что-то волшебное произошло во время ускорений Алисы. Как, например, часы планет могли внезапно стать синхронизированными, когда она замедлилась при повороте?” [6, с.120].
Однако последующий ответ на него, рассуждения о перекосах сетки пространства-времени и о “перемотке времени” через часть жизни Боба, довольно туманны и плохо раскрывают суть возникших преобразований. Интересно замечание, что величина ускорения сама по себе не влияет на изменение возраста Алисы, не вызывает замедления её старения по сравнению с Бобом. На этом, собственно, конструктивное описание парадокса завершено. В качестве корректного научного решения парадокса близнецов принять его сложно.
Интересно замечание, что величина ускорения сама по себе не влияет на изменение возраста Алисы, не вызывает замедления её старения по сравнению с Бобом. На этом, собственно, конструктивное описание парадокса завершено. В качестве корректного научного решения парадокса близнецов принять его сложно.
5. Новый взгляд на парадокс близнецов, Бузмаков И.В.
Данную работу мы рассматриваем критически, несмотря на то, что в интернете, на форуме она была подвергнута весьма серьёзной, даже разгромной критике. Мы не будем сравнивать, совпала наша критика с критикой на форуме или нет, а просто укажем на некоторые ошибки в этой работе. Как заявил автор:
“Доказана невозможность объяснения парадокса в рамках теории относительности при движении одного из близнецов по такой траектории” [8].
Доказательство представлено с помощью схемы движения рис.1 в статье:
Рис.1. Разворот часов U2 в точке B по окружности.
Рассмотрены двое часов U1, находящиеся в неподвижной системе отсчёта K в точке A, и часы U2, в системе отсчёта K‘, движущиеся по замкнутой траектории, состоящей из двух прямолинейных, инерциальных участков, и участка разворота по дуге окружности радиуса r.
Отметим, что схема содержит неинерциальный отрезок пути, поэтому в доказательстве рассматривается эффект падения часов U1 в эквивалентном гравитационном поле. При этом утверждается, что в отличие от известных доказательств используются не приближенные, а точные формулы теории относительности, что, по мнению автора, позволило получить такие же абсолютно точные соотношения.
Тем не менее, некоторые допущения всё-таки довольно условны. Заявлено, что при развороте часы U2 не тормозят, а продолжают лететь с той же скоростью V, но по дуге радиуса r вокруг точки B, что, как считается, вроде бы исключает скачкообразное изменение направления скорости часов U2 в точках начала и конца разворота. Однако такой разворот с изменением скорости на противоположную назвать плавным можно весьма условно, поскольку радиус дуги довольно мал. Тем не менее, это допущение можно принять как вполне безобидное. Но вот следующее рассуждение выглядит весьма двусмысленно:
Однако такой разворот с изменением скорости на противоположную назвать плавным можно весьма условно, поскольку радиус дуги довольно мал. Тем не менее, это допущение можно принять как вполне безобидное. Но вот следующее рассуждение выглядит весьма двусмысленно:
“Так как наблюдаемое из К изменение показаний часов U2, произошедшее при их развороте, имеет некоторую конечную величину, и так как часы U2 при движении вдоль отрезка АВ идут медленнее часов U1, то при достаточно большой длине отрезка АВ часы U2 по возвращении в точку А должны отставать от часов U1 на некоторое время ∆t1” [8].
В действительности всё то же самое можно сказать и о наблюдениях из системы K‘, если учесть, что эта система отсчёта некоторое время является неинерциальной, и часы U1 с её точки зрения на этом этапе идут ускоренно, быстрее часов U2. В результате, согласно приведённой ссылке, отстающими оказываются часы U2 и парадокс снимается сразу же.
В результате, согласно приведённой ссылке, отстающими оказываются часы U2 и парадокс снимается сразу же.
Далее мы изменим порядок рассмотрения ситуации с точек зрения каждой системы отсчёта. Сначала традиционно рассмотрим ситуацию, как она описана в статье, с точки зрения изначально неподвижной системы K.
“В системе отсчета K часы U2 все время двигаются со скоростью V. Учитывая, что согласно специальной теории относительности с точки зрения часов U1 часы U2 идут медленнее в γ раз …, получаем, что время ΔTU2, затраченное часами U2 на путешествие, должно быть равно:
ΔTU2 = ΔTA/γ (7)
Автор использует величину лоренц-фактора γ = (1 – V2/c2)–1/2 > 1. Однако, замечаем, ΔTU2 содержит также и неинерциальную составляющую – время разворота по часам U2. На этом интервале движения медленнее часы идут согласно общей теории относительности, поэтому лоренцев коэффициент в этом случае неприменим.
На этом интервале движения медленнее часы идут согласно общей теории относительности, поэтому лоренцев коэффициент в этом случае неприменим.
Теперь рассмотрим эту же картину с точки зрения движущейся системы отсчёта K‘ с часами U2. Автор указывает, что
“Учитывая, что согласно специальной теории относительности на участках равномерного и прямолинейного движения с точки зрения часов U2 движущиеся часы U1 идут медленнее в γ раз …, имеем:
∆τ′U2 = γ∙∆τ′A (3)
Здесь допущена распространённая ошибка. Дело в том, что в этом уравнении время ∆τ′A – это не суммарное время ∆τ′A, прошедшее по часам U1 на участках равномерного и прямолинейного движения, входящее в уравнение (2):
ΔT′A = ∆τ′A + ∆t′A (2)
Для их различения уравнение (3) следует записать иначе:
∆τ′U2 = γ∙∆τ′′A (3a)
Если же использовать авторское значение ∆τ′A, то уравнение (3) должно иметь инверснвый вид:
∆τ′U2 = ∆τ′A/γ (3б)
Связано это с тем, что длина отрезка AB имеет разную величину с точки зрения систем отсчёта K и K‘. Действительно, с точки зрения движущейся системы K‘ этот отрезок движется ей навстречу, поэтому испытывает лоренцево сокращение. Время на прохождение со скоростью V часами U2 этого интервала с точки зрения часов U1 равно:
Действительно, с точки зрения движущейся системы K‘ этот отрезок движется ей навстречу, поэтому испытывает лоренцево сокращение. Время на прохождение со скоростью V часами U2 этого интервала с точки зрения часов U1 равно:
Соответственно, время на прохождение со скоростью V часами U1 этого интервала с точки зрения часов U2 равно:
Сравнивая эти времена, находим
что отличается от уравнения (3) и совпадает с уравнением (3б). По этой же причине следует изменить и соотношение времени на разворот. Если использовать некорректное, лоренцево сокращение интервалов времени на неинерциальном участке и исправленное уравнение (3б), то в этом случае уравнение (5) примет следующий вид:
ΔT′U2 = ∆τ′A/γ + Δt′A/γ (5)
Воспользовавшись сформулированным в статье правом, приравниваем исправленное уравнение (5) и уравнение (8), получив в результате тождество:
∆τ′A/γ + Δt′A/γ = ∆τ′A/γ + ∆t′A/γ
Получается, что вывод автора о приходе к противоречию специальной теории относительности с ее основным постулатом ошибочен. Заявление автора о том, что все полученные им соотношения абсолютно точны, поскольку в представленных расчетах он не использовал никаких приближений, также неверно. Кроме того, рассуждения в статье содержат явную геометрическую ошибку:
Заявление автора о том, что все полученные им соотношения абсолютно точны, поскольку в представленных расчетах он не использовал никаких приближений, также неверно. Кроме того, рассуждения в статье содержат явную геометрическую ошибку:
“На участке разворота система К′ является вращающейся системой отсчета с центром в точке B, поэтому в ней существует гравитационное поле, в котором часы U2 неподвижны, а часы U1, вращаются с угловой скоростью ω вокруг неподвижной точки B, где находятся точно такие же часы UB” [8].
Это утверждение геометрически некорректно, ошибочно. Очевидно, что часы U1 не могут вращаться вокруг точки B по радиусу r, поскольку они попросту находятся дальше от этой точки. Можно было бы предположить, что по этому радиусу r вокруг часов U2 вращаются синхронные с U1 часы UB, находящиеся в центре вращения B. Однако и это неверно, что легко показать вычислениями. Движение часов U2 вокруг часов UB напоминает движение автомобиля по кольцу. Центр кольца всегда неподвижен относительно автомобиля. Таким же образом часы U2 всегда движутся “лицом вдоль траектории”, поэтому часы UB по отношению к ним на рисунке всегда слева. Следовательно, и падают в эквивалентном гравитационном поле вращающихся часов U2 именно неподвижные часы UB.
Однако и это неверно, что легко показать вычислениями. Движение часов U2 вокруг часов UB напоминает движение автомобиля по кольцу. Центр кольца всегда неподвижен относительно автомобиля. Таким же образом часы U2 всегда движутся “лицом вдоль траектории”, поэтому часы UB по отношению к ним на рисунке всегда слева. Следовательно, и падают в эквивалентном гравитационном поле вращающихся часов U2 именно неподвижные часы UB.
Таким образом, вывод о том, что рассмотренный мысленный эксперимент не может быть непротиворечиво описан в рамках теории относительности является ошибочным.
6. Парадокс часов, Мардер Л.
Парадокс в книге рассматривается в наиболее полном, сложном варианте, в котором движение путешественника разбивается на 5 этапов. Отмечается, что с точки зрения неподвижного, земного участника три участка ускоренного движения занимают непродолжительное время по сравнению с участками инерциального движения [9, с. 83]. Считая, в общем, что продолжительность инерциального движения с обеих точек зрения существенно превышает продолжительность времени ускорения, разворота и торможения, которым можно пренебречь, делается очевидный вывод: время в пути по часам путешественника меньше времени по часам земного наблюдателя.
83]. Считая, в общем, что продолжительность инерциального движения с обеих точек зрения существенно превышает продолжительность времени ускорения, разворота и торможения, которым можно пренебречь, делается очевидный вывод: время в пути по часам путешественника меньше времени по часам земного наблюдателя.
Пренебрегая временем неинерциального движения, мы приходим к традиционной формулировке парадокса близнецов. На участках инерциального движения теперь уже можно неподвижным рассматривать путешественника, вследствие чего, меньшее время должны показать часы на Земле.
Решение парадокса производится на диаграмме Минковского. Отмечается, что критерии одновременности на двух участках инерциального движения в системе отсчёта путешественника не одинаковы. Далее утверждается, что при наблюдении путешественником Земли не будет никаких разрывов, и земные часы не будут “идти в бешеном темпе”. Однако последующее пояснение имеет довольно туманный смысл:
“Быстрое изменение происходит лишь с критерием одновременности, но это не играет физической роли, так как понятие одновременности на расстоянии – дело условное. И все же это понятие прекрасно срабатывает, когда требуется рассчитать абсолютный результат вроде различия времени путешествия часов, сначала разлетающихся друг от друга, а затем вновь встречающихся. [9, с.86].
И все же это понятие прекрасно срабатывает, когда требуется рассчитать абсолютный результат вроде различия времени путешествия часов, сначала разлетающихся друг от друга, а затем вновь встречающихся. [9, с.86].
Далее приводятся достаточно детальные ссылки на взгляды разных авторов на парадокс. В заключение сторонникам мнения, что периоды ускоренного движения путешественника “могут быть последовательно рассмотрены лишь в общей теории относительности” [9, с.87] противопоставляется мнение, что “общая теория относительности мало что добавляет к истолкованию парадокса часов, если нет реальных гравитационных полей, хотя в фокусе всех споров находится именно такой случай” [9, с.202].
Собственно решение парадокса близнецов в рамках специальной теории относительности этим и ограничивается. Назвать его исчерпывающим и убедительным мы не можем.
7. Сказка о двух близнецах, Benguigui L.
В этой работе автор отмечает, что по парадоксу близнецов в специальной теории относительности: “Похоже, что во многих статьях есть ошибки” [1, с. 3] и указывает, что он рассматривает, даёт общий обзор только тех решений, которые, как утверждается, находятся в рамках специальной теории относительности [1, с.25]. В частности автор схематично рассмотрел несколько вариантов применения преобразований Лоренца в контексте парадокса близнецов и получил специфические выводы. Поскольку обозначения переменных в цитатах общепринятые, их расшифровку мы не приводим. Рассматривая продолжительность некоторого процесса в двух относительно движущихся ИСО, автор приходит к классической, наивной формулировке парадокса близнецов:
3] и указывает, что он рассматривает, даёт общий обзор только тех решений, которые, как утверждается, находятся в рамках специальной теории относительности [1, с.25]. В частности автор схематично рассмотрел несколько вариантов применения преобразований Лоренца в контексте парадокса близнецов и получил специфические выводы. Поскольку обозначения переменных в цитатах общепринятые, их расшифровку мы не приводим. Рассматривая продолжительность некоторого процесса в двух относительно движущихся ИСО, автор приходит к классической, наивной формулировке парадокса близнецов:
“Можно считать, что τ – это истекшее время пути для каждого близнеца в его собственной системе (земле или ракете), и каждый из них измеряет время γτ для другого. Вопрос в том, какие времена измеряются в обеих системах, когда они снова встречаются?” [1, с.5].
Наивность заключается в том, что происходит отождествление времён, на самом деле качественно не связанных друг с другом, фактически это времена, относящиеся к двум парам разных событий. Правильнее говорить, что один близнец измеряет времена τ и γτ, а другой – t и γt. Именно такое отождествление и лежит в основе традиционной формулировки парадокса. Точно такое же отождествление автор производит и для расстояний:
Правильнее говорить, что один близнец измеряет времена τ и γτ, а другой – t и γt. Именно такое отождествление и лежит в основе традиционной формулировки парадокса. Точно такое же отождествление автор производит и для расстояний:
“Третий случай интересен для расследования … Какова связь между двумя расстояниями L и L’? Поскольку существует полная симметрия между двумя точками зрения в S и в S’, времена, измеренные в S и S’, должны быть равны. Это приводит к тому, что L = L’ и, в частности, нет “сокращения длины” [1, с.6].
Здесь происходит отождествление теперь уже двух пар расстояний, обозначим их как L1 и L’1 и L2 и L’2. Каждая пара расстояний относится к одной из рассмотренных систем отсчёта и качественно они не эквивалентны, поскольку L1 и L2 – это собственные длины в своих ИСО, это два разных отрезка, два разных стержня. Возникает вопрос: это мнение автора или он приводит мнение других исследователей, с которым он не согласен? Пояснений в статье мы не увидели.
Далее в своём анализе автор демонстрирует возможность применения формализма СТО к ускоренно движущимся системам отсчёта. Для этого интервал движения такой системы разбивается на последовательность инерциальных систем отсчета, имеющих также название мгновенно сопутствующая инерциальная система отсчёта – МСИСО. Эти ИСО можно рассматривать как последовательные интервалы исходной неинерциальной системы отсчета. Для такой неинерциальной системы отсчёта собственное время определяется интегрированием коэффициента Лоренца с переменной скоростью:
Это уравнение позволяет вычислить показания часов, движущихся с переменной скоростью, и показывает, что формализм СТО применим к ускоренно движущимся системам отсчёта с точки зрения обычной инерциальной системы. В качестве примера рассматриваются две ИСО S и S’, движущиеся навстречу, причём перед самой встречей ИСО S’ изменяет свою относительную скорость до нуля, то есть, останавливается в ИСО S. Эта ситуация описывается уравнением:
Эта ситуация описывается уравнением:
Принимается, что часы двух систем обнулены на момент начала движения. Интеграл после первого знака равенства – это общее время движения ИСО S’ с точки зрения неподвижной системы S. Первое слагаемое справа – время инерциального движения S’ с точки зрения S, второе слагаемое – время, в течение которого движущаяся система S’ замедлилась до остановки. Как утверждается, интеграл правой части (6) меньше, чем (t1 – t0), следовательно, t’1 < t1 и при их встрече часы S’ покажут меньшее время, чем часы S. При мгновенной остановке t0 = t1, и интеграл в правой части (6) обращается в ноль. Поэтому t’1 = t1/γ, что является традиционным решением парадокса при мгновенном развороте путешественника.
Описывается также и ещё один корректный вариант решения. Если дистанция между ИСО “привязана” к системе S’, то возникает противоположное решение парадокса: t’1 > t1. Иначе говоря, в этом случае путешественник оказывается старше близнеца, остававшегося неподвижным [1, с.7]. Также корректно рассмотрен последний вариант, когда обе ИСО движутся встречно с одинаковой скоростью относительно третьей, неподвижной системы отсчёта. В этом случае при встрече показания их часов будут тождественными. Отметим небольшую неточность в выкладках. При объяснении взглядов Ланжевена на парадокс близнецов автор приводит схему движения, рис.1 в статье, и поясняет:
Иначе говоря, в этом случае путешественник оказывается старше близнеца, остававшегося неподвижным [1, с.7]. Также корректно рассмотрен последний вариант, когда обе ИСО движутся встречно с одинаковой скоростью относительно третьей, неподвижной системы отсчёта. В этом случае при встрече показания их часов будут тождественными. Отметим небольшую неточность в выкладках. При объяснении взглядов Ланжевена на парадокс близнецов автор приводит схему движения, рис.1 в статье, и поясняет:
“Штриховые линии BK и BL – это мировые линии световых сигналов, посылаемых путешественником. Сигнал BK – это последний сигнал, отправленный непосредственно перед его обратным ходом, а BL – первый сигнал, который он отправил сразу после начала своего обратного хода” [1, с.10].
Как видно на рисунке, при такой трактовке световой сигнал BK должен двигаться в прошлое. Далее делается традиционное замечание по парадоксу с ускорением:
“Поскольку система отсчета путешественника ускоряется относительно системы отсчета Земли, она не является инерциальной. Тем не менее, решение проблемы в ИСО Земли может быть достигнуто с помощью специальной теории относительности, но решение в ИСО путешественника с помощью общей теории относительности даст больше понимания” [1, с.12].
Тем не менее, решение проблемы в ИСО Земли может быть достигнуто с помощью специальной теории относительности, но решение в ИСО путешественника с помощью общей теории относительности даст больше понимания” [1, с.12].
Другими словами, землянин может использовать формализм СТО, а путешественнику следует обратиться к ОТО. Рассмотрен также и вариант с тремя системами отсчёта, названный в статье решением без ускорения. От Земли близнец удаляется инерциально в одной системе, а в точке обычного разворота просто перескакивает в такую же ИСО, но движущуюся к Земле. При этом показания своих часов (возраст) он сохраняет неизменными. Этот вариант, следует заметить, отличается от своего традиционного аналога трёх ИСО, в котором никто не перескакивает, просто возвратно движущиеся часы устанавливаются в показания только что прибывших с Земли. При перескакивании близнец испытывает ускорение. Поэтому следует признать ошибочным утверждение автора статьи, что этот сценарий не использует ускорения, следовательно, совместим со специальной теорией относительности. Это неверно, поскольку ускорение просто завуалировано и соответствует мгновенному развороту.
Это неверно, поскольку ускорение просто завуалировано и соответствует мгновенному развороту.
Вместе с тем, следует признать ошибочным и другое утверждение, отрицающее указанное утверждение о совместимости в части величины ускорения. Это утверждение, высказанное при рассмотрении гравитационного решения Мёллера, что:
“… время в точке поворота, несмотря на то, что оно происходит на нулевом расстоянии, не равно нулю при измерении в системе отсчёта “остающегося дома”! Это приводит к тому, что общее время ΔT имеет разрыв в точке поворота. Это является причиной нарушения симметрии во временах двух близнецов. Меллер объясняет этот особенно удивительный результат тем, что в таком случае (g → ∞) гравитационный потенциал бесконечен. Этот результат очень важен, потому что он показывает, что, даже если времена ускорения очень короткие, существует асимметричное старение. Очень часто утверждается, что, если времена ускорения очень малы, ускорение становится несущественным для проблемы, и это неверно” [1, с. 17].
17].
Вывод о ненулевом времени получен в результате некорректных аналитических выкладок. Нулевое расстояние разворота ведёт к тождественно нулевому времени разворота. А при любом коэффициенте соотношения между временами в движущейся и покоящейся системах второе, относительное время также будет равно нулю. Это верно даже для поля гравитации Чёрной дыры: нулевые интервалы времени под горизонтом событий и над горизонтом – тождественны.
“… столь частый аргумент о том, что короткие времена ускорения делают их ненужными, является ложным. … полные расчеты показывают, что разница в возрасте обусловлена двумя факторами: ускорением и замедлением времени” [1, с.27].
При желании расчёты могут показать любой желаемый результат. Хорошо известны решения, использующие мгновенный разворот путешественника, с нулевым временем ускорения. Это, конечно же, приводит к невозможному, бесконечно большому ускорению, однако в этом гипотетическом случае парадокс решается строго в рамках специальной теории относительности и строго в соответствии с другими корректными решениями, с более молодым путешественником в конце полёта. Формально в этом случае путешественник всё время двигался инерциально, без ускорения. В этой связи следует отметить интересное замечание автора:
Формально в этом случае путешественник всё время двигался инерциально, без ускорения. В этой связи следует отметить интересное замечание автора:
“В неускоренной версии близнецы никогда не находятся в одной и той же системе отсчета, и, таким образом, нет ни поездки одного из них, ни возвращения на Землю” [1, с.23].
Этот вывод, по меньшей мере, является неоправданным упрощением. Неускоренную версию можно назвать традиционной, “жёсткой” версией парадокса близнецов. Действительно, речь идёт о соотношении показаний двух относительно движущихся часов, роль которых нередко исполняют близнецы. Близнецы заметно усложняют задачу, поскольку для них в неускоренной версии общей точкой является только место их рождения. Но для часов это не проблема. В пределах бесконечно протяжённой неподвижной ИСО существует любое число синхронизированных часов. Следовательно, в варианте трёх ИСО из исходной точки могут начать путешествие часы, синхронизированные с неподвижными. А в точке условного разворота обратно могут двигаться такие же часы, синхронизированные с прибывшими в эту точки путешествующими часами. В исходной точке сравниваются неподвижные часы и эти, возвращающиеся. Никаких ускорений в этом случае не требуется и вариант формально полностью эквивалентен “жёсткому” варианту парадокса. Действительно, для того чтобы узнать время на другом конце страны, нам не обязательно ускоряться и ехать туда, поскольку все часы синхронизированы.
В исходной точке сравниваются неподвижные часы и эти, возвращающиеся. Никаких ускорений в этом случае не требуется и вариант формально полностью эквивалентен “жёсткому” варианту парадокса. Действительно, для того чтобы узнать время на другом конце страны, нам не обязательно ускоряться и ехать туда, поскольку все часы синхронизированы.
Рассмотренный обзор решений в статье приводит к выводу, что в классической, “жёсткой” формулировке парадокс не имеет не только решения средствами специальной тории относительности, но он даже не может быть в ней сформулирован просто по определению инерциальной системы отсчёта.
Вместе с тем, хотя и с некоторой долей неуверенности, в расширенных и, по сути, эквивалентных формулировках парадокс близнецов в специальной теории относительности имеет непротиворечивое, корректное решение. Все разногласия и разночтения относятся к разным вариантам его формулировки.
8. О решении Эйнштейна парадокса пары часов, Unnikrishnan C. S.
S.
В данной работе автор критически анализирует решения Эйнштейна и делает вывод, что решение, использующее гравитационное замедление времени, “… страдает от логических и физических недостатков и дает неправильные ответы в общем контексте” [5, с.2009]. Буквально это можно трактовать, что решение парадокса близнецов не нуждается в использовании гравитационных полей. Анализ и выводы автор делает в отношении редко цитируемой работы Эйнштена:
“Поскольку сам документ не очень известен, и поскольку расчет не часто обсуждается в контексте парадокса близнецов, я восстанавливаю его здесь. Вывод здесь более подробный, чем приблизительный расчет, упомянутый в некоторых обсуждениях, и, возможно, более подробный, чем имел в виду Эйнштейн …” [5, с.2011].
В результате восстановления расчетов Эйнштейна, автор приходит к традиционному виду парадокса близнецов [5, с.2012], двум уравнениям, противоречию: близнец А стареет меньше, чем В и, наоборот, близнец B стареет меньше, чем A:
Заметим, что при выводе замедления с точки зрения движущегося близнеца ΔTA-B, автор использует некорректные предположения о равенстве ускорений при развороте с разных точек зрения. Однако ускорение само зависит от времени разворота с точки зрения каждого из близнецов. Получается, что во втором случае, с точки зрения движущегося близнеца B для вычисления времени замедления темпа хода часов A в уравнении требуется использовать (через вычисление ускорения) это самое искомое время. Далее, используя гравитационное замедление, автор приходит к следующему выводу [5, с.2012]:
Однако ускорение само зависит от времени разворота с точки зрения каждого из близнецов. Получается, что во втором случае, с точки зрения движущегося близнеца B для вычисления времени замедления темпа хода часов A в уравнении требуется использовать (через вычисление ускорения) это самое искомое время. Далее, используя гравитационное замедление, автор приходит к следующему выводу [5, с.2012]:
“Общее замедление времени A относительно B равно
“
Однако выкладки выгдядят подозрительно. Проверим их. Для удобства записываем исходные уравнения, использованные в (8):
Подставляем их в первое равенство (8):
Собираем подобные члены:
Подробные преобразования делаем, чтобы не упустить мелкие детали:
Окончательно получаем уравнение (8a) и добавляем для сравнение проверяемое уравнение (8):
Это очень странно, но предложенное автором заключительное выражение не соответствует исходным данным, использованным при его выводе.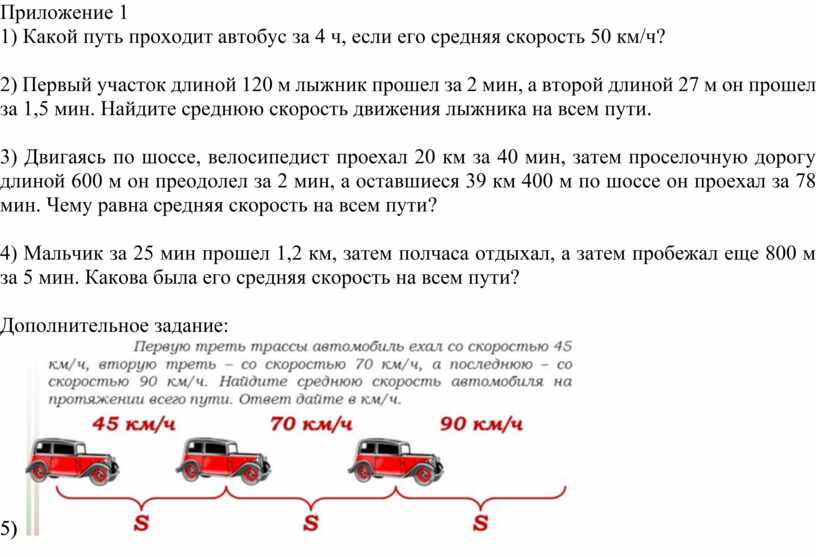 Заодно замечаем, что и уравнение (7) явно не соответствует уравнению (5). Опечатка? Если учесть, что в статье неоднократно делается ссылка на логику, то это более чем странно.
Заодно замечаем, что и уравнение (7) явно не соответствует уравнению (5). Опечатка? Если учесть, что в статье неоднократно делается ссылка на логику, то это более чем странно.
Можно сказать, что в заключение в статье приведены два контрпримера, на основании которых делаются весьма далеко идущие выводы:
“… все стандартные решения парадокса-близнецов, использующие ускорение или эквивалентное псевдо гравитационное поле в качестве физического эффекта, ответственного за асимметричное замедление времени, ошибочны, и решение Эйнштейна не является исключением. Таким образом, решение Эйнштейна, использующее общую теорию относительности, принцип эквивалентности и гравитационное замедление времени, просто не работает, за исключением конкретного случая, состоящего только из двух часов в совершенно особой последовательности движения. Следовательно, это решение парадокса часов, равно как и любое, которое основано на каком-то физическом эффекте, связанном с ускорением, должно быть отвергнуто. … возможность выключения или остановки часов делает все стандартные решения неадекватными” [5, с.2014].
… возможность выключения или остановки часов делает все стандартные решения неадекватными” [5, с.2014].
Надо отметить, что, в общем, мы разделяем позицию о чрезмерности формализма ОТО для решения парадокса близнецов. Для его решения вполне достаточно собственных средств специальной теории относительности. Однако со следующим фундаментальным заявлением, спорным заявлением автора согласиться можно лишь с большой долей осторожности:
“Утверждение … о том, что не существует физического метода измерения скорости движения в пространстве, аннулируется различными маркерами, доступными в космологии …” [5, с.2015].
В заключение отметим, что при наличии объёмной, но всё-таки определённо спорной аргументации, опровержений традиционных гравитационных решений, автор, тем не менее, не привёл хотя бы кратких аналитических доводов, уравнений в пользу решений без формализма ускорений и общей теории относительности.
Библиографический список
- Benguigui L.
 , A tale of two twins, https://arxiv.org/abs/1212.4414
, A tale of two twins, https://arxiv.org/abs/1212.4414 - Eisenlohr H., Another Note on the Twin Paradox, Amer. J. Phys., 36, 635 (1968)
- Grøn Ø., The twin paradox and the principle of relativity, https://arxiv.org/abs/1002.4154
- Lichtenegger H., Iorio L., The twin paradox and Mach’s principle, arXiv:0910.1929v2, 2011
- Unnikrishnan C. S., On Einstein’s resolution of the twin clock paradox. CURRENT SCIENCE, VOL. 89, NO. 12, 25 DECEMBER 2005
- Wittman D.M., The Elements of Relativity. Oxford University Press (2018)
- Борн М. Эйнштейновская теория относительности, перевод с английского Н.В. Мицкевича. – 2-е изд., испр. – М.: МИР, 1972
- Бузмаков И.В., Новый взгляд на парадокс близнецов, // Современные научные исследования и инновации. 2014. № 6. Ч.1 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/06/36247
- Мардер Л., “Парадокс часов”, Пер. с англ. А.А.Бейлинсона, с предисловием Н.В.Мицкевича, Изд. “МИР”, Москва, 1974.
- Мёллер К.
 , Теория относительности, Изд. 2-е. Пер. с англ. Под ред. проф. Д. Иваненко. М.: Атомиздат, 1975, 400 с.
, Теория относительности, Изд. 2-е. Пер. с англ. Под ред. проф. Д. Иваненко. М.: Атомиздат, 1975, 400 с. - Розман Г.А. Теория относительности. – Псков: ПГПУ, 2005. – 256 с.
- Путенихин П.В., Парадокс близнецов – обзор решений. Содержание, URL: http://samlib.ru/p/putenihin_p_w/twin00.shtml
Количество просмотров публикации: Please wait
Все статьи автора «Путенихин Пётр Васильевич»
машин времени | AMNH
Шесть часов в разделе «Время» выставки
AMNH; Фото-студия
Который час? Это зависит от того, как быстро вы путешествуете.

Благодаря Эйнштейну мы знаем, что чем быстрее вы летите, тем медленнее идет время, поэтому очень быстрый космический корабль — это машина времени в будущее. Пять лет на корабле, движущемся со скоростью 99 процентов от скорости света (2,5 года назад и 2,5 года назад), соответствуют примерно 36 годам на Земле. Когда космический корабль вернется на Землю, люди на борту вернутся на 31 год в своем будущем, но они будут всего на пять лет старше, чем в момент отбытия. В самом деле, сам Эйнштейн мог бы быть жив сегодня! Если бы он мог прыгнуть на борт космического корабля, летящего со скоростью 99 процентов скорости света в 1879 году — году его рождения, — ему было бы всего 17 лет, когда он вернулся на Землю сегодня.
Время замедления
Представьте, что каждые из шести показанных часов начали отсчитывать время в день рождения Эйнштейна: 14 марта 1879 года. Пять часов были помещены в космические корабли, а один остался на Земле. Каждый космический корабль движется с разной скоростью, и в результате время на каждом космическом корабле движется с разной скоростью. Чем выше скорость движения, тем медленнее течет время.
Чем выше скорость движения, тем медленнее течет время.
Если бы люди на борту мчащегося корабля вернулись на Землю сейчас, они бы путешествовали во времени с даты, показанной на часах, до сегодняшнего дня — нашего настоящего, но своего будущего.
Эйнштейн родился: 14 марта 1879 г.
часов 1: 0% скорости света
часов 2:25% скорости света
часов 3:50% скорости света
часов 4: 75% скорости света
часов 5 : 99% скорость света
часы 6: 99.99999999% скорость света
ЧАСЫ 1: 0% скорости света (Земля)
Скорость (относительно Земли): 0 километров / час
Длина секунды (относительно Земли): 1,00 секунды
ЧАСЫ 2: 25% скорости света
Скорость (относительно Земли): 25% скорости света
(75000 км / сек или 47000 миль / сек)
Длина секунды (относительно Земли): 1.03 секунды
ЧАСЫ 3: 50% скорости света
Скорость (относительно Земли): 50% скорости света
(150 000 км / сек или 93 000 миль / сек)
Длина секунды (относительно Земли): 1,15 секунды
ЧАСЫ 4: 75% скорости света
Скорость (относительно Земли): 75% скорости света
(225000 км / сек или 140000 миль / сек)
Длина секунды (относительно Земли): 1,51 секунды
ЧАСЫ 5: 99% скорости света
Скорость (относительно Земли): 99% скорости света
(297 000 км / сек или 185 000 миль / сек)
Длина секунды (относительно Земли): 7. 09 секунд
09 секунд
Эйнштейну 17 лет.
ЧАСЫ 6: 99,99999999% скорости света
Скорость (относительно Земли): 99,99999999% скорости света
(299 999,997 км / сек или 185 999,998 миль / сек)
Длина секунды (относительно Земли): 19,6 часа
Эйнштейн один день.
Двойной Парадокс
Парадокс близнецовЧасто задаваемые вопросы о специальной теории относительности
— Парадокс близнецов
Составленный ДокторДжон Симонетти из Кафедра физики в Virginia Tech.
«Пожалуйста, объясните, как работает Парадокс Близнецов». (FAQ, если я когда-нибудь слышал!)
Хотя существует множество возможных примеров Парадокса Близнецов в действии, рассмотрим следующую версию. Prime и Unprime — близнецы; они говорят их прощание, когда Прайм садится в поезд. Прайм едет на поезде в удаленная станция (расстояние L) с постоянной скоростью v (значительная часть скорости света).Достигнув удаленной станции, Прайм берет возвращаться на поезд с той же скоростью, возвращаясь, чтобы встретить Unprime на исходной станция.
 Unprime терпеливо ждал на исходной станции
возвращение Prime. По прибытии на исходную станцию Prime и Unprime
обнаруживают, что Unprime значительно постарел, но Prime не сильно постарел на
все.
Unprime терпеливо ждал на исходной станции
возвращение Prime. По прибытии на исходную станцию Prime и Unprime
обнаруживают, что Unprime значительно постарел, но Prime не сильно постарел на
все.«Парадокс»: Специальная теория относительности утверждает, что физика в отношении кадры, движущиеся относительно друг друга с одинаковой скоростью.Наблюдатели в любые два кадра, движущиеся относительно друг друга, не должны иметь наблюдение, которое указывает, какой из них «фактически» находится в движении. Ну и как что один из близнецов (Прайм) младше другого? Означает ли это один одного из близнецов «на самом деле» было в движении, а другого нет?
Как и все подобные парадоксы, парадокс только кажущийся. В этом случае у Prime
на самом деле совершил поездку. То есть Prime вышел из системы отсчета
Unprime (ощущение первоначального ускорения в начале поездки), затем,
через некоторое время Прайм снова чувствует ускорение, поскольку Прайм замедляется до полной остановки
и разворачивается (садится на обратный поезд), снова набирая скорость,
затем наконец остановился на исходной станции. Прайм испытал много
ускорения; Unprime не почувствовал ускорений. Поэтому Прайм сделал
на самом деле сделать что-то «необычное» — это может быть разумным
чтобы понять, что у Prime и Unprime разный опыт. Действительно, это
похоже, что Prime пережил меньшую продолжительность во время разделения
близнецов, чем испытал Unprime.
Прайм испытал много
ускорения; Unprime не почувствовал ускорений. Поэтому Прайм сделал
на самом деле сделать что-то «необычное» — это может быть разумным
чтобы понять, что у Prime и Unprime разный опыт. Действительно, это
похоже, что Prime пережил меньшую продолжительность во время разделения
близнецов, чем испытал Unprime.
Однако можно возразить, что, хотя у двух близнецов были разные
опыта, совсем не ясно, что один должен быть Моложе другого!
Моя цель здесь — подробно объяснить, почему Prime не так стар, как
Неприятно, когда они встречаются в конце поездки Прайма.Объяснение — это
немного вовлечен, так что не пугайтесь, если вы сначала не все поймете.
Перечитайте его несколько раз. Возможно, вам потребуется обратиться к элементарному тексту на Special
Относительность для объяснения замедления времени, лоренцевского сжатия и
Эффекты относительности одновременности, которые я буду использовать без объяснения причин. В
следующее объяснение, длина и время, измеренные Prime, будут иметь
«штрих» или апостроф, прикрепленный к ним, чтобы различать эти измерения
от Unprime. Итог объяснения: после сравнения
отмечает, что они наблюдают, и Unprime, и Prime согласны с тем, что Prime
старше Unprime.
Итог объяснения: после сравнения
отмечает, что они наблюдают, и Unprime, и Prime согласны с тем, что Prime
старше Unprime.
Давайте проигнорируем продолжительность времени во время ускорений, которым подвергается Prime. Скажем, это ускорение происходит почти мгновенно, поэтому нам не нужно отслеживать, сколько времени они занимают. (Конечно, на самом деле такие внезапные ускорения даст Prime совсем другой опыт, чем Unprime — Prime будет убит! Но давайте проигнорируем эту проблему.) Как вы увидите, ускорения поэтому НЕ ПРИНИМАЙТЕСЬ к количественной разнице в продолжительности разделение, испытанное Prime и Unprime.
Сначала наручные часы Prime и Unprime показывают одинаковое время.
Назовем это время t = t ‘= 0. Чтобы иметь возможность поиграть с числами,
допустим, L = 1 световой год (очень и очень удаленная железнодорожная станция!) и v = 0,80.
c, другими словами, v составляет 80% скорости света (c = скорость света =
186000 миль в секунду).Поезда будут очень быстрыми.
Наблюдения Unprime: в начале
Unprime наблюдает, как его собственные часы показывают t = 0, поскольку Prime мчится со скоростью v. Unprime также видит, что часы Prime показывают t ‘= 0.Наблюдения Непрайма: Когда Прайм достигает далекой станции
Unprime нет на дальней станции, но на станции есть часы платформе, и синхронизируется с часами на запястье Unprime (так же можно было ожидать). Эти часы показывают t = L / v = 1/0.8 = 1,25 года, так как сколько времени потребуется поезду, движущемуся со скоростью v = 0,8c, чтобы проехать расстояние L = 1 световой год. Фотография часов на платформе, сделанная во время прибытие поезда показывает, что часы показывают t = 1,25 года, а фотография передается в Unprime (со скоростью света), поэтому Unprime может проверить это для себя. Когда Прайм на мгновение останавливается и собирается сменить поезд на обратный
поездка, также сделано фото часов Прайма; это фото также передается
на Unprime (со скоростью света), чтобы Unprime мог на него взглянуть. В
На фото видно, что часы Прайма показывают t ‘= 0,75 года. Unprime понимает
этот результат, поскольку Unprime заметил, что наручные часы Prime работают медленно
пока Прайм двигался (в начале поездки). Так что, конечно, меньше времени
истекло бы на часах Прайма. Unprime даже знает, почему: «Я заметил
Часы Прайма должны работать медленно. Любые часы, которые я вижу, я бы наблюдал
бегать медленно; это эффект, называемый замедлением времени. Я могу вычислить
сколько именно времени должно было пройти на вахте Прайма во время его поездки
на дальнюю станцию.2 дюйма до
означает «возведен во 2-ю степень».)
В
На фото видно, что часы Прайма показывают t ‘= 0,75 года. Unprime понимает
этот результат, поскольку Unprime заметил, что наручные часы Prime работают медленно
пока Прайм двигался (в начале поездки). Так что, конечно, меньше времени
истекло бы на часах Прайма. Unprime даже знает, почему: «Я заметил
Часы Прайма должны работать медленно. Любые часы, которые я вижу, я бы наблюдал
бегать медленно; это эффект, называемый замедлением времени. Я могу вычислить
сколько именно времени должно было пройти на вахте Прайма во время его поездки
на дальнюю станцию.2 дюйма до
означает «возведен во 2-ю степень».)
Наблюдения Unprime: на финише
Когда Прайм возвращается на исходную станцию, Unprime отмечает, что его собственная часы показывают t = 2 x 1,25 года = 2,5 года, и Unprime понимает, что это делает здравый смысл: если поезду потребовалось 1,25 года, чтобы преодолеть 1 световой год расстояние до другой станции, то он сядет на второй поезд, едущий на той же скорости еще 1,25 года на обратный путь.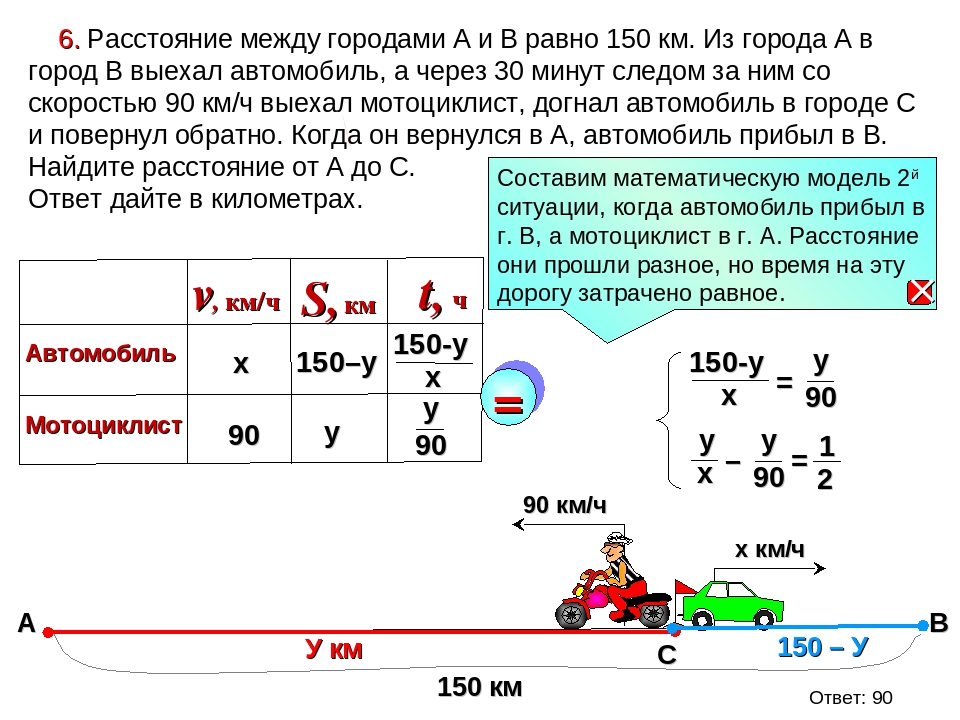 Общая поездка
взял бы t = 2.5 лет.
Общая поездка
взял бы t = 2.5 лет.Unprime теперь смотрит на часы Prime. Он читается как t ‘= 2 x 0,75 года = 1,5. лет. Опять же, Unprime прекрасно понимает этот результат. Unprime увидел фото часов Прайма, сделанное на далекой станции; он показал t ‘= 0,75 лет. Итак, теперь, в конце общей поездки, должно быть t ‘= 1,5 года. Unprime точно понимает, почему t ‘не то же самое, что t: Unprime записывает на мелок все вплоть до Time Dilation.
Unprime резюмирует все это: «Мои часы говорят, что поездка заняла t = 2L / v = 2,5 года, потому что именно столько времени нужно поезду, чтобы преодолеть расстояние L = 1 световой год при скорости v = 0.8c, и вернуться с той же скоростью. Часы Prime записаны всего t ‘= 1,5 года на поездку, потому что часы Прайма шли медленно по сравнению с моим. »
Наблюдения Прайма: в начале
Прайм наблюдает за своими часами, чтобы показать t ‘= 0, а Прайм видит, что часы Unprime также читает t = 0. Движение относительно. Как только мгновенное ускорение В конце Прайм не замечает и не чувствует ничего, что могло бы указывать на движение Прайма; вместо этого Prime наблюдает, как Unprime убегает со скоростью v = 0. 8c.Prime
замечает, что часы Unprime идут медленно. Наконец, Прайм также отмечает
поверхность Земли мчится под поездом со скоростью v = 0.8c.
8c.Prime
замечает, что часы Unprime идут медленно. Наконец, Прайм также отмечает
поверхность Земли мчится под поездом со скоростью v = 0.8c.Наблюдения Прайма: Когда Прайм достигает далекой станции
В конце концов, дальняя станция прибывает на место Прайма (вот как Прайм наблюдает за происходящим). Прайм замечает, что его собственные часы показывают t ‘= 0,75. лет. Прайм прекрасно это понимает. Он знает, по карте, которую он взял поезд, что расстояние между двумя станциями составляет 1 световой год.Prime знает, что это расстояние измеряли люди, державшие линейки из конца в конец (для пример) и стоя на месте относительно станций (так же, как Unprime стоя на исходной станции). Но не это расстояние Прайм будет измерять расстояние между двумя движущимися станциями! Прайм знает (и мог (если он хочет, проверьте путем тщательных измерений), что расстояние между две станции вдоль ДВИЖУЩЕЙСЯ поверхности Земли L / g = 0,6 светового года. Prime знает, что этот результат называется сокращением Лоренца. Прайм говорит:
«Второй станции потребовалось общее время t ‘= (л / г) / v = (1 / 1,6667) / 0,8 =
0,6 / 0,8 = 0,75 года, чтобы добраться до меня, потому что он начинался с расстояния 0,6
на расстоянии световых лет от меня и летел ко мне со скоростью 0,8c «.
Прайм говорит:
«Второй станции потребовалось общее время t ‘= (л / г) / v = (1 / 1,6667) / 0,8 =
0,6 / 0,8 = 0,75 года, чтобы добраться до меня, потому что он начинался с расстояния 0,6
на расстоянии световых лет от меня и летел ко мне со скоростью 0,8c «.Прайм также наблюдает за часами на станции, показывающими t = 1,25 года. Он на мгновение сбит с толку показанием этих часов, но затем вспоминает свой Особый Относительность. Результаты замедления времени и сокращения Лоренца не суммируются все, что есть в специальной теории относительности.Например, есть еще «Относительность одновременности» — события, одновременные в одном система отсчета наблюдателя не будет одновременной в системе отсчета другого наблюдателя. система отсчета (если два наблюдателя движутся относительно друг друга, и если два события имеют некоторое разделение в пространстве по направлению относительное движение).
Итак, как же Прайм объясняет, что t = 1,25 года по сравнению с t ‘= 0,75?
лет? Согласно Unprime, его часы синхронизированы с часами на
дальняя станция. 2.2). В
первый член в этом результате ((L / g) / v) / g и равен расстоянию до
станции перемещаются по наблюдению Prime (L / g), деленное на скорость их движения.
travel (v), все как наблюдал Прайм, но затем уменьшено фактором Лоренца
(g) принять во внимание медленный ход часов станции (временное замедление
эффект). Второй член — это начальная величина, на которую часы станции были
впереди в начале движения. Итак, Прайм говорит: «Время читать
Станционные часы — 1,25 года, и я понимаю, почему.2)) = L / v = 1
световой год / 0,8c = 1,25 года. Это именно то, что показывают часы на станции.
Но, конечно, мои часы показывают только 0,75 года, и я понимаю, почему это так.
также.»
2.2). В
первый член в этом результате ((L / g) / v) / g и равен расстоянию до
станции перемещаются по наблюдению Prime (L / g), деленное на скорость их движения.
travel (v), все как наблюдал Прайм, но затем уменьшено фактором Лоренца
(g) принять во внимание медленный ход часов станции (временное замедление
эффект). Второй член — это начальная величина, на которую часы станции были
впереди в начале движения. Итак, Прайм говорит: «Время читать
Станционные часы — 1,25 года, и я понимаю, почему.2)) = L / v = 1
световой год / 0,8c = 1,25 года. Это именно то, что показывают часы на станции.
Но, конечно, мои часы показывают только 0,75 года, и я понимаю, почему это так.
также.»
Наблюдения Прайма: на финише
Когда исходная станция прибывает в местоположение Прайма, Прайм замечает, что его часы показывают t ‘= 1,5 года, как он и ожидал, так как для первая половина поездки. Теперь Prime смотрит на часы Unprime и видит, что они показывают t = 2,5 года, и
Прайм не удивлен этим, поскольку он заметил, что часы станции показывают t
= 1. 25 лет на полпути эксперимента, а с момента Prime
понимает, почему (как мы только что объяснили выше).
25 лет на полпути эксперимента, а с момента Prime
понимает, почему (как мы только что объяснили выше).
Прайм резюмирует вещи: «По моим наблюдениям, на дальние расстояния потребовалось 0,75 года. станции, чтобы добраться до меня, и еще 0,75 года для исходной станции, чтобы получить назад ко мне. Я точно понимаю, почему, поскольку станции, как я заметил, были разделенные на 0,6 световых года, и двигались на 0,8c. Unprime заметил больше времени на поездку. Его результат (2,5 года) можно понять как результат того, что его часы идут медленно и не синхронизируются (как я заметил их).»
Заключение
Таким образом, оба наблюдателя соглашаются, основываясь на своих собственных наблюдениях, что Unprime’s часы показывают 2,5 года на время их разлуки, а часы Prime читает 1,5 года. Оба наблюдателя также понимают, почему существует такая разница. Прайм теперь младше своего близнеца! Обратите внимание: на обратном пути из-за эффекта относительности одновременности
Прайм замечает, что часы Unprime опережают часы удаленной станции !!
Это с помощью замедления времени объясняет t = 1. 25 лет чтения для возвращения
поездка на вахту Unprime. Если вы озадачены тем, как, по наблюдениям Прайма,
часы удаленной станции были на одну точку впереди часов Unprime, а затем
позже за часами Unprime, причина кроется не в какой-то ошибке в
синхронизация двух часов с помощью Unprime, но вместо этого
Прайм наблюдает за этими часами из РАЗНЫХ систем отсчета на выходе.
и на обратном пути. Помните, еще в самом начале, ПЕРЕД любым
разгона поездом часы Prime и Unprime были синхронизированы (при t
= t ‘= 0), а часы удаленной станции синхронизировались с часами Unprime
часы и часы Prime.Но затем Прайм изменил свою систему взглядов: он
ускоряется (на мгновение) в новую систему с равномерной скоростью. Назад в
Рамка Unprime (исходная рамка Prime), Unprime по-прежнему отмечает, что все часы
в его кадре были синхронизированы. Именно Prime видел часы в Unprime’s
кадр не синхронизирован. Поскольку Прайм тогда двигался к
далекие часы, он заметил, что они были впереди. Однажды Прайм остановился на далеком
станции, он вернулся к системе координат Unprime: Prime видел все часы в
этот кадр будет снова синхронизирован (но чтение 1.
25 лет чтения для возвращения
поездка на вахту Unprime. Если вы озадачены тем, как, по наблюдениям Прайма,
часы удаленной станции были на одну точку впереди часов Unprime, а затем
позже за часами Unprime, причина кроется не в какой-то ошибке в
синхронизация двух часов с помощью Unprime, но вместо этого
Прайм наблюдает за этими часами из РАЗНЫХ систем отсчета на выходе.
и на обратном пути. Помните, еще в самом начале, ПЕРЕД любым
разгона поездом часы Prime и Unprime были синхронизированы (при t
= t ‘= 0), а часы удаленной станции синхронизировались с часами Unprime
часы и часы Prime.Но затем Прайм изменил свою систему взглядов: он
ускоряется (на мгновение) в новую систему с равномерной скоростью. Назад в
Рамка Unprime (исходная рамка Prime), Unprime по-прежнему отмечает, что все часы
в его кадре были синхронизированы. Именно Prime видел часы в Unprime’s
кадр не синхронизирован. Поскольку Прайм тогда двигался к
далекие часы, он заметил, что они были впереди. Однажды Прайм остановился на далеком
станции, он вернулся к системе координат Unprime: Prime видел все часы в
этот кадр будет снова синхронизирован (но чтение 1. 25 лет, пока свое
часы сказали 0,75 года). Затем снова запустился Прайм, теперь путешествуя по
обратное направление: Prime тогда должен был наблюдать за часами Unprime, чтобы опередить
часы удаленной станции, и как раз на нужную величину, чтобы при Prime
прибывает на исходную станцию, часы Unprime будут показывать 2,5 года.
25 лет, пока свое
часы сказали 0,75 года). Затем снова запустился Прайм, теперь путешествуя по
обратное направление: Prime тогда должен был наблюдать за часами Unprime, чтобы опередить
часы удаленной станции, и как раз на нужную величину, чтобы при Prime
прибывает на исходную станцию, часы Unprime будут показывать 2,5 года.
Если вы думаете, что всю эту историю трудно понять, то вы не один. Но это наблюдалось (в экспериментах с частицами) и может быть объяснено (как, например, в вышеприведенной истории) с помощью специальной теории относительности.
Парадокс близнецов без ускорений
В приведенном выше аргументе утверждается, что Prime испытывает ускорение, тогда как Unprime не вызывает, поэтому неудивительно, что опыт разные вещи (в частности, разная продолжительность поездки Прайма). На всякий случай читатель решит, что именно ускорения вызывают разницу в продолжительности жизни близнецов, в этом разделе описано, как парадокс можно объяснить совершенно без ускорений.
Вместо того, чтобы Prime запускался в состоянии покоя, рядом с Unprime, затем ускоряйтесь до
скорости v, затем остановитесь на дальней станции, затем снова ускорьтесь, пока
двигаясь со скоростью v обратно к начальной станции и т. д., представьте себе следующее
демонстрация. Unprime остается на исходной станции. Согласно с
Unprime, Prime движется (и всегда было) со скоростью v, и
передает Unprime в момент, когда часы Unprime и Prime читают t = t ‘=
0. Прайм продолжает свой путь, в конце концов миновав дальнюю станцию.В данный момент
он проходит далекую станцию, часы Прайма показывают t ‘= 0,75 года (по причинам
он понимает, и было объяснено выше). Именно в этот момент Doubleprime
(другой человек), проезжает ту же самую дальнюю станцию в другом направлении поезда
назад к исходной станции на скорости v. Оба Prime и Doubleprime
обратите внимание, что часы станции показывают t = 1,25 года. Также обратите внимание, что оба
их часы показывают время t ‘= t’ ‘= 0,75 года (часы Doubleprime
по совпадению равняется 0. 75 лет). Согласно Unprime (или его когортам)
разбросаны повсюду) Doubleprime всегда шла по этому пути.
В конце концов Doubleprime проходит первоначальную станцию. Когда он проходит, Doubleprime
замечает, что его часы показывают 1,5 года, а часы Unprime’s
на запястье читает 2,5 года. Unprime также замечает две часы. Unprime’s
объяснение — замедление времени (как в приведенном выше объяснении).
Объяснение Doubleprime состоит в том, что Unprime’s
часы работали медленно и не синхронизировались (опять же, как и в
объяснение выше).
75 лет). Согласно Unprime (или его когортам)
разбросаны повсюду) Doubleprime всегда шла по этому пути.
В конце концов Doubleprime проходит первоначальную станцию. Когда он проходит, Doubleprime
замечает, что его часы показывают 1,5 года, а часы Unprime’s
на запястье читает 2,5 года. Unprime также замечает две часы. Unprime’s
объяснение — замедление времени (как в приведенном выше объяснении).
Объяснение Doubleprime состоит в том, что Unprime’s
часы работали медленно и не синхронизировались (опять же, как и в
объяснение выше).
Результирующая разница между показаниями на часах Unprime и показаниями на
Часы Doubleprime не являются результатом каких-либо ускорений, испытанных кем-либо.
(разгонов никто не испытывал). Но обратите внимание, что полный
измеренная продолжительность
Unprime, конечно, измерялся в одной системе отсчета; продолжительность для
полный эксперимент, записанный Prime и Doubleprime, требовал комбинированного
результаты получены в двух разных системах отсчета. Это источник
асимметрия в результатах. Это объяснение парадокса близнецов (без ускорений) показывает, что требуется
ДВЕ разные ссылки
кадров для отслеживания продолжительности времени, которое испытывает
близнец, который на самом деле отправляется в путешествие, в то время как требуется только один кадр, чтобы сохранить
отслеживать продолжительность пребывания близнеца дома.
Их ситуации принципиально
разные, и в результате они испытывают разную продолжительность жизни.
Это объяснение парадокса близнецов (без ускорений) показывает, что требуется
ДВЕ разные ссылки
кадров для отслеживания продолжительности времени, которое испытывает
близнец, который на самом деле отправляется в путешествие, в то время как требуется только один кадр, чтобы сохранить
отслеживать продолжительность пребывания близнеца дома.
Их ситуации принципиально
разные, и в результате они испытывают разную продолжительность жизни.
Вернуться к Часто задаваемые вопросы по астрономии и физике
Эта страница последний раз обновлялась 21 октября 1997 г.
Лекция 23: Специальная теория относительности
Лекция 23: Специальная теория относительностиАстрономия 162: профессор Барбара Райден
Понедельник, 10 февраля
« Здравый смысл — это набор предрассудков приобретен к восемнадцати годам ».
— Альберт Эйнштейн
Ключевое понятие: специальная теория относительности в одном предложении.
- Все скорости относительные ,
кроме скорости света, которая составляет абсолютных .

И специальная теория относительности, и общая теория Теория относительности была сформулирована Альбертом Эйнштейном. (родился 1879, умер в 1955 году).Теории относительности получил репутацию непонятно. Собственно, это что-то бездельника. Теория специальной теории относительности, в частности, очень просто с математической точки зрения. Почему же тогда Специальная теория относительности приобрела репутацию непонятной? В основном потому, что это нарушает « здравый смысл ». В повседневной жизни мы имеем дело с предметами движется намного медленнее скорости света. Специальная теория относительности с объектами, движущимися со скоростью, близкой к скорости света.это неудивительно, что специальная теория относительности не соответствует к набору предрассудков, которые мы накопили из наши наблюдения за медленно движущимися объектами.
Теория Специальная теория относительности , опубликованная Эйнштейном
в 1905 году (когда ему было 26 лет) описывает, как предметы
ведут себя, когда у них постоянная скорость. Десять лет спустя,
в 1915 году Эйнштейн опубликовал свою теорию общих
Теория относительности , описывающая движение объектов
когда они ускоряются силой тяжести.(Общая теория относительности
тема завтрашней лекции;
сегодня мы будем придерживаться
более простой случай специальной теории относительности.)
Десять лет спустя,
в 1915 году Эйнштейн опубликовал свою теорию общих
Теория относительности , описывающая движение объектов
когда они ускоряются силой тяжести.(Общая теория относительности
тема завтрашней лекции;
сегодня мы будем придерживаться
более простой случай специальной теории относительности.)
Специальную теорию относительности можно резюмировать одним коротким предложением:
Все скорости относительны, кроме скорости света, что абсолютно.
Лаконичное предложение — но что оно означает? Давайте начнем
исследуя, что подразумевается под « относительной скоростью ».
Профессор шагает по лекционной платформе.
Ее скорость относительно платформы =
1 метр / секунду
Ее скорость относительно центра Земли =
360 метров / секунду
Ее скорость относительно центра Солнца =
30 000 метров / секунду
Ее скорость относительно центра Галактики =
220 000 метров в секунду
Какая из приведенных выше скоростей является « правильной » скоростью? Все они правильные. Когда вы указываете скорость материального объекта, например, профессор или
звезда, вы указываете скорость относительно некоторого другого объекта.
Для массивных объектов все скорости относительны .
Когда вы указываете скорость материального объекта, например, профессор или
звезда, вы указываете скорость относительно некоторого другого объекта.
Для массивных объектов все скорости относительны .
В качестве еще одного примера относительной природы скоростей, представьте себе преступника, несущегося по Хай-стрит, ведя автомобиль для бегства с места совершения преступления. Как видит невиновный наблюдатель, Автомобиль развивает скорость v = 30 метров в секунду (около 67 миль в час). Преступник вынимает пистолет и стреляет пулей в направление, в котором он движется.По отношению к машине скорость пули u = 250 м / сек (дульное срезание скорость пули из автомата .45).
Обобщая ситуацию:
Скорость автомобиля относительно постороннего = v = 30 м / сек.
Скорость пули относительно машины = u = 250 м / сек.
Чтобы определить скорость пули относительно наблюдателя,
просто сложите скорости вместе:
Скорость пули относительно наблюдателя = v + u = 280 метров в секунду.
Вопрос « Какая скорость пули? » Не дает есть один ответ.Скорость полета пули относительная к машине — 250 метров / сек. Скорость Пуля относительно постороннего составляет 280 метров в секунду. Если на то пошло, скорость пули относительно центр галактики — 220 000 метров в секунду.
Есть важное предостережение, связанное с специальная теория относительности: все скорости относительны, за исключением скорости света , что абсолютно.
В качестве примера абсолютного природы Скорость света, считайте, что тот же преступник рычит вниз Хай-стрит в его машине для побега.По отношению к стороннему наблюдателю, машина имеет такую же скорость v = 30 м / сек. Сейчас же, однако преступник рисует лазер пистолет. Лазер производит электромагнитное излучение, поэтому относительное к машине, лазерный луч будет двигаться со скоростью света: c = 300000000 метров в секунду.
Обобщая новую ситуацию:
Скорость автомобиля относительно постороннего = v = 30 метров / сек.
Скорость светового луча относительно автомобиля = c = 300000000 метров в секунду
Какова скорость светового луча относительно постороннего человека? Классический физик, такой как Галилей или Ньютон, сказал бы: скорость v + c = 300 000 030 м / сек.Однако это неправильно. Правильный ответ, данный Эйнштейном, таков: скорость светового луча относительно постороннего человека c = 300000000.
Скорость света абсолютна; это означает, что это то же самое видно любому наблюдателю, независимо от того, как быстро наблюдатель движется относительно источника света. НАБЛЮДАЕМАЯ СКОРОСТЬ СВЕТА В ВАКУУМЕ ВСЕГДА 299 792 459 КИЛОМЕТРОВ В СЕКУНДУ. (Комментарии в скобках: необходимо добавить квалификацию « в вакууме », поскольку взаимодействие с веществом может замедлить свет луч.Точное значение скорости света обычно округляют. от до 300 000 км / сек для практических целей. Скорость света — скорость всего электромагнитного излучения, от радио до гамма-лучей.)
Тот факт, что скорость света постоянна, был экспериментально подтвержден
подтверждено, сначала парой физиков в Кливленде в 1887 году. Тот факт, что скорость света абсолютна, тогда как все остальные
скорости относительны, имеют странные последствия. Предположим
Я вручаю вам лампочку и отправляю прочь с Земли с
скорость, равная 99% скорости света.Ты говоришь:
Тот факт, что скорость света абсолютна, тогда как все остальные
скорости относительны, имеют странные последствия. Предположим
Я вручаю вам лампочку и отправляю прочь с Земли с
скорость, равная 99% скорости света.Ты говоришь:
« Лампочка стационарная. Свет
от лампочки движется со скоростью c. »
С другой стороны, я говорю:
« Лампочка движется со скоростью 0,99с.
Свет от лампочки движется со скоростью c ».
Два наблюдателя движутся со скоростью 0,99c относительно каждого Другой. Каждый наблюдатель, пользуясь своей меркой и часами, измеряет скорость конкретного луча света, чтобы быть такой же. Единственный способ, которым два наблюдателя могут наблюдать Эйнштейн пришел к выводу, что одна и та же скорость луча света для нечетных что будет происходить с мерками и часами с которой они измеряют скорость света.
Релятивистское замедление времени
Если два наблюдателя движутся относительно каждого другой, каждый видит другой часы идут медленнее.
Чьи часы правильные? Оба верны. ТАМ НЕТ ТАКОЕ ВРЕМЯ. Скорость, с которой течет время отличается для разных наблюдателей.
Релятивистское сокращение длины
Если два наблюдателя движутся относительно каждого другой, каждый видит, что другой сокращается по направлению движения.Чей критерий правильный? Оба верны. НЕТ ТАКОГО АБСОЛЮТНОГО ПРОСТРАНСТВА. Расстояние между две точки разные для разных наблюдателей.
Обратите внимание, что упомянутые релятивистские эффекты выше (замедление времени и сокращение длины) все очень маленькие, если относительная скорость не близка со скоростью света.
Предположим, вы ускоряете объект, применяя постоянная сила к нему. Поскольку скорость объект приближается к скорости света,
- его длина (измеренная вами) приближается к нулю
- время между тактами его часов (измеренное вами) приближается бесконечность
- его ускорение (измеренное вами) приближается к нулю
- и, таким образом, его масса (определяемая как сила / ускорение) приближается к бесконечности.

Понимание Эйнштейна: Масса и энергия кабриолет . «Здравый смысл» подсказывает нам эта масса и энергия — две разные сущности. Однако Эйнштейн выяснилось, что масса может быть преобразована в энергию и наоборот. « Обменный курс » между энергией и массой определяется выражением знаменитая формула:
E = m c 2
Где E — энергия, m — масса, а c — скорость света.поскольку скорость света велика, небольшое количество массы может преобразоваться в большое количество энергии. Один килограмм вещества эквивалентен 10 17 джоулей, или 25 миллиардов киловатт-часов.
Дальнейшее понимание Эйнштейна: Пространство и время межконвертируемый. «Здравый смысл» подсказывает нам, что пространство и время — две разные сущности (пространство это то, что мы измеряем мерками; время то, что мы измерять часами).
 Однако Эйнштейн показал, что
полезнее думать о трех измерениях
пространства и одного измерения времени как бытия
составные части четырехмерного пространства-времени.Два наблюдателя не могут прийти к единому мнению о пространственном расстоянии
между двумя точками (как два конца мерила).
Они не согласятся с промежутком времени между двумя
события (например, два такта часов). Однако раздавит (или сокращение) пространства сопровождается растяжением (или замедление) времени. Таким образом, два наблюдателя согласятся
на четырехмерном пространстве-времени расстояние между
два события.
Однако Эйнштейн показал, что
полезнее думать о трех измерениях
пространства и одного измерения времени как бытия
составные части четырехмерного пространства-времени.Два наблюдателя не могут прийти к единому мнению о пространственном расстоянии
между двумя точками (как два конца мерила).
Они не согласятся с промежутком времени между двумя
события (например, два такта часов). Однако раздавит (или сокращение) пространства сопровождается растяжением (или замедление) времени. Таким образом, два наблюдателя согласятся
на четырехмерном пространстве-времени расстояние между
два события.Профессор Барбара Райден ([email protected])
Обновлено: 10 февраля 2003 г.
Авторское право 2003, Барбара Райден
Дело путешествующих близнецов «Эйнштейн-Онлайн
Почему так называемый «парадокс близнецов» на самом деле не парадокс
Статья Маркуса Пёсселя
В специальной теории относительности Эйнштейна нет такого понятия, как «время» в единственном числе. Время течет по-разному для разных наблюдателей, в зависимости от их движения. Ярким примером являются два гипотетических близнеца: один из них остается дома на Земле. Другие путешествия в космос на сверхбыстрой ракете, почти со скоростью света, перед возвращением домой:
Время течет по-разному для разных наблюдателей, в зависимости от их движения. Ярким примером являются два гипотетических близнеца: один из них остается дома на Земле. Другие путешествия в космос на сверхбыстрой ракете, почти со скоростью света, перед возвращением домой:
После этого, когда близнецы воссоединяются на Земле, странствующий близнец заметно моложе по сравнению с ее братом-домоседом. Точная разница в возрасте зависит от деталей путешествия.Например, может случиться так, что на борту космического корабля прошло два года полета — бортовые часы и календари показывают, что прошло два года, и как космический корабль, так и путешествующий близнец постарели ровно на это количество времени. . Однако на Земле между отправлением космического корабля и его возвращением прошло колоссальные 30 лет. Как и все люди на планете, близнец на Земле за это время постарел на 30 лет. Если увидеть двух (бывших?) Близнецов рядом, разница разительна.
Пока так странно, но, несомненно, реально. Космические путешествия со скоростями, близкими к скорости света, могут быть неизмеримо далеко за пределами досягаемости современных технологий. Но отправка элементарных частиц в оба конца в ускорителе частиц со скоростью 99,99999 процентов от скорости света — обычное дело. Результат полностью согласуется с предсказаниями специальной теории относительности — «внутренние часы» такой движущейся частицы идут намного медленнее, чем у частицы того же вида, которая остается в покое (см.страницу Относительность пространства и времени в разделе Специальная теория относительности элементарного Эйнштейна).
Космические путешествия со скоростями, близкими к скорости света, могут быть неизмеримо далеко за пределами досягаемости современных технологий. Но отправка элементарных частиц в оба конца в ускорителе частиц со скоростью 99,99999 процентов от скорости света — обычное дело. Результат полностью согласуется с предсказаниями специальной теории относительности — «внутренние часы» такой движущейся частицы идут намного медленнее, чем у частицы того же вида, которая остается в покое (см.страницу Относительность пространства и времени в разделе Специальная теория относительности элементарного Эйнштейна).
Поворачивая столы?
Причина, по которой случай странствующих близнецов также известен как «проблема близнецов» или даже «парадокс близнецов», заключается в следующем. С точки зрения близнеца на Земле, разницу в возрасте можно объяснить, обратившись к замедлению времени — основной концепции специальной теории относительности. В нем участвует наблюдатель (точнее: инерционный наблюдатель), например, наблюдатель, который живет на космической станции, плавающей в пустом пространстве. Для такого наблюдателя специальная теория относительности предсказывает следующее: для любых движущихся часов этот наблюдатель придет к выводу, что они идут медленнее, чем его собственные. Будь то часы на другой космической станции, проплывающие мимо, или часы на ракете с приводом от двигателя, за время, необходимое для прохождения секунды на собственных часах наблюдателя, на движущихся часах будет меньше секунды. Это замедление верно не только для часов, но и для всего, что происходит на движущейся космической станции или в летающей ракете.Все процессы, происходящие на этих движущихся объектах, будут казаться нашему наблюдателю замедленными.
Для такого наблюдателя специальная теория относительности предсказывает следующее: для любых движущихся часов этот наблюдатель придет к выводу, что они идут медленнее, чем его собственные. Будь то часы на другой космической станции, проплывающие мимо, или часы на ракете с приводом от двигателя, за время, необходимое для прохождения секунды на собственных часах наблюдателя, на движущихся часах будет меньше секунды. Это замедление верно не только для часов, но и для всего, что происходит на движущейся космической станции или в летающей ракете.Все процессы, происходящие на этих движущихся объектах, будут казаться нашему наблюдателю замедленными.
Характерно, что бывают ситуации, когда замедление времени взаимно. Например, если есть два наблюдателя, дрейфующие в космосе, каждый на своей космической станции, и если эти две космические станции находятся в относительном движении, то для каждого наблюдателя время на другой космической станции кажется медленнее. чем для себя. (Если это уже звучит для вас парадоксом, возможно, вы захотите прочитать популярную тему «Диалектика относительности».)
(Если это уже звучит для вас парадоксом, возможно, вы захотите прочитать популярную тему «Диалектика относительности».)
С помощью замедления времени — часто сокращенно «движущиеся часы идут медленнее» — можно попытаться объяснить, что происходит с близнецами. Неудивительно, что странствующий близнец стареет меньше! В конце концов, близнец на Земле может вызывать замедление времени: движущиеся часы идут медленнее, как и часы движущегося близнеца. На этих более медленных часах — и, соответственно, на всем космическом корабле — проходит меньше времени, чем на Земле, другими словами: когда путешествующий близнец возвращается, он моложе.
Пока парадокса нет.Но почему странствующий близнец не может изменить положение своего брата или сестры? В конце концов, движение относительно. Почему близнец космического корабля не может определить, что находится в состоянии покоя? С этой точки зрения Земля удаляется, прежде чем вернуться на космический корабль. И если это так, не мог ли путешествующий близнец применить замедление времени («движущиеся часы медленнее») ко всем, кто остался на Земле? Согласно этому аргументу, не должны ли люди на Земле оказаться моложе, чем ожидалось, после воссоединения близнецов? Если оба близнеца находятся в равном положении, то каждому следует позволить считать себя в состоянии покоя и вызвать замедление времени. Но в конце концов, когда близнецы снова встречаются, только один из них может быть прав — тогда не может быть никакой двусмысленности: либо один из близнецов моложе, либо другой (или, конечно, аргументы обоих близнецов неверны, и они постарели точно так же). Противоречие — парадокс близнецов?
Но в конце концов, когда близнецы снова встречаются, только один из них может быть прав — тогда не может быть никакой двусмысленности: либо один из близнецов моложе, либо другой (или, конечно, аргументы обоих близнецов неверны, и они постарели точно так же). Противоречие — парадокс близнецов?
Важность инерционных наблюдателей
Чтобы разрешить противоречие, необходимо более пристально взглянуть на замедление времени — в каких ситуациях движущиеся часы действительно идут медленнее? В приведенном выше тексте ключевой критерий был скрыт в скобках: чтобы изречение «Движущиеся часы идут медленнее», выполнялось, вы должны быть инерционным наблюдателем.Приведенный выше пример свободно плавающих космических станций дает представление о том, что означает эта квалификация: в инерциальной системе отсчета все объекты совершенно невесомы. Для таких наблюдателей объект, на который не действуют никакие внешние силы (например, который не толкают и не тянут), либо остается в покое, либо движется с постоянной скоростью по прямой.
Существует лакмусовая бумажка для каждого близнеца: является ли она инерционным наблюдателем и, следовательно, имеет право применять формулу замедления времени, делая вывод о том, что движущиеся часы идут медленнее?
Досадное осложнение: близнец, который остается на Земле, не является инерционным наблюдателем.Она находится в гравитационном поле, в котором объекты падают, а не остаются в покое. Есть два возможных способа продолжить. В любом случае можно использовать теорию гравитации Эйнштейна, общую теорию относительности и вычислить, как гравитационное поле влияет на близнеца на Земле. В результате в данной ситуации гравитация Земли не имеет заметного значения. Если мы игнорируем гравитацию Земли и рассматриваем близнеца на Земле как инерционного наблюдателя, наши результаты относительно относительного старения двух близнецов будут правильными, плюс-минус несколько долей секунды.Если мы выберем ситуации, в которых возможная разница в возрасте близнецов исчисляется годами, сила тяжести не будет иметь значения.
В качестве альтернативы, можно было бы переопределить ситуацию, заставив неподвижного близнеца ждать не на Земле, а на свободно плавающей космической станции в глубоком космосе, вдали от любых массивных объектов. Это определенно сделало бы ее инерциальным наблюдателем.
В обоих случаях результатом является то, что не путешествующий близнец имеет право применить простую формулу замедления времени и сделать вывод, что ее странствующий брат будет моложе, когда они снова встретятся.
А как насчет путешествующего близнеца? Она тоже не инерционный наблюдатель, по крайней мере, не все время. Если бы она просто двигалась с постоянной скоростью по прямой, она никогда не могла бы вернуться на Землю (или, в альтернативной версии, на космическую станцию другого близнеца). Чтобы вернуться, крайне важно, чтобы путешествующий близнец либо остановился и разогнался по направлению к Земле, либо, в качестве альтернативы, запустил свой двигатель, чтобы заставить свой космический корабль свернуть на крутой поворот и направить его обратно к Земле.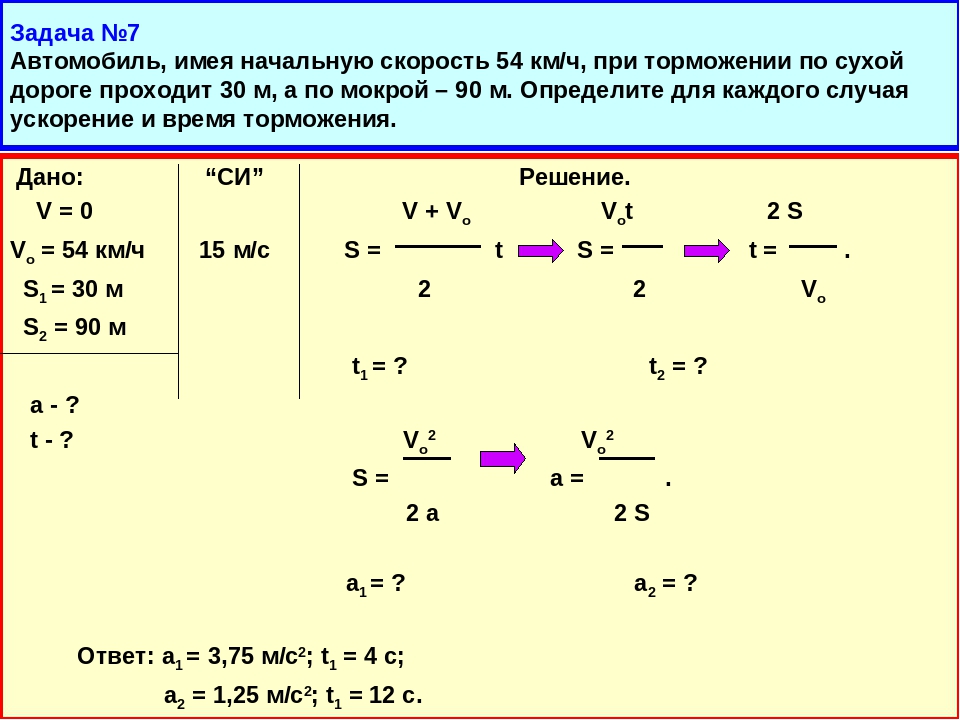 В обоих случаях путешествующий близнец ощущает ускорение — замедление, ее тело ощущает притяжение в направлении полета, повторное ускорение, ее прижимают к сиденью, при полете в повороте ее тянет в сторону. Ускорение неизбежно — и пока она ускоряется, путешествующий близнец определенно не является инерциальным наблюдателем. Например, во время фазы торможения объекты, плавающие внутри кабины космического корабля, не будут просто плавать или двигаться с постоянной скоростью — они будут ускоряться по направлению к передней части космического корабля.И, в отличие от близнеца на Земле, нет никакого небольшого переопределения, которое устранит эти фазы ускорения. Обойти это невозможно: по крайней мере, в течение некоторого времени странствующий близнец не является инерционным наблюдателем.
В обоих случаях путешествующий близнец ощущает ускорение — замедление, ее тело ощущает притяжение в направлении полета, повторное ускорение, ее прижимают к сиденью, при полете в повороте ее тянет в сторону. Ускорение неизбежно — и пока она ускоряется, путешествующий близнец определенно не является инерциальным наблюдателем. Например, во время фазы торможения объекты, плавающие внутри кабины космического корабля, не будут просто плавать или двигаться с постоянной скоростью — они будут ускоряться по направлению к передней части космического корабля.И, в отличие от близнеца на Земле, нет никакого небольшого переопределения, которое устранит эти фазы ускорения. Обойти это невозможно: по крайней мере, в течение некоторого времени странствующий близнец не является инерционным наблюдателем.
Таким образом, очевидный парадокс разрешен. Близнецы не в равных условиях. Ускоренный близнец не может просто применить простую формулу замедления времени, в то время как ее брат на Земле может. Заключение последнего близнеца о том, что часы путешествующего близнеца идут медленнее, и что путешествующий близнец, таким образом, моложе, когда они снова встречаются, верен. (Так какую роль в этом играет ускорение? Узнайте больше в популярной теме «Близнецы на дороге».)
(Так какую роль в этом играет ускорение? Узнайте больше в популярной теме «Близнецы на дороге».)
Дополнительная информация
Что такое относительность? Сногсшибательная теория Эйнштейна объяснила
Когда теория относительности появилась в начале 1900-х годов, она перевернула века науки и дала физикам новое понимание пространства и времени. Исаак Ньютон видел пространство и время как фиксированные, но в новой картине, созданной специальной теорией относительности и общей теорией относительности, они были текучими и податливыми.
Кто придумал теорию относительности?
Альберт Эйнштейн. Он опубликовал первую часть своей теории — специальную теорию относительности — в немецком физическом журнале Annalen der Physik в 1905 году и завершил свою общую теорию относительности только после еще одного десятилетия сложной работы. Он представил последнюю теорию в серии лекций в Берлине в конце 1915 года и опубликовал в Annalen в 1916 году.
Связанные
Что такое специальная теория относительности?
Теория основана на двух ключевых концепциях.
- Во-первых, мир природы не допускает «привилегированных» систем отсчета. Пока объект движется по прямой с постоянной скоростью (то есть без ускорения), законы физики одинаковы для всех. Это немного похоже на то, когда вы смотрите в окно поезда и видите, что соседний поезд движется — но это движется или вы ? Трудно сказать. Эйнштейн признал, что, если движение абсолютно однородно, сказать буквально невозможно — и определил это как центральный принцип физики.
- Во-вторых, свет распространяется с неизменной скоростью 186 000 миль в секунду. Независимо от того, насколько быстро движется наблюдатель или как быстро движется светоизлучающий объект, измерение скорости света всегда дает один и тот же результат.
Исходя из этих двух постулатов, Эйнштейн показал, что пространство и время связаны между собой способами, которые ученые никогда раньше не осознавали. Посредством серии мысленных экспериментов Эйнштейн продемонстрировал, что последствия специальной теории относительности часто противоречат здравому смыслу — даже поразительны.
Посредством серии мысленных экспериментов Эйнштейн продемонстрировал, что последствия специальной теории относительности часто противоречат здравому смыслу — даже поразительны.
Если вы летите на ракете и проехав мимо друга на такой же, но более медленной ракете, например, вы увидите, что часы вашего друга идут медленнее, чем ваши (физики называют это «замедлением времени»).
Более того, ракета вашего друга будет казаться короче вашей собственной.Если ваша ракета разгонится, ваша масса и масса ракеты увеличатся. Чем быстрее вы летите, тем тяжелее становятся вещи и тем сильнее ваша ракета будет сопротивляться вашим усилиям по ускорению. Эйнштейн показал, что ничто, имеющее массу, никогда не может достичь скорости света.
Еще одно следствие специальной теории относительности состоит в том, что материя и энергия взаимозаменяемы с помощью знаменитого уравнения E = mc² (в котором E означает энергию, m — массу, а c² скорость света, умноженную на себя). Поскольку скорость света очень велика, даже небольшое количество массы эквивалентно очень большому количеству энергии и может быть преобразовано в него.Вот почему атомные и водородные бомбы такие мощные.
Поскольку скорость света очень велика, даже небольшое количество массы эквивалентно очень большому количеству энергии и может быть преобразовано в него.Вот почему атомные и водородные бомбы такие мощные.
Что такое общая теория относительности?
По сути, это теория гравитации. Основная идея состоит в том, что гравитация — это не невидимая сила, которая притягивает объекты друг к другу, а искривление или искривление пространства. Чем массивнее объект, тем сильнее он искажает пространство вокруг себя.
Связанные
Например, Солнце достаточно массивно, чтобы искривлять пространство через нашу солнечную систему — это немного похоже на то, как тяжелый шар, лежащий на резиновой пластине, деформирует ее.В результате Земля и другие планеты движутся по изогнутым траекториям (орбитам) вокруг нее.
Эта деформация также влияет на измерения времени. Мы склонны думать, что время уходит с постоянной скоростью. Но точно так же, как гравитация может растягивать или деформировать пространство, она может также замедлять время. Если ваш друг заберется на вершину горы, вы увидите, что его часы тикают быстрее, чем ваши; у другого друга, находящегося на дне долины, будут более медленные часы из-за разницы в силе гравитации в каждом месте.Последующие эксперименты подтвердили, что это действительно происходит.
Если ваш друг заберется на вершину горы, вы увидите, что его часы тикают быстрее, чем ваши; у другого друга, находящегося на дне долины, будут более медленные часы из-за разницы в силе гравитации в каждом месте.Последующие эксперименты подтвердили, что это действительно происходит.
Как выглядит теория относительности «под капотом»?
Специальная теория относительности — это, в конечном счете, набор уравнений, которые связывают то, как вещи выглядят в одной системе отсчета, с тем, как они выглядят в другой — растяжение времени и пространства и увеличение массы. В уравнениях нет ничего сложнее, чем математика средней школы.
Общая теория относительности сложнее. Его «уравнения поля» описывают взаимосвязь между массой и кривизной пространства и замедлением времени, и обычно изучаются на курсах физики в университетах для выпускников.
Тесты специальной и общей теории относительности
За последнее столетие многие эксперименты подтвердили справедливость как специальной, так и общей теории относительности. В ходе первой крупной проверки общей теории относительности астрономы в 1919 году измерили отклонение света от далеких звезд при прохождении звездного света мимо нашего Солнца, доказав, что гравитация действительно искажает или искривляет пространство.
В ходе первой крупной проверки общей теории относительности астрономы в 1919 году измерили отклонение света от далеких звезд при прохождении звездного света мимо нашего Солнца, доказав, что гравитация действительно искажает или искривляет пространство.
В 1971 году ученые проверили обе части теории Эйнштейна, поместив точно синхронизированные атомные часы в авиалайнеры и облетев их вокруг света.Проверка часов после приземления самолетов показала, что часы на борту авиалайнеров идут немного медленнее (менее одной миллионной секунды), чем часы на земле.
Несоответствие возникло из-за скорости самолетов (эффект специальной теории относительности) и их большего расстояния от центра гравитационного поля Земли (эффект общей теории относительности).
В 2016 году открытие гравитационных волн — тонкой ряби в ткани пространства-времени — стало еще одним подтверждением общей теории относительности.
Относительность на практике
Хотя идеи, лежащие в основе теории относительности, кажутся эзотерическими, теория оказала огромное влияние на современный мир.
Атомные электростанции и ядерное оружие, например, были бы невозможны без знания того, что материя может быть преобразована в энергию. И наша спутниковая сеть GPS (глобальная система позиционирования) должна учитывать тонкие эффекты как специальной, так и общей теории относительности; если бы они этого не сделали, они бы дали результаты, отличавшиеся на несколько миль.
ПОДПИСАТЬСЯ НА NBC NEWS MACH В TWITTER, FACEBOOK И INSTAGRAM.
Относительность Эйнштейна, объясненная за 4 простых шага
Теория относительности Альберта Эйнштейна известна тем, что предсказывает некоторые действительно странные, но истинные явления, такие как старение астронавтов медленнее, чем люди на Земле, и твердые объекты, меняющие свою форму с большой скоростью.
Но дело в том, что если вы возьмете копию оригинальной статьи Эйнштейна по теории относительности 1905 года, ее легко прочитать. Его текст ясен и понятен, а его уравнения в основном представляют собой просто алгебру — ничего, что могло бы беспокоить типичного старшеклассника.
Это потому, что Эйнштейн никогда не интересовался причудливой математикой. Он любил мыслить визуально, придумывая эксперименты мысленным взором и работая над ними в своей голове, пока не смог увидеть идеи и физические принципы с кристальной ясностью. (Прочтите «10 фактов, которые вы (возможно) не знали об Эйнштейне».)
Чтобы воплотить этот процесс в жизнь, National Geographic создал интерактивную версию одного из самых известных мысленных экспериментов Эйнштейна: притчу о ударах молнии, видимых из движущегося поезда, которая показывает, как два наблюдателя могут понимать пространство и время по-разному.
Вот как Эйнштейн начал свои мысленные эксперименты, когда ему было всего 16 лет, и как это в конечном итоге привело его к самому революционному уравнению в современной физике.
1895: Бег рядом со световым лучом
К этому моменту из-за плохо замаскированного презрения Эйнштейна к жестким авторитарным методам обучения в своей родной Германии его уже выгнали из школы, эквивалентной средней школе, поэтому он переехал в Цюрих в надежде поступить в Швейцарский федеральный технологический институт (ETH) . (См. Также «Почему ФБР сохранило дело об Эйнштейне на 1400 страниц»).
(См. Также «Почему ФБР сохранило дело об Эйнштейне на 1400 страниц»).
Однако сначала Эйнштейн решил потратить год на подготовку в школе в соседнем городе Аарау — месте, в котором упор делался на такие авангардные методы, как независимое мышление и визуализация концепций. В этой счастливой обстановке он вскоре обнаружил, что задается вопросом, каково это — бегать рядом со световым лучом.
Эйнштейн уже узнал на уроке физики, что такое световой луч: набор колеблющихся электрических и магнитных полей, движущихся со скоростью 186 000 миль в секунду, что является измеренной скоростью света.Эйнштейн рассуждал, что, если бы он бежал рядом с ним с такой скоростью, он должен был бы увидеть ряд колеблющихся электрических и магнитных полей, висящих прямо рядом с ним, казалось бы, неподвижных в космосе.
Но это было невозможно. Во-первых, такие стационарные поля нарушили бы уравнения Максвелла, математические законы, которые систематизировали все, что физики того времени знали об электричестве, магнетизме и свете. Законы были (и остаются) довольно строгими: любая рябь на полях должна двигаться со скоростью света и не может оставаться на месте — никаких исключений.
Законы были (и остаются) довольно строгими: любая рябь на полях должна двигаться со скоростью света и не может оставаться на месте — никаких исключений.
Хуже того, стационарные поля не соответствовали принципу относительности — понятию, которое физики приняли со времен Галилея и Ньютона в 17 веке. По сути, теория относительности гласила, что законы физики не могут зависеть от того, насколько быстро вы двигаетесь; все, что вы могли измерить, — это скорость одного объекта относительно другого.
Но когда Эйнштейн применил этот принцип к своему мысленному эксперименту, это привело к противоречию: теория относительности требовала, чтобы все, что он мог видеть во время бега рядом со световым лучом, включая стационарные поля, также должно было быть тем, что земные физики могли создать в лаборатории.Но ничего подобного никогда не наблюдалось.
Эта проблема будет беспокоить Эйнштейна еще 10 лет, на протяжении всей его университетской работы в ETH и его переезда в столицу Швейцарии Берн, где он стал экспертом в швейцарском патентном бюро. Вот где он решил раз и навсегда разрешить парадокс.
Вот где он решил раз и навсегда разрешить парадокс.
1904: Измерение света от движущегося поезда
Это было непросто. Эйнштейн пробовал все возможные решения, но ничего не помогало.Почти в отчаянии он начал обдумывать простую, но радикальную идею. Он подумал, что, может быть, уравнения Максвелла работают для всех, но скорость света всегда постоянна.
Другими словами, когда вы видели, как луч света проносится мимо, не имеет значения, движется ли его источник к вам, от вас или в сторону, и не имеет значения, насколько быстро он движется. Вы всегда будете измерять скорость этого луча как 186 000 миль в секунду. Среди прочего, это означало, что Эйнштейн никогда не увидит стационарные колеблющиеся поля, потому что он никогда не сможет поймать световой луч.
Это был единственный способ согласовать уравнения Максвелла с принципом относительности, по мнению Эйнштейна. Однако поначалу казалось, что это решение имело свой фатальный недостаток. Позже Эйнштейн объяснил проблему с помощью другого мысленного эксперимента: представьте, что световой луч проходит по насыпи железной дороги, когда поезд движется в том же направлении, скажем, со скоростью 2000 миль в секунду.
Кто-то, стоя на набережной, мог бы измерить скорость светового луча как стандартное число — 186 000 миль в секунду.Но кто-нибудь в поезде увидел бы, как он движется со скоростью всего 184 000 миль в секунду. Эйнштейн пришел к выводу, что если бы скорость света не была постоянной, уравнения Максвелла в вагоне каким-то образом изменились бы, и принцип относительности был бы нарушен.
Это очевидное противоречие заставило Эйнштейна крутиться в колесах почти на год. Но затем, прекрасным майским утром 1905 года, он шел на работу со своим лучшим другом Мишель Бессо, инженером, которого он знал еще со студенческих лет в Цюрихе.Двое мужчин обсуждали дилемму Эйнштейна, как они это часто делали. И вдруг Эйнштейн увидел решение. Он работал над этим всю ночь, и когда они встретились на следующее утро, Эйнштейн сказал Бессо: «Спасибо. Я полностью решил проблему ».
Май 1905: молния поражает движущийся поезд
Эйнштейн открыл, что наблюдатели в относительном движении воспринимают время по-разному: два события вполне могут происходить одновременно с точки зрения одного наблюдателя, но происходить в разное время с точки зрения другого. И оба наблюдателя будут правы.
И оба наблюдателя будут правы.
Позднее Эйнштейн проиллюстрировал это с помощью другого мысленного эксперимента. Представьте, что у вас снова есть наблюдатель, стоящий на железнодорожной насыпи, когда мимо проносится поезд. Но на этот раз в каждый конец поезда попадает молния, когда проходит его середина. Поскольку удары молнии находятся на одинаковом расстоянии от наблюдателя, их свет достигает его глаза в один и тот же момент. Так что он правильно говорит, что они произошли одновременно.
Тем временем еще один наблюдатель в поезде сидит точно в его середине. С ее точки зрения, свет от двух ударов также должен проходить равные расстояния, и она точно так же будет измерять скорость света, чтобы она была одинаковой в любом направлении. Но поскольку поезд движется, свет, исходящий от задней молнии, должен пройти дальше, чтобы догнать ее, поэтому он достигает ее на несколько мгновений позже, чем свет, исходящий спереди. Поскольку световые импульсы приходили в разное время, она может только сделать вывод, что удары были , а не одновременных — что первый действительно произошел первым.
Короче, понял Эйнштейн, одновременность — это то, что относительно. Если вы согласитесь с этим, все странные эффекты, которые мы теперь связываем с теорией относительности, являются вопросом простой алгебры.
Эйнштейн в лихорадке отбросил свои идеи и отправил свою статью для публикации всего несколько недель спустя. Он дал ей название «Электродинамика движущихся тел», что говорило о его борьбе за примирение уравнений Максвелла с принципом относительности. И он завершил его благодарностью Бессо («Я в долгу перед ним за несколько ценных советов»), которые гарантировали его другу легкое бессмертие.
Сентябрь 1905 г .: Масса и энергия
Но на этом первая статья не закончилась. Эйнштейн был одержим теорией относительности все лето 1905 года, а в сентябре он послал вторую статью как своего рода запоздалую мысль.
Он был основан на еще одном мысленном эксперименте. «Представьте себе объект, который неподвижно сидит», — сказал он. А теперь представьте, что он самопроизвольно испускает два одинаковых световых импульса в противоположных направлениях. Объект будет оставаться на месте, но поскольку каждый импульс уносит определенное количество энергии, содержание энергии объекта будет уменьшаться.
Объект будет оставаться на месте, но поскольку каждый импульс уносит определенное количество энергии, содержание энергии объекта будет уменьшаться.
Теперь, сказал Эйнштейн, как бы этот процесс выглядел для движущегося наблюдателя? С ее точки зрения, объект просто продолжал бы двигаться по прямой линии, пока два импульса улетали. Но даже если скорость этих двух импульсов останется одинаковой — скорость света — их энергии будут разными: импульс, движущийся вперед вдоль направления движения, теперь будет иметь более высокую энергию, чем импульс, движущийся назад.
Приложив немного больше алгебры, Эйнштейн показал, что для того, чтобы все это было непротиворечивым, объект должен не только терять энергию при уходе световых импульсов, но и терять немного массы.Или, говоря другими словами, масса и энергия взаимозаменяемы.
Эйнштейн написал уравнение, которое связывает эти два понятия. Используя современные обозначения, в которых скорость света сокращается до буквы c , он легко получил самое известное из когда-либо написанных уравнений: E = mc 2 .
1D Kinematics Review — с ответами № 4
Перейдите к:
Обзорная сессия Домашняя страница — Листинг1D Kinematics — Домашняя страница || Версия для печати || Вопросы и ссылки
Ответы на вопросы: # 1-7 || №8- №28 || # 29- # 42 || # 43- # 50
[# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]Часть E: вычислительные проблемы
43.Определите ускорение (в м / с 2 ) объекта, который ….
- движется по прямой с постоянной скоростью 20,0 м / с в течение 12,0 секунд
- изменяет скорость с 12,1 до 23,5 м / с за 7,81 секунды
- изменяет свою скорость с 0,0 миль / ч до 60,0 миль / ч за 4,20 секунды
- разгоняется с 33,4 м / с до 18,9 м / с на расстоянии 109 м
Ответ: См. Ответы, пояснения и расчеты ниже.
Ответы, пояснения и расчеты ниже.
а. Если скорость и направление объекта постоянны, то ускорение составляет 0 м / с 2 .
г. Ускорение — это отношение изменения скорости за время:
a = (Изменение скорости) / t = (23,5 м / с — 12,1 м / с) / (7,81 с) = 1,46 м / с 2 .г. Ускорение — это отношение изменения скорости за время:
a = (Изменение скорости) / t = (60,0 миль / час — 0,0 миль / час) / (4,20 с) = 14,3 миль / час / с .14.3 мили / час / с * (1,0 м / с) / (2,24 миль / час) = 6,38 м / с 2 .
г. Величина ускорения также может быть рассчитана с использованием кинематических уравнений, если известны три другие кинематические величины. В этом случае известная информация: v o = 33,4 м / с; v f = 18,9 м / с; и d = 109 м. Используя уравнение v f 2 = v o 2 + 2 * a * d, можно вычислить ускорение.
44. Определите величину перемещения (в метрах) объекта, который ….
- перемещается из Hither в Yon (со средней скоростью 28,0 м / с), а затем обратно в Hither (со средней скоростью 28,0 м / с), если оба пути вперед и назад занимают 46 минут каждый.
- движется с постоянной скоростью 8.30 м / с по прямой в течение 15,0 секунд.
- замедляется со скоростью -4,35 м / с / с со скорости 38,1 м / с до скорости 17,6 м / с
- ускоряется из состояния покоя со скоростью 3,67 м / с 2 за 12,1 секунды
- движется со скоростью 12,2 м / с, а затем ускоряется со скоростью +1,88 м / с 2 в течение 17,0 секунд
Ответ: См. Ответы, пояснения и расчеты ниже.
а. Поскольку это поездка туда и обратно, общее смещение составляет 0 м.
г. Поскольку скорость постоянна, смещение можно найти, умножив скорость на время.
d = v * t = (8,30 м / с) * (15,0 с) = 125 мг. Величину смещения также можно рассчитать с использованием кинематических уравнений, если известны три другие кинематические величины. В этом случае известная информация: v o = 38,1 м / с; v f = 17,6 м / с; и a = -4,35 м / с / с. Используя уравнение v f 2 = v o 2 + 2 * a * d, можно вычислить смещение.
d = (v f 2 — v o 2 ) / (2 * a) = [(17,6 м / с) 2 — (38,1 м / с) 2 ] / (2 * -4,35 м / с / с) = 131 м . г. Величину смещения можно рассчитать с помощью других кинематических уравнений, если известен другой набор кинематических величин. Здесь мы знаем, что: v o = 0,0 м / с; t = 12,1 с; и a = 3,67 м / с / с. Используя уравнение d = v o * t + 0,5 * a * t 2 , можно вычислить смещение.
Используя уравнение d = v o * t + 0,5 * a * t 2 , можно вычислить смещение.
e. Здесь величина смещения рассчитывается с использованием того же кинематического уравнения. Мы знаем, что: v o = 12,2 м / с; t = 17,0 с; и a = 1,88 м / с / с. Используя уравнение d = v o * t + 0,5 * a * t 2 , можно вычислить смещение.
d = (12,2 м / с) * (17,0 с) + 0,5 * (1,88 м / с / с) * (17,0 с) 2 = 479 м . [# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]45.Заяц спит в 1200 м от финиша. Черепаха обгоняет его с постоянной скоростью 5,0 см / с. Если заяц наконец просыпается через 6,5 часов, то какое минимальное ускорение (предполагаемое постоянное) должно быть у него, чтобы обогнать черепаху до финиша.
Ответ: 0,0067 м / с 2
Как и во многих других словесных задачах по физике, существует несколько путей к окончательному ответу. Во всех подобных проблемах решение включает в себя обдумывание и хорошие стратегии решения проблем (нарисуйте картинку, перечислите то, что вы знаете, перечислите соответствующие уравнения и т. Д.).
Во всех подобных проблемах решение включает в себя обдумывание и хорошие стратегии решения проблем (нарисуйте картинку, перечислите то, что вы знаете, перечислите соответствующие уравнения и т. Д.).
Черепаха, двигаясь с постоянной скоростью, преодолеет 1200 м за:
t черепаха = d / v черепаха = (1200 м) / (0,050 м / с) = 24000 с = 6,666 … часовЗаяц будет спать 6,5 часов (23400 с) перед стартом, поэтому у него будет всего 0,1666 … часов (600 с), чтобы разогнаться до финиша. Таким образом, ускорение зайца можно определить с помощью кинематического уравнения. Известная информация о движении зайца: t = 600 с; d = 1200 м; v o = 0 м / с.Лучшее уравнение: d = v o * t + 0,5 * a * t 2 . Член v o * t отменяется, и уравнение может быть алгебраически преобразовано и решено для a:
a = 2 * d / t 2 = 2 * (1200 м) / (600 с) 2 = 0,0067 м / с 2 . [# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]
46. Золотая машина движется в 12.0 м / с проезжает Green Car , а Green Car стоит на светофоре. Green Car немедленно ускоряется со скоростью +1,80 м / с / с в течение 11,0 секунд, а затем поддерживает постоянную скорость. Через какое время (относительно начального времени запуска) Green Car должна проехать, прежде чем догнать Gold Car .
Золотая машина движется в 12.0 м / с проезжает Green Car , а Green Car стоит на светофоре. Green Car немедленно ускоряется со скоростью +1,80 м / с / с в течение 11,0 секунд, а затем поддерживает постоянную скорость. Через какое время (относительно начального времени запуска) Green Car должна проехать, прежде чем догнать Gold Car .
Ответ: 14,0 с
(Как упоминалось в предыдущей задаче …) Как и во многих других словесных задачах по физике, существует несколько путей к окончательному ответу.Решение всех таких проблем включает в себя обдумывание и хорошие стратегии решения проблем (нарисуйте картинку, перечислите то, что вы знаете, перечислите соответствующие уравнения и т. Д.).
Здесь золотой автомобиль движется с постоянной скоростью в течение т секунд (где т — общее время в пути для обеих машин). Расстояние, пройденное золотой машиной, определяется кинематическим уравнением d = v o * t + 0,5 * a * t 2 . Второй член отменяется, и расстояние можно выразить как
Второй член отменяется, и расстояние можно выразить как
d золото = 12,0 * t
Для зеленой машины сначала идет период ускорения, а затем период постоянной скорости. Расстояние, пройденное за период ускорения (d 1 зеленый ), определяется из того же кинематического уравнения. Для зеленой машины первый член отменяется, и расстояние равно
. d 1 зеленый = v o * t + 0,5 * a * t 2 = 0,5 * (1,80 м / с 2 ) * (11.0 с) 2 , илиd 1 зеленый = 108,9 м
После того, как зеленый автомобиль ускоряется в течение 11 секунд, он сохраняет постоянную скорость в течение оставшегося времени, определяемого выражением t — 11 с. Скорость, с которой зеленый автомобиль движется за это время, можно рассчитать по формуле:
v f зеленый = v o + a * t = (1,80 м / с 2 ) * (11,0 с) = 19,8 м / с Расстояние, пройденное зеленой машиной во время этого участка движения с постоянной скоростью (d 2green ), можно вычислить с помощью кинематического уравнения. d = v o * t + 0,5 * a * t 2 . Второй член отменяется, и расстояние можно выразить как
d = v o * t + 0,5 * a * t 2 . Второй член отменяется, и расстояние можно выразить как
д 2зеленый = 19,8 * т — 217,8
Таким образом, общее расстояние, пройденное зеленой машиной, определяется выражением:
d зеленый = d 1 зеленый + d 2 зеленый = 108,9 + 19,8 * t — 217,8d зеленый = 19.8 * т — 108,9
Когда зеленая машина догонит золотую, их пройденное расстояние будет таким же. Таким образом, время t можно определить, задав два выражения для расстояния равными друг другу и решив для t.
12,0 * т = 19,8 * т — 108,9108,9 = 7,80 * т
т = (108,9) / (7,80)
t = 13,96 с = 14,0 с
[# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50] 47.Ima Rilla Saari движется со скоростью 28,0 м / с по Лейк-авеню и через лесной заповедник. Она замечает, как олень прыгает на дорогу в 62,0 м перед ней. Има сначала реагирует на событие, затем нажимает на тормоза и замедляет скорость -8,10 м / с 2 , и в конечном итоге останавливает пикометр перед замороженным оленем . Какое время реакции Имы ? (т.е. сколько времени потребовалось Има, чтобы отреагировать на событие до замедления?)
Она замечает, как олень прыгает на дорогу в 62,0 м перед ней. Има сначала реагирует на событие, затем нажимает на тормоза и замедляет скорость -8,10 м / с 2 , и в конечном итоге останавливает пикометр перед замороженным оленем . Какое время реакции Имы ? (т.е. сколько времени потребовалось Има, чтобы отреагировать на событие до замедления?)
Ответ: 0.486 с
Общее пройденное расстояние Имы (62,0 м) можно разделить на два сегмента — расстояние реакции (d rxn ) и тормозной путь (d торможение ). Расстояние реакции — это расстояние, на которое Ima проходит до торможения; она будет двигаться с постоянной скоростью в это время т rxn . Тормозной путь — это расстояние, которое Има проходит, когда ее нога нажимает на тормоз, и она замедляется с 28,0 м / с до 0,0 м / с. Сначала можно рассчитать тормозной путь, используя следующее кинематическое уравнение: v f 2 = v o 2 + 2 * a * d. Известная информация для этого периода торможения: v o = 28 м / с; v f = 0 м / с; и a = -8,10 м / с / с. Замены и решения показаны ниже.
Известная информация для этого периода торможения: v o = 28 м / с; v f = 0 м / с; и a = -8,10 м / с / с. Замены и решения показаны ниже.
Поскольку машине Имы требуется 48,40 м для торможения, она может проехать максимум 13,6 м за время реакции. Связь между временем реакции, скоростью и расстоянием реакции определяется уравнением
d rxn = v * t rxnЗамена 13.6 м для d rxn и 28,0 м / с для v, время реакции можно вычислить:
t rxn = (13,6 м) / (28,0 м / с) = 0,486 с [# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50] 48. Двухступенчатая ракета ускоряется из состояния покоя со скоростью +3,57 м / с / с за 6,82 секунды. Затем он ускоряется со скоростью +2,98 м / с / с еще на 5,90 секунды. После второй стадии он переходит в состояние свободного падения. Определить:
После второй стадии он переходит в состояние свободного падения. Определить:
- максимальная скорость
- максимальная высота
- высота ракеты после 20.0 секунд
- общее время нахождения ракеты в воздухе (при условии, что она запущена с земли)
Ответ: См. Ответы и пояснения ниже.
К этой проблеме можно подойти, используя либо график скорости-времени, либо кинематические уравнения (или их комбинацию). Каким бы ни был подход, необходимо обязательно разбить многоступенчатое движение на три различных периода ускорения. Использование кинематических уравнений подходит только для постоянных периодов ускорения.По этой причине сложное движение необходимо разбить на периоды времени, в течение которых ускорение является постоянным. Эти три периода времени можно увидеть на графике скорость-время тремя линиями с явно разным наклоном. На диаграмме справа показано движение; помечены стратегические точки. Эти моменты будут упомянуты в решениях ниже. График скорости-времени, представленный ниже, будет использоваться во всем решении; обратите внимание, что на графике отмечены те же самые стратегические точки.
График скорости-времени, представленный ниже, будет использоваться во всем решении; обратите внимание, что на графике отмечены те же самые стратегические точки.
а. Максимальная скорость достигается после второй ступени или периода разгона (точка C). По истечении этого времени движущаяся вверх ракета начинает замедляться, поскольку гравитация становится единственной силой, действующей на нее. Для определения этой скорости (v c ) кинематическое уравнение v f = v o + a * t будет использоваться дважды — один раз для каждого периода разгона.
Первая ступень: v B = v A + a * t = 0 м / с + (3,57 м / с / с) * (6,82 с) = 24,3 м / сВторой этап: v C = v B + a * t = 24.3 м / с + (2,98 м / с / с) * (5,90 с) = 41,9 м / с
г. Максимальная высота достигается в точке D, через некоторое время после того, как вторая ступень остановится и у ракеты , наконец, закончится пар . Скорость в этой точке 0 м / с (это пик траектории). Высота в этой точке — это совокупное расстояние, пройденное от t = 0 с до t = t D . Это расстояние — это расстояние для первой ступени, второй ступени и периода замедления (от C до D).Эти расстояния соответствуют площади на графике v-t; на графике они обозначены A 1 , A 2 и A 3 . Они рассчитаны и суммированы ниже.
Скорость в этой точке 0 м / с (это пик траектории). Высота в этой точке — это совокупное расстояние, пройденное от t = 0 с до t = t D . Это расстояние — это расстояние для первой ступени, второй ступени и периода замедления (от C до D).Эти расстояния соответствуют площади на графике v-t; на графике они обозначены A 1 , A 2 и A 3 . Они рассчитаны и суммированы ниже.
A 2 = b * h + 0,5 * b * h (треугольник на вершине квадрата)
A 2 = (24,3 м / с) * (5,9 с) + 0,5 * (41,9 м / с — 24,3 м / с) * (5,9 с) = 195,42 м
Для определения A 3 необходимо знать время от точки C до точки D.Это время можно определить с помощью кинематического уравнения: v f = v o + a * t, для которого v f = 0 м / с и v o = 41,9 м / с и a = -9,8 м / с. с / с.
v D = v C + a * t0 м / с = 41,9 м / с + (-9,8 м / с / с) * t
t = 4,28 с
Теперь A 3 можно определить с помощью графика v-t. Площадь представляет собой треугольник и рассчитывается как
Площадь представляет собой треугольник и рассчитывается как
Максимальная высота складывается из трех расстояний (площадей)
Максимум. высота = 82,86 м + 195,42 м + 89,57 м = 368 мг. Когда ракета достигает точки D, время составляет 17,0 секунды. Высота на отметке 20,0 секунды будет равна 368 м, поднятым над стартовой площадкой от точки A до точки D, за вычетом расстояния, упавшего с пика с 17,0 до 20,0 секунд. Это расстояние будет представлено отрицательной областью на графике скорость-время. Площадь представляет собой треугольник и может быть вычислена, если известна скорость в 20 секунд.Его можно рассчитать с помощью кинематического уравнения, а затем использовать для определения площади треугольника. В качестве альтернативы можно использовать кинематическое уравнение для определения расстояния, пройденного за эти 3,0 секунды. Работа представлена ниже:
d = v o * t + 0,5 * a * t 2 = 0,5 * (-9,8 м / с / с) * (3,0 с) 2 = 44,1 м Таким образом, высота на отметке 20 секунд равна ~ 369 м, набранной за первые 17 секунд минус ~ 44 м, упавшей в следующие 3 секунды. Ответ: 325 м .
Ответ: 325 м .
г. Ракета поднимается на 369 м за первые 17,0 секунды. В последующее время ракета должна упасть на 369 метров. Время падения с высоты 369 м можно определить из того же кинематического уравнения, которое использовалось в части c.
d = v o * t + 0,5 * a * t 2-368 м = 0,5 * (-9,8 м / с / с) * т 2
t = 8,67 секунды
Это время может быть добавлено к 17.0 секундам, чтобы определить время приземления ракеты: 25.7 секунд .
[# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]49. В эстафете на 200,0 м (длина каждого этапа забега составляет 50,0 м) один пловец с опережением на 0,450 секунды плывет с постоянной скоростью 3,90 м / с к противоположному концу бассейна. Какая минимальная скорость должна быть у второго пловца, чтобы догнать первого к концу бассейна?
Ответ: 4,04 м / с
Оба пловца проплывают одинаковое расстояние (50 м) с постоянной скоростью. Пловец А (которого только что назвали произвольно) получает фору в 0,450 секунды. Таким образом, пловец B должен двигаться быстрее, чтобы финишировать за меньшее время, чем пловец A. Во-первых, можно вычислить время, необходимое пловцу A для преодоления 5010 м со скоростью 3,90 м / с. Время
Пловец А (которого только что назвали произвольно) получает фору в 0,450 секунды. Таким образом, пловец B должен двигаться быстрее, чтобы финишировать за меньшее время, чем пловец A. Во-первых, можно вычислить время, необходимое пловцу A для преодоления 5010 м со скоростью 3,90 м / с. Время
Таким образом, пловец B должен финишировать на те же 50,0 м за 12,37 секунды (12,82–0,45 с). Таким образом, скорость пловца B может быть вычислена как
. v B = d / t B = (50.0 м) / (12,37 с) = 4,04 м / с [# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]50. Драгрейсер ускоряется из состояния покоя со средней скоростью +13,2 м / с 2 на расстояние 100 м. Водитель едет по инерции в течение 0,500 секунд, а затем использует тормоза и парашют для замедления до конца трассы. Если общая длина трассы составляет 180 м, какая минимальная скорость замедления должна быть у гонщика, чтобы остановиться до конца трассы?
Ответ: -24 м / с / с
К этой проблеме можно подойти, сначала определив расстояние, на котором драгстер замедляется. Это расстояние будет меньше 80 метров на величину, равную расстоянию, которое драгстер преодолевает после пересечения финишной черты. См. Диаграмму.
Это расстояние будет меньше 80 метров на величину, равную расстоянию, которое драгстер преодолевает после пересечения финишной черты. См. Диаграмму.
Расстояние, пройденное драгстером до торможения, составляет 100 м плюс расстояние наката. Дальность движения накатом можно определить, если определить скорость драгстера на конце 100 м. Итак, сначала кинематическое уравнение будет использоваться для определения скорости, а затем будет вычислено расстояние наката.
Используя уравнение v f 2 = v o 2 + 2 * a * d, можно определить скорость через 100 м.Эта замена и решение показаны ниже.
v f 2 = v o 2 + 2 * a * d = 2 * (13,2 м / с / с) * (100 м) = 2640 м 2 / с 2v f = 51,4 м / с
Выбег со скоростью 51,38 м / с в течение 0,500 с приведет к пройденному расстоянию 25,7 м.
По окончании периода движения накатом остается небольшое расстояние для замедления до остановки. Это расстояние
Это расстояние
Теперь то же кинематическое уравнение можно использовать для определения скорости замедления на последних 54 м пути.Известная информация: v o = 51,4 м / с; v f = 0 м / с; и d = 54 м. Используя уравнение v f 2 = v o 2 + 2 * a * d, можно вычислить ускорение.
a = (v f 2 — v o 2 ) / (2 * d) = = [(51,4 м / с) 2 — (0 м / с) 2 ] / ( 2 * 54 м) = -24 м / с 2 . [# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]Перейдите к:
Обзорная сессия Домашняя страница — Листинг1D Kinematics — Домашняя страница || Версия для печати || Вопросы и ссылки
Ответы на вопросы: # 1-7 || №8- №28 || # 29- # 42 || # 43- # 50
Вам тоже может понравиться…
Пользователи The Review Session часто ищут учебные ресурсы, которые предоставляют им возможности для практики и обзора, которые включают встроенную обратную связь и инструкции. Если это то, что вы ищете, то вам также может понравиться следующее:- Блокнот калькулятора
Блокнот калькулятора включает в себя текстовые задачи по физике, организованные по темам. Каждая проблема сопровождается всплывающим ответом и аудиофайлом, в котором подробно объясняется, как подойти к проблеме и решить ее.Это идеальный ресурс для тех, кто хочет улучшить свои навыки решения проблем.
Визит: Панель калькулятора На главную | Блокнот калькулятора — кинематика
Приложение - Minds On Physics Приложение
Minds On Physics («MOP the App») представляет собой серию интерактивных модулей вопросов для учащихся, которые серьезно настроены улучшить свое концептуальное понимание физики. Каждый модуль этой серии посвящен отдельной теме и разбит на подтемы.

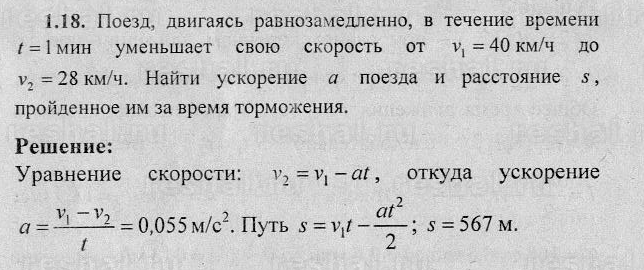 , A tale of two twins, https://arxiv.org/abs/1212.4414
, A tale of two twins, https://arxiv.org/abs/1212.4414 , Теория относительности, Изд. 2-е. Пер. с англ. Под ред. проф. Д. Иваненко. М.: Атомиздат, 1975, 400 с.
, Теория относительности, Изд. 2-е. Пер. с англ. Под ред. проф. Д. Иваненко. М.: Атомиздат, 1975, 400 с.

Leave A Comment