Правильная треугольная призма геометрическое тело

Правильная треугольная призма геометрическое тело — Mnogogranniki.ru
    Вы здесь:
  • Главная
  • Правильная треугольная призма

 

Правильная треугольная призма — это треугольная призма у которой основания правильные треугольники (все стороны которых равны, углы между сторонами основания составляют 60 градусов), а боковые грани прямоугольники.

Основания призмы являются равными правильными треугольниками.

Боковые грани призмы являются прямоугольниками.

Боковые рёбра призмы параллельны и равны.

Размеры призмы можно выразить через длину стороны a и высоту h.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Формула площади поверхности треугольной призмы:

Объём призмы равен произведению её высоты на площадь основания.

Формула объема правильной треугольной призмы:

Правильная треугольная призма может быть вписана в цилиндр.

Формула радиуса цилиндра вписанной треугольной призмы:

Двойственным многогранником прямой призмы является бипирамида.

Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.

Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.

Скачать развертку правильной треугольной призмы для печати на листе А4

 

Геометрические размеры готовой призмы (мм):

Длина =85

Ширина = 74

Высота = 55

 

Скачать развертку правильной треугольной призмы для печати на листе А4

 

Геометрические размеры готовой призмы (мм):

Длина =70

Ширина = 60

Высота = 80

 

Скачать развертку правильной треугольной призмы для печати на листе А4

 

Геометрические размеры готовой призмы (мм):

Длина =31

Ширина = 27

Высота = 94

 

 

посмотреть другие призмы

 

Популярное

Выбрать один продукт

В настоящее время покупатель столкнулся с настолько широким ассортиментом товаров, что сил на то чтобы сделать рациональный выбор уже не хватает. И реклама иногда только усиливает…

Миры Ричарда Суини

Молодой британский дизайнер Ричард Суини (Richard Sweeney) создает удивительные скульптуры из…

Практическое применение развёрток

Достаточно часто возникает вопрос о практическом применении бумажных развёрток. Какой смысл в бумажном моделировании?

Усечённый большой додекаэдр из металла

Памятник многограннику «Усечённый большой додекаэдр» был обнаружен в городе Обнинск, напротив здания «ДОСААФ» (ул.

Шацкого, д.14).

В День Космонавтики сделаем звёзды ближе

  Бывают совпадения, о которых мы даже сами не подозреваем. 12 апреля — День Космонавтики!  

Многогранник – герб города

Основатели города Мирный, находящегося в Архангельской области разместили на флаге и гербе своего города многогранник – «Большой додекаэдр».  

Естественные многогранники

В естественной среде правильные многогранники можно встретить в виде кристаллов (минералов). Форму тетраэдра передает сурьмянистый сернокислый натрий.

2.6. Призма, параллелепипед

2.6. Призма, параллелепипед

Определение 20

Призмой называется многогранник, все вершины которого расположены в двух параллельных плоскостях, причём в этих же двух плоскостях лежат две грани призмы, представляющие собой равные многоугольники с соответственно параллельными сторонами, а все рёбра, не лежащие в этих плоскостях, параллельны.

Эти две равные грани называются основаниями призмы. Все остальные грани призмы называются боковыми, они образуют боковую поверхность призмы. Все боковые грани призмы являются параллелограммами.

Рис. 61

Рис. 62

Рёбра, не лежащие в основаниях, называются боковыми рёбрами призмы. Призму называют n-угольной, если её основаниями являются n-угольники.

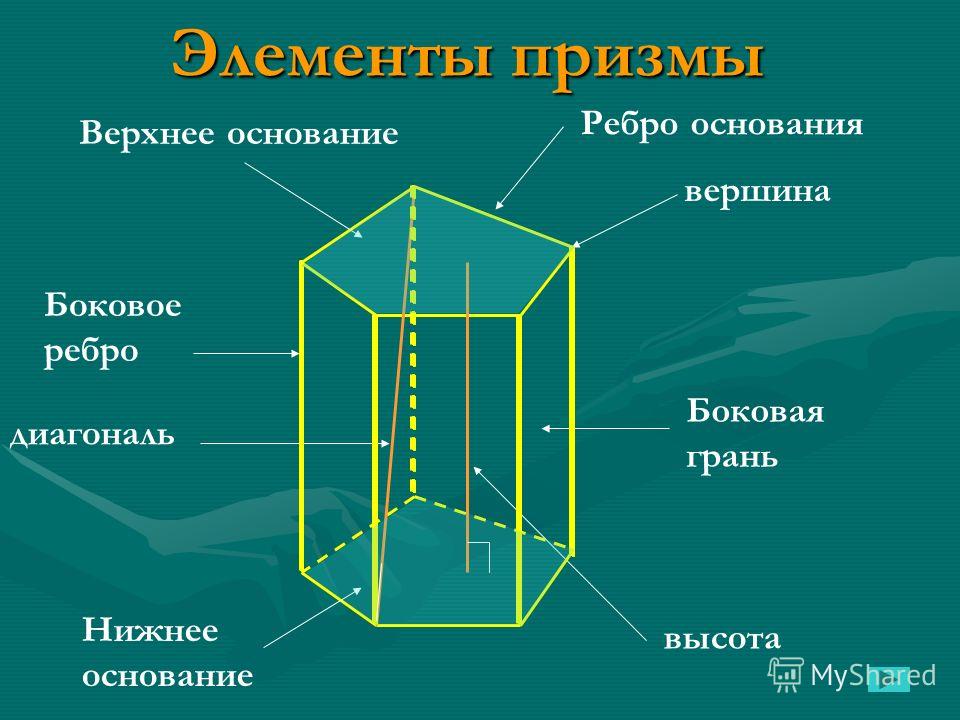
На рисунке 61 изображена пятиугольная призма ABCDEA1B1C1D1E1. Здесь использован наиболее распро- странённый (стандартный) способ обозначения вершин призмы и стандартная запись: сначала в порядке обхода указывают вершины одного основания, а затем в том же порядке — вершины другого; концы каждого бокового ребра обозначают одинаковыми буквами, только вершины, лежащие в одном основании, обозначают буквами без индекса, а в другом — с индексом.

Хорошо известный параллелепипед (рис. 62) является частным случаем призмы: параллелепипед — это четырёхугольная призма, основаниями которой являются параллелограммы. Причём за основание можно взять любую грань параллелепипеда.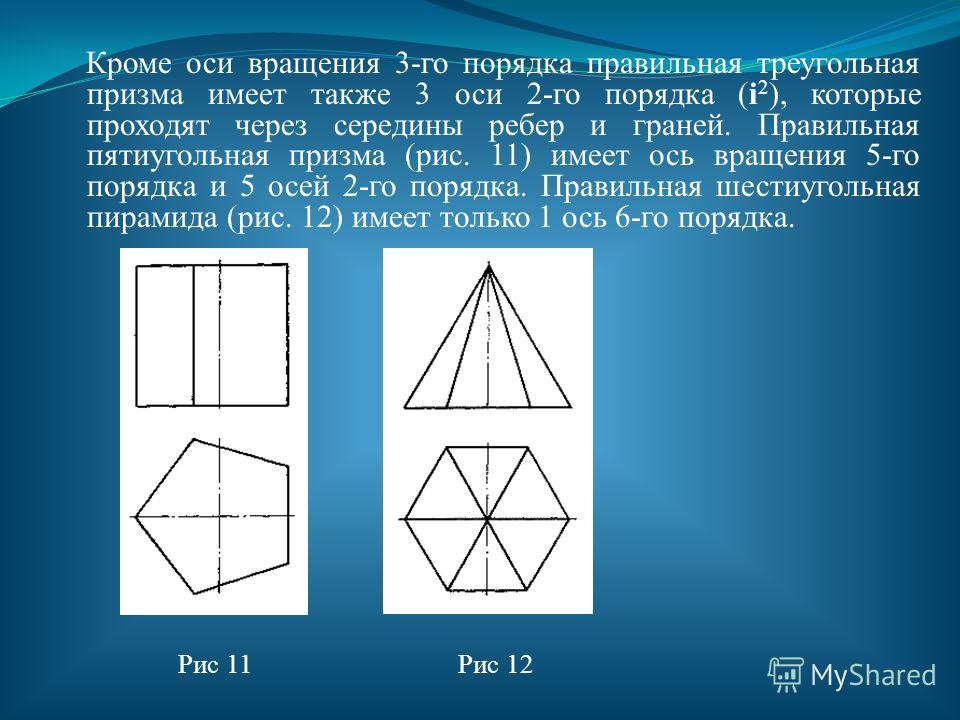

Призма называется прямой, если её боковые рёбра перпендикулярны основаниям.

Призма называется правильной, если она прямая, а её основания — правильные многоугольники.

Как было отмечено, параллелепипед является частным случаем призмы. Особо выделим прямоугольный параллелепипед — параллелепипед, все грани которого прямоугольники (рис. 63).

Рис. 63

Диагональ параллелепипеда — это отрезок, соединяющий его противоположные вершины. У параллелепипеда четыре диагонали.

Теорема 2.7 (свойство диагоналей параллелепипеда)

Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Точка пересечения диагоналей параллелепипеда является центром симметрии параллелепипеда, или просто центром параллелепипеда.

Уточним, что мы называем центром симметрии фигуры или тела точку, при симметрии относительно которой тело переходит само в себя. Заметим также, что образ параллелепипеда при симметрии однозначно задаётся образами его вершин.

Поэтому точка пересечения диагоналей будет центром симметрии параллелепипеда (если мы докажем теорему 2.7).

Доказательство. Рассмотрим параллелепипед ABCDA1B1C1D1 (см. рис. 62). Докажем, что любые две его диагонали пересекаются и делятся точкой пересечения пополам. Возьмём, например, диагонали AC1 и CA1. Рёбра AA1 и CC1 равны и параллельны, поскольку каждое из них равно и параллельно ребру BB1. Значит, AA1C1C — параллелограмм, диагонали AC1 и CA1 которого пересекаются и делятся точкой пересечения пополам. ▼

Следствие

Параллелепипед имеет центр симметрии. Это — точка пересечения его диагоналей. Двенадцать рёбер параллелепипеда образуют три четвёрки соответственно равных между собой и параллельных отрезков.

Теорема 2.8

Диагонали прямоугольного параллелепипеда равны.

Доказательство. Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 (см. рис. 63). Рёбра AA1 и CC1 равны и перпендикулярны граням ABCD и A1B1C1D1, в которых лежат отрезки AC и A1C1. Следовательно, AA1C1C — прямоугольник и AC1 = CA1. То же верно для любой пары диагоналей. ▼

Теорема 2.9 (теорема Пифагора для прямоугольного параллелепипеда)

Пусть a, b и c — длины трёх непараллельных рёбер прямоугольного параллелепипеда, d — его диагональ. Тогда a2 + b2 + c2 = d 2. (Эта теорема представляет собой один из многих пространственных аналогов теоремы Пифагора.)

Доказательство. Пусть в прямоугольном параллелепипеде ABCDA1B1C1D1 (см. рис. 63) AB = a, AD = b, AA1 = c. (Такими же соответственно будут и длины параллельных им рёбер.) Так как AA1C1C — прямоугольник, то

▼

Задачи, задания, вопросы

1.Разрежьте треугольную призму на три треугольные пирамиды.

2.Разрежьте куб на три равные четырёхугольные пирамиды.

3.Сумма трёх чисел, равных количеству вершин, рёбер и граней некоторого многогранника, равна: а) 102; б) 104. Определите вид многогранника, если известно, что это либо пирамида, либо призма.

4(в). Найдите диагональ единичного куба.

5.Три отрезка, не лежащие в одной плоскости, имеют общую точку и делятся этой точкой пополам. Докажите, что концы этих отрезков служат вершинами параллелепипеда.

6.Найдите расстояние от центра грани единичного куба до вершин противоположной грани.

7.Рёбра прямоугольного параллелепипеда равны 2, 3 и 4. Найдите угол между его диагоналями.

8.Проекции отрезка на три попарно перпендикулярные прямые равны 1, 2 и 3. Найдите длину этого отрезка.

9.Найдите расстояние между серединами непараллельных сторон разных оснований правильной треугольной призмы, все рёбра которой равны 2.

10.Покажите, что в кубе можно выбрать четыре вершины, являющиеся вершинами правильного тетраэдра, причём сделать это можно двумя способами.

11.Рассмотрим две треугольные пирамиды, вершинами которых служат вершины данного параллелепипеда. (Каждая вершина параллелепипеда является вершиной одной пирамиды.) Возможно ли, чтобы каждая вершина одной из пирамид принадлежала плоскости грани другой пирамиды, и наоборот?

12.Через точку на ребре треугольной пирамиды проведены две плоскости, параллельные двум граням этой пирамиды. Эти плоскости отсекают две треугольные пирамиды. Разрежьте оставшийся многогранник на две треугольные призмы.

13(в). Диагонали трёх различных граней прямоугольного параллелепипеда равны m, n и p. Найдите диагональ этого параллелепипеда.

14(в). Диагональ прямоугольного параллелепипеда образует с его рёбрами углы a, b и g. Докажите, что

cos2 a + cos2 b + cos2 g = 1.

15(в). В каком отношении диагональ AC1 параллелепипеда ABCDA1B1C1D1 делится плоскостью A1BD ?

16(т). В одном старом учебнике дано такое определение призмы: «Призмой называется многогранник, у которого две грани — равные многоугольники с соответственно параллельными сторонами, а все остальные грани — параллелограммы». Приведите пример многогранника, удовлетворяющего этому определению, но не являющегося призмой.

17(т). Станет ли верным определение, приведённое в предыдущей задаче, если перед словом «многогранник» поставить слово «выпуклый»?

Указание. Возьмём куб и на каждой его грани, как на основании, во внешнюю сторону построим правильную четырёхугольную пирамиду с двугранными углами при основании 45°.

18(т). Найдите ребро куба, одна грань которого лежит в плоскости основания правильной пирамиды, а четыре оставшиеся вершины — на её боковой поверхности, если сторона основания пирамиды равна a, а высота h. Решите эту задачу: а) для правильной четырёхугольной пирамиды; б) для правильной треугольной пирамиды.

19(п). Рёбра прямоугольного параллелепипеда равны a, b и c (a ⩽ b ⩽ c). Найдите: а) углы между его диагоналями; б) угол между диагональю параллелепипеда и скрещивающейся с ней диагональю грани со сторонами a и b; в) угол между скрещивающимися диагоналями двух граней с общим ребром a.

20.Пусть K, L и M — середины рёбер AD, A1B1 и CC1 прямоугольного параллелепипеда ABCDA1B1C1D1, в котором AB = a, AA1 = b, AD = c. Найдите периметр треугольника KLM.

21(т). Укажите все точки на диагонали AC1 параллелепипеда ABCDA1B1C1D1, через которые нельзя провести прямую, пересекающую прямые: а) BC и DD1; б) A1B и B1C.

22(т). Два ребра прямоугольного параллелепипеда равны 1 и 2. Плоскость, параллельная этим рёбрам, делит параллелепипед на два неравных, но подобных между собой параллелепипеда. Найдите длину ребра, отличного от данных.

23(т). На рёбрах A1B1 и A1D1 единичного куба ABCDA1B1C1D1 взяты точки K и M так, что A1K = A1M = x. Найдите x, если известно, что при повороте куба вокруг диагонали AC1 на угол a точка K переходит в M.

24(п). Постройте изображение призмы ABCA1B1C1, если на плоскости даны изображения следующих точек: а) A, B, B1 и C1; б) середин AA1, BC, CC1 и A1C1.

25.Постройте изображение параллелепипеда ABCDA1B1C1D1, если даны изображения следующих точек: а) A, B, D, A1; б) A, B, C, D1; в) A, C, B1, D1; г) середин AB1, BC1, CD, A1D1; д) A, B и центров граней A1B1C1D1 и CDD1C1.

26.Дано изображение призмы ABCA1B1C1. Постройте изображение точки M пересечения плоскостей A1BC, AB1C и ABC1. Пусть высота призмы равна h. Чему равно расстояние от точки M до оснований призмы?

27(пт). Пусть O — середина высоты правильной треугольной пирамиды. Вторая пирамида симметрична данной относительно точки O. Как называется многогранник, являющийся общей частью двух указанных пирамид? (Если вы не знаете его названия, опишите, как он устроен.) Чему равна площадь поверхности этого многогранника, если площадь боковой грани равна S ?

28(т). Рёбра прямоугольного параллелепипеда равны a, b и c (a < b < c). Некоторое сечение этого параллелепипеда является квадратом. Найдите сторону этого квадрата.

29.Проекция вершины A параллелепипеда ABCDA1B1C1D1 на некоторую плоскость лежит внутри проекции треугольника A1BD на эту плоскость. Докажите, что площадь проекции параллелепипеда в два раза больше площади проекции треугольника A1BD.

30(т). Используя результат предыдущей задачи, найдите, чему равно наибольшее значение площади проекции прямоугольного параллелепипеда с рёбрами a, b и c на некоторую плоскость.

31(т). Через центр единичного куба проведена плоскость, делящая его на два многогранника. Докажите, что в каждом из получившихся многогранников найдётся диагональ, длина которой не меньше .

32.Многогранники изучают, их свойства используют представители самых различных профессий. Например, свойствам многогранников посвящены разделы таких наук, как минералогия и кристаллография. Известный русский минералог и кристаллограф Е. С. Фёдоров (1853—1919) сделал немало замечательных открытий, связанных со свойствами многогранников. Некоторые из открытых им многогранников называют «фёдоровскими». Вот один из них.

Возьмём куб и соединим его центр со всеми вершинами. Для каждого из восьми полученных таким образом отрезков построим плоскость, перпендикулярную ему и проходящую через середину. Рассмотрим многогранник, ограниченный этими плоскостями и поверхностью куба (в него входит центр куба). Сколько граней имеет получившийся многогранник? Какими многоугольниками являются его грани? Докажите, что такими многогранниками можно заполнить всё пространство без пропусков и пересечений.

Треугольная призма. Определение, развертка, свойства, примеры

Призма представляет собой объемную фигуру с плоскими гранями, двумя одинаковыми основаниями и одинаковым поперечным сечением по всей длине. Название конкретной призмы зависит от двух оснований призмы, которые могут быть треугольниками, прямоугольниками или любым многоугольником. Например, призма с треугольным основанием называется треугольной призмой, а призма с квадратным основанием называется квадратной призмой и так далее.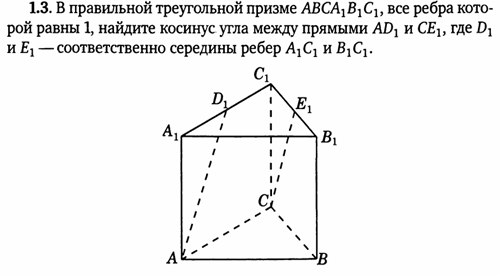 Треугольная призма имеет два треугольных основания и три прямоугольных боковых грани. Давайте узнаем больше о треугольной призме в этой статье.

1. Что такое треугольная призма?
2. Грани треугольной призмы Ребра Вершины
3. Треугольная призматическая сетка
4. Формулы треугольной призмы
5. Часто задаваемые вопросы о треугольной призме

Что такое треугольная призма?

Треугольная призма представляет собой трехмерную фигуру с двумя одинаковыми гранями в форме треугольника, соединенными тремя прямоугольными гранями. Прямоугольные грани называются боковыми гранями, а треугольные — основаниями. Основания также называют вершиной и низом (гранями) призмы.

Треугольная призма Значение: Треугольная призма представляет собой трехмерный многогранник с тремя прямоугольными гранями и двумя треугольными гранями. Две треугольные грани конгруэнтны друг другу, и три боковые грани, имеющие форму прямоугольников, также конгруэнтны друг другу. Таким образом, треугольная призма имеет 5 граней, 9ребер и 6 вершин. Обратите внимание на следующее изображение треугольной призмы, где l представляет собой длину призмы, h представляет собой высоту базового треугольника, а b представляет собой нижний край базового треугольника.

Свойства треугольной призмы

Свойства треугольной призмы помогают нам легко ее идентифицировать. Ниже перечислены некоторые свойства треугольной призмы:

  • Треугольная призма имеет 5 граней, 9 ребер и 6 вершин.
  • Это многогранник с 3 прямоугольными гранями и 2 треугольными гранями.
  • Два треугольных основания конгруэнтны друг другу.
  • Любое поперечное сечение треугольной призмы имеет форму треугольника.

Прямоугольная призма

Прямоугольная призма — это призма, в которой треугольные грани перпендикулярны трем прямоугольным граням. Другими словами, угол, образованный при пересечении граней треугольника и прямоугольника, должен быть равен 90 градусов, поэтому треугольные грани перпендикулярны боковым прямоугольным граням. Прямоугольная призма имеет 6 вершин, 9 ребер и 5 граней.

Грани треугольной призмы Ребра Вершины

Как упоминалось выше, треугольная призма имеет 5 граней, включая 3 боковые прямоугольные грани и 2 треугольных основания, 9 ребер и 6 вершин. Вершины треугольной призмы — это вершины двух треугольных оснований, соединенных линиями, образующими прямоугольники. Его ребра включают 6 ребер двух треугольных оснований (3+3) и 3 стороны, соединяющие основания.

  Лица Края вершин
Треугольная призма 5 9 6

Треугольная призматическая сетка

Сетка треугольной призмы — это узор, который виден, когда поверхность призмы открыта, сплющена и выложена таким образом, что все грани видны четко.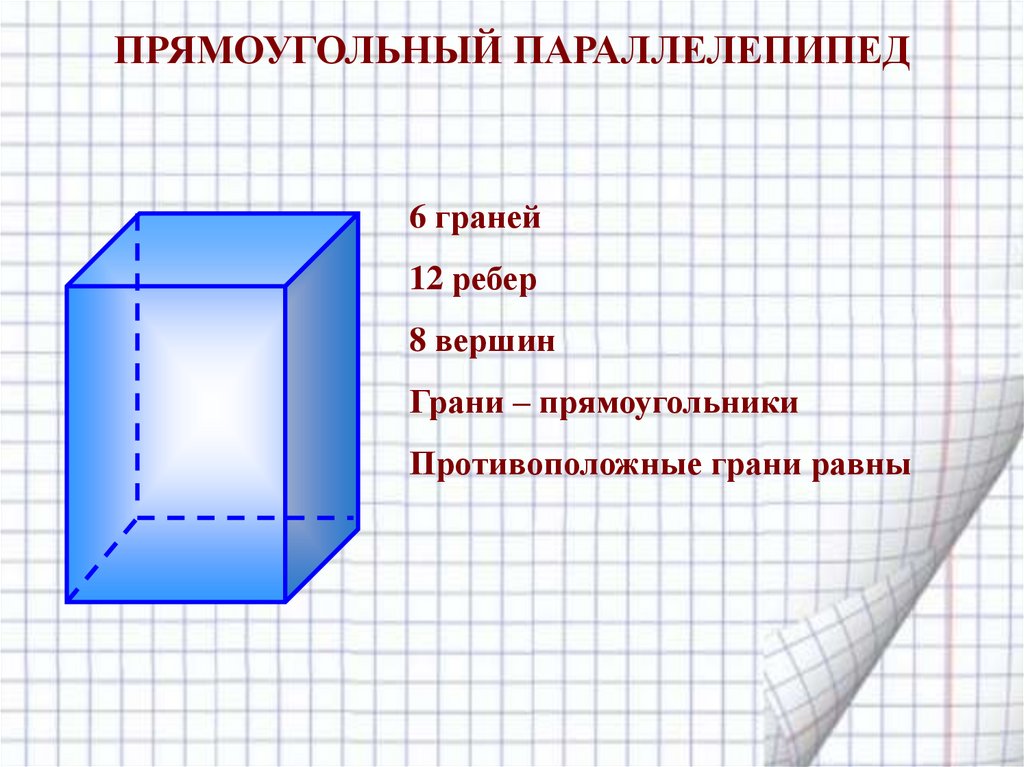 Он двумерный. Эту сетку можно сложить, чтобы получилась треугольная призма. На ней видно, что основания призмы имеют форму треугольника, а боковые грани — прямоугольника. На приведенном ниже рисунке показана сетка треугольной призмы, где четко видны треугольники и прямоугольники.

Формулы треугольной призмы

Существуют две важные формулы треугольной призмы: площадь поверхности и объем. Краткое объяснение обоих приведено ниже вместе с формулой.

Площадь поверхности треугольной призмы

Площадь поверхности треугольной призмы — это площадь, занимаемая ее поверхностью. Это сумма площадей всех граней призмы. Следовательно, формула для расчета площади поверхности:

Площадь поверхности = (Периметр основания × Длина) + (2 × Площадь основания) = ( a + b + c)L + bh

, где

  • b — нижний край основания треугольник,
  • h — высота треугольника основания,
  • L — длина призмы,
  • a, b и c — три ребра (стороны) базового треугольника
  • (bh) — это общая площадь двух треугольных граней, потому что [2 × (1/2 × bh)] = bh.

Для получения дополнительной информации о формуле и расчетах площади поверхности см. статью о площади поверхности треугольной призмы.

Объем треугольной призмы

Объем треугольной призмы равен произведению площади ее треугольного основания и длины призмы. Поскольку мы уже знаем, что основание треугольной призмы имеет форму треугольника, площадь основания будет такой же, как у треугольника. Следовательно, объем треугольной призмы = площадь основания треугольника × длина или его также можно записать как Объем треугольной призмы = ½ × b × h × l , где b — длина основания треугольника, h — высота треугольника, а l — длина призмы.

► Связанные темы

Ниже перечислены несколько интересных тем, связанных с треугольной призмой в геометрии.

  • Квадратная призма
  • Пятиугольная призма
  • Шестиугольная призма

 

Треугольная призма Примеры

  1. Пример 1: Найдите объем треугольной призмы, имеющей следующие размеры: длина основания треугольника = 5 дюймов, высота треугольника = 3 дюйма и длина призмы = 8 дюймов.

    Решение: Дано, длина основания ‘b’ = 5 дюймов, высота ‘h’ = 3 дюйма, а расстояние между треугольными основаниями ‘l’ = 8 дюймов.

    Объем треугольной призмы = ½ × b × h × l

    Объем = ½ × 5 × 3 × 8

    Объем = 60 дюймов 3

    Следовательно, объем данной призмы равен 60 дюймам 3 .

  2. Пример 2: Какова площадь поверхности треугольной призмы, если площадь ее основания 12 квадратных единиц, длина 15 единиц, а периметр основания 21 единица?

    Решение:

    Дано, площадь основания = 12 квадратных единиц, длина = 15 единиц, а периметр основания = 21 единица. Следовательно, площадь поверхности треугольной призмы можно рассчитать по формуле:

    Площадь поверхности = (Периметр основания × Длина) + (2 × Площадь основания)

    Площадь поверхности = (21 × 15) + (2 × 12)

    Площадь поверхности = (315) + (24)

    Площадь поверхности = 339 квадратных единиц

    Следовательно, площадь поверхности данной призмы составляет 339 единиц 2 .

  3. Пример 3: Если объем треугольной призмы, имеющей длину 7 единиц и высоту основания треугольника 4 единицы, равен 35 единицам, найдите длину основания треугольника.

    Решение:

    Дано, длина призмы (l) = 7 единиц, высота основания (h) = 4 единицы, а объем = 35 единиц. Подставляя эти значения в формулу объема треугольной призмы, получаем 70/28 единиц

    b = 2,5 единицы

    Следовательно, основание треугольника составляет 2,5 единицы.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по треугольной призме

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о треугольной призме

Что такое треугольная призма?

Треугольная призма представляет собой трехмерный многогранник, состоящий из двух треугольных граней и трех прямоугольных граней. У него 5 граней, 9ребер и 6 вершин. 2 основания имеют форму треугольника, а остальные 3 грани имеют форму прямоугольника. Некоторыми реальными примерами треугольной призмы являются туристические палатки, шоколадные батончики, крыши домов и т. д.

Каков объем треугольной призмы?

Объем треугольной призмы – это объемлющее ее трехмерное пространство. Это произведение его треугольной площади основания и его длины. Формула для нахождения объема: объем треугольной призмы = площадь основания треугольника × длина, или его также можно записать как ½ × b × h × l, где b — длина основания треугольника, h — высота. треугольника, а l — длина между треугольными основаниями. Объем треугольной призмы выражается в кубических единицах, например, в 3 .

Какова площадь поверхности треугольной призмы?

Площадь поверхности треугольной призмы — это общая площадь, занимаемая ее поверхностью. Формула для нахождения площади поверхности треугольной призмы: (периметр основания × длина) + (2 × площадь основания) квадратных единиц.

Сколько вершин и ребер у треугольной призмы?

Треугольная призма состоит из 6 вершин и 9 ребер. Ребра также известны как стороны, а вершины известны как углы призмы. У него 5 граней, из которых 2 треугольные и 3 прямоугольные.

Что такое прямоугольная призма?

Прямоугольная призма представляет собой призму, в которой угол между гранями треугольных оснований и гранями прямоугольных граней составляет 90 градусов. Остальные свойства треугольной призмы остаются прежними.

Сколько граней у треугольной призмы?

Треугольная призма имеет 5 граней, из которых 3 боковые прямоугольные грани и 2 треугольные грани, образующие верхнее и нижнее основания призмы.

Сколько сторон у треугольной призмы?

Треугольная призма имеет 9 сторон. Эти стороны также называются ребрами призмы.

В чем разница между треугольной призмой и прямоугольной призмой?

Основное различие между треугольной призмой и прямоугольной призмой заключается в том, что основания треугольной призмы — треугольники, а основания прямоугольной призмы — прямоугольники. Кроме того, у прямоугольной призмы 6 граней и 12 ребер, а у треугольной призмы 5 граней и 9 ребер.

Является ли пирамида треугольной призмой?

Нет, пирамида не является треугольной призмой. Треугольная пирамида представляет собой твердое тело с 4 треугольными гранями с центральной вершиной. Принимая во внимание, что треугольная призма представляет собой многогранник с двумя конгруэнтными треугольными основаниями, а остальные являются прямоугольными гранями. Треугольная призма представляет собой трехмерный многогранник с треугольными основаниями и прямоугольными боковыми гранями. Следовательно, пирамида не является треугольной призмой.

Что такое вершины, грани и ребра? Объяснение для начальной школы

Вершины, грани и ребра часто встречаются в начальной школе, когда дети изучают свойства трехмерных фигур. Здесь мы объясним, что означает каждый из них, и как рассчитать количество вершин, граней и ребер для любой формы. Мы также включаем количество ребер, граней и вершин наиболее распространенных форм.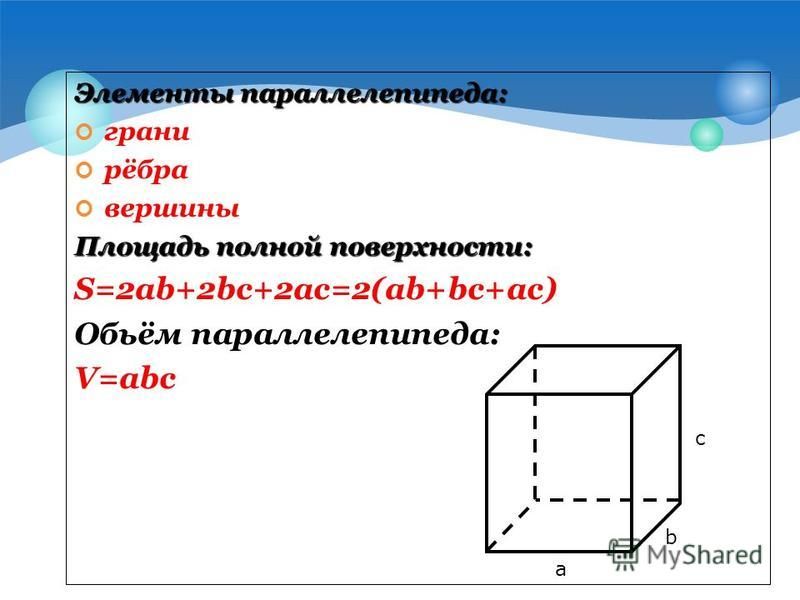

Этот словарь вводится в национальную учебную программу во втором классе, поэтому следующую информацию можно использовать с учащимися в течение всех лет начальной школы. Даже ученики 1-го класса могут начать изучать свойства фигур таким образом, если вы хотите дать им фору!

  • Что такое вершины фигур?
  • Что такое ребра?
  • Что такое лица?
  • Вершины, грани и ребра обычных трехмерных фигур
  • Когда дети узнают о вершинах, гранях и ребрах в начальной школе?
  • Как вершины, грани и ребра связаны с другими областями математики?
  • Как вершины, грани и ребра соотносятся с реальной жизнью?
  • Вершины, грани и ребра примеры вопросов

Что такое вершины в фигурах?

Вершины в фигурах — это точки, в которых встречаются два или более сегмента линии или ребра (например, угол). Единственное число вершин является вершиной. Например, у куба 8 вершин, а у конуса одна вершина.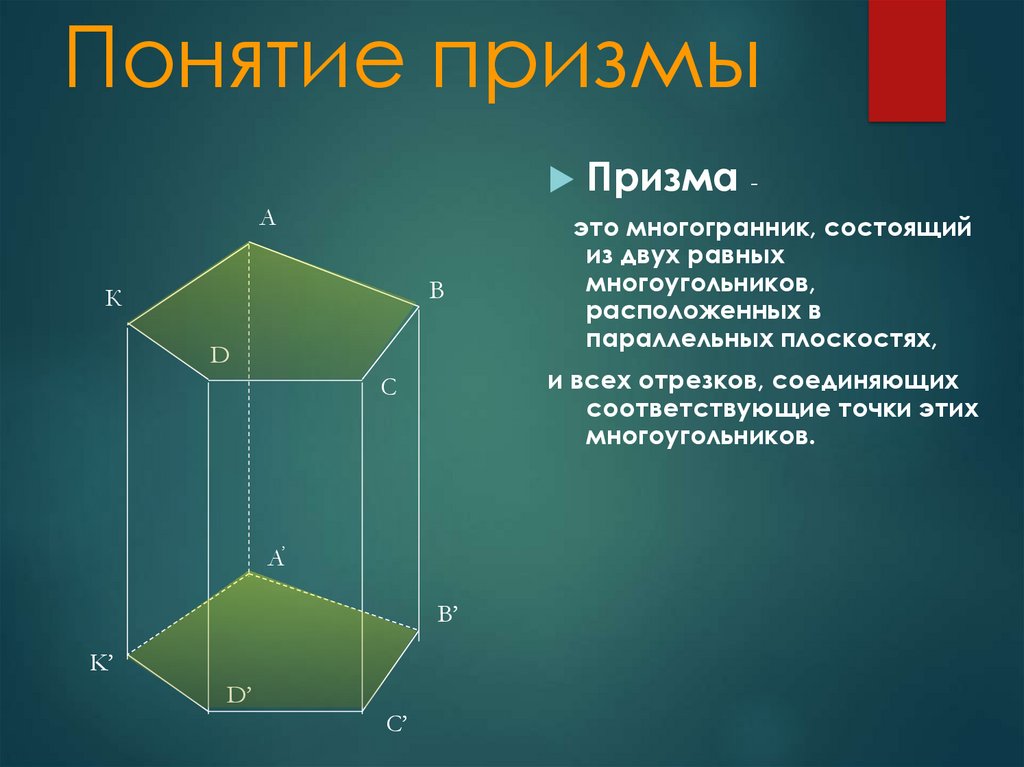

Вершины иногда называют углами, но при работе с 2D- и 3D-формами предпочтительнее слово вершины.

Куб имеет 8 вершин. 7 видны здесь, а один скрыт.

Что такое ребра?

Ребра — это сегменты линии, которые соединяют одну вершину с другой, а также являются местом соединения граней фигуры. Их можно использовать для описания 2d и 3d форм.

Хотя многие фигуры имеют прямые линии и прямые края, существуют формы с изогнутыми краями, например полусфера. Куб будет иметь 12 прямых ребер, как показано ниже; 9 видимых и 3 скрытых.

БЕСПЛАТНЫЕ 3D-шаблоны для самостоятельного подведения итогов

Помогите учащимся 2-го класса (и старше) повторить вершины, грани и ребра с помощью наших бесплатных рабочих листов для независимого подведения итогов.

Что такое лица?

Грани — это плоские поверхности твердотельной формы. Например, кубоид имеет 6 граней. Размышляя о 2D- и 3D-формах, важно знать, что 2D-форма просто представляет собой грань 3D-фигуры.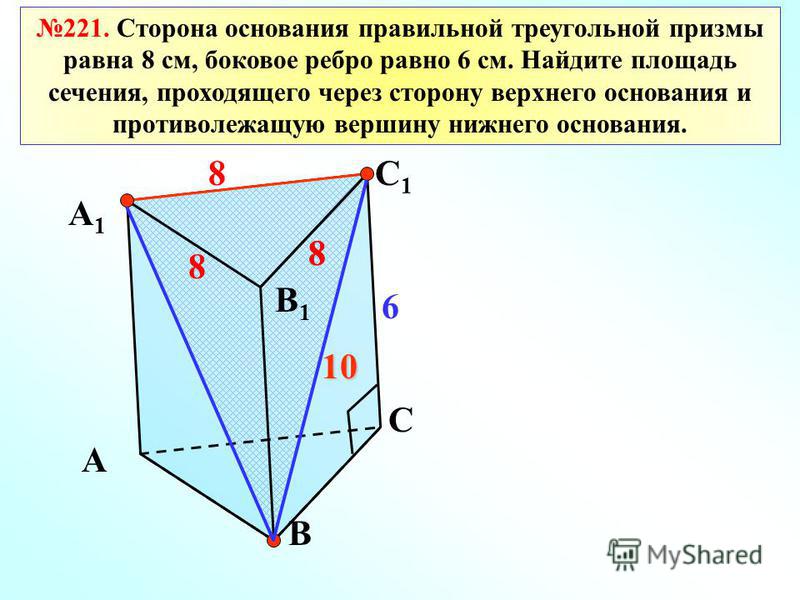

Также важно знать, что поскольку наша реальность построена в трех измерениях, физически невозможно обращаться с двухмерными формами, поскольку мы окружены трехмерными формами. Поэтому, если в вашем классе есть ящик с надписью «2d Shapes», его следует убрать, так как он учит детей неправильному пониманию. Несмотря на то, что это интерактивная концепция для классной комнаты, 2D-формы могут существовать только в виде 2-мерных рисунков.

У вас могут быть как плоские грани, так и изогнутые грани, но я считаю полезным называть изогнутые грани изогнутыми поверхностями, поскольку это хорошо сочетается с визуальным видом формы.

На кубе внизу есть три видимые грани и три скрытые.

Вершины, грани и ребра обычных трехмерных фигур
Сколько граней, ребер и вершин у прямоугольного параллелепипеда?

Кубоид имеет 8 вершин.

Прямоугольный параллелепипед имеет 12 ребер.

Прямоугольный параллелепипед имеет 6 граней.

Сколько граней, ребер и вершин у цилиндра?

Цилиндр имеет 0 вершин.

Цилиндр имеет 2 грани.

Цилиндр имеет 2 грани и 1 изогнутую поверхность.

Сколько граней, ребер и вершин у полушария?

Полусфера имеет 0 вершин.

Полусфера имеет 1 изогнутую кромку.

Полусфера имеет 1 грань и 1 изогнутую поверхность.

Сколько граней, ребер и вершин у конуса?

Конус имеет 1 вершину.

Конус имеет 1 ребро.

Конус имеет 1 грань и 1 изогнутую поверхность.

Сколько граней, ребер и вершин у тетраэдра?

Тетраэдр имеет 4 вершины.

Тетраэдр имеет 6 ребер.

Тетраэдр имеет 4 грани.

Сколько граней, ребер и вершин у сферы?

Сфера имеет 0 вершин.

Сфера имеет 0 ребер.

Сфера имеет 1 изогнутую поверхность.

Сколько граней, ребер и вершин у призмы?

Призма представляет собой твердое тело, геометрическую фигуру или многогранник, у которого грани обоих концов имеют одинаковую форму. Таким образом, учащиеся будут сталкиваться со многими типами призм на протяжении всего обучения. Обычные включают кубы, параллелепипеды, треугольные призмы, пятиугольные призмы и шестиугольные призмы.

Shape Pictorial Faces Edges Vertices
Triangular Prism 5 9 6
Pentagonal Prism 7 15 10
Гексагональная призма 8 18 12
Cube 6 12 8
Cuboid 6 12 8

Когда дети изучают веры, лица и эджа в начальных школах?

Дети должны быть официально ознакомлены со словарем вершин, граней и ребер во 2-м классе при изучении геометрии.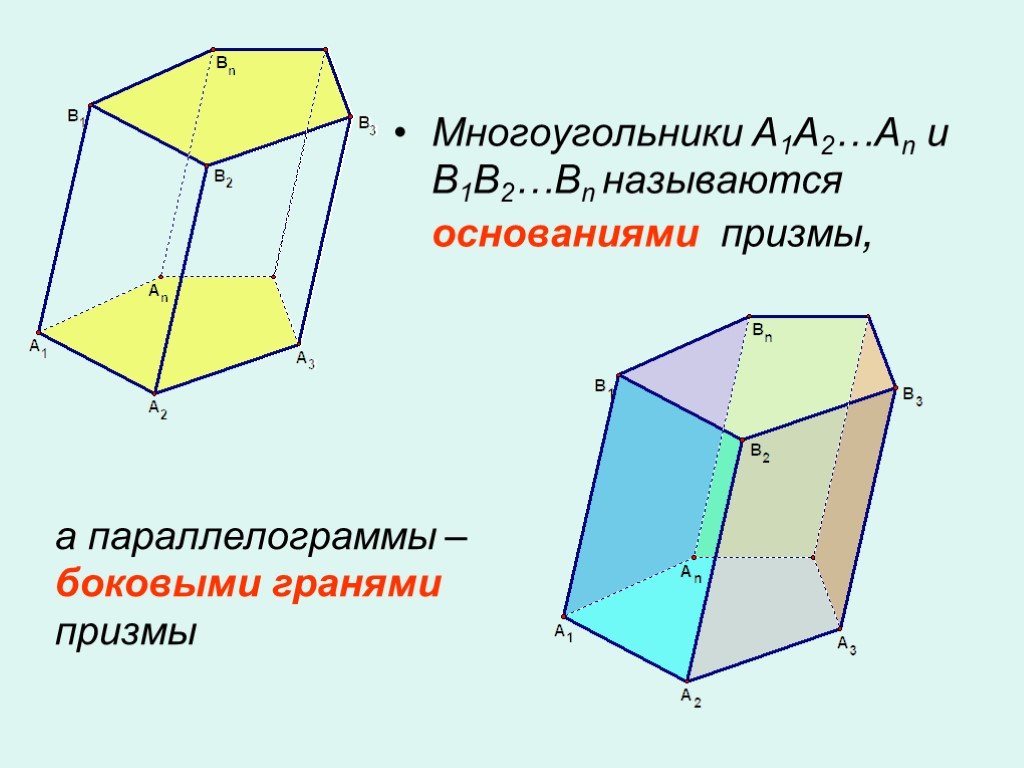 Тем не менее, учителя могут решить ввести эту лексику раньше.

Учащиеся 2 класса должны уметь:

  • определять и описывать свойства трехмерных фигур, включая количество ребер, вершин и граней

В негосударственном руководстве указано, что:

  • Учащиеся обращаются и называют широкий спектр распространенных двумерных и трехмерных фигур, включая четырехугольники и многоугольники, прямоугольные параллелепипеды, призмы и конусы, и определяют свойства каждой формы. (например, количество сторон, количество граней). Ученики идентифицируют, сравнивают и сортируют фигуры на основе их свойств и точно используют словарный запас, например стороны, ребра, вершины и грани.

С этого момента национальная учебная программа больше не ссылается на вершины, грани и ребра явным образом, поэтому учителям других классов придется продолжать использовать этот словарь при рассмотрении формы

Слайд из онлайн-вмешательства Third Space Learning по математике, используя отношения между 2D и 3D фигурами, чтобы помочь ученикам 3 класса идентифицировать вершины, грани и ребра.

Как вершины, грани и ребра связаны с другими областями математики?

Учащиеся будут использовать знания о вершинах, гранях и ребрах при рассмотрении двумерных и трехмерных фигур. Знание того, что такое ребра, и их идентификация на составных фигурах имеет решающее значение для нахождения периметра и площади составных двумерных фигур. Это важная основа для последующих лет работы с различными математическими теоремами, такими как теория графов и параболы.

Как вершины, грани и ребра соотносятся с реальной жизнью?

Любой объект в реальной жизни имеет вершины, грани и ребра. Например, кристалл — это октаэдр — у него восемь граней, двенадцать ребер и шесть вершин. Знание этих свойств различных трехмерных форм закладывает основу для различных отраслей, таких как архитектура, дизайн интерьера, машиностроение и многое другое.

Вершины, грани и ребра Примеры вопросов

1. Объясните, что такое вершина.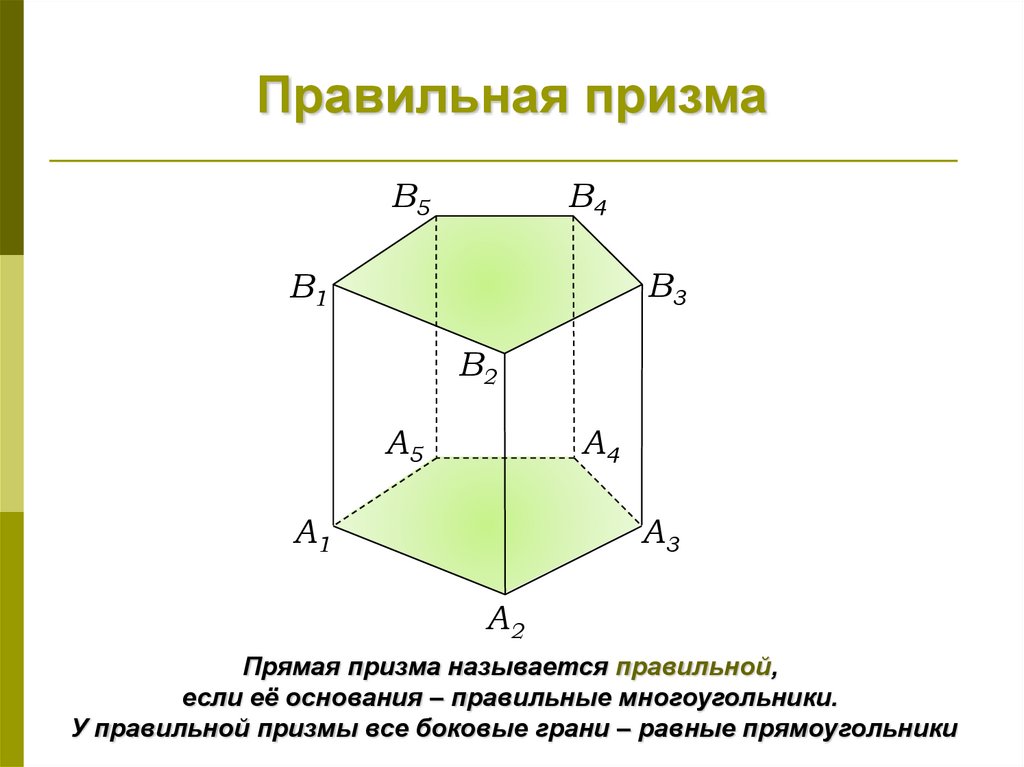

(Ответ: Вершина — это точка пересечения двух прямых)

2. Сколько ребер у треугольной призмы?

(ответ: 9)

3. Сколько вершин у конуса?

(Ответ: 1 вершина)

4. Сколько граней у прямоугольного параллелепипеда? Каковы 2D-формы этих лиц?

(Ответ: 6 граней. Они могут иметь 2 квадратных грани и 4 прямоугольных грани или только 6 прямоугольных граней.)

5. Для всех обычных призм (кубов, параллелепипедов, треугольных, пятиугольных и шестиугольных призм) сложите грани и вершины и вычтите ребра. Что вы заметили в ответах?

(Ответ: Ответ всегда 2. Это известно как формула Эйлера (количество вершин — количество ребер + количество граней = 2) ваших детей? Ознакомьтесь с нашим словарем для начинающих по математике или попробуйте эти:

  • Что такое знание математики?
  • Что такое двумерные фигуры?
  • Что такое трехмерные фигуры?

Вы можете найти множество планов уроков геометрии и печатных рабочих листов для учеников начальных классов в Third Space Learning Math Hub.