Таблица квадратных корней. Онлайн калькулятор
- Онлайн калькулятор
В таблице приведены квадратные корни натуральных чисел от 1 до 100.
|
√1 = 1 √4 = 2 √9 = 3 √16 = 4 √25 = 5 √36 = 6 √49 = 7 √64 = 8 √81 = 9 √100 = 10 |
√121 = 11 √144 = 12 √169 = 13 √196 = 14 √225 = 15 √256 = 16 √289 = 17 √324 = 18 √361 = 19 √400 = 20 |
√441 = 21 √484 = 22 √529 = 23 √576 = 24 √625 = 25 √676 = 26 √729 = 27 √784 = 28 √841 = 29 √900 = 30 |
√961 = 31 √1024 = 32 √1156 = 34 √1225 = 35 √1296 = 36 √1369 = 37 √1444 = 38 √1521 = 39 √1600 = 40 |
|
√1681 = 41 √1764 = 42 √1849 = 43 √1936 = 44 √2025 = 45 √2116 = 46 √2209 = 47 √2304 = 48 √2401 = 49 √2500 = 50 |
√2601 = 51 √2704 = 52 √2809 = 53 √2916 = 54 √3025 = 55 √3136 = 56 √3249 = 57 √3364 = 58 √3481 = 59 √3600 = 60 |
√3721 = 61 √3844 = 62 √3969 = 63 √4096 = 64 √4225 = 65 √4356 = 66 √4489 = 67 √4624 = 68 √4761 = 69 √4900 = 70 |
√5041 = 71 √5184 = 72 √5329 = 73 √5476 = 74 √5625 = 75 √5776 = 76 √5929 = 77 √6084 = 78 √6241 = 79 √6400 = 80 |
|
√6561 = 81 √6724 = 82 √6889 = 83 √7056 = 84 √7225 = 85 √7569 = 87 √7744 = 88 √7921 = 89 √8100 = 90 |
√8281 = 91 √8464 = 92 √8649 = 93 √8836 = 94 √9025 = 95 √9216 = 96 √9409 = 97 √9604 = 98 √9801 = 99 √10000 = 100 |
||
Данный калькулятор поможет вам выполнить извлечение квадратного корня из натурального числа. Просто введите подкоренное число и нажмите кнопку
Просто введите подкоренное число и нажмите кнопку Вычислить
.
Квадратный корень из 28 | Thinkster Math
Методы
Что такое квадратный корень из 28?
Квадратный корень из числа — это значение, которое при умножении само на себя дает исходное число. Например, квадратный корень из 25 равен 5, потому что 5 x 5 = 25. Выражаясь в радикальной форме: √25 = 5. Следовательно, находя квадратный корень из 28, мы находим, что квадратных корней из 28 составляет 5,292 . Всегда помните: ваш ответ может быть как целым, так и десятичным числом.
Является ли квадратный корень из 28 иррациональным?
Числа можно разделить на подмножества, называемые рациональными и иррациональными числами. Примером иррациональных чисел являются десятичные дроби, которые не имеют конца или не заканчиваются. Распространенная путаница заключается в том, что, поскольку у десятичной дроби нет конца, это большое число, стремящееся к бесконечности, хотя это неверно.
Взгляните на экспоненциальную константу e, e имеет значение 2,7182818… и является неограниченным, но не огромным значением, потому что в конце дня e никогда не будет больше 3. С другой стороны, рациональные числа — это десятичные дроби, которые можно записать в виде дробей, делящих два целых числа (если знаменатель не равен 0). Таким образом, для этой задачи, поскольку квадратный корень из 28 или 5,292, является неконечным десятичным числом, поэтому квадратный корень из 28 иррационален.
Методы нахождения квадратного корня из 28
Для начала, есть два способа вычисления квадратного корня из числа: простая факторизация и длинное деление. Обычно простая факторизация используется для идеальных квадратов, а длинное деление используется, когда значение квадратного корня является десятичным.
Поскольку мы знаем, что 28 — десятичное число, мы знаем, что подходящим методом будет деление в длинную сторону. Этот метод работает очень похоже на обычное длинное деление, за исключением того, что в этом методе есть еще несколько правил, которые помогают нам получить ответ. Взгляните на этот пример, в котором подробно рассказывается о том, что представляет собой этот метод, как его использовать, а также приводится несколько решенных примеров. Таким образом, результат после использования метода деления в длину равен 5,29.2.
Взгляните на этот пример, в котором подробно рассказывается о том, что представляет собой этот метод, как его использовать, а также приводится несколько решенных примеров. Таким образом, результат после использования метода деления в длину равен 5,29.2.
Нахождение квадратного корня из других чисел
Нахождение квадратного корня любого числа можно выполнить с помощью того же метода, который показан выше. Посмотрите, как найти квадратный корень из этих других конкретных примеров, нажав на любую из ссылок ниже:
Квадратный корень из 3488
Квадратный корень из 1305
Квадратный корень из 1470
Квадратный корень из 1673
Квадратный корень из 62
Загрузите БЕСПЛАТНЫЕ математические ресурсы
Воспользуйтесь нашими бесплатными загружаемыми ресурсами и учебными материалами для обучения дома.
8 математических хитростей и хитростей, которые превратят вашего «хорошего» студента-математика в чемпиона по математике!
Мы учим наших студентов в Thinkster тому, что есть несколько способов решить математическую задачу. Это помогает нашим ученикам научиться мыслить гибко и нелинейно.
Это помогает нашим ученикам научиться мыслить гибко и нелинейно.
Как сделать так, чтобы ваш ребенок добился больших успехов и стал миллионером
Как родитель, вы надеетесь, что ваш ребенок станет очень успешным и, вероятно, станет следующим Гейтсом, Цукербергом или Мег Уитман. Чтобы направить ребенка на правильный путь, существует множество навыков и качеств, которые вы можете начать формировать и развивать прямо сейчас. Это закладывает семена будущего успеха.
Получить PDFКвадратный корень из 28 — Как найти квадратный корень из 28?
LearnPracticeDownload
Знаете ли вы, что сумма первых пяти простых чисел, то есть 2, 3, 5, 7 и 11, равна 28? Еще один интересный факт о 28 заключается в том, что это совершенное число, потому что сумма всех чисел, которые делят 28 точно, равна 28. 1+2+4+7+14 = 28. Разве это не интересно? Число 28 также является треугольным числом. Это означает, что количество точек в семи рядах треугольных точек равно 28.
Давайте посмотрим, что такое квадратный корень из 28 .
- Квадратный корень из 28
- Квадрат 28: 28 2 = 784
| 1. | Чему равен квадратный корень из 28? |
| 2. | Является ли квадратный корень из 28 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 28? |
| 4. | Часто задаваемые вопросы о квадратном корне из 28 |
Чему равен квадратный корень из 28?
Квадратный корень из 28 в радикальной форме представлен как √ 28, а в экспоненциальной форме он выражается как (28) 1/2 . Неквадратные числа также имеют квадратный корень, просто они не являются целыми числами. Квадратный корень из 28, округленный до 6 знаков после запятой, равен 5,291502.
Квадратный корень из 28, округленный до 6 знаков после запятой, равен 5,291502.
Является ли квадратный корень из 28 рациональным или иррациональным?
Рациональное число — это число в форме p/q, где p и q — целые числа, а q не равно 0. Число, которое нельзя выразить как отношение двух целых чисел, является иррациональным числом. Неконечные десятичные числа, имеющие повторяющиеся числа после запятой, являются рациональными числами.
Как вы думаете, десятичная часть заканчивается после 5,291502322? Нет, она бесконечна. Следовательно, это неконечная десятичная дробь с неповторяющимися числами.
Число 5.291502322… не может быть записано в форме p/q. Итак, √ 28 — иррациональное число.
Как найти квадратный корень из 28?
Квадратные корни можно вычислить двумя способами:
- Путем упрощения радикала чисел, являющихся полными квадратами
- С помощью метода деления в длину для полных и несовершенных квадратов
Число 28 лежит между 25 и 36, поэтому 28 не является полным квадратом целого числа.
Упрощенная радикальная форма квадратного корня из 27
Чтобы упростить квадратный корень из 28, давайте сначала представим 28 как произведение его простых множителей. Разложение числа 28 на простые множители – это 2 × 2 × 7. Следовательно, √ 28 можно еще упростить как √ (2 × 2 × 7) = 2 √ 7. Таким образом, мы выразили квадратный корень из 28 в виде простейшая радикальная форма как 2 √ 7.
Квадратный корень из 27 методом деления в длину
Выполните шаги, указанные ниже, чтобы найти квадратный корень из 28 путем деления в длину.
- Шаг 1. Объединяем цифры 2 и 8 в пару, помещая над ними черту. Поскольку наше число равно 28, давайте представим его внутри символа деления.
- Шаг 2. Находим наибольшее число, произведение которого при умножении на само себя меньше или равно 28. Мы знаем, что 5 × 5 = 25, поскольку 25 < 28.

- Шаг 3: Расставим пары десятичной точки и нулей и продолжим деление. Теперь умножьте частное на 2, и произведение станет начальной цифрой нашего следующего делителя.
- Шаг 4. Выберите наибольшее число вместо единицы для нового делителя, чтобы его произведение на число было меньше или равно 300. Мы знаем, что 0 находится в разряде десятков, а наше произведение должно быть 204 и ближайшим умножение 102 × 2 = 204. Поэтому используйте число 2 в разряде единиц, что дает 102 × 2 = 204.
- . Шаг 5. Сократите следующую пару нулей и умножьте частное 52 (без учета десятичной дроби) на 2, что равно 104, и на начальную цифру нового делителя. Обратите внимание, что квадратный корень из 28 – иррациональное число, т. е. оно никогда не заканчивается. Итак, остановите процесс еще через 2 или 3 итерации, повторив шаги 3 и 4, и вы получите квадратный корень из 28 методом деления в большую сторону.
Исследуйте Квадратные корни с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 22
- Квадратный корень из 26
- Квадратный корень из 27
- Квадратный корень из 29
- Квадратный корень из 30
Важные примечания:
- Квадратный корень из 28 в подкоренной форме выражается как 2 √ 7.

- В форме экспоненты квадратный корень из 28 записывается как (28) 1/2 .
- Десятичное представление √ 28 равно 5,2915.
Аналитический центр:
- Можете ли вы придумать какое-нибудь квадратное уравнение, корни которого равны √ 28?
- Поскольку ( √- 28) 2 = 28, можем ли мы сказать, что √ 28 также является квадратным корнем из 28?
Пример 1: Учитель Майка попросил его решить вопрос a 2 = 28. Вы можете помочь ему решить это?
Решение
Представим 28 как произведение простых чисел. 28 = 2 × 2 × 7,
Рассмотрим уравнение a 2 = 28,
. а 2 = 28
а = √ 28 = √ (2 × 2 × 7) = 2 √ 7Пример 2: Джолли хочет использовать значения квадратного корня из 28 и квадратного корня из 29, чтобы найти квадратный корень из 812.
 Вы можете ей помочь?
Вы можете ей помочь?Решение :
Мы можем записать 812 как: 812 = 28 × 29.
Используя свойство квадратных корней, мы можем записать это как √ 812 = √ 28 ×6.6. Таким образом, Джолли нашел квадратный корень из 812, используя значения квадратного корня из 28 и квадратного корня из 29. перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратном корне из 28Чему равен квадратный корень из 28?
Квадратный корень из 28 равен 2 √ 7.
Как упростить квадратный корень из 28?
Запишите 28 как произведение его простых множителей.



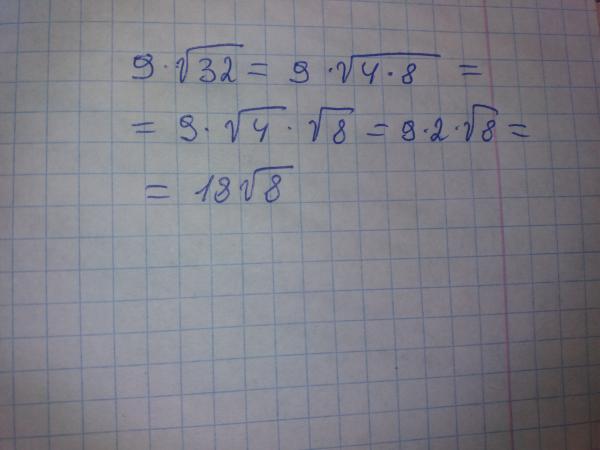
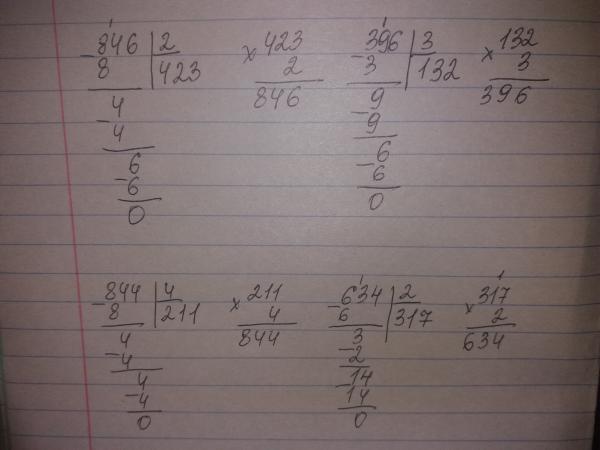 Вы можете ей помочь?
Вы можете ей помочь?
Leave A Comment