Окружность. Основные теоремы
\[{\Large{\text{Центральные и вписанные углы}}}\]
Определения
Центральный угол – это угол, вершина которого лежит в центре окружности.
Вписанный угол – это угол, вершина которого лежит на окружности.
Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.
Теорема
Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.
Доказательство
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка \(B\) – вершина вписанного угла \(ABC\) и \(BC\) – диаметр окружности:
Треугольник \(AOB\) – равнобедренный, \(AO = OB\), \(\angle AOC\) – внешний, тогда \(\angle AOC = \angle OAB + \angle ABO = 2\angle ABC\), откуда \(\angle ABC = 0,5\cdot\angle AOC = 0,5\cdot\buildrel\smile\over{AC}\).
Теперь рассмотрим произвольный вписанный угол \(ABC\). Проведём диаметр окружности \(BD\) из вершины вписанного угла. Возможны два случая:
1) диаметр разрезал угол на два угла \(\angle ABD, \angle CBD\)(для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.
2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла \(\angle ABD, \angle CBD\), у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.
Следствия
1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.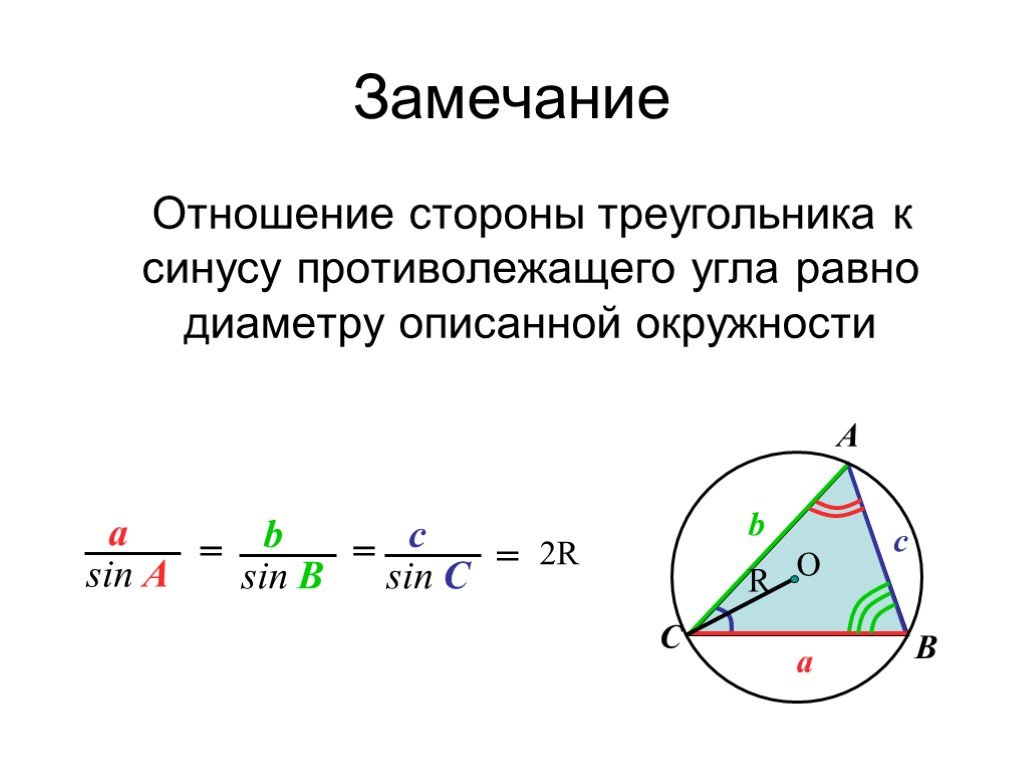
2. Вписанный угол, опирающийся на полуокружность, прямой.
3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
\[{\Large{\text{Касательная к окружности}}}\]
Определения
Существует три типа взаимного расположения прямой и окружности:
1) прямая \(a\) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние \(d\) от центра окружности до прямой меньше радиуса \(R\) окружности (рис. 3).
2) прямая \(b\) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка \(B\) – точкой касания. В этом случае \(d=R\) (рис. 4).
3) прямая \(c\) не имеет общих точек с окружностью (рис. 5).
Теорема
1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.
Следствие
Отрезки касательных, проведенных из одной точки к окружности, равны.
Доказательство
Проведем к окружности из точки \(K\) две касательные \(KA\) и \(KB\):
Значит, \(OA\perp KA, OB\perp KB\) как радиусы. Прямоугольные треугольники \(\triangle KAO\) и \(\triangle KBO\) равны по катету и гипотенузе, следовательно, \(KA=KB\).
Следствие
Центр окружности \(O\) лежит на биссектрисе угла \(AKB\), образованного двумя касательными, проведенными из одной точки \(K\).
\[{\Large{\text{Теоремы, связанные с углами}}}\]
Теорема об угле между секущими
Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.
Доказательство
Пусть \(M\) – точка, из которой проведены две секущие как показано на рисунке:
Покажем, что \(\angle DMB = \dfrac{1}{2}(\buildrel\smile\over{BD} —
\buildrel\smile\over{CA})\).
\circ — \alpha =
\frac12\cdot\buildrel\smile\over{AB}\).
Теорема о дугах, стягиваемых равными хордами
Равные хорды стягивают равные дуги, меньшие полуокружности.
И наоборот: равные дуги стягиваются равными хордами.
Доказательство
1) Пусть \(AB=CD\). Докажем, что меньшие полуокружности дуги \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\).
\(\triangle AOB=\triangle COD\) по трем сторонам, следовательно, \(\angle AOB=\angle COD\). Но т.к. \(\angle AOB, \angle COD\) — центральные углы, опирающиеся на дуги \(\buildrel\smile\over{AB}, \buildrel\smile\over{CD}\) соответственно, то \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\).
2) Если \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\), то \(\triangle AOB=\triangle COD\) по двум сторонам \(AO=BO=CO=DO\) и углу между ними \(\angle AOB=\angle COD\). Следовательно, и \(AB=CD\).
Теорема
Если радиус делит хорду пополам, то он ей перпендикулярен.
Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.
Доказательство
1) Пусть \(AN=NB\). Докажем, что \(OQ\perp AB\).
Рассмотрим \(\triangle AOB\): он равнобедренный, т.к. \(OA=OB\) – радиусы окружности. Т.к. \(ON\) – медиана, проведенная к основанию, то она также является и высотой, следовательно, \(ON\perp AB\).
2) Пусть \(OQ\perp AB\). Докажем, что \(AN=NB\).
Аналогично \(\triangle AOB\) – равнобедренный, \(ON\) – высота, следовательно, \(ON\) – медиана. Следовательно, \(AN=NB\).
\[{\Large{\text{Теоремы, связанные с длинами отрезков}}}\]
Теорема о произведении отрезков хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Доказательство
Пусть хорды \(AB\) и \(CD\) пересекаются в точке \(E\).
Рассмотрим треугольники \(ADE\) и \(CBE\).
Следствие
Произведение секущей, проведённой из точки \(O\), на её внешнюю часть не зависит от выбора секущей, проведённой из точки \(O\):
Теорема синусов
Примечание. В данной главе приводится формулировка и доказательство теоремы синусов. В уроках главы приведены задачи по геометрии с решениями на эту же тему. См. также Теорема косинусов.
Стороны треугольника пропорциональны синусам противолежащих углов
или,
где
R — радиус описанной вокруг треугольника окружности
a, b, c — стороны треугольника
α, β, γ — величины противолежащих этим сторонам углов
Доказательство теоремы синусов
Доказательство теоремы синусов происходит с помощью дополнительных построений.
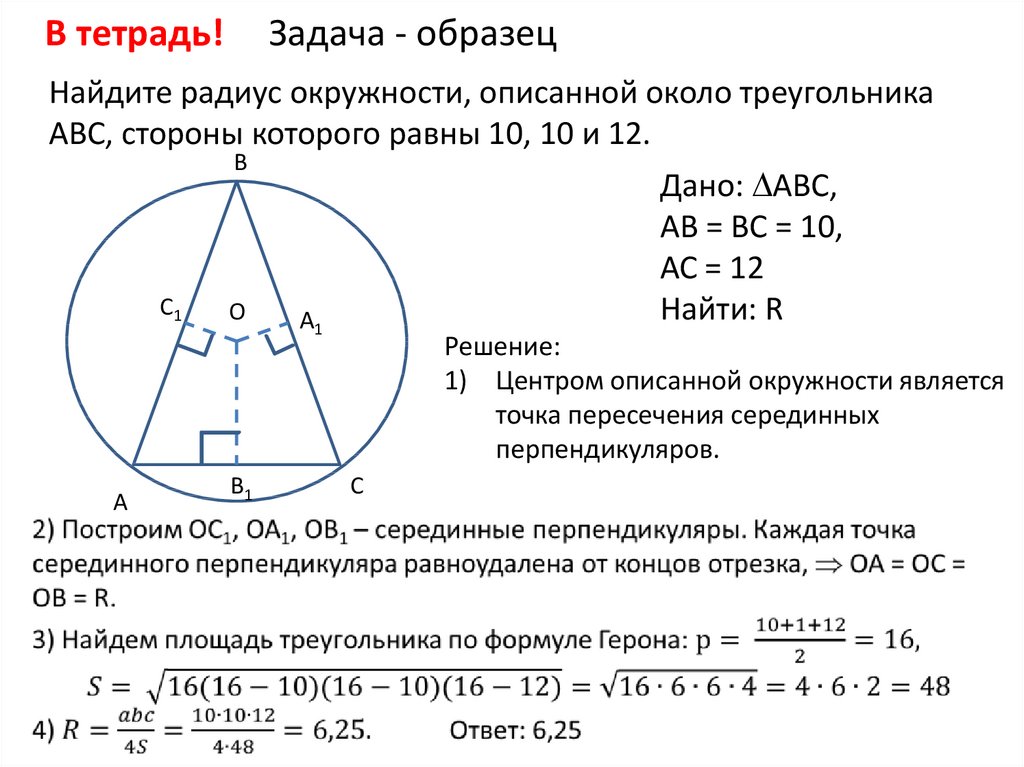
Построим произвольный треугольник, вписанный в окружность. Обозначим его как ABC.
Дополнительно построим диаметр окружности
Примем во внимание, что одним из свойств прямоугольного треугольника, вписанного в окружность является то, что его гипотенуза, является диаметром окружности, в которую он вписан.
Обозначим диаметр для описанной окружности как BD. Образовавшийся треугольник BCD является прямоугольным, поскольку его гипотенуза лежит на диаметре описанной окружности (свойство углов, вписанных в окружность).
Таким образом, дополнительно построенный треугольник, у которого одна общая сторона с построенным ранее произвольным треугольником, а гипотенуза совпадает с диаметром окружности —
Для доказательства всей теоремы, поскольку размеры треугольника ABC выбраны произвольным образом, достаточно доказать, что соотношение одной произвольной стороны к противолежащему ей углу равно 2R.
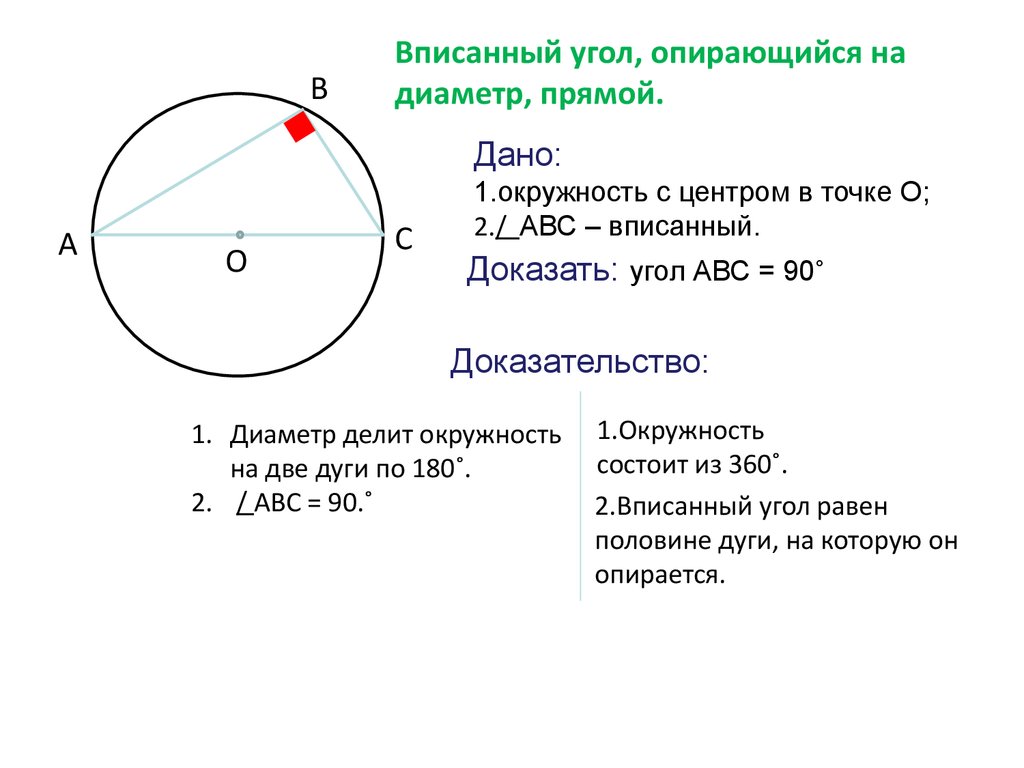
Пусть это будет 2R = a / sin α, то есть если взять по чертежу 2R = BC / sin A.
Поскольку, углы, вписанные в окружность, опирающиеся на одну и ту же дугу, равны, то угол CDB либо равен углу CAB (если точки A и D лежат по одну сторону от прямой BC), либо равен π — CAB (в противном случае).
Обратимся к свойствам тригонометрических функций. Поскольку sin( π − α ) = sin α, то указанные варианты построения треугольника все равно приведут к одному результату.
Вычислим значение 2R = a / sin α, по чертежу 2R = BC / sin A. Для этого заменим sin A на соотношение соответствующих сторон прямоугольного треугольника.
2R = BC / sin A
2R = BC / ( BC / DB )
2R = DB
А, поскольку, DB строился как диаметр окружности, то равенство выполняется.
Повторив то же рассуждение для двух других сторон треугольника, получаем:
Теорема синусов доказана.
Содержание главы:
- Задачи на решение с помощью теоремы синусов
- Теорема синусов (часть 2)
0
Синус | Описание курса | Задачи на решение с помощью теоремы синусов
геометрия — Прямоугольный треугольник $\треугольник ABC$, $D$ лежит на $AB$, вписанный в окружность радиуса $9$.
Найдите меру $CD$$\begingroup$
Сегодня я увидел эту математическую головоломку в посте в Instagram. Как следует из названия, у нас есть прямоугольный треугольник, вписанный в окружность с радиусом $D$ и некоторыми углами. Цель состоит в том, чтобы найти длину $CD$. Я поделюсь своим подходом в качестве ответа ниже. Я не совсем уверен, что мой ответ правильный, поэтому, пожалуйста, не стесняйтесь указывать на любые ошибки в моем подходе и / или публиковать свои собственные подходы!
- геометрия
- тригонометрия
- проверка решения
- евклидова геометрия
- круги
$\endgroup$
2
$\begingroup$
Вот мой подход к проблеме:
Вот мой подход к проблеме:
1.) Растяните $CD$ до $E$, лежащего на окружности.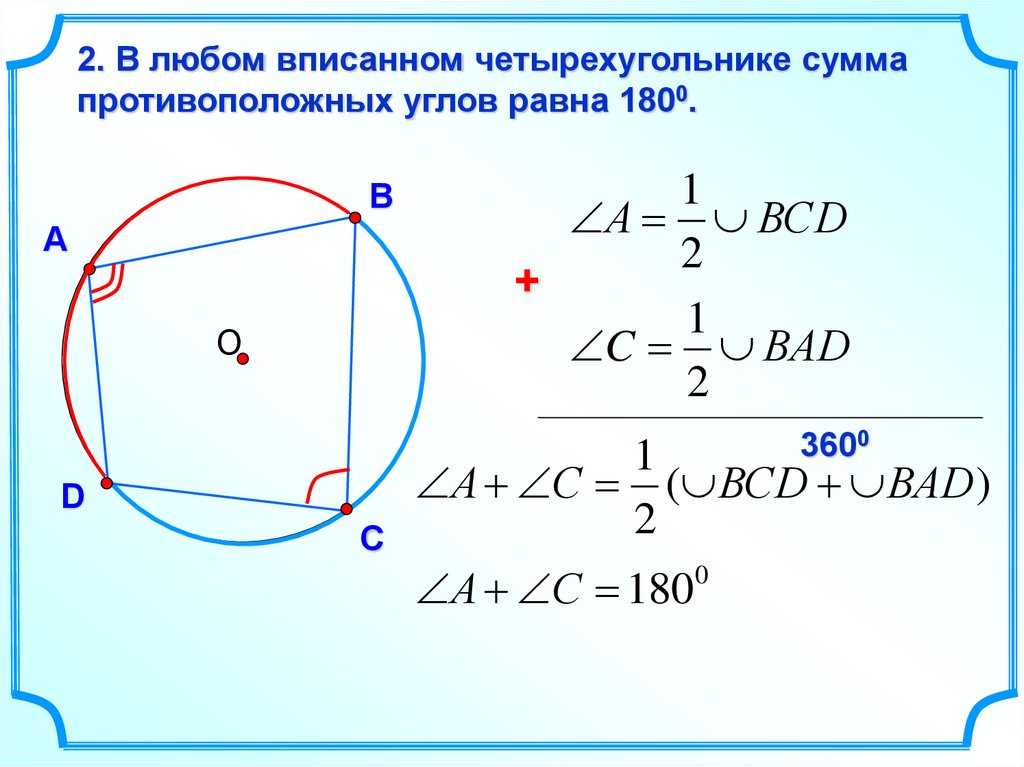
Соедините центр окружности $O$ с $E$ отрезком $OE$. Поскольку $OE$ — это радиус, мы знаем, что $OE=9$. Обратите внимание, что $\angle ECB$ является вписанным углом в $\angle EOC$, поэтому мы можем заключить, что $\angle EOB=2\alpha$
2.) Обратите внимание, что $\angle EOA=\angle EDB=180- 2\alpha$, поэтому $OE=ED=9$. Теперь мы можем использовать теорему о пересекающихся хордах (которую легко доказать через подобие треугольников в любом общем вписанном четырехугольнике) и заключить, что:
$$9\cdot CD=6\cdot12=72$$
$$\Rightarrow CD =8$$
$\endgroup$
2 9{\circ}$, что невозможно.
$\endgroup$
$\begingroup$
Идентификатор триггера: $\displaystyle \;\frac{\sin 3α}{\sin α} — \frac{\cos 3α}{\cosα} = \frac{\sin 2α}{(\sin α)(\cos α)} = 2$
Закон синусов, ΔBCD:
$\displaystyle\frac{x}{\sin (\pi- 3α)} = \frac{BC}{\sin 2α} = \frac{12}{\sin α}$
$→ \;\;\displaystyle \frac{x}{\left(\frac{\sin 3α}{\sin α}\right)} = \frac{BC}{2 \cos α} = 12$
Прямоугольный треугольник ΔABC:
$\;BC = 18\cos(\pi-3α) = -18\cos(3α)$
$\displaystyle \frac{BC}{2 \cos α} = -9 \left(\frac{\sin 3α}{\sin α} — 2\right)$
$\displaystyle → \quad 12 = -9 \left(\frac{x}{12} — 2\ справа) \qquad → \большой\;CD = x = 8$
$\endgroup$
1
$\begingroup$
Фантастическая сила точки wrt.
круговое решение уже найдено Гоку, но позвольте мне показать мою попытку: 92+4x-96=0$ и $x=8$ или $x=-12$. Поскольку $x$ положителен, $x=8$.
$\endgroup$
$\begingroup$
Новый способ вычисления площади двумя разными способами.
Продолжим CD до пересечения окружности в точке E. Пусть $\,x=CD\,\, y=DE$
Площадь (ΔAEB), с основанием = EB
$\displaystyle \frac{(18 \sin α)\,(18\cos α)}{2} = 81\,(\sin 2α)$
Площадь(ΔAEB), с основанием = AB
$\displaystyle \frac{18 × y \,\sin(\pi-2α)}{2} = 9y\,(\sin 2α)$
Площадь, выполненная двумя способами, должна соответствовать: $\quad→y = 9$
$ΔCDB \sim ΔADE\;\;→ \displaystyle\frac{x}{6 }=\frac{12}{y}\quad → x = 8$
Еще лучше, закон синусов на ΔADE:
$\displaystyle \frac{y}{\sin α} = \frac{ 18 \cos α}{\sin 2α}\;\; → у=9$
$\endgroup$
$\begingroup$
Закон касательных , пусть $t = \tan α$
$\displaystyle \frac{x+6}{x-6} = \ гидроразрыва {\ загара \ гидроразрыва {(3α-92-6×12 = (x-6)(x-12) $
$\displaystyle → x = \frac{6×12}{(6+12)÷2} = \frac{72}{9} = 8$
$\endgroup$
1
геометрия — Как найти длину стороны вписанного угла?
спросил
Изменено 4 года, 6 месяцев назад
Просмотрено 291 раз
$\begingroup$
Как найти длину стороны угла, вписанного в окружность с вершиной на самой окружности? Окружность имеет радиус $1$, а образующийся треугольник всегда равнобедренный, как на картинке ниже.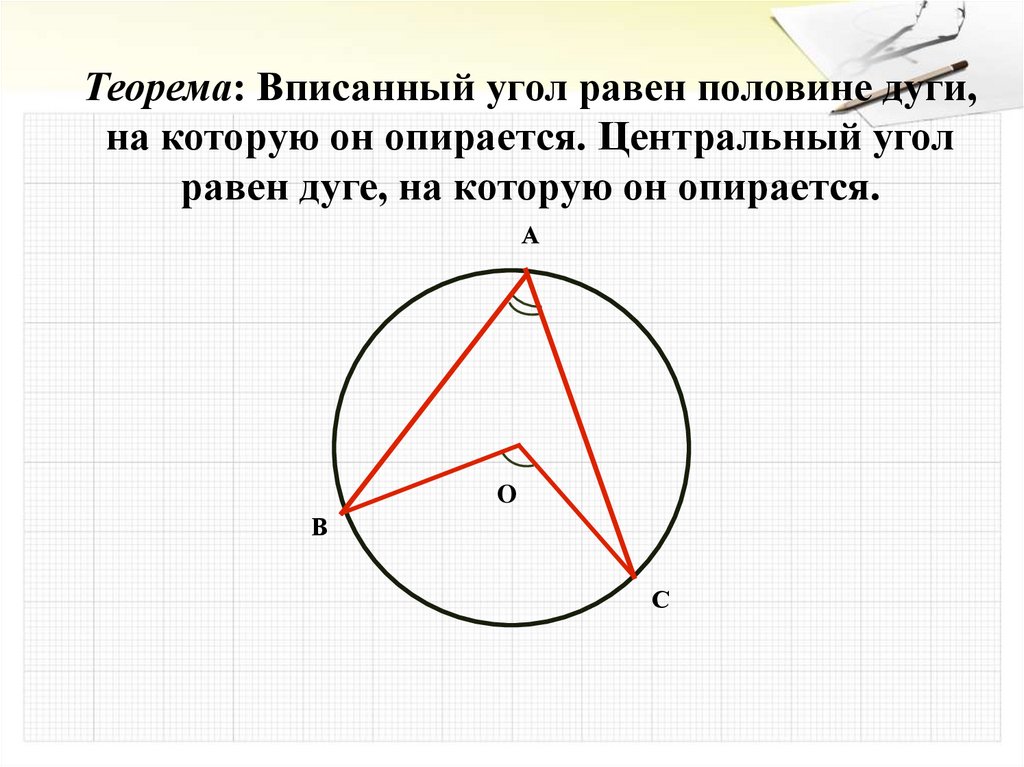
- геометрия
- тригонометрия
$\endgroup$
3 92\альфа ,\\ b&=2R\cos\альфа . \end{align}
Или, просто используя закон синусов,
\begin{align} |AB|&=2R\sin\угол BCA=2R\sin(90-\alpha)=2R\cos\alpha . \end{выравнивание}
$\endgroup$
$\begingroup$
У нас есть несколько способов найти решение. Я думаю, что следующее особенно просто.
Пусть $L$ — длина стороны, которую нужно найти.
Из-за симметрии треугольника радиус от центра описанной окружности до вершины треугольника делит пополам угол при вершине.
То есть этот радиус делит пополам угол $2\alpha$ на два угла меры $\alpha.$
Постройте этот радиус, как показано на рисунке ниже,
а также опустить перпендикуляр из радиуса на одну сторону треугольника, который делит эту сторону пополам на два отрезка длины $L/2.
Leave A Comment