Теорема синусов. Формулы и доказательства
Поможем понять и полюбить математику
Начать учиться
138.2K
Железнодорожные рельсы параллельны друг другу, а деревья растут под наклоном к земле. Увы, с соотношением сторон в треугольнике все не так просто: чтобы их определить, нужна теорема синусов.
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, воспользуемся правилом пропорции и получим:
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
Стороны треугольника, если даны два угла и одна сторона.
Углы треугольника, если даны две стороны и один прилежащий угол.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
,где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.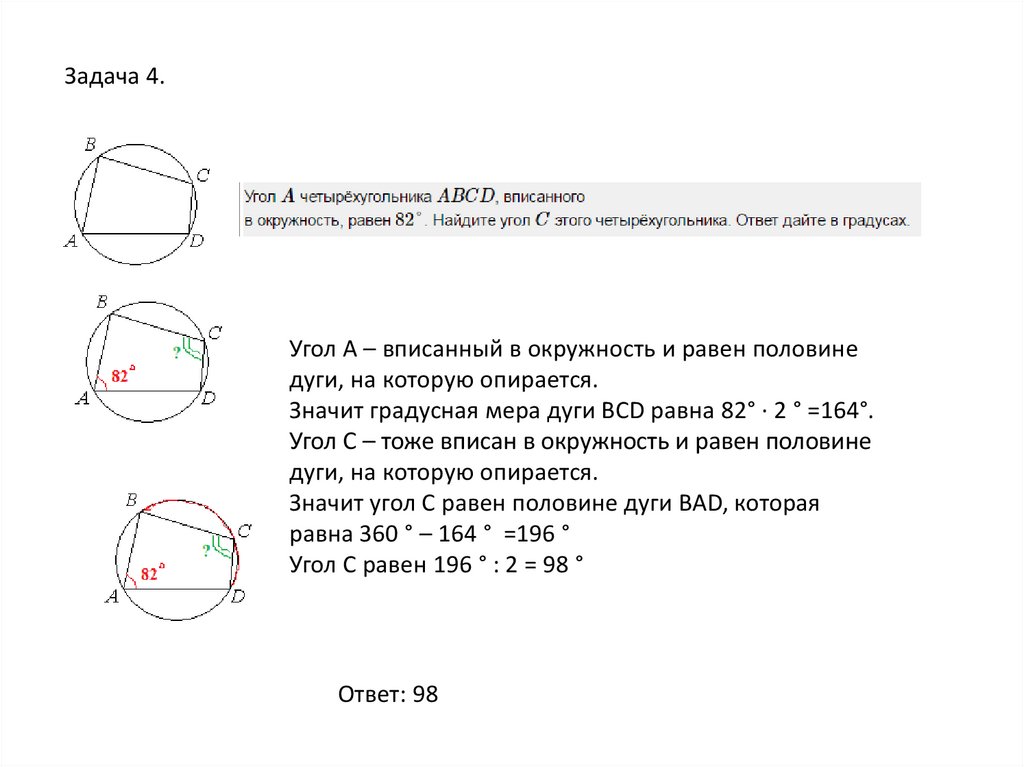
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно:
Для остроугольного треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно:
Для тупоугольного треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
3. Угол ∠А = 90°.
Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Следовательно:
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
Как решаем:
Согласно теореме о сумме углов треугольника:
∠A + ∠B + ∠C = 180°
∠B = 180° — 45° — 15° = 120°
Сторону AC найдем по теореме синусов:
Ответ: AC = 12.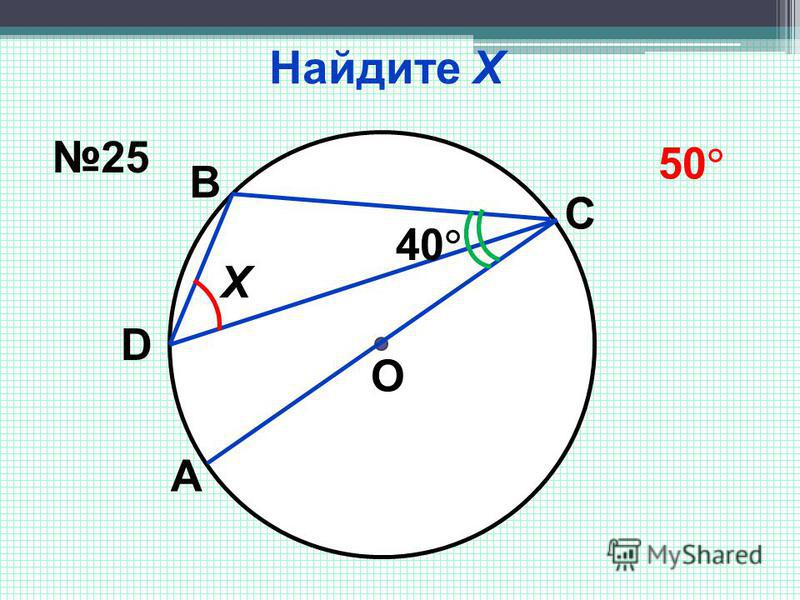
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см соответственно. Найти угол, который расположен напротив данного катета.
Как решаем:
Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Следовательно:
Значит .
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
, где R — радиус описанной вокруг треугольника окружности.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
346. 2K
2K
Разряды и классы чисел
К следующей статье
Прямая и обратная пропорциональность
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Центральный и вписанный угол, свойства
Центральный угол — это угол, вершина которого находится в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее.
Отрезок, соединяющий две точки окружности, называется хорда.
Самая большая хорда проходит через центр окружности и называется диаметр.
На рисунках — центральные и вписанные углы, а также их важнейшие свойства.
Угол, вершина которого лежит в центре окружности, называется центральным. Величина центрального угла равна угловой величине дуги, на которую он опирается. Угол тоже можно назвать центральным. Только он опирается на дугу, которая больше 180
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. Величина вписанного угла равна половине центрального угла, опирающегося на ту же дугу.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Величина центрального угла равна угловой величине дуги, на которую он опирается. Значит, центральный угол величиной в градусов будет опираться на дугу, равную , то есть круга.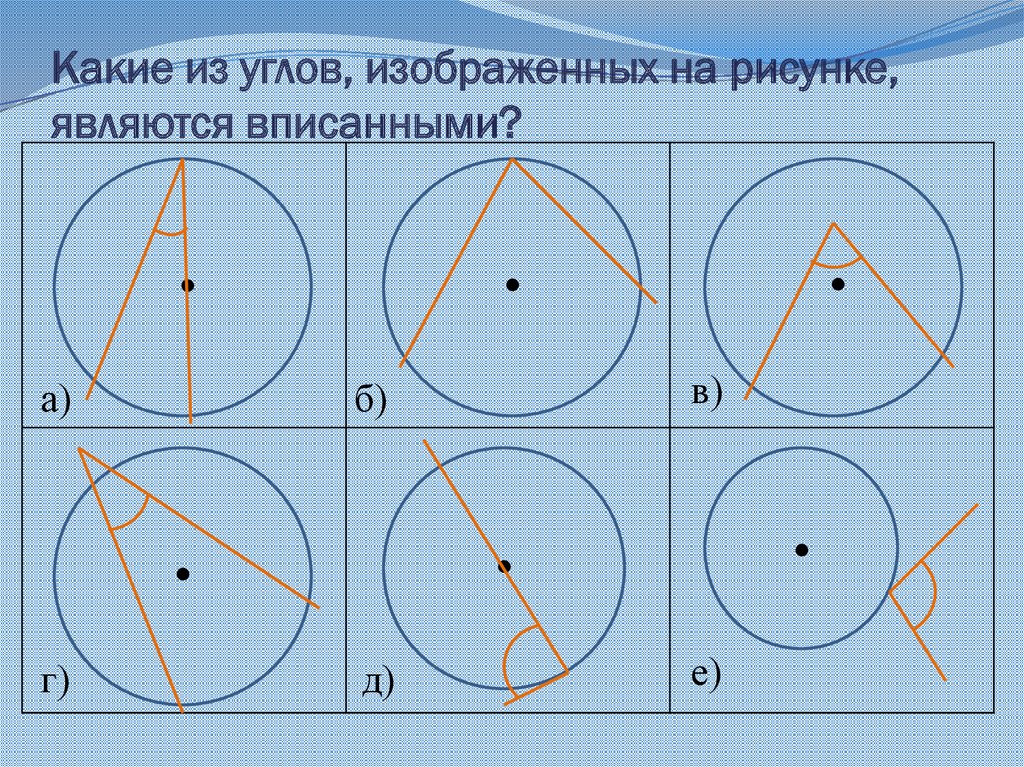 Центральный угол, равный , опирается на дугу в 60 градусов, то есть на шестую часть круга.
Центральный угол, равный , опирается на дугу в 60 градусов, то есть на шестую часть круга.
Докажем, что величина вписанного угла в два раза меньше центрального, опирающегося на ту же дугу.
Пусть угол AOC — центральный и опирается на дугу АС, тогда ОА и ОС — радиусы окружности.
Пусть ABC — вписанный угол, опирающийся на дугу АС,
АВ и ВС — хорды окружности.
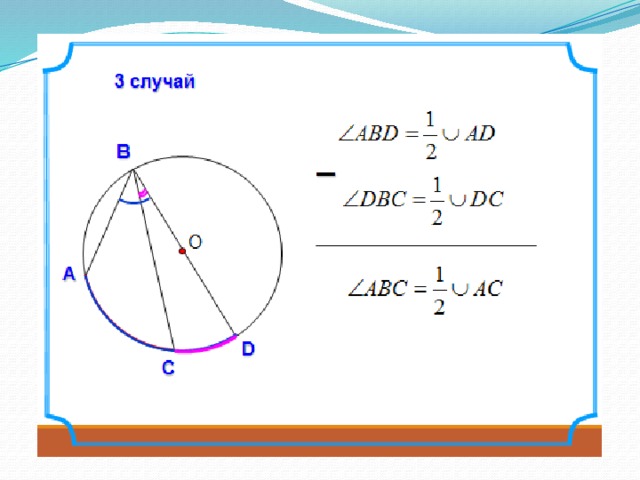
Первый случай: Точка O лежит на BC, то есть ВС — диаметр окружности.
Треугольник AOB — равнобедренный, АО = ОВ как радиусы. Значит,
— внешний угол а внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Получили, что
Второй случай: Центр окружности точка О не лежит на ВС. Построим диаметр BК:
Если точка О лежит внутри вписанного угла АВС, как на рисунке слева, то
Если О лежит вне вписанного угла АВС, как на рисунке справа, то
Мы получили, что в каждом из этих случаев величина центрального угла в два раза больше, чем величина вписанного угла, опирающегося на ту же дугу.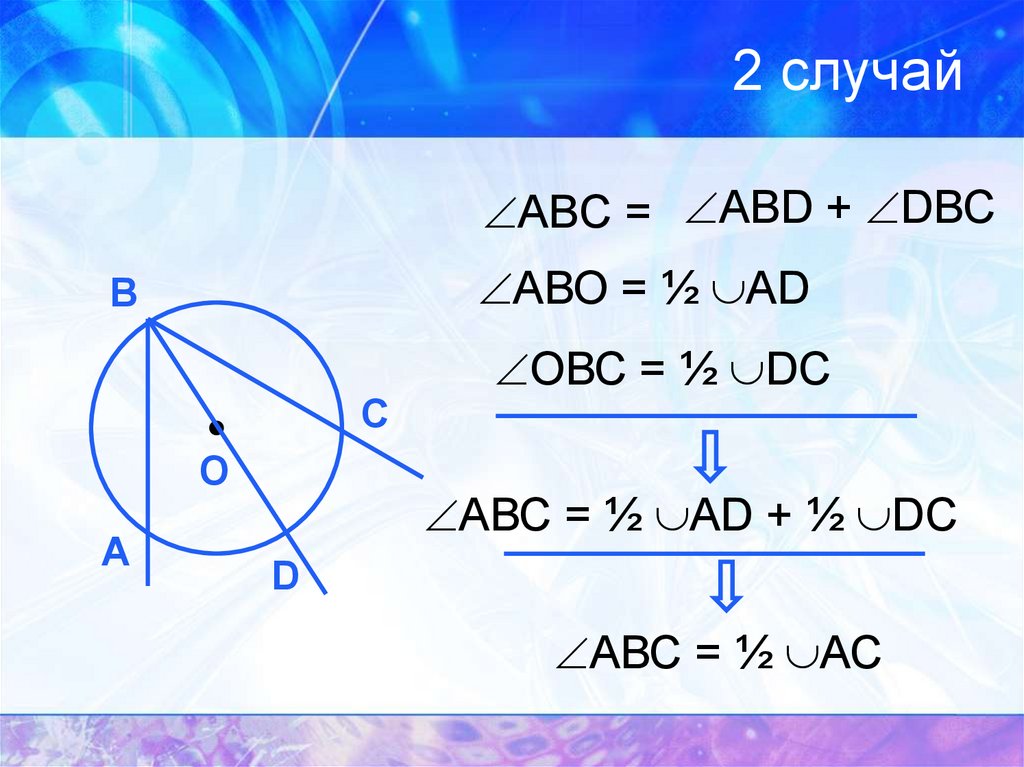
Теорема доказана.
При решении задач по геометрии также применяются следующие теоремы:
1. Равные центральные углы опираются на равные хорды.
2. Равные вписанные углы опираются на равные хорды.
3. Равные хорды стягивают равные дуги.
Докажем теорему 3.
Пусть хорды AB и CD равны. Докажем, что AMB дуги CND имеют одинаковую градусную меру, то есть равны.
Доказательство:
По условию, AB = CD. Соединим концы хорд с центром окружности. Получим: AO = BO = CO = DO = r.
по трем сторонам, отсюда следует, что центральные углы равны, т.е. Значит, и дуги, на которые они опираются, также равны, т.е. дуги AMB и CND имеют одинаковую градусную меру.
Теорема доказана.
Верна и обратная теорема:
Если две дуги окружности равны, то равны и хорды, их стягивающие.
Пусть дуги AMB и CND равны. Тогда как центральные углы, опирающиеся на эти дуги. Значит, треугольники и равны по двум сторонам и углу между ними, и тогда что и требовалось доказать.
Эти две теоремы можно объединить в одну, которая формулируется так:
Хорды окружности равны тогда и только тогда, когда равны дуги, которые они стягивают.
Разберем задачи ЕГЭ и ОГЭ по теме: Окружность, центральный угол, вписанный угол.
Задача 1, ЕГЭ. Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.
Вписанный угол, опирающийся на диаметр, — прямой.
Ответ: 90.
Задача 2, ЕГЭ. Центральный угол на больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Решение:
Пусть центральный угол равен , а вписанный угол, опирающийся на ту же дугу, равен .
Мы знаем, что
Отсюда
Ответ: 36.
Задача 3, ЕГЭ. Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную Ответ дайте в градусах.
Решение:
Пусть хорда AB равна Тупой вписанный угол, опирающийся на эту хорду, обозначим В треугольнике AOB стороны AO и OB равны 1, сторона AB равна Нам уже встречались такие треугольники. Очевидно, что треугольник AOB — прямоугольный и равнобедренный, то есть угол AOB равен 90 Тогда дуга ACB равна 90 а дуга AKB равна Вписанный угол опирается на дугу AKB и равен половине угловой величины этой дуги, то есть 135.
Очевидно, что треугольник AOB — прямоугольный и равнобедренный, то есть угол AOB равен 90 Тогда дуга ACB равна 90 а дуга AKB равна Вписанный угол опирается на дугу AKB и равен половине угловой величины этой дуги, то есть 135.
Ответ: 135.
Задача 4, ЕГЭ. Хорда AB делит окружность на две части, градусные величины которых относятся как 5 : 7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
Решение:
Главное в этой задаче — правильный чертеж и понимание условия. Как вы понимаете вопрос: «Под каким углом хорда видна из точки С?»
Представьте, что вы сидите в точке С и вам необходимо видеть всё, что происходит на хорде AB. Так, как будто хорда AB — это экран в кинотеатре 🙂
Очевидно, что найти нужно угол ACB.
Сумма двух дуг, на которые хорда AB делит окружность, равна то есть
Отсюда и тогда вписанный угол ACB опирается на дугу, равную Величина вписанного угла равна половине угловой величины дуги, на которую он опирается, значит, угол ACB равен
Ответ: 105.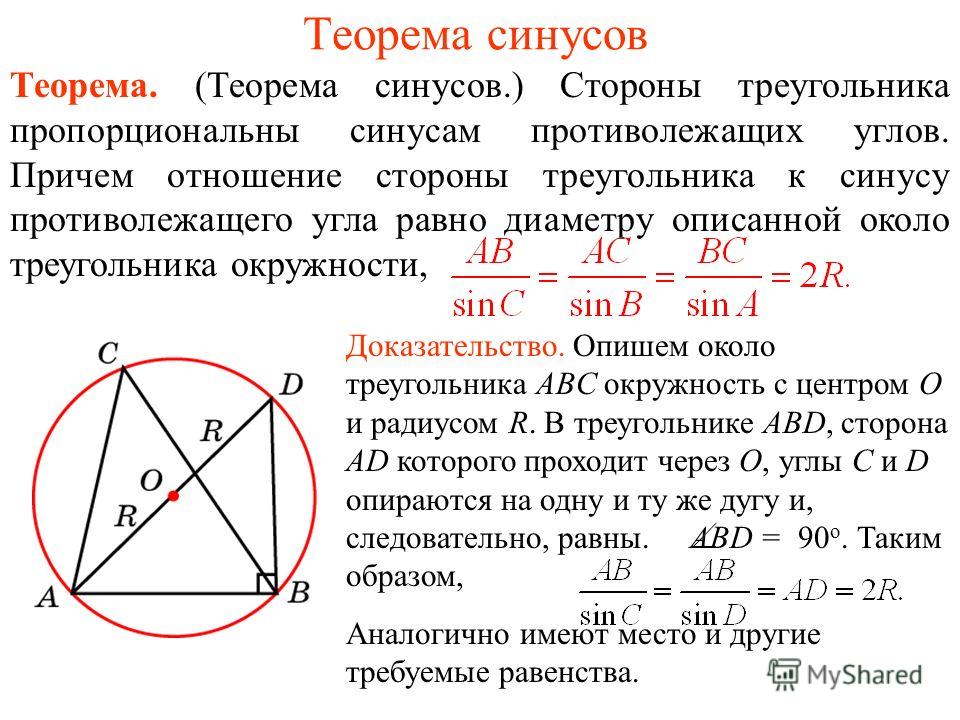
Задача 5, ЕГЭ.
Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32
Решение:
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
Значит,
Ответ: 64.
Задача 6, ЕГЭ. Найдите центральный угол AOB, если он на больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах.
Решение:
Пусть величина угла АОВ равна градусов. Величина вписанного угла АСВ равна половине центрального угла, опирающегося на ту же дугу, то есть градусов.
Получим уравнение: откуда
Ответ: 30.
Задача 7, ЕГЭ. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
Решение.
Рассмотрим треугольник AOB. Он равносторонний, так как AO = OB = AB = R.
Поэтому угол AOB = 60. Вписанный угол ACB равен половине дуги, на которую он опирается, то есть 30
Ответ: 30.
Задача 8, ЕГЭ.
Дуга окружности AC, не содержащая точки B, составляет 200 А дуга окружности BC, не содержащая точки A, составляет 80 Найдите вписанный угол ACB. Ответ дайте в градусах.
Решение:
Вписанный угол равен половине угловой величины дуги, на которую он опирается. Дуга АВ равна Тогда
Ответ: 40.
Задачи ОГЭ по теме: Центральный и вписанный угол, градусная мера дуги.
Задача 9, ОГЭ. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен Найдите радиус окружности.
Решение.
Рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу окружности.
Углы при основании равнобедренного треугольника равны. Пусть AOB равен , тогда где Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.
Ответ: 6.
Задача 10, ОГЭ. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен Найдите величину угла OAB.
Решение.
Вписанные углы ВСD и ВАD опираются на одну и ту же дугу окружности, поэтому они равны, угол
Ответ: 30.
Задача 11, ОГЭ. Найдите градусную меру центрального MON, если известно, что NP — диаметр, а градусная мера MNP равна 18
Решение:
Треугольник MON — равнобедренный. Тогда −
Ответ: 144.
Задача 12, ОГЭ.
Найдите DEF, если градусные меры дуг DE и EF равны и соответственно.
Решение.
Дуга FD, не содержащая точку Е, равна Вписанный угол DEF, опирающийся на эту дугу, равен половине ее угловой величины,
Ответ: 71.
Задача 13, ОГЭ. В окружности с центром O AC и BD — диаметры. Угол ACB равен Найдите угол AOD. Ответ дайте в градусах.
Решение.
Угол ACB — вписанный, он равен половине центрального угла, опирающегося на ту же дугу, то есть AОВ = 52 Угол ВОD — развернутый, поэтому угол AOD равен
Ответ: 128.
Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Окружность. Центральный и вписанный угол» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Информация на странице «Окружность. Центральный и вписанный угол» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена: 09.03.2023
Вопрос Видео: Использование соотношения между правилом синусов и радиусом окружности треугольника для вычисления радиуса
Видеозапись
𝐴𝐵𝐶 — равносторонний треугольник со стороной 12 сантиметров, вписанный в окружность. Найдите радиус окружности, давая ответ с точностью до двух знаков после запятой.
Начнем с наброска схемы. Он не обязательно должен быть точно в масштабе, но он должен быть примерно пропорционален, чтобы мы могли проверить пригодность любых полученных ответов. Поскольку треугольник вписан в окружность, это означает, что все вершины должны лежать на окружности самой окружности. Мы можем построить радиусы окружности, как показано на рисунке. Теперь давайте добавим несколько углов. Мы знаем, что все углы равностороннего треугольника равны 60 градусам. Это означает, что мера угла 𝑂𝐴𝐵 должна быть вдвое меньше. Это 30 градусов.
Поскольку треугольник вписан в окружность, это означает, что все вершины должны лежать на окружности самой окружности. Мы можем построить радиусы окружности, как показано на рисунке. Теперь давайте добавим несколько углов. Мы знаем, что все углы равностороннего треугольника равны 60 градусам. Это означает, что мера угла 𝑂𝐴𝐵 должна быть вдвое меньше. Это 30 градусов.
Точно так же угол 𝑂𝐵𝐴 также должен быть равен 30 градусам. Наконец, поскольку сумма углов в треугольнике равна 180, мы можем вычислить меру угла 𝐴𝑂𝐵, вычитая 30 и 30 из 180, чтобы получить 120 градусов. Если мы посмотрим только на непрямоугольный треугольник 𝐴𝑂𝐵, то увидим, что нам известна мера трех углов и длина одной из его сторон. Мы можем использовать закон синусов для вычисления недостающих длин. Мы знаем, что это не закон косинусов, так как он требует, по крайней мере, двух известных сторон.
Помните, закон синусов можно использовать в любой форме. Поскольку мы пытаемся найти недостающую длину, мы решили использовать первую форму. Эта форма требует от нас меньше перестановок для решения любых уравнений, которые мы получаем. Однако если мы пытаемся найти недостающий угол, мы бы выбрали вторую форму. Назовем стороны нашего треугольника. Сторона, противоположная углу 𝐴, обозначается строчной 𝑎. Сторона, противоположная углу 𝑂, обозначается строчной 𝑜. А сторона, противоположная углу 𝐵, обозначается строчной 𝑏.
Эта форма требует от нас меньше перестановок для решения любых уравнений, которые мы получаем. Однако если мы пытаемся найти недостающий угол, мы бы выбрали вторую форму. Назовем стороны нашего треугольника. Сторона, противоположная углу 𝐴, обозначается строчной 𝑎. Сторона, противоположная углу 𝑂, обозначается строчной 𝑜. А сторона, противоположная углу 𝐵, обозначается строчной 𝑏.
Мы пытаемся вычислить длину радиуса этой окружности. Итак, мы пытаемся найти либо 𝑎, либо 𝑏. Рассчитаем длину стороны 𝑎. Мы знаем меру угла при 𝑂 и длину стороны 𝑜, поэтому будем использовать эти две части формулы: 𝑎 над синусом 𝐴 равно 𝑜 над синусом 𝑂. Обратите внимание, что мы изменили буквы, чтобы они соответствовали нарисованному нами треугольнику. Следующим логическим шагом будет подстановка любых значений, полученных из нашего треугольника, в формулу закона синусов.
Это дает нам 𝑎 на синусе 30 равно 12 на синусе 120. Мы можем решить это уравнение, умножив обе части на синус 30. Это дает нам, что 𝑎 равно 12 на синусе 120, умноженном на синус 30. Вводим это в наш калькулятор и получаем значение 6,9282. Исправьте до двух знаков после запятой, что дает нам 6,93 сантиметра как радиус круга. Полезно знать, что мы можем проверить наш ответ с помощью так называемого расширенного закона синусов.
Вводим это в наш калькулятор и получаем значение 6,9282. Исправьте до двух знаков после запятой, что дает нам 6,93 сантиметра как радиус круга. Полезно знать, что мы можем проверить наш ответ с помощью так называемого расширенного закона синусов.
Это говорит о том, что для треугольника, вписанного в окружность, отношение длины его стороны к синусу противоположного угла равно удвоенному радиусу. Это 𝑎 больше синуса 𝐴 равно 𝑏 больше синуса 𝐵 равно 𝑐 больше синуса 𝐶, что равно двум 𝑟. Если мы просто выберем две части этой формулы, скажем, 𝑐 над синусом 𝐶 равно двум 𝑟, мы сможем быстро вычислить значение радиуса. Мера угла при 𝐶 составляет 60 градусов. А длина стороны 12,
Итак, наша формула станет 12 на синус 60 равно двум 𝑟. Мы можем решить это уравнение, разделив обе части на два. Это дает нам, что радиус равен шести, деленным на синус 60, что снова равно 6,9282, как мы выяснили ранее. Тогда радиус этой окружности равен 6,93 сантиметра.
Углы в круге — макеты
Автор: Мэри Джейн Стерлинг и
Обновлено: 09. 07.2021
07.2021
Из книги: Тригонометрия для чайников0005
Тригонометрия для чайников
Исследуйте книгу Купить на Amazon
Существует несколько способов рисования угла в круге, и каждый из них имеет особый способ вычисления размера этого угла. Четыре различных типа углов: центральный, вписанный, внутренний и внешний. Здесь вы видите примеры этих различных типов углов.Центральный уголок
Центральный угол имеет вершину в центре окружности, а стороны угла лежат на двух радиусах окружности. Мера центрального угла такая же, как мера дуги, которую две стороны вырезают из круга.Вписанный угол
Вписанный угол имеет вершину на окружности, а стороны угла лежат на двух хордах окружности. Вписанный угол равен половине дуги, которую две стороны вырезают из окружности.Угол внутренний
Внутренний угол имеет вершину на пересечении двух прямых, пересекающихся внутри окружности. Стороны угла лежат на пересекающихся прямых. Мерой внутреннего угла является среднее значение двух дуг, которые вырезаются из окружности этими пересекающимися линиями.
Стороны угла лежат на пересекающихся прямых. Мерой внутреннего угла является среднее значение двух дуг, которые вырезаются из окружности этими пересекающимися линиями.Внешний уголок
Внешний угол имеет вершину, где два луча имеют общую конечную точку вне круга. Стороны угла и есть эти два луча. Меру внешнего угла находят, разделив разность между мерами соединяемых дуг на два.Пример: Найдите угол EXT , учитывая, что внешний угол отсекает дуги в 20 градусов и 108 градусов.
Найдите разницу между измерениями двух пересекаемых дуг и разделите на 2:
Угол EXT равен 44 градусам.
Разделение секторов
Сектор круга — это участок круга между двумя радиусами (множественное число от радиуса). Вы можете рассматривать эту часть как кусок пирога, вырезанный из круглой тарелки. Вы можете найти площадь сектора круга, если знаете угол между двумя радиусами. Круг имеет в общей сложности 360 градусов вокруг центра, поэтому, если этот центральный угол, определяющий сектор, имеет угловую меру 60 градусов, то сектор занимает 60/360 или 1/6 градусов на всем протяжении.

Leave A Comment