Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.

- e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.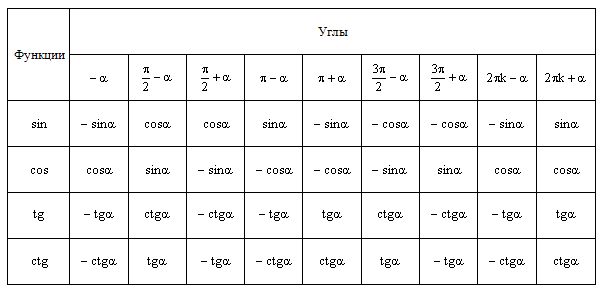 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.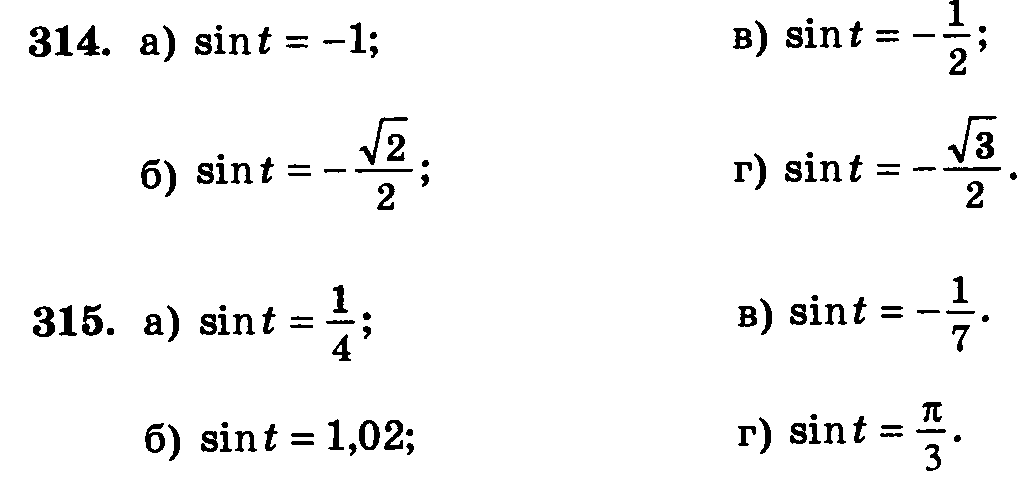 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Math Scene — Тригонометрические функции — Более сложные уравнения и неравенства
Math Scene — Тригонометрические функции — Более сложные уравнения и неравенства — Урок 5 2008 Расмус Эхф | Печать |
Пример 1
Решите уравнение sin x = cos x и затем неравенство
грех x > cos x на интервале 0 x < 2,
Из единичного круга мы видим, что sin x и cos x
может иметь одинаковое значение только в двух местах, в x = /4
и х = 5/4
(45 и 225 ).
Уравнение sin x = cos x также можно решить путем деления на cos x.
тангенс х = 1
x = тангенс −1 (1)
х = 45 ∙ /180 + к∙
x = /4 + k∙ (k — любое целое число, положительное или отрицательное)
Если положить k = 0 и k = 1, получим решения /4 (45 ) и /4 + = 5/4 (45 + 180 = 225 ).
Чтобы решить неравенство sin x > cos x, нам нужно увидеть, что больше sin x или cos x на интервалах между решениями /4 и 5/4. Решения можно увидеть, если мы нарисуем графики f(x) = sin x и g(x) = cos Икс. График sin x лежит над графиком cos x на интервале /4 x 5x/4 (см. заштрихованную область на диаграмме).
sin x cos x на интервале /4 x 5x/4.
Пример 2
Решить уравнение sin x ∙ cos x = 0 и затем неравенство
sin x ∙ cos x > 0 на интервале 0 x < 2.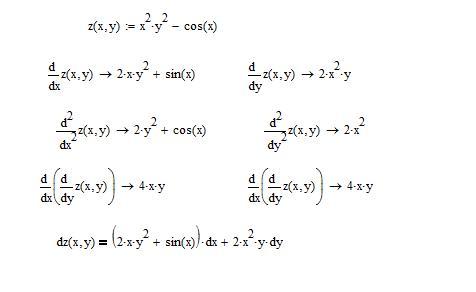
Неравенство не имеет решение, когда sin x или cos x принимают значение 0. Это происходит с интервалом 90.
Решения уравнение sin x ∙ cos x = 0 на интервале 0 x < 2, поэтому 0, /2 и 3/2 (0 , 90 , 180 и 270 ).
Решение sin x
∙ cos x > 0 можно найти, взглянув на единичный круг. Нам нужно найти
где sin x, умноженный на cos x, является положительным. Другими словами, sin x и cos x имеют
иметь один и тот же знак, оба должны быть
положительный или оба отрицательные. Это происходит в первом и третьем квадранте.
поэтому решения
0 < х < /2 и р < х < 3/2.
Мы также можем увидеть это по
построение графика
f(x) = sin x ∙ cos x.
Пример 3
Решите уравнение sin x ∙ cos x − sinx = 0 и тогда неравенство sin x ∙ cos x − sin x > 0 на интервале 0 x < 2,
sin x ∙ cos x − sinx = 0 sin x (cos x − 1) = 0 | Нам нужно
чтобы разложить уравнение на множители, взяв sin x за скобки. |
Уравнение имеет решения когда sin x = 0 или скобка (cos x − 1) = 0,
sin x = 0
x = 0 или (180 ).
или
потому что х — 1 = 0
потому что х = 1
х = 0
Единственные решения уравнение поэтому 0 и .
Неравенство sin x ∙ cos x − sin x > 0 можно переписать как sin x (cos x − 1) > 0,
Теперь полезно сделать таблицу знаков и посмотрите на знаки sin x и cos x − 1.
Решение
Мы видим, что оба фактора
отрицательно на интервале
< x < 2,
Теперь давайте посмотрим, как это подходит
в с графиком
f(x) = sin x ∙ cos x − sin x
Заштрихованная область над крестиком
ось показывает, где
sin x (cos x − 1) > 0, что согласуется с нашими расчетами.
Пример 4
Найти все решения уравнения cos 2 x − cos x = 0,
cos 2 x − cos х = 0
потому что х ∙ (кос х — 1) = 0
Решения можно найти, когда cos x = 0 или cos x − 1 = 0
cos х = 0
x =/ 2 или 3/ 2 (90 или 270 )
х = / 2 + к∙
или
потому что х — 1 = 0
потому что х = 1
x = 0 + k∙2 = k∙2
Все решения укладываются в шаблон x = /2 + к∙
Пример 5
Найти все решения уравнения sin 2 x − 5 sin x + 4 = 0,
Это квадратное уравнение с sin x в качестве
переменная. Поэтому мы можем найти sin x, используя квадратичную формулу. а = 1, б = -5 или с = 4,
Поэтому мы можем найти sin x, используя квадратичную формулу. а = 1, б = -5 или с = 4,
Синус мы не можем принять значение 4 поэтому нам не нужно рассматривать sin x = 4. Другая возможность — sin x = 1, решение которой /2 (90 ). Таким образом, полное решение:
х = / 2 + к∙2
Пример 6
Решите уравнение sin 5x = грех х .
Возможно, что позиция 5х на единичном круге совпадает с позицией x и поскольку эта позиция повторяется с интервалом в 360, мы получаем следующее уравнение:
1) 5x = x + к∙360
4x = к∙360
х = к∙90
Мы показываем эту возможность в диаграмма.
Появляется вторая возможность
от того что
грех x = грех (180 − х ). Это дает нам следующее решение:
5 х = 180 — х + к∙360
6x = 180 + к∙360
х = 30 + к∙60
Это решение показано на
схему справа.
Но мы замечаем, что первое решение содержится в второе решение, поэтому достаточно дать второе решение
х = 30 + к∙60
Пример 7
Решите уравнение cos 2x = cos x на интервале 0 x < 2,
1) Сначала рассмотрим вероятность того, что x и 2x находятся в одном и том же месте на единичной окружности.
2x = x + k∙2 x = k∙2 х = 0 | Вычесть x из обеих частей уравнения, а затем выберите k = 0 (k = 1 дает 2, что находится за пределами интервала |
2) Второй вариант.
с факта
потому что v = cos (-v). Тогда решение будет следующим:
2x = −x + к∙2
3x = k∙2
x = k∙2/ 3
Это дает решения 2/3 (120 )
для k = 1 и 4/3 (240 ) для k = 2.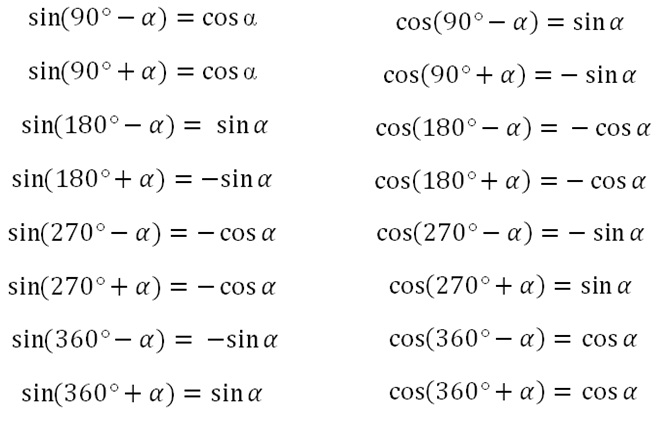 поэтому полное решение:
поэтому полное решение:
0, 2/3 и 4/3.
Пример 8
Решите уравнение tan 3x = загар 2x.
Уравнения Тана во многих способов самое простое из тригонометрических уравнений, так как существует только возможность учтите, что это повторяется с интервалом 180 .
3x = x + k∙180
2x = к∙180
х = к∙90
или в радианах
х = к∙/ 2
Попробуйте викторину 5 по триггерным функциям.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
Синус, косинус и тангенс в четырех квадрантах
Синус, косинус и тангенс
Три основные функции в тригонометрии — это синус, косинус и тангенс.
Их легко вычислить:
Разделить длину одной стороны прямоугольного треугольника
на другую сторону
.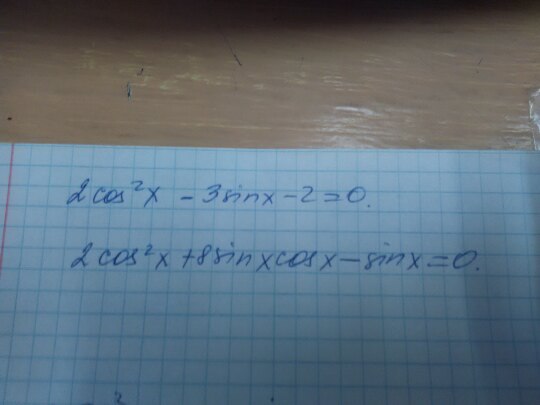 .. но надо знать с каких сторон!
.. но надо знать с каких сторон!
Для угла θ функции вычисляются следующим образом:
Синусоидальная функция: | sin( θ ) = Противоположный / Гипотенуза |
Функция косинуса: | cos( θ ) = Смежный / Гипотенуза |
Функция касания: | tan( θ ) = Противоположный / Смежный |
Пример: чему равен синус 35°?
Используя этот треугольник (длина только до одного десятичного знака): sin(35°) = противоположность / гипотенуза = 2,8/4,9= 0,57… |
Декартовы координаты
Используя декартовы координаты, мы отмечаем точку на графике , как далеко вдоль и , как далеко вверх по :
Точка (12,5) находится на 12 ед. вдоль и на 5 ед. вверх.
вдоль и на 5 ед. вверх.
Четыре квадранта
Когда мы включаем отрицательных значений , оси x и y делят пространство на 4 части:
Квадранты I, II, III и IV
(Нумерация против часовой стрелки)
- В Квадранте I и x, и y положительны,
- в квадранте II x отрицательное (y все еще положительное),
- в квадранте III и x, и y отрицательны, а
- в квадранте IV x снова положительный, а y отрицательный.
Вот так:
| Квадрант | X (по горизонтали) | Y (вертикальный) | Пример |
|---|---|---|---|
| я | Положительный | Положительный | (3,2) |
| II | Отрицательный | Положительный | (−5,4) |
| III | Отрицательный | Отрицательный | (-2,-1) |
| IV | Положительный | Отрицательный | (4,−3) |
Пример: Точка «C» (-2,-1) находится на 2 единицы вперед в отрицательном направлении и на 1 единицу вниз (т. е. в отрицательном направлении).
е. в отрицательном направлении).
И x, и y отрицательны, поэтому эта точка находится в «Квадранте III»
Контрольный угол
Углы могут быть больше 90°
Но мы можем вернуть их ниже 90º, используя ось x в качестве точки отсчета.
Думайте, что «ссылка» означает «ссылка x»
Самый простой способ — сделать набросок!
Пример: 160º
Начните с положительной оси x и поверните на 160º
Затем найдите угол к ближайшей части оси x,
в данном случае 20º
Базовый угол для 160º равен 20º
33Здесь мы видим четыре примера с опорным углом 30º:
Вместо эскиза можно использовать следующие правила:
| Квадрант | Контрольный угол |
| я | θ |
| II | 180º − θ |
| III | θ − 180º |
| IV | 360º − θ |
Синус, косинус и тангенс в Четыре квадранта
Теперь давайте посмотрим на детали прямоугольного треугольника с углом 30° в каждом из 4 квадрантов.
В квадранте I все в норме, а синус, косинус и тангенс положительны:
Пример: синус, косинус и тангенс угла 30°
Синус | sin(30°) = 1/2 = 0,5 |
Косинус | cos(30°) = 1,732 / 2 = 0,866 |
Касательная | тангенс (30°) = 1 / 1,732 = 0,577 |
Но в квадранте II направление x отрицательно , а косинус и тангенс становятся отрицательными:
Пример: синус, косинус и тангенс угла 150°
Синус | sin(150°) = 1/2 = 0,5 |
Косинус | cos(150°) = -1,732 / 2 = -0,866 |
Касательная | тангенс (150°) = 1 / −1,732 = −0,577 |
В квадранте III синус и косинус отрицательны:
Пример: синус, косинус и тангенс 210°
Синус | sin(210°) = −1 / 2 = −0,5 |
Косинус | cos(210°) = −1,732 / 2 = −0,866 |
Касательная | тангенс (210°) = −1 / −1,732 = 0,577 |
Примечание. Тангенс равен положительному числу , потому что деление отрицательного числа на отрицательное дает положительное значение.
Тангенс равен положительному числу , потому что деление отрицательного числа на отрицательное дает положительное значение.
В квадранте IV синус и тангенс отрицательны:
Пример: синус, косинус и тангенс 330°
Синус | sin(330°) = −1 / 2 = −0,5 |
Косинус | cos(330°) = 1,732 / 2 = 0,866 |
Касательная | тангенс (330°) = -1 / 1,732 = -0,577 |
Есть выкройка! Посмотрите, когда синус, косинус и тангенс положительны …
- Все трое положительные в квадранте I
- Синус положительный только в Квадранте II
- Только тангенс положителен в квадранте III
- Косинус положителен только в квадранте IV
Это можно показать еще проще:
На этом графике также отображается «ASTC».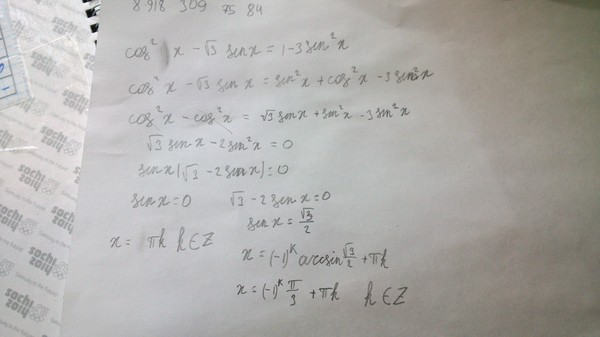

 3
3
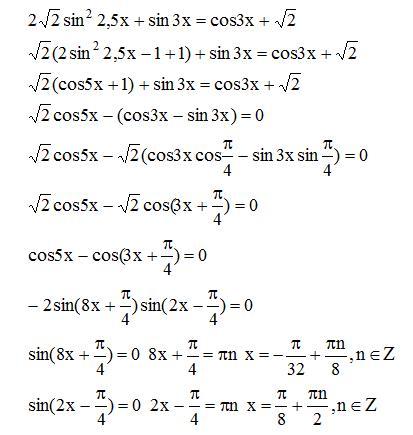
Leave A Comment