Момент силы — как найти? В чем измеряется? Формулы
Покажем, как применять знание физики в жизни
Начать учиться
Возможно, вы никогда не замечали, но каждый раз вы толкаете прозрачные двери в метро, ставя руку не ближе к креплению, а наоборот — ближе к краю. Понятие «Момент силы» объяснит это интуитивное действие.
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
- Сила — это физическая векторная величина, является мерой действия тела на другое тело.
Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.
То есть перпендикуляр, проведенный от точки опоры до линии, вдоль которой действует сила — это плечо силы.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели —
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.
Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Правило равновесия рычага Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил. F1, F2 — силы, действующие на рычаг l1, l2 — плечи этих сил |
Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
Момент силы M = Fl M — момент силы [Н*м] |
Для примера представьте, что вы забыли, как открывать двери.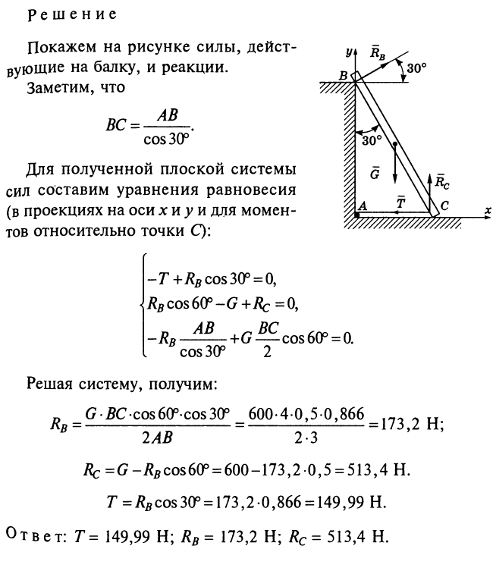
Для начала приложим силу к краю двери — туда, где самый длинный рычаг. Открылась!
А что если толкнуть дверь ближе к креплению — там, где плечо намного короче? Для этого придется приложить силу большего значения.
Вывод: чтобы повернуть дверь, нужен крутящий момент определенного значения. Чем больше плечо силы, тем меньше значение силы, которую нужно приложить — и наоборот. Поэтому нам легче толкать дверь там, где плечо силы больше.
Похожая история с гаечным ключом. Чтобы закрутить гайку, нужно взяться за ручку подальше от гайки. За счет увеличения плеча мы уменьшаем значение силы, которую нужно приложить.
Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
МА=F×AB=F×3м
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
Момент силы относительно точки B:
MB=F×cos30×AB=F×cos30×3м
Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
Момент силы относительно точки B:
MB=F×3м
Правило моментов
Вернемся к нашим баранам качелям. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов M1 + M2 +…+ Mn = M’1 + M’2 +…+ M’n M1 + M2 +…+ Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м] M’1 + M’2 |
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом: — он вращает по часовой.
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
Путешественник несёт мешок с вещами на лёгкой палке.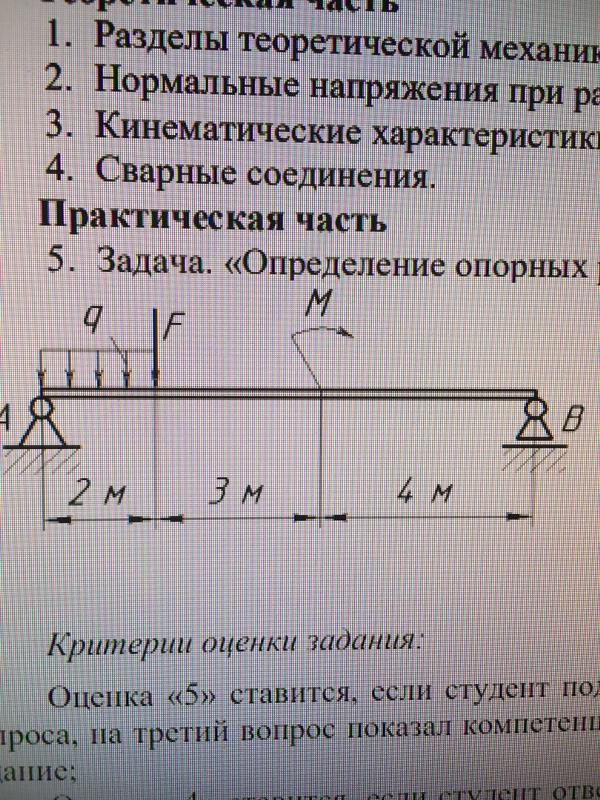 Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Решение:
По правилу рычага:
где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Решение:
По правилу рычага
Отсюда
Ответ: Масса груза равна 0,3 кг
Задача 4 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Уточним, что 0,8 м — это расстояние от центра тяжести груза до опоры, т. е. перпендикуляр до оси вращения. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н
youtube.com/embed/OctfStSExzo» title=»YouTube video player» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»» ssmarticle=»»/>
Карина Хачатурян
К предыдущей статье
189.3K
Закон электромагнитной индукции
К следующей статье
Давление газа на стенки сосуда
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
5. Момент силы относительно центра. Пара сил
5.1 Момент силы относительно центра (или точки)
В
ведем
важное понятие о моменте силы относительно
точки. Точку, относительно которой
берется момент, называют центром
момента, а момент силы относительно
этой точки – моментом относительно
центра.
Точку, относительно которой
берется момент, называют центром
момента, а момент силы относительно
этой точки – моментом относительно
центра.
Если под действием приложенной силы тело может вращаться вокруг некоторой закрепленной точки, то момент силы относительно этой точки будет характеризовать вращательный эффект силы. Вращательное действие силы на тело будет зависеть от модуля силы, расстояния линии действия силы до точки закрепления и от направления вращения в этой плоскости.
Так, например, если к телу, закрепленному
неподвижно в точке О (рисунок 5.1), приложена
в точке A1 сила
,
то тело будет вращаться вокруг оси OZ1,
перпендикулярно плоскости треугольника
OA1B1,
в направлении, указанном на рисунке.
Если к этому же телу приложена сила в точке A2, то тело
будет вращаться вокруг оси OZ2,
перпендикулярно к плоскости треугольника
OA2B2.
Мерой вращательного действия силы на тело с закрепленной точкой является момент силы относительно точки.
Алгебраическая величина момента силы относительно точки, определяется произведением модуля силы на ее плечо.
Рассмотрим силу F, приложенную в точке А (рисунок 5.2). Из некоторого центра О опустим перпендикуляр на линию действия силы ; длину h этого перпендикуляра называют плечом силы относительно центра О.
Рисунок 5.2
Момент силы относительно центра О определяется:
1) модулем момента, равным произведению F·h;
2) положением в пространстве плоскости ОАВ («плоскости поворота»), проходящей через центр О и силу ;
3) направлением поворота в этой плоскости.
Из геометрии известно, что положение
плоскости в пространстве определяется
направлением нормали «n»
(перпендикуляра) к этой плоскости. Таким
образом, момент силы относительно центра
характеризуется не только его числовым
значением, но и направлением в пространстве,
т.е. является величиной векторной.
Таким
образом, момент силы относительно центра
характеризуется не только его числовым
значением, но и направлением в пространстве,
т.е. является величиной векторной.
Моментом силы F относительно центра О называется приложенный в центре О вектор , модуль которого равен произведению модуля силы на ее плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рисунок 5.3).
Согласно этому определению
(5.1)
Этот результат следует из того, что пл.
Δ ОАВ= АВ·h/2=Fh/2. Измеряется момент силы в Ньютон-метрах
(Нм). Выведем формулу, для вектора-момента
силы относительно точки О. Для этого рассмотрим
векторное произведение векторов и (рисунок 5.3). Как известно из векторной
алгебры, это будет вектор, перпендикулярный
к плоскости, в которой расположены
векторы и
,
и направленный в такую сторону, чтобы
с его конца видеть поворот от к кратчайшим путем против хода часовой
стрелки. Модуль этого вектора или
.
Модуль этого вектора или
.
Поэтому
или , (5.2)
где – радиус-вектор точки А, проведенный из центра О.
Таким образом, вектор-момент силы относительно точки равен векторному произведению радиуса-вектора точки приложения силы на вектор силы.
Обозначая алгебраическое значение момента силы относительно точки О через , будет иметь
(5.3)
Из формулы (5.3) следует, момент силы относительно точки, лежащей на линии действия этой силы, равен нулю (т.к. h=0).
Пример.
Вычислить моменты сил , относительно точки O.
Решение
Вектор направлен перпендикулярно плоскости OAEN, т.е. по прямой OL. , т.к. линия действия силы проходит через точку O.
Векторы и перпендикулярны к плоскости ОВDN,
но направлены в противоположные стороны. Вектор перпендикулярен к плоскости ОАВL
и направлен по прямой ON.
Вектор перпендикулярен к плоскости ОАВL
и направлен по прямой ON.
5.2 Пара сил. Момент пары сил
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело (рисунок 5.3, а).
а) б)
Рисунок 5.3
Система сил , , образующих пару, не находится в равновесии (эти силы не направлены вдоль одной прямой). В то же время пара сил не имеет равнодействующей, т.к. равнодействующая любой системы сил равна ее главному вектору , т.е. сумме этих сил, но для пары сил , поэтому свойства пары сил, как особой меры механического взаимодействия тел, рассмотрим отдельно.
Плоскость, проходящая через линии
действия пары сил называется плоскостью действия пары. Расстояние d между линиями
действия сил пары называется плечом пары.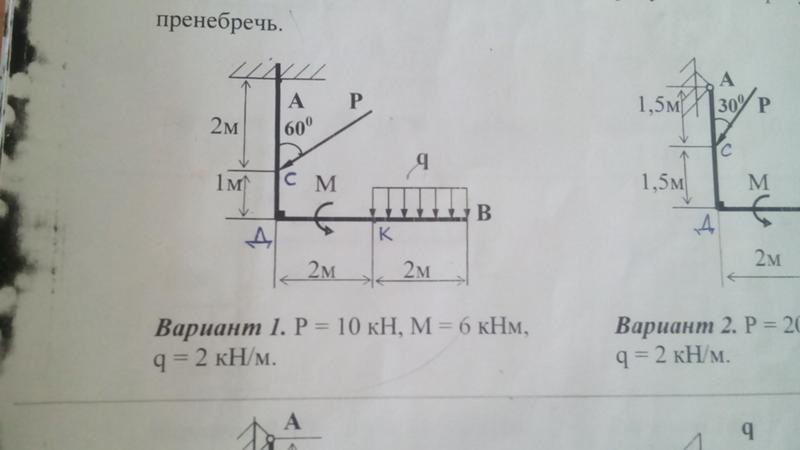 Действие
пары сил на твердое тело сводится к
вращательному эффекту, который
характеризуется величиной, называемой моментом пары. Этот момент
определяется:
Действие
пары сил на твердое тело сводится к
вращательному эффекту, который
характеризуется величиной, называемой моментом пары. Этот момент
определяется:
1) Его модулем, равным произведению F·d;
2) положением в пространстве плоскости действия пары;
3) направлением поворота пары в этой плоскости.
Таким образом, как и момент силы относительно центра, это величина векторная. Поэтому моментом пары сил называется вектор (или ), модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки (рисунок 5.3, б).
Следует отметить, что так как плечо силы относительно точки А равно d
(рисунок 5.3, а), а плоскость, проходящая
через точку А и силу
,
совпадает с плоскостью действия пары,
то одновременно
.
В отличие от момента силы может быть приложен в любой точке (такой вектор называется свободным). Измеряется момент пары, как и момент силы, в Н·м.
Покажем, что моменту пары можно дать другое выражение: момент пары равен сумме моментов относительно любого центра О сил, образующих пару, т.е.
(5.4)
Для доказательства проведем из произвольной точки О (рисунок 5.4) радиусы-векторы и .
Тогда согласно формуле (5.2), учитывая, что , получим ;
и, следовательно,
Так как , то справедливость (5.4) доказана. Отсюда следует, что или (5.5)
т.е. момент пары равен моменту одной из ее сил относительно точки приложения другой силы. Отметим еще, что модуль момента пары
(5.5/)
Так как действие пары сил на твердое
тело определяется значением суммы
моментов сил пары относительно любого
центра О, то из формулы (5. 4) следует, что две пары сил, имеющие одинаковые
моменты, эквивалентны, т.е. оказывают
на тело одинаковое механическое действие.
Это означает, что две пары сил, независимо
от того, где каждая из них расположена
в данной плоскости (или в параллельных
плоскостях) и чему равны в отдельности
модули их сил и их плечи, если моменты
имеют одно и то же значение
,
будут эквивалентны. Так как выбор центра
О произволен, то вектор можно считать приложенным в любой точке,
т.е. это свободный вектор.
4) следует, что две пары сил, имеющие одинаковые
моменты, эквивалентны, т.е. оказывают
на тело одинаковое механическое действие.
Это означает, что две пары сил, независимо
от того, где каждая из них расположена
в данной плоскости (или в параллельных
плоскостях) и чему равны в отдельности
модули их сил и их плечи, если моменты
имеют одно и то же значение
,
будут эквивалентны. Так как выбор центра
О произволен, то вектор можно считать приложенным в любой точке,
т.е. это свободный вектор.
В дальнейшем будем на чертеже вместо пары изображать полностью ее характеризующий вектор . При этом модуль определяет модуль момента пары [формула (5.5)], а направление определяет плоскость действия пары и направление поворота в этой плоскости.
Из формулы (5.4) следует, еще, что если на тело действует несколько пар с моментами ; …., то сумма моментов всех сил, образующих эти пары относительно любого центра будет равна ++…+, а следовательно, вся совокупность этих пар эквивалентна одной паре с моментом
(5. 6)
6)
Этот результат выражает теорему о сложении пар.
Из формулы (5.6) следует, при равновесии системы пар, действующих на твердое тело, должно быть
или (5.6/)
Таким образом, отметим следующие свойства пар сил:
1) Пары сил, лежащие в одной плоскости, эквивалентны, если их моменты численно равны и одинаковы по знаку.
2) Пару сил, не изменяя ее действия на твердое тело, можно переносить в любое место в плоскости ее действия, поворачивать ее плечо на любой угол, не изменяя величины ее момента и направления вращения.
3) Пары сил в пространстве эквивалентны, если их моменты геометрически равны.
4) Не изменяя действия пары сил на твердое
тело, пару сил можно переносить в любую
плоскость, параллельную плоскости ее
действия, а также изменять ее силы и
плечо, сохраняя неизменным модуль и
направление ее момента.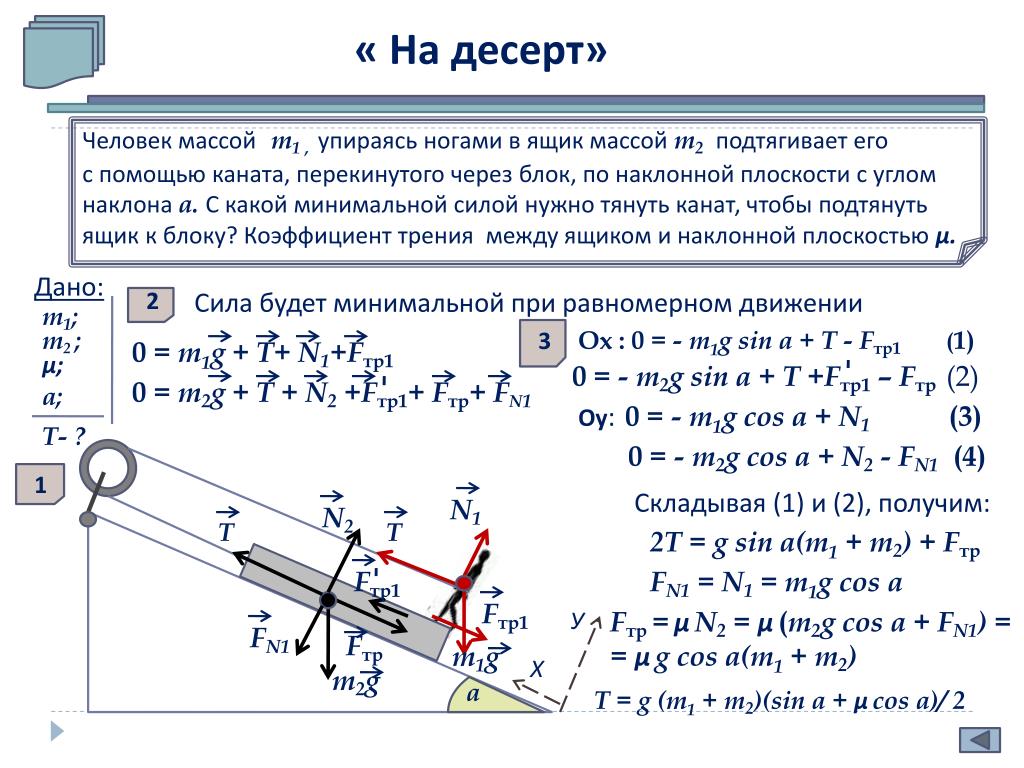 Таким образом,
вектор-момент пары можно переносить в
любую точку, т.е. вектор-момент пары сил
является свободным вектором.
Таким образом,
вектор-момент пары можно переносить в
любую точку, т.е. вектор-момент пары сил
является свободным вектором.
5) Геометрическая сумма моментов составляющих пар равна моменту эквивалентной им пары сил:
или
(5.7)
6) Пары сил, произвольно расположенные в пространстве, взаимно уравновешиваются в том случае, если геометрическая сумма их моментов равна нулю, т.е. условие равновесия пар сил в пространстве имеет вид:
(5.8)
7) Момент пары сил эквивалентной системе пар сил на плоскости, равен алгебраической сумме моментов составляющих пар:
(5.9)
8) Пары сил, расположенные в одной плоскости, взаимно уравновешиваются, если алгебраическая сумма их моментов равна нулю.
(5.10)
Т.е. выражение 5.10 является условием
равновесия пар сил на плоскости, а (5. 8)
– в пространстве.
8)
– в пространстве.
Вопросы для самоконтроля
Момент силы относительно точки
Что называется моментом силы относительно точки?
Как направлен вектор момента силы относительно точки?
Запишите формулу, по которой определяется алгебраический момент силы относительно точки.
Какой площадью можно определить числовое значение момента силы относительно заданной точки?
Изменится ли момент силы относительно данной точки при переносе силы вдоль линии ее действия?
В каком случае момент силы относительно данной точки равен нулю?
Определите геометрическое место точек пространства, относительно которых моменты данной силы:
геометрически равны;
равны по модулю.

Определите момент силы относительно точки O, если F=200H; OA=0.5м (рисунок 5.5).
Рисунок 5.5
9. Определить моменты сил и относительно координатных осей, если КН, КН, ОА = 0,4 м; ОВ = 0,6 м; ОС = 0,3 м (рисунок 5.5).
Объяснение урока: Момент силы относительно точки в 2D: векторы
В этом объяснении мы узнаем, как найти момент плоской системы сил, действующих на тело относительно точки, как вектор.
Мы знаем, что сила или система сил может оказывать вращательное действие на тело, которое описывается моментом
сила или система сил относительно точки. Напомним, что при плоском движении момент 𝑀 силы
⃑𝐹 о точке определяется как скаляр, величина которого определяется выражением
|𝑀|=‖‖⃑𝐹‖‖𝑑,⟂
где 𝑑⟂ — перпендикулярное расстояние между точкой и линией действия силы
⃑𝐹. Затем мы можем определить знак момента, рассмотрев, является ли эффект вращения
идет по часовой стрелке или против часовой стрелки. По соглашению мы определяем момент с действием против часовой стрелки как положительный,
что означает, что момент с эффектом вращения по часовой стрелке определяется как отрицательный.
По соглашению мы определяем момент с действием против часовой стрелки как положительный,
что означает, что момент с эффектом вращения по часовой стрелке определяется как отрицательный.
Хотя это определение хорошо подходит для плоского движения, оно недостаточно, когда мы рассматриваем движение с трехмерным пространство, потому что понятие записи по часовой стрелке или против часовой стрелки здесь не работает. Следовательно, мы хотели бы расширить определение момента для трехмерного движения из скалярного момента, определенного для плоского движения. Чтобы сохранить понятия ориентации вращения, мы определяем момент как вектор следующим образом.
Определение: момент силы
Момент силы ⃑𝐹, действующей на тело относительно точки 𝑂, определяется выражением 𝑀=⃑𝑟×⃑𝐹, где 𝑟 — вектор положения 𝐴, точки приложения силы ⃑𝐹.
В этом определении мы видим, что система координат выбрана так, что ее начало совпадает с точкой около
что мы принимаем момент.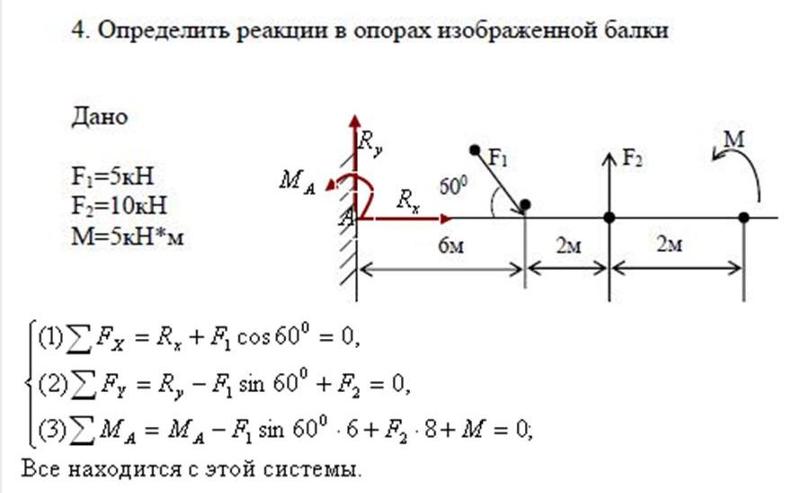 Если бы мы хотели вычислить момент силы ⃑𝐹 относительно точки
𝑃 это не источник, то мы просто заменим ⃑𝑟 на
𝑃𝐴:
𝑀=𝑃𝐴×⃑𝐹.
Если бы мы хотели вычислить момент силы ⃑𝐹 относительно точки
𝑃 это не источник, то мы просто заменим ⃑𝑟 на
𝑃𝐴:
𝑀=𝑃𝐴×⃑𝐹.
Буква 𝑃 была добавлена в качестве нижнего индекса к 𝑀, чтобы указать, что момент взят около точки 𝑃.
В нашем первом примере мы будем использовать эту формулу для вычисления векторного момента силы на плоскости относительно точки.
Пример 1. Нахождение момента вектора силы относительно точки
Если на точку действует сила ⃑𝐹=−5⃑𝑖+𝑚⃑𝑗 𝐴(7,3), определить момент ⃑𝐹 относительно точки 𝐵(7,−2).
Ответ
В этом примере нам нужно найти момент плоской силы относительно точки. Напомним, что векторный момент силы ⃑𝐹, действующий в точке 𝐴 относительно точки 𝐵, определяется выражением 𝑀=𝐵𝐴×⃑𝐹.
Начнем с нахождения вектора 𝐵𝐴: 𝐵𝐴=(7,3,0)−(7,−2,0)=(0,5,0).
Мы можем написать ⃑𝐹 как ⃑𝐹=−5⃑𝑖+𝑚⃑𝑗+0⃑𝑘=(−5,𝑚,0).
Взяв векторное произведение,
𝐵𝐴×⃑𝐹=||||⃑𝑖⃑𝑗⃑𝑘050−5𝑚0||||=(5×0−0×𝑚)⃑𝑖−(0×0−0×(−5))⃑𝑗+(0×𝑚−5×( −5))⃑𝑘=25⃑𝑘.
Заметим, что неизвестная константа 𝑚 в силе ⃑𝐹 сокращалась, когда мы вычислили перекрестное произведение. Следовательно, момент ⃑𝐹 относительно точки 𝐵 равен 25⃑𝑘.
В предыдущем примере мы вычислили векторный момент плоской силы относительно точки по формуле 𝑀=⃑𝑟×⃑𝐹.
Мы видим, что результирующий вектор векторного произведения содержит только компонент ⃑𝑘,
а компоненты ⃑𝑖 и ⃑𝑗 исчезли. Это не
удивительно, если мы рассмотрим геометрическое свойство перекрестного произведения. Напомним, что вектор, полученный в результате перекрестного произведения
двух векторов должны быть перпендикулярны двум векторам. Поскольку 𝑀 определяется как крест
произведение векторов ⃑𝑟 и ⃑𝐹, оно должно быть перпендикулярно обоим
векторы. Мы знаем, что ⃑𝑟 и ⃑𝐹 оба лежат на
𝑥𝑦-плоскость, поэтому 𝑀 должна быть перпендикулярна 𝑥𝑦-плоскости. Вектор, перпендикулярный плоскости 𝑥𝑦, должен быть параллелен единичному вектору
⃑𝑘 в трехмерной системе координат. Это означает
⃑𝑟×⃑𝐹=𝑐⃑𝑘
для некоторого скаляра 𝑐. Поскольку это всегда так, мы можем упростить вычисление этого перекрестного произведения на
используя двумерное перекрестное произведение.
Это означает
⃑𝑟×⃑𝐹=𝑐⃑𝑘
для некоторого скаляра 𝑐. Поскольку это всегда так, мы можем упростить вычисление этого перекрестного произведения на
используя двумерное перекрестное произведение.
Определение: двумерное перекрестное произведение
Для двух двумерных векторов (𝑎,𝑏) и (𝑐,𝑑), двумерное перекрестное произведение определяется как (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.
Как мы видим, двумерное перекрестное произведение вычисляется быстрее. Мы будем использовать эту формулу для вычисления перекрестного произведения двухмерных векторы для оставшейся части этого объяснения.
Далее обсудим величину момента, которая равна величине векторного произведения: ‖‖𝑀‖‖=‖‖⃑𝑟×⃑𝐹‖‖.
Напомним, что перекрестное произведение двух векторов дает площадь параллелограмма, две смежные стороны которого образованы два вектора. Проследим это, используя следующую схему.
На приведенной выше диаграмме площадь выделенной области представляет собой величину векторного произведения ⃑𝑟×⃑𝐹 и, следовательно, величину момента 𝑀. Мы также можем найти площадь этого параллелограмма геометрически, используя геометрическую формулу
длина основанияперпендикулярвысота×.
Мы также можем найти площадь этого параллелограмма геометрически, используя геометрическую формулу
длина основанияперпендикулярвысота×.
На схеме основание этого параллелограмма образовано вектором ⃑𝐹, а высота равна перпендикулярное расстояние от начала координат до линии действия ⃑𝐹, которое обозначается 𝑑⟂.
Это приводит к следующей формуле для величины векторного момента для двумерной силы относительно точки.
Свойство: Величины векторного момента силы
Величина векторного момента плоской силы ⃑𝐹 относительно точки определяется выражением ‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝑑,⟂ где 𝑑⟂ — перпендикулярное расстояние между точкой и линией действия силы ⃑𝐹.
Мы видим, что приведенная выше величина векторного момента равна величине скалярного момента. Следовательно, величина векторного момента согласуется с величиной скалярного момента для плоского движения.
Когда мы переформулируем это уравнение, мы получим полезную формулу для вычисления перпендикулярного расстояния между точкой и линией
действия силы.
Формула: Расстояние по перпендикуляру между точкой и линией действия
Пусть 𝑀 векторный момент силы или системы сил на плоскости относительно точки. Тогда перпендикулярное расстояние между точкой и линией действия силы определяется выражением 𝑑=‖‖𝑀‖‖‖‖⃑𝐹‖‖.⟂
В следующем примере мы вычислим момент плоской силы относительно точки, а затем воспользуемся этой формулой, чтобы найти перпендикулярное расстояние между точкой и линией действия силы.
Пример 2. Нахождение вектора момента силы, действующей в точке, и перпендикуляра между моментом и линией Действие Силы
Учитывая, что сила ⃑𝐹=4⃑𝑖−3⃑𝑗 действует через точки 𝐴(3,6), определить момент 𝑀 относительно происхождение 𝑂 силы ⃑𝐹. Кроме того, вычислить перпендикуляр расстояние 𝐿 между 𝑂 и линией действия силы.
Ответ
В этом примере сначала нужно найти момент 𝑀 относительно 𝑂 силы
⃑𝐹, а затем рассчитайте перпендикулярное расстояние между 𝑂 и линией
действие ⃑𝐹.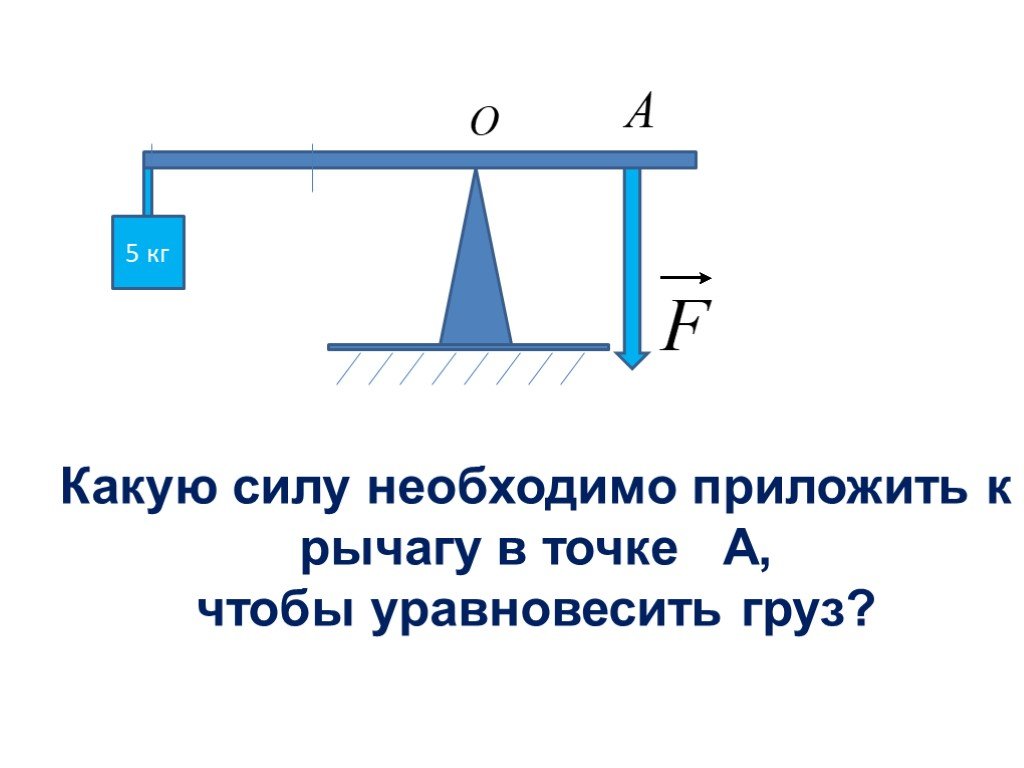 Начнем с поиска момента. Напомним, что векторный момент силы
⃑𝐹, действующий в точке 𝐴 относительно начала координат 𝑂, определяется выражением
𝑀=𝑂𝐴×⃑𝐹.
Начнем с поиска момента. Напомним, что векторный момент силы
⃑𝐹, действующий в точке 𝐴 относительно начала координат 𝑂, определяется выражением
𝑀=𝑂𝐴×⃑𝐹.
Нам даны координаты 𝐴, значит, 𝑂𝐴 — это позиция вектор, заданный 𝑂𝐴=(3,6).
Мы можем записать ⃑𝐹 в компонентной форме как ⃑𝐹=4⃑𝑖−3⃑𝑗=(4,−3).
Теперь мы готовы вычислить перекрестное произведение 𝑂𝐴×⃑𝐹. Напомним, что векторное произведение двумерных векторов определяется формулой (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.
Применяя эту формулу, получаем 𝑂𝐴×⃑𝐹=(3,6)×(4,−3)=(3×(−3)−6×4)⃑𝑘=−33⃑𝑘.
Следовательно, момент ⃑𝐹 относительно начала координат равен −33⃑𝑘.
Далее найдем перпендикулярное расстояние между началом координат и линией действия для ⃑𝐹. Напомним, что модуль векторного момента плоской силы ⃑𝐹 относительно точки определяется выражением
‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝐿,
где 𝐿 — перпендикулярное расстояние между точкой и линией действия силы
⃑𝐹. Мы можем изменить это уравнение, чтобы написать
𝐿=‖‖𝑀‖‖‖‖⃑𝐹‖‖.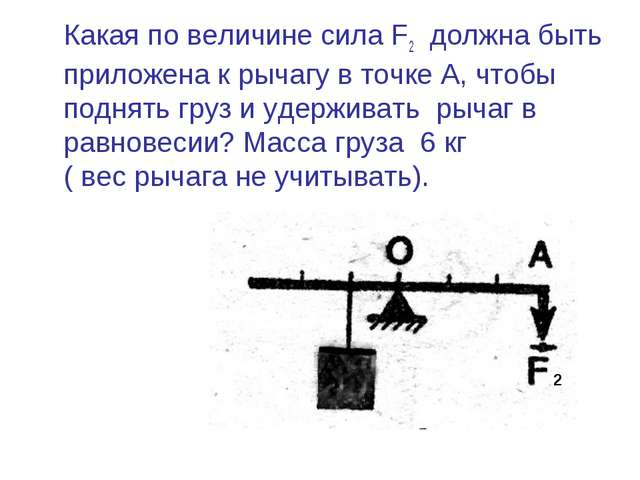
Поскольку мы знаем, что 𝑀=−33⃑𝑘, мы можем получить ‖‖𝑀‖‖=33. Найдем ‖‖⃑𝐹‖‖: ‖‖⃑𝐹‖‖=4+(−3)=√25=5.
Подставив эти значения в формулу для 𝐿, получим 𝐿=335=6,6.
Следовательно, 𝑀=−33⃑𝑘,𝐿=6.6.lengthunits
Мы отметили, что момент силы относительно точки приводит к вектору, параллельному единичному вектору ⃑𝑘. Другими словами, существует некоторый скаляр 𝑐 такой, что 𝑀=𝑐⃑𝑘.
Кроме того, мы заметили, что величина момента равна величине скалярного момента |𝑀|. Это означает, что либо 𝑐=𝑀, либо 𝑐=−𝑀. Чтобы определить, какой из них верен, нам нужно проверить, соответствует ли знак 𝑐 знаку скалярного момента. 𝑀.
Свойства векторного произведения позволяют нам сначала заключить, что 𝑀 является вектором, перпендикулярным
плоскость, определяемая ⃑𝑟 и ⃑𝐹. Направление
𝑀 определяется по правилу правой руки. Это правило иногда объясняют ссылкой на вращение
винта: направление вектора ⃑𝐴×⃑𝐵 соответствует
направление движения (вверх или вниз) крышки бутылки или гайки, которое можно было бы повернуть в том же направлении вращения, что и при переходе от
от ⃑𝐴 до ⃑𝐵, как показано на следующей диаграмме.
Помните, что у нас есть 𝑀=⃑𝑟×⃑𝐹=𝑐⃑𝑘.
Если 𝑐>0, вектор момента будет выходить из плоскости (вверх), что соответствует направлению против часовой стрелки вращение в соответствии с рисунком выше. Если 𝑐0, то вектор момента ушел бы в плоскость (вниз), что указывает на вращение по часовой стрелке. Напомним, что для скалярного момента 𝑀 ориентация против часовой стрелки соответствует к положительному знаку, а вращение по часовой стрелке приводит к отрицательному знаку. Это говорит нам о том, что знак скалярного момента 𝑀 согласуется со знаком скаляра 𝑐. Таким образом, мы показали, что 𝑐=𝑀.
Свойство: двумерный векторный момент силы
Пусть 𝑀 и 𝑀 будут скалярным и векторным моментами силы или системой сил, на плоскости около точки. Затем, 𝑀=𝑀⃑𝑘.
Это свойство твердо устанавливает, почему этот векторный момент является разумным расширением скалярного момента для плоской силы. Кроме того, векторный момент можно обобщить, чтобы представить момент общей трехмерной силы относительно точки, поскольку он получен
используя перекрестное произведение.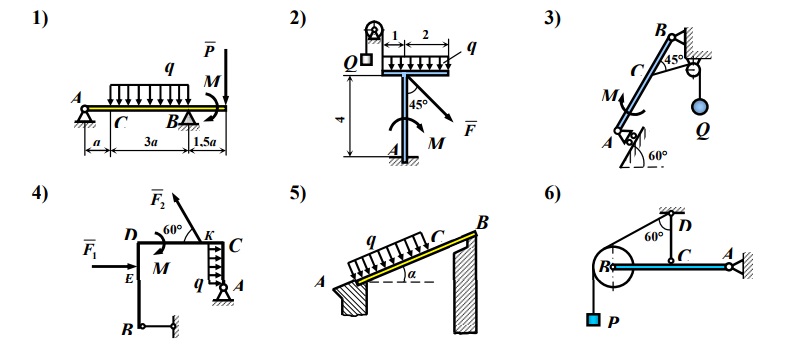
Из этого свойства можно сделать несколько полезных выводов. Во-первых, мы знаем, что скалярный момент не зависит от положение точки, на которую действует сила, если точка лежит на одной линии действия силы. Это потому что скалярный момент получается только с использованием величины силы ‖‖⃑𝐹‖‖ и перпендикулярное расстояние 𝑑⟂. Это означает, что векторный момент также не зависит от местоположения точки, на которую действует сила. Мы сможем понять это лучше, если сравним величину момента, когда мы переместите эту точку вдоль линии действия.
Мы видим, что площади обоих параллелограммов равны, так как длина основания
‖‖⃑𝐹‖‖ и высота 𝑑⟂ одинаковы для обоих
параллелограммы. Это говорит нам о том, что величина момента для этих двух систем одинакова. Кроме того, мы можем видеть
что обе системы будут вызывать вращение по часовой стрелке вокруг начала координат, а это означает, что знак момента будет одинаковым для
обе системы. Следовательно, векторный момент одинаков для этих двух систем. Это приводит к следующему полезному свойству.
Это приводит к следующему полезному свойству.
Свойство: Векторный момент силы
Векторный момент 𝑀 силы относительно точки не зависит от точки, в которой сила действует до тех пор, пока точка лежит на одной линии действия.
В следующем примере мы найдем векторный момент плоской силы относительно точки, когда начальная точка 𝐴 не дается.
Пример 3. Определение момента вектора силы, действующего в точке
Конец 𝐴 из 𝐴𝐵 находится в точке (−6,7) и 𝐴𝐵 имеет середину 𝐷(−7,1). Если линия действия силы ⃑𝐹=−2⃑𝑖−6⃑𝑗 делит пополам 𝐴𝐵, определить момент ⃑𝐹 относительно точки 𝐵.
Ответ
В этом примере нам нужно найти момент плоской силы относительно точки. Напомним, что векторный момент силы ⃑𝐹, действующий в точке 𝑃 относительно точки 𝑂, определяется выражением 𝑀=𝑂𝑃×⃑𝐹.
Хотя нам не известна точка, в которой действует сила, нам известно, что линия действия силы
⃑𝐹 делит 𝐴𝐵 пополам.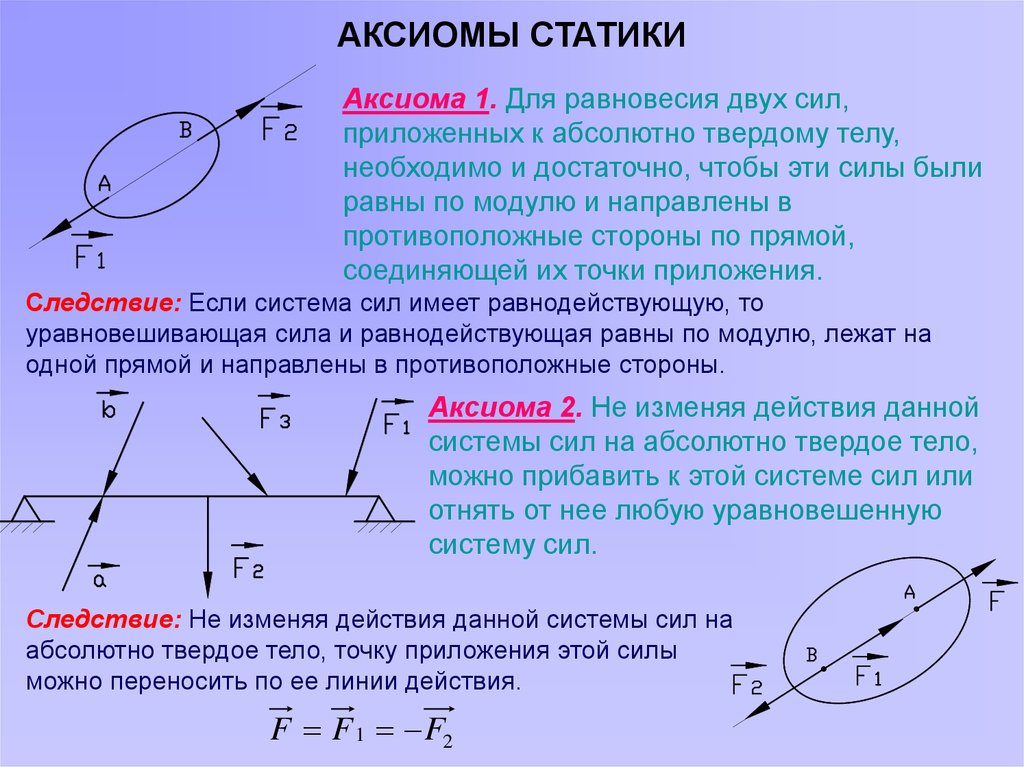 Это означает, что линия действия
проходит через середину 𝐷 отрезка 𝐴𝐵. Напомним, что векторный момент
𝑀 силы, приложенной к точке, не зависит от начальной точки, если точка лежит
в той же линии действия. Следовательно, мы можем вычислить момент, считая, что начальная точка находится в точке
𝐷(−7,1). Это означает, что момент ⃑𝐹 о
𝐵 дается
𝑀=𝐵𝐷×⃑𝐹.
Это означает, что линия действия
проходит через середину 𝐷 отрезка 𝐴𝐵. Напомним, что векторный момент
𝑀 силы, приложенной к точке, не зависит от начальной точки, если точка лежит
в той же линии действия. Следовательно, мы можем вычислить момент, считая, что начальная точка находится в точке
𝐷(−7,1). Это означает, что момент ⃑𝐹 о
𝐵 дается
𝑀=𝐵𝐷×⃑𝐹.
Начнем с поиска вектора 𝐵𝐷. Так как 𝐷 является серединой 𝐴, мы знаем, что ‖‖𝐴𝐷‖‖=‖‖𝐵𝐷‖‖.
Также эти векторы имеют противоположное направление, а значит 𝐵𝐷=−𝐴𝐷.
Мы можем найти 𝐴𝐷, используя координаты точек 𝐴 и 𝐷: 𝐴𝐷=(−7,1)−(−6,7)=(−1,−6).
Следовательно, 𝐵𝐷=-(-1,-6)=(1,6).
Теперь мы готовы вычислить векторное произведение 𝐵𝐷×⃑𝐹. Напомним, что векторное произведение двумерных векторов определяется формулой (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.
Применяя эту формулу, получаем 𝐵𝐷×⃑𝐹=(1,6)×(−2,−6)=(1×(−6)−6×(−2))⃑𝑘=6⃑𝑘.
Следовательно, момент ⃑𝐹 относительно точки 𝐵 равен 6⃑𝑘.
В следующем примере мы найдем момент системы плоских сил, действующих в одной точке относительно другой точки, сначала найти равнодействующую сил.
Пример 4: Расчет момента трех сил, действующих на одну точку относительно данной точки, и расстояния между точками
Учитывая, что ⃑𝐹=−2⃑𝑖+2⃑𝑗, ⃑𝐹=−3⃑𝑖−⃑𝑗, и ⃑𝐹=⃑𝑖−4⃑𝑗 действуют в точке 𝐴(2,3), определить момент ⃑𝑚 равнодействующей сил относительно точки 𝐵(−2,−1) и вычислить длину перпендикулярной линии 𝐿 соединение точки 𝐵 с результирующей линией действия.
Ответ
В этом примере нам дана система плоских сил, действующих в одной и той же точке. Начнем с нахождения равнодействующей
силы. Напомним, что равнодействующая системы сил, действующих в одной точке, равна сумме всех векторов сил в
система. Следовательно, результирующая ⃑𝐹 определяется выражением
⃑𝐹=⃑𝐹+⃑𝐹+⃑𝐹=−2⃑𝑖+2⃑𝑗+−3⃑𝑖−⃑𝑗+⃑𝑖−4⃑𝑗=−2⃑𝑖−3⃑ 𝑖+⃑𝑖+2⃑𝑗−⃑𝑗−4⃑𝑗=−4⃑𝑖−3⃑𝑗.
Это говорит нам о том, что равнодействующая сил равна ⃑𝐹=−4⃑𝑖−3⃑𝑗. Далее найдем момент ⃑𝑚 равнодействующей около точки 𝐵(−2,−1). Напомним, что векторный момент силы ⃑𝐹, действующей в точке 𝐴 о точке 𝐵 дается 𝑀=𝐵𝐴×⃑𝐹.
Используя координаты 𝐴 и 𝐵, мы можем найти 𝐵𝐴=(2,3)−(−2,−1)=(4,4).
Теперь мы готовы вычислить перекрестное произведение 𝐵𝐴×⃑𝐹. Напомним, что перекрестное произведение двумерных векторов определяется выражением (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.
Это приводит к 𝐵𝐴×⃑𝐹=(4,4)×(−4,−3)=(4×(−3)−4×(−4))⃑𝑘=4⃑𝑘.
Следовательно, момент равнодействующей сил относительно точки 𝐵 равен 4⃑𝑘.
Далее найдем длину перпендикуляра 𝐿, соединяющего точку 𝐵 с
результирующая линия действия. Эта длина 𝐿 также известна как перпендикулярное расстояние между точкой
𝐵 и результирующая линия действия. Чтобы вычислить эту длину, вспомним, что величина
векторный момент плоской силы ⃑𝐹 относительно точки определяется выражением
‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝐿,
где 𝐿 — перпендикулярное расстояние между точкой и линией действия для ⃑𝐹. Мы можем изменить это уравнение, чтобы написать
𝐿=‖‖𝑀‖‖‖‖⃑𝐹‖‖.
Мы можем изменить это уравнение, чтобы написать
𝐿=‖‖𝑀‖‖‖‖⃑𝐹‖‖.
Поскольку мы знаем, что 𝑀=4⃑𝑘, мы можем получить ‖‖𝑀‖‖=4. Найдем ‖‖⃑𝐹‖‖: ‖‖⃑𝐹‖‖=(−4)+(−3)=√25=5.
Подставляя эти значения в формулу для 𝐿, получаем 𝐿=45=0,8.
Следовательно, 𝑀=4⃑𝑘,𝐿=0,8.lengthunit
В предыдущем примере мы нашли момент системы плоских сил, действующих в той же точке относительно другой точки. Мы можем отметить что процесс нахождения момента для системы сил такой же, как и для одной силы, если силы действуют в тот же пункт.
Рассмотрим теперь задачу нахождения момента системы плоских сил, когда силы не действуют в одной и той же точке.
Определение: Момент системы плоских сил
Рассмотрим систему сил ⃑𝐹, ⃑𝐹, …,
и ⃑𝐹, действующий в 𝐴, 𝐴, …,
и 𝐴 соответственно. Чтобы найти момент этой системы сил относительно точки 𝑂, найдем
нужно найти моменты 𝑀, 𝑀, …,
и 𝑀 сил ⃑𝐹, ⃑𝐹,
…, и ⃑𝐹 о пункте 𝑂.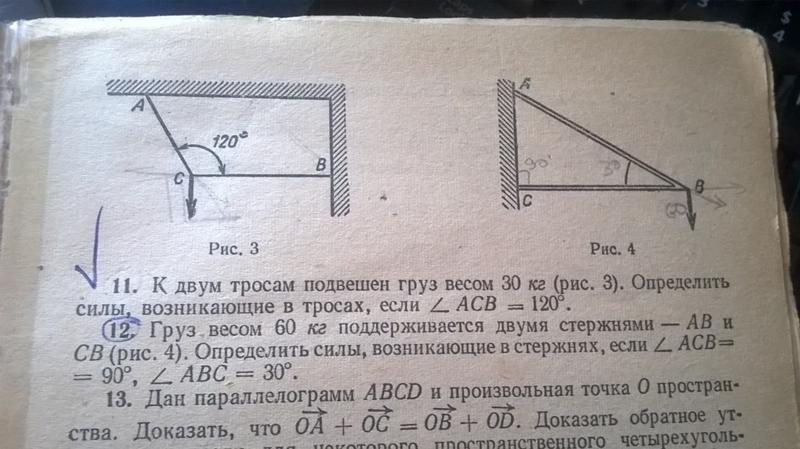 Тогда, момент
система 𝑀 относительно точки 𝑂 задается формулой
𝑀=𝑀+𝑀+⋯+𝑀.
Тогда, момент
система 𝑀 относительно точки 𝑂 задается формулой
𝑀=𝑀+𝑀+⋯+𝑀.
Это определение говорит нам, что момент системы сил равен сумме отдельных моментов каждой силы в система примерно в том же месте.
В нашем последнем примере мы найдем неизвестные константы сил в системе, действующей в разных точках, когда нам задано момент системы сил относительно двух различных точек.
Пример 5. Нахождение неизвестных компонентов двух сил по сумме их моментов относительно двух точек 𝐹 и ⃑𝐹 — две силы, действующие в точках 𝐴(3,1) и 𝐵(−1,−1) соответственно. Сумма моментов относительно точки начала равна нулю. сумма моментов относительно точки 𝐶(1,2) также равна нулю. Определите значения 𝑚 и 𝑛.
Ответ
В этом примере нам нужно найти неизвестные константы 𝑚 и 𝑛 в силах
⃑𝐹 и ⃑𝐹, когда нам известно, что сумма
моменты двух сил относительно начала координат, а также относительно точки 𝐶 равны нулю. Мы можем найти
неизвестные константы путем идентификации пары одновременных уравнений с участием 𝑚 и 𝑛. Мы получим первое уравнение, вычислив сумму моментов ⃑𝐹 и
⃑𝐹 о происхождении и приравнивании их к нулю.
Мы можем найти
неизвестные константы путем идентификации пары одновременных уравнений с участием 𝑚 и 𝑛. Мы получим первое уравнение, вычислив сумму моментов ⃑𝐹 и
⃑𝐹 о происхождении и приравнивании их к нулю.
Напомним, что векторный момент силы ⃑𝐹, действующей в точке 𝑃 относительно точка 𝑄 задается 𝑀=⃑𝑟×⃑𝐹, где ⃑𝑟 — вектор из точки 𝑄 в точку 𝑃. Давайте сначала найдите момент ⃑𝐹 о происхождении. С ⃑𝐹 действует в точке 𝐴, мы можем написать ⃑𝑟=𝑂𝐴=(3,1).
Мы можем записать ⃑𝐹 в компонентной форме как ⃑𝐹=𝑚⃑𝑖+⃑𝑗=(𝑚,1).
Теперь мы готовы вычислить перекрестное произведение 𝑂𝐴×⃑𝐹. Напомним, что перекрестное произведение двумерных векторов определяется выражением (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.
Это приводит к ⃑𝑟×⃑𝐹=(3,1)×(𝑚,1)=(3×1−1×𝑚)⃑𝑘=(3−𝑚)⃑𝑘.
Далее найдем момент ⃑𝐹 относительно начала координат . С ⃑𝐹
действует в точке 𝐵, мы можем написать
⃑𝑟=𝑂𝐵=(−1,−1).
Мы можем записать ⃑𝐹 в компонентной форме как ⃑𝐹=𝑛⃑𝑖−5⃑𝑗=(𝑛,−5).
Взяв векторное произведение, ⃑𝑟×⃑𝐹=(−1,−1)×(𝑛,−5)=(−1×(−5)−(−1)×𝑛)⃑𝑘=(5+𝑛)⃑𝑘.
Тогда сумма этих двух моментов относительно начала координат равна (3−𝑚)⃑𝑘+(5+𝑛)⃑𝑘=(8−𝑚+𝑛)⃑𝑘.
Так как нам дано, что сумма этих моментов должна равняться нулю, то получаем
| 8−𝑚+𝑛=0. | (1) |
Это дает нам одно уравнение, включающее 𝑚 и 𝑛. Мы можем повторить это вычисление на данный момент о точке 𝐶, чтобы получить другое уравнение, но мы также можем найти второе уравнение, используя свойства моменты. Найдем момент ⃑𝐹 относительно точки 𝐶: ⃑𝑟=𝐶𝐴=(3,1)−(1,2)=(2,−1).
Взяв векторное произведение, ⃑𝑟×⃑𝐹=(2,−1)×(𝑚,1)=(2×1−(−1)×𝑚)⃑𝑘=(2+𝑚)⃑𝑘.
Далее, на момент ⃑𝐹 о 𝐶, ⃑𝑟=𝐶𝐵=(−1,−1)−(1,2)=(−2,−3).
Взяв векторное произведение, ⃑𝑟×⃑𝐹=(−2,−3)×(𝑛,−5)=(−2×(−5)−(−3)×𝑛)⃑𝑘=(10+3𝑛)⃑𝑘.
Суммируя эти два моменты про 𝐶,
(2+𝑚)⃑𝑘+(10+3𝑛)⃑𝑘=(12+𝑚+3𝑛)⃑𝑘.
Так как нам дано, что сумма этих моментов должна равняться нулю, то получаем
| 12+𝑚+3𝑛=0. | (2) |
Теперь, когда мы получили два уравнения для 𝑚 и 𝑛, напишем уравнения (1) и (2) здесь: 8−𝑚+𝑛=0,12+𝑚+3𝑛=0.
Мы можем сложить два уравнения, чтобы исключить 𝑚. Это ведет к 20+4𝑛=0.
Преобразование этого уравнения таким образом, что 𝑛 является субъектом, дает нам 𝑛=−5. Мы можем заменить это значение в уравнение (1), чтобы записать 8−𝑚−5=0.
Преобразование этого уравнения таким образом, что 𝑚 является субъектом, приводит к 𝑚=3. Следовательно, у нас есть 𝑚=3,𝑛=−5.
Давайте закончим повторением нескольких важных понятий из этого объяснения.
Ключевые точки
- Вектор момента силы ⃑𝐹, действующей в точке 𝐴 относительно точки 𝑂 дается 𝑀=⃑𝑟×⃑𝐹, где ⃑𝑟 — вектор из точки 𝑂 в точку 𝐴.
- Величина векторного момента плоской силы ⃑𝐹 относительно точки определяется выражением
‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝑑,⟂
где 𝑑⟂ — перпендикулярное расстояние между точкой и линией действия силы
⃑𝐹.

- Векторный момент 𝑀 силы относительно точки не зависит от начальной точки, пока точка лежит на одной линии действия.
- Пусть 𝑀 и 𝑀 — скалярный и векторный моменты силы, или система сил на плоскости относительно точки. Затем, 𝑀=𝑀⃑𝑘.
- Вычисление перекрестного произведения ⃑𝑟×⃑𝐹 для вычисления момент 𝑀 плоской силы относительно точки можно упростить, используя двумерное перекрестное произведение, которое определяется формулой (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.
- Рассмотрим систему сил ⃑𝐹, ⃑𝐹, …, и ⃑𝐹 действующие в 𝐴, 𝐴, … и 𝐴 соответственно. Чтобы найти момент этой системы сил относительно точки 𝑂, нужно найти моменты 𝑀, 𝑀, … и 𝑀 сил ⃑𝐹, ⃑𝐹, …, и ⃑𝐹 о пункте 𝑂. Тогда, момент система 𝑀 относительно точки 𝑂 задается формулой 𝑀=𝑀+𝑀+⋯+𝑀.
Счет, математика и статистика — Набор академических навыков
Моменты (механика)
ContentsToggle Main Menu 1 Моменты 2 Рабочий пример: нахождение момента 3 Рабочий пример: нахождение момента, когда заданное расстояние не перпендикулярно 4 Рабочий пример: тела покоятся в равновесии
Моменты
Вращающее действие силы на тело, на которое она действует, измеряется моментом силы.
Момент силы зависит от величины силы и расстояния от оси вращения.
Момент силы относительно точки равен (величине силы) $\times$ (перпендикулярному расстоянию линии действия силы от точки).
При наличии нескольких сил, действующих на тело, моменты относительно точки могут складываться, если указано положительное направление (по часовой стрелке или против часовой стрелки) и учитывается для каждого момента.
Работал Пример: Нахождение момента 9{\circ}), \\ &= 64,241\mathrm{Нм} \text{ (до 3д.п.).} \end{align} Момент силы измеряется в ньютон-метрах $\mathrm{Н м }$, поэтому момент $F$ относительно $P$ равен $64,241\mathrm{Nm}$.
Сумма моментов
На схеме показан набор сил, действующих на световой стержень. Вычислите сумму моментов относительно точки $P$.
Решение
Каждая сила уже перпендикулярна точке $P$.
Момент силы $6\mathrm{N}$ равен $6 \times 2 = 12 \mathrm{N m}$ против часовой стрелки.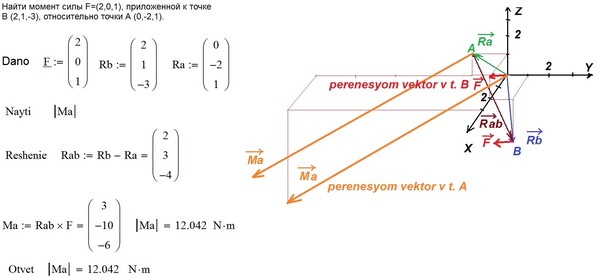
Момент силы $14\mathrm{N}$ равен $14 \times 2 = 28 \mathrm{N m}$ по часовой стрелке.
Момент силы $5\mathrm{N}$ равен $5 \times (2+3) = 25 \mathrm{Nm}$ против часовой стрелки.
Всего по часовой стрелке $= 28 \mathrm{N m}$ и всего против часовой стрелки $= 37 \mathrm{Nm}$. Следовательно, сумма моментов равна $37 — 28 = 9 \mathrm{Nm}$ против часовой стрелки. Поскольку сумма против часовой стрелки была больше, мы выбрали против часовой стрелки в качестве положительного направления.
Рабочий пример: нахождение момента, когда заданное расстояние не перпендикулярно 9{\circ}), \\ & = 66,684 \mathrm{Nm} \text{ против часовой стрелки (3 д.п.).} \end{align}
Рабочий пример: Тела, находящиеся в равновесии
Нахождение нормальных реакций
Предположим, что имеется однородный стержень длины $9\mathrm{m}$ и веса $30\mathrm{N}$. Он опирается на опору $X$ одним концом и опору $Y$, которая находится на расстоянии $5\mathrm{m}$ от опоры $X$. Рассчитайте величину реакции на каждой из опор.
Решение
Мы можем нарисовать схему, показывающую все действующие силы.
Вес стержня будет действовать в его центре масс — так как это однородный стержень, вес действует в средней точке. Стержень находится в равновесии, поэтому суммарные силы, действующие вверх, будут равны суммарным силам, действующим вниз, когда мы разрешим вертикально. \begin{equation} R_X + R_Y = 30. \end{equation} Рассмотрим моменты относительно точки $X$, мы имеем, что моменты по часовой стрелке будут равны моментам против часовой стрелки, поэтому \begin{align} 30 \times 4.5 & = R_Y \times ( 4,5 + 0,5), \\ 135 & = 5R_Y, \\ 27 \mathrm{N} & = R_Y. \end{align} Теперь мы можем использовать это значение, чтобы найти $R_X$ \begin{align} R_X + R_Y & = 30, \\ R _ X & = 30 — 27, \\ & = 3 \mathrm{N}. \end{align} Следовательно, реакция в точке $X$ равна $3 \mathrm{N}$, а реакция в точке $Y$ равна $27\mathrm{N}$.
Нахождение центра масс неоднородного тела
Предположим, что имеется неоднородный стержень $AB$ длины $10\mathrm{m}$ и веса $15\mathrm{N}$.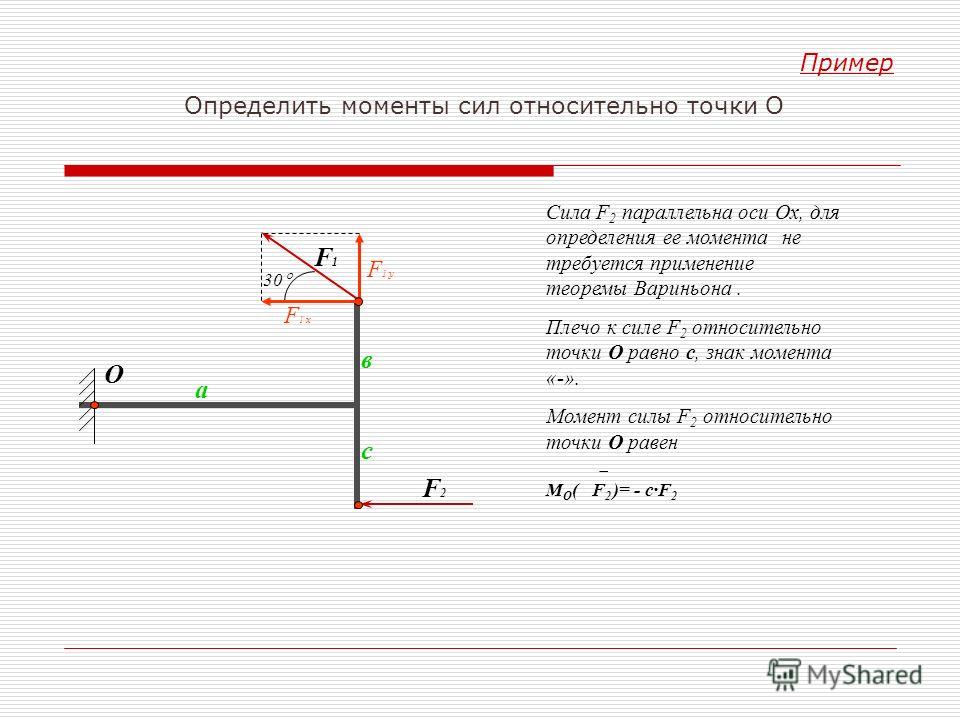

 ..+ M’n — сумма моментов сил, поворачивающих рычаг против часовой стрелке [Н*м]
..+ M’n — сумма моментов сил, поворачивающих рычаг против часовой стрелке [Н*м]

Leave A Comment