Шар объем которого равен 37 п вписан в куб найдите объем куба: Шар, объем которого равен 37п, вписан в куб… — Задание 8 ЕГЭ по математике (Стереометрия)

Шар в заданиях ЕГЭ — презентация онлайн

Шар
в заданиях
ЕГЭ

2. Содержание

Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
• Задачи
Задача №8
Задача №9
Задача №10
Задача №11
Задача №12
Задача №13
Задача №`4
Задача №15
Задача №16
Задача №17
Задача №18
для самостоятельного решения

3. Задача №1

Площадь большого круга шара равна 3. Найдите площадь
поверхности шара
Радиус большого круга является радиусом шара.
Площадь
первого
выражается
через
радиус
как
Skp.=πR², а площадь
поверхности сферы – как Sш.= 4πR². Видно, что
площадь поверхности шара в
4 раза больше
площади поверхности большого круга. Значит
Sш.= 4·3 = 12

4. Задача №2

Во сколько раз увеличится площадь поверхности шара,
если радиус шара увеличить в 2 раза?
Площадь
поверхности
шара
выражается
через
его
радиус
формулой Sш. = 4πR², поэтому при
увеличении радиуса вдвое площадь
увеличится в 22 = 4 раза.

5. Задача №3

Во сколько раз увеличится объем шара, если его радиус
увеличить в три раза?
Т.к. объём шара вычисляется по формуле:
V = 4/3·π·r³, то
при увеличении радиуса втрое, объем
шара увеличится в 27 раз.

6. Задача №4

Объем одного шара в 27 раз больше объема второго. Во
сколько раз площадь поверхности первого шара больше
площади поверхности второго?
Решение. 1) Объемы шаров соотносятся как
V1:V2= R1³: R2³= (R1/R2)³=27 => R1/R2 =3
2) Площади их поверхностей соотносятся как
S1:S2= R1²: R2²= (R1/R2)²=3²=9

7. Задача №5

Даны два шара. Диаметр первого шара в 8 раз больше
диаметра второго. Во сколько раз площадь поверхности
первого шара больше площади поверхности второго?
S1:S2= R1²: R2²= (R1/R2)²=(d1/d2)²=8²=64

8. Задача №6

Однородный шар диаметром 3 см имеет массу 162 грамма.
Чему равна масса шара, изготовленного из того же
материала, с диаметром 2 см? Ответ дайте в граммах.
Масса шара прямо пропорциональна
его объёму. Объёмы шаров относятся
как кубы их радиусов:
V1:V2= R1³: R2³= (R1/R2)³= (d1/d2)²=(2/3)³=8/27
= m1/m2
Следовательно, масса
168·(8/27)= 48 грамм.
второго,
меньшего
шара
равна

9. Задача №7

Даны два шара с радиусами 8 и 4. Во сколько раз площадь
поверхности первого шара больше площади поверхности
второго?
Решение. Т.к. Площадь поверхности шара вычисляется по
формуле: S = 4π·r², то
1) Найдём площадь поверхности первого шара: 256π
2) Найдём площадь поверхности второго шара: 64π
3) Найдём отношение площадей:
256π : 64π = 4

10. Задача №8

Даны два шара с радиусами 2 и 1. Во сколько раз объём
первого шара больше объёма второго?
Решение. Т.к. объём шара вычисляется по формуле:
V = 4/3·π·r³, то
1) Найдём объём первого шара: 4/3·8π
2) Найдём объём второго шара: 4/3·π
3) Найдём отношение объёмов: 4/3·8π : 4/3·π = 8

11. Задача №9

Шар, объём которого равен 6π, вписан в куб. Найдите
объём куба.
Ребро куба равно двум радиусам вписанного
в куб шара, поэтому объем куба,
выраженный через радиус вписанного в него
шара, находится по формуле Vk.=(2R)³= 8R³
Объём шара вычисляется по формуле
V= 4/3·πR³ и это равно 6π.
Значит 4/3·πR³= 6π => R³=18π/4π =9/2.
Тогда Vk.= 8R³= 8·(9/2)=36

12. Задача №10

В куб с ребром 3 вписан шар. Найдите объем этого шара,
деленный на π .
Радиус вписанного в куб шара равен
половине длины ребра:
R=a:2=3:2=1,5
3
4 3 4 3
4 27
9
V R 4,5
3
3 2
3 8
2

13. Задача №11

Объем шара равен 288π. Найдите площадь его
поверхности, деленную на π .
Из формулы объёма шара V = 4/3·π·r³
выразим радиус и вычислим его:
3
V
3
288
R 3
3
6
4
4
Тогда площадь поверхности шара будет равна
S = 4π·r² = 4π·36=144π

14. Задача №12

Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара,
объем которого равен сумме их объемов.
Объёма шара V = 4/3·π·r³
Поэтому cумма объёмов трёх шаров равна
4
4
4
4
3
3
3
6 8 10 (6 3 8 3 10 3 )
3
3
3
3
4
4
4
3
3
3
3
3
3
2 (3 4 5 ) 2 6 12 3
3
3
3
Значит искомый радиус равен 12.

15. Задача №13

Около куба с ребром √3 описан шар. Найдите объем
этого шара, деленный на π .
Пусть длина ребра куба равна а, а его
диагональ равна d. Радиус описанного
шара R равен половине диагонали куба:
1
1
1
3
R d a 3
3 3
2
2
2
2
3
4 3 4 3
9
V R
3
3 2
2
Ответ: 4,5

16. Задача №14

Радиусы двух шаров равны 6, 8. Найдите радиус шара,
площадь поверхности которого равна сумме площадей их
поверхностей.
Из условия S3=S1+S2 и S = 4π·r²
найдём
4 R 4 R 4 R
2
3
2
1
2
2
R3 R R 36 64 10
2
1
2
2

17. Задача №15

Вершина А куба ABCDA1B1C1D1 со стороной 1,6 является
центром сферы, проходящей через точку A1. Найдите
площадь S части сферы, содержащейся внутри куба. В
ответе запишите величину S/π .
Решение. Так как одна из вершин куба является центром
сферы с радиусом, меньшим либо равным стороне куба,
в кубе содержится 1/8 сферы и, соответственно, 1/8 ее
поверхности, равная
1
1
2
2
S 4 R 1,6 1,28
8
8
2

18. Задача №16

Середина ребра куба со стороной 1,9 является центром
шара радиуса 0,95. Найдите площадь S части поверхности
шара, лежащей внутри куба. В ответе запишите S/π .
Решение.
Так как середина ребер куба является центром сферы,
диаметр которой равен ребру куба, в кубе содержится 1/4 сферы
и, соответственно, 1/4 ее поверхности.
1
1
2
2
S 4 R 0,95 0,9025
4
4

19. Задача №17

Конус вписан в шар. Радиус основания конуса равен радиусу
шара. Объем конуса равен 6. Найдите объем шара.
1
1 2
Vk. Soc. h R R 6
3
3
4 3
Vш. R 24
3

20.

Задача №18Куб вписан в шар радиуса √3 . Найдите объем куба.
Диаметр шара, описанного вокруг куба,
совпадает с его диагональю и вдвое
больше радиуса. Поэтому диагональ куба
равна 2√3. Если ребро куба равно а, то
диагональ
куба
вычисляется
по
формуле d=a√3. Следовательно, ребро
куба равно 2, а его объем равен 8.
Задачи
для самостоятельного
решения

22. Задача №1 Решите самостоятельно

1) Площадь большого круга шара равна 41. Найдите
площадь поверхности шара.
Ответ: 164
2) Площадь большого круга шара равна 10. Найдите
площадь поверхности шара
3) Площадь большого круга шара равна 26. Найдите
площадь поверхности шара

23. Задача №2 Решите самостоятельно

1) Во сколько раз увеличится площадь поверхности шара,
если радиус шара увеличить в 45 раз?
Ответ: 2025
2) Во сколько раз увеличится площадь поверхности шара,
если радиус шара увеличить в 16 раз?
3) Во сколько раз увеличится площадь поверхности шара,
если радиус шара увеличить в 1,5 раза?

24.

Задача №3 Решите самостоятельно1) Во сколько раз увеличится объем шара, если его радиус
увеличить в 10 раз?
2) Во сколько раз увеличится объем шара, если его радиус
увеличить в 4 раза?
3) Во сколько раз увеличится объем шара, если его радиус
увеличить в 15 раз?

25. Задача №4 Решите самостоятельно

Задача №4 Решите
1)
самостоятельно
Объем одного шара в 2197 раз больше объема второго. Во
сколько раз площадь поверхности первого шара больше
площади поверхности второго?
Ответ: 169
2) Объем одного шара в 1331 раз больше объема второго. Во
сколько раз площадь поверхности первого шара больше
площади поверхности второго?
3) Объем одного шара в 1000 раз больше объема второго. Во
сколько раз площадь поверхности первого шара больше
площади поверхности второго?

26. Задача №6 Решите самостоятельно

1) Однородный шар диаметром 3 см имеет массу 81
грамма. Чему равна масса шара, изготовленного из того
же материала, с диаметром 5 см? Ответ дайте в
граммах.
Ответ:375

27. Задача №7 Решите самостоятельно

1) Даны два шара с радиусами 5 и 1. Во сколько раз
площадь поверхности первого шара больше площади
поверхности второго?
Ответ: 25
2) Даны два шара с радиусами 3 и 1. Во сколько раз
площадь поверхности первого шара больше площади
поверхности второго?
Ответ: 9
3) Даны два шара с радиусами 14 и 2. Во сколько раз
площадь поверхности первого шара больше площади
поверхности второго?
Ответ: 49

28. Задача №8 Решите самостоятельно

1) Даны два шара с радиусами 4 и 1. Во сколько раз объём
первого шара больше объёма второго?
Ответ: 64

29. Задача №10 Решите самостоятельно

1) В куб с ребром 21 вписан шар. Найдите объем этого
шара, деленный на π .
2) В куб с ребром 9 вписан шар. Найдите объем этого
шара, деленный на π .
3) В куб с ребром 18 вписан шар. Найдите объем этого
шара, деленный на π .

30. Задача №11 Решите самостоятельно

1) Объем шара равен 18 432 π. Найдите площадь его
поверхности, деленную на π .
2) Объем шара равен 12 348π. Найдите площадь его
поверхности, деленную на π .
3) Объем шара равен 26.244π. Найдите площадь его
поверхности, деленную на π .
4) Объем шара равен 972π. Найдите площадь его
поверхности, деленную на π .

31. Задача №12 Решите самостоятельно

1) Радиусы трех шаров равны 2, 12 и 16. Найдите радиус
шара, объем которого равен сумме их объемов.
Ответ:18
2) Радиусы трех шаров равны 1, 6 и 8. Найдите радиус
шара, объем которого равен сумме их объемов.
3) Радиусы трех шаров равны 15, 20 и 25. Найдите радиус
шара, объем которого равен сумме их объемов.

32. Задача №13 Решите самостоятельно

1) Около куба с ребром √243 описан шар. Найдите
объем этого шара, деленный на π . Ответ:
2) Около куба с ребром √300 описан шар. Найдите
объем этого шара, деленный на π .
3) Около куба с ребром √507 описан шар. Найдите
объем этого шара, деленный на π .

33. Задача №14 Решите самостоятельно

1) Радиусы двух шаров равны 21, 72. Найдите радиус
шара, площадь поверхности которого равна сумме
площадей их поверхностей.
Ответ: 75
2) Радиусы двух шаров равны 8, 15. Найдите радиус шара,
площадь поверхности которого равна сумме площадей
их поверхностей.
3) Радиусы двух шаров равны 32, 60. Найдите радиус
шара, площадь поверхности которого равна сумме
площадей их поверхностей.

34. Задача №15 Решите самостоятельно

1) Вершина А куба ABCDA1B1C1D1 со стороной 1,2 является
центром сферы, проходящей через точку A1. Найдите
площадь S части сферы, содержащейся внутри куба. В ответе
запишите величину S/π .
2) Вершина А куба ABCDA1B1C1D1 со стороной 0,7 является
центром сферы, проходящей через точку A1. Найдите
площадь S части сферы, содержащейся внутри куба. В ответе
запишите величину S/π .
3) Вершина А куба ABCDA1B1C1D1 со стороной 0,9 является
центром сферы, проходящей через точку A1. Найдите
площадь S части сферы, содержащейся внутри куба. В ответе
запишите величину S/π .

35. Задача №16 Решите самостоятельно

1) Середина ребра куба со стороной 1,8 является центром
шара радиуса 0,8. Найдите площадь S части
поверхности шара, лежащей внутри куба. В ответе
запишите S/π .
2) Середина ребра куба со стороной 2,4 является центром
шара радиуса 1,2. Найдите площадь S части
поверхности шара, лежащей внутри куба. В ответе
запишите S/π .

36. Задача №17 Решите самостоятельно

1) Конус вписан в шар. Радиус основания конуса равен
радиусу шара. Объем конуса равен 27. Найдите объем
шара.
2) Конус вписан в шар. Радиус основания конуса равен
радиусу шара. Объем конуса равен 45. Найдите объем
шара.
3) Конус вписан в шар. Радиус основания конуса равен
радиусу шара. Объем конуса равен 12√3. Найдите
объем шара.

37. Задача №18 Решите самостоятельно

Задача №18 Решите
1)
2)
3)
4)
самостоятельно
Куб вписан в шар радиуса 0,5√3 . Найдите объем
куба.
Ответ: 1
Куб вписан в шар радиуса 10,5√3 . Найдите объем
куба.
Куб вписан в шар радиуса 8√3 . Найдите объем
куба.
Куб вписан в шар радиуса 15,5√3 . Найдите объем
куба.

38. Используемые ресурсы

• Шаблон подготовила
учитель русского языка и литературы
Тихонова Надежда Андреевна
• «Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ.
Режим доступа: http://mathb.reshuege.ru
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
Автор и источник заимствования неизвестен
http://www.ourcity.ru/images/art/img_big_1274700246.jpg
http://oboi.ucoz.de/_ph/4/980025544.jpg
http://gym1517.narod.ru/awg/d55.jpg

Задание 7. Решите задачи — Студопедия

Поделись с друзьями: 

1. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ AB = 2 см, AA₁ = 5 см. Найдите площадь боковой поверхности призмы.

2. Высота конуса равна 12, а длина образующей — 15. Найдите диаметр основания конуса.

3. В Кубе ABCDA₁B₁C₁D₁ сторона основания равна 5 см. Найдите площадь боковой поверхности куба.

4. Площадь куба равна 24 см². Найдите сторону куба.

5. Площадь боковой поверхности цилиндра равна 24π, а его высота равна 4. Найдите диаметр основания цилиндра.

6. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ AB = 5, AВ = , CC₁ = . Найдите длину диагонали параллелепипеда AC₁.

7. Объем цилиндра равен π. Найдите высоту цилиндра, если диаметр его основания равен 1.

8. Объем правильной треугольной пирамиды SABC с вершиной S равен 30. Найдите площадь треугольника ABC, если высота пирамиды SO равна 10.

9. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ AB = 5, AВ = 7, A₁D₁ = , AA₁ = 1.

Найдите длину диагонали параллелепипеда DB₁.

10. Площадь боковой поверхности цилиндра равна 18π, а его высота равна 3. Найдите радиус основания цилиндра.

11. В цилиндрическом сосуде уровень жидкости достигает 192 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ выразите в сантиметрах.

12. В сосуд в виде конуса налита жидкость до 1/3 высоты. Объем налитой жидкости 16 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху?

13. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в 8 раз?

14. В цилиндрический сосуд налили 4000 см³ воды. Уровень жидкости оказался равным 22 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 11 см. Чему равен объем детали? Ответ выразите в см³.

15. В сосуд, имеющий форму правильной треугольной призмы, налили 2500 см

3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 20 см до отметки 31 см. Чему равен объем детали? Ответ выразите в см³.

16. Объем цилиндра равен 1 см³. Радиус основания уменьшили в 2 раза, а высоту увеличили в 3 раза. Найдите объем получившегося цилиндра. Ответ дайте в см³.

17. Шар, объем которого равен 29π, вписан в куб. Найдите объем куба.

18. В правильной треугольной призме ABCA₁B₁C₁, площадь основания равна 9, а боковое ребро равно 4. Найдите объем пирамиды BAСС

1.

19. Прямоугольный параллелепипед описан вокруг сферы радиуса 4. Найдите его объем.

20. Шар, объем которого равен 16π, вписан в куб. Найдите объем куба.

21. Шар, объем которого равен 37π, вписан в куб. Найдите объем куба.

22. В цилиндрическом сосуде уровень жидкости достигает 12 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.

23. Прямоугольный параллелепипед описан вокруг сферы радиуса 5. Найдите его объем.

24. Шар, объем которого равен 9π, вписан в куб. Найдите объем куба.

25. В кубе ABCDA₁B₁C₁D₁ точки E, F, E₁ и F₁ являются серединами ребер BC, DC, B₁C₁ и D₁C₁ соответственно. Объем треугольной призмы, отсекаемой от куба плоскостью EFF₁, равен 29. Найдите объем куба.

---

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:  

---



3$?

Задавать вопрос

спросил 12 лет, 10 месяцев назад

Изменено 5 месяцев назад

Просмотрено 92к раз

$\begingroup$

Я узнал, что объем сферы равен $\frac{4}{3}\pi r^3$, но почему? $\pi$ имеет смысл, потому что он круглый, как круг, а $r^3$ потому что он трехмерный, но $\frac{4}{3}$ такой случайный! Как кто-то мог предположить что-то подобное для формулы?

• геометрия
• объем
• объемная геометрия
• сферы

$\endgroup$

6

$\begingroup$

Помимо уже упомянутых методов исчисления, Паппа и Архимеда, для подобных задач может быть полезен принцип Кавальери.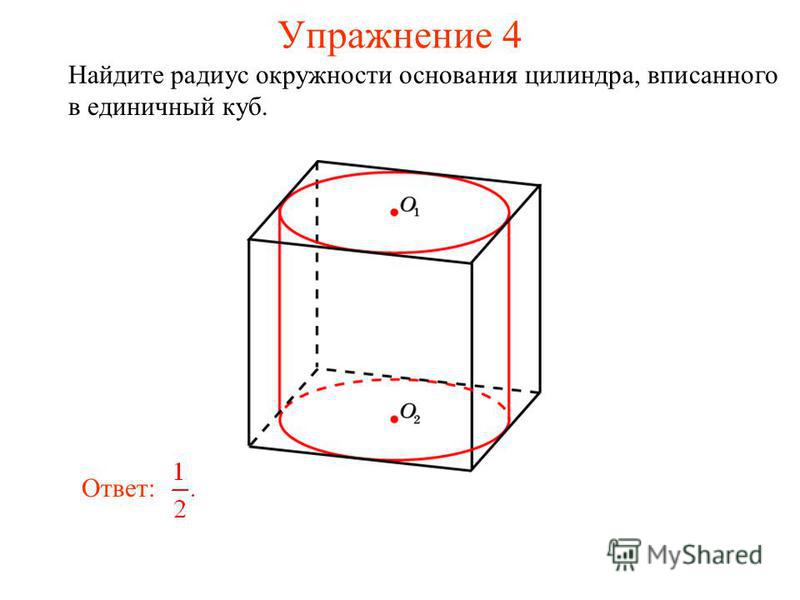

Предположим, у вас есть две сплошные фигуры, выстроенные рядом друг с другом, каждая из которых помещается между одними и теми же двумя параллельными плоскостями. (Например, две стопки монет одной высоты, лежащие на столе). Затем рассмотрите возможность разрезания двух твердых тел плоскостью, параллельной данным двум и находящейся между ними. Если образованная таким образом площадь поперечного сечения каждого из тел одинакова для любой такой плоскости, то объемы тел одинаковы.

Если вы согласны с тем, что знаете, что объем конуса составляет 1/3 объема цилиндра с тем же основанием и высотой, вы можете использовать Кавальери, сравнивая полушарие с цилиндром с вписанным конусом, чтобы получить объем сферы. Эта диаграмма (из Википедии) иллюстрирует конструкцию: смотрите здесь

Рассмотрим цилиндр радиуса $R$ и высоты $R$, внутри которого находится перевернутый конус с основанием радиуса $R$, совпадающим с вершиной цилиндр, и снова высота $R$. Поместите рядом с ним полусферу радиуса $R$. 2)$. То же самое и с поперечным сечением полусферы, как вы можете видеть, выполняя теорему Пифагора с любым вектором из центра сферы в точку на сфере на высоте y, чтобы получить радиус поперечного сечения (которое круглое). 93. \end{выравнивание*}

$\endgroup$

4

$\begingroup$

Добавлю китайскую версию для интереса.

У древних китайцев был другой способ расчета этого объема.

Принцип тот же, что и принцип Кавальери; разница заключается в использовании пересечения двух перпендикулярных цилиндров, «бицилиндра», для упаковки сферы. Китайское название этой формы — 牟合方蓋 или «моухефангай» (что означает два квадратных зонтика). 92}=\dfrac{\pi}{4}$.

Теперь встает вопрос расчета объема бицилиндра (белого цвета). Это тоже очень сложно, поэтому добавьте куб (красный), упаковывающий бицилиндр (белый). Теперь, когда плоскость пересекает куб, он образует еще один квадрат большего размера. Дополнительная площадь в большом квадрате (большой квадрат из куба минус меньший квадрат из бицилиндра) такая же, как $4$ маленьких квадратов (синие). При движении плоскости, пересекающей твердые тела, эти синие квадраты образуют в углах куба $4$ маленьких пирамиды со сторонами равнобедренного треугольника и вершиной на краю куба. При перемещении по всему бицилиндру получается всего $8$ пирамид. 93$.

Теперь вы видите, что $3$ — это пирамиды, а $4$ — кубы! Они не случайны.

На этом рисунке показаны геометрические соотношения.

$\endgroup$

$\begingroup$

Теорема Паппа о центроиде (вторая теорема) утверждает, что объем твердого тела, образованного вращением области вокруг оси, равен произведению площади области на расстояние, пройденное центром тяжести области при ее вращении. Сфера может быть образована вращением полукруга вокруг края диаметра. 92$. Центр тяжести полукруга можно найти путем пересечения двух прямых, которые делят площадь полукруга на две равные части. Одна такая линия проходит перпендикулярно ребру диаметра через центр полуокружности (это линия симметрии полуокружности).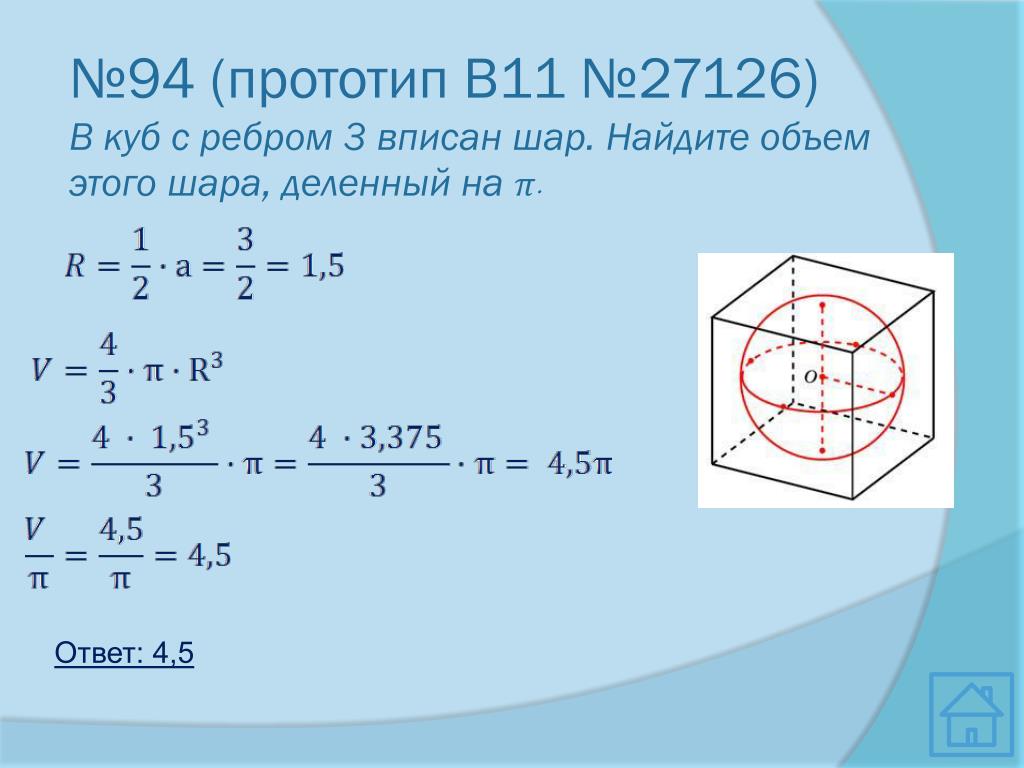 3$. 91}{3!!} = \frac{4 \pi}{3}$.

Смысл этого в том, чтобы показать вам, что общая формула также включает множители в знаменателе и что формула для $n=3$ не является «случайной», а скорее соответствует общей схеме.

$\endgroup$

1

$\begingroup$

На приведенной ниже диаграмме слева будем считать, что размер $\треугольника PQR$ бесконечно мал по сравнению с $\треугольником PNO$, и, таким образом, зеленая дуга и отрезок $\overline{PR}$ равны практически равны по длине. Обратите внимание, что $\angle NPO$ и $\angle QPR$ дополняют $\angle OPQ$ и, следовательно, равны. Таким образом, прямоугольные треугольники $\triangle PNO$ и $\triangle PQR$ подобны (соответствующие стороны окрашены одинаково). Поскольку $\треугольник PNO$ и $\треугольник PQR$ подобны, $$ \overline{NP}\cdot\overline{PR}=\overline{OP}\cdot\overline{PQ}\tag{1} $$ Внутренняя окружность зеленого кольца на сфере справа равна $2\pi\overline{NP}$, а внешняя окружность равна $2\pi\left(\overline{NP}+\overline{QR}\right)$, а его ширина $\overline{PR}$. Следовательно, его площадь находится между $2\pi\overline{NP}\cdot\overline{PR}$ и $2\pi\left(\overline{NP}+\overline{QR}\right)\cdot\overline{PR} $.

Окружность красной полосы на цилиндре справа равна $2\pi\overline{OP}$, а ширина — $\overline{PQ}$. Следовательно, его площадь равна $2\pi\overline{OP}\cdot\overline{PQ}$.

Согласно $(1)$, разница между площадью зеленого кольца на сфере и красной полосой на цилиндре меньше $2\pi\overline{QR}\cdot\overline{PR}$. Суммирование $\overline{QR}$ при движении вниз по сфере дает $2\overline{OP}$ (один при увеличении $\overline{NP}$ и один при уменьшении), таким образом, разница между площадью сферы и площадь цилиндра меньше, чем $4\pi\overline{OP}\cdot\max\overline{PR}$, которую можно сделать равной нулю, сделав $\overline{PR}$ сколь угодно малой. 93\тег{2} $$

$\endgroup$

0

$\begingroup$

Это впервые «угадал» Архимед, на какую долю объема цилиндра приходится сфера. То есть сфера, которая содержится внутри этого цилиндра. Из этого он вычислил $4/3$.

В наши дни это можно сделать с помощью математических инструментов. Один из способов — использовать [Метод диска] над графом полукруга. Другой вариант — использовать сферические координаты и вычислить 3D-интеграл. 93$. Но это может быть то, что вы сказали, но просто уточняю.

$\endgroup$

$\begingroup$

Я хотел опубликовать это как комментарий к ответу Джастина Л., но это моя первая публикация здесь, поэтому я не смог. Архимед так гордился своим доказательством того, что объем сферы составляет две трети объема цилиндра той же высоты и диаметра, что попросил поставить на его могиле скульптуру, иллюстрирующую это. Позже гробница была найдена римским оратором Цицероном, который описывает ее следующим образом:

«Мне удалось разыскать его могилу. Сиракузяне ничего о ней не знали, да и вообще отрицали существование чего-либо подобного. Но вот она, полностью окруженная и скрытая зарослями терновника и терновника. Я вспомнила, что слышала о какой-то простой строки стихов, которые были начертаны на его могиле, относящиеся к сфере и цилиндру, вылепленным из камня на вершине могилы. Итак, я внимательно осмотрел все многочисленные гробницы, стоящие рядом с Агригентинскими воротами. Наконец, я заметил кое-что. колонна едва видна над кустарником: она была увенчана сферой и цилиндром».

Американский художник Бенджамин Уэст вообразил эту сцену на своей картине 1797 года «Цицерон, обнаруживающий гробницу Архимеда».

$\endgroup$

0

$\begingroup$

Чтобы расширить то, что сказал anosov_diffeomorphism:

Предположим, мы согласны с тем, что площадь поверхности сферы равна 4 π r ² (Если мы не согласны с этим, это был бы отличный вопрос, чтобы задать на этом сайте , а затем кто-то может отредактировать этот ответ, чтобы сослаться на него!). Теперь, если у меня есть сфера радиуса r , и я немного увеличиваю радиус, dr , тогда новая, расширенная сфера имеет больший объем, на объем только что добавленной тонкой сферической оболочки.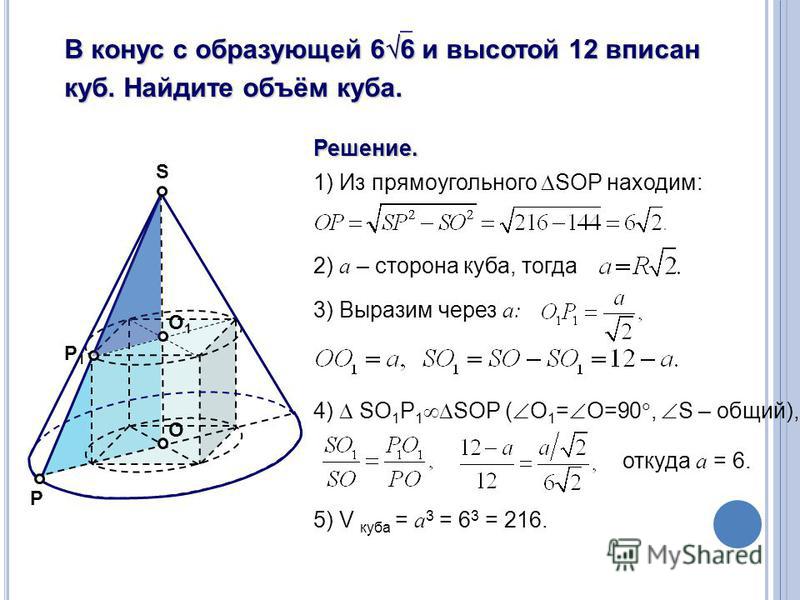

{r_2}$ 4 π r 93$.

(Хотя должен признать, что мне это больше нравилось как способ вывести формулу площади поверхности из объема.)

$\endgroup$

5

$\begingroup$

Архимед обнаружил, что объем мяча составляет 2/3 объема окружающего его цилиндра: внутри помещается шляпная коробка с баскетбольным мячом. Почему именно 2/3  ? Это чистая красота математики. Архимед нашел этот прекрасный результат и так полюбил сферы и цилиндры.

Каков объем цилиндра ?

V _C = площадь основного диска × высота

1. Площадь основного диска π r ² 901 72 . Архимед также нашел этот результат и доказал его. Примем это пока.
2. Высота цилиндра равна общей высоте шара, поэтому 2  r .

So V _C  = π r ²  × 2  92 .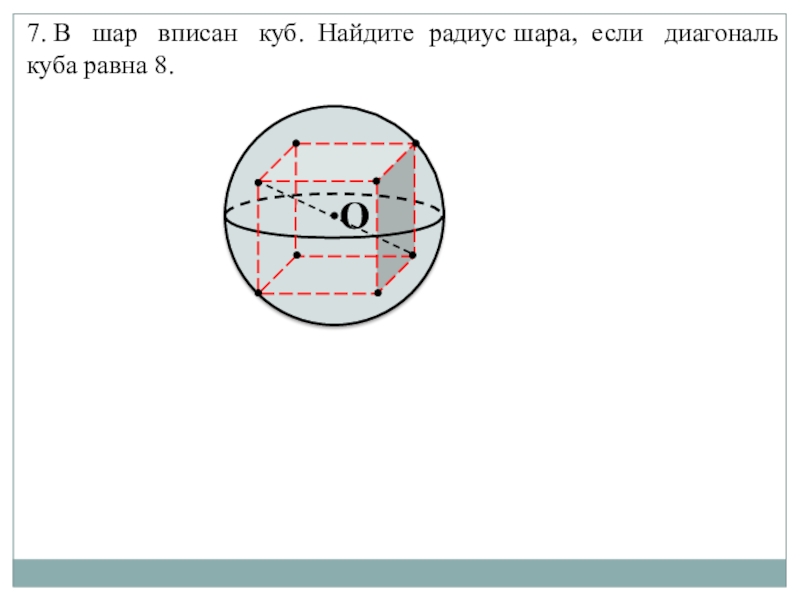 t$ действителен при использовании школьной математики и без исчисления.

Смоделируем сферу (радиус $R$) как набор концентрических, соприкасающихся оболочек общей толщины $t$. Самая внешняя оболочка определяется внешней сферой (нулевой толщины) радиуса $R$ и внутренней сферой (нулевой толщины) радиуса $R-t$. Самая внутренняя оболочка определяется внешней (нулевой толщины) сферой радиуса $t$, а ее внутренней границей является центр сферы; поэтому самая внутренняя оболочка представляет собой небольшую сферу. 93$.

Примечание. Я использую термин в масштабе специально, чтобы избежать путаницы в использовании умножения и сложения.

Доказательство (противоречие): Если вы сложите горизонтальную и вертикальную поверхности-компоненты сферы, вы обнаружите, что у вас есть длина окружности, умноженная на скалярный коэффициент 2 или $(2\pi r)_{ xy}+(2\pi r)_{xz}=4\pi r=2*2\pi r$.

Доказательство (путем концептуализации): Вы интегрируете трехмерный объект, высота которого (в плоскости xy) = $r_{xy}$, а ширина (в плоскости xz) = $r_{xz }$.

9{2}} \ underbrace {\, {\ rm d} \ left (h ‘\ over h \ right)} _ {\ vphantom {\ Large A} 1} \конец{массив} $$

Также по теореме Гаусса любой объем есть сумма пирамид: $$ В «=» \int_{V}{\rm d}V «=» \int_{V}{\nabla\cdot\vec{r} \over 3}\,{\rm d}V «=» \int_{V}{\vec{r}\cdot{\rm d}\vec{S} \более 3} $$ Мы можем думать, что конус — это «идеальная сумма пирамид», так как нам просто нужно интегрировать (с вершинами в качестве начала координат) над основанием.

$\endgroup$

$\begingroup$ 93$$

$\endgroup$

2

$\begingroup$

Рассмотрим следующую сферу радиуса r с вписанной пирамидой с площадью основания G:

Объем вписанной пирамиды можно вычислить следующим образом:

$V_{pyramid} = \frac{1}{ 3} \cdot G \cdot r$

Обратите внимание, что теперь мы можем выразить $V_{сфера}$ как сумму объемов бесконечно малых пирамид по всей площади поверхности сферы, где $A_{сфера} = 4 \cdot \pi \cdot r^2$. При этом получаем следующий результат: 93$

Итак, что мы из этого вынесем? Множитель $\frac{4}{3}$ можно интуитивно рассматривать как композицию множителя $4$, полученного из площади сферы, и множителя $\frac{1}{3}$, полученного из объема пирамида.

$\endgroup$

Калькулятор объема | Число Пи

Сфера

Радиус

Объем

Цилиндр

Радиус

Высота

Объем

Куб

Объем

Конус

Радиус

Высота

Объем

Прямоугольный параллелепипед

Длина

Высота

Объем 900 03

Вернуться на страницу калькуляторов

Калькулятор объема определит объем наиболее распространенных геометрических тел.

Что такое объем?

Объем — это общее пространство внутри твердого тела. Зная определение объема, мы можем теперь сосредоточиться на формулах объема обычных геометрических тел. Использовать эти формулы вручную не составит труда, но для получения быстрых и точных результатов каждый раз используйте калькулятор объема. 9{3}\), где r — радиус.

Просто введите размеры в калькулятор, чтобы найти объем. Единицы объема всегда будут кубическими, по сравнению с квадратными единицами площади поверхности.

@mometrixНужен калькулятор объема? Ссылка в био. ##pi ##piday ##volume ##sphere ##math ##mathhelp ##mometrix ##fyp

♬ оригинальный звук – Подготовка к тесту Mometrix

Вычисление объема куба Пример

Вот пример для расчет объема куба. 9{2}(4)=12\pi\) кубических сантиметров

Можно задаться вопросом, где этот калькулятор может быть полезен в реальных условиях. Это очень важно с точки зрения архитектуры и строительства. Одним из таких примеров является строительство дорог или тротуаров, где необходимо соорудить бетонные плиты. Как правило, бетонные плиты представляют собой прямоугольные тела, поэтому можно использовать калькулятор прямоугольной призмы.