Ср 14 движение тела брошенного вертикально вверх. Свободное падение и движение тела, брошенного вертикально вверх
Пусть тело начинает свободно падать из состояния покоя. В этом случае к его движению применимы формулы равноускоренного движения без начальной скорости с ускорением. Обозначим начальную высоту тела над землей через, время его свободного падения с этой высоты до земли — через и скорость, достигнутую телом в момент падения на землю, — через . Согласно формулам § 22 эти величины будут связаны соотношениями
(54.1)
(54.2)
В зависимости от характера задачи удобно пользоваться тем или другим из этих соотношений.
Рассмотрим теперь движение тела, которому сообщена некоторая начальная скорость , направленная вертикально вверх. В этой задаче удобно считать положительным направление кверху. Так как ускорение свободного падения направлено вниз, то движение будет равнозамедленным с отрицательным ускорением и с положительной начальной скоростью. Скорость этого движения в момент временивыразится формулой
а высота подъема в этот момент над исходной точкой — формулой
(54. 5)
5)
Когда скорость тела уменьшится до нуля, тело достигнет высшей точки подъема; это произойдет в момент, для которого
После этого момента скорость станет отрицательной и тело начнет падать вниз. Значит, время подъема тела
Подставляя в формулу (54.5) время подъема, найдем высоту подъема тела:
(54.8)
Дальнейшее движение тела можно рассматривать как падение без начальной скорости (случай, рассмотренный в начале этого параграфа) с высоты. Подставляя эту высоту в формулу (54.3), найдем, что скорость, которой тело достигнет в момент падения на землю, т. е. вернувшись в точку, откуда оно было брошено вверх, будет равна начальной скорости тела (но, конечно, будет направлена противоположно — вниз). Наконец, из формулы (54.2) заключим, что время падения тела с высшей точки равно времени поднятия тела в эту точку.
5 4.1. Тело свободно падает без начальной скорости с высоты 20 м. На какой высоте оно достигнет скорости, равной половине скорости в момент падения на землю?
54. 2. Покажите, что
тело, брошенное вертикально вверх, проходит каждую точку своей траектории с
одной и тон же по модулю скоростью на пути вверх и на пути вниз.
2. Покажите, что
тело, брошенное вертикально вверх, проходит каждую точку своей траектории с
одной и тон же по модулю скоростью на пути вверх и на пути вниз.
54.3. Найдите скорость при ударе о землю камня, брошенного с башни высоты : а) без начальной скорости; б) с начальной скоростью , направленной вертикально вверх; в) с начальной скоростью , направленной вертикально вниз.
54.4. Камень, брошенный вертикально вверх, пролетел мимо окна через 1 с после броска на пути вверх и через 3 с после броска на пути вниз. Найдите высоту окна над землей и начальную скорость камня.
54.5. При вертикальной стрельбе по воздушным целям снаряд, выпущенный из зенитного орудия, достиг только половины расстояния до цели. Снаряд, выпущенный из другого орудия, достиг цели. Во сколько раз начальная скорость снаряда второго орудия больше, чем скорость первого?
54.6. Какова максимальная высота, на которую поднимется камень, брошенный вертикально вверх, если через 1,5 с его скорость уменьшилась вдвое?
1588. Как определить ускорение свободного падения, имея в своем распоряжении секундомер, стальной шарик и шкалу высотой до 3 м?
Как определить ускорение свободного падения, имея в своем распоряжении секундомер, стальной шарик и шкалу высотой до 3 м?
1589. Какова глубина шахты, если свободно падающий в нее камень достигает дна через 2 с после начала падения.
1590. Высота Останкинской телебашни 532 м. С ее самой верхней точки уронили кирпич. За какое время он упадет на землю? Сопротивление воздуха не учитывать.
1591. Здание Московского государственного университета на Воробьевых горах имеет высоту 240 м. С верхней части его шпиля оторвался кусок облицовки и свободно падает вниз. Через какое время он достигнет земли? Сопротивление воздуха не учитывать.
1592. Камень свободно падает с обрыва. Какой путь он пройдет за восьмую секунду с начала падения?
1593. Кирпич свободно падает с крыши здания высотой 122,5 м. Какой путь пройдет кирпич за последнюю секунду своего падения?
1594. Определите глубину колодца, если камень, упавший в него, коснулся дна колодца через 1 с.
1595. Со стола высотой 80 см на пол падает карандаш. Определить время падения.
1596. Тело падает с высоты 30 м. Какое расстояние оно проходит в течение последней секунды своего падения?
1597. Два тела падают с разной высоты, но достигают земли в один и тот же момент времени; при этом первое тело падает 1 с, а второе — 2 с. На каком расстоянии от земли было второе тело, когда первое начало падать?
1598. Докажите, что время, в течение которого движущееся вертикально вверх тело достигает наибольшей высоты h, равно времени, в течение которого тело падает с этой высоты.
1599. Тело движется вертикально вниз с начальной скоростью. На какие простейшие движения можно разложить такое движение тела? Напишите формулы для скорости и пройденного пути этого движения.
1600. Тело брошено вертикально вверх со скоростью 40 м/с. Вычислите, на какой высоте будет тело через 2 с, 6 с, 8 с и 9 с, считая от начала движения. Ответы объясните. Для упрощения расчетов принять g равным 10 м/с2.
Ответы объясните. Для упрощения расчетов принять g равным 10 м/с2.
1601. С какой скоростью надо бросить тело вертикально вверх, чтобы оно вернулось назад через 10 с?
1602. Стрела пущена вертикально вверх с начальной скоростью 40 м/с. Через сколько секунд она упадет обратно на землю? Для упрощения расчетов принять g равным 10 м/с2.
1603. Аэростат равномерно поднимается вертикально вверх со скоростью 4 м/с. К нему на веревке подвешен груз. На высоте 217 м веревка обрывается. Через сколько секунд груз упадет на землю? Принять g равным 10 м/с2.
1604. Камень бросили вертикально вверх с начальной скоростью 30 м/с. Через 3 с после начала движения первого камня бросили также вверх второй с начальной скоростью 45 м/с. На какой высоте камни встретятся? Принять g = 10 м/с2. Сопротивлением воздуха пренебречь.
1605. Велосипедист поднимается вверх по уклону длиной 100 м. Скорость в начале подъема 18 км/ч, а в конце 3 м/с. Предполагая движение равнозамедленным, определите, как долго длился подъем.
Предполагая движение равнозамедленным, определите, как долго длился подъем.
1606. Санки движутся вниз по горе равноускоренно с ускорением 0,8 м/с2. Длина горы 40 м. Скатившись с горы, санки продолжают двигаться равнозамедленно и останавливаются через 8 с….
Как нам уже известно, сила тяжести действует на все тела , которые находятся на поверхности Земли и вблизи неё. При этом не важно, находятся ли они в состоянии покоя или совершают движение.
Если некоторое тело будет свободно падать на Землю, то при этом оно будет совершать равноускоренное движение , причем скорость будет возрастать постоянно, так как вектор скорости и вектор ускорения свободного падения будут сонаправлены между собой.
Суть движения вертикально вверх
Если же подбросить некоторое тело вертикально вверх, и при этом считать что сопротивление воздуха отсутствует, то можно считать что оно тоже совершает равноускоренное движение, с ускорением свободного падения, которое вызвано силой тяжести. Только в этом случае, скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться.
Только в этом случае, скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться.
Через некоторое время наступит момент, когда скорость станет равняться нулю. В этот момент тело достигнет своей максимальной высоты и на какой-то момент остановится. Очевидно, что, чем большую начальную скорость мы придадим телу, тем на большую высоту оно поднимется к моменту остановки.
- Далее, тело начнет равноускоренно падать вниз, под действием силы тяжести.
Как решать задачи
Когда вы столкнетесь с задачами на движение тела вверх, при котором не учитывается сопротивление воздуха и другие силы, а считается, что на тело действует только сила тяжести, то так как движение равноускоренное, то можно применять те же самые формулы, что и при прямолинейном равноускоренном движении с некоторой начальной скорость V0.
Необходимо также учитывать, что при движении вверх вектор ускорения свободного падения направлен вниз, а вектор скорости вверх, то есть они разнонаправлены, а следовательно, их проекции будут иметь разные знаки.
Например, если Ось Ох направить вверх, то проекция вектора скорости при движении вверх, будет положительна, а проекция ускорения свободного падения отрицательна. Это надо учитывать, подставляя значения в формулы, иначе получится совершенно неверный результат.
Движение тела, брошенного вертикально вверх
I уровень. Прочитайте текст
Если некоторое тело будет свободно падать на Землю, то при этом оно будет совершать равноускоренное движение, причем скорость будет возрастать постоянно, так как вектор скорости и вектор ускорения свободного падения будут сонаправлены между собой.
Если же подбросить некоторое тело вертикально вверх, и при этом считать что сопротивление воздуха отсутствует, то можно считать что оно тоже совершает равноускоренное движение, с ускорением свободного падения, которое вызвано силой тяжести. Только в этом случае, скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться.
Только в этом случае, скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться.
Через некоторое время наступит момент, когда скорость станет равняться нулю. В этот момент тело достигнет своей максимальной высоты и на какой-то момент остановится. Очевидно, что, чем большую начальную скорость мы придадим телу, тем на большую высоту оно поднимется к моменту остановки.
Все формулы для равноускоренного движения применимы для движения тела, брошенного вверх. V0 всегда > 0
Движение тела, брошенного вертикально вверх является прямолинейным движением с постоянным ускорением. Если направить координатную ось OY вертикально вверх, совместив начало координат с поверхностью Земли, то для анализа свободного падения без начальной скорости можно использовать формулу https://pandia.ru/text/78/086/images/image002_13. gif»>
gif»>
Вблизи поверхности Земли, при условии отсутствия заметного влияния атмосферы скорость тела, брошенного вертикально вверх, изменяется во времени по линейному закону: https://pandia.ru/text/78/086/images/image004_7.gif»>.
Скорость тела на некоторой высоте h, можно найти по формуле:
https://pandia.ru/text/78/086/images/image006_6.gif»>
Высота подъема тела за некоторое время, зная конечную скорость
https://pandia.ru/text/78/086/images/image008_5.gif»>
II I уровень. Решите задачи. Для 9 б. 9а решает из задачника!
1. Мяч бросили вертикально вверх со скоростью 18 м/с. Какое перемещение совершит он за 3 с?
2. Стрела, выпущенная из лука вертикально вверх со скоростью 25 м/с, поражает цель через 2 с. Какую скорость имела стрела к моменту достижения цели?
3. Из пружинного пистолета выстрелили вертикально вверх шариком, который поднялся на высоту 4,9 м. С какой скоростью вылетел шарик из пистолета?
4. Мальчик бросил вертикально вверх мячик и поймал его через 2 с. На какую высоту поднялся мячик и какова его начальная скорость?
Мальчик бросил вертикально вверх мячик и поймал его через 2 с. На какую высоту поднялся мячик и какова его начальная скорость?
5. С какой начальной скоростью нужно бросить тело вертикально вверх, чтобы через 10 с оно двигалось со скоростью 20 м/с вниз?
6. «Шалтай-Болтай сидел на стене (высотой 20 м),
Шалтай-Болтай свалился во сне.
Нужна ли вся королевская конница, вся королевская рать,
чтобы Шалтая, чтобы Болтая, Шалтая-Болтая,
Болтая-Шалтая собрать»
(если он разбивается только при скорости 23 м/с?)
Так нужна ли вся королевская конница?
7. Теперь гром сабель, шпор, султан,
И камер-юнкерский кафтан
Узорчатый — красавицам прельщенье,
Не то ли ж было искушенье,
Когда из гвардии, иные от двора
Сюда на время приезжали!
Кричали женщины: ура!
И в воздух чепчики бросали.
«Горе от ума» .
Девица Екатерина кидала свой чепчик вверх со скоростью 10 м/с. При этом она стояла на балконе 2 этажа (на высоте 5 метров). Сколько времени чепчик будет находиться в полете, если упадет он под ноги храброму гусару Никите Петровичу (естественно стоящему под балконом на улице).
Сколько времени чепчик будет находиться в полете, если упадет он под ноги храброму гусару Никите Петровичу (естественно стоящему под балконом на улице).
Само по себе тело вверх, как известно, не движется. Его нужно «бросить», т. е. сообщить ему некоторую начальную скорость направленную по вертикали вверх.
Брошенное вверх тело движется, как показывает опыт, с таким же ускорением, как и свободно падающее тело. Это ускорение равно и направлено вертикально вниз. Движение тела, брошенного вверх, — это тоже прямолинейное равноускоренное движение, и формулы, которые были написаны для свободного падения тела, годны и для описания движения тела, брошенного вверх. Но при написании формул надо учесть, что вектор ускорения направлен против вектора начальной скорости: скорость тела по абсолютному значению не увеличивается, а уменьшается. Поэтому, если ось координат направить вверх, проекция начальной скорости будет положительна, а проекция ускорения — отрицательна, и формулы примут вид:
Так как тело, брошенное вверх, движется с уменьшающейся скоростью, то наступит такой момент, когда скорость станет равной нулю. В этот момент тело будет находиться на максимальной высоте. Подставив в формулу (1) значение получим:
В этот момент тело будет находиться на максимальной высоте. Подставив в формулу (1) значение получим:
Отсюда можно найти время, которое требуется для того, чтобы тело поднялось до максимальной высоты:
Максимальную высоту определяем из формулы (2).
Подставив в формулу получим
После того как тело достигнет высоты оно начнет падать вниз; проекция его скорости станет отрицательной, а по абсолютной величине будет возрастать (см. формулу 1), высота же будет уменьшаться со временем согласно формуле (2) при
Пользуясь формулами (1) и (2), легко убедиться в том, что скорость тела в момент его падения на землю или вообще туда, откуда оно было брошено (при h = 0), равна по абсолютной величине начальной скорости а время падения тела равно времени его подъема.
Падение тела можно рассматривать и отдельно как свободное падение тела с высоты Тогда мы можем воспользоваться формулами, приведенными в предыдущем параграфе.
Задача. Тело брошено вертикально вверх со скоростью 25 м/сек. Какова скорость тела через 4 сек? Какое перемещение совершит тело и какова длина пути, пройденного телом за это время? Решение. Скорость тела вычисляется по формуле
Какова скорость тела через 4 сек? Какое перемещение совершит тело и какова длина пути, пройденного телом за это время? Решение. Скорость тела вычисляется по формуле
К исходу четвертой секунды
Знак означает, что скорость направлена против координатной оси, направленной вверх, т. е. в конце четвертой секунды тело уже двигалось вниз, пройдя через высшую точку своего подъема.
Величину перемещения тела найдем по формуле
Это перемещение отсчитывается от того места, откуда тело было брошено. Но в этот момент тело уже двигалось вниз. Поэтому длина пройденного телом пути равна максимальной высоте подъема плюс расстояние, на которое оно успело опуститься вниз:
Значение вычислим по формуле
Подставив значения получаем: сек
Упражнение 13
1. Стрела выпущена из лука вертикально вверх со скоростью 30 м/сек. На какую высоту она поднимется?
2. Тело, брошенное с земли вертикально вверх, упало через 8 сек. Найдите, на какую высоту оно поднялось и какова была его начальная скорость?
3. Из пружинного пистолета, находящегося на высоте 2 м над землей, вылетает вертикально вверх шарик со скоростью 5 м/сек. Определите, на какую максимальную высоту он поднимется и какую скорость шарик будет иметь в момент падения на землю. Сколько времени шарик находился в полете? Каково его перемещение за первые 0,2 сек полета?
Из пружинного пистолета, находящегося на высоте 2 м над землей, вылетает вертикально вверх шарик со скоростью 5 м/сек. Определите, на какую максимальную высоту он поднимется и какую скорость шарик будет иметь в момент падения на землю. Сколько времени шарик находился в полете? Каково его перемещение за первые 0,2 сек полета?
4. Тело брошено вертикально вверх со скоростью 40 м/сек. На какой высоте оно окажется через 3 и 5 сек и какие при этом у него будут скорости? Принять
5 Два тела брошены вертикально вверх с различными начальными скоростями. Одно из них достигло вчетверо большей высоты, чем другое. Во сколько раз его начальная скорость была больше начальной скорости другого тела?
6. Брошенное вверх тело пролетает мимо окна со скоростью 12 м/сек. С какой скоростью оно будет пролетать мимо того же окна вниз?
Решение типовых задач по физике. Механика. Кинематика :: Класс!ная физика
Здесь есть всё!
На этой странице представлены условия типовых задач по физике из сборника задач Бендрикова Г.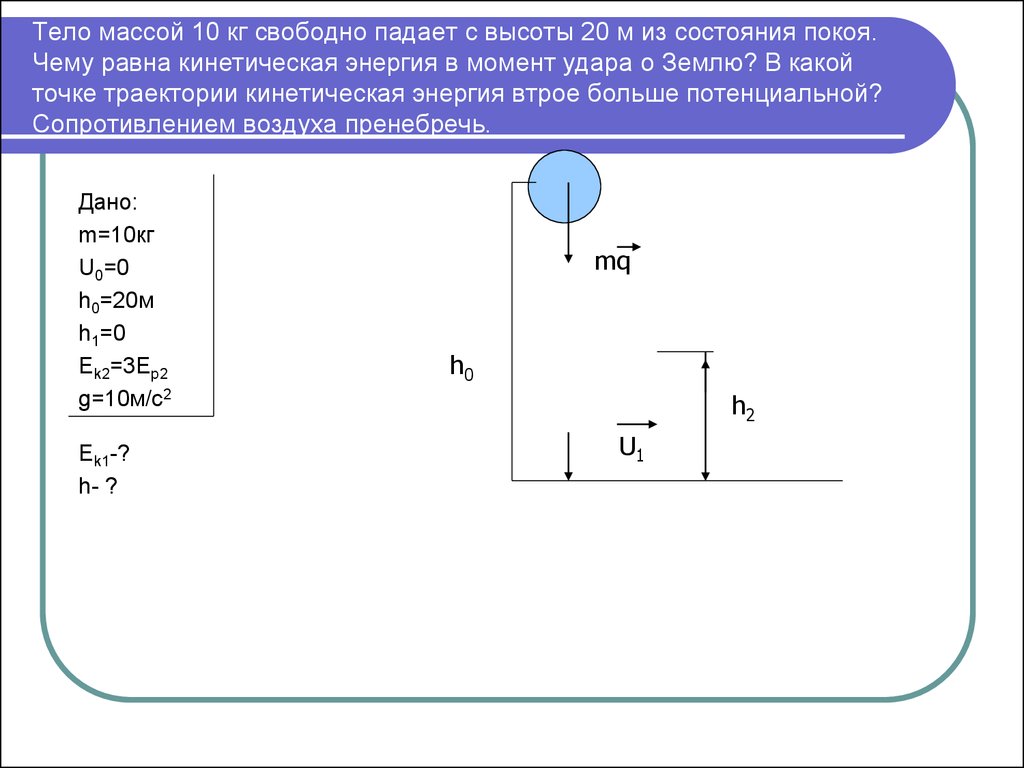 А. для школьников 9-11 классов и студентов.
А. для школьников 9-11 классов и студентов.
Решения этих задач даны на плейлисте видео — СМОТРИ ЗДЕСЬ —
Номера задач здесь и на плейлисте совпадают.
Счастливого разбора «полетов»!
Задачи на прямолинейное равномерное и равнопеременное движение
1. Товарный поезд идет со скоростью 10 м/с. Спустя 30 мин. с той же станции по тому же направлению вышел экспресс со скоростью 20 м/с. Через какое время после выхода товарного поезда и на каком расстоянии от станции экспресс догонит товарный поезд.
2. Из городов А и В, расстояние между которыми равно 54 км одновременно выехали навстречу друг другу две автомашины со скоростями 4 м/с и 6 м/с. Через какое время и на каком расстоянии от города, находящемся на полпути между А и В встретятся автомашины?
3. Стержень АВ длины l опирается концами о пол и стену. Найти зависимость координаты y — конца стержня В от времени t при движении конца стержня А с постоянной скоростью v в направлении, указанном на рисунке.
4. Товарный поезд длины 630 м и экспресс длины 120 м идут по двум параллельным путям в одном направлении со скоростями 13 м/с и 28 м/с соответственно. В течении какого времени экспресс будет обгонять товарный поезд?
5. Два поезда идут навстречу друг другу со скоростями 10 м/с и 15 м/с. Пассажир в первом поезде замечает, что второй поезд проходит мимо него в течении 6 секунд. Какова длина второго поезда?
6. Теплоход, имеющий длину 300 м, движется по прямому курсу в неподвижной воде со скоростью v. Катер, имеющий скорость 25 м/с, проходит расстояние от кормы движущегося теплохода до его носа и обратно, за 37,5 секунды. Найти скорость v теплохода.
7. На наклонную плоскость, составляющую с линией горизонта угол альфа, опирается стержень, который может перемещаться только по вертикали, благодаря направляющему устройству АВ. С какой скоростью поднимается стержень?
8. Капли дождя на окнах неподвижного трамвая оставляют полосы, наклоненные под углом 30 градусов к вертикали. При движении трамвая со скоростью 5 м/с полосы от дождя вертикальные. Найти скорость капель дождя в безветренную погоду и скорость ветра.
При движении трамвая со скоростью 5 м/с полосы от дождя вертикальные. Найти скорость капель дождя в безветренную погоду и скорость ветра.
9. Пловец переплывает реку, имеющую ширину h. Под каким углом альфа к направлению течения он должен плыть, чтобы переправиться на противоположный берег в кратчайшее время?
10. Лодочник, переправляясь через реку ширины H, из пункта А в пункт В все время направляет лодку под углом альфа к берегу. Найти скорость лодки относительно воды, если скорость течения реки равна u, а лодку снесло ниже пункта В на расстояние l.
11. Корабль идет на запад со скоростью v. Известно, что ветер дует с юго-запада. Скорость ветра, измеренная на палубе корабля, равна u0. Найти скорость ветра u относительно Земли.
12. Тело 1 начинает двигаться из точки А по направлению к точке В со скоростью V1. Одновременно тело 2 начинает двигаться из точки В по направлению к точке С со скоростью V2. Расстояние AB=L. Острый угол ABC равен альфа. В какой момент времени t расстояние r между телами 1 и 2 будет минимальным, и каково это расстояние?
13. Один поезд шел первую половину пути S1 со скоростью 80 км/ч, а вторую половину — со скоростью 40 км/ч. Второй поезд шел первую половину времени со скоростью 80 км/ч, а вторую половину времени со скоростью 40 км/ч. Какова средняя скорость каждого поезда?
Один поезд шел первую половину пути S1 со скоростью 80 км/ч, а вторую половину — со скоростью 40 км/ч. Второй поезд шел первую половину времени со скоростью 80 км/ч, а вторую половину времени со скоростью 40 км/ч. Какова средняя скорость каждого поезда?
14. Тело, имея начальную скорость v1=2 м/с двигалось в течении времени t1=3c равномерно, t2=2 cекунды с ускорением а2=2 м/с2, t3=5 cекунд с ускорением а3=1 м/с2. Найти среднюю скорость на этом пути.
15. Самолет, летящий горизонтально со скоростью V, попадает в полосу дождя, капли которого падают вертикально со скоростью омега. Кабина пилота имеет два стекла: верхнее горизонтальное и переднее, наклоненное к горизонту под углом альфа. Каждое из стекол имеет площадь S. Найдите отношение числа капель воды, падающих в единицу времени на переднее стекло к числу капель, падающих в единицу времени на верхнее стекло.
16. Тело, имея начальную скорость v0 = 1 м/с, двигалось равноускоренно и приобрело, пройдя некоторое расстояние, скорость v = 7 м/с. Какова была скорость тела у на половине этого расстояния?
Какова была скорость тела у на половине этого расстояния?
17. Тело, имея некоторую начальную скорость, движется равноускоренно из некоторого положения. Известны координаты тела, отсчитанные вдоль направления движения от произвольного начала отсчета в моменты времени. Найти ускорение тела.
18. Парашютист спускается с постоянной скоростью v = 5 м/с. На расстоянии h = 10 м от земли у него выпал предмет. На сколько позже приземлится парашютист, чем этот предмет? Сопротивлением воздуха для падающего предмета пренебречь. Считать ускорение свободного падения g = 10 м/с2.
19. Тело, имея некоторую начальную скорость, движется равноускоренно. За время t тело прошло путь s, причем его скорость увеличилась в n раз. Найти ускорение тела.
20. По одному направлению из одной точки одновременно начали двигаться два тела: одно — равномерно со скоростью v = 980 см/с, а другое — равноускоренно без начальной скорости с ускорением а = 9,8 см/с2. Через какое время второе тело догонит первое?
21. Два поезда прошли одинаковый путь s за одно и то же время /, однако один поезд, имея начальную скорость, равную нулю, прошел весь путь с ускорением а = 3 см/с2, а другой поезд половину пути шел со скоростью v, = 18 км/ч, а половину пути — со скоростью v2 = 54 км/ч. Найти путь s, пройденный поездами.
Два поезда прошли одинаковый путь s за одно и то же время /, однако один поезд, имея начальную скорость, равную нулю, прошел весь путь с ускорением а = 3 см/с2, а другой поезд половину пути шел со скоростью v, = 18 км/ч, а половину пути — со скоростью v2 = 54 км/ч. Найти путь s, пройденный поездами.
22. Автомобиль, трогаясь с места, едет с ускорением а. Достигнув скорости v, он некоторое время едет равномерно, а затем тормозит с ускорением а2 до остановки. Найти время t движения автомобиля, если он прошел путь s.
23. Поезд прошел путь s = 60 км за время t = 52 мин. Сначала он шел с ускорением +а, в конце с ускорением -а, остальное время с максимальной скоростью v =72 км/ч. Найти модуль ускорения, если начальная и конечная скорости равны нулю.
24. Какая предельная скорость приземления v парашютиста допустима, если человек, не имея парашюта, может безопасно прыгать с высоты 2 м?
25. Камень брошен с высоты h = 28 м вертикально вверх с начальной скоростью v0 = 8 м/с. Найти скорость v падения камня на землю.
Найти скорость v падения камня на землю.
26. Тело падает без начальной скорости с высоты h = 45 м. Найти среднюю скорость падения на второй половине пути.
27. За какое время t свободно падающее без начальной скорости тело пройдет сотый сантиметр своего пути?
28. Свободно падающее без начальной скорости тело в последнюю секунду падения прошло 2/3 своего пути. Найти путь s, пройденный телом.
29. Тело брошено с некоторой высоты вертикально вверх с начальной скоростью v0 = 30 м/с. Найти координату h и скорость v тела через время t = 10 с, а также пройденный за это время путь Считать ускорение свободного падения g = 10 м/с2.
30. Свободно падающее без начальной скорости тело спустя некоторое время после начала падения находилось на высоте h2 = 1100 м, а еще через время t1 = 10 с — на высоте h3 = 120 м над поверхностью земли. С какой высоты h падало тело?
31. Тело, брошенное вертикально вверх, дважды проходит через точку на высоте h. Промежуток времени между этими прохождениями равен At.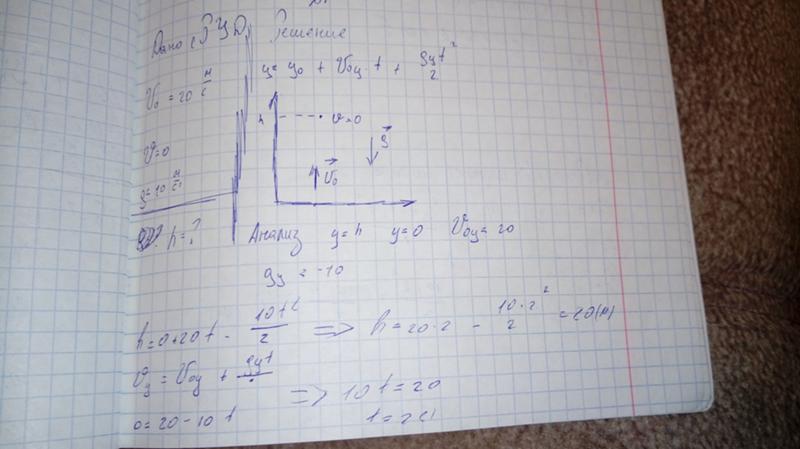 Найти начальную скорость тела v0 и время t0 от начала движения тела до возврата в начальное положение.
Найти начальную скорость тела v0 и время t0 от начала движения тела до возврата в начальное положение.
32. Одно тело брошено вертикально вверх с начальной скоростью v0, другое падает с высоты h без начальной скорости. Движения начались одновременно и происходят по одной прямой. Найти зависимость расстояния s между телами от времени t.
33. С башни, имеющей высоту h, бросают одновременно два шарика: один — вертикально вверх со скоростью v1, другой — вертикально вниз со скоростью v2. Найти промежуток времени At, отделяющий моменты их падения на землю.
34. С крыши падают одна за другой две капли. Через время t2 = = 2 с после начала падения второй капли расстояние между каплями стало равным s = 25 м. На сколько раньше первая капля оторвалась от крыши?
35. С высоты /i] = 10 м без начальной скорости падает камень. Одновременно с высоты h3 = 5 м вертикально вверх бросают другой камень. С какой начальной скоростью и{) брошен второй камень, если камни встретились на высоте h = 1 над землей?
36. Два тела брошены вертикально вверх с одинаковыми начальными скоростями с интервалом времени At. С какой скоростью будет двигаться второе тело относительно первого?
Два тела брошены вертикально вверх с одинаковыми начальными скоростями с интервалом времени At. С какой скоростью будет двигаться второе тело относительно первого?
37. Лодка подтягивается к высокому берегу озера при помощи веревки, которую наматывают с постоянной скоростью v = 1 м/с на цилиндрический барабан, находящийся на высоте h = 6 м над уровнем воды . Найти зависимость скорости лодки от длины веревки . Найти также скорость лодки в момент времени, когда I = 10 м, и перемещение лодки из этого положения за время t = 1 с.
38. По наклонной плоскости одновременно начали двигаться два тела: одно — вверх с начальной скоростью ц, = 0,5 м/с, другое — вниз без начальной скорости. Через какое время t тела встретятся и какой будет их относительная скорость в месте встречи, если первоначальное расстояние между телами I = 2,5 м?
39. По наклонной плоскости одновременно начали двигаться два тела: одно — вверх с начальной скоростью ц, = 0,5 м/с, другое — вниз без начальной скорости.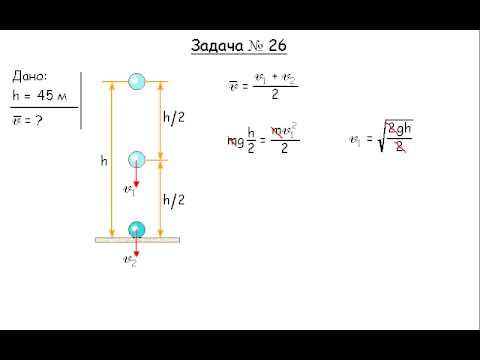 Через какое время t тела встретятся и какой будет их относительная скорость в месте встречи, если первоначальное расстояние между телами I = 2,5 м?
Через какое время t тела встретятся и какой будет их относительная скорость в месте встречи, если первоначальное расстояние между телами I = 2,5 м?
40. Стальной шарик, упавший с высоты h = 1,5 м на стальную доску, отскакивает от нее с потерей 25% скорости. Найти время t, которое проходит от начала движения шарика до его второго падения на доску.
41. Мяч свободно падает с высоты h — 120 м на горизонтальную плоскость. При каждом отскоке скорость его уменьшается вл = 2 раза. Построить график скорости и найти пройденный мячом путь от начала движения до остановки.
42. На движущуюся вертикально вверх со скоростью и горизонтальную гладкую плиту свободно падает шарик. Расстояние от точки начала падения шарика до его места встречи с плитой равна h0- На какую высоту h от этого места подскочит шарик после соударения с плитой? Плита, обладая очень большой массой, не изменяет своей скорости в результате соударения с шариком. Считать соударение абсолютно упругим.
РЕШЕНИЯ ЭТИХ ЗАДАЧ даны на плейлисте видео — СМОТРИ ЗДЕСЬ —
Номера задач здесь и на плейлисте совпадают.
Набор вопросов 1/Ответы
Набор вопросов 1/Ответы
1. Использование Галилеем наклонных плоскостей позволило ему эффективно
а. Замедлить ускорение свободного падения
б. Увеличьте ускорение выше, чем при свободном падении.
в. Устранить ускорение свободного падения
д. Все эти
е. Ни один из этих
Рассуждение : Перекатывание предметов по наклонной плоскости позволяют ему изучать их движение с меньшим ускорением, чем свободное падать. См. стр. 24 текста.
2. Самолет, летящий со скоростью 100 км/ч при попутном ветре 10 км/ч. движется со скоростью 110 км/ч относительно земли. Если он вместо этого летит при встречном ветре 10 км/ч его путевая скорость составляет
и . 90 км/ч
б. 100 км/ч
в. 110 км/ч
д. 120 км/ч
3. Два измерения, необходимые для расчета средней скорости
Два измерения, необходимые для расчета средней скорости
а. Ускорение и время
б. Скорость и время
c . Расстояние и время
д. Расстояние и ускорение
е. Скорость и расстояние
Рассуждение : Определение среднего скорость (пройденное расстояние)/(прошедшее время).
4. Средняя скорость лошади, проехавшей галопом расстояние 10 километров за 30 минут это
а. 10 км/ч
б. 20 км/ч
в. 30 км/ч
д. Более 30 км/ч
Рассуждение : V(среднее) = (10 км) / (0,5 ч) = 20 км/ч
5. Каково ускорение автомобиля при сохранении постоянного скорость 100 км/ч за 10 секунд?
и . 0
б. 10 км/ч/с
в. Оба эти
д. Ни один из этих
Обоснование : Ускорение связано с изменением
в скорости. Поскольку скорость остается постоянной, это означает, что ускорение
равен нулю.
6. Поскольку объект свободно падает вниз, его
а. Скорость увеличивается
б. Ускорение увеличивается
в. Оба эти
д. Ни один из этих
Рассуждение : В свободном падении скорость сохраняется увеличение. Однако ускорение остается постоянным и составляет = 90,8 м/с/с.
7. Если бы объект, свободно падающий вниз, был каким-либо образом оборудован со спидометром на планете, где ускорение за счет силы тяжести составляет 20 метров в секунду в секунду, то его скорость будет увеличивать каждую секунду на
а. 10 м/с
б. 20 м/с
в. 30 м/с
д. 40 м/с
е. Зависит от его начальной скорости.
8. Если предмет, свободно падающий вниз, был каким-то образом оборудован одометром для измерения пройденного пути, то расстояние, которое он проходит каждую последующую секунду, будет:
а. Константа
б.Меньше и меньше
c. Терка сильнее, чем предыдущая.
Рассуждение : расстояние, пройденное за каждую секунду увеличивается из-за того, что скорость увеличивается. См. стр. 46.
9. Через десять секунд после старта из состояния покоя объект падает. свободно вниз будет иметь скорость около:
а. 10 м/с
б. 50 м/с
в. 100 м/с
д. Более 100 м/с
Обоснование : Скорость увеличивается со скоростью 10 м/с (фактически 9,8 м/с) каждую секунду. Таким образом, через 10 секунд скорость 10 х 10 = 100 м/с.
10. Если тело падает с постоянным ускорением, скорость объекта необходимо:
а. Будьте также постоянными
b. Непрерывное изменение на одну и ту же величину каждую секунду
в. Непрерывно меняйте на разную величину в зависимости от скорости
д. Постоянно уменьшать
е. Ни один из них.
11. Одновременно падают тяжелый и легкий предметы.
время покоя в вакууме. Более тяжелый объект достигает земли:
Одновременно падают тяжелый и легкий предметы.
время покоя в вакууме. Более тяжелый объект достигает земли:
а. Раньше, чем более легкий объект
b. Одновременно с более легким объектом
в. Позже, чем более легкий объект.
Рассуждение : В вакууме нет воздуха сопротивление. Ускорение легкого и тяжелого тела одинаково.
12. Если автомобиль увеличивает скорость от нуля до 60 км/ч в 10 секунд, его ускорение:
а. 3 км/ч с
б . 6 км/ч с
в. 10 км/ч с
д. 60 км/ч с
е. 600 км/ч с.
Обоснование : ускорение = (изменение в V) / (время) = (60 — 0 км/ч) / (10 с) = 6 км/ч/с
13. Если ракета, первоначально находящаяся в состоянии покоя, разгоняется со скоростью 50 м/с2 в течение одной минуты, его скорость будет равна
а. 50 м/с
б. 500 м/с
в. 3000 м/с
д.3600 мм/с
е. Ни один из них.
Обоснование : Скорость увеличивается со скоростью 50 м/с каждую секунду. Таким образом, за одну минуту (т.е. за 60 секунд) скорость = (5 м/с/с) х (60 с) = 3000 м/с.
14. Бросьте камень с высоты 5 м, и он разгонится до 10 м/с2 и ударяется о землю через 1 с. Бросьте тот же камень из высота 2,5 м, а ускорение падения:
а. Около половины
б . Тот самый
в. Более.
15. При движении автомобиля по круговой трассе с постоянной скорость его:
а. Ускорение равно нулю
б. Скорость равна нулю
в. Оба этих
d . Ни один из них.
Рассуждение : Скорость вокруг круговой дорожки меняется, потому что меняется его направление. Ускорение меняется как хорошо. Таким образом, (d) является ответом.
16. Автомобиль разгоняется из состояния покоя со скоростью 2 метра в секунду за
второй. Какова его скорость через 3 с после начала движения автомобиля?
Какова его скорость через 3 с после начала движения автомобиля?
а. 2 м/с
б. 3 м/с
в. 4 м/с
d . 6 м/с
е. Ни один из них.
17. Мяч подброшен вверх и пойман при возвращении вниз. Если пренебречь сопротивлением воздуха, его скорость в момент захвата:
.а. Больше, чем скорость, которую он имел, когда его подбрасывали вверх.
б. Меньше, чем скорость, которую он имел при броске вверх.
в. Такая же скорость, как при броске вверх.
18. Объект проходит 8 метров за первую секунду пути, Снова 8 метров на третьей секунде. Его ускорение в метрах в секунду:
и . 0
б. 5
в. 8
д. 10
е. Более 10.
19. В один момент объект в свободном падении движется вверх со скоростью 50 метров в секунду. Через одну секунду его скорость составляет примерно:
а.
100 м/с
б. 60 м/с
в. 55 м/с
д. 50 м/с
e . 40 м/с.
Рассуждение : При свободном падении ускорение составляет около 10 м/с/с. Таким образом, скорость объектов будет уменьшаться на 10 м/с каждую секунду.
20. Без учета сопротивления воздуха предметы падают с постоянной скоростью:
а. Скорость
б. Скорость
в . Ускорение
д. Расстояние каждую последующую секунду.
21. Мяч подброшен вверх и пойман при возвращении вниз. При наличии сопротивления воздуха скорость, с которой поймано это:
а. Больше, чем скорость, которую он имел, когда его подбрасывали вверх.
б. Меньше, чем скорость, которую он имел при броске вверх.
в. Такой же, как скорость, которую он имел при броске вверх.
Рассуждение : При наличии сопротивления воздуха,
мяч достигнет своей высшей точки, которая короче корпуса
когда нет сопротивления воздуха. При падении мяча его ускорение равно
быть менее 9,8 м/с2. Таким образом, в конце его конечная скорость будет меньше
Случай отсутствия воздуха.
При падении мяча его ускорение равно
быть менее 9,8 м/с2. Таким образом, в конце его конечная скорость будет меньше
Случай отсутствия воздуха.
22. Яблоко падает с дерева и падает на землю на 5 метров ниже. Это бьет по земле со скоростью около:
а. 5 м/с
б. 10 м/с
в. 15 м/с
д. 20 м/с
е. Недостаточно информации для оценки.
Рассуждение : Чтобы яблоко упало с высоты 5 м его падение, оно должно падать примерно 1 секунду (прочитайте страницы 46-47 и нажмите Таблица 3.3). Таким образом, за одну секунду его скорость увеличивается примерно на 10 м/с. Это бьет землю со скоростью 10 м/с.
23. Камень падает на дно за 6 секунд. шахтный ствол. Насколько глубока шахта?
а. Около 60 м
б. Около 120 м
c . Около 180 м
д. Более 200 м
Рассуждение : Используя d = (1/2) g t2 = (1/2)(9. 8)(36)
= около 180 м. (см. стр. 46).
8)(36)
= около 180 м. (см. стр. 46).
24. За каждую секунду падения расстояние свободного падения объекта упадет это:
а. Около 5 м
б. Около 10 м
в. То же, но не 5 м и не 10 м
д. Увеличение
е. Ни один из них.
Рассуждение : В первую секунду (после предмет падает) расстояние = 5 м. Но каждую секунду после этого расстояние продолжает увеличиваться. См. Таблицу 3.3 на стр. 47.
25. Если снаряд выпущен прямо вверх со скоростью 10 м/с, время, необходимое для достижения вершины своего пути, составляет примерно:
и . 1 секунда
б. 2 секунды
в. 10 секунд
д. Недостаточно информации для оценки.
Рассуждение : Наверху его скорость должна идти
до нуля. Но ускорение (т.е. изменение скорости в каждую секунду) составляет 10 м/с/с.
Таким образом, его скорость уменьшается на 10 м/с каждую секунду. Так как она началась с 10 м/с,
ему потребуется 1 секунда, чтобы его скорость уменьшилась до нуля и достигла вершины.
Так как она началась с 10 м/с,
ему потребуется 1 секунда, чтобы его скорость уменьшилась до нуля и достигла вершины.
Как решать квадратичные задачи о движении снаряда
General Word ProblemsMax/Min Problems
Purplemath
Исчисление включает в себя поиск максимумов, минимумов и нулей. Вы почувствуете это с квадратичными задачами. На самом деле, если/когда вы дойдете до исчисления, вы обнаружите, что некоторые из домашних упражнений будут идентичны тем, которые вы делаете сейчас; просто у вас будут новые инструменты для поиска ответов.
Содержание продолжается ниже
MathHelp.com
Основная категория текстовых задач с квадратными уравнениями связана с так называемым движением снаряда. Для наших целей снаряд — это любой объект, который бросают, стреляют или бросают. Почти всегда в этом контексте объект изначально движется прямо вверх или прямо вниз. (Если он начинает движение вверх, то, естественно, позже он снова пойдет вниз.) Эта начальная скорость движения и есть скорость.
В упражнениях с движением снаряда объект, который высвобождается (выстреливается, падает или что-то еще
Что говорит об объекте знак скорости?
Начальная скорость объекта в этих упражнениях говорит нам, как объект был освобожден. Начальное значение скорости будет либо нулевым (значит, объект был только что брошен), либо положительным (значит, он был брошен или выстрелен вверх), либо отрицательным (значит, объект был брошен вниз).
Что означает »
g «обозначает?В упражнениях на движение снаряда коэффициент при квадрате члена равен −½ g . g обозначает постоянную силы тяжести (на Земле), которая составляет -9,8 метра в секунду. квадрат (то есть метры в секунду в секунду) в метрических единицах или -32 фута в секунду в квадрате в имперских единицах. Знаки «минус» отражают тот факт, что гравитация Земли тянет нас и рассматриваемый объект вниз
Что означает «в секунду в квадрате»?
Ускорение (являющееся изменением скорости, а не самой скоростью) измеряется с точки зрения того, насколько скорость изменяется в единицу времени. Итак, если скорость объекта измеряется в футах в секунду, то ускорение этого объекта говорит о том, насколько эта скорость изменяется в единицу времени; то есть ускорение измеряет, насколько футы в секунду изменяются в секунду. И это дубликат «в секунду» — это то, как мы получаем «секунду в квадрате». Это из физики ситуации.
Итак, если скорость объекта измеряется в футах в секунду, то ускорение этого объекта говорит о том, насколько эта скорость изменяется в единицу времени; то есть ускорение измеряет, насколько футы в секунду изменяются в секунду. И это дубликат «в секунду» — это то, как мы получаем «секунду в квадрате». Это из физики ситуации.
Какое значение следует использовать для гравитации?
Если упражнение по движению снаряда выражено в футах, милях или других имперских единицах измерения, то используйте −32 для силы тяжести; если единицами измерения являются метры, сантиметры или другие метрические единицы, используйте −9,8 для силы тяжести.
Что такое уравнение движения снаряда?
Уравнение движения снаряда составляет S ( T ) = −½ G x 2 + V 0 0 + 5.
5.
5.
5.
5.
5.
5.
5.0375 — гравитационная постоянная, v 0 — начальная скорость (то есть скорость в момент времени t = 0), ч 0 — начальная высота объекта (то есть высота объекта в t = 0, время выпуска).
Да, вам нужно следить за всеми этими вещами при работе с движением снаряда.
- Объект запускается со скоростью 19,6 метра в секунду (м/с) с платформы высотой 58,8 метра. Уравнение для высоты объекта с в момент времени t секунд после запуска равно с ( t ) = −4,9 t 2 + 19,6 t 7 м 3 ≥ 590,8 Когда предмет ударяется о землю?
На какой высоте (над уровнем земли) объект врезается в землю? Ну, очевидно же, ноль. Итак, я ищу время, когда высота с = 0. Я установлю с равным нулю и решу:
0 = −4,9 t 2 + 19,6 t + 58,8
0 = t 2 − 4 t − 12
0 = ( t — 6)( t + 2)
Тогда t = 6 или t = -2. Второе решение — за две секунды до запуска, что не имеет смысла в данном контексте. (На графике это имеет смысл, потому что линия пересекает ось x в точке -2, но отрицательное время не работает в этой задаче со словами.) Итак, » t = −2″ является посторонним решением, и я его проигнорирую.
(На графике это имеет смысл, потому что линия пересекает ось x в точке -2, но отрицательное время не работает в этой задаче со словами.) Итак, » t = −2″ является посторонним решением, и я его проигнорирую.
Вместо этого мой ответ на это упражнение (то есть правильный ответ в контексте) является другим значением решения. Они спросили меня о времени , а время здесь измеряется в секундах, поэтому мой ответ:
Объект ударяется о землю через шесть секунд после запуска
Обратите внимание на построение уравнения высоты в задаче выше (да, мы рассмотрели это в начало, но вам действительно понадобится эта информация, так что мы вернемся.)
Начальная высота пуска была 58,8 метра, а постоянный срок был «58,8». Начальная скорость (или стартовая скорость) составляла 19,6 м/с, а коэффициент при линейном члене равнялся «19,6». Это всегда верно для этих проблем с движением снаряда вверх/вниз. (Если у вас есть упражнение с боковым движением, уравнение будет иметь другую форму, но они всегда дадут вам это уравнение. ) Начальная скорость — это коэффициент для среднего члена, а начальная высота — это постоянный член. .
) Начальная скорость — это коэффициент для среднего члена, а начальная высота — это постоянный член. .
А коэффициент при старшем члене получается от силы тяжести. Этот коэффициент отрицательный, так как гравитация тянет вниз, и значение будет либо «−4,9» (если ваши единицы измерения «метры»), либо «–16» (если ваши единицы измерения — «футы»). Да, эти значения составляют половину значений гравитационной постоянной, перечисленных в начале этой страницы; они умножили ½.
В общем, формат уравнения движения снаряда следующий:
с ( t ) = − gt 2 + v 0 t + h 0
9 …где « g 9″ получено из «6» или « g 9″ здесь. сила тяжести (технически это сила тяжести на Земле ), « v 0 » («ви-ноль» или «ви-минус-ноль») — начальная скорость, и « h 0 «(«aitch-naught» или «aitch-sub-zero») — начальная высота. Запомните это уравнение (или хотя бы его значение), потому что оно может понадобиться вам на тесте. Хм… На этот раз мне не дали уравнение. Но это нормально, потому что я могу составить уравнение из информации, которую мне дали. Начальная высота составляет 80 футов над землей, а начальная скорость — 64 фута/с вверх. Поскольку моими единицами измерения являются футы, то число для силы тяжести будет равно −16, и мое уравнение: s ( t ) = −16 t 2 + 64 t + 80 Они хотят, чтобы я нашел максимальную высоту. Для такого отрицательного квадратичного уравнения максимум будет в вершине перевернутой параболы. Так что они действительно хотят, чтобы я нашел вершину. Из графика я знаю, как найти вершину; в этом случае вершина находится в точке ( h , k ) = (2, 144): h = − b / 2 a = −(64)/2(−16) = −64/−32 = 2 Но что говорят мне координаты этой вершины? Согласно моему уравнению, я подставляю значения времени и извлекаю значения высоты, поэтому ввод 2 — это время, а вывод 144 — высота. Требуется две секунды, чтобы достичь максимальной высоты в 144 фута. Пока вы четко маркируете, вам не нужно полное предложение (как я использовал выше) для вашего ответа. Таким образом, вы также можете дать ответ: «время: 2 секунды; высота: 144 фута». На этот раз я использую метры, поэтому гравитационное число будет −4,9. Поскольку объект начинался на уровне земли, начальная высота была равна 0. Тогда мое уравнение: s ( t ) = −4,9 t 2 + 39,2 t 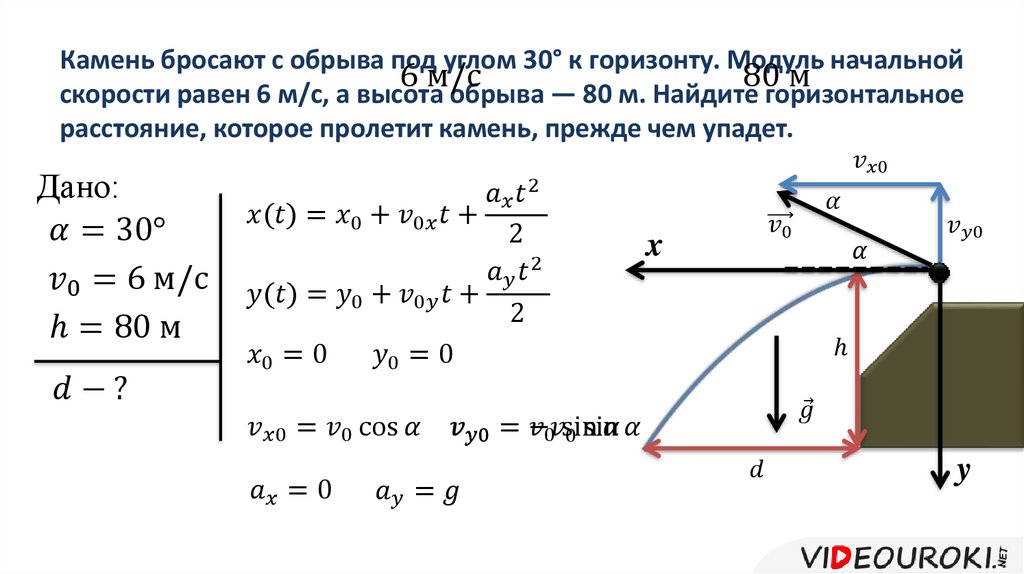
k = с (2) = −16(2) 2 + 64(2) + 80 = -16(4) + 128 + 80 = 208 — 64 = 144
Почему «два раза» и как узнать, что период времени находится между этими двумя временами? Потому что первый раз будет, когда объект пройдет высоту 34,3 метра на пути к своей максимальной высоте, а второй раз, когда он преодолеет 34,3 метра, падая обратно на землю. Итак, я должен решить следующее:
Итак, я должен решить следующее:
-4,9 t 2 + 39,2 t = 34,3
t 2 — 8 5 0 + 5 0 + ( t − 7)( t − 1) = 0
Два решения: в моменты времени t = 1 и t = 7. Таким образом, объект находится на высоте 34,3 метра через одну секунду после запуска (поднимается вверх). ) и снова через семь секунд после запуска (спуск). Вычитая, чтобы найти разницу, я обнаружил, что:
Объект находится на высоте 34,3 метра или выше в течение шести секунд.
Опять же, технически вам не нужно полное предложение для вашего прямого ответа; сказать «6 секунд», вероятно, достаточно. Но обязательно включите в свой ответ единицу измерения «секунды».
Не удивляйтесь, если многие из ваших упражнений сработают так же «аккуратно», как и в приведенных выше примерах. Многие учебники до сих пор тщательно разрабатывают свои упражнения, чтобы вы могли решать их с помощью факторизации (то есть, быстро выполняя алгебраические операции).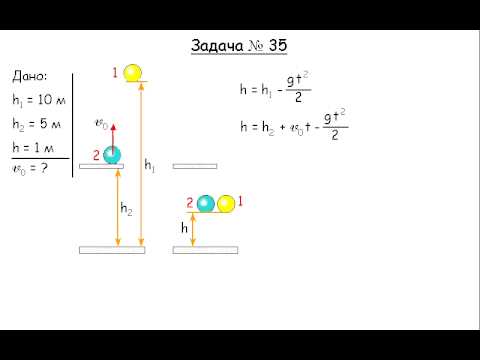
Однако (справедливое предупреждение!), сильная зависимость от калькуляторов приводит к тому, что больше текстов приводит к созданию «интересных» (то есть излишне сложных) упражнений, поэтому некоторые (или все) ваши упражнения могут включать гораздо более беспорядочные вычисления, чем здесь отображались. Если это так, внимательно изучите эти «хорошие» примеры, пока не будете уверены, что следуете рассуждениям.
- После окончания семестра вы обнаруживаете, что математический факультет (снова) изменил учебники, поэтому книжный магазин не выкупит вашу почти новую книгу. Вы и ваш друг Герман решаете проявить творческий подход. Вы идете на крышу двенадцатиэтажного здания и смотрите через край на отражающий бассейн в 160 футах ниже. Вы бросаете свою книгу через край в тот самый момент, когда Герман бросает свою книгу прямо вниз со скоростью 48 футов в секунду. На сколько секунд его книга опережает вашу? (Округлите ответ до двух знаков после запятой.)
Наши начальные высоты запуска будут одинаковыми: мы оба запускаем с высоты 160 футов над землей. А гравитационное число, поскольку мы работаем в футах, будет −16. Моя начальная скорость равна нулю, так как я только что уронил свою книгу, но скорость моего приятеля Германа равна минус 48, отрицательная скорость возникает из-за того, что он бросил свою книгу вниз , а не вверх. Итак, наши уравнения «высоты»:0374 т 2 + 160
А гравитационное число, поскольку мы работаем в футах, будет −16. Моя начальная скорость равна нулю, так как я только что уронил свою книгу, но скорость моего приятеля Германа равна минус 48, отрицательная скорость возникает из-за того, что он бросил свою книгу вниз , а не вверх. Итак, наши уравнения «высоты»:0374 т 2 + 160
его: с ( t ) = −16 t 2 − 48 t + 160
В каждом случае мне нужно найти время, за которое книги достигнут нулевой высоты (высоты нулевой из нулевого «уровня земли»), так:
шахта: 0 = −16 T 2 + 160
T 2 — 10 = 0
T =
668 .1868 9056.1868 .1868 .168968 8 9056.18968 68 9056.18968 9056.18968 9056.18 68 9056.18 9056.18 68 9056.18905 — 10 = 0 0003. 10)
его: 0 = −16 T 2 — 48 T + 160
T 2 + 3 T — 10 = 0
( T 9037 + 5) 5) 5) 5) 5) 5) 5) 5) 5) 5) 5) 5) 5) 5) 5) 5) 5) ( + 5) 5) 5). t = −5, +2
t = −5, +2
Я буду игнорировать отрицательные значения времени, поскольку они не имеют значения в данном контексте. (В какой-то момент в каком-то упражнении может возникнуть случай, когда отрицательное значение оказывается полезным в данном контексте, поэтому мне нужно помнить, что нужно думать о значениях и контексте, а не рефлекторно отбрасывать любые и все отрицательные решения.)
Книга Германа падает в воду через две секунды, а моя — через
sqrt (10) секунд, или примерно через 3,16 секунды. То есть:
Книга Германа падает на воду примерно на 1,16 секунды раньше, чем моя.
Время от времени они будут хитрить и помещать «снарядную» проблему в другую среду. Уравнение останется прежним по структуре, но вам, возможно, придется учитывать другое значение гравитации.
- Международное космическое агентство наконец посадило робота-исследователя на внесолнечную планету.
 Некоторые зонды выдвигаются из корпуса спускаемого аппарата для проведения различных тестов. Чтобы продемонстрировать сокрушительный вес гравитации на этой планете, камера посадочного модуля направлена на порт выброса зонда на уровне земли, и порт запускает бейсбольный мяч прямо вверх со скоростью 147 футов в секунду (фут/с), что примерно соответствует максимальной скорости профессиональный кувшин. Сила гравитации на этой планете составляет 98 фут/с 2 . Если предположить, что ветра нет и что зонд может вовремя уйти в сторону, сколько времени потребуется, чтобы шар снова врезался в поверхность?
Некоторые зонды выдвигаются из корпуса спускаемого аппарата для проведения различных тестов. Чтобы продемонстрировать сокрушительный вес гравитации на этой планете, камера посадочного модуля направлена на порт выброса зонда на уровне земли, и порт запускает бейсбольный мяч прямо вверх со скоростью 147 футов в секунду (фут/с), что примерно соответствует максимальной скорости профессиональный кувшин. Сила гравитации на этой планете составляет 98 фут/с 2 . Если предположить, что ветра нет и что зонд может вовремя уйти в сторону, сколько времени потребуется, чтобы шар снова врезался в поверхность?
Чтобы составить уравнение для этого упражнения, мне нужно иметь в виду, что значение коэффициента g из приведенного выше уравнения движения снаряда составляет половину значения силы гравитации в данном месте. .
В физике существует «универсальная гравитационная постоянная» G , представляющая собой гравитационное притяжение, присущее нашей Вселенной (или, по крайней мере, нашей ее области). Каждый объект оказывает свою гравитационную силу, которая связана с его собственной массой и универсальной постоянной 9.0374 Г . В формуле «движение снаряда» « г » — это половина значения силы гравитации для этого конкретного тела. Например, гравитационная сила на Земле направлена вниз со скоростью 32 фута/с 2 , но мы использовали 16 в уравнении.
Каждый объект оказывает свою гравитационную силу, которая связана с его собственной массой и универсальной постоянной 9.0374 Г . В формуле «движение снаряда» « г » — это половина значения силы гравитации для этого конкретного тела. Например, гравитационная сила на Земле направлена вниз со скоростью 32 фута/с 2 , но мы использовали 16 в уравнении.
Итак, г для моего уравнения на этот раз будет на 98 ÷ 2 = 49 футов в секунду в квадрате. Тогда:
с = −49 t 2 + 147 t
0 = −49 т 2 + 147 т
0 = t 2 − 3 t
0 = t ( t − 3)
Тогда t = 0 или t = 3. Первое решение представляет момент запуска мяча, поэтому мне нужно второе решение.
Чтобы мяч коснулся земли, требуется три секунды.
Примечание: на Земле мячу потребовалось бы немногим более девяти секунд, чтобы упасть на землю.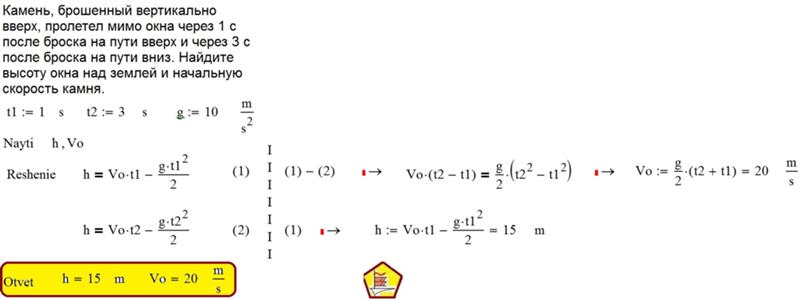

 Меньше и меньше
Меньше и меньше  3600 мм/с
3600 мм/с  100 м/с
100 м/с  Некоторые зонды выдвигаются из корпуса спускаемого аппарата для проведения различных тестов. Чтобы продемонстрировать сокрушительный вес гравитации на этой планете, камера посадочного модуля направлена на порт выброса зонда на уровне земли, и порт запускает бейсбольный мяч прямо вверх со скоростью 147 футов в секунду (фут/с), что примерно соответствует максимальной скорости профессиональный кувшин. Сила гравитации на этой планете составляет 98 фут/с 2 . Если предположить, что ветра нет и что зонд может вовремя уйти в сторону, сколько времени потребуется, чтобы шар снова врезался в поверхность?
Некоторые зонды выдвигаются из корпуса спускаемого аппарата для проведения различных тестов. Чтобы продемонстрировать сокрушительный вес гравитации на этой планете, камера посадочного модуля направлена на порт выброса зонда на уровне земли, и порт запускает бейсбольный мяч прямо вверх со скоростью 147 футов в секунду (фут/с), что примерно соответствует максимальной скорости профессиональный кувшин. Сила гравитации на этой планете составляет 98 фут/с 2 . Если предположить, что ветра нет и что зонд может вовремя уйти в сторону, сколько времени потребуется, чтобы шар снова врезался в поверхность?
Leave A Comment