неравенства | Справочник по математике
1. Если a > b, то b < a; наоборот, если а < b, то b > a.
Пример. Если 5х – 1 > 2x + 1, то 2х +1< 5x – 1.
2. Если a > b и b > с, то а > с. Точно так же, а < b и b < с, то a < с.
Пример. Из неравенств x > 2у, 2y > 10 следует, что x >10.
3. Если a > b, то a + c > b + с и a – c > b – c. Если же а < b, то а + с<b+c и a – c<b – c, т.е. к обеим частям неравенства можно прибавить (или вычесть) одну и ту же величину
 Дано неравенство х + 8>3. Вычитая из обеих частей неравенства число 8, находим х > – 5.
Дано неравенство х + 8>3. Вычитая из обеих частей неравенства число 8, находим х > – 5.
Пример 2. Дано неравенство х – 6 < – 2. Прибавляя обеим частям 6, находим х < 4.
4. Если a > b и с > d, то a + c >b + d; точно так же если а < b и с < d, то a + с < b + d, т. е. два неравенства одинакового смысла ) можно почленно складывать. Это справедливо и для любого числа неравенств, например, если
Пример 1. Неравенства – 8 > – 10 и 5 > 2 верны. Складывая их почленно, находим верное неравенство – 3 > – 8.
Пример 2. Дана система неравенств (1/2)х + (1/2)у < 18; (1/2)х – (1/2)у < 4. Складывая их почленно, находим x < 22.
Дана система неравенств (1/2)х + (1/2)у < 18; (1/2)х – (1/2)у < 4. Складывая их почленно, находим x < 22.
5. Если a > b и c < d, то а – с > b – d; если а < b и с – d, то 
Пример 1. Неравенства 12 < 20 и 15 > 7 верны. Вычитая почленно второе из первого и оставляя знак первого, получаем верное неравенство – 3 < 13. Вычитая почленно первое из второго и оставляя знак второго, находим верное неравенство 3 > – 13.
Пример 2
6. Если а > b и m — положительное число, то ma > mb и a/n > b/n, т. е. обе части неравенства можно разделить или умножить на одно и то же положительное число (знак неравенства остается тем же).Если же a > b и n – отрицательное число, то na < nb и a/n < b/n, т. е. обе части неравенства можно умножить или разделить на одно и то же отрицательное число, но при том знак неравенства нужно изменить на противоположный.
е. обе части неравенства можно умножить или разделить на одно и то же отрицательное число, но при том знак неравенства нужно изменить на противоположный.
Пример 1. Разделив обе части верного неравенства 25 > 20 на 5, получим верное неравенство 5 > 4. Если же мы делим обе части неравенства 25 > 20 на – 5, то нужно переменить знак > на < , и тогда получим верное неравенство – 5 < – 4.
Пример 2. Из неравенства 2х < 12 следует, что х < 6.
Пример 3. Из неравенства -(1/3)х – (1/3)х > 4
Пример 4. Дано неравенство х/к > у/l; из него следует, что lx > ky, если знаки чисел l и k одинаковы, и что lx < ky, если знаки чисел l и k противоположны. {2}-2|x-1| \leq 0\)
{2}-2|x-1| \leq 0\)
Вопрос B15 #3421 Математика (профиль)
Решите неравенство: Подробнее Узнать ответ КомментироватьВопрос B15 #3650 Математика (профиль)
Решить неравенство: Подробнее Узнать ответ КомментироватьВопрос B15 #3669 Математика (профиль)
Решить неравенство Подробнее Узнать ответ КомментироватьВопрос B15 #3793 Математика (профиль)
Решите неравенство:Подробнее Узнать ответ КомментироватьВопрос B15 #3812 Математика (профиль)
Решить неравенство: Подробнее Узнать ответ КомментироватьВопрос B15 #3831 Математика (профиль)
Решите неравенство Подробнее Узнать ответ КомментироватьПутеводитель по неравенствам (задачи №15 ЕГЭ по математике)
Решите неравенство
!!! Смотрите также подборку задач С3 (с ответами) для подготовки к ЕГЭ !!!Список всех неравенств (С3), разобранных на сайте:
-9.
Ответ: Видеорешение New*
-8. (Реальный ЕГЭ, 2019) Решите неравенство
Ответ: Решение Видеорешение New*
-7. (Реальный ЕГЭ, 2019) Решите неравенство
Ответ: Решение
-6. (Реальный ЕГЭ, 2018) Решите неравенство
Ответ: Решение Видеорешение New*
-5. (Досрочный резервный ЕГЭ, 2018) Решите неравенство
Ответ: Решение Видеорешение New*
-4. (Досрочный ЕГЭ, 2018) Решите неравенство
Ответ: Решение Видеорешение New*
-3. (Резервный ЕГЭ, 2017) Решите неравенство
Ответ: Решение
-2. (Резервный ЕГЭ, 2017) Решить неравенство
Ответ: {} Решение Видеорешение New*
-1. (Реальный ЕГЭ, 2017) Решить неравенство
Ответ: {}Решение
0. (Реальный ЕГЭ, 2017) Решить неравенство
(Реальный ЕГЭ, 2017) Решить неравенство
Ответ: {} Решение
1.
Ответ: Решение Видеорешение New*
2. (Резервн. ЕГЭ, 2016) Решите неравенство
Ответ: Решение Видеорешение New*
3. (ЕГЭ, 2016) Решите неравенство
Ответ: Решение
4. (Т/Р, 2016) Решите неравенство
Ответ: Решение
5. (Досрочн. ЕГЭ, 2016) Решите неравенство
Ответ: . Решение Видеорешение New*
6. (ЕГЭ, 2015) Решите неравенство
Ответ: {}Решение
7. (Т/Р 2013)
Ответ: Решение
8. (Т/Р 2013) Решите систему неравенств
Ответ: Решение
9. (Т/Р 2013) Решите систему неравенств
(Т/Р 2013) Решите систему неравенств
Ответ: {}. Решение
10. (ДЕМО 2014) Решите систему неравенств
Ответ: Решение
11. (ЕГЭ 2013) Решите систему неравенств
Ответ: {} Решение
12. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
13. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
14. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
15. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение Видеорешение
16. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
17. (Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
18. (Т/Р А. Ларина) Решите неравенство
Ларина) Решите неравенство
Ответ: {}. Решение
19. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
20. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
21. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
22. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
23. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
24. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
25. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
26. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
27. (Т/Р А.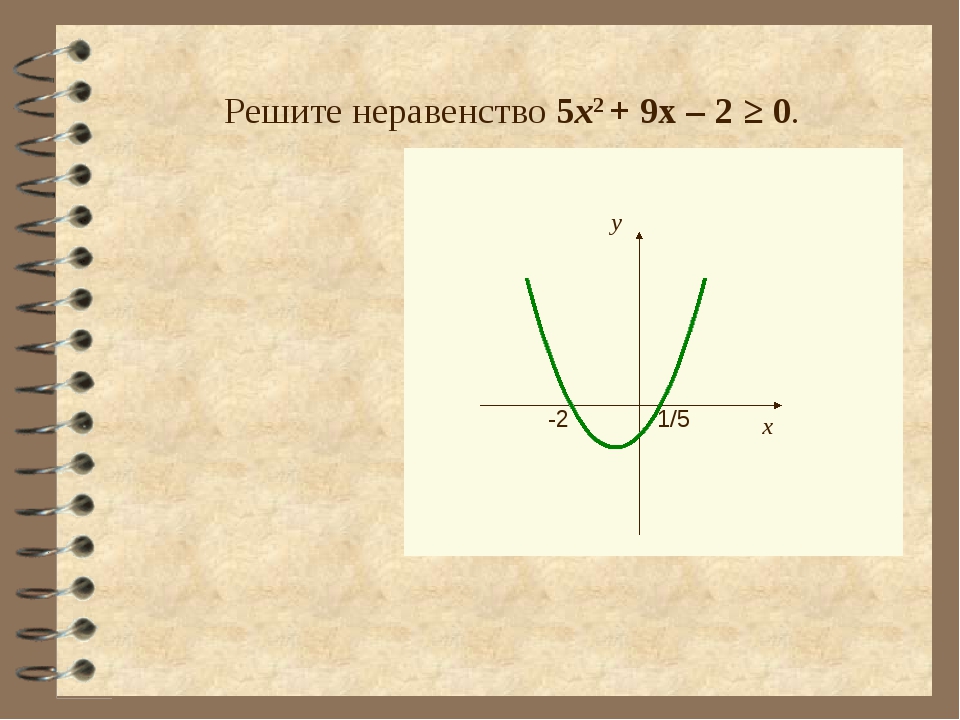 Ларина) Решите неравенство
Ларина) Решите неравенство
Ответ: Решение
28. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
29. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
30. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
31. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
33. (Т/Р А. Ларина) Решите неравенство
.
Ответ: {}Решение
34. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
35. (Т/Р А. Ларина) Решите неравенство
.
Ответ: {}Решение
36. (Т/Р А. Ларина) Решите неравенство
Ответ: {}. Решение
37. (Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
38. (Т/Р А. Ларина) Решите неравенство
(Т/Р А. Ларина) Решите неравенство
Ответ: {} Решение
39. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
40. (Т/Р А. Ларина) Решите неравенство
.
Ответ: Решение
41. (Т/Р А. Ларина) Решите неравенство
Ответ: {}. Решение
42. (Т/Р А. Ларина) Решите неравенство
Ответ: {}. Решение
43. (Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
44. (Т/Р А. Ларина) Решите неравенство
Ответ: {}. Решение
45. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
46. (Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
47. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
48. (Т/Р А. Ларина) Решите неравенство
(Т/Р А. Ларина) Решите неравенство
.
Ответ: Решение
49. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
50. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
51. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
52. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
53. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
54. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
55. (Т/Р А. Ларина) Решите неравенство
.
Ответ: Решение
56. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
57. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
58. (Т/Р А. Ларина) Решите неравенство
(Т/Р А. Ларина) Решите неравенство
Ответ: Решение
59. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
60. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
61. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
62. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
63. (Т/Р А. Ларина) Решите неравенство
Ответ: {}. Решение
64. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
65. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
66. (Т/Р А. Ларина) Решите неравенство
Ответ: (]. Решение
67. (Т/Р А. Ларина) Решите неравенство
Ответ: [)(]. Решение
Решение
68. (Т/Р А. Ларина) Решите неравенство
Ответ: [). Решение
69. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
70. (Т/Р А. Ларина) Решите систему неравенств
Ответ: Решение
71. (Т/Р А. Ларина) Решите систему неравенств
Ответ: [spoiler]{}Решение
72. (Т/Р А. Ларина) Решите систему неравенств
Ответ: Решение
73. (Т/Р А. Ларина) Решите неравенство
Ответ: {} Решение
74. (Т/Р А. Ларина) Решите неравенство
Ответ: {}, Решение
75. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
76. (Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
77. (Т/Р А. Ларина) Решите неравенство
(Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
78. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
79. (Т/Р А. Ларина) Найдите область определения функции
Ответ: {}Решение
80. (Т/Р А. Ларина) Решите неравенство
Ответ: {}. Решение
81. (Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
82. (Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
83. (Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
84. (Т/Р А. Ларина) Решите неравенство
Ответ: {}. Решение
85. (Т/Р, 2017) Решите неравенство
Ответ: Решение
86. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
87. (Т/Р А. Ларина) Решите неравенство
(Т/Р А. Ларина) Решите неравенство
Ответ: Решение
88. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
89. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
90. (Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
91. (Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
92. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
93. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
94. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
95. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
96. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
97. (Т/Р А. Ларина) Решите неравенство
(Т/Р А. Ларина) Решите неравенство
Ответ: Решение
98. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
99. (Т/Р А. Ларина) Решите неравенство
Ответ: {}. Решение
100. (Т/Р А. Ларина) Решите неравенство
Ответ: {}Решение
101. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
102. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
103. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
104. (Т/Р 283 А. Ларина) Решите неравенство
Ответ: Видеорешение
Ошибки в неравенствах / math5school.ru
Неравенства по праву считаются одним из самых трудных разделов школьной математики, и при их решении допускается наибольшее количество ошибок. Рассмотрим наиболее часто встречающиеся из них.
Рассмотрим наиболее часто встречающиеся из них.
Некоторые общие ошибки
K Упражнение | L Неправильно | J Правильно |
Указать наименьшее целое решение неравенства: x > 4 | х ∈ (4; +∞), наименьшее целое число 4. Ответ:x = 4 | х ∈ (4; +∞), наименьшее целое число 5. Ответ: x = 5. |
Решить неравенство: –х < 1 | x < –1 Ответ: (–∞; –1) | x > –1 Ответ: (–1; +∞) |
Сравнить a и b, если 1/a < 1/b | Ответ: если a и bположительные, то a > b; если a и b отрицательные, то a < b | Ответ: если a · b > 0, то a > b; |
Оценить х из 0,25 ≤ 1/x ≤ 2 | Ответ:4 ≥ х ≥ 0,5 | Ответ: 0,5 ≤ х ≤ 4 |
\[a< x< b\] | \[\left[\begin{matrix} x> a\\ x< b \end{matrix} \right. | \[\begin{cases} x> a\\ x< b \end{cases} \] |
Ошибки в квадратных неравенствах
Квадратные(квадратичные)неравенства – неравенства вида
aх2 + bx + c > 0, (< 0, ≥ 0, ≤ 0)
часто решаются разложением левой части на линейные множители, то есть
aх2 + bx + c = a (x – x1) (x – x2) > 0,
где x1 и x2 – корни квадратного трехчлена aх2 + bx +c. Это возможно сделать, когда корни квадратного трехчлена являются действительными числами. Однако в некоторых случаях при решении неравенств этим способом можно легко прийти к неверному заключению.
K Решить неравенство | L Неправильное решение | J Правильное решение |
– х2 + 5x– 6 < 0 | – (x – 2) (x – 3) < 0, х ∈ (2; 3). Ответ: (2; 3) | х2 – 5x + 6 < 0, (x – 2) (x – 3) > 0, х ∈ (–∞; 2)∪(3; +∞). Ответ: (–∞; 2)∪(3; +∞) |
х2 + 6x + 9 ≥ 0 | (х+ 3)2 ≥ 0, х + 3 ≥ 0, х ≥ –3. Ответ: [–3; +∞) | Неравенство (х + 3)2 ≥ 0 выполняется для всех значений х, значит х – любое число. Ответ: (–∞; +∞) |
х2 – 4x + 4 > 0 | Неравенство (х– 2)2 > 0 выполняется для всех значений х, значит х – любое число. Ответ: (–∞; +∞) | При х = 2 (х– 2)2 = 0, значит, х ≠ 2. Ответ: (–∞; 2)∪(2; +∞) |
х2 + 10x + 25 ≤ 0 | (х + 5)2 ≤ 0 – решений нет. Ответ: Ø | Неравенство (х + 5)2 ≤ 0 выполняется при единственном значении х = –5. Ответ: –5 |
х2 + x + 2 > 0 | Так как D = 12 – 2·2 = –3 < 0, то решений нет. Ответ: Ø | Так как старший коэффициент положительный и D < 0, то при любом значении х левая часть неравенства положительна. Ответ: (–∞; +∞) |
х2 – 9 ≤ 0 | х2 ≤ 9, х ≤ 3. Ответ: (–∞; 3] | х2 ≤ 9, |х| ≤ 3, \[\begin{cases} x\geq -3,\\ x\leq +3. \end{cases}\] Ответ: [–3; 3] |
х2 – 9 ≥ 0 | х2 ≥ 9, х ≥ 3. Ответ: [3; +∞). Комментарий. Необходимо помнить, что, вообще говоря, нельзя извлекать корень из обеих частей неравенства. | х2 ≥ 9, |х| ≥ 3, \[\left[\begin{matrix} x\geq +3,\\ x\leq -3. Ответ: (–∞; –3]∪[3; +∞) |
Ошибки в дробно-рациональных неравенствах
Нередко ошибки появляются при сведении неравенств к системе неравенств, совокупности неравенств или совокупности систем неравенств.
K Упражнение. Решить неравенство \(\large \frac{x+6}{x}>0.\)
L Неправильное решение.
\(\begin{cases} x+6>0,\\ x>0; \end{cases}\;\;\; \begin{cases} x>-6,\\ x>0; \end{cases}\;\;\; x>0.\)
Ответ: (0; +∞).
Комментарий. Дробь может быть положительной в двух случаях: когда числитель и знаменатель одновременно положительны, и когда числитель и знаменатель отрицательны.
J Правильное решение.
\(\left[\begin{matrix} \begin{cases} x + 6 > 0, \\ x > 0, \end{cases}\\ \begin{cases} x + 6 < 0,\\ x < 0; \end{cases} \end{matrix} \right.\;\;\;\;\left[\begin{matrix} \begin{cases} x > — 6,\\ x > 0, \end{cases}\\ \begin{cases} x < — 6,\\ x < 0; \end{cases} \end{matrix} \right. \;\;\;\;\left[\begin{matrix} x > 0,\;\;\\ x < -6.\end{matrix} \right.\)
\;\;\;\;\left[\begin{matrix} x > 0,\;\;\\ x < -6.\end{matrix} \right.\)
Ответ: (–∞; –6)∪(0; +∞).
Часто учащиеся допускают ошибки при умножении неравенства на знаменатель, который не имеет определенного знака при любых значениях переменной.
K Упражнение 1. Решить неравенство \(\large \frac{2x+3}{x-1}>1.\)
L Неправильное решение.
2x + 3 > x – 1;
x > – 4.
Ответ: (–4; +∞).
Комментарий. Нельзя умножать обе части неравенства на знаменатель, который содержит неизвестное, если заранее не известен его знак. Если же вы все-таки не можете обойтись без умножения, то нужно рассматривать два варианта:
х –1 > 0 или х – 1 < 0.
J Правильное решение.
Рассмотрим один из возможных способов решения данного неравенства:
\(\left[\begin{matrix} \begin{cases} 2 x + 3 > x — 1, \\ x — 1 > 0, \end{cases}\\ \begin{cases} 2 x + 3 < x — 1, \\ x — 1 < 0; \end{cases} \end{matrix} \right. 2}>0.\)
2}>0.\)
L Неправильное решение.
х2 + 81 > 0 при х ≠ ±2.
Ответ: (–∞; –2)∪(–2; 2)∪(2; +∞).
J Правильное решение.
Так как дробь больше нуля, и числитель принимает положительные значения для любого допустимого значения х, то
4 –х2 > 0,
х2 < 4,
–2 < x < 2.
Ответ: (–2; 2).
K Упражнение 3. Решить неравенство 1/x ≥ 2.
L Неправильное решение.
2x ≤ 1;
x ≤ 1/2.
Ответ: (–∞; 1/2].
J Правильное решение.
Так как обе части неравенства представлены стандартными функциями, то легко использовать графические метод решения неравенства:
Очевидно, что значения функции у = 1/x достигают 2 и более при х ∈ (0; 1/2]. 2}>0\), которое, очевидно, равносильно неравенству х2 – 81 > 0, полученному из первого умножением на положительное число 4 + х2.
2}>0\), которое, очевидно, равносильно неравенству х2 – 81 > 0, полученному из первого умножением на положительное число 4 + х2.
Ошибки при использовании метода интервалов
Рассмотрим типичные ошибки, возникающие при решении неравенств с применением метода интервалов.
K Упражнение 1. Решить неравенство х (х – 6) (х + 1) ≥ 0.
L Неправильное решение.
Ответ: х ∈ (–∞; –1]∪[6; +∞).
Комментарий. В данном решении не учтено, что сравнивается с нулем произведение трех множителей, а не двух. Таким образом, получаются не три интервала, а четыре.
J Правильное решение.
Ответ: х ∈ [–1; 0]∪[6; +∞).
K Упражнение 2. Решить неравенство (х– 5) (х + 3) (2 – х) ≥ 0.
L Неправильное решение.
Ответ: х ∈ [–3; 2]∪[5; +∞).
Комментарий. В данном примере знаки в интервалах проставлены неверно. Часто учащиеся не задумываясь проставляют знаки, чередуя их справа налево, начиная со знака +.
В данном примере знаки в интервалах проставлены неверно. Часто учащиеся не задумываясь проставляют знаки, чередуя их справа налево, начиная со знака +.
J Правильное решение.
Числовая ось с проставленными знаками на промежутках должна выглядеть в данном случае следующим образом:
Ответ: х ∈ (–∞; –3]∪[2; 5].
K Упражнение 3. Решить неравенство
| (х – 8) (х + 7) | ≥ 0. |
| х + 2 |
L Неправильное решение.
Ответ: х ∈ [–7; –2]∪[8; +∞).
Комментарий. В дробно-рациональных неравенствах нули знаменателя на числовую ось наносятся пустыми(выколотыми)точками, и это не зависит от строгости неравенства.
J Правильное решение.
Ответ: х ∈ [–7; –2)∪[8; +∞).
K Упражнение 4. Решить неравенство (х – 5) (х + 3)2 ≤ 0.
L Неправильное решение.
Ответ: х ∈ [–3; 5].
Комментарий. В данном упражнении знаки на интервалах проставлены неверно, так как при переходе через корень четной кратности знак не меняется.
J Правильное решение.
Ответ: х ∈ (–∞; 5].
K Упражнение 5. Решить неравенство (х – 1) (х – 10)2 > 0.
L Неправильное решение.
Ответ: х ∈ (1; +∞).
Комментарий. При записи ответа к данному неравенству не учтено то, что в точке х = 10 левая часть неравенства обращается в ноль, что не соответствует знаку данного неравенства.
J Правильный ответ: х ∈ (1; 10)∪(10; +∞).
K Упражнение 6. Решить неравенство (х – 5)2 (х + 3) ≤ 0.
L Неправильное решение.
Ответ: х ∈ (–∞; –3].
Комментарий. При решении данного неравенства потеряно одно решение. При х = 5 левая часть неравенства обращается в ноль, что тоже удовлетворяет данному неравенству.
J Правильный ответ: х ∈ (–∞; –3]∪{5}.
Ошибки в иррациональных неравенствах
Самый распространенный вид ошибок при решении иррациональных неравенств связан с тем, что учащимися не учитывается область допустимых значений неизвестного для корня четной степени.
K Упражнение. Решить неравенство √x – 5 < 2.
L Неправильное решение.
x – 5 < 4;
x < 9.
Ответ: х ∈ (–∞; 9).
Комментарий. Неравенство имеет смысл лишь при x – 5 ≥ 0.
J Правильное решение.
\(\begin{cases} x — 5 < 4,\\ x — 5 \geq 0; \end{cases}\;\;\;\; \begin{cases} x < 9,\\ x \geq 5; \end{cases}\;\;\;\; 5 \leq x < 9.\)
Ответ: х ∈ [5; 9).
Нередко учащиеся не учитывают ограничения, которые накладываются на выражения, стоящие вне знака корня четной степени и содержащие неизвестную величину.2-9x-10\leq 0,\\ x\geq -26,\\ x\geq 4; \end{cases} \\ \begin{cases} x\geq -26,\\ x < 4;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{cases} \end{matrix}\right.\;\;\; \left[\begin{matrix}\begin{cases} (x+1)(x-10)\leq 0,\\ x\geq -26,\\ x\geq 4; \end{cases} \\ \begin{cases} x\geq -26,\\ x < 4.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{cases} \end{matrix}\right.\;\;\;\)
Решением первой системы является промежуток [4; 10], решением второй – промежуток [–26; 4). Таким образом, решением совокупности систем является объединение этих промежутков.
Ответ: х ∈ [–26; 10].
Ошибки в показательных и логарифмических неравенствах
При решении показательных и логарифмических неравенств возникновение ошибок, как правило, вызвано тем, что учащиеся неверно применяют свойства показательной и логарифмической функции.
Например, не учитывают, что при положительном, меньшем единицы основании, и показательная, и логарифмическая функции являются убывающими.
K Упражнение. Решить неравенство 0,8 х ≥ 0,8 – 1/3.
L Неправильный ответ: х ≥ – 1/3.
Комментарий. Так как 0 < 0,8 < 1, то при переходе от неравенства степеней с одинаковыми основаниями к неравенству показателей необходимо было поменять знак основания.
J Правильный ответ: х ≤ – 1/3.
Пренебрежение областью допустимых значений неизвестного – еще одна распространенная причина ошибок при решении показательных и, особенно, логарифмических неравенств.
K Упражнение. Решить неравенство log4 (x2 + 3x) ≤ 1.
L Неправильное решение.
x2 + 3x ≤ 4;
x2 + 3x – 4 ≤ 0;
(x – 1) (x + 4) ≤ 0;
х ∈ [–4; 1].
Ответ: [–4; 1].
J Правильное решение.2-7x+6 \leq 0; \end{cases} \end{matrix} \right.\;\;\;\; \left[\begin{matrix} \begin{cases} 0 < x < 0,5, \\ (x-2)(x-3) > 0,\\ (x-1)(x-6) \geq 0; \end{cases}\\ \begin{cases} x > 0,5, \\ (x-2)(x-3) > 0,\\ (x-1)(x-6) \leq 0. \end{cases} \end{matrix} \right.\;\;\;\;\)
В первом случае решением системы является промежуток (0; 0,5), а во втором – объединение промежутков [1; 2)∪(3; 6].
Таким образом, после объединения ответов получим (0; 0,5)∪[1; 2)∪(3; 6].
Ответ: х ∈ (0; 0,5)∪[1; 2)∪(3; 6].
K Упражнение 2. Решить неравенство х 3х + 1 > х 4.
L Неправильное решение.
\(\begin{cases} x > 0, \\ 3x+1 > 4; \end{cases}\;\;\;\; \begin{cases} x > 0, \\ x > 1; \end{cases}\;\;\;\; x > 1.\)
Ответ: х ∈ (1; +∞).
J Правильное решение.
\(\left[\begin{matrix} \begin{cases} 0 < x < 1, \\ 3x+1 < 4; \end{cases}\\ \begin{cases} x > 1, \\ 3x+1 > 4; \end{cases} \end{matrix} \right.\;\;\;\; \left[\begin{matrix} \begin{cases} 0 < x < 1, \\ x < 1; \end{cases}\\ \begin{cases} x > 1, \\ x > 1; \;\;\;\;\;\; \end{cases} \end{matrix} \right.\;\;\;\; \left[\begin{matrix} 0 < x < 1,\\ x > 1.\;\;\;\;\;\; \end{matrix} \right.\)
Ответ: х ∈ (0; 1)∪(1; +∞).
При решении неравенств методом замены переменной учащиеся достаточно часто путают, знак совокупности и знак системы, то есть не понимают, что в первом случае решением неравенства является объединение нескольких множеств, а во втором случае – их пересечение.
K Упражнение 1. Решить неравенство lg2x + lg x – 2 ≥ 0.
L Неправильное решение.
Пусть lg x = t, тогда
t 2 + t – 2 ≥ 0;
(t – 1) (t + 2) ≥ 0;
\(\begin{cases} t \geq 1, \\ t \leq -2; \end{cases}\;\;\;\; \begin{cases} \lg x \geq 1, \\ \lg x \leq -2; \end{cases}\;\;\;\; \begin{cases} x \geq 10, \\ x \leq 0,01. \end{cases}\;\;\;\;\)
Ответ: Ø.
Комментарий. Решение должно сводиться к объединению, а не к пересечению двух промежутков, то есть к решению совокупности неравенств.
J Правильное решение.
\(\left[\begin{matrix} t \geq 1,\;\;\;\\ t \leq -2; \end{matrix} \right.\;\;\;\; \left[\begin{matrix} \lg x \geq 1,\;\;\;\\ \lg x \leq -2; \end{matrix} \right.\;\;\;\; \begin{cases} \left[\begin{matrix} x \geq 10,\;\;\;\\ x \leq 0,01; \end{matrix} \right. \\ \; x > 0. \end{cases}\)
Ответ: х ∈ (0; 0,01]∪[10; +∞).
K Упражнение 2. Решить неравенство x – 3√x + 2 ≤ 0.
L Неправильное решение.
Пусть √x =t; тогда
t 2 – 3t + 2 ≤ 0;
(t – 1) (t – 2) ≤ 0;
\(\left[\begin{matrix} t \geq 1,\\ t \leq 2; \end{matrix} \right.\;\;\;\; \left[\begin{matrix} \sqrt{x} \geq 1,\\ \sqrt{x} \leq 2; \end{matrix} \right.\;\;\;\; \left[\begin{matrix} x \geq 1,\\ x \leq 4; \end{matrix} \right.\;\;\;\; x\in (-\infty;\; +\infty).\)
Ответ: все числа.
Комментарий. Во-первых, в представленном решении не учтена область допустимых значений переменной, а во-вторых, решение должно сводиться к пересечению двух промежутков, а не к их объединению, то есть к решению системы неравенств или двойного неравенства.
J Правильное решение.
1 ≤ t ≤ 2;
1 ≤ √x ≤ 2;
1 ≤ x ≤ 4.
Ответ: [1; 4].
Смотрите так же:
Ошибки в тождественных преобразованиях
Ошибки в уравнениях
Ошибки в системах уравнений
Ошибки в упражнениях с параметрами
Ошибки в упражнениях о функциях
Ошибки в упражнениях из начал анализа
Ошибки в геометрических задачах
Общие сведения о неравенствах
Данный материал может показаться сложным для понимания. Рекомендуется изучать его маленькими частями.
Предварительные навыкиОпределения и свойства
Неравенством мы будем называть два числовых или буквенных выражения, соединенных знаками >, <, ≥, ≤ или ≠.
Пример: 5 > 3
Данное неравенство говорит о том, что число 5 больше, чем число 3. Острый угол знака неравенства должен быть направлен в сторону меньшего числа. Это неравенство является верным, поскольку 5 больше, чем 3.
Если на левую чашу весов положить арбуз массой 5 кг, а на правую — арбуз массой 3 кг, то левая чаша перевесит правую, и экран весов покажет, что левая чаша тяжелее правой:
Если 5 > 3, то 3 < 5. То есть левую и правую часть неравенства можно поменять местами, изменив знак неравенства на противоположный. В ситуации с весами: большой арбуз можно положить на правую чашу, а маленький арбуз на левую. Тогда правая чаша перевесит левую, и экран покажет знак <
Если в неравенстве 5 > 3, не трогая левую и правую часть, поменять знак на <, то получится неравенство 5 < 3. Это неравенство не является верным, поскольку число 3 не может быть больше числа 5.
Числа, которые располагаются в левой и правой части неравенства, будем называть членами этого неравенства. Например, в неравенстве 5 > 3 членами являются числа 5 и 3.
Рассмотрим некоторые важные свойства для неравенства 5 > 3.
В будущем эти свойства будут работать и для других неравенств.
Свойство 1.
Если к левой и правой части неравенства 5 > 3 прибавить или вычесть одно и то же число, то знак неравенства не изменится.
Например, прибавим к обеим частям неравенства число 4. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем вычесть из обеих частей неравенства 5 > 3 какое-нибудь число, скажем число 2
Видим, что левая часть по-прежнему больше правой.
Из данного свойства следует, что любой член неравенства можно перенести из одной части в другую часть, изменив знак этого члена. Знак неравенства при этом не изменится.
Например, перенесём в неравенстве 5 > 3, член 5 из левой части в правую часть, изменив знак этого члена. После переноса члена 5 в правую часть, в левой части ничего не останется, поэтому запишем там 0
0 > 3 − 5
0 > −2
Видим, что левая часть по-прежнему больше правой.
Свойство 2.
Если обе части неравенства умножить или разделить на одно и то же положительное число, то знак неравенства не изменится.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь положительное число, скажем на число 2. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь число. Разделим их на 2
Видим, что левая часть по-прежнему больше правой.
Свойство 3.
Если обе части неравенства умножить или разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь отрицательное число, скажем на число −2. Тогда получим:
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь отрицательное число. Давайте разделим их на −1
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Само по себе неравенство можно понимать, как некоторое условие. Если условие выполняется, то неравенство является верным. И наоборот, если условие не выполняется, то неравенство не верно.
Например, чтобы ответить на вопрос является ли верным неравенство 7 > 3, нужно проверить выполняется ли условие «больше ли 7, чем 3». Мы знаем, что число 7 больше, чем число 3. То есть условие выполнено, а значит и неравенство 7 > 3 верно.
Неравенство 8 < 6 не является верным, поскольку не выполняется условие «8 меньше, чем 6».
Другим способом определения верности неравенства является составление разности из левой и правой части данного неравенства. Если разность положительна, то левая часть больше правой части. И наоборот, если разность отрицательна, то левая часть меньше правой части. Более точно это правило выглядит следующим образом:
Число a больше числа b, если разность a − b положительна. Число a меньше числа b, если разность a − b отрицательна.
Например, мы выяснили, что неравенство 7 > 3 является верным, поскольку число 7 больше, чем число 3. Докажем это с помощью правила, приведённого выше.
Составим разность из членов 7 и 3. Тогда получим 7 − 3 = 4. Согласно правилу, число 7 будет больше числа 3, если разность 7 − 3 окажется положительной. У нас она равна 4, то есть разность положительна. А значит число 7 больше числа 3.
Проверим с помощью разности верно ли неравенство 3 < 4. Составим разность, получим 3 − 4 = −1. Согласно правилу, число 3 будет меньше числа 4, если разность 3 − 4 окажется отрицательной. У нас она равна −1, то есть разность отрицательна. А значит число 3 меньше числа 4.
Проверим верно ли неравенство 5 > 8. Составим разность, получим 5 − 8 = −3. Согласно правилу, число 5 будет больше числа 8, если разность 5 − 8 окажется положительной. У нас разность равна −3, то есть она не является положительной. А значит число 5 не больше числа 8. Иными словами, неравенство 5 > 8 не является верным.
Строгие и нестрогие неравенства
Неравенства, содержащие знаки >, < называют строгими. А неравенства, содержащие знаки ≥, ≤ называют нестрогими.
Примеры строгих неравенства мы рассматривали ранее. Таковыми являются неравенства 5 > 3, 7 < 9.
Нестрогим, например, является неравенство 2 ≤ 5. Данное неравенство читают следующим образом: «2 меньше или равно 5».
Запись 2 ≤ 5 является неполной. Полная запись этого неравенства выглядит следующим образом:
2 < 5 или 2 = 5
Тогда становится очевидным, что неравенство 2 ≤ 5 состоит из двух условий: «два меньше пять» и «два равно пять».
Нестрогое неравенство верно в том случае, если выполняется хотя бы одно из его условий. В нашем примере верным является условие «2 меньше 5». Значит и само неравенство 2 ≤ 5 верно.
Пример 2. Неравенство 2 ≤ 2 является верным, поскольку выполняется одно из его условий, а именно 2 = 2.
Пример 3. Неравенство 5 ≤ 2 не является верным, поскольку не выполняется ни одно из его условий: ни 5 < 2 ни 5 = 2.
Двойное неравенство
Число 3 больше, чем число 2 и меньше, чем число 4. В виде неравенства это высказывание можно записать так: 2 < 3 < 4. Такое неравенство называют двойным.
Двойное неравенство может содержать знаки нестрогих неравенств. К примеру, если число 5 больше или равно, чем число 2, и меньше или равно, чем число 7, то можно записать, что 2 ≤ 5 ≤ 7
Чтобы правильно записать двойное неравенство, сначала записывают член находящийся в середине, затем член находящийся слева, затем член находящийся справа.
Например, запишем, что число 6 больше, чем число 4, и меньше, чем число 9.
Сначала записываем 6
Слева записываем, что это число больше, чем число 4
Справа записываем, что число 6 меньше, чем число 9
Неравенство с переменной
Неравенство, как и равенство может содержать переменную.
Например, неравенство x > 2 содержит переменную x. Обычно такое неравенство нужно решить, то есть выяснить при каких значениях x данное неравенство становится верным.
Решить неравенство означает найти такие значения переменной x, при которых данное неравенство становится верным.
Значение переменной, при котором неравенство становится верным, называется решением неравенства.
Неравенство x > 2 становится верным при x = 3, x = 4, x = 5, x = 6 и так далее до бесконечности. Видим, что это неравенство имеет не одно решение, а множество решений.
Другими словами, решением неравенства x > 2 является множество всех чисел, бóльших 2. При этих числах неравенство будет верным. Примеры:
3 > 2
4 > 2
5 > 2
Число 2, располагающееся в правой части неравенства x > 2, будем называть границей данного неравенства. В зависимости от знака неравенства, граница может принадлежать множеству решений неравенства либо не принадлежать ему.
В нашем примере граница неравенства не принадлежит множеству решений, поскольку при подстановке числа 2 в неравенство x > 2 получается не верное неравенство 2 > 2. Число 2 не может быть больше самого себя, поскольку оно равно самому себе (2 = 2).
Неравенство x > 2 является строгим. Его можно прочитать так: «x строго больше 2″. То есть все значения, принимаемые переменной x должны быть строго больше 2. В противном случае, неравенство верным не будет.
Если бы нам было дано нестрогое неравенство x ≥ 2, то решениями данного неравенства были бы все числа, которые больше 2, в том числе и само число 2. В этом неравенстве граница 2 принадлежит множеству решений неравенства, поскольку при подстановке числа 2 в неравенство x ≥ 2 получается верное неравенство 2 ≥ 2. Ранее было сказано, что нестрогое неравенство является верным, если выполняется хотя бы одно из его условий. В неравенстве 2 ≥ 2 выполняется условие 2 = 2, поэтому и само неравенство 2 ≥ 2 верно.
Как решать неравенства
Процесс решения неравенств во многом схож с процессом решения уравнений. При решении неравенств мы будем применять свойства, которые изучили вначале данного урока, такие как: перенос слагаемых из одной части неравенства в другую часть, меняя знак; умножение (или деление) обеих частей неравенства на одно и то же число.
Эти свойства позволяют получить неравенство, которое равносильно исходному. Равносильными называют неравенства, решения которых совпадают.
Решая уравнения мы выполняли тождественные преобразования до тех пор, пока в левой части уравнения не оставалась переменная, а в правой части значение этой переменной (например: x = 2, x = 5). Иными словами, заменяли исходное уравнение на равносильное ему уравнение до тех пор, пока не получалось уравнение вида x = a, где a значение переменной x. В зависимости от уравнения, корней могло быть один, два, бесконечное множество, либо не быть совсем.
А при решении неравенств мы будем заменять исходное неравенство на равносильное ему неравенство до тех пор, пока в левой части не останется переменная этого неравенства, а в правой части его граница.
Пример 1. Решить неравенство 2x > 6
Итак, нужно найти такие значения x, при подстановке которых в 2x > 6 получится верное неравенство.
Вначале данного урока было сказано, что если обе части неравенства разделить на какое-нибудь положительное число, то знак неравенства не изменится. Если применить это свойство к неравенству, содержащему переменную, то получится неравенство равносильное исходному.
В нашем случае, если мы разделим обе части неравенства 2x > 6 на какое-нибудь положительное число, то получится неравенство, которое равносильно исходному неравенству 2x > 6.
Итак, разделим обе части неравенства на 2.
В левой части осталась переменная x, а правая часть стала равна 3. Получилось равносильное неравенство x > 3. На этом решение завершается, поскольку в левой части осталась переменная, а в правой части граница неравенства.
Теперь можно сделать вывод, что решениями неравенства x > 3 являются все числа, которые больше 3. Это числа 4, 5, 6, 7 и так далее до бесконечности. При этих значениях неравенство x > 3 будет верным.
4 > 3
5 > 3
6 > 3
7 > 3
Отметим, что неравенство x > 3 является строгим. «Переменная x строго больше трёх».
А поскольку неравенство x > 3 равносильно исходному неравенству 2x > 6, то их решения будут совпадать. Иначе говоря, значения, которые подходят неравенству x > 3, будут подходить и неравенству 2x > 6. Покажем это.
Возьмём, например, число 5 и подставим его сначала в полученное нами равносильное неравенство x > 3, а потом в исходное 2x > 6.
Видим, что в обоих случаях получается верное неравенство.
После того, как неравенство решено, ответ нужно записать в виде так называемого числового промежутка следующим образом:
В этом выражении говорится, что значения, принимаемые переменной x, принадлежат числовому промежутку от трёх до плюс бесконечности.
Иначе говоря, все числа, начиная от трёх до плюс бесконечности являются решениями неравенства x > 3. Знак ∞ в математике означает бесконечность.
Учитывая, что понятие числового промежутка очень важно, остановимся на нём подробнее.
Числовые промежутки
Числовым промежутком называют множество чисел на координатной прямой, которое может быть описано с помощью неравенства.
Допустим, мы хотим изобразить на координатной прямой множество чисел от 2 до 8. Для этого сначала на координатной прямой отмечаем точки с координатами 2 и 8, а затем выделяем штрихами ту область, которая располагается между координатами 2 и 8. Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8
Числа 2 и 8 назовём границами числового промежутка. Рисуя числовой промежуток, точки для его границ изображают не в виде точек как таковых, а в виде кружков, которые можно разглядеть.
Границы могут принадлежать числовому промежутку либо не принадлежать ему.
Если границы не принадлежат числовому промежутку, то они изображаются на координатной прямой в виде пустых кружков.
Если границы принадлежат числовому промежутку, то кружки необходимо закрасить.
На нашем рисунке кружки были оставлены пустыми. Это означало, что границы 2 и 8 не принадлежат числовому промежутку. Значит в наш числовой промежуток будут входить все числа от 2 до 8, кроме чисел 2 и 8.
Если мы хотим включить границы 2 и 8 в числовой промежуток, то кружки необходимо закрасить:
В данном случае в числовой промежуток будут входить все числа от 2 до 8, включая числа 2 и 8.
На письме числовой промежуток обозначается указанием его границ с помощью круглых или квадратных скобок.
Если границы не принадлежат числовому промежутку, то границы обрамляются круглыми скобками.
Если границы принадлежат числовому промежутку, то границы обрамляются квадратными скобками.
На рисунке представлено два числовых промежутка от 2 до 8 с соответствующими обозначениями:
На первом рисунке числовой промежуток обозначен с помощью круглых скобок, поскольку границы 2 и 8 не принадлежат этому числовому промежутку.
На втором рисунке числовой промежуток обозначен с помощью квадратных скобок, поскольку границы 2 и 8 принадлежат этому числовому промежутку.
С помощью числовых промежутков можно записывать ответы к неравенствам. Например, ответ к двойному неравенству 2 ≤ x ≤ 8 записывается так:
x ∈ [ 2 ; 8 ]
То есть сначала записывают переменную, входящую в неравенство, затем с помощью знака принадлежности ∈ указывают к какому числовому промежутку принадлежат значения этой переменной. В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.
Обратим внимание на то, что ответ записан с помощью квадратных скобок, поскольку границы неравенства 2 ≤ x ≤ 8, а именно числа 2 и 8 принадлежат множеству решений этого неравенства.
Множество решений неравенства 2 ≤ x ≤ 8 также можно изобразить с помощью координатной прямой:
Здесь границы числового промежутка 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x ≤ 8.
В некоторых источниках границы, которые не принадлежат числовому промежутку, называют открытыми.
Открытыми их называют по той причине, что числовой промежуток остаётся открытым из-за того, что его границы не принадлежат этому числовому промежутку. Пустой кружок на координатной прямой математики называют выколотой точкой. Выколоть точку значит исключить её из числового промежутка или из множества решений неравенства.
А в случае, когда границы принадлежат числовому промежутку, их называют закрытыми (или замкнутыми), поскольку такие границы закрывают (замыкают) собой числовой промежуток. Закрашенный кружок на координатной прямой также говорит о закрытости границ.
Существуют разновидности числовых промежутков. Рассмотрим каждый из них.
Числовой лучЧисловым лучом называют числовой промежуток, который задаётся неравенством x ≥ a, где a — граница данного неравенства, x — решение неравенства.
Пусть a = 3. Тогда неравенство x ≥ a примет вид x ≥ 3. Решениями данного неравенства являются все числа, которые больше 3, включая само число 3.
Изобразим числовой луч, заданный неравенством x ≥ 3, на координатной прямой. Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее
Здесь точка 3 соответствует границе неравенства x ≥ 3, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x ≥ 3.
Точка 3, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≥ 3 принадлежит множеству его решений.
На письме числовой луч, заданный неравенством x ≥ a, обозначается следующим образом:
[ a ; +∞ )
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница числового луча принадлежит ему, а другая нет, поскольку бесконечность сама по себе границ не имеет и подразумевается, что по ту сторону нет числа, замыкающего этот числовой луч.
Учитывая то, что одна из границ числового луча закрыта, данный промежуток часто называют закрытым числовым лучом.
Запишем ответ к неравенству x ≥ 3 с помощью обозначения числового луча. У нас переменная a равна 3
x ∈ [ 3 ; +∞ )
В этом выражении говорится, что переменная x, входящая в неравенство x ≥ 3, принимает все значения от 3 до плюс бесконечности.
Иначе говоря, все числа от 3 до плюс бесконечности, являются решениями неравенства x ≥ 3. Граница 3 принадлежит множеству решений, поскольку неравенство x ≥ 3 является нестрогим.
Закрытым числовым лучом также называют числовой промежуток, который задаётся неравенством x ≤ a. Решениями неравенства x ≤ a являются все числа, которые меньше a, включая само число a.
К примеру, если a = 2, то неравенство примет вид x ≤ 2. На координатной прямой граница 2 будет изображаться закрашенным кружком, а вся область, находящаяся слева, будет выделена штрихами. В этот раз выделяется левая часть, поскольку решениями неравенства x ≤ 2 являются числа, меньшие 2. А меньшие числа на координатной прямой располагаются левее
Здесь точка 2 соответствует границе неравенства x ≤ 2, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x ≤ 2.
Точка 2, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≤ 2 принадлежит множеству его решений.
Запишем ответ к неравенству x ≤ 2 с помощью обозначения числового луча:
x ∈ ( −∞ ; 2 ]
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x ≤ 2. Граница 2 принадлежит множеству решений, поскольку неравенство x ≤ 2 является нестрогим.
Открытый числовой луч
Открытым числовым лучом называют числовой промежуток, который задаётся неравенством x > a, где a — граница данного неравенства, x — решение неравенства.
Открытый числовой луч во многом похож на закрытый числовой луч. Различие в том, что граница a не принадлежит промежутку, как и граница неравенства x > a не принадлежит множеству его решений.
Пусть a = 3. Тогда неравенство примет вид x > 3. Решениями данного неравенства являются все числа, которые больше 3, за исключением числа 3
На координатной прямой граница открытого числового луча, заданного неравенством x > 3, будет изображаться в виде пустого кружка. Вся область, находящаяся справа, будет выделена штрихами:
Здесь точка 3 соответствует границе неравенства x > 3, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x > 3. Точка 3, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x > 3 не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x > a, обозначается следующим образом:
( a ; +∞ )
Круглые скобки указывают на то, что границы открытого числового луча не принадлежат ему.
Запишем ответ к неравенству x > 3 с помощью обозначения открытого числового луча:
x ∈ ( 3 ; +∞ )
В этом выражении говорится, что все числа от 3 до плюс бесконечности, являются решениями неравенства x > 3. Граница 3 не принадлежит множеству решений, поскольку неравенство x > 3 является строгим.
Открытым числовым лучом также называют числовой промежуток, который задаётся неравенством x < a, где a — граница данного неравенства, x — решение неравенства. Решениями неравенства x < a являются все числа, которые меньше a, исключая число a.
К примеру, если a = 2, то неравенство примет вид x < 2. На координатной прямой граница 2 будет изображаться пустым кружком, а вся область, находящаяся слева, будет выделена штрихами:
Здесь точка 2 соответствует границе неравенства x < 2, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x < 2. Точка 2, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x < 2 не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x < a, обозначается следующим образом:
( −∞ ; a )
Запишем ответ к неравенству x < 2 с помощью обозначения открытого числового луча:
x ∈ ( −∞ ; 2 )
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x < 2. Граница 2 не принадлежит множеству решений, поскольку неравенство x < 2 является строгим.
ОтрезокОтрезком называют числовой промежуток, который задаётся двойным неравенством a ≤ x ≤ b, где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2, b = 8. Тогда неравенство a ≤ x ≤ b примет вид 2 ≤ x ≤ 8. Решениями неравенства 2 ≤ x ≤ 8 являются все числа, которые больше 2 и меньше 8. При этом границы неравенства 2 и 8 принадлежат множеству его решений, поскольку неравенство 2 ≤ x ≤ 8 является нестрогим.
Изобразим отрезок, заданный двойным неравенством 2 ≤ x ≤ 8 на координатной прямой. Для этого отметим на ней точки с координатами 2 и 8, а располагающуюся между ними область выделим штрихами:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x ≤ 8. Точки 2 и 8, являющиеся границами отрезка, изображены в виде закрашенных кружков, поскольку границы неравенства 2 ≤ x ≤ 8 принадлежат множеству его решений.
На письме отрезок, заданный неравенством a ≤ x ≤ b обозначается следующим образом:
[ a ; b ]
Квадратные скобки с обеих сторон указывают на то, что границы отрезка принадлежат ему. Запишем ответ к неравенству 2 ≤ x ≤ 8 с помощью этого обозначения:
x ∈ [ 2 ; 8 ]
В этом выражении говорится, что все числа от 2 до 8 включительно, являются решениями неравенства 2 ≤ x ≤ 8.
Интервал
Интервалом называют числовой промежуток, который задаётся двойным неравенством a < x < b, где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2, b = 8. Тогда неравенство a < x < b примет вид 2 < x < 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая числа 2 и 8.
Изобразим интервал на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 < x < 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 < x < 8. Точки 2 и 8, являющиеся границами интервала, изображены в виде пустых кружков, поскольку границы неравенства 2 < x < 8 не принадлежат множеству его решений.
На письме интервал, заданный неравенством a < x < b, обозначается следующим образом:
( a ; b )
Круглые скобки с обеих сторон указывают на то, что границы интервала не принадлежат ему. Запишем ответ к неравенству 2 < x < 8 с помощью этого обозначения:
x ∈ ( 2 ; 8 )
В этом выражении говорится, что все числа от 2 до 8, исключая числа 2 и 8, являются решениями неравенства 2 < x < 8.
Полуинтервал
Полуинтервалом называют числовой промежуток, который задаётся неравенством a ≤ x < b, где a и b — границы данного неравенства, x — решение неравенства.
Полуинтервалом также называют числовой промежуток, который задаётся неравенством a < x ≤ b.
Одна из границ полуинтервала принадлежит ему. Отсюда и название этого числового промежутка.
В ситуации с полуинтервалом a ≤ x < b ему (полуинтервалу) принадлежит левая граница.
А в ситуации с полуинтервалом a < x ≤ b ему принадлежит правая граница.
Пусть a = 2, b = 8. Тогда неравенство a ≤ x < b примет вид 2 ≤ x < 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, включая число 2, но исключая число 8.
Изобразим полуинтервал 2 ≤ x < 8 на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x < 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x < 8.
Точка 2, являющаяся левой границей полуинтервала, изображена в виде закрашенного кружка, поскольку левая граница неравенства 2 ≤ x < 8 принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде пустого кружка, поскольку правая граница неравенства 2 ≤ x < 8 не принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a ≤ x < b, обозначается следующим образом:
[ a ; b )
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница полуинтервала принадлежит ему, а другая нет. Запишем ответ к неравенству 2 ≤ x < 8 с помощью этого обозначения:
x ∈ [ 2 ; 8 )
В этом выражении говорится, что все числа от 2 до 8, включая число 2, но исключая число 8, являются решениями неравенства 2 ≤ x < 8.
Аналогично на координатной прямой можно изобразить полуинтервал, заданный неравенством a < x ≤ b. Пусть a = 2, b = 8. Тогда неравенство a < x ≤ b примет вид 2 < x ≤ 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая число 2, но включая число 8.
Изобразим полуинтервал 2 < x ≤ 8 на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 < x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 < x ≤ 8.
Точка 2, являющаяся левой границей полуинтервала, изображена в виде пустого кружка, поскольку левая граница неравенства 2 < x ≤ 8 не принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде закрашенного кружка, поскольку правая граница неравенства 2 < x ≤ 8 принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a < x ≤ b, обозначается так: ( a ; b ]. Запишем ответ к неравенству 2 < x ≤ 8 с помощью этого обозначения:
x ∈ ( 2 ; 8 ]
В этом выражении говорится, что все числа от 2 до 8, исключая число 2, но включая число 8, являются решениями неравенства 2 < x ≤ 8.
Изображение числовых промежутков на координатной прямой
Числовой промежуток может быть задан с помощью неравенства или с помощью обозначения (круглых или квадратных скобок). В обоих случаях нужно суметь изобразить этот числовой промежуток на координатной прямой. Рассмотрим несколько примеров.
Пример 1. Изобразить числовой промежуток, заданный неравенством x > 5
Вспоминаем, что неравенством вида x > a задаётся открытый числовой луч. В данном случае переменная a равна 5. Неравенство x > 5 строгое, поэтому граница 5 будет изображаться в виде пустого кружкá. Нас интересуют все значения x, которые больше 5, поэтому вся область справа будет выделена штрихами:
Пример 2. Изобразить числовой промежуток (5; +∞) на координатной прямой
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью неравенства, а с помощью обозначения числового промежутка.
Граница 5 обрамлена круглой скобкой, значит она не принадлежит промежутку. Соответственно, кружок остаётся пустым.
Символ +∞ указывает, что нас интересуют все числа, которые больше 5. Соответственно, вся область справа от границы 5 выделяется штрихами:
Пример 3. Изобразить числовой промежуток (−5; 1) на координатной прямой.
Круглыми скобками с обеих сторон обозначаются интервалы. Границы интервала не принадлежат ему, поэтому границы −5 и 1 будут изображаться на координатной прямой в виде пустых кружков. Вся область между ними будет выделена штрихами:
Пример 4. Изобразить числовой промежуток, заданный неравенством −5 < x < 1
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью обозначения промежутка, а с помощью двойного неравенства.
Неравенством вида a < x < b, задаётся интервал. В данном случае переменная a равна −5, а переменная b равна единице. Неравенство −5 < x < 1 строгое, поэтому границы −5 и 1 будут изображаться в виде пустых кружка. Нас интересуют все значения x, которые больше −5, но меньше единицы, поэтому вся область между точками −5 и 1 будет выделена штрихами:
Пример 5. Изобразить на координатной прямой числовые промежутки [-1; 2] и [2; 5]
В этот раз изобразим на координатной прямой сразу два промежутка.
Квадратными скобками с обеих сторон обозначаются отрезки. Границы отрезка принадлежат ему, поэтому границы отрезков [-1; 2] и [2; 5] будут изображаться на координатной прямой в виде закрашенных кружков. Вся область между ними будет выделена штрихами.
Чтобы хорошо увидеть промежутки [−1; 2] и [2; 5], первый можно изобразить на верхней области, а второй на нижней. Так и поступим:
Пример 6. Изобразить на координатной прямой числовые промежутки [-1; 2) и (2; 5]
Квадратной скобкой с одной стороны и круглой с другой обозначаются полуинтервалы. Одна из границ полуинтервала принадлежат ему, а другая нет.
В случае с полуинтервалом [-1; 2) левая граница будет принадлежать ему, а правая нет. Значит левая граница будет изображаться в виде закрашенного кружка. Правая же граница будет изображаться в виде пустого кружка.
А в случае с полуинтервалом (2; 5] ему будет принадлежать только правая граница, а левая нет. Значит левая граница будет изображаться в виде пустого кружка. Правая же граница будет изображаться в виде закрашенного кружка.
Изобразим промежуток [-1; 2) на верхней области координатной прямой, а промежуток (2; 5] — на нижней:
Примеры решения неравенств
Неравенство, которое путём тождественных преобразований можно привести к виду ax > b (или к виду ax < b), будем называть линейным неравенством с одной переменной.
В линейном неравенстве ax > b, x — это переменная, значения которой нужно найти, а — коэффициент этой переменной, b — граница неравенства, которая в зависимости от знака неравенства может принадлежать множеству его решений либо не принадлежать ему.
Например, неравенство 2x > 4 является неравенством вида ax > b. В нём роль переменной a играет число 2, роль переменной b (границы неравенства) играет число 4.
Неравенство 2x > 4 можно сделать ещё проще. Если мы разделим обе его части на 2, то получим неравенство x > 2
Получившееся неравенство x > 2 также является неравенством вида ax > b, то есть линейным неравенством с одной переменной. В этом неравенстве роль переменной a играет единица. Ранее мы говорили, что коэффициент 1 не записывают. Роль переменной b играет число 2.
Отталкиваясь от этих сведений, попробуем решить несколько простых неравенств. В ходе решения мы будем выполнять элементарные тождественные преобразования с целью получить неравенство вида ax > b
Пример 1. Решить неравенство x − 7 < 0
Прибавим к обеим частям неравенства число 7
x − 7 + 7 < 0 + 7
В левой части останется x, а правая часть станет равна 7
x < 7
Путём элементарных преобразований мы привели неравенство x − 7 < 0 к равносильному неравенству x < 7. Решениями неравенства x < 7 являются все числа, которые меньше 7. Граница 7 не принадлежит множеству решений, поскольку неравенство строгое.
Когда неравенство приведено к виду x < a (или x > a), его можно считать уже решённым. Наше неравенство x − 7 < 0 тоже приведено к такому виду, а именно к виду x < 7. Но в большинстве школ требуют, чтобы ответ был записан с помощью числового промежутка и проиллюстрирован на координатной прямой.
Запишем ответ с помощью числового промежутка. В данном случае ответом будет открытый числовой луч (вспоминаем, что числовой луч задаётся неравенством x < a и обозначается как ( −∞ ; a)
x ∈ ( −∞ ; 7 )
На координатной прямой граница 7 будет изображаться в виде пустого кружка, а вся область, находящаяся слева от границы, будет выделена штрихами:
Для проверки возьмём любое число из промежутка ( −∞ ; 7 ) и подставим его в неравенство x < 7 вместо переменной x. Возьмём, например, число 2
2 < 7
Получилось верное числовое неравенство, значит и решение верное. Возьмём ещё какое-нибудь число, например, число 4
4 < 7
Получилось верное числовое неравенство. Значит решение верное.
А поскольку неравенство x < 7 равносильно исходному неравенству x − 7 < 0, то решения неравенства x < 7 будут совпадать с решениями неравенства x − 7 < 0. Подставим те же тестовые значения 2 и 4 в неравенство x − 7 < 0
2 − 7 < 0
−5 < 0 — Верное неравенство
4 − 7 < 0
−3 < 0 Верное неравенство
Пример 2. Решить неравенство −4x < −16
Разделим обе части неравенства на −4. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Мы привели неравенство −4x < −16 к равносильному неравенству x > 4. Решениями неравенства x > 4 будут все числа, которые больше 4. Граница 4 не принадлежит множеству решений, поскольку неравенство строгое.
Изобразим множество решений неравенства x > 4 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 3. Решить неравенство 3y + 1 > 1 + 6y
Перенесём 6y из правой части в левую часть, изменив знак. А 1 из левой части перенесем в правую часть, опять же изменив знак:
3y − 6y> 1 − 1
Приведём подобные слагаемые:
−3y > 0
Разделим обе части на −3. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства y < 0 являются все числа, меньшие нуля. Изобразим множество решений неравенства y < 0 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 4. Решить неравенство 5(x − 1) + 7 ≤ 1 − 3(x + 2)
Раскроем скобки в обеих частях неравенства:
Перенесем −3x из правой части в левую часть, изменив знак. Члены −5 и 7 из левой части перенесем в правую часть, опять же изменив знаки:
Приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 8
Решениями неравенства являются все числа, которые меньше . Граница принадлежит множеству решений, поскольку неравенство является нестрогим.
Изобразим множество решений неравенства на координатной прямой и запишем ответ в виде числового промежутка:
Пример 5. Решить неравенство
Умножим обе части неравенства на 2. Это позволит избавиться от дроби в левой части:
Теперь перенесем 5 из левой части в правую часть, изменив знак:
После приведения подобных слагаемых, получим неравенство 6x > 1. Разделим обе части этого неравенства на 6. Тогда получим:
Решениями неравенства являются все числа, которые больше . Граница не принадлежит множеству решений, поскольку неравенство является строгим.
Изобразим множество решений неравенства на координатной прямой и запишем ответ в виде числового промежутка:
Пример 6. Решить неравенство
Умножим обе части на 6
После приведения подобных слагаемых, получим неравенство 5x < 30. Разделим обе части этого неравенства на 5
Решениями неравенства x < 6 являются все числа, которые меньше 6. Граница 6 не принадлежит множеству решений, поскольку неравенство является x < 6 строгим.
Изобразим множество решений неравенства x < 6 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 7. Решить неравенство
Умножим обе части неравенства на 10
В получившемся неравенстве раскроем скобки в левой части:
Перенесем члены без x в правую часть
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 10
Решениями неравенства x ≤ 3,5 являются все числа, которые меньше 3,5. Граница 3,5 принадлежит множеству решений, поскольку неравенство является x ≤ 3,5 нестрогим.
Изобразим множество решений неравенства x ≤ 3,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 8. Решить неравенство 4 < 4x < 20
Чтобы решить такое неравенство, нужно переменную x освободить от коэффициента 4. Тогда мы сможем сказать в каком промежутке находится решение данного неравенства.
Чтобы освободить переменную x от коэффициента, можно разделить член 4x на 4. Но правило в неравенствах таково, что если мы делим член неравенства на какое-нибудь число, то тоже самое надо сделать и с остальными членами, входящими в данное неравенство. В нашем случае на 4 нужно разделить все три члена неравенства 4 < 4x < 20
Решениями неравенства 1 < x < 5 являются все числа, которые больше 1 и меньше 5. Границы 1 и 5 не принадлежат множеству решений, поскольку неравенство 1 < x < 5 является строгим.
Изобразим множество решений неравенства 1 < x < 5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 9. Решить неравенство −1 ≤ −2x ≤ 0
Разделим все члены неравенства на −2
Получили неравенство 0,5 ≥ x ≥ 0. Двойное неравенство желательно записывать так, чтобы меньший член располагался слева, а больший справа. Поэтому перепишем наше неравенство следующим образом:
0 ≤ x ≤ 0,5
Решениями неравенства 0 ≤ x ≤ 0,5 являются все числа, которые больше 0 и меньше 0,5. Границы 0 и 0,5 принадлежат множеству решений, поскольку неравенство 0 ≤ x ≤ 0,5 является нестрогим.
Изобразим множество решений неравенства 0 ≤ x ≤ 0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 10. Решить неравенство
Умножим обе неравенства на 12
Раскроем скобки в получившемся неравенстве и приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 2
Решениями неравенства x ≤ −0,5 являются все числа, которые меньше −0,5. Граница −0,5 принадлежит множеству решений, поскольку неравенство x ≤ −0,5 является нестрогим.
Изобразим множество решений неравенства x ≤ −0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 11. Решить неравенство
Умножим все части неравенства на 3
Теперь из каждой части получившегося неравенства вычтем 6
Каждую часть получившегося неравенства разделим на −1. Не забываем, что при делении всех частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства 3 ≤ a ≤ 9 являются все числа, которые больше 3 и меньше 9. Границы 3 и 9 принадлежат множеству решений, поскольку неравенство 3 ≤ a ≤ 9 является нестрогим.
Изобразим множество решений неравенства 3 ≤ a ≤ 9 на координатной прямой и запишем ответ в виде числового промежутка:
Когда решений нет
Существуют неравенства, которые не имеют решений. Таковым, например, является неравенство 6x > 2(3x + 1). В процессе решения этого неравенства мы придём к тому, что знак неравенства > не оправдает своего местоположения. Давайте посмотрим, как это выглядит.
Раскроем скобки в правой части данного неравенство, получим 6x > 6x + 2. Перенесем 6x из правой части в левую часть, изменив знак, получим 6x − 6x > 2. Приводим подобные слагаемые и получаем неравенство 0 > 2, которое не является верным.
Для наилучшего понимания, перепишем приведение подобных слагаемых в левой части следующим образом:
Получили неравенство 0x > 2. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль не может быть больше, чем число 2. Значит неравенство 0x > 2 не имеет решений.
А если не имеет решений приведённое равносильное неравенство 0x > 2, то не имеет решений и исходное неравенство 6x > 2(3x + 1).
Пример 2. Решить неравенство
Умножим обе части неравенства на 3
В получившемся неравенстве перенесем член 12x из правой части в левую часть, изменив знак. Затем приведём подобные слагаемые:
Правая часть получившегося неравенства при любом x будет равна нулю. А ноль не меньше, чем −8. Значит неравенство 0x < −8 не имеет решений.
А если не имеет решений приведённое равносильное неравенство 0x < −8, то не имеет решений и исходное неравенство .
Ответ: решений нет.
Когда решений бесконечно много
Существуют неравенства, имеющие бесчисленное множество решений. Такие неравенства становятся верными при любом x.
Пример 1. Решить неравенство 5(3x − 9) < 15x
Раскроем скобки в правой части неравенства:
Перенесём 15x из правой части в левую часть, изменив знак:
Приведем подобные слагаемые в левой части:
Получили неравенство 0x < 45. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль меньше, чем 45. Значит решением неравенства 0x < 45 является любое число.
А если приведённое равносильное неравенство 0x < 45 имеет бесчисленное множество решений, то и исходное неравенство 5(3x − 9) < 15x имеет те же решения.
Ответ можно записать в виде числового промежутка:
x ∈ ( −∞; +∞ )
В этом выражении говорится, что решениями неравенства 5(3x − 9) < 15x являются все числа от минус бесконечности до плюс бесконечности.
Пример 2. Решить неравенство: 31(2x + 1) − 12x > 50x
Раскроем скобки в левой части неравенства:
Перенесём 50x из правой части в левую часть, изменив знак. А член 31 из левой части перенесём в правую часть, опять же изменив знак:
Приведём подобные слагаемые:
Получили неравенство 0x > −31. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль больше, чем −31. Значит решением неравенства 0x < −31 является любое число.
А если приведённое равносильное неравенство 0x > −31 имеет бесчисленное множество решений, то и исходное неравенство 31(2x + 1) − 12x > 50x имеет те же решения.
Запишем ответ в виде числового промежутка:
x ∈ ( −∞; +∞ )
Задания для самостоятельного решения
Задание 1. Решите неравенство:
Задание 2. Решите неравенство:
Задание 3. Решите неравенство:
Задание 4. Решите неравенство:
Задание 5. Решите неравенство:
Задание 6. Решите неравенство:
Задание 7. Решите неравенство:
Задание 8. Решите неравенство:
Задание 9. Решите неравенство:
Задание 10. Решите неравенство:
Задание 11. Решите неравенство:
Задание 12.2\)
\(x_1=\frac{-1-11}{2 \cdot 2}=-3;\) \(x_2=\frac{-1+11}{2 \cdot 2}=\frac{5}{2}\)
\(2(x-\frac{5}{2})(x+3)>0\) \(|:2\)
\((x-\frac{5}{2})(x+3)>0\)
Отметим, что здесь применено разложение на множители квадратного трехчлена.
Найдите корни числителя и знаменателя (т.е. такие значения икса, которые превратят их в ноль).
\(x=\frac{5}{2}; x=-3\)
Нанесите найденные значения на числовую ось.
Если неравенство строгое, то корни числителя обозначьте «выколотой» точкой, если нет — закрашенной. Корни знаменателя «выколоты» всегда, независимо от строгости знака сравнения.
Расставьте знаки на интервалах числовой оси. Напомню правила расстановки знаков:
— В крайнем правом интервале ставим знак плюс;
— Дальше двигаемся влево;
|
— Переходя через число: |
— меняем знак, если скобка с этим числом была в нечетной степени (1, 3, 5…) |
|
|
|
— не меняем знак, если скобка с этим числом была в четной степени (2, 4, 6…)
|
Выделите нужные промежутки.2+64\) – однозначно положительно при любом значении икса, то есть это выражение никак не влияет на знак левой части. Поэтому можно смело делить обе части неравенства на это выражение.
Поделим неравенство так же на \(-1\) , чтобы избавиться от минуса.
\((x-8)(x+8)≥0\)
Теперь можно применять метод интервалов
\(x=8;\) \(x=-8\)
Запишем ответ
Ответ: \((-∞;-8]∪[8;∞)\)
Смотрите также:
Квадратные неравенства
Дробно-рациональные неравенства
Алгебра для 8 класса
Необходимо решить уравнение: х*(143)=2х-30:
1
-2
2
Необходимо решить уравнение: 2*(х2х3х4х)=600:
30
20
4
Необходимо решить уравнение: 3*(5х7х)2=576:
7
9
8
Какие из представленных значений С и М соответствует уравнению С(ХМ)=0, если Х=-7. С и М – больше нуля:
М=3
С=0
М=0
С=0
М=7
С=2
Укажите квадратный корень из 16:
-4
8
4
Укажите квадратный корень из 25:
10
5
2,5
Укажите квадратный корень из 64:
16
18
8
При каких значениях x график функции y=2x-7 расположен выше оси x:
при x>3,5
при x< -3,5
при x< 3,5
Необходимо найти наименьшее целочисленное решение неравенства 2x-5< 4×7:
6
1
-5
Необходимо решить уравнение х2 – 2х = 0. В ответе укажите сумму корней:
1
2
4
Если дискриминант квадратного уравнения отрицательный, то уравнение:
не имеет корней
имеет 1 корень
имеет 2 корня
Книга стоила 320 р., цена была увеличена на 20%. Сколько стоит эта книга теперь:
364
384
380
Понятие этих чисел вызвано потребностью счёта предметов. Какое они название носят:
Натуральные
простые
целые
Какие цифры мы используем в школе:
Римские
Индийские
Арабские и Римские
Какое из чисел является решением неравенства 3х > х 3:
0
-2
3
Неравенству х < 5 соответствует промежуток:
[5; ∞)
( – ∞; 5)
(5; ∞)
Необходимо решить неравенство: 3х < 18:
[6; ∞)
(6; ∞)
( – ∞; 6)
Какое из чисел является решением неравенства 4х – 3 > х:
0
2
1
Неравенству х > 4 соответствует промежуток:
(-∞; 4]
(-∞; 4)
(4; ∞)
Необходимо решить неравенство: 6х ≤ 30:
(5; ∞)
( – ∞; 5]
[5; ∞)
Какое из чисел не является решением неравенства 4,5 3у >0:
-1,5
3
4,5
Необходимо решить неравенство: 6 -7х > 3х – 7:
(0,1; ∞)
(-∞; 1,3)
(-∞; 0,1)
Сколько целых решений неравенства 2с < -1,3 принадлежит промежутку (-6; 3]:
4
3
5
Какое из предложенных неравенств является верным при любых значениях х и у, удовлетворяющих условию х > у:
у – х < -1
х – у > -2
х – у > 3
Какое из чисел не является решением неравенства 2,6 2у < 0
4,5
-3
-1,3
Необходимо решить уравнение: 3х-4*(82х)-710х=2х3*(6х7):
-2
-4
2
Выберите число, заключенное между числами 3,128 и 3,131:
3,12(8)
3,127
3,1(3)
Необходимо сравнить числа 0,791(6) и 37/48:
0,791(6) < 37/48
0,791(6) = 37/48
0,791(6) > 37/48
Порядок числа 20331,22 равен:
6
4
2
Наибольшее из предложенных цифр:
2,5
√7
√5
Решение рациональных неравенств
Рациональный
Рациональное выражение выглядит так:
Неравенства
Иногда нам нужно решить такие рациональные неравенства:
Символ | слов | Пример |
|---|---|---|
| | | |
> | больше | (х + 1) / (3-х)> 2 |
< | менее | х / (х + 7) <−3 |
≥ | больше или равно | (x − 1) / (5 − x) ≥ 0 |
≤ | меньше или равно | (3−2x) / (x − 1) ≤ 2 |
| | | |
Решение
Решение неравенств очень похоже на решение уравнений… вы делаете почти то же самое.
| Когда мы решаем неравенств , мы пытаемся найти интервалов , , например, отмеченные «<0» или «> 0» |
Это шаги:
- найти «достопримечательности»:
- точки «= 0» (корни) и
- «вертикальные асимптоты» (где функция не определена)
- между «точками интереса», функция либо больше нуля (> 0), либо меньше нуля (<0)
- , затем выберите тестовое значение, чтобы узнать, какое оно (> 0 или <0)
Вот пример:
Пример:
3x − 10 x − 4 > 2Первый , давайте упростим!
Но вы не можете умножить на (x − 4)
Потому что «x − 4» может быть положительным или отрицательным…. мы не знаем, следует ли нам менять направление неравенства или нет. Все это объясняется в разделе «Устранение неравенств».
Вместо этого переместите «2» влево:
3x − 10 x − 4 -2> 0
Затем умножьте 2 на (x − 4) / (x − 4):
3x − 10 x − 4 -2 x − 4 x − 4 > 0
Теперь у нас есть общий знаменатель, давайте все вместе:
3x − 10-2 (x − 4) x − 4 > 0
Упростить:
x − 2 x − 4 > 0
Второй , поищем «достопримечательности».
При x = 2 имеем: (0) / (x − 4)> 0, что является точкой «= 0», или корень
При x = 4 имеем: (x − 2) / (0)> 0, что составляет undefined
Третий , сделайте контрольные точки, чтобы увидеть, что он делает между:
При x = 0:
- x − 2 = −2, что составляет отрицательное значение
- x − 4 = −4, что также является отрицательным
- Итак, (x − 2) / (x − 4) должно быть положительным
Мы можем сделать то же самое для x = 3 и x = 5 и получить следующие результаты:
| х = 0 | х = 2 | х = 3 | х = 4 | х = 5 | |
|---|---|---|---|---|---|
| х − 2 <0 | х − 2> 0 | х − 2> 0 | |||
| х − 4 <0 | х − 4 <0 | х − 4> 0 | |||
| (x − 2) / (x − 4) равно | > 0 | 0 | <0 | undefined | > 0 |
Это дает нам полную картину!
А где это> 0?
Итак, наш результат:
(−∞, 2) U (4, + ∞)
Все это мы сделали без рисования сюжета!
Но вот график (x − 2) / (x − 4), поэтому вы можете видеть:
Сложные неравенства — объяснение и примеры
Сложные неравенства — это производная форма неравенств, которые очень полезны в математике, когда вы имеете дело с диапазоном возможных значений.
Например, вы получаете два решения после решения определенного линейного неравенства, x> 3 и x <12. Вы можете прочитать это как «3 меньше x, что меньше 12. Теперь вы можете переписать его в форма 3 Давайте посмотрим, что такое сложное неравенство? Есть и другие случаи, когда неравенство может использоваться для представления более чем одного ограничивающего значения.В таких ситуациях применяется сложное неравенство. Следовательно, мы можем определить составное неравенство как выражение, содержащее два утверждения неравенства, соединенные словами « И » или « ИЛИ. » Конъюнкция« и »указывает, что два утверждения верны одновременно. С другой стороны, слово « или » означает, что все составное утверждение истинно, пока истинно одно из утверждений. Термин «Или» используется для обозначения комбинации наборов решений для отдельных операторов. Пример 1 Решите относительно x: 3 x + 2 <14 и 2 x - 5> –11. Решение Чтобы решить это сложное неравенство, мы начнем с решения каждого уравнения отдельно.А поскольку соединяющее слово — «и», то это означает, что желаемое решение является перекрытием или пересечением. 3x + 2 <14 Вычтите 2 и разделите на 3 в обеих частях уравнения. 3x + 2-2 <14-2 3x / 3 <12/3 x <4 А; 2x - 5> -11 Добавьте 5 к обеим сторонам и разделите все на 2 2x — 5 + 5> -11 + 5 2x> -6 x> -3 Неравенство x <4 означает все числа слева от 4, а x> –3 означает все числа справа от –3.Следовательно, пересечение этих двух неравенств включает в себя все числа от –3 до 4. Решение для этого сложного неравенства, следовательно, x> –3 и x <4 Пример 2 Решите 2 + x <5 и -1 <2 + x Решение Решите каждое неравенство отдельно. 2 + x <5 Чтобы выделить переменную из первого уравнения, нам нужно вычесть обе части на 2, что дает; х <3. Мы снова вычитаем 2 из обеих частей второго уравнения -1 <2 + x. -3 <х. Следовательно, решение для этого сложного неравенства: x <3 и -3 Пример 3 Решить 7> 2x + 5 или 7 <5x - 3. Решение Решите каждое неравенство отдельно: Для 7> 2x + 5 мы вычитаем обе части на 5, чтобы получить; 2> 2х. Теперь разделите обе стороны на 2, чтобы получить; 1> х. Для 7 <5x - 3 сложите обе стороны на 3, чтобы получить; 10 <5x. Если разделить каждую сторону на 5, получим; 2 <х. Решение: x <1 или x> 2 Пример 4 Решите 3 (2x + 5) ≤18 и 2 (x − 7) <- 6 Решение Решите каждое неравенство отдельно 3 (2x + 5) ≤ 18 => 6x + 15 ≤ 18 6x ≤ 3 x ≤ ½ And 2 (x − 7) <- 6 = > 2x −14 <−6 2x <8 x <4 Следовательно, решение: x ≤ ½ и x <4 Пример 5 Решить: 5 + x> 7 или x — 3 <5 Решение Решите каждое неравенство отдельно и объедините решения. Для 5 + x> 7; Вычтем обе части на 5, чтобы получить; x> 2 Решить x — 3 <5; Добавьте 3 к обеим сторонам неравенства, чтобы получить; x <2 Объединение двух решений со словом «или» дает; X> 2 или x <2 Пример 6 Решите для x: –12 ≤ 2 x + 6 ≤ 8. Решение Если составное слово написано без связующее слово предполагается как «и».”Следовательно, x — 12 ≤ 2 x + 6 ≤ 8 можно перевести в следующее сложное предложение: –12 ≤ 2 x + 6 и 2 x + 6 ≤ 8. Теперь каждое неравенство можно решить отдельно. Для –12 ≤ 2 x + 6; => –18 ≤ 2 x –9 ≤ x А для 2 x + 6 ≤ 8; => 2 x≤ 2 Неравенство –9 ≤ x означает, что все числа справа от –9 включительно и находятся в пределах решения, а x ≤ 1 означает, что все числа слева от 1 включительно находятся в пределах решения.Поэтому решение этого составного неравенства можно записать как {x | x ≥ –9 и x ≤ 1} или {x | –9 ≤ x ≤ 1} Пример 7 Решить для x: 3x — 2> –8 или 2 x + 1 <9. Решение Для 3x — 2> –8; => 3x — 2 + 2> –8 + 2 => 3x> — 6 => x> — 2 Для 2 x + 1 <9; Вычтем 1 из обеих частей уравнения; => 2 х <8.=> x <4. Неравенство x> –2 означает, что решение верно для всех чисел справа от –2, а x <4 означает, что решение верно для всех чисел слева от 4. Решение записывается как; {x | x <4 или x > — 2} \ (<\) \ (2x-1 <7 \) \ (\ le \) \ (2x-1 \ le 7 \) \ (> \) \ (2x-1> 7 \) \ (\ ge \) \ (2x-1 \ ge 7 \) \ (- 5x + 24 <3x-8 \) \ (- 24 \) \ (- 5x + 24 + (- 24) <3x-8 + (- 24) \) \ (- 5x <3x-32 \) \ (- 3x \) \ (- 5x + (- 3x) <3x-32 + (- 3x) \) \ (- 8x <-32 \) \ (8 \) \ (\ frac {-8x} {8} <- \ frac {32} {8} \) \ (- х <-4 \) \ (- х \ раз -1 <-4 \ раз -1 \) \ (х> 4 \) \ (x> 4 \) \ (4 \) Линейное неравенство похоже на линейное уравнение в том, что наибольший показатель степени переменной равен \ (\ text {1} \). Ниже приведены примеры линейных неравенств. Методы, используемые для решения линейных неравенств, аналогичны тем, которые используются для решения линейных уравнений.Единственная разница возникает при умножении или делении со знаком минус. Например, мы знаем, что \ (8> 6 \). Если обе части неравенства разделить на \ (- \ text {2} \), то мы получим \ (- 4> -3 \), что неверно. Следовательно, знак неравенства нужно поменять местами, получая \ (- 4 <-3 \). Чтобы сравнить неравенство с нормальным уравнением, мы сначала решим уравнение. Решить \ (2x + 2 = 1 \): Если представить этот ответ в числовой строке, получим: Теперь решим относительно \ (x \) в неравенстве \ (2x + 2 \ le 1 \): Если представить этот ответ в числовой строке, получим: Мы видим, что для уравнения существует только одно значение \ (x \), для которого уравнение верно.Однако для неравенства существует диапазон значений, для которых неравенство верно. В этом главное отличие уравнения от неравенства. Помните: , когда мы делим или умножаем обе стороны неравенства на отрицательное число, направление неравенства меняется. Например, если \ (x <1 \), то \ (- x> -1 \). Также обратите внимание, что мы не можем делить или умножать на переменную. Следующее видео знакомит с линейными неравенствами. Видео: 2FGH Примеры: \ (\ left (4; 12 \ right) \) Круглые скобки указывают на то, что номер не включен. Этот интервал включает все действительные числа, большие, но не равные \ (\ text {4} \) и меньшие, но не равные \ (\ text {12} \). \ (\ left (- \ infty; -1 \ right) \) Круглые скобки всегда используются для положительной и отрицательной бесконечности.Этот интервал включает все действительные числа, меньшие, но не равные \ (- \ text {1} \). \ (\ left [1; 13 \ right) \) Квадратная скобка означает, что номер включен. Этот интервал включает все действительные числа, большие или равные \ (\ text {1} \) и меньшие, но не равные \ (\ text {13} \). Важно отметить, что это обозначение может использоваться только для представления интервала действительных чисел. Мы представляем вышеприведенный ответ в обозначении интервалов как \ (\ left (- \ infty; — \ frac {1} {2} \ right] \) Решить относительно \ (r \): Представьте ответ в числовой строке и в виде интервалов. Что такое сложное неравенство?
Как решить сложные неравенства?
Решение сложных неравенств зависит от того, используются ли слова «и» или «или» для соединения отдельных утверждений.
Предыдущий урок | Главная страница | Следующий урок Алгебра Неравенства — Задачи | Неравенства
Неравенство повсюду вокруг нас.Некоторые из них могут быть настолько знакомы, что вы их даже не замечаете. Рассмотрим следующие сценарии: максимальное количество людей, которым разрешено находиться в лифте, ограничение скорости на дорожном знаке, минимальный балл теста, необходимый для прохождения класса, количество мегабайт, которое вы можете использовать в месяц по тарифному плану мобильного телефона и т. Д. Все это неравенство. Вы можете записать их следующим образом: 1. Количество человек, которым разрешено находиться в лифте ≤ 12
2. Максимально допустимое количество миль в час ≤ 60
3. Баллы, необходимые для прохождения класса ≥ 50
4.Количество мегабайт использования интернета в месяц ≤ 2000 Формально алгебраическое неравенство — это выражение, в котором вместо знака равенства, используемого в регулярных уравнениях, используется один из следующих знаков: 1. Решение линейных неравенств | Уравнения и неравенства
4.7 Решение линейных неравенств (EMA3H)
Обозначение интервалов (EMA3J)
Рабочий пример 17: Решение линейных неравенств
Переставьте и решите для \ (r \)
\ begin {align *}
-r &> 2-6 \\
-r &> -4
\ end {align *} Умножить на \ (- \ text {1} \) и отменить знак неравенства
\ [г <4 \]
Изобразите ответ в числовой строке
Представьте ответ в виде интервалов
\ [\ влево (- \ infty; 4 \ вправо) \]Рабочий пример 18: Решение линейных неравенств
Решите относительно \ (q \):
\ [4q + 3Представьте ответ в числовой строке и в интервальной записи.
Раскладной кронштейн
\ begin {align *} 4q + 3 & <2 (q + 3) \\ 4q + 3 & <2q + 6 \ end {align *}Переставьте и решите для \ (q \)
\ begin {align *} 4q + 3 & <2q + 6 \\ 4q - 2q & <6 - 3 \\ 2q & <3 \ end {align *}Разделите обе стороны на \ (\ text {2} \)
\ begin {align *} 2q & <3 \\ д & <\ frac {3} {2} \ end {align *}Представьте ответ в числовой строке
Представьте ответ в виде интервалов
\ (\ left (- \ infty; \ frac {3} {2} \ right) \)Рабочий пример 19: Решение сложных линейных неравенств
Решить относительно \ (x \):
\ [5 \ le x + 3Представьте ответ в числовой строке и в интервальной записи.
Вычтем \ (\ text {3} \) из всех частей неравенства
\ [\ begin {array} {ccccc} 5 — 3 & \ le & x + 3 — 3 & <& 8 - 3 \\ 2 & \ le & x & <& 5 \ конец {массив} \]Изобразите ответ в числовой строке
Представьте ответ в виде интервалов
\ (\ left [2; 5 \ right) \)Зарегистрируйтесь, чтобы получить фору по стипендии и возможностям карьерного роста.Используйте практику Сиявулы, чтобы получить наилучшие возможные оценки.
Зарегистрируйтесь, чтобы разблокировать свое будущее Упражнение 4.6\ (x <-1 \ text {и} x \ ge 6; x \ in \ mathbb {R} \)
\ (3 <х <6; х \ в \ mathbb {R} \)
\ (x \ neq 3; x \ neq 6; x \ in \ mathbb {R} \)
\ (х> -10; х \ в \ mathbb {R} \)
\ begin {align *} 3х + 4 &> 5х + 8 \\ 3х — 5х &> 8 — 4 \\ -2x> 4 \\ 2xОбозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; -2) \)
\ (3 (х — 1) — 2 \ le 6x + 4 \)
\ begin {align *} 3 (x — 1) — 2 & \ le 6x + 4 \\ 3x — 5 & \ le 6x + 4 \\ 3х — 6х & \ ле 4 + 5 \\ -3x \ le 9 \\ х \ ge — \ frac {9} {3} \\ х \ ge -3 \ end {выровнять *}Обозначается в числовой строке:
В интервальном обозначении: \ ([- 3; \ infty) \)
\ (\ dfrac {x — 7} {3}> \ dfrac {2x — 3} {2} \)
\ begin {align *} \ frac {x — 7} {3} &> \ frac {2x — 3} {2} \\ 2 (х — 7) &> 3 (2x — 3) \\ 2х — 14> 6х — 9 \\ -4x> 5 \\ xОбозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; — \ frac {5} {4}) \)
\ begin {align *} -4 (x — 1) & \ frac {2} {5} \ end {выровнять *}Обозначается в числовой строке:
В интервальном обозначении: \ ((\ frac {2} {5}; \ infty) \)
\ (\ dfrac {1} {2} x + \ dfrac {1} {3} (x — 1) \ ge \ dfrac {5} {6} x — \ dfrac {1} {3} \)
\ begin {align *} \ frac {1} {2} x + \ frac {1} {3} (x — 1) & \ ge \ frac {5} {6} x — \ frac {1} {3} \\ \ frac {1} {2} x + \ frac {1} {3} x — \ frac {1} {3} & \ ge \ frac {5} {6} x — \ frac {1} {3} \ \ \ frac {1} {2} x + \ frac {1} {3} x — \ frac {5} {6} x & \ ge \ frac {1} {3} — \ frac {1} {3} \ \ \ frac {3} {6} x + \ frac {2} {6} x — \ frac {5} {6} x & \ ge 0 \\ 0x \ ge 0 \ end {выровнять *}Неравенство верно для всех действительных значений \ (x \).
\ [\ begin {array} {ccccc} -2 & \ le & x — 1 &В числовой строке:
В интервальном обозначении: \ ([- 1; 4) \)
\ [\ begin {array} {ccccc} -5 иОбозначается в числовой строке:
В интервальном обозначении: \ ((- 1; 5] \)
\ (7 (3x + 2) — 5 (2x — 3)> 7 \)
\ begin {align *} 7 (3x + 2) — 5 (2x — 3) &> 7 \\ 21х + 14 — 10х + 15 &> 7 \\ 11x &> -22 \\ х &> -2 \ end {выровнять *}Обозначается в числовой строке:
В интервальном обозначении: \ ((- 2; \ infty) \)
\ (\ dfrac {5x — 1} {- 6} \ ge \ dfrac {1 — 2x} {3} \)
\ begin {align *} \ frac {5x — 1} {- 6} & \ ge \ frac {1 — 2x} {3} \\ 5x — 1 & \ ge -2 (1 — 2x) \\ 5x — 1 & \ ge -2 + 4x \\ 5x — 4x & \ ge -1 \\ х & \ ge -1 \ end {выровнять *}Обозначается в числовой строке:
В интервальном обозначении: \ ([- 1; \ infty) \)
\ [\ begin {array} {ccccc} 3 & \ le & 4 — х & \ le & 16 \\ -1 & \ le & -x & \ le & 12 \\ 1 & \ ge & x & \ ge & -12 \ конец {массив} \]Обозначается в числовой строке:
В интервальном обозначении: \ ([1; 12] \)
\ (\ dfrac {-7y} {3} — 5> -7 \)
\ begin {align *} \ frac {-7y} {3} — 5 &> -7 \\ -7л — 15 &> -21 \\ -7лет &> -6 \\ y &Обозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; \ frac {6} {7}) \)
\ [\ begin {array} {ccccc} 1 & \ le & 1-2y & & -4 \\ -4 иОбозначается в числовой строке:
В интервальном обозначении: \ ((- 4; 0] \)
\ (- 2 <\ dfrac {x - 1} {- 3} <7 \)
\ [\ begin {array} {ccccc} -2 & & x — 1 &> & -21 \\ 7 &> & x &> & -20 \\ -20 иОбозначается в числовой строке:
В интервальном обозначении: \ ((- 20; 7) \)
\ begin {align *} 2 х -1 & <3 (х +11) \\ 2 х -1 & <3 х +33 \\ 2 х -3 х & <33 +1 \\ -1 х & <34 \\ \ поэтому x &> -34 \ end {align *}
\ [\ влево (-34; \ infty \ вправо) \]
\ begin {align *} х -1 & <-4 (х -6) \\ х -1 & <-4 х +24 \\ х +4 х & <24 +1 \\ 5 х & <25 \\ \ поэтому x & <5 \ end {align *}
\ [\ влево (- \ infty; 5 \ вправо) \]
\ (\ dfrac {x-1} {8} \ leq \ dfrac {2 (x-2)} {3} \)
\ begin {align *} \ frac {x-1} {8} & \ leq \ frac {2 (x-2)} {3} \\ 3 (х-1) & \ leq 16 (х-2) \\ 3х-3 & \ leq 16х-32 \\ 3х -16х & \ leq -32 +3 \\ -13x & \ leq -29 \\ \ поэтому x & \ geq \ frac {29} {13} \ end {выровнять *}\ (\; x \ in \ left [\ frac {29} {13}; \ infty \ right) \).
\ (\ dfrac {x + 2} {4} \ leq \ dfrac {-2 (x-4)} {7} \)
\ begin {align *} \ frac {x + 2} {4} & \ leq \ frac {-2 (x-4)} {7} \\ 7 (х + 2) & \ leq -8 (х-4) \\ 7x + 14 & \ leq -8x + 32 \\ 7x + 8x & \ leq 32-14 \\ 15x & \ leq 18 \\ \ поэтому x & \ leq \ frac {6} {5} \ end {выровнять *}\ (\; x \ in \ left (- \ infty; \ frac {6} {5} \ right] \).
\ (\ dfrac {1} {5} x — \ dfrac {5} {4} (x + 2)> \ dfrac {1} {4} x + 3 \)
\ begin {align *} \ frac {1} {5} x — \ frac {5} {4} (x + 2) &> \ frac {1} {4} x +3 \\ 4х — 25 (х + 2) &> 5х +60 \\ 4х — 25х-50 &> 5х +60 \\ 4х — 25 х -5х &> 60 + 50 \\ -26x &> 110 \\ \ поэтому x & <- \ frac {55} {13} \ end {align *}
Интервал: \ [\ left (- \ infty; — \ frac {55} {13} \ right) \]
\ (\ dfrac {1} {5} x — \ dfrac {2} {5} (x + 3) \ geq \ dfrac {4} {2} x +3 \)
\ begin {align *} \ frac {1} {5} x — \ frac {2} {5} (x + 3) & \ geq \ frac {4} {2} x +3 \\ 2x — 4 (x + 3) & \ geq 20x +30 \\ 2х — 4 х-12 & \ geq 20x +30 \\ 2х — 4 х -20х & \ geq 30 + 12 \\ -22x & \ geq 42 \\ \ поэтому x & \ leq — \ frac {21} {11} \ end {align *}
Интервал: \ [\ left (- \ infty; — \ frac {21} {11} \ right] \]
\ (4x +3 <-3 \ quad \ text {или} \ quad 4x +3> 5 \)
Решите неравенство: \ [\ begin {array} {rclcrcl} 4x +3 & <& -3 & \ text {или} & 4x +3 &> & 5 \\ 4x & <& -3-3 & \ text {or} & 4x &> & 5-3 \\ x & <& \ frac {-3-3} {4} & \ text {или} & x &> & \ frac {5-3} {4} \\ x & <& - \ frac {3} {2} & \ text {или} & x &> & \ frac {1} {2} \\ \ end {array} \]
\ [\ left (- \ infty; — \ frac {3} {2} \ right) \ cup \ left (\ frac {1} {2}; \ infty \ right) \]
Решите неравенство: \ [\ begin {array} {rcccl} 4 & \ ge & -6x -6 & \ ge & -3 \\ 4 + 6 & \ ge & -6x & \ ge & -3 + 6 \\ \ frac {4 + 6} {- 6} & \ le & x & \ le & \ frac {-3 + 6} {- 6} \\ — \ frac {5} {3} & \ le & x & \ le & — \ frac {1} {2} \\ \ end {array} \]
\ [\ left [- \ frac {5} {3}; — \ frac {1} {2} \ right] \]
\ (6b — 3> b + 2, ~ b \ in \ mathbb {Z} \)
\ begin {align *} 6b — 3> b + 2, ~ b \ in \ mathbb {Z} \\ 5b> 5 \\ b> 1 \ end {выровнять *}\ (3a — 1 <4a + 6, ~ a \ in \ mathbb {N} \)
\ begin {align *} 3а — 1-7 \ end {выровнять *}Однако нам говорят, что \ (a \ in \ mathbb {N} \) и поэтому \ (a> 0 \).
\ (\ dfrac {b-3} {2} + 1 <\ dfrac {b} {4} - 4, ~ b \ in \ mathbb {R} \)
\ begin {align *} \ frac {b-3} {2} + 1\ (\ dfrac {4a +7} {3} — 5> a — \ dfrac {2} {3}, ~ a \ in \ mathbb {N} \)
\ begin {align *} \ frac {4a +7} {3} — 5> a — \ frac {2} {3} \\ 4а + 7-15> 3а — 2 \\ а> 6 \ end {выровнять *}Решение полиномиальных неравенств
Решение полиномиальных неравенств Вот шаги, необходимые для решения полиномиальных неравенств:| Шаг 1 : | Запишите многочлен в правильной форме.Многочлен должен быть записан в порядке убывания и должен быть меньше, больше, меньше или равен или больше или равен нулю. |
| Шаг 2 : | Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, приравняйте уравнение к нулю и решите. |
| Шаг 3 : | Сделайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки. |
| Шаг 4 : | Выполните анализ знаков. Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. Знак этого ответа (положительный или отрицательный) будет знаком всего раздела. Вы можете проверить другой номер из того же раздела, если хотите проверить свой ответ. |
| Шаг 5 : | Используйте диаграмму знакового анализа, чтобы определить, какие разделы удовлетворяют неравенству.Если неравенство меньше нуля или меньше или равно нулю, тогда вам нужны все отрицательные участки, найденные в диаграмме анализа знаков. Если неравенство больше нуля или больше или равно нулю, тогда вы хотите, чтобы все положительные участки были найдены в диаграмме анализа знаков. |
| Шаг 6 : | Используйте интервальную запись, чтобы написать окончательный ответ. |
Пример 1 — График:
| Шаг 1 : Напишите многочлен в правильной форме.Многочлен должен быть записан в порядке убывания и должен быть меньше, больше, меньше или равен или больше или равен нулю. | |
| Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, приравняйте уравнение к нулю и решите. | |
| Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки. | |
| Шаг 4 : Выполните анализ знаков. Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –3, что дает +7, x = 0, что дает –8, и x = 5, что дает +7. | |
| Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству.В этом случае у нас больше или равно нулю, поэтому нам нужны все положительные секции. | |
| Шаг 6 : Используйте интервальную нотацию, чтобы написать окончательный ответ. |
Пример 2 — График:
| Шаг 1 : Напишите многочлен в правильной форме. Многочлен должен быть записан в порядке убывания и должен быть меньше, больше, меньше или равен или больше или равен нулю. | |
| Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, приравняйте уравнение к нулю и решите. | |
| Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки. | |
| Шаг 4 : Выполните анализ знаков.Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –4, что дает +3, x = –2, что дает –1, и x = 0, что дает +3. | |
| Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству. В этом случае у нас меньше или равно нулю, поэтому нам нужен отрицательный участок. | |
| Шаг 6 : Используйте интервальную нотацию, чтобы написать окончательный ответ. |
Щелкните здесь для практических задач
Пример 3 — График:
| Шаг 1 : Напишите многочлен в правильной форме. Многочлен должен быть записан в порядке убывания и должен быть меньше, больше, меньше или равен или больше или равен нулю. | |
| Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, приравняйте уравнение к нулю и решите. | |
| Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки. | |
| Шаг 4 : Выполните анализ знаков.Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –4, что дает –35, x = 0, что дает +9, x = 2, что дает –5, и x = 4, что дает +21. | |
| Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству. В этом случае у нас меньше нуля, поэтому нам нужны все отрицательные секции. | |
| Шаг 6 : Используйте интервальную нотацию, чтобы написать окончательный ответ. |
Щелкните здесь для практических задач
Пример 4 — График:
| Шаг 1 : Напишите многочлен в правильной форме. Многочлен должен быть записан в порядке убывания и должен быть меньше, больше, меньше или равен или больше или равен нулю. | |
| Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, приравняйте уравнение к нулю и решите. | |
| Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки. | |
| Шаг 4 : Выполните анализ знаков.Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –5, что дает +56, x = –2, что дает –16, x = 0, что дает +16, и x = 3, что дает –56. | |
| Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству. В этом случае у нас больше нуля, поэтому нам нужны все положительные секции. | |
| Шаг 6 : Используйте интервальную нотацию, чтобы написать окончательный ответ. |
Щелкните здесь для практических задач
неравенств | S-cool, сайт доработки
4x — 5 Например: (Это означает, что, когда значение x меньше 2, выполняется неравенство 4x — 5 Приведенный выше пример представляет собой линейное неравенство (нет степеней x, кроме x 1 , и оно было решено как обычное уравнение). Все неравенства одинаковы, за исключением того, что нужно заметить одну или две уловки.В основном при работе с негативом или ответом. Обратите внимание, что для следующих примеров знак неравенства изменился. (Вы понимаете, почему?) Пример То же верно и для получения обратных величин. В этом случае мы умножаем и делим величины следующим образом: Пример Проверьте это сами, умножив обе стороны на 5x и разделив обе стороны на 12. (Дополнительная проверка заключается в замене значений и проверке соответствия решение работает.) Как и при решении квадратных уравнений, желательно разложить на множители (или использовать формулу), а затем нарисовать кривую, помня, что a + x 2 — это ∪-образная форма, а — x 2 —образная форма. Пример: Решить 3x 2 <7x + 6 3x 2 — 7x — 6 <0 (3x + 2) (x — 3) <0 График равен ноль, когда x = -2/3 или x = 3 Поскольку график имеет-образную форму, график находится ниже оси y, когда -2/3 После факторизации функции можно найти, где она равна нулю, и, рассматривая числа между этими значениями, мы можем определить, где кривая является положительной и отрицательной, и, следовательно, решить неравенство. Например: Решить (x-1) (x + 2) (x + 4) ≥ 0 Он равен нулю, когда x = 1, -2 и -4. Чтобы узнать, что происходит, когда x принимает другие значения, мы заполнили быструю таблицу. Быстрый набросок кривой покажет эти результаты более четко: Итак, решения следующие: -4 ≤ x ≤ 2 и x ≥ 1. Примечание: Если вы знаете форму графика, в таблице больше нет необходимости, так как вы можете заполнить детали после того, как нанесете точки, где график пересекает оси x и y. В этом разделе предполагается, что вы знаете, как находить корни многочлена.
Также поможет, если вы посетили секцию разминки. Предположим, вы хотите решить неравенство x 2 -4 x +3 <0. Шаг 1 . Решите уравнение f ( x ) = x 2 -4 x + 3 = 0. В этом случае мы можем «угадать»: x 2 -4 x + 3 = ( x -1) ( x -3), Шаг 2. Наши решения разделяют ось x на три интервала. Выберите точку (на ваш выбор!) В каждом интервале. Возьмем x = 0, x = 2 и x = 4. Вычислите f ( x ) для этих точек: Эти три точки являются репрезентативными для того, что происходит в интервалах, в которых они содержатся: Поскольку f (0)> 0, f ( x ) будет положительным для все x в интервале .Точно так же, поскольку f (2) <0, f ( x ) будет отрицательным для всех x в интервале (1,3). Поскольку f (4)> 0, f ( x ) будет положительным для все x в интервале .
Вы можете указать это на оси x , вставив знаки плюс или минус на оси x . Вместо этого я использую цветовую кодировку: синий для положительного, красный для отрицательного: Шаг 3. Мы хотим решить неравенство x 2 -4 x +3 <0, Почему это работает? Посмотрим на график f ( x ): Обратите внимание на ключевую роль, которую играют «желтые точки», x — точки пересечения f ( x ). f ( x ) может изменить свой знак, только пройдя через точку пересечения x , , т.е. , решение f ( x ) = 0 всегда будет разделять части графика f ( x ) над осью x от деталей ниже оси x . Таким образом, достаточно выбрать представителя в каждом из трех интервалов, разделенных «желтыми точками», чтобы проверить, является ли f ( x ) положительным или отрицательным в интервале. Это замечательное свойство полиномов называется свойством промежуточного значения полиномов; ваш учитель может также называть это свойство непрерывностью . Вот еще один пример: Найдите решения неравенства Опять же, мы можем «угадать»: x 2 -3 x + 2 = ( x -1) ( x -2), Шаг 2. Наши решения разделяют ось x на три интервала. Выберите точку (на ваш выбор!) В каждом интервале.Возьмем x = 0, x = 1,5 и x = 3. Вычислите f ( x ) для этих точек: Эти три точки являются репрезентативными для того, что происходит в интервалах, в которых они содержатся: Поскольку f (0)> 0, f ( x ) будет положительным для все x в интервале .
Точно так же, поскольку f (1.5) <0, f ( x ) будет отрицательным для всех x в интервале (1,2).Поскольку f (3)> 0, f ( x ) будет положительным для для всех x в интервале .
Вы можете указать это на оси x , вставив знаки плюс или минус на оси x . Вместо этого я использую цветовую кодировку: синий для положительного, красный для отрицательного: Шаг 3. Мы хотим решить неравенство Наш следующий пример: Решить x 3 > 2 x . Сделайте , а не разделите на x с обеих сторон! Если вы это сделаете, вы никогда не сможете прийти к правильному ответу.
Вместо этого повторите узор; сделать одну часть неравенства равной нулю: x 3 -2 x > 0. Шаг 1 . Решите уравнение f ( x ) = x 3 -2 x = 0. Мы можем довольно легко разложить на факторы: Шаг 2. Наши решения разделяют ось x на четыре интервала.Выберите точку (на ваш выбор!) В каждом интервале. Возьмем x = -2, x = -1, x = 1 и x = 2. Вычислите f ( x ) для этих точек: Эти четыре точки являются репрезентативными для того, что происходит в интервалах, в которых они содержатся: Поскольку f (-2) <0, f ( x ) будет отрицательным для все x в интервале .
Точно так же, поскольку f (-1)> 0, f ( x ) будет положительным для все x в интервале .Поскольку f (1) <0, f ( x ) будет отрицательным для все x в интервале .
Так как f (2)> 0, f ( x ) будет положительным для все x в интервале .
Вы можете указать это на оси x , вставив знаки плюс или минус на оси x . Вместо этого я использую цветовую кодировку: синий для положительного, красный для отрицательного: Шаг 3. Мы хотим решить неравенство x 3 -2 x > 0, Вот мой последний пример: Решите Шаг 1 .Решите уравнение f ( x ) = x 3 +3 x 2 + x +3. Мы можем разложить на множители либо путем нахождения рационального нуля, либо путем умной группировки: x 3 +3 x 2 + x + 3 = ( x 3 +3 x 2 ) + ( x +3) = x 2 ( x +3) +1 ( x +3) = ( x 2 +1) ( x +3), Многочлен x 2 +1 неприводим, он не имеет действительных корней. Его сложные корни не имеют отношения к нашим целям. Шаг 2. Наше решение разделяет ось x на два интервала. Выберите точку (на ваш выбор!) В каждом интервале. Возьмем x = -4 и x = 0. Вычислите f ( x ) для этих точек: Эти две точки являются репрезентативными для того, что происходит в интервалах, в которых они содержатся: Поскольку f (-4) <0, f ( x ) будет отрицательным для все x в интервале .Аналогичным образом, поскольку f (0)> 0, f ( x ) будет положительным для все x в интервале .
Вы можете указать это на оси x , вставив знаки плюс или минус на оси x . Вместо этого я использую цветовую кодировку: синий для положительного, красный для отрицательного: Шаг 3. Мы хотим решить неравенство Пора попробовать самому: x 3 < x . x 3 + x 2 -6 x > 0. Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S. 4x — 5 3x <6 х <2 Диапазон x: Знак каждой скобки: Общий знак: x <-4 (-) (-) (-) -ve х = -4 0 -4 (-) (-) (+) + ve x = -2 0 -2 (-) (+) (+) -ve x = 1 0 x> 1 (+) (+) (+) + ve Аналитическое решение полиномиальных неравенств
Аналитическое решение полиномиальных неравенств
поэтому корни уравнения f ( x ) = 0 равны x = 1 и x = 3. Нарисуйте изображение оси x и отметьте эти точки.
поэтому мы ищем все x такие, что f ( x ) <0.
Следовательно, интервал (1,3) содержит все решения неравенства.
Для работы нашего метода важно, чтобы правая часть неравенства была равна нулю! Итак, давайте изменим наше неравенство на
Шаг 1 . Решите уравнение f ( x ) = x 2 -3 x + 2 = 0.
поэтому корни уравнения f ( x ) = 0 равны x = 1 и x = 2. Нарисуйте изображение оси x и отметьте эти точки.
поэтому мы ищем все x такие, что .Следовательно, множество содержит все решения неравенства. (Поскольку наше неравенство только оговаривает, что , x = 1 и x = 2 — решения, поэтому мы включаем их. «» и «» — это только символы; они никогда не будут включены в качестве решений.)
поэтому корни уравнения f ( x ) = 0 равны , x = 0 и .
Нарисуйте изображение оси x и отметьте эти точки.
поэтому мы ищем все x такие, что f ( x )> 0.
Следовательно, множество содержит все решения неравенства. (Поскольку наше неравенство предусматривает, что f ( x )> 0, не считаются решениями, поэтому мы их исключаем. «» и «» — это только символы; они никогда не будут включены в качестве решений.)
поэтому существует только один действительный корень уравнения f ( x ) = 0, а именно x = -3.Нарисуйте изображение оси x и отметьте эту точку.
поэтому мы ищем все x такие, что .Следовательно, множество — множество решений неравенства. (Поскольку наше неравенство предусматривает, что , x = -3 также является решением, поэтому мы включаем его. «» и «» — это только символы; они никогда не будут включены в качестве решений.) Упражнение 1.
Найти решения неравенства
Отвечать.
Упражнение 2.
Найти решения неравенства Отвечать.
Упражнение 3.
Найти решения неравенства Отвечать.
Упражнение 4.
Найти решения неравенства
Отвечать.
Упражнение 5.
Найти решения неравенства
Отвечать.
[Назад] [Следующий] [Алгебра] [Тригонометрия] [Комплексные переменные] [Исчисление] [Дифференциальные уравнения] [Матричная алгебра] С.Домашняя страница O.S MATHematics

 \]
\]


 \end{matrix} \right.\]
\end{matrix} \right.\]
Leave A Comment