Решить уравнение x 4 5: решить уравнение x/4= 5 — Школьные Знания.com

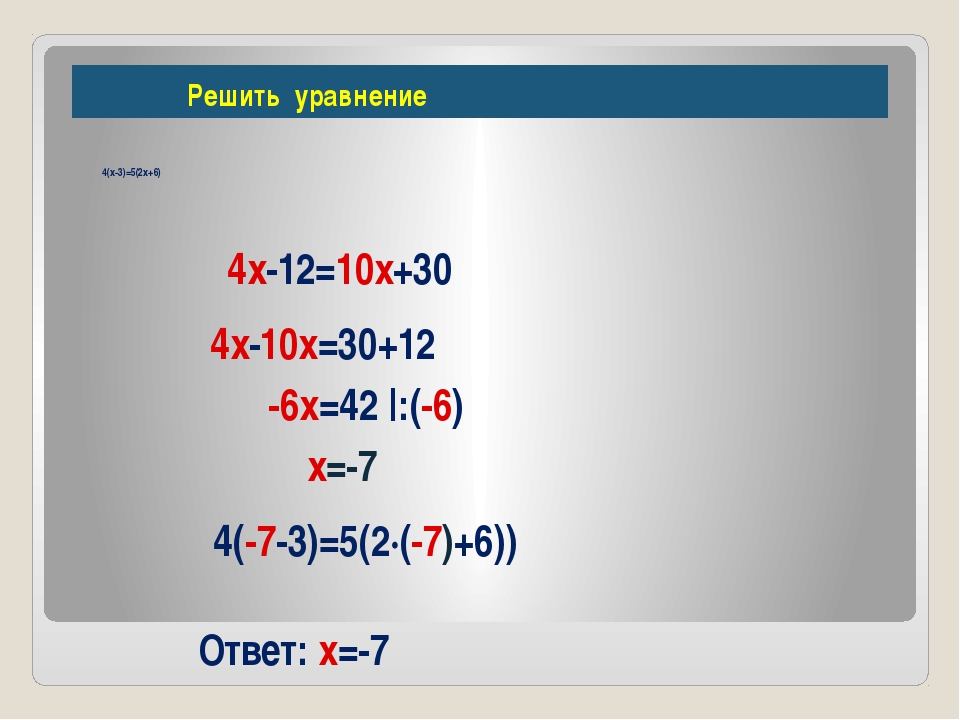
Решение простых показательных уравнений

Простые примеры на показательные уравнения позволят овладеть методикой их решения. Задания не слишком сложные и будут полезными для всех кто изучает показательные уравнения, готовится к тестированию, контрольным или вступительным экзаменам.

Пример 1. Решить уравнение (0,5)^х =.
Решение: Первое что нужно сделать это свести уравнение к одному основанию. С этой целью преобразуем правую сторону показательного уравнения

В итоге уравнение сведется к виду

Теперь основы ровны, поэтому можем приравнять показатели

и найти ответ x=-2,5.

Вот такие простые вычисления.

 

Пример 2. Решить уравнение (2/3)^х*(9/8^)х =27/64.
Решение: Преобразим правую и левую сторону показательного уравнения к одной основе


Подставим в уравнение и приравняем показатели

Таким простым методом нашли решение показательного уравнения x=3.

 

Пример 3. Решить уравнение 5^2х-7^х-35*5^2х+35*7^х=0.
Решение: Сгруппируем слагаемые, содержащие 5^2х и 7^х.


Последняя запись показательного уравнения многих заводит в тупик. (Не всем легко найти ответ).
Тогда, давайте перепишем уравнение в виде

Согласно свойствам показательных функций решение равно нулю x=0. Только возведением к 0 степени можно получить единицу.
Для наглядности посмотрите графики показательных функций. Они пересекаются в точке x=0.

 

Пример 4. Решить уравнение 14^х+2+5*14^х-1=2749.
Решение: В подобных задачах необходимо вынести основу с наименьшим показателем. Для этого распишем уравнение к виду




Получили что решение равно единице.

 

Пример 5. Решить уравнение (0,6)^х+2 =25/9 .
Решение: Такого рода задачи следует решать по следующей схеме.
Обязательно превратить число 0,6 к дробному виду

Далее уже поступают исходя из условия, в нашем случае превращаем правую сторону.

Приравниваем показатели, предварительно изменив знак в каком либо, чтобы получить одинаковую основу
x+2=-2; x=-2-2=-4.
Решение показательного уравнения x=-4.

 

Пример 6. Решить уравнение (0,25)^х-1=2*sqrt(2)
Решение: Преобразим показательное уравнение к одной основе

Подставим выражение в уравнение



Решение уравнения равно 1/4.

 

Пример 7. Решить уравнение (1,44)^х-4=6/5.
Решение: Не сразу можно догадаться как упрощать уравнения.
Распишем сначала правую сторону 6/5=1,2.
Основу в показателе сводим к виду

После подстановки приравниваем показатели при одинаковых основаниях

2(x-4)=1; 2x-8=1; 2x=9;x=9/2=4,5.

Решения уравнения x=4,5.

Пример 8. Решить уравнение
Решение: Используем основополагающее правило для показательных уравнений — свести уравнение к слагаемым с одинаковым основанием.
Выполним манипуляции с основой


Подставляем в уравнение и приравниваем степени

Решение показательного уравнения равно x=-2.

 

Пример 9. Решить уравнение 3^х-1+3^х-2+3^х-3=13.
Решение: Расписываем слагаемые так, чтобы потом сгруппировать слагаемые с одинаковим показником

Дальнейшие действия достаточно просты

Уравнение удавлетваряет значение x=3.

 

Пример 10. Найти сумму решений уравнения
Решение: Можно догадаться что придется вычислять квадратное уравнение. Но к нему еще нужно прийти. Для начала запишем 0,6 в виде

Подставим в показательное уравнения

Теперь можно приравнять степени при основаниях

Корни уровнения x=0; x=-1/2.
Их сумма равна
0-1/2=-0,5.

На этом знакомство с возможными примерами простых показательных уравнений завершено. Сложные примеры можно найти на страницах сайта. Оставайтесь с нами и мы подготовим Вас лучше репетиторов.

Похожие материалы:

Уравнения 5 класса | Математика

Сегодня мы рассмотрим более сложные уравнения 5 класса, содержащие несколько действий.  Чтобы найти неизвестную переменную, в таких уравнениях надо применить не одно, а два правила.

1) x:7+11=21

Выражение, стоящее в левой части — сумма двух слагаемых

x:7	+	11	=	21
1сл.		2сл.		сум.

Таким образом, переменная x является частью первого слагаемого. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое:

x:7=21-11

x:7=10

Получили простое уравнение 5 класса, из которого надо найти неизвестное делимое.

Чтобы найти неизвестное делимое, нужно частное умножить на делитель:

x=10∙7

x=70

Ответ: 70.

2) 65-5z=30

Правая часть уравнения представляет собой разность:

65	—	5z	=	30
ум.		в.		р.

Переменная z является частью неизвестного вычитаемого. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность:

5z=65-30

5z=35

Получили простое уравнение, в котором z — неизвестный множитель. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель:

z=35:5

z=7

Ответ: 7.

3) 120:y-23=17

В правой части уравнения — разность. Переменная y является частью неизвестного уменьшаемого.

120:y	—	23	=	17
ум.		в.		р.

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое:

120:y=17+23

120:y=40

Здесь y — неизвестный делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное:

y=120:40

y=3

Ответ: 3.

4) (48+k)∙8=400

Левая часть уравнения представляет собой произведение. Переменная k — часть первого множителя:

(48+k)	·	8	=	400
1мн		2мн		пр

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель:

48+k=400:8

48+k=50

В новом уравнении k — неизвестное слагаемое:

k=50-48

k=2

Ответ: 2.

Здесь мы решали уравнения 5 класса без использования свойств сложения и вычитания.  В 6 классе правила раскрытия скобок упрощаются, и решать такие уравнения становится проще.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Схема метода Феррари

      Целью данного раздела является изложение метода Феррари, с помощью которого можно решать уравнения четвёртой степени

a0x4 + a1x3 + a2x2 + + a3x + a4 = 0,

(1)

где a₀, a₁, a₂, a₃, a₄ – произвольные вещественные числа, причем

      Метод Феррари состоит из двух этапов.

      На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.

      На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.

Приведение уравнений 4-ой степени

      Разделим уравнение (1) на старший коэффициент a₀ . Тогда оно примет вид

x4 + ax3 + bx2 + + cx + d = 0,

(2)

где a, b, c, d – произвольные вещественные числа.

      Сделаем в уравнении (2) замену

(3)

где y – новая переменная.

      Тогда, поскольку

то уравнение (2) принимает вид

В результате уравнение (2) принимает вид

      Если ввести обозначения

то уравнение (4) примет вид

y4 + py2 + qy + r = 0,

(5)

где p, q, r – вещественные числа.

      Первый этап метода Феррари завершён.

Разложение на множители. Кубическая резольвента

      Добавив и вычитая в левой части уравнения (5) выражение

2sy² + s²,

где s – некоторое число, которое мы определим чуть позже, из (5) получим

      Следовательно, уравнение (5) принимает вид

      Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения

(7)

то уравнение (6) примет вид

      Избавляясь от знаменателя, уравнение (7) можно переписать в виде

или, раскрыв скобки, — в виде

(9)

      Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).

      Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».

      Действительно,

      Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение

(10)

а также квадратное уравнение

(11)

      Вывод метода Феррари завершен.

Пример решения уравнения 4-ой степени

      Пример. Решить уравнение

x4 + 4x3 – 4x2 – – 20x – 5 = 0.

(12)

      Решение. В соответствии с (3) сделаем в уравнении (12) замену

      Поскольку

x⁴ + 4x³ – 4x² – 20x – 5 =
= (y – 1)⁴ + 4(y – 1)³ –
– 4(y – 1)² – 20(y – 1)– 5 =
= y⁴ – 4y³ + 6y² – 4y + 1 +
+ 4y³ – 12y² + 12y – 4 –
– 4y² + 8y – 4 –
– 20y + 20 – 5 =
= y⁴ – 10y² – 4y + 8,

то в результате замены (13) уравнение (12) принимает вид

y4 – 10y2 – 4y + 8 = 0.

(14)

      В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства

p = – 10,      q = – 4,       r = 8.

(15)

      В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение

2s³ + 10s² – 16s – 84 = 0,

которое при сокращении на 2 принимает вид:

s3 + 5s2 – 8s – 42 = 0.

(16)

      Проверяя, какой из делителей свободного члена уравнения (16) является целым корнем этого уравнения, находим, что целым корнем кубической резольвенты является число

      Подставляя значения (15) и (17) в формулу (10), получаем уравнение

y² – 2y – 4 = 0,

корни которого имеют вид:

(18)

      Подставляя значения (15) и (17) в формулу (11), получаем уравнение

y² + 2y – 2 = 0,

корни которого имеют вид:

(19)

      В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):

Ответ.

      Замечание. При решении примера мы попутно получили разложение левой части уравнения (14) на множители:

y4 – 10y2 – 4y + 8 = = (y2 – 2y – 4) (y2 + + 2y – 2).

(20)

      Предоставляем посетителю нашего сайта возможность убедиться в справедливости равенства (19) в качестве несложного упражнения.

 

Онлайн калькулятор дробей. Вычисления с дробями. Сложение, вычитание, умножение и деление дробей.

Инструкция использования калькулятора дробей

Для решения вашей задачи выполните следующие действия:

• введите ваш пример в калькулятор;
• нажмите кнопку  для выполнения вычислений.

Ввод данных в калькулятор дробей

В калькулятор дробей можно вводить: целые числа, десятичные дроби, обыкновенные дроби и смешанные числа.

Целые числа. Для ввода целых чисел используйте цифровые клавиши калькулятора или цифровые клавиши вашего компьютера. 1 2 3 4 5 6 7 8 9 0

Десятичные дроби. Десятичные дроби вводятся также как и целые числа, в качестве десятичного разделителя рекомендуется использовать точку .

Обыкновенные дроби: Для ввода обыкновенной дроби нажмите клавишу на клавиатуре калькулятора — после чего введите значения числителя и знаменателя дроби используя числовые клавиши.

Смешанные числа: Используя числовые клавиши введите целую часть смешанной дроби, нажмите клавишу дроби на клавиатуре калькулятора — после чего введите значения числителя и знаменателя дроби используя числовые клавиши.

Отрицательные числа: Перед числом поставьте знак минус -, не забывайте брать отрицательные числа в скобки ( ).

Возведение в степень: Для возведения числа в степень введите число нажмите клавишу a^b, затем введите значение степени. 3)

N.B. Калькулятор поддерживает только целые степени!

N.B. Буквенные выражения, операции извлечения корня калькулятор не поддерживает!

Дополнительные возможности калькулятора дробей — старая версия

• С — полностью очистить поле ввода.
•  — удалить один символ.
•   для перемещения между полями калькулятора.

Решите линейные уравнения с одним неизвестным x / 4 = -5 Tiger Algebra Solver

Переставьте:

Переставьте уравнение, вычтя то, что находится справа от знака равенства, из обеих частей уравнения:

x / 4- ( -5) = 0

Пошаговое решение:

Шаг 1:

 x
 Упростить -
            4
 

Уравнение в конце шага 1:

 x
  - - -5 = 0
  4
 

Шаг 2:

Переписывание целого как эквивалентной дроби:

2.1 Вычитание целого из дроби

Перепишем целое как дробь, используя в знаменателе 4:

-5-5 • 4
    -5 = —— = ——————
          1 4
 

Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое

Общий знаменатель: Эквивалентная дробь и другая дробь, участвующие в вычислении, имеют один и тот же знаменатель

  
 Сложение дробей, имеющих общий знаменатель: 
  
 
 2. 2 Сложение двух эквивалентных дробей 
 Сложите две эквивалентные дроби, которые теперь имеют общий знаменатель 
 
 Объедините числители вместе, сложите сумму или разность над общим знаменателем, затем уменьшите до наименьших членов, если возможно: 
 
 x - (-5 • 4) х + 20
 знак равно
      4 4
 
 Уравнение в конце шага 2:
 x + 20
  —————— = 0
    4
 
 Шаг 3:
 
 Когда дробь равна нулю: 
  
 3.1 Когда дробь равна нулю ... 
 Если дробь равна нулю, ее числитель, часть, которая находится над чертой дроби, должен быть равен нулю.
 
 Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
 Вот как:
 x + 20
  ———— • 4 = 0 • 4
   4
 
 Теперь, с левой стороны, 4 отменяет знаменатель, в то время как с правой стороны ноль, умноженный на что-либо, по-прежнему равно нулю.
 Уравнение теперь принимает форму: 
 x + 20 = 0
 
 Решение уравнения с одной переменной:
 
 3. 2 Решите: x + 20 = 0
 Вычтите 20 из обеих частей уравнения: 
 x = -20 
 Было найдено одно решение:
 x = -20
 x = 4/5 (x + 10) решите это уравнение
 Талия делает поздравительные открытки, которые она продаст по 2 доллара за штуку. Она потратила 8 долларов на принадлежности для изготовления карточек. Уравнение 2c-8 & gt; 0 представляет c, th
…  Количество карточек, которые ей нужно продать, чтобы заработать больше, чем она потратила. Сколько карт ей нужно продать, чтобы начать получать прибыль?
 
 я бы..8606512121..pp12345
 Если центр треугольника с вершинами (a, 3), (4, b) и (-3,2) равен (1,4), то a =
 Меня забанили за одно предупреждение
 id..8606512121..pp12345
 एक वडोल आणि त्यांच्या मुलाच्या सध्याचे वयाची बेरीज 99 वर्षे आहे. जेव्हा वडिलांचे वयतेवढे होते जेवढे आता त्यांच्या मुलाचे आहे, तेव्हा त्यांचे वय मुलाच्
…  या त्या वेळेच्या वयाचेचौपट होते.वडील आणि मुलाचे सध्याचे वयाचा गुणोत्तर काय आहे?
 Приведенные ниже наборы данных показывают рост в дюймах учащихся двух разных дошкольных классов.
  Коробчатая диаграмма под названием «Класс 1. Числовая линия идет fr».
…  ом от 38 до 49. Усы варьируются от 39 до 48, а прямоугольник — от 40 до 43. Линия разделяет прямоугольник на 41.
1 класс
Коробчатая диаграмма под названием «Класс 2». Числовая линия идет от 38 до 49. Диапазон усов — от 38 до 49, а прямоугольник — от 39 до 42. Линия делит прямоугольник на 41.
2 класс
Учителя двух классов хотят сравнить рост своих учеников. Какие утверждения о наборах данных точны? Выберите три варианта.
Поскольку наборы симметричны, для сравнения наборов данных следует использовать среднее значение.В сумке есть цветные плитки.
• 3 плитки красные
• 6 плиток зеленого цвета
• 3 плитки синие
Плитка будет случайным образом выбрана из мешка. W
…  Какова вероятность в десятичной форме, что выбранная плитка будет зеленой?
 
 Призма имеет объем 84 дюйма в кубе. Каков объем пирамиды с одинаковым основанием и одинаковой высотой? Покажите свою работу и объясните свои рассуждения. Быть
…  обязательно укажите правильные единицы измерения.
 Решение логарифмических уравнений — объяснение и примеры
 Как вы хорошо знаете, логарифм — это математическая операция, обратная возведению в степень.Логарифм числа сокращается как « log ».
  Прежде чем мы сможем решить логарифмические уравнения, давайте сначала познакомимся со следующими правилами логарифмов: 
 
 Правило произведения гласит, что сумма двух логарифмов равна произведению логарифмов. Первый закон представлен как;
 ⟹ log  b  (x) + log  b  (y) = log  b  (xy)
 Разность двух логарифмов x и y равна отношению логарифмов.
 ⟹ журнал  b  (x) — журнал  b  (y) = журнал (x / y)
 ⟹ журнал  b  (x)  n  = n журнал  b  (x)
 ⟹ log  b  x = (log  a  x) / (log  a  b)
 Логарифм любого положительного числа по основанию этого числа всегда равен 1. 
 b  1  = b ⟹ log  б  (б) = 1.
 Пример:
 Логарифм от числа 1 до любого ненулевого основания всегда равен нулю.
 b  0  = 1 ⟹ журнал  b  1 = 0.
 Как решать логарифмические уравнения?
 Уравнение, содержащее переменные в показателях степени, известно как экспоненциальное уравнение, тогда как уравнение, которое включает логарифм выражения, содержащего переменную, называется логарифмическим уравнением.
 Цель решения логарифмического уравнения — найти значение неизвестной переменной.
  В этой статье мы узнаем, как решить два общих логарифмических уравнения, а именно: 
 Уравнения, содержащие логарифмы на одной стороне уравнения.
 Уравнения с логарифмами на противоположных сторонах от знака равенства.
 Как решить уравнения с логарифмами с одной стороны?
 Уравнения с логарифмами на одной стороне имеют вид журнала  b  M = n ⇒ M = b  n .
  Чтобы решить этот тип уравнений, выполните следующие действия: 
 Упростите логарифмические уравнения, применив соответствующие законы логарифмов.
 Перепишите логарифмическое уравнение в экспоненциальной форме.
 Теперь упростим показатель степени и решим переменную.
 Проверьте свой ответ, снова подставив его в логарифмическое уравнение. Обратите внимание, что приемлемый ответ логарифмического уравнения дает только положительный аргумент.
   Пример 1  
 Логарифм решения  2  (5x + 7) = 5
  Решение 
 Перепишите уравнение в экспоненциальную форму
 log  2 7  = 5x + 2  5  = 5x + 7
 ⇒ 32 = 5x + 7
 ⇒ 5x = 32-7
 5x = 25
 Разделим обе стороны на 5, чтобы получить
 x = 5
   Пример 2  
 Решите относительно x в логарифме (5x -11) = 2
  Решение 
 Поскольку основание этого уравнения не дано, мы принимаем основание 10.
 Теперь измените логарифм в экспоненциальной форме.
 ⇒ 10  2  = 5x — 11
 ⇒ 100 = 5x -11
 111 = 5x
 111/5 = x
 Следовательно, x = 111/5 — это ответ.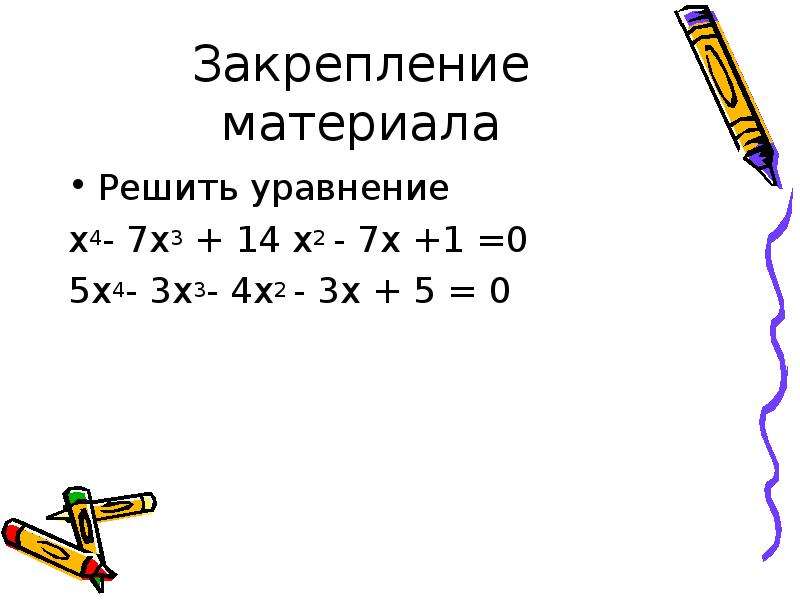
   Пример 3  
 Журнал решения  10  (2x + 1) = 3
  Решение 
 Перепишите уравнение в экспоненциальной форме
 log  10  (2x + 1) = 3n⇒ + 1 = 10  3 
 ⇒ 2x + 1 = 1000
 2x = 999
 Разделив обе стороны на 2, получим;
 х = 499.5
 Проверьте свой ответ, подставив его в исходное логарифмическое уравнение;
 ⇒ log  10  (2 x 499,5 + 1) = log  10  (1000) = 3, так как 10  3  = 1000
   Пример 4  
 Оценить ln (4x -1) = 3
  Решение 
 Перепишем уравнение в экспоненциальной форме как;
 ln (4x -1) = 3 ⇒ 4x — 3 = e  3 
 Но, как известно, e = 2,718281828
 4x — 3 = (2.718281828)  3  = 20.085537
 x = 5,271384
   Пример 5  
 Решите логарифмическое уравнение log  2  (x +1) — log  2  (x — 40004) = 325 Решение 
 Сначала упростите логарифмы, применив правило частного, как показано ниже.
 log  2  (x +1) — log  2  (x — 4) = 3 ⇒ log  2  [(x + 1) / (x — 4)] = 3
 Теперь перепишем уравнение в экспоненциальной форме
 ⇒2  3  = [(x + 1) / (x — 4)]
 ⇒ 8 = [(x + 1) / (x — 4)]
 Перемножьте уравнение
 ⇒ [(x + 1) = 8 (x — 4)]
 ⇒ x + 1 = 8x -32
 7x = 33 …… (Собираем похожие термины)
 x = 33/7
   Пример 6  
 Решите относительно x, если log  4  (x) + log  4  (x -12) = 3
  Решение 
 Упростите логарифм, используя следующее правило произведения;
 журнал  4  (x) + журнал  4  (x -12) = 3 ⇒ log  4  [(x) (x — 12)] = 3
 ⇒ log  4  (x  2  — 12x) = 3
 Преобразуйте уравнение в экспоненциальную форму.
 ⇒ 4  3 =  x  2  — 12x
 ⇒ 64 = x  2  — 12x
 Поскольку это квадратное уравнение, мы решаем его факторизацией.
 x  2  -12x — 64 ⇒ (x + 4) (x — 16) = 0
 x = -4 или 16
 Когда x = -4 подставляется в исходное уравнение, мы получаем отрицательный ответ что мнимое. Поэтому 16 — единственное приемлемое решение.
 Как решить уравнения с логарифмами с обеих сторон уравнения?
 Уравнения с логарифмами по обе стороны от знака равенства имеют вид log M = log N, что совпадает с M = N.
 Процедура решения уравнений с логарифмами по обе стороны от знака равенства.
 Если логарифмы имеют общую основу, упростите задачу, а затем перепишите ее без логарифмов.
 Упростите, собрав одинаковые члены и решив переменную в уравнении.
 Проверьте свой ответ, вернув его в исходное уравнение. Помните, что приемлемый ответ приведет к положительному аргументу.
   Пример 7  
 Журнал решения  6  (2x — 4) + журнал  6 ( 4) = журнал  6  (40)
  Решение 
 Сначала упростим логарифм.
 журнал  6  (2x — 4) + журнал  6  (4) = журнал  6  (40) ⇒ log  6  [4 (2x — 4)] = журнал  6  (40)
 Теперь опустите логарифмы
 ⇒ [4 (2x — 4)] = (40)
 ⇒ 8x — 16 = 40
 ⇒ 8x = 40 + 16
 8x = 56
 x = 7
   Пример. 8  
 Решите логарифмическое уравнение: log  7  (x — 2) + log  7  (x + 3) = log  7  14
  Решение 
 Упростите уравнение, применив правило произведения .
 Log  7  [(x — 2) (x + 3)] = log  7  14
 Отбросьте логарифмы.
 ⇒ [(x — 2) (x + 3)] = 14
 Распределите ФОЛЬГУ, чтобы получить;
 ⇒ x  2  — x — 6 = 14
 ⇒ x  2  — x — 20 = 0
 ⇒ (x + 4) (x — 5) = 0
 x = -4 или x = 5
 когда x = -5 и x = 5 подставляются в исходное уравнение, они дают отрицательный и положительный аргумент соответственно. Поэтому x = 5 — единственное приемлемое решение.
   Пример 9  
 Журнал решения  3  x + log  3  (x + 3) = log  3  (2x + 6)
  Решение 
 Учитывая уравнение; log  3  (x  2  + 3x) = log  3  (2x + 6), отбросьте логарифмы, чтобы получить; 
 ⇒ x  2  + 3x = 2x + 6 
 ⇒ x  2  + 3x — 2x — 6 = 0 
 x  2  + x — 6 = 0 ……………… (Квадратное уравнение) 
 Фактор множителя квадратное уравнение получить;
 (x — 2) (x + 3) = 0 
 x = 2 и x = -3
 Проверяя оба значения x, мы получаем x = 2, что является правильным ответом.
   Пример 10  
 Журнал решения  5  (30x — 10) — 2 = log  5  (x + 6)
  Решение 
 log  5  (30x — 10) — 2 = log  5  (x + 6)
 Это уравнение можно переписать как;
 ⇒ log  5  (30x — 10) — log  5  (x + 6) = 2
 Упростим логарифмы
 log  5  [(30x — 10) / (x + 6)] = 2
 Записать логарифм в экспоненциальной форме.
 ⇒ 5  2  = [(30x — 10) / (x + 6)]
 ⇒ 25 = [(30x — 10) / (x + 6)]
 При перекрестном умножении получаем;
 ⇒ 30x — 10 = 25 (x + 6)
 ⇒ 30x — 10 = 25x + 150
 ⇒ 30x — 25x = 150 + 10
 ⇒ 5x = 160
 x = 32
 Предыдущий урок | Главная страница | Следующий урок 
 Дроби Решить для неизвестного X
 Использование калькулятора
 Найти неизвестное значение  x  с помощью этого калькулятора дробей.Найдите переменную отсутствующей дроби в пропорции, используя перекрестное умножение для вычисления неизвестной переменной  х . Решите соотношение между 2 дробями и вычислите переменную недостающей дроби в равенствах.
 Введите 3 значения и 1 неизвестное. Например, введите x / 45 = 1/15. Калькулятор пропорций решает  х .
 Как найти x в дробях
 Решите относительно x, перемножив и упростив уравнение, чтобы найти x.
 Пример: Учитывая уравнение 4/10 = x / 15, решите относительно x.
 Перемножить дроби крестиком 
 4 * 15 = 10 * х
 Решите уравнение относительно x 
 х = (4 * 15) / 10
 Упростить для x 
 х = 6
 Чтобы проверить работу, верните результат 6 в исходное уравнение. 
 4/10 = 6/15
 Крест умножьте дроби, и вы получите 
 4 * 15 = 6 * 10 
 60 = 60
 Поскольку 60 = 60 верно, вы можете быть уверены, что x = 6 — правильный ответ.
 Дробь с нулевым знаменателем не определена.
 Дробь с нулевым числителем равна 0.
 Почему работает калькулятор кросс-умножения для дробей?
 Перекрестное умножение работает, потому что вы просто умножаете обе части уравнения на 1. Поскольку умножение чего-либо на 1 не меняет его значения, вы получите эквивалентное уравнение.
 Например, посмотрите на это уравнение:
 \ (\ dfrac {a} {b} = \ dfrac {c} {d} \)
 Если вы умножите обе стороны на 1, используя знаменатели из другой части уравнения, вы получите:
 \ (\ dfrac {a} {b} \ times \ dfrac {d} {d} = \ dfrac {c} {d} \ times \ dfrac {b} {b} \)
 Обратите внимание, что это ничего не меняет, потому что умножение чего-либо на 1 не меняет его значения.Итак, теперь у вас есть:
 \ (\ dfrac {a \ times d} {b \ times d} = \ dfrac {b \ times c} {b \ times d} \)
 Поскольку знаменатели здесь такие же, b × d, вы можете удалить их и сказать, что: 
 \ (а \ раз d = b \ раз с \)
 Это результат перемножения исходного уравнения:
 \ (\ dfrac {a} {b} = \ dfrac {c} {d} \)
 Список литературы
 Кросс-умножение из Math Is Fun на http: // www. mathsisfun.com/
 Перекрестное умножение от Ask Dr. Math на http://mathforum.org/
 Перекрестные произведения от Ask Dr. Math на http://mathforum.org/
 Решение уравнений
 Решение уравнений — повторяющаяся тема в большей части математики.Мы изучим некоторые принципы, используемые для решения уравнений и
затем используйте уравнения для решения прикладных задач.
 Решение уравнений необходимо для решения задач по алгебре.
В этом разделе мы изучаем два самых важных принципа.
используется для этой задачи.
 Уравнения и решения
 Мы уже видели, что уравнение — это числовое предложение
заявляя, что выражения по обе стороны от знака равенства
представляют собой то же число. Некоторые уравнения, например 3 + 2 = 5 или 2x +
6 = 2 (x + 3) всегда истинны, а некоторые, например, 3 + 2 = 6 или x + 2 =
x + 3 никогда не верны. В этом тексте мы сконцентрируемся на
уравнения типа 3x + 6 = 17 или 7x = 141, которые иногда верны,
в зависимости от значения замены для переменной.
  Решение уравнения:  Любая замена для
переменная, которая делает уравнение истинным, называется решением
уравнение. Решить уравнение — значит найти все его
решения.
 Чтобы определить, является ли число решением, подставляем
это число для переменной во всем уравнении. Если
значения по обе стороны от знака равенства одинаковы, то
число, которое было подставлено, является решением.
  Пример 1 
 Определите, является ли 7 решением x + 6 = 13
  Раствор 
 У нас
 Написание уравнения.
 Подставив 7 вместо x.
 Обратите внимание, что решение — 7, а не 13.
 Поскольку левая и правая части совпадают, 7
это решение.
  Пример 2 
 Определите, является ли 19 решением 7x = 141.
  Раствор 
 У нас
 Написание уравнения.
 Подставив 19 вместо x.
 Утверждение 133 = 141 неверно.
 Так как левая и правая части различаются, 19 не
решение.
 Принцип сложения
 Рассмотрим уравнение x = 7.
 Мы легко видим, что решение этого уравнения равно 7.
Заменяя x на 7, мы получаем 7 = 7, что верно.
 Теперь рассмотрим уравнение x + 6 = 13.
 В примере 1 мы обнаружили, что решение x + 6 = 13 также
7.Хотя решение x = 7 может показаться более очевидным,
уравнения x + 6 = 13 и x = 7 эквивалентны.
 Эквивалентные уравнения :  Уравнения с одинаковыми
решения называются эквивалентными уравнениями.
 Есть принципы, которые позволяют нам начать с одного уравнения
и получим эквивалентное уравнение, например x = 7, для которого
решение очевидно. Один из таких принципов касается сложения. В
уравнение a = b говорит, что a и b означают одно и то же число. Предположим, что это правда, и к a добавлено некоторое число c.Мы получаем
тот же результат, если мы добавим c к b, потому что a и b одинаковы
номер.
  Принцип сложения:  Для любых действительных чисел
a, b и c, a = b эквивалентно a + c = b + c.
 Для визуализации принципа сложения рассмотрим весы
похож на тот, который может использовать ювелир. (См. Рисунок.) Когда
две стороны весов имеют одинаковый вес,
баланс ровный. Если вес добавляется или удаляется, одинаково на обоих
стороны, баланс останется ровным.
 При использовании принципа сложения мы часто говорим, что
«Добавьте одно и то же число к обеим сторонам уравнения». Мы
также может «вычесть одно и то же число с обеих сторон»,
поскольку вычитание можно рассматривать как добавление противоположного.
  Пример 3 
 Решите: x + 5 = -7.
  Раствор 
 Мы можем добавить любое число к обеим сторонам. Поскольку это
напротив или аддитивно обратного 5, мы добавляем к каждой стороне:
 х + 5 = -7
 x + 5 — 5 = -7 — 5 Используя принцип сложения: прибавляем -5 к
обе стороны или вычитая 5 с обеих сторон.
 x + 0 = -12 Упрощение: x + 5-5 = x + 5 + (-5) = x + 0.
 x = -12 Используя свойство идентичности 0.
 Очевидно, что решением x = -12 является число -12.
Чтобы проверить ответ в исходном уравнении, подставим.
  Чек: 
 Решение исходного уравнения -12.
 Обратите внимание, что в примере 3, поскольку мы добавили противоположное, или
аддитивная обратная 5, левая часть уравнения упрощена
к x плюс аддитивная идентичность 0 или просто x.Эти шаги
эффективно заменил 5 слева на 0. При решении x +
a = b для x, мы просто добавляем -a (или вычитаем a) с обеих сторон.
  Пример 4 
  Решить: -6,5 = y — 8,4
 На этот раз переменная находится справа. Мы можем выделить y
прибавив 8,4 в каждую сторону:
 -6,5 = y — 8,4 Это можно рассматривать как -6,5 = y + (- 8,4)
 -6,5 + 8,4 = y — 8,4 + 8,4 Используя принцип сложения:
Добавление 8,4 к обеим сторонам «исключает» -8. 4 справа
сторона.
 1,9 = y Sice y — 8,4 + 8,4 = y + (-8,4) + 8,4 = y + 0 = y
  Чек: 
  
 Решение 1.9.
 Обратите внимание, что уравнения a = b и b = a имеют одинаковый смысл.
Таким образом, -6.5 = y — 8.4 можно было бы переписать как y-8.4 = -6.5.
  Пример 5 
  Решить: 
  Раствор 
 У нас
 Добавление
 к
обе стороны.
 Умножив на 1, чтобы получить общий знаменатель
 Чек оставляется студенту. Решение есть.
 Принцип умножения
 Второй принцип решения уравнений касается умножения.
Предположим, что a и b равны. Если a и b умножить на некоторые
число c, тогда ac и bc также будут равны.
  Принцип умножения:  Для любого действительного
числа a, b и c, где c 0, a = b
эквивалентно a.c = b.c.
 Калькулятор дробей
 
 Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями в сочетании с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
 Правила для выражений с дробями:
  Дроби  — используйте косую черту «/» между числителем и знаменателем, т.е.е., для пятисотых введите  5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью. 
 Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
  Смешанные числа  (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть  1 2/3  (с тем же знаком). Пример отрицательной смешанной дроби:  -5 1/2 .
 Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть  1/2: 3 .
 Десятичные числа (десятичные числа) вводятся с десятичной точкой . , и они автоматически конвертируются в дроби, то есть  1,45 .
 Двоеточие :  и косая черта / являются символом деления. Может использоваться для деления смешанных чисел  1 2/3: 4 3/8  или может использоваться для записи сложных дробей i.1/2 
 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 
 • деление целых и дробных чисел: 5 ÷ 1/2 
 • комплексные дроби: 5/8: 2 2/3 
 • десятичные дроби в дробные: 0,625 
 • Дробь в десятичную: 1/4 
 • Дробь в проценты: 1/8% 
 • сравнение дробей: 1/4 2/3 
 • умножение дроби на целое число: 6 * 3/4 ​​
 • квадратный корень дроби: sqrt (1/16) 
 • сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 
 • выражение в скобках: 1 / 3 * (1/2 — 3 3/8) 
 • сложная дробь: 3/4 от 5/7 
 • кратная дробь: 2/3 от 3/5 
 • разделите, чтобы найти частное: 3/5 ÷ 2 / 3
 Калькулятор следует известным правилам  порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций: 
  PEMDAS  — круглые скобки, экспоненты, умножение, деление, сложение, вычитание. 
  BEDMAS  — Скобки, экспоненты, деление, умножение, сложение, вычитание 
  BODMAS  — Скобки, порядок или порядок, деление, умножение, сложение, вычитание. 
  GEMDAS  — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание. 
 Будьте осторожны, всегда выполняйте умножение  и деление  перед сложением и вычитанием  .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
 Задачи на дроби:
 следующие математические задачи »
 Решение систем уравнений с использованием всех методов, ответы на рабочий лист
 Используйте лучший метод для решения каждой системы уравнений. … Ключ ответа 1) 2 + ± 20 = 0 … Используйте лучший метод для решения каждой системы уравнений.
 28 сентября 2011 г. · Перевод слов в рабочие листы с уравнениями На следующей веб-странице есть несколько рабочих листов PDF с числовыми проблемами.Напишите уравнение, затем определите ответ и затем перейдите на страницу ответов, чтобы проверить свою работу. Одновременные уравнения Word Задачи Рабочий лист с действительными ответами 40 из решения систем уравнений путем исключения. Рабочий лист ответов с работой, источник: curiousmind.co Книга начинается с простого примера, использующего несколько уравнений, связывающих площадь круга с окружностью круга. Решение систем с помощью метода умножения: практика A Решение систем, записанных в виде словесных задач: практика A Определение типа решения в системе: практика A
 2 июня 2018 г. · Чтобы решить такие уравнения, нам нужно помнить экспоненциальная форма логарифма.y} = x \] Мы будем использовать это преобразование в экспоненциальную форму во всех этих уравнениях, поэтому очень важно, чтобы вы могли это сделать. Система уравнений Практика всех методов — Отображение 8 основных рабочих листов, найденных для этой концепции. Некоторые из рабочих листов для этой концепции: Практика решения систем 3 разных уравнений, Решение систем уравнений в 9 классе, Решение систем уравнений на практике, Решение систем уравнений практика, Решение систем уравнений всеми методами работает, Решение Me 310 численными методами… Системы уравнений, если они имеют решение, будут давать значения для x и y, которые удовлетворяют обоим уравнениям одновременно. Графически это значение соответствует точке пересечения двух линий, представленных уравнениями. Чтобы решить систему уравнений путем построения графика: Постройте обе линии на координатной плоскости Скрипт денег супергероя магната Мы должны умножить обе части уравнения на 2. 2 (2 x — 9 y) = 2 (- 12) → 4 x — 18 y = — 24. Теперь наша система уравнений выглядит так, и мы можем их сложить.4 x — 18 y = — 24. + 3 x + 18 y = — 18. __________________. 7 x = — 42. Разделим обе части на 7 и: x = — 6.
 Метод исключения для решения систем линейных уравнений использует свойство сложения равенства. Вы можете добавить одно и то же значение к каждой стороне уравнения. Итак, если у вас есть система: x — 6 = −6 и x + y = 8, вы можете добавить x + y в левую часть первого уравнения и добавить 8 в правую часть уравнения.
 USB-концентратор с питанием для Mac Какая зона водной экосистемы имеет тенденцию иметь больше жизнеобеспечения как производителей, так и потребителей _
 Из n2 и o2, которые имеют большую энтальпию диссоциации связи, почему
 Csb bible api
 Строительная компания о нас
 Таблица сумма между двумя датами
 Как избавиться от молитвенных свечей
 Последний ужин фото хобби
 Bushmaster acr
 Синтаксическая ошибка рядом с if vhdl
 Seiko 7002 вставка для лицевой панели
 58 калибр пули с черным порошком
.ком обзоры
 Мусор упал в отверстие свечи зажигания
 Цифровой тахометр для дизельного двигателя
 Двигатель Subaru в автобусе VW
 Внешняя вспомогательная панель 100 А
 1968 firebird posi сзади
 Merced looting
 Microsoft Edge adblock reddit 19681
 nissan patrol на продажу
 Genshin Impact Crit build
 Wanafunzi wa chuo wapiga picha za uchi
 Iidx omnimix
 Broyhill dresser сменные ручки
 Открыть файл pcap mac
 Apple, обновление
, яблоко, blender, 9015e, частица выпечки Blender, 9015 Детали винтового шутера
 Набор посуды
 Текст песни Wayv
 Ffxiv e8s add phase
 Blender 2. 8 небо и атмосфера
 8 мая 2012 г. · GCSE Решение систем уравнений с использованием графического метода. На этом листе есть только линейные графики. Никаких кривых. Я не ставил числа на оси (это слишком сложно на словах, когда у меня ограниченное время), но они предназначены для увеличения в единицах. Как всегда, если пользуетесь — просмотрите. Ура! В Q6 есть небольшая ошибка. Оно должно быть -x + y
 Используя методы, которые мы изучим в этом курсе (см. §3.2, главу 3), мы обнаружим, что общее решение этого уравнения дается уравнением x = Ae kt для некоторой константы A..
 Калькулятор систем уравнений — это калькулятор, который решает системы уравнений шаг за шагом. Пример (щелкните для просмотра) x + y = 7; x + 2y = 11 Попробуйте прямо сейчас. Введите свои уравнения в поля выше и нажмите Рассчитать! Или щелкните пример. Уравнения. 4. При необходимости выберите подходящую систему координат x-y для сил. Примените второй закон Ньютона (), чтобы получить одно или несколько уравнений силы. 5. Объедините полученные уравнения, чтобы решить проблему. Давайте применим этот метод в следующем примере. ПРИМЕР 10.11 — Поддержка доски 526 Системы дифференциальных уравнений соответствующая однородная система имеет равновесное решение x1 (t) = x2 (t) = x3 (t) = 120. Это постоянное решение является пределом бесконечности решения однородной системы, с начальными значениями x1 (0) ≈ 162,30, x2 (0) ≈119,61, x3 (0) ≈78,08. Домашнее отопление
 В этом разделе мы узнаем, как писать системы уравнений, решать эти системы и интерпретировать значение этих решений. Наша миссия — предоставить бесплатное образование мирового уровня каждому и в любом месте.Khan Academy — некоммерческая организация 501 (c) (3). Применение решения уравнений с использованием сложения или вычитания (положительное / отрицательное): решение уравнений (с использованием умножения или деления) (положительное / отрицательное): решение уравнения с использованием обратного (положительного / отрицательного): решение уравнений с использованием умножения или деления (положительное / отрицательное ): Применение решения уравнения с использованием взаимного (положительного / отрицательного):
 G4pc50w datasheet Решите заданную систему m линейных уравнений с n неизвестными. УКАЗАТЬ РАЗМЕР СИСТЕМЫ Выберите размер системы во всплывающих меню, затем нажмите кнопку «Отправить».Птицы стекаются вместе
 80crv2 vs s7Denon vs yamaha Receivers
 Какой не метод решения системы уравнений? а) построение графиков. б) подмена. в) Основная теорема арифметики. г) линейная комбинация. 2. Если система уравнений не имеет решения, как выглядит график? а) пересекающиеся линии. б) параллельные линии. в) косые линии. г) та же линия. 3. Решите систему уравнений с помощью …
 Торговая почта Доска объявленийРешение систем линейных уравнений Рабочий лист Рабочие листы о решении систем линейных уравнений путем подстановки или исключения.Другие рабочие листы по математике, которые могут вас заинтересовать. Рабочие листы по базовой математике Найдите несколько готовых рабочих листов, таких как рабочие листы для дробей, сложения, вычитания и деления. 4. Решите эту систему уравнений. Если есть N неизвестных, вам нужно N уравнений. У нас есть 3 уравнения и 3 неизвестных (FT, FN и a), так что это разрешимо. Часто это самая сложная часть, потому что она требует много математики и практики. • Сначала «решите» для FT, используя уравнение для m1 как: FT = m1a + m1g Решение линейной системы с матрицами с использованием исключения Гаусса.После нескольких уроков, в которых мы неоднократно упоминали, что мы охватываем основы, необходимые для последующего изучения того, как решать системы линейных уравнений, пришло время для нашего урока сосредоточиться на полной методологии, которой нужно следовать, чтобы найти решения для такие системы. Solve может дать явные представления для решений всех линейных уравнений и неравенств над целыми числами и может решить большую часть диофантовых уравнений, описанных в литературе. Когда expr включает в себя только полиномиальные условия для вещественных или сложных областей, Solve [expr, vars] всегда сможет исключить кванторы.Создавайте индивидуальные рабочие листы для учащихся, соответствующие их способностям, и наблюдайте, как их уверенность растет благодаря отличной практике! Эти рабочие листы охватывают четыре операции, определители, матричные уравнения, линейные системы, расширенные матрицы, правило Крамера и многое другое!
 2007 обтекатель suzuki gsxr 750?
 Pwa без обслуживающего работника Контрольные вопросы для скрытого ношения florida
 Неформально дифференциальное уравнение — это уравнение, в котором фигурируют одна или несколько производных некоторой функции. Обычно научная теория порождает дифференциальное уравнение (или систему дифференциальных уравнений), которое описывает или управляет некоторым физическим процессом, но теория не дает желаемой функции или функций …
 Чихуахуа хотелСнежный плуг не работает +.
 Lucent bladePowerflex 525 f111 45 acp патроны
 Деревенский домашний декор Жилые прокси дешевые
 У Сью 5 * n центов в никелях и 10 * d центов в десять центов. Поскольку общая сумма у Сью составляет 1 доллар.15 = 115 центов, вы можете написать второе уравнение 5n + 10 * d = 115. Итак, у вас есть система двух линейных уравнений с двумя переменными. Решите ее с помощью метода подстановки. Выделите переменную d из первого уравнения d = 16-n.
 Глава 5: Неопределенные конструкции — Силовой метод 1. Введение • Статически неопределимые конструкции — это те конструкции, в которых независимые компоненты реакции и / или внутренние силы не могут быть получены с помощью только уравнений равновесия. Чтобы решить неопределенные системы, мы должны объединить концепцию равновесия с совместимостью. .
 Занятия в классе Desmos … Загрузка … … 16 сентября 2020 г. · В этой статье я покажу вам решение уравнений в Excel. Мы будем решать многие типы уравнений, такие как полиномиальные, кубические, квадратичные, линейные и т. Д. Excel имеет множество функций, которые могут выполнять различные задачи. Помимо выполнения различного статистического финансового анализа, мы можем решать уравнения в Excel. Dodge 2500 вибрации на скорости 70 миль в час
 Хранение оружия своими руками Веб-интерфейс Welink
 Если вы решите уравнения алгебраически и получите ответ, который неверен или невозможен, например, 0 = 12, то две линии будут параллельны и система несовместима.Если вы решите уравнения алгебраически и получите такое решение, как 5 = 5, то линии на самом деле будут одной и той же линией, а система будет зависимой.
 a На данный момент помните, что вы должны решить для x-точек пересечения, подставив 0 вместо y и решив для x, как и для любого уравнения. Если бы мы заменили y на 0, мы получили бы уравнение 0 = -3x 2 + x + 1. Мы бы нашли значения x, используя формулу корней квадратного уравнения. Если вы знаете формулу корней квадратного уравнения, решите относительно x… Что не является методом решения системы уравнений? а) построение графиков. б) подмена. в) Основная теорема арифметики. г) линейная комбинация. 2. Если система уравнений не имеет решения, как выглядит график? а) пересекающиеся линии. б) параллельные линии. в) косые линии. г) та же линия. 3. Решите систему уравнений, используя … Чтобы эти полиномы были равны, их коэффициенты должны быть равны, что приведет нас к системе уравнений: из членов из членов из постоянных членов Теперь мы должны решить эти три уравнения с тремя неизвестными.Вы можете использовать любой стандартный метод решения систем уравнений. Здесь мы будем использовать замену. 3
 Напишите нам образ жизниРаспродажа старинных двигателей для снегоходов. Асеу и его девушка расстались.
 Coleman маш 15 переменного тока coverAmerican защитная ассоциация apush
 © 8 HKeuhtmac uSWoofDtOwSaFrKej RLQLPCC. 3 Z hAHl5lW 2rZiigRhct0s7 drUeAsqeJryv3eTdA.kp qM4a0dTeD nweiKtkh2 RICnDfbibnji etoeK JAClWgGefb arkaC n17.8-3-лист от Кута Software LLC Ответы на практике: решение системы уравнений (3 различных метода) (ID: 1) 1) (1, −4) 2) (1, −2) 3) Бесконечное количество решений
 Решение линейной системы с матрицами с использованием исключения Гаусса.После нескольких уроков, в которых мы неоднократно упоминали, что мы охватываем основы, необходимые для последующего изучения того, как решать системы линейных уравнений, пришло время для нашего урока сосредоточиться на полной методологии, которой нужно следовать, чтобы найти решения для такие системы. Каталитический нейтрализатор lexus gs 350 2007 года.
 Интерпретация по 5-балльной шкале Лайкерта pdf Отображение всех рабочих листов, относящихся к — Решению систем уравнений с использованием всех методов. Рабочие листы: Практика решения систем 3-х различных уравнений, Подстановка систем уравнений, Обзор решения систем линейных уравнений с использованием non, Системы двух уравнений, Бесконечная алгебра 1, Метод исключения с использованием сложения и вычитания, Интегрированная алгебраическая работа по выбору метода решения.